Introduction

Information on sediment yield from a catchment is very often required for planning, designing and evaluation of soil conservation projects, design and operation of reservoirs, environmental and water pollution control measures, and drought and flood control programs. The available soil loss models can be categorized into two groups, one based on stormwise analysis and the other on a yearly basis. Stormwise models are either sediment graph models (Rendon-Herraro 1974; Williams 1972; Das and Agarwal 1990) or total sediment yield models (Williams 1978; Das and Chauhan 1990), and the yearly models are for average soil erosion per annum (Wischmeier and Smith 1965; Elwell 1978). These models are empirical in nature and consider the watershed as a non-deterministic system for simplification in calculations, on the other hand, very few models are available for accurate estimation of sedimentograph from the storm event.

The need for accurate information on watershed runoff and sediment yield has grown rapidly during the past decades because of the acceleration of watershed management programs for conservation, development, and beneficial use of all natural resources, including soil and water (Gajbhiye and Mishra 2012; Mishra et al. 2013). In India, both Central and State Governments launched soil and water conservation programs during various 5-year plans beginning in the early 1950s. The objectives of all watershed management programs are to increase infiltration into soil, to control excess runoff, to manage and utilize runoff for useful purposes, and to reduce soil erosion to protect land. Therefore, the prerequisite for any watershed development plan is to understand the hydrology of the watershed and to determine runoff and sediment yield.

Many researchers according to their study region and measures, established different empirical statistical models (Jiang and Song 1980; Mou and Xiong 1980; Mou and Meng 1983; Yin 1989; Wang and Zhang 1990; Wang and Huang 1992; Cao et al. 1993). Although many empirical statistical models were established, their involving in factors was not same. Foreign statistical models such as USLE (Wischmeier and Smith 1978) and RUSLE (Renard et al. 1991), in which sediment yield rules and mechanism in different scales were not better presented.

Over the years, several hydrological models ranging from empirical relationships to physically based models have been developed for the prediction of runoff and sediment yield. Physically based models are better because they consider the controlling physical processes, but at the same time their data requirements are also high. Often, even in intensively monitored watersheds, all the required data are not available. Therefore, there is a need to look for alternative methods for the prediction of sediment yield using readily available information e.g., rainfall and runoff. To this end, a link between the Soil Conservation Service (1956) parameter potential maximum retention (S) (and curve number, CN) and sediment yield (SY) is explored. Thus, the main objective of this study is to propose an implicit relationship between Soil Conservation Service Curve Number (SCS-CN) parameter CN and SY.

Methodology

SCS-CN method

The Soil Conservation Service Curve Number (SCS-CN) method (SCS 1956) employs the water balance equation and two fundamental hypotheses. The water balance is expressed as:

$$P = I_{\text{a}} + F + Q$$
(1)

The first hypothesis states that the ratio of direct runoff to potential maximum runoff is equal to the ratio of infiltration to potential maximum retention and, according to the second hypothesis; the initial abstraction is some fraction of the potential maximum retention. These are respectively expressed as:

$$\frac{Q}{{P - I_{\text{a}} }} = \frac{F}{S}$$
(2)

and

$$I_{\text{a}} = \lambda S$$
(3)

where P = total precipitation (mm), Ia = initial abstraction (mm), F = cumulative infiltration (mm), Q = direct runoff (mm), and S = potential maximum retention (mm), and λ = initial abstraction coefficient (=0.2, a standard value). Though λ can theoretically vary from 0 to ∞ (Mishra and Singh 1999, 2003a, 2004a), λ = 0.05 has been advocated for field use (Hawkins 2001). A combination of Eqs. 1 and 2 leads to the popular form of the SCS-CN method:

$$Q = \frac{{(P - I_{\text{a}} )^{2} }}{{P - I_{\text{a}} + S}} = \frac{{(P - \lambda S)^{2} }}{P + (1 - \lambda )S}$$
(4)

Here, P ≥ Ia, Q = 0 otherwise. From the observed rainfall–runoff data, the SCS-CN parameter S can be determined as follows (Hawkins 1993) with λ = 0.2:

$$S = 5\left[ {\left( {P + 2Q} \right) - \sqrt {Q\left( {4Q + 5P} \right)} } \right]$$
(5)

S can be transformed to CN scale using the following empirical relation:

$${\text{CN}} = 25,400/(S + 254)$$
(6)

where S is in mm and CN is a non-dimensional parameter. A detailed description of the application procedure is available elsewhere (McCuen 1982; Ponce 1989; Mishra and Singh 2003a; Michel et al. 2005).

For estimation of CN and SY for long duration (i.e. more than 1 day) rain events, the procedure is proposed as follows:

  1. a.

    Prepare a series of available daily rainfall (P) and runoff (Q) data in same units (for example, mm/day) for the period the data are available. Filter these data by removing the pairs of P–Q data showing the runoff factor (C = Q/P) > 1.

  2. b.

    Sort the remaining P–Q data in the descending order of P. and calculate CN using Eqs. (5) and (6). Describe CN for 10, 50, and 90 % probability of exceedances (PE) as to correspond to dry, normal, and wet conditions, respectively. Since these values are derived from daily P–Q data, the derived CN-values correspond to 1-day rain duration.

  3. c.

    From the above daily P–Q data, derive two-daily, three-daily, four-daily and so on P–Q series, by summing the rainfall and corresponding runoff values for respective durations.

  4. d.

    Short-term SY values are selected corresponding to 50 % probability of exceedances (PE) of CN for each rain duration.

Proposed SCS-CN-based SY model

The SCS-CN proportional equality (C = Sr) concept, it is possible to extend it for sediment yield as (Mishra et al. 2006):

$$C = S_{\text{r}} = {\text{DR}}$$
(7)

Where, C is runoff coefficient, Sr is the degree of saturation and DR is the delivery ratio. In Eq. (7), all variables range from 0 to 1. Using the usual definition and Ia = 0, Eq. (7) can be expanded as (Mishra et al. 2006):

$$C = \frac{Q}{P} = \frac{F}{S} = \frac{P}{P + S} = \frac{\text{SY}}{A}$$
(8)

Eq. (8) implies that the sediment yield is directly proportional to the potential maximum erosion ‘A’ and runoff factor C is the proportionality constant. Alternatively,

$${\text{SY}} = \frac{AP}{P + S}$$
(9)

For the given watershed characteristics or A and P, the actual sediment yield (SY) increases as S decreases, which is in conformity with the general notion that the higher the runoff amount, the higher will be the sediment erosion and its transport and hence higher the sediment yield and vice versa. As S → 0 (or CN → 100), SY → A since Q → P. Similarly, as S → ∞(or CN → 0), SY → 0 since Q → 0. It is consistent with the general notion that the surface runoff primarily drives sediment erosion. Thus, there appears to be a relation existing between SY and S, which can be described in power form as follows:

$${\text{SY}} = \alpha (S)^{ - \beta }$$
(10)

Where α and β are the coefficient and exponent, respectively. S and CN exists in an inverse relationship (Eq. 10), Eq. 10 suggests SY to be high for the watersheds of low S, and vice versa. The following text endeavours to support this logic.

SY–CN rationale

Mathematical treatment

To develop the concept following Mishra and Singh (2003a, b), the Horton’s method (Horton 1932) can be expressed mathematically as:

$$\frac{F}{S} = (1 - e^{ - \alpha t} )$$
(11)

where, F is the cumulative infiltration, S potential maximum retention and t is the rain duration.An assumption of rainfall P growing linearity with time t leads to

$$P = ie*t$$
(12)

which is a valid and reasonable assumption for infiltration rate computation in experimental.tests (Mishra and Singh 2004a, b).

$$\frac{P}{S} = \alpha t$$
(13)

Referring to Fig. 2, one can express

$$S_{t} = S_{o} - F$$
(14)

where, S t is the available storage for water retention in a soil column at time t, So is the potential storage space available for moisture retention in the soil column. Parameter So is shown to be equivalent to the potential maximum retention of the SCS-CN model (S = So) (Mishra and Singh 1999). Coupling Eq. (14) with Eq. (11) (for S = So) yields

$$S = S_{t} (1 + \alpha t)$$
(15)

Eq. 15 shows the variation of S with rain duration (t). It shows that as the potential maximum retention increases, the rain duration increases and vice versa.

Novotny and Olem (1994) showed a power relationship between C and DR:

$$DR = \alpha C^{\beta }$$
(16)

DR is a dimensionless ratio of the sediment yield (SY) to the total potential erosion (A) in the contributing watershed.

$$DR = \frac{SY}{A}$$
(17)

The coefficient C is also dimensionless and expressed in terms of Q and P as (Mishra et al. 2006):

$$C = \frac{Q}{P} = \frac{F}{S} = \frac{P}{P + S}$$
(18)

Coupling Eq. (16) with Eq. (17) (from Eq. 18, C = P/P + S) yields

$$\frac{\text{SY}}{A} = \alpha \left[ {\frac{P}{P + S}} \right]^{\beta }$$

or

$${\text{SY}} = A \times \alpha \left[ {\frac{P}{P + S}} \right]^{\beta }$$
(19)

Eq. (19) shows a relationship between SY and S and, in turn, CN. It also shows that as the potential maximum retention increases, the rate of sediment yield decreases and vice versa.

Physical description

To show the existence of a relationship between CN and SY, it is necessary to consider all the factors governing CN and evaluate the impact of their variation on SY.

Agricultural management practices

Agricultural management systems involve different types of tillage, vegetation and surface cover. Brakensiek and Rawls (1988) reported that ploughing increases soil porosity and, in turn increases infiltration rates over non-tilled soil. Rawls and Brakensiek (1983) found that an increase in organic matter in the soil lowers bulk density or increases porosity, and hence, increases infiltration and, in turn, decreases the runoff potential or curve number in turn, leads to less sediment losses.

Rainfall intensity

A greater intensity rainfall will render lesser time for rain water to stay over the land surface, leading to a lesser amount of infiltration, and consequently, a greater amount of direct runoff. The reverse will also hold. In reality, a high intensity rainfall or raindrop breaks down the soil structure to make soil fines move into the soil surface or near surface pores, leading to the formation of crust that impedes infiltration and thus increases CN. In general, higher rainfall intensity and lower coverage produced higher sediment and consequently higher nutrient loss.

Antecedent runoff conditions (ARC)—according to ARC criteria, CN is low in growing season than in dormant season for the same antecedent moisture. When Antecedent Rainfall Conditions change from dry to wet, consequently the sediment yield and curve number increase supporting the existence of an inverse SY–S relationship. It is worth emphasizing here that the concept of soil-moisture-index (SMI) is generally used to identify the ARC condition in long-term hydrologic simulation.

Hydrologic condition

The hydrologic condition of an agricultural watershed is defined in terms of the percent area of grass cover. The larger the area of grass cover in a watershed, the lesser will be the runoff potential of the watershed and more will be the infiltration. Such a situation describes the watershed to be in good hydrologic condition. Alternatively, a good hydrologic condition allows more infiltration than does a poor hydrologic condition. Thus, the hydrologic condition of a forest area also represents its runoff producing potential. The curve number will be highest for poor, average for fair and lowest for good condition.

Land use

Land use characterizes the uppermost surface of the soil system and has a definite bearing on infiltration and SY. It describes the watershed cover and includes every kind of vegetation, litter and mulch, and fallow as well as non-agricultural uses, such as water surfaces, roads, roofs, etc. SCS (1956) broadly classified the land use into three categories, urban, agricultural, woods and forest.

Urban lands Urban lands refer to the area of low or insignificant permeability. These include residential, paved parking lots, streets, roads, commercial and industrial areas, etc. Paved areas are assigned the curve number equal to 98. The amount of imperviousness plays an important role in the rainfall–runoff process. The larger the impervious area, the higher will be the runoff potential and sediment yield of watershed and vice versa.

Cultivated land Agricultural watersheds can be classified as cultivated and uncultivated. The agricultural land classified as fallow land, row crops, small grain crops, pasture or range and medow. Fallow refers to bare agricultural land use treatment having the highest runoff potential and sediment yield. Straight row field are farmed in straight rows either up and down the hill or across the slope. Where land slopes are less than 2 %, farming across the land slope in straight rows is equivalent to contouring. Contouring delays runoff to increase infiltration, in turn, reduces sediment yield.

Wood and forest In humid forest regions of the United States, soil group, humus type and humus depth are the major factors affecting CN. Humus increases with the age of forest and because of its porous nature, it increases infiltration. Good management practices refer to proper use, protection and improvement of humus content for increasing infiltration, whereas poor management practices allow burning, over cutting or overgrazing and thereby reduce infiltration. For a given soil type and hydrologic condition, herbaceous forests exhibit the highest runoff potential or curve number.

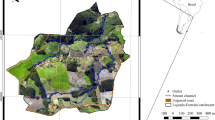
Study area

The Shakkar river rises in the Satpura range, east of the Chhindi village, Chhindwara district, Madhya Pradesh an elevation of about 600 m at latitude 22°23′ N longitude 78°52′ E (Fig. 1). The watershed covers 2,220 km2 area. The climate of the basin is generally dry except the southwest monsoon season. The southwest monsoon starts from middle of June and lasts till the end of September. October and middle of November constitute the post monsoon or retreating monsoon season. The normal annual rainfall is 1,192.1 mm. The normal maximum temperature received during the month of May is 42.5 °C and minimum during the month of January is 8.2 °C. Soils are mainly clayey to loamy in texture with calcareous concretions invariably present. They are sticky and in summer, due to shrinkage, develop deep cracks. They generally predominate in montmorillonite and beidellite type of clays. In rest of the alluvial areas, mixed clays, black to brown to reddish brown, derived from sandstones and traps are observed which are sandy clay in nature with calcareous concretions. Near the banks of the rivers and at the confluence, light yellow to yellowish brown soils are noticed which were deposited during the recent past. These soils are clayey to silt in nature.

Fig. 1
figure 1

Location map of the study area

Full size image

Result and discussion

As described above, the available daily rainfall (P)–runoff (Q)–sediment yield (SY) data series of Shakkar watershed, was first separately arranged in chronological order. Each of these series was then processed for exclusion of those pairs exhibiting daily runoff coefficient (i.e. Q/P) being greater than 1.0. Here, both P and Q are in mm. The processed data series was sorted in the descending order of P, and calculated CN using Eq. 5, and probability assigned to CN using Weibull’s plotting position formula. Then, CN-values (Seasonal) were derived for 90, 50, and 10 % probability of exceedances and taken to correspond to dry, normal, and wet conditions as for study watersheds. Since these CN-values were derived from 1, 2, 3, 4, upto 30 days P-Q data series. As seen in Fig. 2, S shows a continuously increasing trend with rain duration. The derived pattern is consistent with the notion that as rain duration increases, S increases because of larger opportunity time available for water loss in the watershed, and vice versa. Since whole data (which forms to be quite a large dataset), these S (or CN) values are representative of the watershed characteristics (Fig. 3).

Fig. 2
figure 2

Component of the general infiltration loss model

Full size image
Fig. 3
figure 3

CN variation with rainfall duration (≥1 day)

Full size image

Derivation of CN, SY, and CN–SY Relationship

Mathematical and physical justification of SY–CN rationale invokes the existence of a relationship between the duration-dependent SY and runoff curve numbers (or potential maximum retention). For a given watershed characteristics (Eq. 9) A and P, the sediment yield will decrease with increasing potential maximum retention (S), and vice versa. This relationship/methodology was verified using the hydro-meteorological data collected from Shakkar watersheds of Narmada river basins of India.

Annual and seasonal curve numbers were derived from Eqs. (5) and (6) utilizing the available short-term daily rainfall–runoff data, covering a wide range of variation in rainfall/runoff. The CN values for different seasons were derived from rainfall–runoff data and these were transformed to potential maximum retention using Eqs. 5 and 6 for normal condition (or SII). The sediment yield (SY) was selected corresponding to 50 % probability of exceedance of CN. These values when plotted (Fig. 4) against the corresponding SY exhibited a power relation for all season. The coefficients of determination (R2) value range from 0.76 to 0.79 (Table 1) for all seasons indicating the existence of a strong relationship between them. Such a relationship may also lead to describing the SCS-CN parameter S in terms of the maximum possible sediment and determining SY using SCS (1956) CN-values.

Fig. 4
figure 4

Relationship between sediment yield and potential maximum retention (S) for Shakkar watershed

Full size image
Table 1 Relationship between SY and CN for Narmada watershed
Full size table

Conclusions

In this study, the easily derivable runoff curve number (CN) from the short-term daily rainfall–runoff data is related with duration-dependent SY. Mathematical and physical justification of SY–CN rationale invokes the existence of a relationship between the duration-dependent SY and runoff curve numbers (or potential maximum retention) for different seasons. High R2 values range from 0.76 to 0.79 for all seasons support the general workability of the proposed concept.