Abstract
Biofilm process is widely used for the treatment of a variety of wastewater especially containing slowly biodegradable substances. It provides resistance against toxic environment and is capable of retaining biomass under continuous operation. Development of kinetics is very much pertinent for rational design of a biofilm process for the treatment of wastewater with or without inhibitory substances. A simple approach for development of such kinetics for an aerobic biofilm reactor has been presented using a novel biofilm model. The said biofilm model is formulated from the correlations between substrate concentrations in the influent/effluent and at biofilm liquid interface along with substrate flux and biofilm thickness complying Monod’s growth kinetics. The methodology for determining the kinetic coefficients for substrate removal and biomass growth has been demonstrated stepwise along with graphical representations. Kinetic coefficients like K, k, Y, b t, b s, and b d are determined either from the intercepts of X- and Y-axis or from the slope of the graphical plots.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Biofilms are natural, heterogeneous, multiphase material consisting primarily of microbial cells in slouble extracellular polymeric substances (EPS), and interstitial water (Hinson et al. 1996) attached on a solid surface which are used to combat high organic strengths in wastewater. Due to some, inherent advantages like low energy consumption, easy maintenance, better physical and chemical stability, and excellent biomass retention capacity, importance of biofilm is increasing in biological treatment of wastewater. A unique feature of biofilm process lies in the operation of continuous flow mode with minimal biomass loss compared to the traditional suspended growth bioreactor. Biofilm has an additional advantage having no contamination at its inner depth under inhibitory condition. There is a limited number of methods available for determining the kinetic coefficients required for the solution of the model of an aerobic biofilm bioreactor. In the process design of an aerobic biofilm bioreactor, the kinetic coefficients act as an essential tool for predicting the substrate utilization and biomass growth under a specific condition. The biomass yield coefficient (Y) indicates the portion of the biomass growth from the utilization of substrates. Specific biomass growth rate (µ) represents the biomass growth rate per unit biomass per day. Maximum value of specific biomass growth rate (µ max) is attained when substrates are not in limiting condition. Half-velocity constant (K) is the substrate concentration corresponding to half of maximum specific biomass growth rate (µ max). The maximum specific substrate utilization rate (k) represents the substrate utilization rate per day per unit biomass corresponding to µ max. Biomass decay coefficient (b d) is the rate of biomass loss due to endogenous decay and is taken into consideration for determining the net biomass growth rate.
In the biofilm process, the rate of total biomass loss (b t) consists of the rates of biomass shear loss (b s) and biomass decay (b d).Y, k, K, b t, b s, and b d are the kinetic coefficients required for the solution of a specific biofilm model. Substrate mass balance is accomplished with the simultaneous occurrence of both diffusion and utilization of substrates. The molecular diffusion coefficient of the substrate in water (D) and in the biofilm (D f) represent internal mass transport resistance in the bulk liquid and in the biofilm, respectively. The thickness of the effective diffusion layer of the bulk liquid (L) represents the external mass transport resistance. The biomass concentration (X f) in the biofilm can be determined from the total biofilm thickness (L f). Biofilm thickness primarily depends on the substrate concentration in the bulk liquid and the liquid hydraulics. The biomass per unit surface area, i.e., (X f L f) is constant indicating the steady state condition of biofilm. Various research studies have been reported on modeling of biofilm reactor (Williamson and McCarty 1976; Rittmann and McCarty 1980; Suidan and Wang 1985; Strand 1986; Kim and Suidan 1989; Golla and Thomas 1990; Heath et al. 1990; Saez and Rittman 1991; Lee 1997; Rauch et al. 1999; Tsuno et al. 2002; Pritchett and Dockery 2001; Perez et al. 2005; Shaoying et al. 2005; Hsien and Lin 2005; Mudliar et al. 2008; Jiang et al. 2009; Qi and Morgenroth 2005; Rao et al. 2010; Liao et al. 2012; Eldyasti et al. 2012; Gullicks et al. 2011), but no simplified method was developed for determining the kinetic coefficients. Indeed, the kinetic coefficients are needful for solving the biofilm model and hence for the process design of the biofilm reactor. A kinetic study was performed in an aerobic biofilm bioreactor for evaluation of efficiency of COD removal from organic wastewater (Dey and Mukherjee 2010). The half-velocity constant (K) was determined from the experimental results using Monod’s kinetics. The inhibition kinetics was used in another research work for predicting the response of biofilms to toxic compounds in wastewater (Gheewala and Annachhatre 2003). Although the relationship between the effectiveness factor of biofilm and the half-velocity constant (K) was shown, no guideline was stipulated for arriving the values of K. Hsien and Lin (2005) has conducted one batch test for determining the kinetic coefficients for simulation study in a biofilm reactor.
Therefore, development of kinetics for an aerobic biofilm reactor for the treatment of wastewater finds its relevance and having an importance in this research work. The present method employs a series of biofilm model equations complying Monod’s growth kinetics. The graphical solutions for evaluating the kinetics coefficient like K, k, Y, b t, b s, and b d for both the substrate removal and biomass growth have been presented sequentially.
Materials and methods
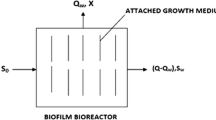
The schematic diagram of Biofilm model considering purely attached biomass is shown in Fig. 1.
The concept of biofilm model is based upon three basic assumptions, i.e., (1) the nature of the kinetics for substrate utilization in suspended growth and attached growth are in similar nature, (2) external substrate transport from the bulk liquid to the biofilm through biofilm Liquid interface follows Fick’s first law of molecular diffusion and (3) the substrate transport within the biofilm follows the Fick’s second law of molecular diffusion. Now, the equation for external mass transport according to Fick’s first law
where, J is the substrate flux into the biofilm (mg/cm2/day), D is the Molecular diffusion coefficient in liquid (cm2/day), L is the thickness of effective diffusion layer (cm), S 0, S s is the substrate concentrations in the bulk liquid and at the biofilm liquid interface, respectively (mg/cm3). Now, from the substrate mass balance within the biofilm is.
where, a is the specific surface area of supporting media (cm−1), θ is the Hydraulic Retention time (h), S w is the effluent substrate concentration (mg/cm3), therefore, from Eq. 2 we get,
Again from the mass balance equation for substrate in the biofilm considering Monod’s’ kinetics we get,
where, S f is the substrate concentration at a point in the biofilm (mg/cm3), k is the maximum specific rate of substrate use (per day), X f is the active biomass density within the biofilm (mg/cm3), D f is the molecular diffusion coefficient of the substrate in the biofilm (cm2/day), K is the half-velocity coefficient (mg/cm3).
Referring Fig. 1, the boundary conditions for solving above second-order differential Eq. (3) may be taken as below:
At the attachment surface (i.e., at z = 0) there will be no flux, i.e., \(\frac{{{\text{d}}S_{f} }}{{{\text{d}}z}} = 0\).
At the biofilm/liquid interface, i.e., at z = L e,
Now, the solution of the above second-order differential Eq. (3) on substrate utilization considering both the boundary condition within the biofilm is shown below:
Analytical procedure for determining the kinetic coefficients
To determine the kinetic coefficient from, the Biomass growth curve, Eqs. (1), (2) and (4) can be systematically used in the following Steps.
Step 1
µ is the specific growth rate of biomass for biofilm bioreactor (h−1), X 2 is the final Biomass density for attached phase at the end of batch period (mg/cm3), X 1 is the initial Biomass density for attached phase at the end of batch period (mg/cm3), θ is the batch period under consideration (h).
Now, biomass density can be determined by washing the biofilm attached surface with 25 ml 0.1 (N) NaOH after heating the solution at 80 °C (Lazarova et al. 1994; Cox and Deshusses 1999) and subsequently by measuring the protein concentration with Lowry’s method as below:
Steps for determining the protein concentration by Lowry’s method:
-
1.
Preparation of following reagents are as follows:
-
(a)
5 % Na2CO3 solution.
-
(b)
CuSO4 solution (0.5 mg CuSO4, 5H20 + 100 ml of 1 % sodium potassium tartrate solution)
-
(c)
Alkali copper reagent(50 ml of reagent a + 2 ml of reagent b)
-
(d)
Folin reagent solution (folin reagent:distilled water = 1:1
-
(e)
1 (N) NaOH solution
-
(f)
Standard BSA solution of concentration 200 mg/l.
-
(a)
-
2.
0.5 ml of the cell suspension (BSA solution) + 0.5 ml 1(N) NaOH solution were kept in boiling water bath for 5 min.
-
3.
The content was then cooled in cold water. A 5 ml of freshly prepared reagent (c) was added to the content and allowed to stand for 10 min.
-
4.
Now 0.5 ml folin reagent solution was added and the whole mixture was allowed to stand for 30 min for color development.
-
5.
The blank was prepared taking 0.5 ml distilled wastewater instead of bacterial suspension and was treated in the same way as above.
-
6.
The absorbance value was measured at 750 nm using visible spectrophotometer against distilled water blank.
BSA standards ranged between 0 and 200 µg/ml were processed in the same manner as samples for developing the calibration curve.
Step 2
The ‘µ’ values can be plotted in Y-axis with respect to ‘S w’ values in X-axis, which should have an ascending asymptotic nature as shown in Fig. 2. The half-velocity constant K can be obtained corresponding to half of the maximum specific growth rate, i.e., µ m, as indicated in the same figure.
Step 3
\(\left( {\frac{{S_{0} - S_{\text{W}} }}{a}} \right)^{2} = 2kX_{\text{f}} D_{\text{f}} \partial^{2} \left[ {\left\{ {S_{0} - \frac{L}{D}\frac{{S_{0} - S_{W} }}{a\theta }) - Sw} \right\} + ks\ln \left\{ {\frac{{k + S_{W} }}{{k + s_{o} - \frac{L}{D}\left( {\frac{{S_{0} - s_{w} }}{a\theta }} \right)}}} \right\}} \right]\). Now, \(\left( {\frac{{S_{0} - S_{\text{W}} }}{a}} \right)^{2}\) values can be plotted with respect to 2X
f
D
f
 2
\(\left[ {\left\{ {S_{0} - \frac{L}{D}\left( {\frac{{S_{0} - S_{W} }}{a\theta }} \right) - S_{W} } \right\} + K\ln \left\{ {\frac{{k + S_{W} }}{{k + s_{0} - \frac{L}{D}\left( {\frac{{s_{0} - s_{w} }}{a\theta }} \right)}}} \right\}} \right]\) and a best-fit line can be drawn as shown in Fig. 3 below. The slope of a best-fit line passing through the origin will result in the value of k.
2
\(\left[ {\left\{ {S_{0} - \frac{L}{D}\left( {\frac{{S_{0} - S_{W} }}{a\theta }} \right) - S_{W} } \right\} + K\ln \left\{ {\frac{{k + S_{W} }}{{k + s_{0} - \frac{L}{D}\left( {\frac{{s_{0} - s_{w} }}{a\theta }} \right)}}} \right\}} \right]\) and a best-fit line can be drawn as shown in Fig. 3 below. The slope of a best-fit line passing through the origin will result in the value of k.
Step 4
Now the total biofilm thickness L
f can be estimated as \(L_{\text{f}} = \frac{JY}{{X_{\text{f}} b_{\text{t}} }}\, \Rightarrow L_{\text{f}} = \left( {\frac{{S_{0} - S_{W} }}{{X_{f} a\theta bt}}} \right)Y\)where, J is the substrate flux, X
f is the Biofilm density, b
t is the overall specific biofilm loss rate in (h−1), µ
m = kY or Y = µ
m/k. Therefore, the value of L
f
X
f
 can be plotted with respect to \(\left( {\frac{{S_{0} - S_{W} }}{a}} \right)Y\) to find out b
t.
can be plotted with respect to \(\left( {\frac{{S_{0} - S_{W} }}{a}} \right)Y\) to find out b
t.
Step 5
To determine the shear loss coefficient (b s), the sloughed off biomass from the attached surface may be equated to the final suspended biomass after batch period in the reactor. Y·a·θ·J·\(\frac{{b_{\text{s}} }}{{b_{\text{t}} }}\) = X, the portion of biomass which is sloughed off from the attached biofilm and take part into the suspended one. or \(\frac{Ya\theta J}{{b_{\text{t}} }} = \frac{X}{{b_{s} }}\) or, \(\frac{{Y(S_{0} - S_{w} )}}{{b_{\text{t}} }} = \frac{X}{bs}\), where θ is the HRT (Hydraulic retention time), X is the suspended biomass contributed from the attached biofilm in the reactor. Now, \(Y{ \cdot }\left( {\frac{{S_{O} - S_{W} }}{{b_{t} }}} \right)\) can be plotted with respect to X as shown in Fig. 4 below. The slope of the best-fit line will denote the value of 1/b s.
Results
The semi-batch study results are tabulated in the Table 1 below.
Illustrative example
In the laboratory, semi-batch studies on municipal wastewater in an aerobic biofilm bioreactor in three consecutive days were performed at an interval of 3 h. ‘µ’ is calculated from the expression \(\mu = \frac{{(X_{\text{attached 2}} - X_{\text{attached 1}} )}}{{(X_{\text{attached 1}} )\theta }}\) as shown in Table 1. Consequently, ‘µ’ Vs. ‘S w’ graph is plotted as shown in Fig. 5 to find out µ max and K.
From Fig. 5, µ max and K are obtained as µ max = 0.11 h−1 = 2.64 day−1 and K = 60 mg/l = 0.06 mg/cc. Now, the values of (S 0 − S w / a)2 are plotted against 2*X f*D f*θ2*[S 0 − L/D{(S 0 − S w)/aθ} − S w + Kln{(K + S w)/(K + S 0 − L/D{(S 0 − S w)/aθ}] as shown in Fig. 6 to determine the value of k and Y.
From the Fig. 6, it is observed that k = 2.6 day−1 Therefore, Y = µ max/k = 2.64/2.6 = 0.99. Now, L fθX f are plotted against (S 0 − S w)Y/a as shown in Fig. 7 to determine the value of b t.
It is observed from Fig. 7 that 1/b t = 0.501 day, hence total biomass loss rate, b t = 1.996 day−1. Now, Y(S 0 − S w)/b t are plotted against X as shown in Fig. 8 to determine the value of b s.
From Fig. 8, 1/b s = 0.552 day, hence biomass shear loss, b s = 1.81 day−1. Hence biomass decay b d = 0.186 day−1.
The simulation study was conducted with the proposed model varying the organic loadings and hydraulic retention times and the performance of the biofilm reactor was envisaged as shown in Table 2.
The kinetic coefficients and physical data in this regard are as follows.
k = 8 day−1, Y = 0.5, K = 0.01 mg/cm3, b t = 0.1 day−1, D = 0.8 cm2/day, Df = 0.64 cm2/day, L = 0.01 cm.
Discussion
The specific growth curve of biomass as shown in Fig. 2 essentially depicts the Monod’s kinetics, which is valid for non-inhibitory environment. In case of inhibitory environment, the specific growth curve will show a maximum value (i.e., µ m) and then it will move downward. As the specific growth curve significantly influences the values of µ m and K, it should be plotted with a set of data as large as possible. The maximum specific substrate utilization rate (k) can be calculated from the slope of Fig. 3, provided the biomass density of the biofilm reactor is known. On the other hand, the ‘b t’ value evaluated from the slope of Fig. 9 represents the rate of total biomass loss in the biofilm reactor. The rate of shear loss (b s) is evaluated by plotting \(Y \cdot (\frac{{S_{0} - S_{W} }}{{b_{t} }}\)) against X as shown in Fig. 5. In these cases also the slope of the ‘best-fit line’ considerably influences the values of b s and b d and therefore Figs. 5, 9 should be drawn with a large set of data. The use of the present method in determining the kinetic coefficient for the treatment of municipal wastewater in a biofilm reactor clearly demonstrates its efficacy and compatibility. All such kinetic data also show good removal rate of organic substrate in the biofilm reactor as indicated in Table 2. The output results of Table 2 were also compared with Pseudo-analytical solution by Rittman and McCarty (1980) with the same set of kinetic coefficients and found okay. The values of kinetic coefficients obtained in batch study are more or less in similar nature of that of suspended growth process in earlier research work (Ref Mardani et al. 2011)
Conclusion
So far, no simplified method for determining the kinetic coefficients of the biofilm bioreactor was developed in any earlier research. An attempt was made to present a simple method with straight-line equations and graphical representation for determining the kinetic coefficients of an aerobic biofilm reactor. The proposed development for kinetic coefficients of an aerobic biofilm reactor thus finds its relevance for process design of an aerobic biofilm bioreactor. The proposed method is an accurate, fast, and simplified one to find out the kinetic coefficients of an aerobic biofilm bioreactor. It is possible to simply calculate the kinetic coefficients from the graphs either from the intercepts of both x- and y-axis or from the slope of the graph applying mass balance equations both for substrates and biomass. All necessary kinetic coefficients like K, k, Y, b s, b t, and b d can be determined by the proposed method required for the solution of the modeling of an aerobic biofilm bioreactor. In reality the application of biofilm bioreactor model suffers due to lack of accuracy of kinetic models and uncertainty in the kinetic parameters. Successful modeling of the biofilm reactor therefore requires accurate determination of biokinetic parameters.
References
Cox HJ, Deshusses A (1999) Chemical removal of biomass from waste air biotrickling filters: screening of chemicals of potential interest. Water Res 33:2383–2391
Dey S, Mukherjee S (2010) Kinetic studies for an aerobic packed bed biofilm reactor for treatment of organic wastewater with and without phenol. Water Res Protect 2:731–738
Gheewala SH, Annachhatre AP (2003) Efficacy of biofilms under toxic conditions. J Environ Eng ASCE 129(6):576–599
Golla PS, Thomas J (1990) Simple solutions for steady-state biofilm reactors. J Environ Eng ASCE 116(5):829–836
Hinson RK, Kocher WM (1996) Model for effective diffusivities in aerobic biofilms. J Environ Eng ASCE 122(11):1023–1030
Hsien TY, Lin YH (2005) Biodegradation of phenolic wastewater in a fixed biofilm reactor. Biochem Eng J 27:95–103
Jiang F, Leung DHW, Li S, Chen GH, Okabe S, van Loosdrechte MC (2009) A biofilm model for prediction of pollutant transformation in sewers. Water Res 43:3187–3198
Kim R Byung, Suidan T Makram (1989) Approximate algebraic solution for a biofilm model with the Monod kinetic expression. Water Res 23(12):1491–1498
Lazarova V, Pierzo V, Fontvielle D, Manem J (1994) Integrated approach for biofilm characterization and biomass activity control. Water Sci Technol 29(7):345–354
Lee Chi Y (1997) Model of bacterial-supplement kinetics. J Environ Eng ASCE 123(8):634–646
Liao Q, Wang YJ, Wang YZ, Chen R, Zhu X, Pu YK, Lee DJ (2012) Two-dimension mathematical modeling of photosynthetic bacterial biofilm growth and formation. Int J Hydrogen Energy 37:15607–15615
Mardani et al (2011) Determination of biokinetic coefficients for activated sludge processes on municipal wastewater. Iran J Environ Health Sci Eng 8(1):25–34
Mudliar S, Banerjee S, Vaidya A, Devotta S (2008) Steady state model for evaluation of external and internal mass transfer effects in an immobilized biofilm. Bioresource Technol 99:3468–3474
Perez J, Picioreanu C, van Loosdrecht M (2005) Modeling biofilm and flock diffusion processes based on analytical solution of reaction-diffusion equations. Water Res 39:1311–1323
Pritchett LA, Dockery JD (2001) Steady state solutions of a one-dimensional biofilm model. Math Comp Model 33:255–263
Qi S, Morgenroth E (2005) Modeling steady-state biofilms with dual-substrate limitations. J Environ Eng ASCE 131(2):320–326
Rao K, Rama ST, Venkateswarlu Ch (2010) Mathematical and kinetic modeling of biofilm reactor based on ant colony optimization. Process Biochem 45:961–972
Rauch W, Vanhooren H, Vanrolleghem PA (1999) A simplified mixed-culture biofilm model. Water Res 33(9):148–2162
Rittmann BE, McCarty PL (1980) Model of steady state biofilm kinetics. Biotechnol Bioeng XXII:2343–2357
Saez PB, Rittman BE (1991) Accurate pseudo analytical solution for steady state bio films. Biotechnol Bioeng 39:790–793
Strand SE (1986) Model of ammonia and carbon oxidation in biofilms. J Environ Eng 112(4):785–804
Suidan MT, Wang YT (1985) Unified analysis of bio film kinetics. J Environ Eng 3(5):634–646
Szilágyi N, Kovács R, Kenyeres I, Csikor Zs (2011) Performance of a newly developed biofilm-based wastewater treatment technology. In: 1st IWA Central Asian Regional Young Water Professionals Conference. Sept. 22–24. Almaty, Kazahstan, Accepted
Tsuno H, Hidakaa T, Nishimura F (2002) A simple biofilm model of bacterial competition for attached surface. Water Res 36:996–1006
Williamson K, McCarty PL (1976) A model of substrate utilization by bacterial films. Water Environ Feder 48(1):9–24
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Goswami, S., Sarkar, S. & Mazumder, D. A new approach for development of kinetics of wastewater treatment in aerobic biofilm reactor. Appl Water Sci 7, 2187–2193 (2017). https://doi.org/10.1007/s13201-016-0389-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13201-016-0389-0