Accurate evaluation for the biofilm-activated sludge reactor using graphical techniques

Abstract

A complete graphical solution is obtained for the completely mixed biofilm-activated sludge reactor (hybrid reactor). The solution consists of a series of curves deduced from the principal equations of the hybrid system after converting them in dimensionless form. The curves estimate the basic parameters of the hybrid system such as suspended biomass concentration, sludge residence time, wasted mass of sludge, and food to biomass ratio. All of these parameters can be expressed as functions of hydraulic retention time, influent substrate concentration, substrate concentration in the bulk, stagnant liquid layer thickness, and the minimum substrate concentration which can maintain the biofilm growth in addition to the basic kinetics of the activated sludge process in which all these variables are expressed in a dimensionless form. Compared to other solutions of such system these curves are simple, easy to use, and provide an accurate tool for analyzing such system based on fundamental principles. Further, these curves may be used as a quick tool to get the effect of variables change on the other parameters and the whole system.

Introduction

Activated sludge process (ASP) reinforced by biofilm carrier to get aerobic hybrid system has become a major concern (Gautam et al. 2013). Today this technique can eliminate most problems of ASP like unavailability of large space requirement to construct new plants or extension of other existing plants and complaints such as low resistance, low stability, and low efficiency (Lessel 1994; Randall 1996; Muller 1998; Wanner et al. 1998). Despite of widespread use of this system, the design criteria for most of its parameters are still unclear. The analysis of this system seems very complicated due to difficulty of the biofilm analysis, differentiation between the suspended and the attached culture behavior, and complexity of the combined system (Islam et al. 2013; Goswami et al. 2017). Describing this system using any steady state model based on Monod kinetics, often yields, a set of algebraic equations not having an explicit solution even for biofilm reactor only (Kim and Suidan 1989). At present, hybrid reactors are normally designed using experimental results for a recommended ratio of the biofilm carrier based on field experience, some iteration steps do not include all of its parameters (Lee 1992) or the system is simplified as a two separate reactors run in series (Gebara 1999). These methods of application neither give precise results nor a good estimation for system parameters (Goswami et al. 2017; Sarkar and Mazumder 2017). The present study has focused on deducing an easy graphical solution, which can be used for design and control of this system. In this technique, the basic parameters of the system could be computed from its basic equations (substrate and biomass balance). The relationship between variables and dimensionless parameters are drawn in the form of a set of curves. From these curves, the hybrid system can be designed and controlled accurately based on fundamental principles and according to the kinetics of its cultures (attached and suspended). Further, these curves are easy to use and can be considered a good tool to approve the performance and the characteristics of such system. In addition these curves has the value of substrate flux into biofilm (J) in implicit form, so many steps has been saved in evaluating this value, which is required in any analytical solution (Fouad and Renu 2005c). Only knowledge of hydraulic retention time (HRT), influent substrate concentration (S_o), stagnant liquid layer thickness (L), the minimum substrate concentration which can maintain the biofilm growth (S_min), and the desired value of substrate concentration in the bulk (S) permit computation of suspended biomass concentration (X) and food to biomass ratio (F/M) for that system. Further, the additional knowledge of fraction YK/K_d permits computation of sludge residence time (SRT) and wasted mass of sludge (Q_w X_u). Computation the value of J in this solution is not required, but J can be determined easily if it is needed in other applications.

Development of the graphical solution

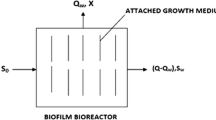
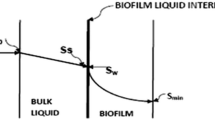
The process diagram of aerobic hybrid system is shown in Fig. 1a while Fig. 1b defines its schematic, which is used for the present study. The system is assumed to run under a steady sate condition with a rate limiting substrate concentration through the reactor and has same kinetics for both cultures (suspended and attached). For this system, the graphical solution for X, SRT, Q_wX_u, and F/M can be deduced.

Fig. 1

Aerobic hybrid process a Basic component of aerobic hybrid process. b Schematic of aerobic hybrid process

Biomass concentration

The substrate balance for the hybrid system can be written as follows,

$$ \frac{{d{\text{S}}}}{{d{\text{t}}}} = Q (S_{o} - S )- a{\text{VJ}} - {\text{VX}}\frac{\text{K S}}{{K_{\text{s}} + S}} $$

(1)

where dS/dt = the growth rate of substrate concentration in the bulk, Q = flow rate, a = specific surface area of the biofilm, V = reactor volume, K = maximum specific rate of substrate utilization, and K_S = Monod half-velocity coefficient. At steady state dS/dt vanish and the resulting equation after rearranging the terms is:

$$ \frac{\text{X K}}{a} \, = \left[ {\frac{{ (S_{\text{o}} - S )}}{\theta \, a} - J} \right]\frac{{ \, K_{\text{s}} + S}}{S} $$

(2)

where θ = empty retention time in the reactor.

Rewriting (2) in dimensionless parameters for S, S_o, J, and θ yields,

$$ X^{*} \frac{{ \, S^{*} }}{{1 + S^{*} }} = \frac{{(S_{\text{o}}^{*} - S^{*} )}}{{\theta^{*} }} - J^{*} $$

(3)

where X^* = (X/a) $\sqrt { (K ) / (K_{\text{s}} \, X_{\text{f}} \, D_{\text{f}} )}$, J^* = J/ $\sqrt {(K_{{\text{s}}} {\text{KX}}_{{\text{f}}} D_{{\text{f}}} )}$, S^* = S/K_s, $S_{\text{o}}^{ *}$ = $S_{o}$/K_s, and θ^* = a θ$\sqrt { (K \, X_{\text{f}} \, D_{\text{f}} ) / (K_{\text{s}} ) { }}$

In which D_f = molecular diffusion coefficient in biofilm, and X_f = biofilm microbial density. The following solution of J^* has been developed by Suidan et al. (1989).

Sáez and Rittmann (1988, 1992) presented the following set of parametric equations, which give a unique value of J^* for each value of S^* > $S_{\text{min} }^{*}$.

$$ S^{*} = S_{\text{s}}^{ *} \, + J^{*} \, L^{*} $$

(4)

$$ J^{ *} = f \, J_{\text{deep}}^{ *} \, $$

(5)

$$ f \, = \tanh \, \left[ {\upalpha \, \left( {\frac{{S_{\text{s}}^{*} \, }}{{S_{\text{min} }^{*} \, }} \, - 1} \right)^{\upbeta} } \right] $$

(5a)

$$ \upalpha = \, 1.5557 \, - \, 0.4110 \, \tanh \, \left( {\log \, S_{\text{min} }^{*} } \right) $$

(5b)

$$ \upbeta = \, 0.5035 \, - \, 0.0257 \, \tanh \, \left( {\log \, S_{\text{min} }^{*} } \right) $$

(5c)

$$ J_{\text{deep}}^{ *} = [2(S_{\text{s}}^{ *} \, \text{ - }{\text{ln (1}} + S_{\text{s}}^{ *} ))]^{0.5} $$

(6)

where $S^{*}_{\text{s}}$ = dimensionless minimum substrate concentration at diffusion layer, f = ratio between flux into actual and deep biofilm, α and β are product and exponentional coefficients respectively in factor f expression (Eq. 4), and $J^{*}_{\text{deep}}$ = dimensionless substrate flux into deep biofilm,

$S_{\text{min} }^{*}$ = dimensionless minimum substrate concentration that can sustain biofilm, and L^* = L $\sqrt { ( {\text{K X}}_{\text{f}} ) / (K_{\text{s}} \, D_{\text{f}} ) { }}$ (D_f/D_w) in which D_w = molecular diffusion coefficient in water.

This model is the most widely accepted model, used for biofilm application. It is simplified in one-dimension and consider a single substrate as a limiting factor.

After combining Eqs. (4–6) and (3), X^* can be expressed as a function of (S^*, $S_{\text{o}}^{*}$, $S_{\text{min} }^{*}$, L^*,θ^*). Figure 2 represents the relation between X^* and ($S_{\text{o}}^{*}$−S^*)/θ^* for a fixed values of $S_{\text{min} }^{*}$ = 0.10 with L^* = 0.0 and L^* = 1.0 and $S_{\text{min} }^{*}$ = 1.0 with L^* = 0.0 and L^* = 1.0. Each chart contains different values of S^* ranging from 0.10 to 100.0 and from 1.0 to 100.0 for $S_{\text{min} }^{*}$ = 0.10 and $S_{\text{min} }^{*}$ = 1.0 respectively.

Fig. 2

X^* as a function of S^* and ($S_{\text{o}}^{*}$−S)/HRT at a L^* = 0.0, $S_{\text{min} }^{*}$ = 0.10, b L^* = 0.0, $S_{\text{min} }^{*}$ = 1.0, c L^* = 1.0, $S_{\text{min} }^{*}$ = 0.10 and d L^* = 1.0, $S_{\text{min} }^{*}$ = 1.0

Wasted mass of sludge

At steady state, biomass balance for hybrid system is:

$$ \frac{{d{\text{X}}}}{{d{\text{t}}}} = {\text{VX}}\left[ {\frac{\text{Y K S}}{{K_{\text{s}} + S}} - K_{\text{d}} } \right] + {\text{YaVJ}}\frac{{b_{\text{s}} }}{{b_{\text{t}} }} - Q_{\text{w}} X_{\text{u}} $$

(7)

where dX/dt = changing rate of biomass concentration in the reactor, Y = yield coefficient, b_s = specific shear loss rates, b_t = sum of specific decay and shear loss rates, Q_wX_u = mass of wasted sludge, and k_d = specific decay rate. At steady state dX/dt will vanish then combining (2) and (7) and substituting b_t = k_d + b_s (Rittmann 1982a) the resulting equation is obtained as:

$$ Q_{\text{w}} X_{\text{u}} = {\text{YQ(}}S_{\text{o}} - S )- {\text{VXK}}_{\text{d}} - {\text{YaVJ}}\frac{{K_{\text{d}} }}{{b_{\text{t}} }} $$

(8)

By rearranging (8), the following equation can be obtained

$$ \frac{K}{{\text{aV }k_{\text{d}} }}Q_{\text{w}} X_{\text{u}} = \frac{{Y\text{(}S_{\text{o}} - S\text{)}}}{{\text{a}\theta }}\frac{K}{{\text{ }k_{\text{d}} }} - \frac{{\text{XK}}}{a} - J\frac{{\text{YK}}}{{b_{\text{t}} }} $$

(9)

Making substitution for $\frac{\text{YK}}{{b_{\text{t}} }}$ as $( 1 /S_{\text{min} }^{*} + 1 )$ (Suidan et al. 1989; Rittmann 1982a) and transferring (9) in dimensionless form yield.

$$ (Q_{\text{w}} X_{\text{u}} )^{ *} = \frac{\text{YK}}{{ \, k_{\text{d}} }}\frac{{ (S_{\text{o}}^{ *} - S^{ *} )}}{{\theta^{ *} }} - X^{ *} - J^{ *} \left( {\frac{ 1}{{S^{ *}_{\text{min} } }} + 1} \right) $$

(10)

where (Q_wX_u)^* = $Q_{{\text{w}}} X_{{\text{u}}} \frac{K}{{{\text{aV }}k_{{\text{d}}} }}/\sqrt {(K_{{\text{s}}} {\text{KX}}_{{\text{f}}} D_{{\text{f}}} )}$.

Substituting X^* from (3) the final equation for (Q_wX_u)^* can be obtained as follow.

$$ (Q_{\text{w}} X_{\text{u}} )^{ *} = \frac{{ (S_{\text{o}}^{ *} - S^{ *} )}}{{\theta^{ *} }}\left( {\frac{\text{YK}}{{K_{\text{d}} }} - \frac{{ 1+ \, S^{ *} }}{{S^{ *} }}} \right) + {\text{J}}^{ *} \left( {\frac{{ 1+ \, S^{ *} }}{{S^{ *} }} - \frac{ 1}{{S_{\text{min} }^{*} }} - 1} \right) $$

(11)

After combining (4–6) and (11) the term (Q_w X_u)^* can be expressed as a function of S^*, $S_{\text{o}}^{*}$,$S_{\text{min} }^{*}$, L^*, θ^*, YK/K_d. Figures 3 and 4 represent the relation between (Q_wX_u)^* and ($S_{\text{o}}^{*}$−S^*)/θ^* for a specific set of $S_{\text{min} }^{*}$ L^*, and S^* which are used earlier for computation X^*, but for two different values of YK/K_d, 50 and 500.

Fig. 3

(Qw Xu)^* as a function of S^* and ($S_{\text{o}}^{*}$−S)/HRT at Y K/K_d = 50.0, a L^* = 0.0, $S_{\text{min} }^{*}$ = 0.10, b L^* = 0.0, $S_{\text{min} }^{*}$ = 1.0, c L^* = 1.0, $S_{\text{min} }^{*}$ = 0.10 and d L^* = 1.0, $S_{\text{min} }^{*}$ = 1.0

Fig. 4

(Qw Xu)^* as a function of S^* and ($S_{\text{o}}^{*}$−S)/HRT at Y K/K_d = 500.0, a L^* = 0.0, $S_{\text{min} }^{*}$ = 0.10, b L^* = 0.0, $S_{\text{min} }^{*}$ = 1.0, c L^* = 1.0, $S_{\text{min} }^{*}$ = 0.10 d L^* = 1.0, $S_{\text{min} }^{*}$ = 1.0

Sludge residence time

By definition, SRT for the combined biomass (suspended and fixed) is given by the following relationship after neglecting the biomass in the final effluent.

$$ {\text{SRT}}_{\text{ave}} = \frac{{M_{{{\text{sus}} .}} + M_{{{\text{bio}} .}} }}{{ (M_{\text{w}} )_{{{\text{sus}} .}} + (M_{\text{w}} )_{{{\text{bio}} .}} }} = \frac{\text{Total active biomass}}{\text{Total wasted sludge}} $$

(12)

where M_bio = the active mass of biofilm which is given by

$$ M_{\text{bio}} = \, a \, V \, L_{\text{f}} X_{\text{f}} $$

(13a)

where L_f = biofilm thickness which equals (JY)/(b_tX_f) (Rittmann 1982a; Suidan et al. 1989) then

$$ M_{\text{bio}} = \, a \, V \, J \, Y \, /b_{{{\text{t}} .}} $$

(14b)

Substituting total wasted sludge from (8) yields,

$$ {\text{SRT}}_{\text{ave}} = \frac{{{\text{aJV}}\frac{Y}{{b_{\text{t}} }} + {\text{XV}}}}{{{\text{YQ(}}S_{\text{o}} - S )- {\text{VXK}}_{\text{d}} - {\text{aVJY}}\frac{{K_{\text{d}} }}{{b_{\text{t}} }}}} $$

(14)

Multiplying both sides of (14) by K_d and the right hand side (numerator and denominator) by K/aV yields,

$$ {\text{SRT}}_{\text{ave}} \, K_{\text{d}} = \frac{{J\frac{\text{YK}}{{b_{\text{t}} }} + \frac{\text{XK}}{a}}}{{\frac{\text{YK}}{{K_{\text{d}} }}\frac{{ (S_{\text{o}} - S )}}{{{\text{a}}\theta }} - \frac{\text{XK}}{a} - J\frac{\text{YK}}{{b_{\text{t}} }}}} $$

(15)

Equation (15) can be expressed in a dimensionless form as:

$$ {\text{SRT}}^{ *} = \frac{{J^{ *} ( 1 /S_{ \text{min} }^{ *} + 1) + X^{ *} }}{{{\text{YK/}}K_{\text{d}} (S_{\text{o}}^{ *} - S^{ *} ) /\theta^{ *} - X^{ *} - J^{ *} ( 1 /S_{ \text{min} }^{ *} + 1)}} $$

(16)

where SRT^* = SRT_ave K_d. Combining (3) and (16) the SRT^* may be written as:

$$ {\text{SRT}}^{ *} = \frac{{J^{ *} \left( {\frac{1}{{S_{\text{min} }^{*} }} + 1 - \frac{{1 + \, S^{*} }}{{S^{ *} }}} \right) + \left( {\frac{{ (S_{o}^{*} - S^{ *} )}}{{\theta^{ *} }}} \right)\left( {\frac{{ 1+ \, S^{ *} }}{{S^{ *} }}} \right)}}{{\frac{{ (S_{o}^{*} - S^{ *} )}}{{\theta^{ *} }}\left( {\frac{\text{YK}}{{K_{\text{d}} }} - \frac{{ 1+ \, S^{ *} }}{{S^{ *} }}} \right) + J^{ *} \left( {\frac{{ 1+ \, S^{ *} }}{{S^{ *} }} - \frac{ 1}{{S_{\text{min} }^{*} }} - 1} \right)}} $$

(17)

After substituting J^* from (4 to 6), SRT^* is plotted as a function of S^* for a fixed value of $S_{\text{min} }^{*}$ = 0.10 with L^* = 0.0 and L^* = 1.0 and $S_{\text{min} }^{*}$ = 1.0 with L^* = 0.0 and L^* = 1.0 (Figs. 5, 6). Each chart contains different values of ($S_{\text{o}}^{*}$−S^*)/θ^* ranging from 0.01 to 1000. Also the curves are prepared for two values of YK/Kd (50 and 500). In these curves, it is better and easy to fix the values of ($S_{\text{o}}^{*}$−S^*)/θ^* instead of S^* as in the previous curves (Figs. 3, 4). The use of the figures in design is exemplified in illustrative example at the end of this paper.

Fig. 5

SRT^* as a function of S^* and ($S_{\text{o}}^{*}$−S)/HRT at Y K/K_d = 50.0, a L^* = 0.0, $S_{\text{min} }^{*}$ = 0.10, b L^* = 0.0, $S_{\text{min} }^{*}$ = 1.0, c L^* = 1.0, $S_{\text{min} }^{*}$ = 0.10 and d L^* = 1.0, $S_{\text{min} }^{*}$ = 1.0

Fig. 6

SRT^* as a function of S^* and ($S_{\text{o}}^{*}$−S)/HRT at Y K/K_d = 50.0, a L^* = 0.0, $S_{\text{min} }^{*}$ = 0.10, b L^* = 0.0, $S_{\text{min} }^{*}$ = 1.0, c L^* = 1.0, $S_{\text{min} }^{*}$ = 0.10 and d L^* = 1.0, $S_{\text{min} }^{*}$ = 1.0

Food/biomass ratio

For the hybrid system F/M can be written as:

$$ \frac{F}{M} = \frac{{Q(S_{o} - S )}}{{{\text{aVJY/}}b_{\text{t}} + {\text{VX}}}} $$

(18)

Multiplying both sides of (18) by 1/K and the right hand side (numerator and denominator) by 1/aV yields,

$$ \frac{F}{M}\frac{1}{K} = \frac{{ (S_{\text{o}} - S ) / {\text{a }}\theta }}{{{\text{J Y K/}}b_{\text{t}} + {\text{XK/a}}}} $$

(19)

Equation (19) can be converted in a dimensionless form as:

$$ F/M^{ *} = \frac{{ (S_{{_{\text{o}} }}^{*} - S^{ *} ) /\theta^{ *} }}{{ \, J^{ *} ( 1 /S_{ \text{min} }^{ *} + 1 )+ X^{ *} }} $$

(20)

where F/M^* = F/M (1/K). Substituting X^* from (3) yields,

$$ F/M^{ *} = \frac{{ (S_{\text{o}}^{ *} - S^{ *} ) /\theta^{ *} }}{{ \, J*(1/S_{ \text{min} }^{ *} + 1 )+ [ (S_{\text{o}}^{ *} - S^{ *} ) /\theta^{ *} - J^{ *} { ](1/}S^{ *} + 1 )}} $$

(21)

After substituting J^* from (4 to 6), F/M^* can be expressed as a function of (S^*, $S_{\text{o}}^{*}$, $S_{\text{min} }^{*}$, L^*, and ($S_{\text{o}}^{*}$−S^*)/θ^*. Figure 7 represents the relation between F/M^* as a function of ($S_{\text{o}}^{*}$−S^*)/θ^* for the same values of $S_{\text{min} }^{*}$ L^*, and S^* as in previous curves (5,6) except that these curves are not dependent on YK/Kd. It must be noted that in all these curves the value of S^* must be greater than or at least equals $S_{\text{min} }^{*}$. When the value of S^* equals $S_{\text{min} }^{*}$ the J^* will be zero and the role of biofilm in the reactor will vanish converting the system to a pure suspended reactor. At that time the value of X, SRT, Q_wX_u, and F/M shall not depend on the value of $S_{\text{min} }^{*}$ or L^*.

Fig. 7

F/M^* as a function of S^* and (S^*−S)/HRT at a L^* = 0.0, $S_{\text{min} }^{*}$ = 0.10, b L^* = 0.0, $S_{\text{min} }^{*}$ = 1.0, c L^* = 1.0, $S_{\text{min} }^{*}$ = 0.10 and d L^* = 1.0, $S_{\text{min} }^{*}$ = 1.0

Illustrative example

Consider a true specific domestic wastewater having the following kinetics (Heath et al. 1990; Lee 1992).

S_o = 430.0 mg/L, S = 4.0 mg/L, K_s = . 01 mg/cm³, K = 10/day, Y = 0.45, K_d = 0.09 day⁻¹,

b_t = 0.41 day⁻¹, b_s = 0.32 day⁻¹, S_min = 1.0 mg/L, L = 0.0078 cm, HRT = 0.5 day, a = 1. 8 cm⁻¹, D_w = 1.25 cm² day^−1, X_f = 25 mg/cm³, Q = 10,000 m³/day, and D_f = 0.75 cm² day⁻¹.

Converting variables to dimensionless form:

$S_{\text{o}}^{*}$ = 430/10 = 43, S^* = 4/10 = 0.4, $S_{\text{min} }^{*}$ = 1.0/10 = 0. 1, L^* = . 0078 $\sqrt { ( 1 0 ) ( { 25)/[(} . 0 1 ) (. 7 5 ) ] { }}$(.75/1.25) = . 85, θ^* = (1.8)(0.5) $\sqrt { ( 1 0 { )(25)(} . 7 5 ) / (. 0 1 ) { }}$ = 123.24,

$$ (S_{\text{o}}^{*} - S^{*} )/q^{*} \, = \, \left( {43 - 0.4} \right)/123.24 \, = \, 0.346. $$

For the above variables, X^* = 0.0 at L^* = 0.0 and X^* = 0.59 at L^* = 1.0 from Fig. 2a and c respectively giving X^* = 0.501 at L^* = . 85 by using linear interpolation.

From the definition of X^*, X = (0.501) (1.8)/ $\sqrt { ( 1 0 ) / [ (. 0 1 ) ( { 25)(} . 7 5 ) { ]}}$ = 0.124 mg/cm³ = 124.0 mg/L.

Further the value of J can deduced easily from (3) to be

J^* = 0.346−(0.501)(0.4)/(1 + 0.4) = 0.203, so J = (0.203) $\sqrt { (. 0 1 ) ( 1 0 ) ( { 25)(} . 7 5 ) { }}$ = . 278 mg cm⁻² day⁻¹.

These results for X and J conform to Lee (1992), He obtained the same results by analytical solution after five iterations. In additions, These results conform to Fouad and Renu (2005a, b, 2012).

Further the present technique can be used to get the values of SRT, Q_wX_u, and F/M easily (as given below) which are not available before. Repeating the same steps at L^* = . 85 and YK/K_d = 50.0, the values of SRT^*, (Q_wX_u)^*, and F/M^* can be deduced to be 0.189, 14.7, 0.127 from which SRT, Q_wX_u, and F/M are 2.2 day, 1664.0 kg 1.26 day⁻¹.

Conclusion

This paper presents a graphical solution for design and control of the biofilm-activated sludge reactor when it runs under steady state and rate limiting substrate condition. The solution, which is presented by a series of curves, can be used to estimate suspended biomass concentration, sludge residence time, wasted mass of sludge, and food to biomass ratio. The applicability of these curves has been proven by compared with results of other researchers. The accuracy of this technique may be about 98% because of the inaccuracy in reading from the curves and use of the linear interpolation to get the final results. Equations 3, 11, 17, and 21 can also be used to determine the solution with accuracy reach to of 100%.