Abstract
A simplified approach for analyzing the biofilm process in deriving an easy model has been presented. This simplified biofilm model formulated correlations between substrate concentration in the influent/effluent and at biofilm–liquid interface along with substrate flux and biofilm thickness. The model essentially considered the external mass transport according to Fick’s Law, steady state substrate as well as biomass balance for attached growth microorganisms. In substrate utilization, Monod growth kinetics has been followed incorporating relevant boundary conditions at the liquid–biofilm interface and at the attachment surface. The numerical solution of equations was accomplished using Runge–Kutta method and accordingly an integrated computer program was developed. The model has been successfully applied in a distinct set of trials with varying range of representative input variables. The model performance was compared with available existing methods and it was found an easy, accurate method that can be used for process design of biofilm reactor.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
A biofilm is a layer-like aggregation of bacteria and their extra cellular polymers (Rittmann and McCarty 1980; Hinson and Kocher 1996) that is attached to a solid surface and thus a common form of microbial ecosystem associated with surfaces. Biofilms are increasingly important in biological treatment of wastewater like attached growth process because of some inherent advantages such as low energy consumption, easy maintenance, better stability, excellent biomass retention and volumetric reaction rates. Immobilized biofilms are better alternatives to the traditional suspended growth bioreactor systems because biofilm process can be easily operated under continuous flow mode with minimal biomass loss. There is also no contamination at the inner depth of a biofilm under toxic environment to make it applicable for treating refractory substances. Moreover, the biofilm process exhibits improved physical and chemical stability of the biocatalyst along with low power requirement (Mudliar et al. 2008).
Various researchers have developed their steady state biofilm models in due course of their study on biological attached growth process in wastewater treatment which have certain limitations (Jiang et al. 2009; Pritchett and Dockery 2001; Perez et al. 2005; Liao et al. 2012; Qi and Morgenroth 2005; Suidan and Wang 1985; Tsuno et al. 2001; Wik et al. 2006).
Runge–Kutta finite difference technique was applied in approximate solution of second-order differential equation of mass balance of substrate in the biofilm (Williamson and McCarty 1976). The above biofilm model had a drawback that it had not considered any substrate balance in attached growth including the terms specific surface area, hydraulic retention time, etc. which are the crucial parameters in design of biofilm reactor. Moreover to maintain the steady state biofilm layer it is necessary to check whether the value of effluent substrate concentration is higher than minimum substrate concentration (S min) or not. However, no such consideration was addressed in the biofilm model by Williamson and McCarty (1976). Moreover, in that biofilm model nomographs were used to cause an approximation in calculation of output results.
In the later developments of the steady state biofilm model, the mass balance on active biomass inside the biofilm derived the total biofilm thickness (Rittmann and McCarty 1980; Huang and Jih 1997). However, the effective thickness of biofilm, which is highly relevant to a deep biofilm, could not be measured using this model. Moreover no simplified analytical solution was formulated against the second-order differential equation of mass balance of substrate within the biofilm. To overcome this lacuna, pseudo analytical/graphical analysis was done which is an approximate and rigorous process. Pseudo analytical solution with various dimensionless parameters is very complicated, time consuming and cumbersome. In the pseudo analytical method, two levels of iteration are simultaneously required to get the value of effluent substrate concentration.
Consequently, the differential equation on substrate balance was eliminated by semi-empirical algebraic expression resulting in a single substrate dimensionless biofilm model developed by Kim and Suidan (1989). The above model was solved numerically to generate a nomograph that relates dimensionless substrate concentration at biofilm–liquid interface, dimensionless substrate flux, dimensionless biofilm thickness and dimensionless minimum substrate concentration required to sustain the flux (Kim and Suidan 1989). The solution of this model was also an approximate one and only the total biofilm thickness could be determined as before.
Another biofilm model was developed using normalized loading curves with dimensionless variables (Heath et al. 1990). This model also represented an approximate solution and still the effective biofilm thickness could not be obtained. In addition, there is a chance of human error while investigating the output results from the normalized loading curves. Normalized loading curve can be used to determine the substrate flux only with a known effluent substrate concentration.
An accurate pseudo analytical solution for steady state biofilms was also proposed by Saez et al. (1991). However, it did not consider any substrate balance within the biofilm incorporating the variables like specific surface area, hydraulic retention time, etc. The effective thickness of biofilm could not also be calculated from this model.
In view of all such constraints and limitations, a biofilm model is thus developed with a computer programming in FORTRAN to easily calculate the output parameters like effluent substrate concentration, substrate flux as well as effective and total biofilm thickness. The performance of this biofilm model has been examined with a set of representative input variables and standard kinetic data.
Materials and methods
Model description
The schematic diagram of a typical biofilm reactor containing attached phase biomass is shown in Fig. 1.
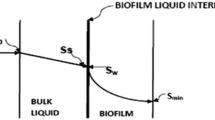
In the above system substrate flows through the biofilm–liquid interface and then through the biofilm as shown in Fig. 2.
Now, from the external mass transport according to Fick’s first law
where J substrate flux into the biofilm (mg/cm2/day),
D molecular diffusion coefficient in liquid (cm2/day),
L thickness of effective diffusion layer (cm),
S 0, S s substrate concentrations in the bulk liquid and at the biofilm–liquid interface, respectively (mg/cm3)
The steady state substrate balance for the attached growth is
where a specific surface area of supporting media (cm−1),
θ empty bed hydraulic detention time (h),
S w effluent substrate concentration (mg/cm3)
From Eqs. (1) and (2), \(J = \frac{{S_{0} - S_{\text{w}} }}{a\theta } = \left( {D/L} \right) \times \left( {S_{0} - S_{\text{s}} } \right)\)
Hence, (S 0 − S s) = \(\frac{L}{D}\) × \({\left\{ \left({S_{0} \text{ - }S_{\text{w}}) /{a\theta }} \right.\right\}} \)
Again, from the mass balance equation for substrate in the biofilm considering Monod’s’ kinetics,
where S f substrate concentration at a point in the biofilm (mg/cm3),
k maximum specific rate of substrate use (per day),
X f active biomass density within the biofilm (mg/cm3),
D f molecular diffusion coefficient of the substrate in the biofilm (cm2/day),
K half velocity coefficient (mg/cm3)
Referring Fig. 2, the boundary conditions for solving above second-order differential equation may be taken as,
-
1.
At the attachment surface (i.e. at z = 0) there will be no flux, i.e. \(\frac{{{\text{d}}S_{\text{f0}} }}{{{\text{d}}z}}\) = 0.
-
2.
At the biofilm/water interface (i.e., at z = L e) \(J = D_{\text{f }} \times \frac{{{\text{d}}S_{f} }}{{{\text{d}}z}} = D \times \frac{{(S_{0} \text{ - }S_{\text{s}} )}}{L}\)
Methodology of solution
Applying Runge–Kutta method, solution of Eq. (4) can be obtained as follows: \({\text{d}}^{2} S_{\text{f}}/{\text{d}}z^{2} = f \, \left( {z,{\text{d}}S_{\text{f}}/{\text{d}}z}\right),\) \({\text{ d}}S_{\text{f}}/{\text{d}}z\) \(\left( {z_{0} } \right) = {\text{ d}}S_{\text{f0}}/{\text{d}}z\) = K1 = 0 [S f0 = S w at z = 0]
\({\text{d}}S_{\text{f1}} /{\text{d}}z = {\text{d}}S_{\text{f0}}/{\text{d}}z\) + 0.5 × L1 × h = K2, where h = step = effective biofilm thickness (cm), h is the distance between z = 0 (at the attachment surface) and z = L e (at the biofilm/water interface)
\({\text{d}}S_{\text{f2}} /{\text{d}}z = {\text{d}}S_{\text{f0}}/{\text{d}}z\) + 0.5 × L2 × h = K3
\({\text{L3 }} = h \times f \, (z0 + {h}/{2},{{{\text{d}}S_{f2} }}/{{{\text{d}}z}}) = h \times{{{\text{d}}^{2}S_{\text{f2}} }}/{{{\text{d}}z^{2} }} = {{[kX_{\text{f}} (S_{\text{f0}} + 0.5{\text{K2}} \times h)] \, }}/{{[D_{\text{f}} \, (K + S_{\text{f0}} + 0.5{\text{K2}} \times h)]}}\) \({\text{d}}S_{\text{f3}} /{\text{d}}z = {\text{d}}S_{\text{f0}}/{\text{d}}z\) + L3 × h = K4
\(L4 = h \times f \, (z0 + h,\frac{{{\text{ d}}S_{\text{f3}} }}{{{\text{d}}z}}) = h \times \frac{{{\text{ d}}^{2} S_{\text{f3}} }}{{{\text{d}}z^{2} }} = \frac{{[kX_{\text{f}} (S_{\text{f0}} + {\text{K3}} \times h)] \, }}{{[D_{\text{f}} \, (K + S_{\text{f0}} + {\text{K3}} \times h)]}}\)
where ΔY (1) stands for increment of substrate concentration, ΔY (2) stands for \(\frac{{{\text{d}}S_{\text{f}} }}{{{\text{d}}z}}\)
The substrate concentration and the respective flux at the liquid–biofilm interface can be denoted as S s and J, respectively. Therefore,
The Eq. (4) can also be solved without considering the effective biofilm thickness to find out ‘J’ as follows:
However, a minimum bulk substrate concentration is always required to support the attached phase biomass, which can be calculated as, S min = K × \({b_{t}/\left(Y \times k{ - }b_{t}\right)}\), where b t = an overall biofilm specific loss rate (day−1), Y = bacteria yield coefficient, S min = minimum bulk concentration of rate-limiting substrate able to support a steady state biofilm (mg/cm3) Now, from the steady state mass balance of active micro- organisms in a biofilm,
The above model equation is useful to determine the total biofilm thickness in a biofilm reactor system where purely attached growth is considered. In order to calculate S s, S w and J using Eqs. (3), (4) and (9), two detailed FORTRAN programs have been developed on the basis of flowsheets for which the corresponding author may kindly be referred
Essence of flowcharts constructed
Two flowcharts for computer programming in FORTRAN have been prepared approaching the iteration processes, with a view to calculate unknown effluent substrate concentration S w (Fig. 3) and S s, J and L e (Fig. 4). In the first flowchart, equations 3, 4 and 9 as stated earlier are simultaneously iterated to calculate the unknown effluent substrate concentration S w. The initial iteration value S w was assumed in this Flowchart as S min, which is required to sustain a steady biofilm growth. The second flowchart utilized the value of S w as obtained from the Flowchart 1 to calculate S s, J and L e following the concept of Runge–Kutta method of analysis. The convergence of iteration was attributed at the liquid/biofilm interface when computed substrate concentration (S s) and substrate flux J become equal to those calculated earlier.
Modality of application of the developed model
The developed model can be applied to find out the effluent substrate concentration (S w), the substrate concentration at liquid–biofilm interface (S s) and the substrate flux (J) by running the FORTRAN program based on the Flowchart as shown in Fig. 3. However, those output parameters can also be determined analytically by a 7-step trial procedure as demonstrated in Table 1. Firstly, a trial value of S w needs to be assumed taking into account the minimum substrate concentration (S min), required to maintain a steady biofilm layer. Thereafter, the substrate concentration at the liquid–biofilm interface (S s) can be calculated. Thus, the value of S w is explicitly obtained using three sequential expressions and is compared with the assumed value. The process of iteration gets completed when the assumed and calculated values of S w become almost equal. Under such condition, the substrate flux (J) can be calculated using Step 7. Therefore, this analytical tool represents a simplified method of determining the effluent substrate concentration and the substrate flux in a Biofilm process, even without using a computer program. Once the values of S w, S s and J are estimated, the FORTRAN program based on the Flowchart as shown in Fig. 4 can be run for determining both the total and effective biofilm thickness L f and L e.
Illustrative example of model solution using 7-steps procedure
The solution of a problem on typical Biofilm process by the developed model has been illustrated as follows.
A biofilm system is operated with undermentioned process condition
S 0 (initial substrate concentration mg/cc) = 0.43
k (maximum specific rate of substrate utilization, per day) = 10
θ (HRT, h) = 1
Y (bacteria yield coefficient) = 0.45
a (specific surface area, per cm) = 0.9
K (half velocity constant, mg/cc) = 0.01
b t (total biomass loss rate, per day) = 0.41
D (molecular diffusivity in liquid, cm2/day) = 1.25
D f (molecular diffusivity in biofilm, cm2/day) = 0.75
L (thickness of liquid layer, cm) = 0.078
X f (biomass concentration in biofilm, mg/cc) = 25
The effluent substrate concentration (S w) and the substrate flux (J) for the above biofilm process has been predicted using 7-Steps procedure as shown in Table 2.
Results of analysis
In the present biofilm model, the analytical solution has been presented in two different ways, i.e., Case 1 and Case 2 as stipulated below. At the same time, pseudo analytical solution by Rittmann and McCarty (2001) and normalized loading curves by Heath et al. (1990) are considered as Case 3 and Case 4, respectively. The relevant output parameters like S s, J, L e and L f have been computed under 6(six) distinct input conditions in all the four cases, wherever those are suitable for determination. A Comparison chart of the output results as stated above with similar kinetic coefficients [as adopted by Rittmann and McCarty (2001) is shown in Table 3].
The kinetic coefficients and physical data in this regard are as follows.
k = 8 day−1, Y = 0.5, K = 0.01 mg/cm3, b t = 0.1 day−1, D = 0.8 cm2/day, D f = 0.64 cm2/day, L = 0.01 cm.
Case 1
Iteration performed by equating 3 Nos of J values i.e. J1 = J2 = J3, where,
\({\text{J1}} = D/L \, \left( {S_{0} - S_{\text{s}} } \right), \, J2 = \left( {S_{0} - S_{\text{w}} } \right)/\left( {a \, \partial } \right),{\text{ J3 }} = \sqrt {2kX_{\text{f}} D_{\text{f}} (S_{\text{s}} - S_{\text{w}} + K\ln ({\raise0.5ex\hbox{$\scriptstyle {K + S_{\text{w}} }$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle {K + Ss}$}}))}\)
Case 2
\({\text{J1}} = \frac{D}{L}\) ×(S 0 − S s), J2 = (S 0 − S w)/(a Ə), J3 has been solved by Runge–Kutta Method by solving \(\frac{{{\text{d}}^{2} S_{\text{f}} }}{{{\text{d}}z^{2} }}\) = \(\frac{{kX_{\text{f}} S_{\text{f}} \, }}{{D_{\text{f}} \, (K + S_{\text{f}} )}}\) with iteration of biofilm thickness.
Case 3
As per formula applied in Pseudo = analytical solution as accomplished in Rittmann and McCarty (2001).
Case 4
By using normalized loading curve as per Heath et al. (1990).
Discussion on results
As stated above the comparison has been made with a well-known pseudo analytical solution by Rittmann and McCarty (2001) and normalized loading curves by Heath et al. (1990). It is evident from Table 3 that the substrate concentration at biofilm–liquid interface (S s), found in case 3, i.e., in pseudo analytical solution by Rittmann and McCarty (2001) exactly tallies with that obtained in the proposed biofilm model. However, S s can not be determined in case 4, i.e., in normalized loading curves by Heath et al. (1990). It is also to note that the process of evaluating S s by Rittmann and McCarty (2001) is cumbersome involving a series of tedious calculations. It establishes the simplicity of the proposed biofilm model for determining S s, which is a crucial parameter to calculate the substrate flux (J).
Similarly, the substrate flux (J) found in case 1 and case 2 (i.e., in the proposed model) is in a good agreement with that in pseudo analytical solution by Rittmann and McCarty (2001). However, a nominal deviation in the value of J has been observed with respect to case 4, i.e., in normalized loading curves by Heath et al. (1990). This may be attributed to the approximation in studying the values by interpolation from the normalized loading curves, which causes observation error.
It is interesting to note that no existing method (like case 3 or case 4) could determine the L e (effective biofilm thickness) value. It has been possible to evaluate the same by the proposed biofilm model (case 1 or case 2) only. Therefore, it would be useful to get an idea about the nature of biofilm (i.e., shallow or deep), provided the total biofilm thickness is already calculated.
The value of L f, i.e., total biofilm thickness in case 3, i.e., in pseudo analytical solution by Rittmann and McCarty (2001) is almost equal to that in the proposed biofilm model. However, there is a slight deviation in the value of L f, obtained from the proposed model with respect to case 4, i.e., in normalized loading curves by Heath et al. (1990). This deviation is reasonably attributed to the nominal difference in ‘J’ values under those two respective cases.
Conclusion
The comparison of results using various biofilm models reveals that all relevant outputs like S s, J, L e and L f can be determined only in the proposed model (case 1 and case 2 combined). The effective biofilm thickness L e could neither be found out in case 3, i.e., in pseudo analytical solution by Rittmann and McCarty (2001) nor in case 4, i.e., in normalized loading curves by Heath et al. (1990). So there is no scope for ascertaining whether the biofilm is deep or shallow in those two existing methods. It can be further concluded that the substrate concentration at biofilm–liquid interface (S s) could not be evaluated in case 4. The main drawback of this existing model is availability of no kinetic relationship between the substrate flux (J) and the substrate concentration S s at biofilm–liquid interface. The existing Biofilm model proposed by Rittmann and McCarty (2001), i.e., case 3 is complicated, cumbersome and time consuming because of two levels iterations simultaneously using various dimensionless parameters.
The accuracy of the proposed model analysis lies with the fact that all the output results are exactly matching with those obtained from classical models especially by Rittmann and McCarty. The proposed model provides simple tools to estimate the effluent substrate concentration, substrate concentration at liquid–biofilm interface, substrate flux and effective biofilm thickness. Since, the proposed biofilm model does not consider any nomographs, normalized loading curves, etc., there is no chance of any manual error. Moreover complicated analysis like pseudo analytical solution with two levels iteration simultaneously was also totally avoided in this proposed biofilm model making an easy solution thereby. The simplicity of the proposed biofilm model lies in the fact that it can determine all relevant output parameters required for the process design of the biofilm reactor without going for complicated two-level iterations simultaneously and also without involving any graphical outputs.
References
Heath MS, Wirtel SA, Rittman BE (1990) Simplified design of biofilm processes using normalized loading curves. Water Pollut Control Fed 62:185–191
Hinson RK, Kocher WM (1996) Model for effective diffusivities in aerobic biofilms. ASCE J Environ Eng vol. 122. No. 11. ASCE, pp 1023–1030
Huang JS, Jih CG (1997) Deep biofilm kinetics of substrate utilization in anaerobic filters. Water Res 31(9):2309–2317
Jiang F, Leung DH, Li S, Chen G-H, Okabe S, van Loosdrechte MCM (2009) A biofilm model for prediction of pollutant transformation in sewers. Water Res 43:3187–3198
Kim BR, Suidan MT (1989) Approximate algebraic solution for a biofilm model with the monod kinetic expression. Wat Res 23(12):1491–1498
Liao Q, Wang Y-J, Wang Y-Z, Chen R, X Zhu, Pu Y-K, Lee D-J (2012) Two-dimension mathematical modeling of photosynthetic bacterial biofilm growth and formation. Int J Hydrogen Energy 37:15607–15615
Mudliar S, Banerjee S, Vaidya A, Devotta S (2008) Steady state model for evaluation of external and internal mass transfer effects in an immobilized biofilm. Bioresour Technol 99:3468–3474
Perez J, Picioreanu C, van Loosdrecht M (2005) Modeling biofilm and flock diffusion processes based on analytical solution of reaction-diffusion equations. Water Res 39:1311–1323
Pritchett LA, Dockery JD (2001) Steady state solutions of a one dimensional biofilm model. Math Comput Model 33(2001):255–263
Qi S, Morgenroth E (2005) Modeling steady-state biofilms with dual-substrate limitations. J Environ Eng ASCE, vol 131, No. 2, pp 320–326
Rittmann BE, McCarty PL (1980) Model of steady state biofilm kinetics. Biotechnol Bioeng XXII:2343–2357
Rittmann BE, McCarty PL (2001) Environmental biotechnology: principles and applications, McGraw-Hill, New York
Saez PB, Rittman BE (1991) Accurate pseudoanalytical solution for steady state biofilms. Biotechnol Bioeng 39:790–793
Suidan MT, Wang Y-T (1985) Unified analysis of biofilm kinetics. J Environ Eng 111(5):634–646
Tsuno H, Hidakaa T, Nishimura F (2001) A simple biofilm model of bacterial competition for attached surface. Water Res 36:996–1006
Wik T, Goransson E, Breitholtz C (2006) Low model order approximations of continuously stirred biofilm reactors with Monod kinetics. Biochem Eng J 30:16–25
Williamson K, McCarty PL (1976) A model of substrate utilization by bacterial films. Water Pollut Control Fed 48(1):9–23
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Sarkar, S., Mazumder, D. Development of a simplified biofilm model. Appl Water Sci 7, 1799–1806 (2017). https://doi.org/10.1007/s13201-015-0353-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13201-015-0353-4