Introduction

Managing sustainability of limited water resources is a challenging task in the face of ever-increasing demand for water and the geotechnical problems associated with overuse of available water. Proper resource management techniques based on precise information of groundwater response to recharge and withdrawal activities can help in improving sustainability and efficiency of an aquifer. In this context, mathematical and numerical models have emerged as effective tools to determine what is currently happening in an aquifer and what will happen as a result of variation in hydrologic and hydraulic parameters.

In areas where overdevelopment has depleted groundwater resources, artificial recharge is often used for augmentation of subsurface water reservoir and to enhance the sustainable yield of the region. Analytic models are extensively used for assessing the temporal development of groundwater system in response to controlled activities such as localized replenishment and pumping from wells. Evolution and stabilization of the free surface in unconfined semi-infinite aquifers subjected to rectangular recharge at uniform rate was first analyzed by Glover (1960) and Hantush (1967). Since then, numerous mathematical models have been developed to predict the dynamic behavior of groundwater in response to the constant or periodically applied recharge in an unconfined aquifer (Hunt 1971; Marino 1974; Rao and Sarma 1981; Manglik et al. 1997; Rai and Manglik 1999). Numerical model developed by Zomorodi (1991) highlighted the effects of unsaturated zone on the recharge rate and the effect of in-transit water in reducing the fillable pore space. The calculation presented in his study demonstrated that estimation of the recharge rate by a constant value can severely misjudge the actual results. Rastogi and Pandey (1998) simulated numerically the phreatic head distribution in response to constant recharge from recharge basins of different geometry but of equal areas. They showed that the mound height underneath a basin decreased when the perimeter of the recharge basin increased. Manglik et al. (1997) proposed a new method for simulating the discontinuous cycles of recharge operation by a sequence of line segments of varying lengths and slopes. Rai et al. (2006) and Rai and Manglik (2012) applied this scheme to predict the water head distribution in unconfined aquifers for multi-recharge and pumping operations. Although, these studies provide useful insight into the groundwater flow system; the upland watershed hydrology concerning subsurface drainage over hillslope cannot be satisfactorily explained with these results.

The movement of groundwater depends considerably on the stratigraphical and structural units of the region. In hillslope terrains, the flow of groundwater inherits certain unique features that are seldom seen in horizontal strata. Most importantly, aquifers in hillslope regions are underlain by sloping impervious beds. In such cases, approximation of groundwater flow based on the assumption that the streamlines are nearly parallel to the sloping bed (Dupuit–Forchheimer assumption) yields more accurate results. Childs (1971) formulated the unsteady groundwater flow in skewed coordinate system (along and perpendicular to the sloping base) by a nonlinear Boussinesq equation. Chapman (1980) converted this approximation in rectangular coordinate system. Analytic solutions of linearized Boussinesq equation under varying hydrologic conditions are presented by a number of investigators (Brutsaert 1994; Verhoest and Troach 2000; Upadhyaya and Chauhan 2001; Bansal and Das 2009, 2011; Bansal 2012). Using finite Fourier transform, effects of localized recharge from single basin on the evolution of groundwater mound in downward sloping aquifers of rectangular shape were analyzed by Ram and Chauhan (1987), Singh et al. (1991) and Ramana et al. (1995). By considering varying hydraulic conductivities along x- and y-axes, Chang and Yeh (2007) analyzed two-dimensional transient groundwater flow in a sloping aquifer due to time-varying recharge from single recharge basin and extraction from multi-wells. Closed form analytic expressions for spatio-temporal variations in water head over semi-infinite sloping bed due to localized recharge is presented by Bansal and Das (2010) and Bansal (2013). The aforementioned studies highlight the importance of bed slope in the determination of transient profiles of phreatic surface; however, the results are either exceedingly complicated or suffer from slow convergence.

The aim of the current study is to develop new analytic model for prediction of groundwater mound in a sloping ditch–drain aquifer system due to multiple localized recharge. The study uses a simple approach to develop analytical expressions for water head distribution in the aquifer due to uniform percolation from a single recharge basin. The solution is then extended to multiple basins of varying recharge rate which are arbitrarily located in the model domain. Unlike previous works based on Laplace transform technique, the current study treats the entire aquifer as a single zone system. Closed form analytic expressions for water head distribution in the aquifer and discharge rate into the ditches are obtained by solving the linearized Boussinesq equation with eigenvalue–eigenfunction method. Some special cases such as no slope and uniform localized recharge are derived as limiting cases of the analytic results. Combined effects of bed slope, spatial coordinate of recharge basin, and the recharge rate parameter on the transient profiles of groundwater mound are illustrated with the help of a numerical example.

Development of model for single recharge basin

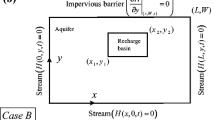
The hydrologic setting of the problem considered in this study consists of an unconfined aquifer of lateral extent L overlaying an impermeable bed with an upward slope tan β. As shown in Fig. 1, the aquifer is hydrologically connected with two ditches of constant water level h 0 and receives localized recharge from a recharge basin PQ extending from x = x 1 to x = x 1′. With Dupuit–Forchheimer assumptions that the streamline are nearly parallel to the sloping impervious bed, the discharge rate per unit width of the aquifer along x-axis can be approximated by the following relation (Chapman 1980):

$$q = - K\,h\,\cos^{2} \beta \quad\frac{\partial \hbar }{\partial x}$$
(1)

where ħ (x, t) is the variable water head height measured in the vertical direction from a horizontal datum, and h (x, t) is the water head height measured in the vertical direction from the impermeable sloping bed. K is the hydraulic conductivity, and tan β is the bed slope. Applying the principle of mass balance across a vertical slice, the equation of subsurface seepage flow over sloping bed is given by

$$\frac{\partial q}{\partial x} + S\frac{\partial \hbar }{\partial t} = R\left( {x, t} \right)$$
(2)

where S is the specific yield of the aquifer, and R(x, t) are the spatial and temporal varying net rates of the vertical accretion to the free surface. If the spatial variations in K and S are neglected, then Eqs. (1) and (2) imply that

Fig. 1
figure 1

Definition sketch of upward-sloping ditch-drained aquifer receiving localized recharge

Full size image
$$K\cos^{2} \beta \,\frac{\partial }{\partial x}\left( {h\frac{\partial \hbar }{\partial x}} \right) + R\left( {x, t} \right) = S\frac{\partial \hbar }{\partial t}$$
(3)

Since ħ = h + x tan β, Eqs. (1) and (3) can be respectively, written as

$$q = - K \, h\left\{ {\frac{\partial h}{\partial x} + \tan \beta } \right\}\cos^{2} \beta$$
(4)

and

$$K\left\{ {\frac{\partial }{\partial x}\left( {h\frac{\partial h}{\partial x}} \right) + \tan \beta \left( {\frac{\partial h}{\partial x}} \right)} \right\}\cos^{2} \beta + R\left( {x, t} \right) = S\frac{\partial h}{\partial t}$$
(5)

The rate of replenishment R(x, t) of groundwater resources often varies with time due to initial swelling and dispersion of soil particles and further due to release of entrapped air in soil pores. A cycle of recharge typically consists of a rising limb, a peak point, and a recession limb. The recession limb of recharge hydrograph can be approximated by an exponentially decaying function of time. It is assumed here that the recharge rate decreases from an initial value N i to final value N f by the following exponential law:

$$R\left( {x,\,t} \right) = \left\{ \begin{array}{ll} N_{\text{f}} + \,\left( {N_{\text{i}} - N_{\text{f}} } \right)\,{\text{e}}^{ - \lambda t} &\quad x_{1} \le x \le x^{\prime}_{1} \\ 0&\quad{\text{otherwise}} \\ \end{array} \right.$$
(6)

where λ is a positive constant. The groundwater flow equation is based on the assumption that the streamlines are nearly parallel to the sloping impermeable bed. Thus, the initial profile of free surface in the aquifer can be considered parallel to the sloping bed, and its height from the sloping bed, measured in vertical direction, is the same as the initial elevation of water level in the drains. We prescribe the initial and boundary conditions as follows:

$$h\left( {x, \, t = 0} \right) = h_{0}$$
(7)
$$h\left( {x = 0, \, t} \right) = h\left( {x = L, \, t} \right) = h_{0}$$
(8)

Equation (5) is a second-order parabolic partial differential equation, analytic solution of which is not tractable. However, approximate analytic solutions can be obtained by taming the nonlinearity around some mean saturated depth D. Rewrite equation (5) as

$$\frac{{\partial^{2} h}}{{\partial x^{2} }} + \frac{\tan \beta }{D}\frac{\partial h}{\partial x} + \frac{R}{{K\,D \cos^{2} \beta }} = \frac{S}{{K\,D \cos^{2} \beta }}\frac{\partial h}{\partial t},\quad 0 \le x \le L$$
(9)

In fact, this technique invokes linearization of the flow rate q around D, given by

$$q\left( {x, t} \right) = - K\,\left( {D\frac{\partial h}{\partial x} + h\tan \beta } \right)\cos^{2} \beta$$
(10)

The average saturated depth D of the aquifer is successively approximated using an iterative formula D = (h 0 + h t )/2, where h 0 is the initial water table height, and h t is the varying water table height at time t at the end of which D is approximated (Marino 1974). Now use the following dimensionless variables and substitutions:

$$H = \frac{{h\left( {x, \, t} \right) - h_{0} }}{L};\quad X = \frac{x}{L};\quad \tau = \frac{{K\,D \cos^{2} \beta }}{{S\,L^{2} }}t;\quad\,\alpha = \frac{L\tan \beta }{2\,D}$$
(11a-d)

that translates Eq. (9) into the following form:

$$\frac{{\partial^{2} H}}{{\partial X^{2} }} + 2\alpha \frac{\partial H}{\partial X} + R^{\prime}\left( {X, \tau } \right) = \frac{\partial H}{\partial \tau },\quad 0 \le X \le 1$$
(12)

where

$$R^{\prime}\left( {X, \tau } \right) = \left\{ \begin{array}{ll} N^{\prime}_{\text{f}} + \left( {N_{\text{i}}^{\prime } - N^{\prime}_{\text{f}} } \right)\,{\text{e}}^{{ - \lambda^{\prime}\,\tau }}&\quad X_{1} \le X \le X^{\prime}_{1} \hfill \\ 0&\quad{\text{otherwise}} \hfill \\ \end{array} \right.$$
(13)
$$N_{\text{i}}^{\prime } = \frac{{N_{i} \,L}}{{K\,D\,\cos^{2} \beta }},\quad N^{\prime}_{\text{f}} = \frac{{N_{f} \,L}}{{K\,D\,\cos^{2} \beta }},\quad \lambda^{\prime} = \frac{{S\,L^{2} }}{{K\,D\quad\cos^{2} \beta }}\lambda ;\quad X_{1} = \frac{{x_{1} }}{L},\quad X^{\prime}_{i} = \frac{{x^{\prime}_{1} }}{L}$$
(14a-e)

and the initial and boundary conditions reduce to

$$H(X, \, \tau = 0) = 0$$
(15a)
$$H(X = 0, \, \tau ) = 0$$
(15b)
$$H(X = 1, \, \tau ) = 0$$
(15c)

Equation (12) along with conditions (15a)–(15c) can be solved analytically by several techniques (Laplace transform, Fourier transform, etc.). In the current study, the advection term of Eq. (12) is eliminated using the substitution:

$$H(X, \, \tau ) = G\left( {X,\tau } \right){\text{e}}^{\, - \alpha X} \,{\text{e}}^{{ - \alpha^{2} \,\tau }}$$
(16)

The transformed equation reads

$$\frac{{\partial^{2} G}}{{\partial X^{2} }} + R^{\prime}\left( {X, \tau } \right){\text{e}}^{\,\alpha X} \,{\text{e}}^{{\alpha^{2} \,\tau }} = \frac{\partial G}{\partial \tau }$$
(17)

Furthermore, conditions (15a)–(15c) in terms of G(X, τ) become

$$G(X, \, \tau = 0) = 0$$
(18a)
$$G(X = 0, \, \tau ) = 0$$
(18b)
$$G(X = 1, \, \tau ) = 0$$
(18c)

Now, the eigenvalue–eigenfunction method is used for solving Eq. (17) along with conditions (18a)–(18c). First, the homogeneous part of Eq. (17) is solved. That is,

$$\frac{{\partial^{2} G}}{{\partial X^{2} }} = \frac{\partial G}{\partial \tau }$$
(19)

Let the solution of Eq. (19) be

$$G(X, \, \tau ) = A\left( X \right)B\left( \tau \right)$$
(20)

which yields two ordinary differential equations:

$$\frac{{{\text{d}}^{2} A}}{{{\text{d}}X^{2} }} + \omega^{2} A = 0$$
(21)

and

$$\frac{{{\text{d}}B}}{{{\text{d}}\tau }} + \omega^{2} B = 0$$
(22)

Conditions (18a)–(18c), in terms of variables A(X) and B(τ) read

$$B\left( {\tau = 0} \right) = 0,\quad A(X = 0) = 0\quad and \quad A\left( {X = 1} \right) = 1$$
(23a-c)

Equation (21) can be solved by ordinary methods, yielding solution\(A = C\sin \omega X + C^{\prime}\cos \omega X\). Using conditions (23b) and (23c), we obtain C′ = 0, and the eigenvalues ω n  = nπ where n = 1, 2,… Moreover, the orthogonal property of eigenfunction A n implies that the solution is of the form:

$$A_{n} = \sqrt 2 \sin \left( {n\,\pi \,X} \right)$$
(24)

Thus, the solution of Eq. (17) can be written as

$$G(X, \, \tau ) = \sum\limits_{n = 0}^{\infty } {\sqrt 2 \sin \left( {n\pi X} \right)B_{n} \left( \tau \right)}$$
(25)

Equation (25) is now used in Eq. (17). The resulting equation is multiplied by sin (nπ X) and integrated with respect to variable X from X = X1 to X2. We obtain

$$\begin{aligned} \frac{{{\text{d}}B_{n} }}{{{\text{d}}\tau }} + n^{2} \pi^{2} B_{n} = \frac{{\sqrt 2 \,{\text{e}}^{{\alpha^{2} \tau }} }}{{\alpha^{2} + n^{2} \pi^{2} }}\left[ {{\text{e}}^{{\alpha \,X_{1} }} \left\{ {n\pi \cos \left( {n\pi X_{1} } \right) - \alpha \sin \left( {n\pi \,X_{1} } \right)} \right\}} \right. \hfill \\ \quad\quad \left. { - \,{\text{e}}^{{\alpha \,X_{2} }} \left\{ {n\pi \cos \left( {n\pi X_{2} } \right) - \alpha \sin \left( {n\pi \,X_{2} } \right)} \right\}} \right]\,\left\{ {N_{1}^{\prime } + \left( {N_{0}^{\prime } - N_{1}^{\prime } } \right){\text{e}}^{{ - \lambda^{\prime}\,\tau }} } \right\} \hfill \\ \end{aligned}$$
(26)

Equation (26) can also be solved by ordinary methods. Its general solution subject to condition (23a) is

$$B_{n} \left( \tau \right) = \frac{\sqrt 2 \,}{{\alpha^{2} + n^{2} \pi^{2} }}\left\{ {\frac{{N_{1}^{\prime } \left( {{\text{e}}^{{\alpha^{2} \tau }} - {\text{e}}^{{ - n^{2} \pi^{2} \tau }} } \right)}}{{\alpha^{2} + n^{2} \pi^{2} }} + \frac{{\left( {N_{0}^{\prime } - N_{1}^{\prime } } \right)\left( {{\text{e}}^{{(\alpha^{2} - \lambda^{\prime})\tau }} - {\text{e}}^{{ - n^{2} \pi^{2} \tau }} } \right)}}{{\alpha^{2} + n^{2} \pi^{2} - \lambda^{\prime}}}} \right\}\varOmega_{n}$$
(27)

where

$$\varOmega_{n} = {\text{e}}^{{\alpha \,X_{1} }} \left\{ {n\pi \cos \left( {n\pi X_{1} } \right) - \alpha \sin \left( {n\pi \,X_{1} } \right)} \right\} - {\text{e}}^{{\alpha \,X_{2} }} \left\{ {n\pi \cos \left( {n\pi X_{2} } \right) - \alpha \sin \left( {n\pi \,X_{2} } \right)} \right\}$$
(28)

which provides the solution of Eq. (17) as

$$G\left( {X,\tau } \right) = 2\sum\limits_{n = 0}^{\infty } {\frac{{\sin \left( {n\pi X} \right)\quad\varOmega_{n} }}{{\alpha^{2} + n^{2} \pi^{2} }}\left\{ {\frac{{N_{1}^{\prime } \left( {{\text{e}}^{{\alpha^{2} \tau }} - {\text{e}}^{{ - n^{2} \pi^{2} \tau }} } \right)}}{{\alpha^{2} + n^{2} \pi^{2} }} + \frac{{\left( {N_{0}^{\prime } - N_{1}^{\prime } } \right)\left( {{\text{e}}^{{(\alpha^{2} - \lambda^{\prime})\tau }} - {\text{e}}^{{ - n^{2} \pi^{2} \tau }} } \right)}}{{\alpha^{2} + n^{2} \pi^{2} - \lambda^{\prime}}}} \right\}}$$
(29)

Finally, using Eq. (29) in (16), the solution of the governing flow Eq. (12) can be expressed as follows:

$$\begin{aligned} H\left( {X,\tau } \right) = 2\,{\text{e}}^{ - \alpha X} \sum\limits_{n = 0}^{\infty } {\frac{{\sin \left( {n\pi X} \right)\varOmega_{n} }}{{\alpha^{2} + n^{2} \pi^{2} }}} \hfill \\ \left. {\quad\quad \left\{ {\frac{{N_{1}^{\prime } \left( {1 - {\text{e}}^{{ - (\alpha^{2} + n^{2} \pi^{2} )\tau }} } \right)}}{{\alpha^{2} + n^{2} \pi^{2} }}} \right. + \frac{{\left( {N_{0}^{\prime } - N_{1}^{\prime } } \right)\left( {{\text{e}}^{{ - \lambda_{1} \tau }} - {\text{e}}^{{ - (\alpha^{2} + n^{2} \pi^{2} )\tau }} } \right)}}{{\alpha^{2} + n^{2} \pi^{2} - \lambda_{1} }}} \right\} \hfill \\ \end{aligned}$$
(30)

Equation (30) provides closed form analytic expressions for spatio-temporal distribution of water head in the aquifer. For downward sloping aquifers, the results can be modified by replacing α by −α. For horizontal aquifer (α = 0), the expression reduces to

$$\begin{aligned} H\left( {X,\tau } \right) = 2\,\sum\limits_{n = 0}^{\infty } {\frac{{\sin \left( {n\pi X} \right)}}{n\,\pi }\left\{ {\cos \left( {n\pi X_{1} } \right) - \cos \left( {n\pi X_{2} } \right)} \right\}} \times \hfill \\ \quad \left\{ {\frac{{N_{1}^{\prime } \left( {1 - e^{{ - n^{2} \pi^{2} \tau }} } \right)}}{{n^{2} \pi^{2} }}} \right.\left. { + \frac{{\left( {N_{0}^{\prime } - N_{1}^{\prime } } \right)\left( {e^{{ - \lambda^{\prime}\,\tau }} - e^{{ - n^{2} \pi^{2} \tau }} } \right)}}{{n^{2} \pi^{2} - \lambda^{\prime}}}} \right\} \hfill \\ \end{aligned}$$
(31)

Extension of the model for multirecharge basins

Now suppose that the model domain 0 ≤ x ≤ L contains m recharge basins of varying lengths and recharge rates. The kth basin (k = 1, 2,…, m) extends from x = x k to x = x k ′ and has a transient recharge rate which varies from an initial value N ki to the final value N kf by an exponentially decaying function of time with controlling rate parameter λ k . The normalized subsurface seepage flow equation can be expressed in the form:

$$\frac{{\partial^{2} H}}{{\partial X^{2} }} + 2\alpha \frac{\partial H}{\partial X} + R^{\prime}_{m} \left( {X, \tau } \right) = \frac{\partial H}{\partial \tau },\quad\quad 0 \le X \le 1$$
(32)

where the source term R m ′ (X, τ) simulates the combined effects of m recharge basins, given by

$$R^{\prime}_{m} \left( {X, \tau } \right) = \left\{ \begin{array}{ll} N^{\prime}_{{1{\text{f}}}} + \left( {N^{\prime}_{{1{\text{i}}}} - N^{\prime}_{{1{\text{f}}}} } \right)\,{\text{e}}^{{ - \lambda^{\prime}_{1} \,\tau }} &\quad X_{1} \le X \le X^{\prime}_{1} \hfill \\ N^{\prime}_{{2{\text{f}}}} + \left( {N^{\prime}_{{2{\text{i}}}} - N^{\prime}_{{2{\text{f}}}} } \right)\,{\text{e}}^{{ - \lambda^{\prime}_{2} \,\tau }}& \quad X_{2} \le X \le X^{\prime}_{2} \hfill \\ &\quad \vdots \hfill \\ N^{\prime}_{{m{\text{f}}}} + \left( {N^{\prime}_{{m{\text{i}}}} - N^{\prime}_{{m{\text{f}}}} } \right)\,{\text{e}}^{{ - \lambda^{\prime}_{m} \,\tau }} &\quad X_{m} \le X \le X^{\prime}_{m} \hfill \\ 0&\quad {\text{otherwise}} \hfill \\ \end{array} \right.$$
(33)

where

$$\begin{aligned} N^{\prime}_{{k\,{\text{i}}}} = \frac{{N_{{k{\text{i}}}} \,L}}{{K\,D\,\cos^{2} \beta }};\quad N^{\prime}_{{k{\text{f}}}} = \frac{{N_{{k{\text{f}}}} \,L}}{{K\,D\,\cos^{2} \beta }}\,;\quad\lambda^{\prime}_{k} = \frac{{S\,L^{2} }}{{K\,D\quad\cos^{2} \beta }}\lambda_{k} ; \hfill \\ X_{k} = \frac{{x_{k} }}{L};\quad X^{\prime}_{k} = \frac{{x^{\prime}_{k} }}{L}\quad k = 1,\,2,\, \ldots ,\,m \hfill \\ \end{aligned}$$
(34a-e)

Following the procedure described in preceding section, the solution of seepage flow is obtained as

$$\begin{aligned} H\left( {X,\tau } \right) = 2\,{\text{e}}^{ - \alpha X} \sum\limits_{n = 0}^{\infty } {\sum\limits_{k = 1}^{m} {\frac{{\sin \left( {n\pi X} \right)\varOmega_{n,k} }}{{\alpha^{2} + n^{2} \pi^{2} }}} } \left\{ {\frac{{N^{\prime}_{{k\,{\text{f}}}} }}{{\alpha^{2} + n^{2} \pi^{2} }}\left( {1 - {\text{e}}^{{ - (\alpha^{2} + n^{2} \pi^{2} )\tau }} } \right)} \right. \hfill \\ \left. {\quad\quad\quad\quad\quad + \frac{{N^{\prime}_{{k\,{\text{i}}}} - N^{\prime}_{{k\,{\text{f}}}} }}{{\alpha^{2} + n^{2} \pi^{2} - \lambda^{\prime}_{k} }}\left( {{\text{e}}^{{ - \lambda^{\prime}_{k} \,\tau }} - {\text{e}}^{{ - (\alpha^{2} + n^{2} \pi^{2} )\tau }} } \right)} \right\} \hfill \\ \end{aligned}$$
(35)

where

$$\varOmega_{n,\,k} = {\text{e}}^{{\alpha \,X_{k} }} \left\{ {n\pi \cos \left( {n\pi X_{k} } \right) - \alpha \sin \left( {n\pi \,X_{k} } \right)} \right\} - {\text{e}}^{{\alpha \,X^{\prime}_{k} }} \left\{ {n\pi \cos \left( {n\pi X^{\prime}_{k} } \right) - \alpha \sin \left( {n\pi \,X^{\prime}_{k} } \right)} \right\}$$
(36)

For horizontal aquifers, the corresponding results become

$$\begin{aligned} H\left( {X,\tau } \right) = 2\,\sum\limits_{n = 0}^{\infty } {\sum\limits_{k = 1}^{m} {\frac{{\sin \left( {n\pi X} \right)}}{n\,\pi }\left\{ {\cos \left( {n\pi X_{k} } \right) - \cos \left( {n\pi X^{\prime}_{k} } \right)} \right\}} } \hfill \\ \quad\quad\quad \left\{ {\frac{{N^{\prime}_{{k{\text{f}}}} }}{{n^{2} \pi^{2} }}\left( {1 - e^{{ - n^{2} \pi^{2} \tau }} } \right)} \right.\left. {\, + \frac{{N^{\prime}_{{k{\text{i}}}} - N^{\prime}_{{k{\text{f}}}} }}{{n^{2} \pi^{2} - \lambda_{1} }}\left( {{\text{e}}^{{ - \lambda^{\prime}_{k} \,\tau }} - {\text{e}}^{{ - n^{2} \pi^{2} \tau }} } \right)} \right\} \hfill \\ \end{aligned}$$
(37)

As time progresses, the mound height beneath recharge basins converges to a steady-state value. The corresponding expression can be obtained by setting τ → ∞. We get

$$H^{ * } = 2\,{\text{e}}^{ - \alpha X} \sum\limits_{n = 0}^{\infty } {\sum\limits_{k = 1}^{m} {\frac{{N^{\prime}_{{k{\text{f}}}} }}{{\left( {\alpha^{2} + n^{2} \pi^{2} } \right)^{2} }}\,\varOmega_{n,\,k} \sin \left( {n\pi X} \right)} }$$
(38)

implying that the stabilized profiles are dependent on the bed slope and final value of the recharge rate.

Discharge rate into drains

Flow rate per unit width of the aquifer along x-axis is given by Eq. (4). Using dimensionless variables of Eq. (11a–d), and defining a dimensionless flow rate

$$Q\left( {X, \tau } \right) = \frac{q}{{K\,L\,\cos^{2} \beta }}$$
(39)

yielding

$$Q\left( {X, \tau } \right) = - \left( {H + \frac{{h_{\,0} }}{L}} \right)\left( {\frac{\partial H}{\partial X} + \tan \beta } \right)$$
(40)

where the term ∂H/∂X is obtained from Eq. (35). The discharge rates into the drains located at x = 0 and x = L are given by

$$Q\left( {X = 0,\tau } \right) = - \frac{{h_{\,0} }}{L}\left[ {\left( {\frac{\partial H}{\partial X}} \right)_{X = 0} + \tan \beta } \right]$$
(41)
$$Q\left( {X = 1,\tau } \right) = - \frac{{h_{\,0} }}{L}\left[ {\left( {\frac{\partial H}{\partial X}} \right)_{X = 1} + \tan \beta } \right]$$
(42)

Plugging the values of the first-order partial derivatives, one obtains

$$\begin{aligned} Q\left( {X = 0,\tau } \right) &= - \frac{{h_{\,0} }}{L}\left[ {\sum\limits_{n = 0}^{\infty } {\sum\limits_{k = 1}^{m} {\frac{2n\,\pi }{{\alpha^{2} + n^{2} \pi^{2} }}\varOmega_{n,k} } } \left\{ {\frac{{N^{\prime}_{{k\,{\text{f}}}} }}{{\alpha^{2} + n^{2} \pi^{2} }}\left( {1 - {\text{e}}^{{ - (\alpha^{2} + n^{2} \pi^{2} )\tau }} } \right)} \right.} \right. \hfill \\ &\quad\left. {\left. { + \frac{{N^{\prime}_{{k\,{\text{i}}}} - N^{\prime}_{{k{\text{f}}}} }}{{\alpha^{2} + n^{2} \pi^{2} - \lambda^{\prime}_{k} }}\left( {{\text{e}}^{{ - \lambda^{\prime}_{k} \,\tau }} - {\text{e}}^{{ - (\alpha^{2} + n^{2} \pi^{2} )\tau }} } \right)} \right\} + \tan \beta } \right] \hfill \\ \end{aligned}$$
(43)

and

$$\begin{aligned} Q\left( {X = 1,\tau } \right) = - \frac{{h_{\,0} }}{L}\left[ {\sum\limits_{n = 0}^{\infty } {\sum\limits_{k = 1}^{m} {\frac{{2n\pi {\text{e}}^{\alpha } ( - 1)^{n} }}{{\alpha^{2} + n^{2} \pi^{2} }}\varOmega_{n,\,k} } } } \times \right.\left\{ {\frac{{N^{\prime}_{{k{\text{f}}}} }}{{\alpha^{2} + n^{2} \pi^{2} }}\left( {1 - {\text{e}}^{{ - (\alpha^{2} + n^{2} \pi^{2} )\tau }} } \right)} \right. \hfill \\ \left. {\left. {\quad + \frac{{N^{\prime}_{{k{\text{i}}}} - N^{\prime}_{{k{\text{f}}}} }}{{\alpha^{2} + n^{2} \pi^{2} - \lambda^{\prime}_{k} }}\left( {{\text{e}}^{{ - \lambda^{\prime}_{k} \,\tau }} - {\text{e}}^{{ - (\alpha^{2} + n^{2} \pi^{2} )\tau }} } \right)} \right\} + \tan \beta } \right] \hfill \\ \end{aligned}$$
(44)

Numerical solution of the nonlinear flow equation

In order to examine the validity of linearization technique, analytic solution of the linearized Boussinesq equation is compared with the numerical solution of the corresponding nonlinear equation. For this purpose, a fully explicit Mac Cormack finite difference computational scheme (Mac Cormack 1969) is employed. This scheme is conditionally stable, convergent, and provides second-order accuracy with respect to time and space. To use this scheme, Eq. (5) is written as

$$\frac{\partial h}{\partial t} = C_{1} \frac{\partial }{\partial x}\left( {h\frac{\partial h}{\partial x}} \right) + C_{2} \frac{\partial h}{\partial x} + \frac{{R\left( {x, t} \right)}}{S}$$
(45)

where \(C_{1} = \left( {K\cos^{2} \beta } \right)/S\) and \(C_{2} = \left( {K\sin 2\beta } \right)/2S\). The Mac Cormack scheme consist two steps, namely, predictor and corrector. In the first step, the value of variable h is predicted by replacing the spatial and temporal derivatives present in Eq. (45) by forward difference

$$\begin{aligned} h_{k, \, n + 1}^{*} = h_{k, \, n} + C_{1} \frac{\Delta t}{{\left( {\Delta x} \right)^{2} }}\left[ {h_{k + 1, \, n} \left( {h_{k + 1, \, n} - h_{k, \, n} } \right) - h_{k, \, n} \left( {h_{k, \, n} - h_{k - 1, \, n} } \right)} \right] \hfill \\ \, + \,C_{2} \frac{\Delta t}{\Delta x}\left( {h_{k + 1, \, n} - h_{k, \, n} } \right) + \frac{{R\left( {x, t} \right)}}{S}\Delta t \hfill \\ \end{aligned}$$
(46)

In the second step, the temporal derivative is approximated by forward difference; however, the spatial derivatives are still approximated by backward difference. This approximation can be put as

$$\begin{aligned} h_{k, \, n + 1}^{**} = h_{k, \, n} + C_{2} \frac{\Delta t}{\Delta x}\left( {h_{k, \, n + 1}^{*} - h_{k - 1, \, n + 1}^{*} } \right) \hfill \\ \, + C_{1} \frac{\Delta t}{{\left( {\Delta x} \right)^{2} }}\left[ {h_{k, \, n + 1}^{*} \left( {h_{k + 1, \, n + 1}^{*} - h_{k, \, n + 1}^{*} } \right)} \right.\left. { - h_{k - 1, \, n + 1}^{*} \left( {h_{k, \, n + 1}^{*} - h_{k - 1, \, n + 1}^{*} } \right)} \right] + \frac{{R\left( {x, t} \right)}}{S}\Delta t \hfill \\ \end{aligned}$$
(47)

The corrected value of h k, n+1 is given as an arithmetic mean of \(h_{k, \, n + 1}^{*}\) and \(h_{k, \, n + 1}^{**}\), i.e.,

$$\begin{aligned} h_{k, \, n + 1} = \frac{1}{2}\left[ {h_{k, \, n} + h_{k, \, n + 1}^{*} + C_{ 2} \frac{\Delta t}{\Delta x}\left( {h_{k, \, n + 1}^{*} - h_{k - 1, \, n + 1}^{*} } \right)} \right. + C_{ 1} \frac{\Delta t}{{\left( {\Delta x} \right)^{2} }} \times \hfill \\ \, \left. {\left\{ {h_{k, \, n + 1}^{*} \left( {h_{k + 1, \, n + 1}^{*} - h_{k, \, n + 1}^{*} } \right) - h_{k - 1, \, n + 1}^{*} \left( {h_{k, \, n + 1}^{*} - h_{k - 1, \, n + 1}^{*} } \right)} \right\}} \right] + \frac{{R\left( {x, t} \right)}}{S}\Delta t \hfill \\ \end{aligned}$$
(48)

Mac Cormack scheme is conditionally stable. It is not possible to obtain a simple stability criterion for Mac Cormack scheme (Tannehill et al. 1975). Numerical experiments are carried out with various values of ∆t and ∆x, and it is observed that the stability of the numerical solution requires

$$\Delta t \le 0.06\frac{{\left( {\Delta x} \right)^{2} }}{{C_{1} }};\quad \Delta t \le 0.9\frac{\Delta x}{{C_{2} }}$$
(49)

Discussions of results

To demonstrate the combined effects of bed slopes and time-varying localized recharges, a numerical example is considered with K = 2.5 m/d, S = 0.25, h 0 = 5 m, and L = 200 m. Recharge schemes are applied through two basins R1 and R2 extending in the ranges of 25 ≤ x ≤ 50 m and 150 ≤ x ≤ 175 m, respectively. In the current example, it is assumed that the recharge schemes applied in both R1 and R2 are the same. The initial recharge rate is 4 mm/h which finally drops to 2 mm/h by the exponential function 2 + 2 e−0.2t. Three different values of sloping angle are considered, namely, β = 10°, 0°, and −10°. Analytic values of water head are computed using Eq. (35) in which the mean saturated depth D of the aquifer is successively approximated using an iterative formula D = (h 0 + h t )/2, where h t is the water table height at time t at the end of which D is approximated. From computational viewpoint, implementation of Eq. (35) is simple and straightforward. Numerical experiments with various values of aquifer parameters indicate that the infinite sequence in the right-hand side of Eq. (35) converges very fast to a final value. We have taken first 50 terms of the sequence to represent the sum of the whole infinite series. Performance of analytic solution is tested against numerical solution of the nonlinear Boussinesq equation at 200 equally spaced grid points of length 1 m for t = 2, 5, 10, 20, and 50 days. It is observed that the two solutions are in excellent agreement during the initial stages (t = 2, 5, 10, and 20 days). As time increases (e.g., 50 days), analytic solutions marginally underestimate the numerical solutions. Numerical experiments do not reveal any definite interplay between the relative percentage difference (RPD) and the aquifer parameters. However, a clear observation is that the RPD is least in the proximity of aquifer–drain interfaces, and decreases as λ decreases.

Distributions of water head for t = 2, 5, 10, 20, and 50 days in 10°, 0°, and −10° sloping aquifers are plotted against the spatial coordinate x in Fig. 2. The profiles of free surface develop in the form of groundwater mound which expands with time at varying rates. It is observed that the dynamic profiles of mound in horizontal aquifer evolve symmetrically about the center of the basins (Fig. 2a). In sloping aquifers, the profiles remain symmetric during initial stages; however, for large values of time, the phreatic surface becomes asymmetric and drifts along the bed slope (Fig. 2b, c), justifying the extended Dupuit–Forchheimer assumptions. Another interesting point to note is that the height of free surface beneath recharge basins is significantly influenced by the bed slope. In upward sloping aquifer, the mound height below R1 is more than that of R2 (Fig. 2b), although the applied recharge schemes in R1 and R2 are identical. This is because when the recharge water percolates through R2 and meets the groundwater, it gradually seeps along the down slope. When this water reaches the recharge zone under R1, it contributes to the mound height under R1. As a result, the height of free surface under R1 attains comparatively higher level than that of R2. In downward sloping aquifers, the mound beneath R2 is higher than that of R1 (Fig. 2c). For large values of time, the mound profiles converge to a steady-state value, given by Eq. (38). The time taken in stabilization of free surface depends on the interplay between the bed slope, the final recharge rate, and the dimensions of recharge basins. Although the recharge rate variation parameter λ does not influence the steady-state values, it has significant impact on the transient profiles of free surface. In Tables 1 and 2, we present the comparison of water head height at the centers of R1 and R2, respectively, when the recharge rate is approximated at constant rate (λ = ∞) and at time-varying rates (λ = 0.2 d−1). It can be observed from these tables that the actual results can be seriously misjudged, if the rate of recharge is approximated by a constant value.

Fig. 2
figure 2

Dynamic profiles of groundwater mound at t = 2, 5, 10, 20, and 50 days in a horizontal, b 10° upward sloping, and c 10° downward sloping aquifer

Full size image
Table 1 Comparison of water head height under the midpoint of R1 (x = 37.5 m) due to constant (λ = ∞) and time-varying (λ = 0.2 d−1) recharge
Full size table
Table 2 Comparison of water head height under the midpoint of R2 (x = 162.5 m) due to constant (λ = ∞) and time-varying (λ = 0.2 d−1) recharge
Full size table

To investigate the combine effects of sloping angle β and recharge rate variation parameter λ on the evolution and stabilization of groundwater mound, the water head heights at the midpoints of the recharge basins R1 and R2 are plotted against time t in Fig. 3 for β = 10° and λ = 0.02, 0.2, and 1 d−1. The mound height increases with time, and eventually when the inflow and outflow strike equilibrium, it converges to a final value. It is shown in these diagrams that for large values of parameter λ, the time taken to achieve the stabilized level is less. The profiles eventually merge irrespective of the value of λ.

Fig. 3
figure 3

Variations in water head height with λ at a x = 37.5 m, and b x = 162.5 m

Full size image

Initial discharge rate in the drains can be obtained by setting t = 0 in Eq. (4). With initial water head height \(h\left( {x = 0,t = 0} \right) = h\left( {x = L,t = 0} \right) = h_{0} \,{\text{and}}\;\left( {\partial h/\partial x} \right)_{t = 0} = 0\), one obtains \(q\left( {x = 0,t = 0} \right) = q\left( {x = L,t = 0} \right) = - \left\{ {K h_{0} \sin \left( {2\beta } \right)} \right\}/2\) for all x. For upward sloping base, the initial value of flow rate is negative, indicating outflow at x = 0 and inflow at x = L. For downward sloping aquifer, both q(x = 0, t = 0) and q(x = 1, t = 0) are positive, indicating inflow at x = 0 and outflow at x = L. In case of horizontal aquifer, there is no exchange of water at the initial stage. Transient discharge rates into the ditches located at x = 0 (referred as D1) and at x = L (referred as D2) are simulated using Eqs. (43) and (44). In this illustration, three different values of recharge rate-controlling parameter, namely λ = 0.02, 0.2, and 1 d−1 for each of the values of β = 10°, −10°, and 0°. These simulations are presented in Fig. 4. It is observed that as the recharge water from basins R1 and R2 meets the groundwater; it influences the discharge rate into both drains according to the slope of impervious bed. Since most of the recharge water in upward sloping aquifer flows along x = 0, the discharge rate in D1 increases with time. At the same time, the evolving groundwater mound beneath R2 deters inflow at x = L; the rate at which water enters at this end decreases with time (Fig. 4a). The flow direction reverses in case of down sloping aquifer. As a result, the discharge rate into drain D2 increases, and the influx of water at x = 0 decreases with the increasing values of time (Fig. 4b). In zero-sloping case, the discharge rate profiles are symmetric with respect to the time axis, implying identical flow patterns in both D1 and D2 (Fig. 4c). Parameter λ plays an important role in the determination of transient profiles of q(x, t). It can be observed from these figures that the magnitude of flow rate increases as the value of parameter λ decreases. For large value of time t, the flow rates in D1 and D2 attain a steady-state value, given by

Fig. 4
figure 4

Discharge rates into drains D1 (continuous curves) and D2 (dotted curves) for λ = 0.02, 0.2, and 1 d−1 in a 10° upward sloping, b 10° downward sloping, and c horizontal aquifer

Full size image
$$Q_{0}^{ * } = - \frac{{h_{\,0} }}{L}\left[ {\sum\limits_{n = 0}^{\infty } {\sum\limits_{k = 1}^{m} {\frac{{2n\,\pi N^{\prime}_{{k{\text{f}}}} }}{{\left( {\alpha^{2} + n^{2} \pi^{2} } \right)^{2} }}\varOmega_{k} \left( n \right) + \tan \beta } } } \right]$$
(50)
$$Q_{1}^{ * } = - \frac{{h_{\,0} }}{L}\left[ {\sum\limits_{n = 0}^{\infty } {\sum\limits_{k = 1}^{m} {\frac{{2( - 1)^{n} n\,\pi {\text{e}}^{\alpha } N^{\prime}_{k\,f} \,}}{{\left( {\alpha^{2} + n^{2} \pi^{2} } \right)^{2} }}\varOmega_{k} \left( n \right)} } + \tan \beta } \right]$$
(51)

Conclusions

New analytic solutions are developed and tested for estimation of spatio-temporal variations in unconfined water table over sloping ditch–drain aquifer system due to localized transient recharge from multiple basins. The mathematical model presented in this study is based on Dupuit–Forchheimer assumptions in which spatial coordinates of recharge basins are treated as additional parameters. Unlike existing studies that invoke Laplace transform methods and yield the solution in terms of error function with complex argument, the present work combines a substitution with eigenvalue–eigenfunction method and produces the analytic expressions for water head and flow rate in the form of a fast converging infinite sequence. A computational example is considered to simulate the combine effects of bed slopes (upward, zero, and downward slope), spatial locations of basins, and variation rate in the downward recharge. The study brings out certain new facts, some of which are summarized as follows:

  • Unlike horizontal aquifers, the groundwater mound in sloping aquifers is asymmetric and its peak drifts along the bed slope.

  • Given two basins of equal dimensions and subjected to same recharge rate, the mound height beneath the upslope-located basin is lesser than that of the down slope-located basin.

  • The bed slope accelerates the process of stabilization of water head profiles and significantly controls the mound height.

  • The prediction of spatio-temporal variations of water head distribution can be erroneous if the recharge rate is approximated by a constant value.