Abstract
The purpose of this study was to develop a group fuzzy multi-criteria decision-making method to be applied in rating problems associated with water resources management. Thus, here Chen’s group fuzzy TOPSIS method extended by a difference technique to handle uncertainties of applying a group decision making. Then, the extended group fuzzy TOPSIS method combined with a consistency check. In the presented method, initially linguistic judgments are being surveyed via a consistency checking process, and afterward these judgments are being used in the extended Chen’s fuzzy TOPSIS method. Here, each expert’s opinion is turned to accurate mathematical numbers and, then, to apply uncertainties, the opinions of group are turned to fuzzy numbers using three mathematical operators. The proposed method is applied to select the optimal strategy for the rural water supply of Nohoor village in north-eastern Iran, as a case study and illustrated example. Sensitivity analyses test over results and comparing results with project reality showed that proposed method offered good results for water resources projects.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Generally, the problems related to water resources management consist of managing the water supply and consumption. Since these problems depend on different qualitative and quantitative criteria, an integrated decision is required, which is difficult. Selecting the optimal strategy for water supply in rural and urban areas is one of the most important issues in water supply management. One of the approaches applicable for solving these problems is using multi-criteria decision-making (MCDM) methods. To date, different MCDM methods have been presented, consisting: Compromise Programming (CP) (Charnes and Cooper 1961); Elimination Et Choice Translating Reality I (ELECTRE I) (Benayoun et al. 1966; Roy 1968); ELECTRE II (Roy and Bertier 1973) and ELECTRE III (Roy 1978); Analytic Hierarchy Process (AHP) (Saaty 1980); Simple Additive Weighting (Hwang and Yoon 1981); Technique for Order Preference by Simulation of Ideal Solution (TOPSIS) (Hwang and Yoon 1981); Analytic Network Process (ANP) (Saaty 1996); preference ranking organization method for enrichment evaluations (PROMETHEE) (Brans et al. 1986); Gray Relational Analysis (Deng 1989); Weighted Sum Method (Janssen 1996); Vise Kriterijumska optimizacija I Kompromisno Resenje (VIKOR) (Opricovic 1998; Opricovic and Tzeng 2002) and Data Development Analysis (Cooper et al. 2000).
But traditionally these methods employ the mathematical classic numbers, which cannot appropriately cover the uncertainties. On the other hand, due to the complex nature of the problems associated with water resources management and its dependence on the qualitative parameters, some uncertainties are involved that can be treated by fuzzy logic. As a result, we have to combine MCDM methods with fuzzy logic to achieve so-called fuzzy MCDM methods. MCDM and fuzzy MCDM methods have been used in different water engineering disciplines (Table 1).
Technique for Order Preference by Similarity to Ideal Solution (TOPSIS), first introduced by Hwang and Yoon (1981), is known as one of the most important MCDM methods. TOPSIS is a technique to assess the performance of alternatives through the similarity with an ideal solution. According to this technique, the best alternative would be the one that is closest to the positive-ideal solution (PIS) and farthest from the negative-ideal solution (NIS). This method uses precise numbers in the rating of alternatives, causing limitations in dealing with uncertainties. To consider them, this technique is enhanced by combining it with fuzzy logic, which became known as the “Fuzzy TOPSIS” method.
An impressive variety of fuzzy TOPSIS methods and their applications have been developed in recent years. Chen (2000) evaluated the rating of alternatives and the weight of criteria by linguistic judgments which were expressed in triangular fuzzy numbers (TFNs). A vertex method was proposed to determine the distance between two TFNs. According to the TOPSIS concept, a closeness coefficient was defined to determine the ranking order of all alternatives by calculating simultaneously the distance to both the fuzzy PIS (FPIS) and the fuzzy negative-ideal solution (FNIS). Triantaphyllou and Lin (1996) introduced a fuzzy TOPSIS method based on fuzzy arithmetic operations that would lead to a fuzzy relative closeness for each alternative. Wang and Chang (2007) developed an evaluation approach based on TOPSIS to help the Air Force Academy in Taiwan in choosing an optimal initial training aircraft in a fuzzy environment where the vagueness and subjectivity were handled with linguistic terms parameterized by TFNs. Wang and Lee (2007) extended TOPSIS in a fuzzy environment where two operators, Up and Low, were used to find the positive- and negative-ideal solutions instead of usual maximum and minimum operations, respectively. Kahraman et al. (2007) proposed a fuzzy hierarchical TOPSIS method for the multi-criteria assessment of the industrial robotic systems. Jahanshahloo et al. (2006) extended the TOPSIS method for decision-making problems with fuzzy data. They used a cut level concept for normalizing fuzzy numbers. Wang and Elhag (2006) developed a non-linear programming solution procedure using a fuzzy TOPSIS method based on a cut level concept. The preference of the method was evaluated using a risk assessment undertaken on a bridge.
Fuzzy TOPSIS methods has been used for a variety of specific applications in decision-making problems, including: Selecting plant location, (Chu 2002), robot selection, (Chu and Lin 2003), service quality in hotel industry, (Benitez et al. 2007), plant layout design, (Yang and Hung 2007), transshipment site selection, (Onut and Soner 2008), the evaluation of the competitive advantage of shopping websites, and selecting the most appropriate blast design (Sun and Lin 2009).
In this study, using the Chen’s group fuzzy TOPSIS method, (Chen 2000), a group fuzzy TOPSIS method with a consistency check and a difference technique to handle uncertainties of applying a group decision making is presented. These are the main advantages over Chen’s method and other group fuzzy TOPSIS methods. The proposed methodology is then applied to select the optimal strategy for rural water supply, as a case study.
In Sect. 2, the details of the method are presented. In Sect. 3, the real case study, the effective criteria and proposed strategy are described. Then the results for selecting the optimal strategy for water supply are given. The last section concludes the paper.
Method
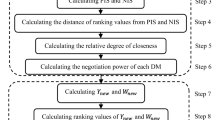
The method used in this study is a group fuzzy TOPSIS with detailed explications of two proposed improvements, namely, a consistency analysis of experts’ opinions and using a difference technique regarding to handle uncertainties of applying a group decision making to substantiate the advantages and differences over the Chen’s group fuzzy TOPSIS method (see Chen 2000). In fact, the method proposed in this study is an extension over the Chen’s method. In this research, a questionnaire was employed to pool the real opinions of the experts by an iterative technique of questioning with a consistency analysis. General steps of the proposed approach can be summarized as in Fig. 1 and are described as follows:
Step 1. Form a committee for decision making. This committee involves experts and decision makers.
Step 2. The effective criteria in the decision-making process are determined by using a comprehensive literature review and the opinions of experts, then the potential alternatives are proposed based on the determined criteria.
Step 3. The experts’ real opinions regarding the importance of the decision-making elements are pooled by employing a questionnaire with an iterative technique of questioning including a consistency analysis.
Step 4. Consistency check of experts’ opinions, A comparison matrix is established based on each expert opinion for each decision element using Saaty’s technique (Saaty, 1980), Letting El1, El2, …, El n denote a set of decision elements, their comparison matrix is according to \(A = [x_{ij} ]_{n \times n}\) in which \(x_{ij} = 1,\,\,\,\left( {i,\,j = 1,\,2,\, \ldots ,\,n.,\,\,\,i = j} \right)\) and \(x_{ij} = \lambda_{i} /\lambda_{j} ,\,\,\,\left( {i,\,j = 1,\,2,\, \ldots ,\,n.,\,\,\,i \ne j} \right),\)
where x ij is a number of precise mathematics that expresses the relative importance (or the relative rating) of element i (λ i ), then the relative importance (or the relative rating) of element j (λ j ). λ i and λ j are obtained from the linguistic judgments inserted in the questionnaires by experts.
To convert the linguistic judgments into numbers of precise mathematics, a scale is used as Table 2.
Determine whether the input data satisfies a “consistency check”. If it does not, go back to step 3 and redo the comparisons. For an n × n square matrix, an index represented by the II is defined as follows:
where λmax is the biggest eigenvalue of an n × n square matrix.
The value of the II is calculated by random numbers, which are called RII. Table 3 shows the values of the RII for (1–10) dimensional matrices (Saaty 1980).
For each n × n square matrix, the result of II divided by RII is called IR:
The closer the IR is to zero, the more consistent is the result. If IR is more than 0.1, the decision should be reviewed.
Step 5. Applying group fuzzy TOPSIS approach, the decision maker’s opinions are aggregated and fuzzy decision matrix \(\tilde{D} = \left[ {\tilde{a}_{ij} } \right]_{m \times n}\) is established.
where \(\tilde{a}_{ij}\) is a TFN that indicates the performance of the alternative i with respect to criterion j. The values of \(\tilde{a}_{ij}\) are calculated as shown in Eqs. 3–6 (see Fig. 2). This manner of formation \(\tilde{a}_{ij}\) is different from the other ones used in fuzzy TOPSIS methods (for comparison see Chen 2000).
where \(a_{ij} \, \le b_{ij} \le c_{ij}\), \(\lambda_{ijk}\) indicates the importance of alternative i with respect to criterion j based on the opinion of expert k; i is the number of alternatives, j the number of criteria; and k is the number of experts involved in the decision making.
The decision makers’ opinions about the importance weight of criteria are aggregated and the criteria weighted matrix is obtained as follows:
where \(\tilde{w}_{j}\) is the aggregated fuzzy weight of criterion j, and it is a TFN as follows:
where \(\tilde{w}_{j}\) is a TFN that expresses the importance weight of the criterion j. The \(\delta_{jk}\) indicates the importance weight of criterion j based on the opinion of expert k.
The normalized fuzzy decision matrix \(\tilde{R} = [\tilde{r}_{ij} ]_{m \times n}\) with i = 1,…,m, and j = 1,…,n arrived at as follows, (Chen 2000):
where B and C are the set of benefit criteria (+) and cost criteria (−), respectively.
The normalized weighted fuzzy decision matrix \(\tilde{V} = [\tilde{v}_{ij} ]_{m \times n}\) is then obtained as:
The fuzzy positive ideal solution (FPIS, A*) indicates the most preferable alternative, and the negative ideal solution (FNIS, A−) indicates the least preferable alternative, so they are determined as follows:
The distance of each alternative from FPIS (\(S_{i}^{ * }\)) and the distance of each alternative from FNIS (\(S_{i}^{ - }\)) are obtained as shown below:
The closeness coefficient of each alternative (C i ) is calculated as follows:
The overall ranking of alternatives is obtained using the closeness coefficient. Each alternative with the higher closeness coefficient has the higher priority.
Case study
An aim of this study is selecting an optimal strategy to supply the drinking water and the water needed for agriculture and livestock in Nohoor village, located in north-eastern Iran, 90 km south of Khaf city in Khorasan Razavi province and is at a distance of 130 km north-east of Ghaen, one of the cities of South Khorasan province (actually on the border of these two towns but a part of Khaf county; see Fig. 3).
The main occupation of the village inhabitants is animal husbandry and they play a major role in meat and dairy production of Khorasan Razavi Province. Although there are fertile lands, agriculture is not flourishing because of water shortage, but it can be revived if enough water could be supplied. It is a hot and dry place located near desert, having 3 month of sand storms (called 120 days of winds). Precipitations are limited to winter and spring (which is really limited). It is mostly small and leads to the recreation of pastures in spring; however, dams would not be filled. In spring, people immigrate to the higher places nearby village to find grazing lands where water supplements are important to find. Grazing lands are located in a circular area with radiation of 13 km around the village which is fertile. Note that grazing lands are fertile considering small precipitations, which includes enduring plants and fertile soil, and also optimal and planed usage of the lands.
Geometrically, this village shares a boundary with Afghanistan country and villagers are loyal to Iran government. Therefore, it is important to maintain and reform policy and security of the village.
In the past, the water demands have been met by a spring named Nohoor, located at a distance of 2 km south of the village. Today, this spring is almost dry and its volume of water is limited. Considering all said, it is a very important issue for local authorities to solve the problem of village water supply. Due to the shortage of rain, the large evaporation rate and the lack of appropriate watershed, constructing a dam is not an appropriate way to supply water to this village. In addition, because of low quantity and quality of underground water supplies in this area, well digging is not a proper way out, either. As a result, the only solution is to transfer water from underground water resources of adjacent villages through a pipeline or tankers.
Alternatives (strategies)
As it was said, the only way to supply the water of the village is to transfer water from nearby villages. Therefore, based on investigations, four strategies to supply drinking and agricultural water for this village are proposed. Figure 3 shows the proposed paths (which are shown by blue line and letters, A, B, C, and D). These strategies are as follows:
-
A.
Water supplied through pipeline via path A: In this strategy, water is extracted from underground water resources near Chahpayab village (a village belonging to Haji Abad county), by a well and is transferred by pipelines. Given the area’s topography, it is difficult to transfer water from this resource by tankers. The obvious advantageous characteristic of this strategy is that the ground slopes toward the Nohoor village from the water resource, which facilitates the transfer of water and decreases the costs of pumping and thereby ensuring pressure in the pipeline. As a result, the probability of pipe failure and water supply cuts is reduced. But it is anticipated that the damage to the transmission system due to the existence of many rivers along the path as well as the probability of seasonal floods would be too high. On the other hand, the distance of transmission is also too long. The opportunity for using the water along the transmission line and profit making for villagers would be quite rife.
-
B.
Water supplied via pipeline path B: In this strategy, water is transferred from the water distribution network of Chahzool village through a pipeline. The main water resource in this strategy is the underground water resources around Mazhnabad village, previously transferred to the Chahzool by a pipeline, in fact, a continuation of the formerly established system. The clear drawback of this strategy is that the ground slopes from the end toward the source at a steep angle. But the transmission distance of water is neither long nor difficult. It is predicted that water supply cuts and the damages to the water facilities would be mostly due to the steepness of the ground. On the other hand, because the water transmission line from Mazhnabad (the main water resource) to the Chahzool village was established to meet the demands only of this village in the past, adding the pipeline of Nohoor village to the end of this pipeline would result in the loss of water pressure and hamper the delivery of water to both villages.
-
C.
Transferring water from path B by tankers and storing it in reservoirs located in the village: In this strategy, the water of Chahzool village network is stored in a reservoir (constructed from concrete). Then, it is transferred to Nohoor village by a tanker and stored in a pool. The main water supply resource in this strategy is similar to that in the second strategy. The significant characteristic of this strategy is its comparably low initial cost. But, this system does not have the capacity to meet all the demands and in an inappropriate weather condition the risk of water shortage in the village increases. Therefore, in the present strategy, the water security for the inhabitants is low.
-
D.
Transferring water by pipeline using path C: In this strategy water is provided from underground water resources near Mazhnabad village from a well and transferred by pipeline. The significant characteristic of this strategy is that the ground slopes from the source to the end, as is the case between the first and second strategies but the distance is greater than in the former. Although the source of water supply is the same, the water security of this strategy is higher than of the second and third strategies. This is due to the direct connection to the main resource. In the second and third strategies, water is first transferred to the Chahzool village and then to the Nohoor village. Therefore, the level of water consumption at Chahzool village would have a strong influence on the loss of pressure and water cuts in the future. In this strategy, the feasibility of using water along the line and also the prospects of profit making are somehow beneficial for the villagers.
Criteria
The most effective criteria in this process are determined using a comprehensive literature review and relying on experts’ opinions. Selected criteria are discussed here:
Initial cost (C1): This includes expenses due to the procurement of pipeline, pumping stations, tanker, as well the expenses of salaries and wages, and energy supply costs; in general, the initial cost contains all the costs needed for initial launching of the project.
Maintenance cost (C2): This includes the expenses due to the possible failure of the pipeline, pumping stations and other facilities in the future in addition to the costs of maintaining the tanker. For instance, the maintenance costs of the second strategy are expected to be high due to the high slope of the ground. In view of the number of the pumping stations needed, the costs of energy and maintenance would be higher. Furthermore, due to the slope, and the water pressure, the water hammer in the pipeline causes damage to the facilities resulting in higher maintenance costs.
Water quality (C3): The quality of water is important for different uses such as drinking, agriculture and animal husbandry.
Environmental destruction (C4): Given the fact that the main occupation of the villagers is herding and therefore using the grassland and natural resources, while it is necessary to dig canals and construct roads to execute pipelines, the resulting damages to the grassland vegetation is generally very important from an environmental point of view. On the other hand, the continuous movement of livestock between the grassland and their water resource causes further damage to the environment. Therefore, water should be transferred by a path that reduces the movement of livestock around the grassland.
Water security and satisfaction of inhabitants (C 5 ): In general, this area of Iran is located in a warm and dry area at a desert margin. Consequently it faces a shortage of surface and underground water resources. On the other hand, Nohoor village has an important role in the local meat and dairy industries and it has a politically strategic location close to the border of Afghanistan country. In this situation, preventing the migration of inhabitants is important from a politico-economic point of view. Consequently, in efforts to prevent migration, water security and customer satisfaction is instrumental which means that their water demands should be met by a suitable resource to minimize water cuts caused by shortage of resources and damaged systems.
The impact on water security of the inhabitants living close to the water resource (C6): Due to the shortage of water resources in this part of Iran, supplying water to Nohoor from, resources available in neighboring villages even in a low quantity would have a significant impact on the water security of the inhabitants in these villages. As a result, it should be supplied from a source that would have a minimum negative effect on the villagers.
Using water along the transmission line and the level of profits thus generated (C7): The main occupation of the villagers is livestock breeding and the major part of the landscape close to this village consists of seasonal grasslands where sheep graze. Therefore, the herd has to travel a long way to return to the village to drink. This traveling distance influences the rate of breeding and increases the risk of damage to the grassland. The path of the water transfer system is important in supplying water for livestock at different parts of the grassland without returning to the village. This will have a positive effect on the village economy.
Applying the proposed method
At this stage, the proposed method was applied to select the optimal strategy. First, to determine the importance weight of the criteria and to rate the strategies using the proposed method, a questionnaire was designed according to Table 4; and the four experts (E1, E2, E3 and E4) involved in the Nohoor project were asked to express the importance weight of each criterion and the rating of alternatives in regard to each criterion using linguistic variables inserted in the questionnaire. Then, a consistency check was applied. Where they did not correlate, the opinions were sent back to the experts. This process was repeated until the consistency check became acceptable. Table 5 shows the opinions of experts on the importance weight of the criteria and Table 6 shows the opinions of the experts on the rating of the alternatives with respect to each criterion in the final repetition.
For example, the calculations of the consistency check for the alternatives with respect to C1 are performed as follows:
-
1.
The opinions of experts to determine the rating of the alternatives with respect to C1 in the final repetition are collected according to the first row in Table 6.
-
2.
The expert opinions are converted into precise numbers using Table 2, and the results are presented in Table 7.
Table 7 The rating of the alternatives with respect to C1 -
3.
The comparison matrices of the alternatives with respect to C1, based on each expert’s opinion, are established according to Table 8.
Table 8 Comparison of the alternatives with respect to C1: a based on opinion of E1, b based on opinion of E2, c based on opinion of E3, d based on opinion of E4
The RI values for these matrices are calculated using Eq. 2 and the results are presented at the bottom of Table 8a–d. As can be observed, the values of the RI are <0.1, thus, these matrices are consistent, and the judgments about the alternatives with respect to C1 are acceptable. Similar calculations were made to obtain the comparison matrices of the criteria (using opinions inserted in Table 5), the comparison matrices of the alternatives with respect to the other criteria (using opinions inserted in Table 6) and their RI values.
In the next stage, the fuzzy decision matrix was calculated using Eqs. 3–6, the resulting matrix is shown in Table 9. The criteria weighted matrix was constructed by Eqs. 7–11, according to Table 10.
The fuzzy decision matrix was normalized using Eqs. 12 and 13. The resulting matrix is shown in Table 11.
Using the Eqs. 14 and 15, the normalized weighted fuzzy decision matrix is calculated and the result is presented in Table 12.
FPIS and FNIS were determined as follows (see Eqs. 16–19):
A* = {(21.00, 21.00, 21.00), (15.00, 15.00, 15.00), (9.00, 9.00, 9.00), (21.00, 21.00, 21.00), (9.00, 9.00, 9.00), (21.00, 21.00, 21.00), (7.00, 7.00, 7.00)}.
A− = {(3.00, 3.00, 3.00), (6.43, 6.43, 6.43), (0.78, 0.78, 0.78), (0.43, 0.43, 0.43), (0.78, 0.78, 0.78), (2.14, 2.14, 2.14), (0.56, 0.56, 0.56)}.
The distance of each alternative from FPIS and FNIS was calculated as (see Eqs. 20–23):
For example:
The results are shown in Tables 13 and 14.
Consequently, the closeness coefficient of each alternative can be calculated using Eq. 24, as shown below:
The closeness coefficients clearly show the rating of the strategies. Based on these values, the four proposed strategies were ranked A, D, C and B, respectively. This means that, strategy A is the optimal alternative for the water supply to Nohoor village. This problem is resolved by the Chen’s group fuzzy TOPSIS method (Chen, 2000). It is essential to note that for solving the problem by Chen’s method, a fuzzy scale should be used. Therefore, a fuzzy scale, similar to the one used in the proposed method (see Table 2) is applied as in Table 15. The results (The values of the C i ) of the Chen’s method in comparison with the one proposed in this study are shown in Table 16. As can be observed, the rating of the alternatives obtained from the proposed method is similar to the results obtained from the Chen’s method.
Sensitivity analysis
To test the ranking sensitivity of the alternatives, an extended sensitivity analysis was done based on the criterion importance and then performances of the Chen’s fuzzy TOPSIS method and the presented methods were being compared with each other. During one of these tests, the influence of the importance of each criterion was surveyed by one level decrement of the importance of that criterion.
If the importance of criterion C1, C2, C4 decreases and the influence of each of them is tested separately, the ranking of options does not change based on none of the two methods.
If the importance of criterion C3 decreases as much as one level, ranking of the options both based on Chen’s method and the presented method will be pursuant to Fig. 4.
As it is observed, according to Chen’s method, ranking of alternatives A, B and D does not change, but the ranking of alternative C will equal option D (the 2nd rank). However, based on the presented method, only the ranking of alternative B remains unchanged, and the ranks of other alternatives change, somehow that option D replaces alternative A and gains the 1st rank.
If the importance of criterion C5 decreases as much as one level, the rank of alternatives A and B does not change according to Chen’s method. However, alternative C replaces in the situation of alternative D (Fig. 5), but according to the presented method just the rank of alternative B remains unchanged (Fig. 5).
If the importance of criterion C6 decreases as much as one level, ranking change of the alternatives will be pursuant to Fig. 6. Based on Chen’s method, only rank of alternative C changes and rank of other options remains unchanged. However, according to the presented method, rank of all options—except than option B—changes. Alternative D replaces alternative A in the 1st rank and alternative D rises from 3rd rank to the 2nd.
If the importance of criterion C7 decreases as much as one level, then according to Fig. 7 and based on Chen’s method, ranks of options A and B do not change but ranks of options C and D are being replaced with each other. However, based on the presented method, option C replaces option A in the 1st rank and ranks of other options remain unchanged.
Other sensitivity tests also were implemented according to the importance of criteria. Based on all these tests and the way it is observed in Figs. 3, 4, 5 and 6, the sensitivity of the alternatives to the importance of criteria is more in the presented method rather than in Chen’s method. In fact, influence of the importance of criteria on ranking of the options is more intense in the presented method. According to Figs. 4, 5, 6 and 7 and other implemented tests, in Chen’s method, changing the importance of criteria does not have influence on the rank of alternatives A and B and alternative A is always in the 1st rank, as alternative B is always in the last rank (4th rank). But in the presented method, alternatives ranking always change with changing the importance level of criteria, and in each test, the alternative occupying 1st rank is different. After local survey and group discussion on options’ ranks in each test, it was shown that the presented method has a better function in introducing the alternative with 1st rank (the selected alternative) as well as ranking other alternatives.
Discussion
Chen’s method (Chen 2000) is one of the most functional methods for multi-criteria problems, but studying the method on the case study in this research, there are two main discussions: (1) there are many beneficiaries in decision-making situations including water supplement management. Therefore, ideas should be in accordance to make best decisions, and it is needed in Chen’s method, as presented in this paper. (2) Using sensitivity test and comparing the results with real project by working experts showed that, changing weight criteria, Chen’s method presented unexpected priorities and less sensitive to the criteria in some cases where local studies showed more needed sensitivity. In Chen’s method, experts’ opinions first turn to triangle fuzzy numbers and, then, three mathematical operators (maximum, minimum and arithmetic mean), combine the opinions and decision-making matrix is introduced. But, in the proposed method, each expert’s opinion is turned to accurate mathematical numbers and, then, to apply uncertainties, the opinions of group are turned to fuzzy numbers using three mathematical operators (maximum, minimum and geometric mean). Using sensitivity test and local studies, it was concluded that adding these expansions to Chen’s method leads to more acceptable results.
Conclusions
Present study aimed to develop Chen’s fuzzy TOPSIS method and choose the best strategy to transfer water supplement in Nohoor village, Iran. Results and local studies showed that in comparison with other methods, presented method in this study offered more practical and more acceptable results in such cases, and it is easier to calculate.
In group decision making, it is necessary to control and analyze opinions to make the best decision, as the result a technique called compatibility study is added to Chen’s method, which results in priority of proposed method in comparison with Chen’s method. It helps to make the opinions more compatible in projects like water resources, which includes many beneficiaries. Turning group opinions to fuzzy numbers and creating decision matrix leads to higher sensitivity to changes of criteria weight in comparison with Chen’s method which is expected according to local studies. Of course, it is better to compare the functions of these two methods in other topics, too. Present study, also, included effective criteria to choose water transfer route to an immigrant village (Nohoor village, Iran) which was analyzed by proposed method. As the result, alternative A was selected as the most practical among others (alternatives A, B, C and D) to transfer water to the village. Local studies showed that proposed method was a proper method for compatibility of the opinions and group decision making in multi-criteria problems like water resources. It is suggested to compare this method and some other MCDM methods in future and, also, apply and investigate the techniques used this study in other methods.
References
Abrishamchi A, Ebrahimian A, Tajrishi M (2005) Case study: application of multicriteria decision making to urban water supply. J Water Res Pl ASCE 131:326–335
Afshar A, Mariño MA, Saadatpour M, Afshar A (2011) Fuzzy TOPSIS multi-criteria decision analysis applied to Karun Reservoirs System. Water Resour Manage 25:545–563
Anand Raj P (1995) Multicriteria methods in river basin planning—a case study. Water Sci Technol 31(8):261–272
Anane M, Bouziri L, Limam A, Jellali S (2012) Ranking suitable sites for irrigation with reclaimed water in the Nabeul-Hammamet region (Tunisia) using GIS and AHP-multicriteria decision analysis. Resour Conserv Recycl 65:36–46
Benayoun R, Roy B, Sussman N (1966) Manual de reference du programme electre. Note De Synthese et Formaton, 25th edn. Direction Scientifique SEMA, Paris
Bender MJ, Simonovic SP (2000) A fuzzy compromise approach to water resource systems planning under uncertainty. Fuzzy Sets Syst 115(1):35–44
Benitez JM, Martin JC, Roman C (2007) Using fuzzy number for measuring quality of service in the hotel industry. Tour Manag 28:544–555
Bojan S (2007) Linking analytic hierarchy process and social choice methods to support group decision-making in water management. Decis Support Syst 42:2261–2273
Brans JP, Vincke P, Mareschal B (1986) How to select and how to rank projects: the PROMETHEE method. Eur J Oper Res 24:228–238
Charnes A, Cooper WW (1961) Management models and industrial applications of linear programming. Wiley, New York
Chen CT (2000) Extensions of the TOPSIS for group decision-making under fuzzy environment. Fuzzy Sets Syst 114:1–9
Chen Z, Ngo HH, Guo WS, Listowski A, O’Halloran K, Thompson M, Muthukaruppan M (2012) Multi-criteria analysis towards the new end use of recycled water for household laundry: a case study in Sydney. Sci Total Environ 438(1):59–65
Chu TC (2002) Selecting plant location via a fuzzy TOPSIS approach. Int J Adv Manuf Technol 20:859–864
Chu TC, Lin YC (2003) A fuzzy TOPSIS method for robot selection. Int J Adv Manuf Technol 21:284–290
Cooper WW, Sieford LM, Tone K (2000) Data envelopment analysis: a comprehensive text with models, applications, references and DEA-Solver Software. Kluwer Academic Publishers, Boston
Czyżak P, Skowiiński R (1996) Possibilistic construction of fuzzy outranking relation for multiple-criteria ranking. Fuzzy Sets Syst 81(1):123–131
Deng JL (1989) Introduction to grey system theory. J Grey Syst 1:1–24
Fouladgar MM, Yazdani-Chamzini A, Zavadskas EK (2012) Risk evaluation of tunneling projects. Arch Civ Mech Eng 12(1):1–12
Hwang CL, Yoon K (1981) Multiple attribute decision making. Springer, Berlin
Jahanshahloo GR, Hosseinzadeh Lotfi F, Izadikhah M (2006) Extension of the TOPSIS method for decision-making problems with fuzzy data. Appl Math Comput 181:1544–1551
Janssen R (1996) Multiobjective decision support for environmental management. Kluwer Academic Publishers, Netherlands
Kahraman C, Çevik S, Ates NY, Gülbay M (2007) Fuzzy multi-criteria evaluation of industrial robotic systems. Comput Ind Eng 52:414–433
Khodabakhshi B, Jafari HR (2011) Application of fuzzy ELECTRE TRI method for determination of environmental impact significance of water resource development projects (The case of Ardebil dam, drainage and irrigation network project). Environ Res 1(2):31–42
Kodikara PN, Perera BJC, Kularathna MDUP (2010) Stakeholder preference elicitation and modelling in multi-criteria decision analysis—a case study on urban water supply. Eur J Oper Res 206(1):209–220
Lee CS, Wen CG (1997) Fuzzy goal programming approach for water quality management in a river basin. Fuzzy Sets Syst 89(2):181–192
Minatour Y, Khazaei J, Ataei M (2012) Earth dam site selection using the analytic hierarchy process (AHP): a case study in the west of Iran. Arab J Geosci. doi:10.1007/s12517-012-0602-x
Nasiri H, Darvishi Boloorani A, Faraji Sabokbar HA, Jafari HR, Hamzeh M, Rafii Y (2013) Determining the most suitable areas for artificial groundwater recharge via an integrated PROMETHEE II-AHP method in GIS environment (case study: Garabaygan Basin, Iran). Environ Monit Assess 185(1):707–718
Nitirach S, Vilas N (2011) Strategic decision making for urban water reuse application: a case from Thailand. Desalination 268:141–149
Onut S, Soner S (2008) Transshipment site selection using the AHP and TOPSIS approaches under fuzzy environment. Waste Manag 28:1552–1559
Opricovic S (1998) Multi-criteria optimization of civil engineering systems. Faculty of Civil Engineering, Belgrade
Opricovic S (2011) Fuzzy VIKOR with an application to water resources planning. Expert Syst Appl 38(10):12983–12990
Opricovic S, Tzeng GH (2002) Multicriteria planning of post earthquake sustainable reconstruction. Comput Aided Civ Infrastruct Eng 17:211–220
Panagopoulos GP, Bathrellos GD, Skilodimou HD, Martsouka FA (2012) Mapping urban water demands using multi-criteria analysis and GIS. Water Resour Manag 26(5):1347–1363
Prodanovic P, Simonovic SP (2002) Comparison of fuzzy set ranking methods for implementation in water resources decision-making. Can J Civ Eng 29(5):692–701
Razavi Toosi SL, Samani JMV (1999) Evaluating water transfer projects using analytic network process (ANP). Water Resour Manag 26(7):1999–2014
Roy B (1968) Classement et choix en presence de points de vue multiples: la methode ELECTRE. RIRO 8:57–75
Roy B (1978) ELECTRE III: un algorithme de classement fondé sur une représentation floue des préférencesen présence de critères multiples. Cahiers du CERO 20:3–24
Roy B, Bertier P (1973) La methode Electre II: Une application au media-planing. In: Ross M (ed) Vlleme Conference Internationale de Recherche Operationnelle, Dublin, OR72, North Holland, Amsterdam, pp 291–302
Saaty TL (1980) The analytic hierarchy process. McGraw-Hill, New York
Saaty TL (1996) Decision making with dependence and feedback: the analytic network process. RWS Publications, Pittsburgh
Simon U, Brüggemann R, Pudenz S (2004) Aspects of decision support in water management—example Berlin and Potsdam (Germany) I—spatially differentiated evaluation. Water Res 38(7):1809–1816
Sun C, Lin GTR (2009) Using fuzzy TOPSIS method for evaluating the competitive advantages of shopping websites. Expert Syst Appl 36:11764–11771
Triantaphyllou E, Lin CT (1996) Development and evaluation of five fuzzy multiattribute decision-making methods. Int J Approx Reason 14:281–310
Wang TC, Chang TH (2007) Application of TOPSIS in evaluating initial training aircraft under a fuzzy environment. Expert Syst Appl 33:870–880
Wang YM, Elhag TMS (2006) Fuzzy TOPSIS method based on alpha level sets with an application to bridge risk assessment. Expert Syst Appl 31:309–319
Wang YJ, Lee HS (2007) Generalizing TOPSIS for fuzzy multiple-criteria group decision-making. Comput Math Appl 53:1762–1772
Wei LH, Jing LY, Wu W, Mou L (2011) Research on security assessment model of water supply system based on leakage control. Procedia Environ Sci 11:749–756
Yang T, Hung CC (2007) Multiple-attribute decision making methods for plant layout design problem. Robot Comput Integr Manuf 23:126–137
Zarghami M, Abrishamchi A, Ardakanian R (2008a) Multi-criteria decision making for integrated urban water management. Water Resour Manage 22(8):1017–1029
Zarghami M, Szidarovszky F, Ardakanian R (2008b) A fuzzy-stochastic OWA model for robust multi-criteria decision making. Fuzzy Optim Decis Mak 7(1):1–15
Zekri S, Romero C (1993) Public and private compromises in agricultural water management. J Environ Manage 37(4):281–290
Zou Q, Zhou J, Zhou C, Song L, Guo J (2013) Comprehensive flood risk assessment based on set pair analysis-variable fuzzy sets model and fuzzy AHP. Stoch Environ Res Risk Assess 27(2):525–546
Acknowledgments
The authors would like to express their appreciation to the Rural Water and Wastewater Company of Khaf County and the residents of Nohoor Village for their assistance in this research. The authors are also grateful to the reviewers for their valuable and useful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This article is published under license to BioMed Central Ltd. Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Minatour, Y., Bonakdari, H., Zarghami, M. et al. Water supply management using an extended group fuzzy decision-making method: a case study in north-eastern Iran. Appl Water Sci 5, 291–304 (2015). https://doi.org/10.1007/s13201-014-0191-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13201-014-0191-9