Introduction

Copper exploitation causes a major water quality problem due to acid mine drainage (AMD) generation in Sarcheshmeh mine, Kerman Province, southeast Iran. The oxidation of sulphide minerals particularly pyrite exposed to atmospheric oxygen during or after mining activities generates acidic waters with high concentrations of dissolved iron (Fe), sulphate (SO4) and both of the heavy and toxic metals (Williams 1975; Moncur et al. 2005). The low pH of AMD may cause further dissolution and the leaching of additional metals (Mn, Zn, Cu, Cd, and Pb) into aqueous system (Zhao et al. 2007). AMD containing heavy and toxic metals has detrimental impact on aquatic life and the surrounding environment. Shur River in the Sarcheshmeh copper mine area is polluted by AMD with pH values ranging between 2 and 4.5 and high concentrations of heavy and toxic metals. The prediction of toxic metals in Shur River is useful in developing proper remediation and monitoring methods. Environmental problems due to the oxidation of sulphide minerals and hence AMD generation in the Sarcheshmeh copper mine and its impact on the Shur River have been investigated in the past (Marandi et al. 2007; Shahabpour and Doorandish 2008; Doulati Ardejani et al. 2008; Bani Assadi et al. 2008; Derakhshandeh and Alipour 2010). In addition, several investigations have been carried out using artificial neural networks (ANN) multiple linear regression (MLR) in different fields of environmental engineering in the past few decades (Karunanithi et al. 1994; Lek and Guegan 1999; Govindaraju 2000; Karul et al. 2000; Bowers and Shedrow 2000; Kemper and Sommer 2002; Dedecker et al. 2004; Kuo et al. 2004, 2007; Khandelwal and Singh 2005 Almasri and Kaluarachchi 2005; Kurunc et al. 2005; Sengorur et al. 2006; Messikh et al. 2007; Palani et al. 2008; Hanbay et al. 2008; Chenard and Caissie 2008; Dogan et al. 2009; Singh et al. 2009).

Recently, a novel machine learning technique, called support vector machine (SVM), has drawn much attention in the fields of pattern classification and regression forecasting. SVM was first introduced by Vapnik (1995). SVM is a kind of classification methods on statistic study theory. This algorithm derives from linear classifier, and can solve the problem of two-kind classifier, later this algorithm applies in non-linear fields, i.e. to say, we can find the optimal hyperplane (large margin) to classify the samples set. It is an approximate implementation to the structure risk minimization (SRM) principle in statistical learning theory (SLT), rather than the empirical risk minimization (ERM) method (Kwok 1999). Compared with traditional neural networks, SVM can use the theory of minimizing the structure risk to avoid the problems of excessive study, calamity data, local minimal value and etc. For the small samples set, this algorithm can be generalized well. SVM has been successfully used for machine learning with large and high-dimensional datasets. These attractive properties make SVM become a promising technique. This is due to the fact that the generalization property of a SVM does not depend on the complete training data but only a subset, the so-called support vectors. Now, SVM has been applied in many fields as follows: handwriting recognition, three-dimension objects recognition, faces recognition, text images recognition, voice recognition, regression analysis, and so on (Carbonneau et al. 2008; Chen and Hsieh 2006; Huang 2008; Seo 2007; Trontl et al. 2007; Wohlberg et al. 2006). The aim of this paper is to predict the concentration of two toxic metals namely Fe and Ni using SVM. For making a good comparison, the obtained results will be compared with those given by a back-propagation neural network (BPNN).

Study area

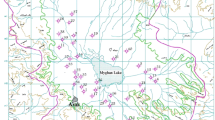
Sarcheshmeh copper mine is located 160 km to southwest of Kerman and 50 km to southwest of Rafsanjan in Kerman province, Iran. The main access road to the study area is Kerman-Rafsanjan-Shahr Babak road. This mine belongs to Band Mamazar-Pariz Mountains. The average elevation of the mine is 1,600 m. The mean annual precipitation of the mine area varies from 300 to 550 mm. The temperature varies from +35°C in summer to −20°C in winter. The area is covered with snow about 3–4 months per year. The wind speed sometimes exceeds to 100 km/h. A rough topography is predominant at the mining area. Figure 1 shows the geographical position of the Sarcheshmeh copper mine.

Fig. 1
figure 1

Location of the Sarcheshmeh cooper mine and Shur River

Full size image

The orebody in Sarcheshmeh is oval shaped with a long dimension of about 2,300 m and a width of about 1,200 m. This deposit is associated with the late Tertiary Sarcheshmeh granodiorite porphyry stock (Waterman and Hamilton 1975). The porphyry is a member of a complex series of magmatically related intrusives emplaced in the Tertiary volcanics at a short distance from the edge of an older near-batholith-sized granodiorite mass. Open pit mining method is used to extract copper ore in the Sarcheshmeh mine. A total of 40,000 tons of ore (average grades 0.9% Cu and 0.03% molybdenum) are approximately extracted per day from the Sarcheshmeh mine (Banisi and Finch 2001).

Sampling and field methods

Sampling of water in the Shur River downstream from the Sarcheshmeh mine was carried out in February 2006. Water samples consist of water from the Shur River (Fig. 1) originating from the Sarcheshmeh mine, acidic leachates of heap structure, run-off of leaching solution into the River and tailings along the Shur River. The water samples were immediately acidified by adding HNO3 (10 cc acid to 1,000 cc sample) and stored under cool conditions. The equipments used in this study consisted of sample container, GPS, oven, autoclave, pH meter, atomic adsorption and ICP analysers. The pH of the water samples was measured using a portable pH meter in the field. Other field measured quantities were total dissolved solids (TDS), electric conductivity (EC) and temperature. Analyses for dissolved metals were performed using atomic adsorption spectrometer (AA220) in the Water Laboratory of the National Iranian Copper Industries Company (NICIC). The ICP (model 6000) analysis method was also used to analyze the concentrations of those metals, usually detected in the range of ppb. Table 1 gives the minimum, maximum and the mean values of the some physical and chemical measured quantities.

Table 1 Maximum, minimum and mean physical and chemical constituents including toxic metals of the Shur River (concentrations of elements are given in ppm)
Full size table

Support vector machine

In pattern recognition, the SVM algorithm constructs nonlinear decision functions by training a classifier to perform a linear separation in some high dimensional space which is nonlinearly related to input space. To generalize the SVM algorithm for regression analysis, an analog of the margin is constructed in the space of the target values (y) using Vapnik’s ε-insensitive loss function (Fig. 2) (Quang-Anh et al. 2005; Stefano and Giuseppe 2006).

Fig. 2
figure 2

Concept of ε-insensitivity. Only the samples out of the ±ε margin will have a non-zero slack variable, so they will be the only ones that will be part of the solution

Full size image
$$ \left| {y - f(x)} \right|_{\varepsilon } : = \max \left\{ {0,\left| {y - f(x) - \varepsilon } \right|} \right\} $$
(1)

To estimate a linear regression

$$ f(x) = \left( {w \cdot x} \right) + b $$
(2)

where w is the weighted matrix, x is the input vector and b is the bias term. With precision, one minimizes

$$ \frac{1}{2}\left\| w \right\|^{2} + C\sum\limits_{i = 1}^{m} {\left| {y - f(x)} \right|_{\varepsilon } } $$
(3)

Where C is a trade-off parameter to ensure the margin ε is maximized and error of the classification ξ is minimized. Considering a set of constraints, one may write the following relations as a constrained optimization problem:

$$ L(w,\xi ,\xi^{\prime}) = \frac{1}{2}\left\| w \right\|^{2} + C\sum\limits_{i = 1}^{N} {(\xi_{i} + \xi^{\prime}_{i} } ) $$
(4)

That according to relations (5) and (6), any error smaller than ε does not require a nonzero ξ i or \( \xi^{\prime}_{i} \), and does not enter the objective function (4) (Lia et al. 2007; Hwei-Jen and Jih Pin 2009; Eryarsoy et al. 2009).

By introducing Lagrange multipliers (α and α′) and allowing for C > 0, ε > 0 chosen a priori, the equation of an optimum hyper plane is achieved by maximizing of the following relations:

$$ L(\alpha ,\alpha^{\prime}) = \frac{1}{2}\sum\limits_{i = 1}^{N} {\sum\limits_{i = 1}^{N} {(\alpha_{i} - \alpha^{\prime}_{i} } )x^{\prime}_{i} x_{i} (\alpha_{i} - \alpha^{\prime}_{i} ) + \sum\limits_{i = 1}^{N} {((\alpha_{i} - \alpha^{\prime}_{i} )y_{i} - (\alpha_{i} + \alpha^{\prime}_{i} )\varepsilon )} } $$
(8)
$$ {\text{Subject to }}0 \le (\alpha_{i} - \alpha^{\prime}_{i} ) \le C $$
(9)

Where, x i only appears inside an inner product. To get a potentially better representation of the data in non-linearized case, the data points can be mapped into an alternative space, generally called feature space (a pre-Hilbert or inner product space) through a replacement:

$$ x_{i} \cdot x_{j} \to \phi (x_{i} ) \cdot \phi (x_{j} ) $$
(10)

The functional form of the mapping φ(x i ) does not need to be known since it is implicitly defined by the choice of kernel: k(x i , x j ) = φ(x i ).φ(x j ) or inner product in Hilbert space. With a suitable choice of kernel, the data can become separable in feature space while the original input space is still non-linear. Thus, whereas data for n-parity or the two spirals problem are non-separable by a hyper plane in input space, it can be separated in the feature space by the proper kernels (Scholkopf et al. 1998; Walczack and Massart 1996; Rosipal and Trejo 2004; Mika et al. 1999; Scholkopf and Smola 2002; Gunn 1997). Table 2 gives some of the common kernels.

Table 2 Polynomial, normalized polynomial and radial basis function (Gaussian) kernels (Wang 2005)
Full size table

Then, the nonlinear regression estimate takes the following form:

$$ y_{i} = \sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{N} {(\alpha_{i} - \alpha^{\prime}_{i} )\phi (x_{i} )^{T} \phi (x_{j} ) + b = \sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{N} {(\alpha_{i} - \alpha^{\prime}_{i} )K(x_{i} ,x_{j} ) + b} } } } $$
(11)

Where b is computed using the fact that equation (5) becomes an equality with ξ i  = 0 if 0 < α i  < C, and relation (6) becomes an equality with \( \xi^{\prime}_{i} \) = 0 if 0 < \( \alpha^{\prime}_{i} \) < C (Chih-Hung et al. 2009; Sanchez 2003).

Network training: the over-fitting problem

One of the most common problems in the training process is the over fitting phenomenon. This happens when the error on the training set is driven to a very small value, but when new data are presented to the network the error is large. This problem occurs mostly in case of large networks with only few available data. Demuth and Beale (2002) have shown that there are a number of ways to avoid over-fitting problem. Early stopping and automated Bayesian regularization methods are the most common. However, with immediate fixing the error and the number of epochs to an adequate level (not too low/not too high) and dividing the data into two sets: training and testing, one can avoid such problem by making several realizations and selecting the best of them. In this paper, the necessary coding was added through MATLAB multi-purpose commercial software to implement the automated Bayesian regularization for training both the SVM and BPNN. In this technique, the available data are divided into two subsets. The first subset is the training set, which is used for computing the gradient and updating the network weights and biases. The second subset is the test set. This method works by modifying the performance function, which is normally chosen to be the sum of squares of the network errors on the training set. The typical performance function that is used for training neural networks is the mean sum of squares of the network errors according to the following equation:

$$ {\text{mse}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {(e_{i} } )^{2} = \frac{1}{N}\sum\limits_{i = 1}^{N} {(t_{i} } - a_{i} )^{2} $$
(12)

where N represents the number of samples, a is the predicted value, t denotes the measured value and e is the error.

It is possible to improve generalization if we modify the performance function by adding a term that consists of the mean of the sum of squares of the network weights and biases which is given by:

$$ {\text{msereg}} = \gamma {\kern 1pt} {\text{mse}} + (1 - \gamma ){\kern 1pt} {\kern 1pt} {\text{msw}} $$
(13)

Where, \( {\text{msereg}} \) is the modified error, γ is the performance ratio, and \( {\text{msw}} \) can be written as:

$$ {\text{msw}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {w_{i} } $$
(14)

Performance function will cause the network to have smaller weights and biases, and this will force the network response to be smoother and less likely to over fit (Demuth and Beale 2002).

Data set

One of the main objectives of this study is to predict the concentrations of Ni and Fe in the samples collected from the Shur River nearby the Sarcheshmeh cooper mine using SVM and BPNN methods. In this regard, physical and chemical constitutions (given in Table 1) are considered as the inputs, whereas Ni and Fe concentrations are taken as the output of the network in the both methods. In view of the requirements of the SVM and back-propagation neural computation algorithms, the data of both the input and output variables were normalized to an interval by a transformation process. In this study, normalization of data (inputs and outputs) was carried out that the normalized results were transformed to the range of (−1, 1) using equation (15) and the number of train data (40) and test data (16) were then selected randomly.

$$ p_{n} = 2\frac{{p - p_{\min } }}{{p_{\max } - p_{\min } }} - 1 $$
(15)

where, pn is the normalized parameter, p denotes the actual parameter, pmin represents the minimum of the actual parameters and pmax stands for the maximum of the actual parameters. In addition, the leave-one-out (LOO) cross-validation of the whole training set was used for adjusting the associated parameters of the networks (Liu et al. 2006).

Prediction of toxic metals concentration by SVM

Similar to other multivariate statistical models, the performance of SVM for regression depend on the combination of several parameters. They are capacity parameter C, ε of ε-insensitive loss function, the kernel type K and its corresponding parameters. C is a regularization parameter that controls the trade-off between maximizing the margin and minimizing the training error. If C is too small then insufficient stress will be placed on fitting the training data. If C is too large then the algorithm will overfit the training data. However, Wang et al. (2003) indicated that prediction error was scarcely influenced by C. To make the learning process stable, a large value should be set up for C (e.g., C = 100).

The optimal value for ε depends on the type of noise present in the data, which is usually unknown. Even if enough knowledge of the noise is available to select an optimal value for ε, there is the practical consideration of the number of resulting support vectors.ε-insensitivity prevents the entire training set meeting boundary conditions, and so allows for the possibility of sparsity in the dual formulations solution. So, choosing the appropriate value of ε is critical from theory.

Since in this study the nonlinear SVM is applied, it would be necessary to select a suitable kernel function. The obtained results of previous published researches (e.g. Dibike et al. 2001; Han and Cluckie 2004) indicate the Gaussian radial basis function has superior efficiency than other kernel functions. As seen in the Table 1, the form of the Gaussian kernel is as follow:

$$ K(x_{i} ,x_{j} ) = e^{{ - \left| {x_{i} - x_{j} } \right|^{2} /2\sigma^{2} }} $$
(16)

In addition, where σ is a constant parameter of the kernel and can either control the amplitude of the Gaussian function and the generalization ability of SVM. We have to optimize σ and find the optimal one.

To find the optimum values of two parameters (σ and ε) and prohibit the overfitting of the model, the dataset was separated into a training set of 40 compounds and a test set of 16 compounds randomly and the LOO cross-validation of the whole training set was performed. The LOO procedure consists of removing one example from the training set, constructing the decision function on the basis only of the remaining training data and then testing on the removed example (Liu et al. 2006). In this fashion one tests all examples of the training data and measures the fraction of errors over the total number of training examples. The root mean square (RMS) error was used as an error function to evaluate the quality of model.

Detailed process of selecting the parameters and the effects of every parameter on generalization performance of the corresponding model are shown in Fig. 3. To obtain the optimal value of σ, the SVM with different σ were trained, the σ varying from 0.01 to 0.3, every 0.01. We calculated the RMS errors for different σ, according to the generalization ability of the model based on the LOO cross-validation for the training set to determine the optimal one. The curve of RMS error versus the sigma was shown in Fig. 3. The optimal σ was found as 0.13. To find an optimal ε, the RMS errors for different εs, were calculated. The curve of the RMS error versus ε was shown in Fig. 3. From Fig. 3, the optimal ε was found as 0.08.

Fig. 3
figure 3

RMS error versus σ (left) and RMS error versus ε (right) in LOO cross-validation stage

Full size image

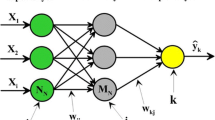
From the above discussion, the σ, ε and C were fixed to 0.13, 0.08 and 100, respectively, when the support vector number of the SVM model was 48. Figure 4 is a schematic diagram showing the construction of the SVM.

Fig. 4
figure 4

Schematic diagram of optimum SVM for prediction of Ni and Fe concentration

Full size image

Afterward, the most relevant input variables for predicting the concentration of Ni and Fe among many combinations of attributes (different physical and chemical parameters provided in the Table 1), the best input variables were selected by the trial and error method (Table 3). Two criteria were used to evaluate the effectiveness of each network and its ability to make accurate predictions. The RMS error can be calculated as follows:

Table 3 Correlation coefficient (R) and RMS error of the prediction based on the different input variables
Full size table
$$ {\text{RMS}} = \sqrt {\frac{{\sum\nolimits_{i = 1}^{n} {(y_{i} - \hat{y}_{i} )^{2} } }}{n}} $$
(17)

where, \( y_{i} \) is the measured value, \( \hat{y}_{i} \) denotes the predicted value, and n stands for the number of samples. RMS error indicates the discrepancy between the measured and predicted values. The lowest the RMS, the more accurate the prediction is. Furthermore, the efficiency criterion, R, is given by:

$$ R = \sqrt {1 - \frac{{\sum\nolimits_{i = 1}^{n} {(y_{i} - \hat{y}_{i} )^{2} } }}{{\sum\nolimits_{i = 1}^{n} {y_{i}^{2} } - \frac{{\sum\nolimits_{i = 1}^{n} {\hat{y}_{i}^{2} } }}{n}}}} $$
(18)

Where, R efficiency criterion represents the percentage of the initial uncertainty explained by the model. The best fitting between measured and predicted values, which is unlikely to occur, would have RMS = 0 and R = 1. It was found that combination of seven parameters (pH, SO4, HCO3, TDS, EC, Mg, and Ca) is the most suitable input variable. Table 3 gives the correlation coefficient (R) and RMS of the prediction based on the different input variables.

In the next stage, the performance of SVM was evaluated using the measured and predicted concentrations. Figure 5 can provide a good insight into the process of prediction.

Fig. 5
figure 5

Relationship between the measured and predicted concentration by SVM; Fe (left) and Ni (right)

Full size image

As it is quite observed in Fig. 5, there is an acceptable agreement (correlation coefficient of 0.92 for the Fe and correlation coefficient of 0.95 for Ni) between the predicted and measured dataset. Based on the Fig. 5, the SVM is a proper method for the prediction of toxic metal concentration. Nonetheless, the performance of this method should be compared with another suitable method for highlighting the highly performance of the SVM.

Back-propagation neural network

Back-propagation neural networks are usually recognized for their prediction capabilities and ability to generalize well on a wide variety of problems. These models are a supervised type of networks, in other words, trained with both inputs and target outputs. During training, the network tries to match the outputs with the desired target values. Learning starts with the assignment of random weights. The output is then calculated and the error is estimated. This error is used to update the weights until the stopping criterion is reached. It should be noted that the stopping criteria are usually the average error of epoch.

The optimal network for this study is a multilayer perceptron (Cybenko 1989, Hornik et al. 1989, Haykin 1994, Noori et al. 2009, 2010), that has one input layer with seven inputs (i.e. pH, SO4, HCO3, TDS, EC, Mg, and Ca), one hidden layers with six neurons that each neuron has a bias and is fully connected to all inputs and utilizes sigmoid activation function. The output layer has two neurons (Fe and Ni) with linear activation function (purelin) without any bias. Figure 6 can properly show the performance of BPNN in the prediction process.

Fig. 6
figure 6

Relationship between the measured and predicted concentration by BPNN; Fe (left) and Ni (right)

Full size image

As seen in Fig. 6, BPNN provides a good prediction for the Ni and Fe concentrations, but it is not as good as the SVM prediction. Nonetheless, there is good agreement between the measured and predicted concentration provided by BPNN (correlation coefficient of 0.88 for the Fe and correlation coefficient of 0.901 for Ni). Hence, BPNN can be considered as an alternative approach after the SVM for the prediction of the toxic metal concentration.

Discussion

In this research work, we have demonstrated one of the applications of SVM in forecasting the concentration of toxic metals. We interrogate the performance of this method by comparing the results with the best performed work of BPNN model. When compared SVM with this model (Table 4), we can see overall better performance of SVM over BPNN approach in terms of RMS error in both training and testing steps.

Table 4 Comparing the performance of SVM and BPNN methods in the training and testing steps
Full size table

According to this table, the RMS error of SVM model is quite smaller than that of the BPNN. In terms of running time, In addition, the SVM consumes a considerably less time for prediction compared with that of the BPNN. For determining the relative running time of each network, Matlab multipurpose software has been used (i.e. relative codes of both networks have written in the Matlab software environment). As it is completely clear in the Table, the associated running time of SVM in training set is even less than that of the BPNN in the testing process. All of these expressions can introduce the SVM as a robust algorithm for the prediction process.

Conclusions

Support vector machine is a novel machine learning methodology based on SLT, which has considerable features including the fact that requirement on kernel and nature of the optimization problem results in a uniquely global optimum, high generalization performance, and prevention from converging to a local optimal solution. In this research work, we have shown the application of SVM compared with BPNN model for prediction of the concentrations of two toxic metals, namely Fe and Ni, based on those chemicals and physical parameters obtained by conducting a sampling program nearby the Sarcheshmeh cooper mine, Iran. Although both methods are data-driven models, it has been found that SVM makes the running time considerably faster with the higher accuracy. In terms of accuracy, the SVM technique resulted in a less RMS error compared with that of the BPNN model (Table 4). Regarding the running time, SVM requires a small fraction of the computational time used by BPNN, which is an important factor to choose an appropriate and high-performance data-driven model.