1 Introduction

Anaemia is a serious global health problem that specifically affects young children and pregnant women (Jiahong et al. 2021; Chaparro and Suchdev 2019; WHO 2015; Gutema et al. 2014). It may result from several factors, the iron deficiency is the main contributor, but the proportion probably varies among population groups in different areas or according to the local conditions (Steven et al. 2013; Stoltzfus 2004). Other causes of anaemia include micronutrient deficiencies (e.g., folate, riboflavin, vitamin A and B12), acute and chronic infections (e.g., malaria, cancer, tuberculosis, and HIV), and inherited or acquired disorders that affect haemoglobin synthesis, red blood cell production or red blood cell survival (e.g., hemoglobinopathies) (Dey et al. 2013; Balarajan et al. 2011; Tolentino and Friedman 2007).

Iron deficiency anaemia is considered one of the ‘Top Ten Risk Factors’ causing death (Dubey 1994). People suffering from anaemia lack red blood cells that are responsible to carry oxygen to the body’s tissues. Its symptoms may include fatigue, skin pallor, shortness of breath, light-headedness, dizziness or fast heartbeat, low body weight, etc. (Cho et al. 2021). If untreated it can lead to severe complications among children and adults, either in the short or long term. As far as the children are concerned, especially children below 5 years of age, anaemia affects them with behavioural delay, low cognitive development and intelligence, difficulty with concentration, low learning outcomes, low immunity, and susceptibility to frequent infections, increased mortality, and disability (Agaoglu et al. 2007; Katzman et al. 1972; Zou and Hastie 2005). It also affects adults, especially women, in the form of pregnancy complications such as premature birth, abortion, and low birth weight of babies, and the same is for adolescents too (Lokeshwar et al. 2011; Qiaoyi et al. 2009). Finally, untreated anaemia also results in heart attack and heart failure (Shah et al. 2013). Recent studies suggest that anaemia is associated with poor outcomes for patients hospitalized with COVID-19 infections (Faghih et al. 2021; Rajanna et al. 2021).

According to the World Health Organization (WHO), children of 6–59 months of age, and women in the child-bearing age group, especially those who are pregnant, are prone to anaemia. WHO (2021) further states that the prevalence of anaemia among 6–59-month-old children across the world in 2019 was around 40% while the same in the case of pregnant women was around 36.5%. Thus, anaemia among the 6–59 age group of children is a matter of serious concern in the world.

However, the prevalence of anaemiaFootnote 1 varies widely across the regions and countries in the world. It is as high as 60% in Africa and as low as 7% in North America. And within Africa, it is as high as 69% in western and central Africa, the poorest regions of the continent. As far as the individual countries are concerned, Yemen records the highest rate (around 79.5%), and the lowest in the USA (around 6%). Owing to internal conflict and infighting, Yemen suffers from the worst humanitarian crisis—nearly three fourth of its population, especially women, suffer from extreme poverty (World Bank 2021), whereas, the USA is one of the richest countries in the world. In fact, going by strict economic criteria, the prevalence of anaemia in low-income countries is as high as 74% whereas the same in the case of high-income countries is around 13% (Fig. 1).

Fig. 1
figure 1

Source: Authors’ calculations based on data published by Our World in Data (https://ourworldindata.org)

Prevalence of anaemia in children (6–59 months) in the world.

Full size image

Clearly, the pattern of anaemia prevalence in the world indicates its possible negative correlation with income. However, impressively no such pattern is apparent in the context of South Asia in general and India in particular.

Despite being one of the poorest regions of Asia, South Asia has anaemia prevalence to an extent of 52%. Most of the countries in the region do not show a similar pattern. Countries like Afghanistan, Bangladesh, Nepal, and Pakistan exhibit a lower prevalence of anaemia than India (Fig. 2).

Fig. 2
figure 2

Source: Same as Fig. 1

Prevalence of anaemia in children (6–59 months) in SAARC countries. (Arranged in descending order of GDP (PPP)).

Full size image

As per the National Family Health Survey (NFHS)-4 (2015–16) survey report, anaemia prevalence rate is 58.5%, which of course is higher than the WHO figures for 2019. It also suggests that the economically developed regions, states, and UTs in the country have a higher prevalence of anaemia than their poorer counterparts, both in terms of its severity and proportion. Economically sound regions in North and South India have a higher and more severe prevalence of anaemia than economically weak regions like North-East India. Similarly, the proportion and severity of anaemia are higher in the richer states like Punjab, Haryana, Delhi, Gujarat, Maharashtra, Andhra Pradesh, Telangana, etc. whereas, it is the opposite in the case of economically less well-off states like Arunachal Pradesh, Assam, Manipur, Meghalaya, etc., All the states in North-East India are having a lesser prevalence than the national average, with Sikkim (55.1%) having the highest followed by Arunachal Pradesh (54.2%), while the rest of the states in the region have reported a prevalence of less than 50%. The available factsheets of the NHFS-5 (2019–21) survey report also suggests a similar pattern in a more alarming situation (Fig. 3).

Fig. 3
figure 3

Source: Authors’ Compilations Based on NFHS-4 and NFHS-5, Published by MoHFW, Govt. of India

Heat map of child anaemia as per NFHS-4 and NFHS-5.

Full size image

The national prevalence rate has gone up drastically from 58.6 in NFHS-4 to 67.1% in NHFS-5 and across the states and UTs barring the state of Kerala, there has a been rise in child anaemia during the same period. However, on the one hand, high prevalence of anaemia in India compared to its South Asian neighbours, and on the other hand within India, relatively low prevalence of anaemia in some North-Eastern states, Himachal Pradesh, Uttarakhand, and Sikkim, more or less counter the global scenario of anaemia that depicts its negative correlation with the income.

1.1 Broad research question and review of literature

The major research question that arises is ‘Do factors other than income matter in the prevalence of anaemia among the children in the 6–59 months age group?’ The present study seeks to explore an answer to the aforesaid research question in the context of North-East Indian states. This is because, as mentioned earlier, the region is relatively less well-off in terms of economy, child and woman welfare, and has a lower prevalence of anaemia. Besides, North-East India is home to a large chunk of tribal population whose living environment, social norms, culture and consumption pattern, etc., vary markedly from the economically well-off states in India. Further, the region is usually considered an economically less developed region of India and hence since 2014, it has been the focus of the central government. The gross budgetary support of the central government for the North-East has gone up from Rs. 36,108 Crores in 2014–15 to Rs. 76,040 Crores in 2022–23, an increase of 110%. Pertinently, there can’t be economic development without human development.

As far as the available literature is concerned, although there are a plethora of studies on the prevalence of child anaemia in India, there is hardly any specific study conducted in the context of North-East India. In this respect, however, we could trace one direct study and a couple of related studies.

Dey S et al. (2013), examined the factors that influence the occurrence of anaemia among children of 0–6 years in North-East India. They used a data set of 10,317 children from the Reproductive and Child Health-II (RCH-II) survey conducted between 2002 and 2004. Using the chosen data, the authors attempted to predict the probability of anaemia occurrence among the target group by fitting a multinomial logistic model. They found that the geographical location (rural or urban), religion, fertility and literacy of the mother, and age of the mother at marriage are significant determinants for the prevalence of anaemia among children of 0–6 years in North-East India. Meshram I. et al. (2020) assessed the prevalence of anaemia and vitamin A deficiency (VAD) among women and pre-school children in North-East India through a small sample survey. The study found the prevalence of anaemia to be low among pre-school children. The authors however suggest that Anaemia and VAD are important public health problems among the tribal population of North-East India, despite their rich biodiversity. Bezboruah et al. (2021) conducted a cross-sectional study of 104 HIV-positive children in one of the tertiary care centers in North-East India. According to their study, compared to the older age group preschool children had a higher prevalence of anaemia. Further, the authors put forth that those rural children are more affected both in terms of prevalence and severity of anaemia. And in their study malnutrition is found to be an important risk factor for anaemia. Accordingly, the authors prescribe nutritional programs for improving the quality of life among HIV-infected children, especially those belonging to rural India.

De M et al. (2006) studied the prevalence of anaemia and hemoglobinopathies in the tribal population of North-East India through a sample survey of 1726 cases. Out of the total number of cases, approximately 73% were from the tribal population, collected from three states in the region, namely, Arunachal Pradesh, Assam, and Tripura, and the rest were non-tribal populations, collected from the state of West Bengal, as a control group. The incidence of anaemia among the tribal population of North-East states was significantly different from that of West Bengal. In particular, the study found the incidence of anaemia in Arunachal Pradesh, Assam, and Tripura were around 54%, 60%, and 57% respectively. Finally, the authors opined that the presence of hemoglobinopathies and thalassemia accounted for anaemia in a sizeable population of certain tribes in North-East India and urgent public health programmes were needed to address the issue.

Thus, the available literature suggests that the demographic variables like tribal and rural inhabitations, nutritional deficiency, literacy of mother, age of the mother during the marriage, fertility of women, etc., are responsible for anaemia in children of 6–59 months age group in North-East India. However, over the years there has been a rapid stride in the collection of family health statistics in India—we have moved from RCH to NHFS. Compared to RCH data used in Dey S et al. (2013), the NHFS-4 is a large database both in terms of sample size and variables. Moreover, the statistical techniques applied to analyze the survey has gone up tremendously—from multinomial logistics used in Dey S et al. (2013) to machine learning (ML) techniques like penalized regression. Of course, there has been a number of studies on child anaemia using NHFS-4 data and applying ML techniques but not in the context of North-East India. A few important of them are worth highlighting in this context.

Meena et al. (2019) applied data mining techniques such as decision tree and association rule mining to NHFS-4 to predict child anaemia in India. Similarly, Jain et al. (2021) analyzed the NHFS-4 data for child malnutrition. Using multilevel analysis, the authors found households as an important source of clustering and variation in child malnutrition outcomes. In predicting anaemia and malnutrition in children, ML techniques have also been used outside India at a global level. Talukder and Ahammed (2020) also compared various ML algorithms to predict malnutrition status for children under the age of five using the Bangladesh Demographic and Health Survey (BDHS). Similarly, Wallner et al. (2022) tried to predict the occurrence of anaemia among children in the UK through CART analysis and ML techniques. Qusay and Emrullah (2022) have compared the performance of different ML techniques for aneamia prediction among children using various social factors. The authors viewed that the ML techniques like Multilayer Perceptron (MLP) and Decision Tree (DT) better predict the prevalence of anaemia among children than the traditional statistical methods. Bitew et al. (2022) using the data from the Ethiopian Demographic and Health Survey of 2016 compared 5 different ML algorithms to predict the socio-demographic risk factors for undernutrition. Dukhi et al. (2021) have reviewed the studies pertaining to the use of artificial intelligence in analyzing the prevalence of anaemia among children and adolescents in India, South Africa, and Russia. The authors opined that although the use of ML approach for the study of child anaemia is at a nascent stage, it could be used as a potential tool in identifying the risk associated with child anaemia at preliminary levels.

Thus, in recent years ML techniques have been widely used, as an improvement over the traditional methods, in predicting child anaemia and related health issues of children. However, we could not find a single study that has used either NHFS-4 data or any of the ML techniques in predicting child anaemia in North-East India, given the central government’s focus on it in recent years.

Nevertheless, taking the aforesaid gaps in literature into consideration, the present study intends to evaluate the prevalence of anaemia among children (6–59 months) and examine the role of a wide variety of factors in it, using a sufficiently large set of the latest available demographic data i.e., NHFS-4 data. For this purpose, we have used one of the important ML techniques known as penalized logistic regression methods with the help of classification and regression training (CARET) (Kuhn M 2008) package in R. Thus, the present study is distinguished from the previous studies in terms of a wide variety of factors/determinants, a large sample size from the latest available data and use of sophisticated analytical methods.

The study is organized as follows. Apart from the current introductory section which includes research question and literature review, there are 4 more sections. The Sect. 2 is devoted to a threadbare discussion of methodology. In Sect. 3, we outline the nuance of the data, select the independent variables and evaluate the appropriate model suitable for the analysis. The results are discussed in the Sect. 4. Finally, we summarise and conclude the entire discussion by highlighting the limitations of the study.

2 Methodology

Machine Learning (ML) is an emerging analytical technique in quantitative research (Donepudi 2017). Being a data-centric technique, ML follows a large number of algorithms and widely used among them is supervised ML. Some of the popular supervised ML algorithms are decision tree, random forest, support vector machine, k nearest neighbourhood, penalised regression, etc. Penalised regression is widely used in analysing health and demographic data.

2.1 Penalized regression: the supervised ML algorithm

Traditionally, logistic regression is one of the most popular linear classification methods in the field of healthcare, banking, and other related areas. It has been found useful for binary classification wherein the dependent variable is known to have only 2 classes. One of the major limitations of using logistic regression is the high dimensionality of the data under investigation, especially in those cases where the sample size is less than the number of variables, in areas such as genomics, fMRI data, etc. Further, the use of too many predictive variables makes the regression exercise complex, and it even affects the predictive accuracy of the model. Also, it encounters the problems of multi-collinearity and over-fitting. These problems are well addressed when we use penalized regression methods (Greenwood et al. 2020, Abram et al. 2016, Aitor and Juan 2011). Penalized regression is an improvement over binary logistic regression as it allows us to handle complex regression problems and attain higher predictive accuracy. Penalized regression models impose a penalty on the logistic regression coefficients for having many explanatory variables. This in turn results in the shrinking of the regression coefficients of less important variables towards zero. This process is also known as ‘Regularization’.

The prominent penalized regression methods are ridge, LASSO (Least Absolute Shrinkage and Selection Operator), and elastic-net. The ridge regression (Arthur and Robert 1970) also known as the ‘Quadratic Regularization’ approach is the oldest penalized regression method. The ridge regression shrinks the regression coefficients by imposing \({l}_{2}\)-norm penalty for having a large value. It is also known to shrink the coefficients of the correlated explanatory variables towards each other by acquiring strength from each other (Friedman et al. 2010). However, one important drawback of ridge regression is its inability to select the important variables. An improvement over a ridge could be LASSO, purposed by Robert (1996) using the \({l}_{1}\)-norm penalty. It eliminates the least important variables by forcing their coefficients to be exactly zero. Hence, LASSO is otherwise known as the variable selection method. In fact, it not only improves the accuracy of the classification but also makes the interpretation of the model easier (Pourahmadi 2013). Although this method demonstrated encouraging results, Zou and Hastie (2005) pointed out some shortcomings. The LASSO method is known to have problems when the explanatory variables are correlated and variables more than the size of the sample. Hence, we use elastic-net proposed by Zou and Hastie as an improvement over LASSO. Basically, elastic-net is a combination of the ridge and LASSO that overcome their individual drawbacks.

Penalised regression technique, as an improvement over classical logistic regression can be seen though its various functional forms.

$$P\left( {y{|}x} \right) = \pi \left( x \right) = logit^{ - 1} \left( {\beta_{0} + \mathop \sum \limits_{j = 1}^{m} \beta_{j} x_{i} } \right)$$
(1)

here \({logit}^{-1}\) is the inverse of the logit transformation, \({\beta =(\beta }_{0},{\beta }_{1}{,\beta }_{2},\dots ,{\beta }_{m})\) are the regression coefficients and \({x=(x}_{1},{x}_{2}{,x}_{3},\dots ,{x}_{m})\) are the explanatory variables. These coefficients are obtained by maximizing the log-likelihood function, \(l\left(\beta \right)\) over the total given observations \(n\).

$$\ell \left( \beta \right) = \mathop \sum \limits_{i = 1}^{n} \left\{ {y_{i} \log \left( {\pi \left( {x_{i} } \right)} \right) + (1 - y_{i} )\log \left( {1 - \pi \left( {x_{i} } \right)} \right)} \right\}$$
(2)

Then the penalized logistic regression, \(l{\left(\beta \right)}^{p}\) can be defined as below:

$$\ell \left( \beta \right)^{p} = \mathop \sum \limits_{i = 1}^{n} \left\{ {y_{i} \log \left( {\pi \left( {x_{i} } \right)} \right) + \left( {1 - y_{i} } \right)\log \left( {1 - \pi \left( {x_{i} } \right)} \right)} \right\} + \lambda P\left( \beta \right)$$
(3)

\(\lambda \ge 0\), is the tuning parameter and controls the shrinkage of the coefficients of the explanatory variables of the model. The larger the value of this tuning parameter the more the weight to the penalty term \(P\left(\beta \right)\). When this penalty term is replaced by \({l}_{2}\)-norm penalty, we have ridge regression;

$$\ell \left( \beta \right)_{ridge}^{p} = \mathop \sum \limits_{i = 1}^{n} \left\{ {y_{i} \log \left( {\pi \left( {x_{i} } \right)} \right) + \left( {1 - y_{i} } \right)\log \left( {1 - \pi \left( {x_{i} } \right)} \right)} \right\} + \lambda \mathop \sum \limits_{j = 1}^{m} \beta_{j}^{2}$$
(4)

And the solution to the likelihood Eq. (4) is

$$\hat{\beta }_{ridge} = \arg \mathop {\min }\limits_{\beta } \left\{ {\ell \left( \beta \right) + \lambda \mathop \sum \limits_{j = 1}^{m} \beta_{j}^{2} } \right\}$$
(5)

In the ridge regression, the tuning parameter \(\lambda\) only controls the amount of shrinkage in the regression coefficient but never takes them exactly equal to zero. When \(P\left(\beta \right)\) is put equal to \({l}_{1}\)-norm penalty we have the LASSO regression;

$$\ell \left( \beta \right)_{lasso}^{p} = \mathop \sum \limits_{i = 1}^{n} \left\{ {y_{i} \log \left( {\pi \left( {x_{i} } \right)} \right) + \left( {1 - y_{i} } \right)\log \left( {1 - \pi \left( {x_{i} } \right)} \right)} \right\} + \lambda \mathop \sum \limits_{j = 1}^{m} \left| {\beta_{j} } \right|$$
(6)

And the solution to the likelihood Eq. (6) is

$$\hat{\beta }_{lasso} = \arg \mathop {\min }\limits_{\beta } \left\{ {\ell \left( \beta \right) + \lambda \mathop \sum \limits_{j = 1}^{m} \left| {\beta_{j} } \right|} \right\}$$
(7)

Unlike the ridge, in LASSO, the tuning parameter will make some of the regression coefficient equal to zero, and thus eliminating the least important variable from the model.

When \({l}_{1}\)-norm and \({l}_{2}\)-norm penalties are used simultaneously we have the elastic net regression;

$$\ell \left( \beta \right)_{elastic}^{p} = \mathop \sum \limits_{i = 1}^{n} \left\{ {y_{i} \log \left( {\pi \left( {x_{i} } \right)} \right) + \left( {1 - y_{i} } \right)\log \left( {1 - \pi \left( {x_{i} } \right)} \right)} \right\} + \lambda \left[ {\left( {\frac{1 - \alpha }{2}} \right)\mathop \sum \limits_{j = 1}^{m} \beta_{j}^{2} + \alpha \mathop \sum \limits_{j = 1}^{m} \left| {\beta_{j} } \right|} \right]$$
(8)

here the \({l}_{1}\)-norm is responsible for variable selection by setting coefficients some of the variables exactly zero and \({l}_{2}\)-norm does the job of shrinking the coefficient of the correlated variables with each other. In this way, the elastic net automatically handles the problem of multicollinearity in the model.

In (8), if \(\alpha =0\), then the elastic net will give ridge, and if \(\alpha =1\) then it will give LASSO regression. Thus \(\frac{\lambda }{2}\) is equivalent to the tuning parameter of the ridge and \(\lambda\) is the LASSO tuning parameter.

Packages like CARET can handle both classification and regression models.

3 Data

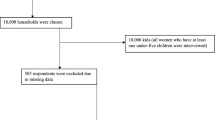
We have used the data from National Family Health Survey-4 conducted by the International Institute for Population Science during 2015–2016 under the Ministry of Health and Family Welfare, Government of India. In the NFHS-4, haemoglobin testing was conducted on the children (6–59 months) using the capillary blood for identifation and categorisation of aneamia. The anaemia was categorised as: severely anaemic (i.e., > 7.0 g/dl Hb level), moderate anaemic (i.e., 7.0–9.9 g/dl Hb level), and mild anaemic (10–10.9 g/dl Hb level). In the survey, total number of eligible children in North-East India was 29,312, out of which 10,504 children were found to be anaemic.Footnote 2 A total of 17 demographic variables were identified for our study and basis on it, we dropped all the rows with any missing observation. As a result, we were left with 10,460 anaemic and 18,725 non-anaemic children. Further, to make the data symmetric in terms of child anaemic status, 10,540 non-anaemic children are selected using the simple random sampling technique from 18,725 making the total dataset into 21,000 children.

3.1 Independent variables

The set of sixteen independent variables considered is based on child-mother, household and socio-economic characteristics. Child characteristics include Sex (male, female), Child Age (in months) (6–23, 24–59), Child’s Size (large, average, small), Breastfeeding (no, yes). Mother’s characteristics have Mother’s Age (in years) (15–19, 20–29, 30–39, 40–49), Mother’s Education (no education, primary, secondary, higher), Mother’s Anaemic Status (severe, moderate, mild, no). Household characteristics include Place of Residence (urban, rural), Sanitation (Hygienic, No-Hygienic), Disposal of Youngest Child Stool (safe, unsafe), Safe Drinking Water (yes, no), Household Size (< = 4, 5–7, >  = 8) and Number of Living Child (1, 2, 3, >  = 4). The socioeconomic information includes Wealth Quintile (poorest, poorer, middle, richer, richest), Religion (Hindu, Muslim, Others), Social Status (Schedule Caste, Schedule Tribe, OBC, and Others). Thus, in the aggregate 48 independent variables have been considered comprising aforesaid sixteen variables along with their subclasses. Table 1 gives the complete list of variables and their associated acronym.

Table 1 List of independent variables.
Full size table

3.2 Model evaluation

The performance of the models is evaluated based on receiver operating characteristic (ROC) curve, sensitivity, and specificity for the training outcomes whereas accuracy, sensitivity, specificity, precision (positive predictive value), negative predictive value F1 score, and Cohen’s Kappa value will be used for testing evaluation. The ROC curve is one of the best methods of accessing the performance of a classification algorithm. The area under the ROC curve (AUROC) is used as a basis for checking the discriminative adeptness of the model. AUROC or simply ROC value of a test is categorized as: 0.5–0.6 (fail), 0.6–0.7 (poor), 0.7–0.8 (fair), 0.8–0.9 (good) and 0.9–1.0 (very good). Accuracy is the degree of closeness to the true value of the population parameters. It is used for evaluating classification models to measure the proportion of cases of reproducibility (i.e., repeating the same value) of the measure set. Sensitivity is the proportion of true positives predicted as true by the classifier whereas specificity is the proportion of true negative cases predicted as negative by the classifier. Precision, also known as the positive predictive value, gives the proportion of the true positive out of the total predicted positive while negative predictive value is the proportion of true negative out of the total predicted negative. The harmonic mean of accuracy and precision is defined as the F1 score or F-value. It evaluates the overall model’s accuracy. F-measure affects the false positives and false negatives. A good F-measure means the model has low false positives and low false negatives. For a model, an F1 score of 1 is considered as a perfect model whereas a value of 0 is a total failure. And finally, Cohen’s k Statistics measures are useful in those problems where the data is imbalanced or involves a multiclass classification or both. This metric gives information about the agreement between predicted and estimated values.

4 Results and discussions

4.1 Bivariate analysis

A bivariate analysis is conducted before applying the ML techniques. In child characteristics, out of 21,000 children, 7,158 have come under the age group of 6–23 months having 63.06% (4514) prevalence of anaemia, the remaining children are under 24–59 months with 42.96% (5946) prevalence and p-value < 0.001 indicating that there is a highly significant relationship between CAS and CA. The data have a total of 10,860 male children with a prevalence rate of 50.17% (5449) and females have a prevalence of 48.88% (5,011) and the p-value, in this case, is greater than 5%, highlighting that there is no significant relationship between CAS and Sex. The average-sized children have the highest prevalence of 50.48% (7377) followed by large-sized children 49.15% (1882) and the small-sized children have 46.99% (1201). The prevalence rate of breastfeed children is 51.4% (7374) than the children without breastfeeding 46.37% (3086). The p-values for the CS and BF indicate that there are significant relationships of CAS with both CS and BF (Details can be seen from Table 2).

Table 2 Bivariate results of child characteristics.
Full size table

Mothers with moderate anaemic status have the highest prevalence of anaemic child 66.43% (1,304) followed by severely anaemic mothers 63.72% (72) and then mothers with mild anaemia 55.66% (4,090). Non-anaemic mothers have the lowest prevalence of 43.14% (4994). The p-value for the chi-square test also indicates a strong significance between CAS and MAS. The prevalence rate of child anaemia is highest among secondary educated mothers, 53.59% (1896), and lowest among illiterate mothers, 41.03% (556). In the meanwhile, there was a prevalence of 53.22% (2484) and 48.29% (5524) among the mothers with primary and higher educational backgrounds. In the different age groups of mothers, 348 children were found to be anaemic with a prevalence rate of 56.4% for mothers under the age group of 15–19 years, followed by a prevalence rate of 51.20% (6252) among the mothers in the age group of 20–29 years, 48.09% (504) for the age group of 40–49 years and finally, 47.10% (3356) for mother in the age group of 30–39 years. The p-values of ME, and MAGE are all less than 0.001, indicating a strong relationship between CAS and ME, MAGE (Details can be seen from Table 3).

Table 3 Bivariate results of mother’s characteristics.
Full size table

In household characteristics, households with non-hygienic sanitation facilities have a higher prevalence of 50.66% (7145) than hygienic sanitation facility households with 48.07% (3315). The prevalence is higher among the children with access to safe drinking water 50.66% (7145) than unsafe 48.07% (3315). In the disposal of the youngest child stool, unsafe disposal has 52.63% (7316) whereas safe disposal has 44.28% (3144). The household size less than 4 has the highest prevalence of 51.22% (3478) and the greater than 8 has the least 48.48% (1836). In the case of number of living children, families with more than 4 living children have the highest prevalence 53.64% (2240) and the least in those families with 2 living children, 48.38% (3302). Children who live in rural areas have a higher prevalence of 49.97% (8618) as compared to the children in urban areas 49.05% (1842). The chi-square values in Table 4 indicate that except for a place of residence, CAS is showing a strong relationship between sanitation, disposal of the youngest child stool, safe drinking water, household size and the number of living children.

Table 4 Bivariate results of household characteristics.
Full size table

In the wealth quintile, the middle-class has the highest prevalence 51.39% (2558), followed by the poorer and poorest class which have an almost similar prevalence of 49.52% (3631) and 49.88% (2411). Richer people have a prevalence of 49.02% (1372) while the richest people have the lowest prevalence of 46.21% (488). In religion, Hindu and Muslims have prevalence 42.16% (3327) and 36.99% (1419) respectively, while others have the highest prevalence of 61.62% (5714). Among the social strata, ST has the highest prevalence of 61.23% (6212) followed by OBC, others and SC with 43.19% (612), 39.84% (1159) and 37.94% (24,477) respectively. The chi-square values in Table 5 indicate there is a good degree of association between CAS and WI, REL, SS.

Table 5 Bivariate results of socio-economic characteristics.
Full size table

4.2 Training reports

Before we develop the machine learning models, the hot encoding process is used to convert all the (categorical) variables into multiple variables, each with a value of 1 or 0. The whole data is randomly partitioned into 80:20 as commonly practiced in ML techniques (Gholamy et al. 2018). Eighty percent as training (16,800) and twenty percent as testing (4200) datasets. The method of repeated cross-validation is considered to avoid the problem of overfitting.

The training outputs are then compared based on ROC, sensitivity, and specificity. Table 6 presents these performance measures and the best values of alpha and lambda on the training dataset. We can see from the table that the ROC values of the three models are almost the same with LASSO having a slightly higher value of average ROC and closely followed by elastic net and ridge respectively. LASSO also has the highest average values of both sensitivity and specificity. When it comes to the best median values, elastic net has the best ROC and specificity. LASSO again has the best median value for sensitivity. Figures 4 and 5 also give the model comparison based on box plots and 95% confidence intervals (CI).

Table 6 Comparison of training results.
Full size table
Fig. 4
figure 4

Accuracy comparison in terms of ROC, Sensitivity and Specificity

Full size image
Fig. 5
figure 5

Accuracy comparison in terms of 95% confidence intervals

Full size image

The models depicted in Figs. 6, 7 and 8 are ridge, LASSO and elastic net models respectively. These figures represent the plotting of penalized variables as a function of the regularisation parameter. Each colour represents a different variable in the plots.

Fig. 6
figure 6

Final ridge model, lambda = 0.0232

Full size image
Fig. 7
figure 7

Final LASSO model, lambda = 0.0020

Full size image
Fig. 8
figure 8

Final elastic model, lambda = 0.030 and alpha = 0.02

Full size image

In Fig. 6, we can see that all variables are shrinking towards zero because of the property of ridge regression in which correlated variables shrink towards each other. The variables that shrink initially are the least important whereas the most important variables shrink at last. In Fig. 7, variables follow the LASSO property of selecting only one variable among the correlated variables and eliminating others by making them equal to zero. In Fig. 8, the plotting pattern follows both shrinking and selection of variables as it is the generalised case of ridge and LASSO regression.

4.3 Testing reports

The models are now tested with the test data. All the models are giving almost the same level of accuracy. LASSO with an accuracy of 0.6429 and Kappa 0.2856 is the best. LASSO is closely followed by ridge and elastic net with an accuracy of 0.6419 and 0.6417 respectively. LASSO also has the highest values of sensitivity, positive predictive value, negative predictive value and F1, whereas ridge has the highest value of specificity. Detailed values of the performance metric of the three models can be seen in Table 7.

Table 7 Predictive performance of the three classification methods.
Full size table

After having a detailed investigation about the prevalence of anaemia through bivariate analysis and predicting it with acceptable levels of accuracy with the help of penalized regression models using ML techniques, we now turn to a brief discussion on major outcomes. Figure 9 gives VIP plots of the top 25 variables for ridge, LASSO and elastic net respectively.

Fig. 9
figure 9

VIP plots of ridge, LASSO and elastic net

Full size image

The results also suggest that gender, wealth index, and place of residence are not the most important variables for the prevalence of anaemia which is in contrast to that of Dey S et al. (2013). The VIP plots (Fig. 9) across the models reveal that the variables such as mother anaemic status, age of the child, social status, mother’s age, mother’s education, and religion are important factors in predicting the prevalence of anaemia. However, there is a little variation in the degree of their respective importance across the models. For example, mother’s anaemic status of moderate grade is the most important predictor in elastic and ridge models whereas in the case of LASSO, age of the child below 2 years is the most important one.

Now, as far as the social status is concerned, it is the ST category that dominates the prediction. As for maternal age, the mothers in the age group of 15–19 years are identified as the most important factor. In the mother’s education category, mothers with low education contribute more to the prediction than those with high education. This corroborates the findings of NFHS-4 reports and other studies (Dey S et al. 2013). In religious categories, it is the non-Hindu and non-Muslim, levelled as others (Table 1) appears to be prominent across the models. This could be because of the fact that a large proportion of the population belongs to the ST category and many of them do not follow either Hindu or Muslim religion. Apart from important variables, the models have identified a group of variables that moderately contribute to the prediction of anaemia, viz. disposal of youngest child’s stool, access to safe drinking water and wealth index.

Finally, the remaining variables like gender of the child, size of the child, number of living children, breastfeeding, household size, sanitation facility, and place of residence are identified by the models as least or unimportant variables for predicting anaemia.

5 Conclusion

We analysed NFHS-4 data in context of North-East India through penalized regression with three different models, namely, ridge, LASSO and elastic net. Of the 3 models, LASSO is giving the best results but the difference is negligible. We have achieved a ROC value of above 70% with training data and accuracy of above 64% with testing data, which is a reasonably acceptable outcome when working with the survey data. This study demonstrates the efficiency of ML algorithms in analysing and drawing inferences from demographic data. The major finding suggests that the prevalence of anaemia depends on various factors such as mother’s anaemic status, age of child, social status, mother’s age, religion, etc. which are important in predicting the prevalence of anaemia. Hence, the aforesaid factors should be taken into consideration in designing any affirmative action program in controlling anaemia among children (6–59 months).

Certainly, there are some limitations of this study that need to be specified to bring the complete aspects of accuracy. Firstly, the data of the study, which is based on NFHS-4 (2015–16), can have limitations in the consistency of the survey questionnaire as per demographic requirements. Responses to the questionnaire may not be correct or truthful, because of the number of missing entries in the data, and the chances of biasness by respondents or interviewers. Secondly, it could be due to the lack of the availability of related literature. As per our knowledge, there is scant literature on the application of machine learning techniques in general and penalized logistic regression in particular for predicting anaemic children using demographic data. Thirdly, there might be some important variables that are missing in the analysis due to the unavailability of appropriate data sets. However, a detailed investigation is necessary for specific socio-ethnic communities who are more prone to anaemia using different datasets.

Future research should focus on applying alternate ML techniques and using different data sets in predicting child anaemia and assess their relative efficacies. As far as different data sets are concerned, predicting child anaemia using medical image processing data could be another potential research direction that can be explored. Further, since ML algorithms are capable of identifying trends and patterns easily, the future research can look at applying those in predicting other disease such as heart disease, lung cancer, etc. Nevertheless, in spite of its limited scope, the present study aims to draw the attention of the Indian policy makers towards the various socio-economic factors in the fight against the child anaemia.