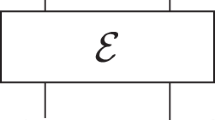Evidence for interactive common causes. Resuming the Cartwright-Hausman-Woodward debate

Abstract

The most serious candidates for common causes that fail to screen off (‘interactive common causes’, ICCs) and thus violate the causal Markov condition (CMC) refer to quantum phenomena. In her seminal debate with Hausman and Woodward, Cartwright early on focussed on unfortunate non-quantum examples. Especially, Hausman and Woodward’s redescriptions of quantum cases saving the CMC remain unchallenged. This paper takes up this lose end of the discussion and aims to resolve the debate in favour of Cartwright’s position. It systematically considers redescriptions of ICC structures, including those by Hausman and Woodward, and explains why these are inappropriate, when quantum mechanics (in an objective collapse interpretation) is true. It first shows that all cases of purported quantum ICCs are cases of entanglement and then, using the tools of causal modelling, it provides an analysis of the quantum mechanical formalism for the case that the collapse of entangled systems is best described as a causal model with an ICC.

1 Introduction

The common wisdom is that common causes screen off their effects: If two variables a and b have a common cause c and are not directly causally related (neither is a a cause of b nor vice versa), then a and b are marginally correlated but statistically independent given knowledge about c. This statistical characterization is widely believed to be a central feature of common causes and is captured by the causal Markov condition (CMC),¹ which is part of our best theories of causation (the CMC is an axiom of the theory of causal Bayes nets by Spirtes et al. (1993) and Pearl (2000), and a purported consequence of the interventionist theory of Woodward (2003)).

Some philosophers have challenged this view by a number of counterexamples: They have adduced situations in which conditional on the common cause the correlation persists and in this sense the common cause fails to screen off its effects from another. Referring to Salmon’s interactive forks (Salmon, 1978, 1984), which were the first putative counterexamples, we shall call such common causes that do not screen off ‘interactive common causes’ (ICC) and qualify usual common causes, that do screen off, as ‘conjunctive common causes’. Today it is well-known that many cases of purported ICCs, among them Salmon’s original proposals, are artefacts of incorrect descriptions of the system in question (cf. Spirtes et al., 1993, 61-3): described properly, all common causes in such systems do screen off and the CMC holds. We call such cases ‘apparent ICCs’ as opposed to ‘genuine ICCs’ that persist even in a correct description. While apparent ICCs are an epistemological challenge and occur frequently in scientific practice, it is of course genuine ICCs, violating the CMC, which are conceptually most interesting.

It is controversial whether all reported cases of ICCs are apparent,

• (Q1) Are there genuine ICCs in our world?,

and it is this question that I shall treat in the present paper. I shall answer (Q1) in the affirmative by arguing that not all cases of purported ICCs can plausibly be redescribed such that the CMC holds: There are systems in our world that involve a causal anomaly that genuinely has the structure of an ICC. Such genuine ICCs are not the result of a misdescription, but are real structures in our world.

Since the debate about possible violations of the CMC by common causes is ramified, I emphasize that (Q1) is to be distinguished from the following related but logically independent questions (Q2)–(Q6), which I do not treat in this paper:

• (Q2) Do all causal systems fulfil the CMC?²

• (Q3) If there is a failure of the CMC by a genuine ICC, how can one explain the correlation between the effects of the ICC (which are stronger than a usual common cause would explain)?

• (Q4) Do all causal systems fulfil modularity, i.e. the condition, roughly, that every effect in a system comes about by its own separate mechanism?

• (Q5) If there is a failure of modularity by genuine ICCs, how can one explain the violation?

• (Q6) Does modularity imply the CMC?

In this paper I focus on discussing the evidence for the case that there are genuine ICC structures (Q1) without treating (Q2)–(Q6).

As ICCs violate usual principles of causal modelling – by definition the CMC and, as a matter of fact, as I shall explain, also modularity and independent fixability – I further emphasize that in this paper I neither treat the question what the existence of ICC structures implies for the status of these principles of causal modelling. There are two rough options: either systems with genuine ICCs are not causal and hence the principles of causal modelling are not affected since they should not be applied to such systems. Or such systems are causal, and the principles of causal modelling are violated and need to be revised (at least for those domains in which ICCs occur). The reader may have a preference for the one or the other position but I shall not attempt to decide between them in this paper.

My main claim that there are genuine ICCs is not new. After the very first examples by Salmon and others had turned out to be apparent ICCs, it were van Fraassen (1980, 1982a, b) and especially Cartwright (1988, 1989) who provided the most promising candidates for genuine ICCs violating the CMC. The common characteristic of the examples is that common causes act indeterministically and produce their effects in pairs (e.g. due to conservation laws). Since indeterminism is required, realistic examples refer to the quantum domain (in an indeterministic collapse interpretation): A prominent example is the indeterministic decay of a molecule into two halves, where the momenta (or the size) of the halves is perfectly anti-correlated, but the state prior to decay does not screen off this strong correlation; another is the measurement of entangled properties in EPR experiments.

The position that there are genuine ICCs has not been very popular in the causal modelling literature, and has been defended for the last three decades or so nearly exclusively by Nancy Cartwright (Suárez (1997, §4.2) is an exception; among the few recent advocates is Näger (2014, 2016)). While her early writings on the subject were based on clear quantum cases of ICCs, Cartwright later mainly focussed on the example of a chemical factory (first in Cartwright (1993), and repeated in many following publications), which let her defence of ICCs turn out not as strong as it could have been, for at least two reasons. First, unlike the factory example, the quantum cases are particularly strong because they rest on a precise mathematical description that is empirically well-confirmed. Second, combining the claim with other controversial theses has watered down the position. In particular, the case of the chemical factory assumes controversial macro indeterminism, which has been shrugged off as fictitious (Glymour, 1999; Hausman and Woodward, 2004a). Finally, Cartwright’s defence suffered from the fact that she shifted focus from the central question (Q1) to related questions such as (Q2).

The debate between Cartwright on the one, arguing for genuine ICCs, and Hausman and Woodward on the other side, defending the CMC against Cartwright’s criticism, is the deepest and most intense debate about ICCs up to date, treating or at least touching upon all of questions (Q1)–(Q6); it took place in a series of long and intricate papers (Hausman & Woodward, 1999, 2004a, b; Cartwright, 2002, 2006) and illustrates the shift in discussion. In their first response to Cartwright, Hausman and Woodward (1999) extensively discuss the example of entangled quantum states and propose that even the quantum examples only apparently violate the CMC because the causal structure is misrepresented. In her subsequent answers, however, Cartwright does not reply to these questionable proposals (without giving reasons), and the debate focusses on her factory example, that Hausman and Woodward easily dismiss, and then continues to treat questions (Q2)–(Q6).

In this way it happened that up to now Hausman and Woodward’s proposals that would save the CMC in the quantum realm are undisputed; a debate about the plausibility of their claims is still missing. In general, the debate about proposed quantum ICCs has never been led conclusively and, since quantum ICCs are the most serious candidates for genuine ICCs, there exists considerable unclarity whether there are such ICCs.

This paper investigates in detail the central evidence for and against assuming a genuine ICC model for the quantum cases. Against arguments by Hausman and Woodward (and others) I defend the view that, if quantum theory in a dynamical collapse interpretation is true, there are genuine ICCs. In this sense this paper aims to catch up what Cartwright could have said in response to Hausman and Woodward 20 years ago and to make her case for ICCs as strong as it can be made. My main argument will be an analysis of the quantum mechanical formalism that yields an appropriate causal model for the theory. In this way, the present work is also a contribution to the emerging field of quantum causal modelling.

Since there are different interpretations of the quantum realm I should mention at the outset that this paper presupposes an interpretation of quantum theory that conforms to the following assumptions:

• (i) Strong quantum state realism: Fundamental quantum states describe objective and fundamental features of physical systems, and jointly with state independent variables (mass, charge, ...) they provide a complete description of these features.

• (ii) Indeterministic collapse dynamics: There are processes, in particular measurements with macroscopic devices, that are correctly described as a collapse of the quantum state, and the collapse is indeterministic in an ontic sense.

These assumptions are met by so called objective (or: dynamical) collapse theories. In most of the paper I shall assume the most simple version of such a theory, namely the Ghirardi-Rimini-Weber theory (GRW; Ghirardi et al., 1986), which assumes that the collapse is discrete and instantaneous. Only at the end of the paper (Section 5) I shall generalize the results to continuous collapse theories (e.g. the CSL theory; Pearle 1989, Ghirardi et al., 1990). The question whether there are ICCs is controversial even given the assumption of a dynamical collapse theory.

The paper is organised in five main sections. After a short characterization of ICCs that also introduces some terminology (Section 2), I review diverse phenomena from the quantum realm that purportedly are serious candidates for genuine ICCs and argue that all such examples are cases of entanglement (Section 3). The question whether there are genuine ICCs then reduces to the question whether entangled systems involve genuine ICCs. Analyzing the quantum mechanical formalism, I argue that entangled systems involve genuine ICCs; I also examine in detail why the main rival proposals are not viable (Section 4). Finally, I generalize my result from discrete collapse theories to continuous ones (Section 5) and shortly discuss the existence of ICCs according to other interpretations of quantum theory (Section 6).

2 Characterizing ICCs

2.1 Cartwright’s paradigmatic case and a decaying molecule

Cartwright proposes one of the paradigmatic examples in the debate: A ‘particle collides with an atom and the atom emits two new particles as a consequence’ (Cartwright, 1988, 184). Here we consider a variant of her example that there is a molecule in an unstable state z₁, which is disposed to decay and at some point decays into two even smaller objects, say, two atoms of the same kind. So according to both cases a pair of particles is produced that, due to the conservation of momentum, move in opposite direction, such that their total momentum remains zero.³ What is undetermined about this process is along which direction the particles fly off. Cartwright assumes the most simple case that there are only two possible directions (0 or 1), i.e. either, with a certain probability q, we have the momenta x₀ and y₀ (with x₀ = −y₀), or, with probability 1 − q, we have the momenta x₁ and y₁ (with x₁ = −y₁; see Fig. 1). By these assumptions, the probability distribution of this case is

$$ \begin{array}{@{}rcl@{}} P(x_{0} y_{0} |z_{1}) = q \qquad P(x_{0} y_{1} |z_{1}) = 0 \qquad P(x_{1} y_{0} |z_{1}) = 0 \qquad P(x_{1} y_{1} |z_{1}) = 1 - q,\\ \end{array} $$

(1)

which implies the conditional probabilities for each single atom,

$$ \begin{array}{@{}rcl@{}} P(x_{0} | z_{1}) = q \qquad P(y_{0}| z_{1}) = q \qquad P(x_{1} | z_{1}) = 1-q \qquad P(y_{1} | z_{1}) = 1-q.\\ \end{array} $$

(2)

Fig. 1

A molecule in state z₁ decays indeterministically into two oppositely moving parts along one of two directions

Here we have described physical properties or states, respectively, by values of variables x_0/1, y_0/1 and z₁. We shall denote the corresponding variables by bold symbols x, y, z and describe causal structures, as is usual in causal modelling, as between variables. Assuming, as it seems natural in the present case, that the state z of the molecule prior to decay both causes the momentum x as well as the momentum y of the emerging smaller molecules, and that these momenta do not influence each other after decay, yields a common cause structure $\boldsymbol x \leftarrow \boldsymbol z \rightarrow \boldsymbol y$. Since causal models consist of a causal structure (typically, a directed acyclic graph involving a set of variables as nodes and directed edges between the nodes such that there are no loops of arrows) and a probability distribution over the variables, this completes the causal model of the decaying molecule.

In causal modelling one usually requires certain axioms that constrain which probability distributions are consistent with which structures. The central assumption is the

Causal Markov condition (CMC):⁴ A variable a in a given causal structure is probabilistically independent of its non-effects (NE) conditional on its direct causes (DC):

$$ \begin{array}{@{}rcl@{}} \big[ \boldsymbol B = \text{NE}(\boldsymbol a) \wedge \boldsymbol C = \text{DC}(\boldsymbol a) \big] \quad \rightarrow \quad \ I(\boldsymbol a, \boldsymbol B | \boldsymbol C). \end{array} $$

The CMC is typically required to hold for all variables in a causal structure represented by a directed acyclic graph. For a common cause structure $\boldsymbol x \leftarrow \boldsymbol z \rightarrow \boldsymbol y$ the condition requires the statistical independence

$$ I(\boldsymbol x, \boldsymbol y | \boldsymbol z) \leftrightarrow \forall x,y,z: P(xy|z) = P(x|z)P(y|z), $$

(3)

which is also denoted as ‘z screening off x from y’.

A simple comparison between (1) and (2), however, yields that according to the causal model describing the decaying molecule, the value z₁ of the common cause, the considered state of the molecule before decay, in general does not screen off the perfect correlation between the atoms’ momenta x₀ and y₀:

$$ \begin{array}{@{}rcl@{}} P(x_{0} y_{0}| z_{1}) = q \neq q^{2} = P(x_{0} | z_{1}) P(y_{0} | z_{1}). \end{array} $$

(4)

The common cause model of the decaying molecule thus clearly violates the CMC.

Let me make two comments. First, the result that z₁ does not screen off does not depend on the exact value of q, as long as q is not 0 or 1. When q is 0 or 1 (‘determinism’), however, the equations reveal that screening-off holds trivially. Hence, indeterminism is a necessary ingredient for genuine ICCs.

It is an open question whether proposed ICCs such as the decaying molecule, besides violating the CMC, violate the condition of modularity. The condition, which has been introduced by Hausman and Woodward (1999), expresses the idea that every effect in a causal model comes about by its own separate process or mechanism. In mathematical causal models this is reflected in the fact that every variable has its own separate equation that determines its value by the values of its causes. If modularity holds, every causal process of the model is, in principle, independently disruptable, i.e. can be stopped without interfering with any other causal process that is not an effect of the stopped process. Hausman and Woodward (1999, 2004b) claim that modularity (plus some additional conditions) imply the CMC. If this were true, an ICC violating the CMC would also violate modularity (or one of the additional assumptions); however, Cartwright (2002) and Cartwright (2006) and Steel (2006) criticise the implication and it seems an open question whether the proposed cases of ICCs in fact violate modularity. We shall come back to this question in Section 4.3.3.

2.2 Conjunctive vs. interactive common causes

Here we shall not attempt at a general definition of ICCs in terms of necessary and sufficient conditions, which would be against the spirit of an axiomatic characterization of causal structures that causal modelling by causal Bayes nets provides (cf. Glymour, 2004). Rather, we discern and characterize conjunctive and interactive common causes via general paradigmatic causal models, of which the model for the decaying molecule is an instance.

The most simple, paradigmatic causal models with these types of common causes are shown in Fig. 2a and b. The models are to be understood as sufficient conditions: If there is a causal structure as indicated and the statistics is as indicated, then z is a conjunctive or interactive common cause, respectively. ICCs are marked by drawing an arc between the outgoing arrows, indicating that screening-off by the common cause fails.

Fig. 2

Two kinds of common cause models. a Conjunctive common cause structure. b Interactive common cause structure

These paradigmatic cases involving three variables might also be found as substructures of causal models. Note further that by these paradigmatic cases we have not said what it means to be an ICC in more complex cases (especially when x and y are additionally connected by a directed causal path or if there are further common causes of x and y) — this would require an axiomatic characterization. Since here we are about to argue that there are ICCs at all, it suffices to show that there are ICCs of the paradigmatic kind; so in the rest of the paper we shall concentrate on the simple paradigmatic causal structures.

An ICC z in a causal model M is apparent when according to the system S (a system in the world, a model of a theory or a causal model itself) that M describes, z is in fact a conjunctive common cause, i.e. M misrepresents the ontology of S with regard to z’s interactiveness. An ICC is genuine when it is not apparent.

It is well-known that one can generate models with ICCs by misrepresenting the causal structure in question. Figure 3 provides an overview of the central cases. It shows structures with the three variables z, x and y that yield z as an apparent ICC of x and y (a), if one wrongly omits those elements of the structures that are depicted in grey (b-h). We shall comment on each of these possible misrepresentations when discussing the causal structure of the quantum mechanical formalism in Section 4.

Fig. 3

Generation of apparent ICCs. Omitting the grey elements in the causal structures (b)–(j) yields an apparent ICC (a). a Interactive common cause structure. b Fine-grained common cause structure. c Latent common cause structure. d Intermediate common cause structure. e Direct cause structure. f Cyclic direct cause structure. g Non-separable structure. h Single effect structure 1: unity by identity. i Single effect structure 2: unity by composition. j Single effect structure 3: unity by dependent fixability

3 Promising candidates for genuine ICCs

3.1 Quantum ICCs are the most serious candidates for genuine ICCs

There is a number of purported cases that have exactly the same formal structure as the paradigmatic example (or can at least be simplified to have that structure). One needs to distinguish fictitious examples from realistic ones: The former are simply cooked up by assuming a suitable formal structure, however, without providing (enough) evidence that in fact there are such systems in our world (e.g. van Fraassen’s dividing bullet and Cartwright’s chemical factory have been claimed to be of this kind). Realistic examples, in contrast, agree in their structure with our best scientific theories or models, and it is controversial whether there are such examples.

Since indeterminism is a necessary ingredient for ICCs, the scientific background theory required for the realistic cases must be indeterministic. While many special sciences involve theories or models with indeterministic dynamics, such cases can easily be dismissed as involving only epistemic indeterminism, i.e. a more detailed description, which might epistemically not be accessible, would reveal that determinism and consequently screening-off holds.⁵ The matter is difficult to assess,⁶ but in the absence of strong arguments for ontic macro indeterminism, the genuineness of most macro cases from the special sciences remains at best unclear and potentially threatened by the reductionist claim.

In contrast, quantum theory (in a dynamical collapse reading) is ontically indeterministic and since the theory furthermore happens to be the most successful one in scientific history, quantum ICCs are the most serious examples for genuine ICCs.

3.2 Prima facie classification of proposed quantum ICCs

Prima facie, there seem to be four basic classes of quantum ICCs. (i) The example of unstable molecules belongs to the category of decay or division. Radioactive alpha decay is another clear case in this category: The ICC candidate is the unstable state of the radium nucleus that, in a certain amount of time, indeterministically decomposes into a helium nucleus and a radon nucleus, or not. Either both the radium and the radon nucleus are present or both are not – which fulfils the typical formal scheme of an ICC.

(ii) Other types of radioactivity like beta decay (a nucleus emits an electron and an anti-electron neutrino and a neutron inside the nucleus is transformed into a proton), or gamma decay (where a nucleus emits a high-energy photon and enters a lower energy state), might rather be subsumed under the class of emission processes: A system emits with a certain probability another system and thereby enters a new state itself. Another example would be atoms (or molecules) in an excited state, which in a certain time span with probability q emit a photon and (due to energy conservation) transit to their ground states, or (with probability 1 − q) do not emit a photon and just remain in the excited state.

(iii) Examples for a third class, jointly generated objects, are numerous in high energy physics, where collisions of two particles produce with a certain probability two (or more) particles, but due to conservation laws (especially energy and momentum, but also charge, spin, isospin, etc.) only certain combinations of particles can occur. For instance, one might have the case that collisions of an electron with its anti-particle (positron) with probability q produce an up quark and its anti-particle (up anti-quark) while with probability 1 − q the collision produces a down quark and its anti-particle (down anti-quark).

(iv) Fourth, entangled states

$$ \begin{array}{@{}rcl@{}} |z_1\rangle = \sqrt{q}|x_{0}\rangle |y_{0}\rangle + \sqrt{1-q} |x_{1} \rangle |y_{1}\rangle, \end{array} $$

(5)

as they are prepared in EPR experiments (maximally entangled for $q=\frac {1}{2}$, e.g. the entangled polarization state of two photons), yield exactly the same probability distribution as in Cartwright’s example (when measured at parallel settings): At measurement, the entangled state collapses onto one of the two product states

$$ \begin{array}{@{}rcl@{}} \begin{array}{ll} & |x_{0}\rangle |y_{0}\rangle \qquad \text{with probability } q \quad\quad~~ \text{or} \\ & |x_{1}\rangle |y_{1}\rangle \qquad \text{with probability } 1-q. \end{array} \end{array} $$

(6)

Since it is well-known that it is a peculiarity of entangled quantum states to be delocalized such that they can produce the correlated polarization measurements at space-like separation, we should note that our present considerations about ICCs do not hinge on this quantum non-locality in any way (causal graphs and statistics do not involve spatio-temporal features).

3.3 All proposed quantum ICCs are due to quantum entanglement

Despite the differences between the four classes of ICCs, there is a common feature (which at first sight might seem unintuitive): All mentioned processes defining a class are in fact cases of quantum entanglement. The reason is simple: According to the quantum mechanical formalism, if there are two alternative scenarios, say, x₀ and y₀ happening with a certain probability q, and x₁ and y₁ occurring with probability 1 − q (as in our paradigmatic scheme for an ICC), then the only way of the quantum mechanical formalism to express this is exactly to ascribe an entangled state as in Eq. 5.

Prior to its decay, Cartwright’s molecule is in the state (5), where the momentum states of the one particle (|x₀〉, |x₁〉) are entangled with that of the other (|y₀〉, |y₁〉). Or consider again the case of an excited atom that emits a photon (an excitation of the mode of the electromagnetic field) and thereby transits to its ground state: Since atomic states are always coupled to the electromagnetic field, the excited state is, in fact, an entangled state of an atom’s excitation state and the excitation state of a mode of the electro-magnetic field, which eventually transits to a product state of the two (see Walls and Milburn, 2008). While entanglement is usually only associated with its paradigm cases in EPR experiments, this consideration points to the fact, which is well-known among physicists, that entanglement is widespread in quantum systems with more than one object.

Consequently, the prima facie categorisation of quantum ICCs into different classes (i)–(iv) is somewhat misleading. In fact, all classes of proposed quantum ICCs are instances of quantum entanglement. Hence, entangled quantum systems are the most serious candidates for genuine ICCs in our world. This insight allows to narrow down our quest for genuine ICCs: The question whether there are genuine ICCs reduces to the question whether entangled systems involve genuine ICCs.

4 Causal analysis of the quantum mechanical formalism

We shall now examine whether measurements at an entangled system are correctly described by an ICC structure. According to a discrete dynamical collapse interpretation (GRW), which we presuppose here, the system is described by an entangled state (5), which shortly after contact with the measurement device collapses (with some probability) into one of two possible product states (6). Which causal structure appropriately represents this formal description? I propose that the entangled state z is an ICC of the states of the disentangled particles x and y after collapse (Fig. 3a). While this view is not new (van Fraassen, cf. 1982a; Cartwright, cf. 1989; Butterfield, cf. 1989) I here present a detailed analysis of the quantum mechanical formalism in terms of causal modelling. In developing my answer I shall contrast the proposed model with rival models claiming quantum ICCs to be apparent (see Fig. 3). I first discuss whether the variables are appropriately chosen before I treat the connections between them.

4.1 Modelling the entangled state prior to collapse as a single variable

The proposed ICC model describes the entangled quantum state (5) prior to collapse as a single variable z because entangled states are non-separable.

One might object that despite its non-separability the entangled state in the quantum mechanical description is composed of states for each of its two components and also that at measurement the entangled system decays into two systems. It might therefore have some appeal to assume the entangled system as being composed of two subsystems, each of whose states should be described by the value of a distinct variable ($\boldsymbol {x^{\prime }}$ and $\boldsymbol {y^{\prime }}$, respectively) and at the same time be closely related due to being non-separable. One might wish to symbolize the intimate relation between the two by an undirected edge, resulting in the model $\boldsymbol {x^{\prime }}-\boldsymbol {y^{\prime }}$ for the entangled state.

The so modelled entangled state can be integrated in the causal graph in two ways: one can either conceive of $\boldsymbol {x^{\prime }}$ and $\boldsymbol {y^{\prime }}$ as distinct variables, though connected by a relation of non-separability, such that each $\boldsymbol {x^{\prime }}$ and $\boldsymbol {y^{\prime }}$ can be a cause, i.e. the origin of an arrow in the graph (Fig. 4a). Or one can assume that the non-separable state $\boldsymbol {x^{\prime }-y^{\prime }}$ acts as one cause (Fig. 4b), in which case, however, one is essentially back to describing the entangled state as one variable in the causal diagram (modulo an internal structure). So we leave aside the latter proposal and discuss the former.

Fig. 4

Proposals for modelling the non-separable entangled state. a Non-separability 1. b Non-separability 2

There are at least three difficulties with the proposal. A minor problem is that one would have to make clear, how to derive probabilistic consequences from a structure with the unusual element of an undirected edge (I think that this can be overcome).

Second, since variables in causal modelling must have definite values, each $\boldsymbol {x^{\prime }}$ and $\boldsymbol {y^{\prime }}$ would have to have a definite value, i.e. each describes a well-defined state of the corresponding component system (and the connection between them presumably indicates that there are restrictions for the possible combinations of values). In quantum theory without hidden variables (see presumption (i) in Section 1) the only reasonable candidate for such states are the reduced density matrices of the component systems; however, pairs of such reduced density matrices are well-known not to be able to reproduce the strong correlations between the outcomes x and y.

Third, even if one could redescribe the entangled state in a more fine-grained way by two connected variables, that would not help to save the CMC. Whatever the exact meaning of the substructure $\boldsymbol {x^{\prime }-y^{\prime }}$ is: Since in the causal graph it has the role of a common cause, it is a requirement of the CMC that conditional on $\boldsymbol {x^{\prime }-y^{\prime }}$, the correlation between x and y is screened off. Since, however, $\boldsymbol {x^{\prime }-y^{\prime }}$ represents the entangled state and the entangled state is known to not screen off the correlation between x and y, $\boldsymbol {x^{\prime }-y^{\prime }}$ does not screen off. Hence, the CMC will be violated in that description as well.

In sum, it is questionable whether the description of an entangled state by two connected variables can succeed; and even if it does it does not seem to make a difference for the violation of the CMC. For these reasons I shall describe the entangled state prior to collapse by a single variable z.

4.2 There are no further relevant variables prior to collapse

According to the proposed model, the entangled quantum state z is the only variable prior to collapse. As it is well-known that omitting proper common causes can lead to apparent ICCs (Fig. 3b–d),⁷ it is a central requirement in causal modelling that one has accounted for all common causes of the set of considered variables (‘causal sufficiency’).

First, since here we are presupposing that the quantum mechanical formalism is complete (see presumption (i) in Section 1), we can safely rule out that there are states beyond the quantum mechanical formalism that need to be considered. This precludes structures that presuppose that the entangled quantum state is an incomplete description requiring a more precise characterization by hidden variables u (Fig. 3b) or that there is a further latent common cause (Fig. 3c).

Second, neither does the spatial component of the wave function, which we have not considered, play any essential role when it is separable from the spin component (as we have presumed), nor does one need to consider the state independent properties of the entangled quantum objects like mass and charge, since these do not change over the measurement.

Finally, according to the quantum mechanical description, there neither is an intermediate common cause u (as in Fig. 3d) that screens off. The entangled quantum state is the last state before collapse and the transition from the entangled state z to the collapsed states x and y is temporally not extended: The entangled system described by z exists up to the very point in time at which the separate objects described by the product state start to exist. Especially, there is no instance in time at which an intermediate state u might exist.

4.3 The product state after collapse is not a unit

The state immediately after collapse of the entangled state is a product state and reads |x₀〉⊗|y₀〉 or |x₁〉⊗|y₁〉, respectively, where the sign ‘⊗’ denotes the tensor product. (In short notation one often omits the sign, cf. e.g. Eq. 6). While we have seen that the entangled state is plausibly modelled as one variable, the product state lacks all the peculiar features that make the entangled state so special. There are four essential differences that speak for the case that one should model a product state by the two distinct variables x and y that describe its components.

First, the product state assigns definite states to each component system (according to both central interpretations of quantum states).⁸ The two states connected by the tensor product (in a two-particle product state) are definite (one-particle) states, each describing one of the objects that have been disentangled by the collapse. That the values of the component variables are well-defined is a necessary requirement for regarding them as variables of a causal model.

Second, the component states of product states are synchronically separable. Describing the state of the one object by |x₀〉 or |x₁〉, respectively, is a complete description of its state (at a certain instant). There is no need to refer to the state of the other object. There is no connection between the components of product states. Joining states by the tensor product is quantum mechanics’ rule to form the joint state of two (or more) separate systems. Any correlation between the components of such systems must be due to their common causal history.

Third, the joint product state supervenes on the component states and it is therefore the latter which should be regarded as fundamental. There is no further variable besides the product state that describes the joint system. Consequently, describing the joint system by one variable would describe a non-fundamental level and therefore not fit well with the structure of the quantum mechanical description.

Fourth, the component states of product states are diachronically separable if the objects do not interact: In this case one can separate the dynamical equations for each component system (in quantum mechanics: Schrödinger equation) and treat them independently. Without interactions, there is no connection between the component states of product states.

In sum, the component states of quantum product states are as separate and distinct as are states in classical physics (whose joint state is described by a Cartesian product state). Quantum theory, which is our best theory of entangled systems including their dynamics, describes the systems after collapse by two distinct variables, and there is no evidence in its description for counting them as one joint variable. For these reasons, the proposed model describes the state of each subsystem as values of distinct variables x or y, respectively.

Against this direct, literal reading of the quantum mechanical description one might object that there are features of the product state after collapse that speak for the case that x and y in fact are not separate and distinct and therefore should be described as one variable. Three options have some prima facie plausibility: (i) x and y denote the same event by different descriptions (Fig. 3h, unity by identity) or (ii) x and y describe different parts of one event (Fig. 3i, unity by composition) or (iii) x and y are not independently fixable (for some other reason than identity; Fig. 3j, unity by dependent fixability). In each of these cases, if one wrongly considers x and y as two different events, their cause appears to be an ICC. Note that, when talking about entanglement in EPR experiments in the following, the states after collapse x and y are also called ‘measurement outcomes’ or simply ‘outcomes’.

4.3.1 Against unity by identity

An example for the proposal that x and y denote the same event would be the case that z₁ describes the decay of a radium atom, x describes whether an alpha particle is emitted, and y whether a helium nucleus is emitted. Clearly, x and y are identical and therefore perfectly correlated; it is clear that in such situations the same formal scheme as in Cartwright’s example holds, hence z₁ appears to be an ICC.

The descriptions referring to the same event need not be analytically equivalent as in the given example; it suffices that they non-analytically refer to the same event (as for Frege’s morning and evening star). Since in any such case x and y, represented as distinct variables, would violate the requirement that variables in a causal graph must describe distinct states, I suggest to represent such situations by including both x and y in one node and indicating the identity of their referent by an identity sign (Fig. 3h). Then the correlation internal to the node is explained by the identity of the variables, and there is no external correlation between distinct variables that could violate the CMC.

There is, however, no question that this proposal cannot be true in the case of entanglement. For it would amount to saying that one electron turning out spin up is the very same event as the other electron turning out spin down. A claim of identity in this case would contradict the uncontroversial facts that, first, there are two electrons, and, second, that the electrons (in the present example and generally) differ in their properties.

4.3.2 Against unity by composition

The idea that x and y should be described as one event because they describe different parts of an event that should be considered as a unit amounts to the claim that the ICC is apparent due to a mereological misdescription. As an instructive example one can consider the case of a radium atom emitting an alpha particle, consisting of two protons and two neutrons, with a certain probability lower than 1.⁹ If by z₁ one describes the decay event, by x, whether two protons are emitted, and by y, whether two neutrons are emitted, we again get the same formal situation as in Cartwright’s example (1).

This model, however, misdescribes the situation, since the alpha particle is one object, so its emission should not be described by two different variables. Rather one should represent x and y as one node in the graph (Fig. 3j), i.e. z is not a common cause but a usual single cause. In this example ontological—more precisely: mereological—considerations play a crucial role: It is the unity of the alpha particle which requires to summarize x and y as one variable and leads to accept the correlation between the variables as not in need of causal explanation.

One might be tempted to advance a similar claim for entangled systems: Rather than describing each component of the product state after collapse separately, e.g. one electron having spin up and the other having spin down, one might think that these states compose a joint state that must be described as a unit. Then, x and y should not be considered as separate variables but as a composite variable xy. According to this re-description there simply would be no correlation between distinct variables that needs to be explained, hence the CMC could not be violated.

In contrast to the case of the alpha particle, however, I deny that the description of the product state after collapse as a causal unit is correct because there is no criterion according to which a quantum mechanical product state should be regarded to be a unit. First, it is clear that entanglement cannot help to lay the foundations of a unit in this case since the emerging objects after collapse are not entangled any more.

Second, our examples of entangled systems show that the objects emerging after collapse are not generally bound to each other (e.g. a decaying molecule or an atom emitting a photon).¹⁰ (In the case of the alpha particle this criterion is fulfilled, since the alpha particle consists of two protons and two neutrons binding with each other.)

Third, the sub-states of the product state, which are candidates for the parts of the composite state, can be arbitrarily spatially separated: In typical setups of EPR experiments, the states after collapse describe objects that are non-locally related without borders. (The components of the alpha particle, in contrast, are close to each other.)

In sum, there is no evidence to describe the product state after collapse as a unit that emerges by composition.

4.3.3 Against unity by dependent fixability

Woodward’s position

A third reason for regarding the product state after collapse as one variable is discussed by Hausman and Woodward (1999): x and y are not sufficiently distinct to be separate variables in causal models. The criterion for distinctness of variables that Hausman and Woodward appeal to is today widely called ‘independent fixability’ (IF; ‘independent disruptability’ in their paper from 1999) and is a central and necessary requirement for (purely) causal models according to an interventionist theory of causation: The set of variables in a causal model has to be chosen such that ‘it is possible to intervene on every variable [...] and to set each such variable to each of its values independently of the values to which other variables are set.’ (Woodward, 2015, 312) If a set of variables contains a pair of variables that cannot be intervened on independently, the set is not suited to serve as the basis for a (purely) causal model.¹¹

Hausman and Woodward illustrate their idea with the already mentioned case of a radium atom emitting an alpha particle (cf. Section 4.3.2). They caution that one should not choose one variable x to describe whether two protons are emitted, and another y to describe whether two neutrons are emitted, because that would violate independent fixability: One could not intervene on x without intervening at the same time on y (and vice versa). In other words, one cannot break the causal mechanism from z to x without breaking the one from z to y (and vice versa). Accordingly, they claim that the emission should be described by one variable, i.e. x and y are represented as one node in the graph (Fig. 3j), such that z is not a common cause but a usual single cause.

Now, for entangled systems (Hausman and Woodward, 1999, 564–7)¹² advance a similar claim: They maintain that the state after collapse, i.e. the product state, which consists of the two measurement results x and y should in fact be described as one variable, avoiding z to be an ICC, because independent fixability fails for x and y:

The notion of an intervention with respect to one of the measurement events is not well-defined in the EPR phenomena, because the distinction between intervening with respect to [x] and acting directly on both [x] and [y] cannot be drawn. The reason given for this within the standard interpretation is that the correlated particles are in a so-called non-separable or entangled state. In some way that is difficult to understand, the two particles constitute a single composite object, even though they may be at space-like separation from each other. The measurement result on one wing [of an EPR experiment] is not really a distinct event from the result on the other wing but rather both comprise ‘a single, indivisible non-local event’ (Skyrms [1984], p. 255).

                                                                                                                     (Hausman & Woodward, 1999, 566)

The central idea here is that the measurement outcomes x and y should not be considered distinct causal variables since they are not independently fixable.¹³ This would amount to saying that one may not consider one electron having spin up (x) as a distinct event from the other having spin down (y), but needs to consider the two as one joint event xy. According to this re-description there simply would be no correlation between distinct variables that needs to be explained, hence the CMC could not be violated.

Different readings

The truth of the claim that the measurement outcomes are not independently fixable crucially depends on what exactly one means by ‘measurement outcomes’. I shall now discern three different readings only one of which makes the claim true. Subsequently, I shall explain why even in the reading according to which the assumption of distinct variables would violate IF there are good reasons to regard the variables to be distinct.

Let us make clear the measurement process according to a discrete dynamical collapse interpretation of quantum mechanics: We have a system of two particles, say two electrons, in an entangled state, which above I have argued to be appropriately described by one variable z. Each particle moves towards a measurement device¹⁴ and at the point in time t₁, when the first particle, say the left one, hits the detector, the entangled state collapses instantaneously to a product state, described by quantum mechanics as |x₀〉|y₀〉 or |x₁〉|y₁〉. From this moment on the dynamical evolution of the two particles is decoupled: The first particle further interacts with the matter of the detector (either it is scattered or absorbed), however, since the particles are disentangled, without affecting the second particle, which is still on its flight to the other detector. In the physical description of such experiments one is not interested in the states of a particle after it has hit the detector; rather what is important is that the interaction changes the physical state of the detector such that the detector outputs a signal that is transferred to a humanly readable display; say, the left measurement result is displayed starting from t₂. When the right particle hits the detector (say at t₃ > t₂), it interacts with the detector, which starts a process that causes the right display of the measurement result starting at t₄.

This somewhat detailed description will now help us to discern different readings of Hausman’s and Woodward’s claim. Let us call the immediate states of the electrons after collapse (at t₁) x and y, the non-immediate states of the electrons after collapse x^′ and $\boldsymbol y^{\prime }$ (at some t > t₁) and the state of the displays of the measurement devices $\boldsymbol x^{\prime \prime }$ (at t₂) and $\boldsymbol y^{\prime \prime }$ (at t₄). Any of these pairs of variables might with some reason be called ‘measurement outcomes’ and Hausman and Woodward do not say explicitly which of these events they mean when they claim that the measurement outcomes are not independently fixable — so let us assess their claim for all three possible meanings.¹⁵

First, in the debate about EPR experiments and entanglement ‘the measurement outcomes’ usually denote the displays of the measurement devices $\boldsymbol x^{\prime \prime }$ and $\boldsymbol y^{\prime \prime }$. Understood in this way, it would, however, be false to claim that the measurement outcomes are not independently fixable: One can clearly fix the state of the display of the measurement device $\boldsymbol x^{\prime \prime }$ by some intervention, e.g. one can intervene on the position of the displaying pointer just as one can intervene on a barometer dial (the latter is one of Hausman and Woodward’s example of a valid intervention, see their 1999, 536).

Second, also the non-immediate states $\boldsymbol x^{\prime }$ or $\boldsymbol y^{\prime }$ of the electrons after collapse are independently fixable. Since at the time of the non-immediate states the intimate connection due to entanglement has ceased to exist, the process from x to $\boldsymbol x^{\prime }$ is independently disruptable from the process from y to $\boldsymbol y^{\prime }$; and since the time interval between the collapse and the non-immediate states is finite, there is no principled obstacle to perform an intervention. Intervening on the spin of the one electron ($\boldsymbol y^{\prime }$), is possible and would not change the spin of the other ($\boldsymbol x^{\prime }$). Consider, for instance, the state $\boldsymbol y^{\prime }$ of the electron that is still on its way to the right detector: One can perform all sorts of local physical manipulations on the state of this particle (e.g. reversing the spin by magnetic fields) that will not affect the other particle (since the particles are disentangled since t₁) and that, if suitable, fix the value of the variable.

Third, concerning the immediate states x and y after collapse (at t₁), however, the claim that independent fixability fails is true. One cannot intervene on x (by disrupting the process to x) without disturbing y because the processes leading from z to x and from z to y are both described by the collapse. There is no way to interrupt the collapse for one variable but not for the other. (The reason for the failure of IF is emphatically not that x and y are non-separable – forming a product state they are separable!) Consequently, the best reading of Hausman’s and Woodward’s claim that the measurement outcomes are not independently fixable is that it is the immediate states of the quantum objects after collapse, described as two distinct variables, which are not independently fixable.

Discussion

In its best reading, Hausman and Woodward’s argument then is to say that the outcomes immediately after collapse should be described as one variable, because they are not independently fixable and independent fixability is a necessary criterion for variables in causal models to be distinct. Upholding independent fixability would also save the CMC because the problematic correlation between the outcomes is hidden in the joint variable. This description is in accordance with usual principles of causal modelling.

Although it would be desirable to uphold all usual principles of causal modelling, I think that there are at least three good reasons to describe the immediate outcomes after collapse of the entangled state as two variables and to accept a violation of independent fixability and modularity, and, hence, to acknowledge an anomaly for interventionist theories of causation requiring the principles.

First, at the beginning of Section 4.3 I have argued that according to quantum mechanics the states immediately after collapse are described by two separate variables. So our best scientific theory of such systems makes a clear choice, and I think it is reasonable to require that causal models should be in accordance with our best scientific theories. One might object that quantum theory should not be taken too seriously when it comes to judging matters of causation because it is not based on the principles of causal modelling. That, however, seems a questionable assessment. Quantum theory does provide information that is relevant for causal models: It is an essential part of the quantum theoretical description (i) how to segment systems into distinct variables and (ii) how these variables evolve dynamically over time, especially which variable influences which — and this is exactly the information that is summarized in causal models. Quantum mechanics provides well-tested and the best description of this kind for entangled systems that we have.

Similarly, second, causal models should agree with our best ontological models. I have argued above that there is no reasonable criterion of composition that would require to regard the variables as one. According to all criteria the variables should be considered to be distinct. Then, to assume the immediate states after collapse as one variable would be in tension with our ontological assessments.

Third, describing the immediate states after collapse as one variable would have the consequence that the deep and mysterious EPR correlations are not recognizable in the model, since they are then hidden inside the joint variable. Since causal models only require explanation of correlations between distinct variables, this assumption would dispose the EPR correlations of the need to be explained. It is, however, difficult to believe, that the notorious EPR correlations should turn out as a mere artefact of misdescription, a scheinproblem in the modern philosophy of physics. While one can challenge that the EPR correlations can be explained causally (although I think they can), causal models should definitely not hide them, but rather make them explicit by describing the case with two variables.

In sum, I think that the reasons for describing the immediate states after collapse as two separate variables are quite strong such that the resulting violation of independent fixability is well-founded.

The violation of IF appealed to here does not seem to be restricted to the quantum realm. As an illustration, imagine the case of dividing a piece of twine in two halves with scissors. Let z describe the position of the scissor relative to the undivided twine before the cut and x and y denote the length of the left and right piece of twine, respectively, immediately after division. Clearly, the processes towards x and y are not independently disruptable: One cannot interrupt the process to the one without interrupting the process to the other. This does not imply, however, that x and y are not separate variables. Then, IF and modularity fail for the twine as for entangled systems.

As a result of the considerations about the quantum mechanical formalism so far, we note that the quantum mechanical description of entangled states should be understood to involve three distinct variables: the entangled state z and the components of the product state after collapse, the measurement outcomes x and y. We now turn to the question which connections hold between these distinct variables.

4.4 The entangled state is a common cause of the collapsed states

The proposed model involves a causal relation from z to x and from z to y, such that z is a common cause of x and y.

It is natural to think that the entangled state is a cause of its collapsed state, and none of the usual models denies this. To justify the claim, the causal relations in question can be inferred by interventions. Interventions on the entangled quantum state are in most cases unproblematic since in typical EPR experiments the experimenter prepares, and hence controls the quantum state. There is no evidence that the preparation of the entangled state might not be an intervention. An experimenter can vary the entangled stated at will (e.g. vary the value of q in Eq. 5) and then observe that under such interventions on z, z is correlated with x as well as with y. Hence, by usual standards of causation z is a common cause of x and of y.

4.5 There is no connection between the collapsed states

The proposed model assumes that there is no direct connection between the collapsed states x and y. If this is true, the CMC is violated because even conditional on the common cause z, x and y remain correlated to some degree – and this ‘excess correlation’ that is not screened off by z cannot be explained by the CMC.

It is clear that conservatives about causal modelling, who acknowledge that the outcomes are separate variables (as we have argued above), have a high motivation to assume a model according to which there is a connection of some kind between x and y that might explain the failure of screening off in a way consistent with the CMC. The connection might be either causal in one direction (Fig. 3e) or bidirectionally causal (which would be a loop of two causal processes in opposite direction; Fig. 3f), or symmetrically non-causal (here depicted as a non-directed edge, Fig. 3g).^16,17

Most proponents of a connection between the outcomes have assumed the connection to be non-causal because causation has been associated with a flow of conserved quantities and the ability to send signals, but it is well-known that there is neither a flow of conserved quantities from one wing of an EPR experiment to the other, nor can one send signals (and furthermore both seems to be forbidden between space-like separated events by the principles of relativity). The abstract approach to causation assumed by causal modelling, however, is not committed to such characterizations of causation, and, in fact, a recent analysis has revealed that quantum mechanics explains the failure to send signals by a fine-tuning of the causal parameters (Näger, 2016). So we here generally discuss the evidences for a connection, whether causal or non-causal. What is important is that in any case we need to look for a real physical connection; a mere correlation and any epistemic relation that is implied by mere correlations like ‘knowing A entails B’ would not suffice (correlations are the explanandum, not the explanans).

There is one noteworthy difference, though: While models with a causal relation would save the CMC, models involving a non-causal relation would literally violate the principle. However, Gebharter and Retzlaff (2020) explain that – in contrast to models without any connection – the main idea of the causal Markov condition (and Bayes net modelling), that correlations are to be explained by structure, can be saved in such scenarios when one generalizes the CMC to structures including non-causal relations (‘global Markov condition’, GMC). If the GMC is correct, it solves the additional challenge for a view that assumes acausal connections, namely to provide a rule for how to derive probabilistic consequences from a structure with the unusual element of a symmetric non-causal relation (compare a similar problem for the proposal in Section 4.1).

4.5.1 Hausman’s view

Hausman and Woodward (1999) are among the proponents of a non-causal connection between the outcomes. They present the position (which seems to be Hausman’s view) as an alternative to their view that assumed the unity of x and y (which is Woodward’s position; see our discussion in Section 4.3.3 and especially Fn. 12):

[The measurement results of EPR experiments] are distinct events, but they are not probabilistically dependent on one another in virtue of being cause and effect or effects of a common cause. Instead they bear a different kind of non-causal (but non-accidental) relation to one another.

                                                                                                                     (Hausman & Woodward, 1999, 564f.)

Since they advance this claim in the context of a discussion of common cause models $\boldsymbol x \leftarrow \boldsymbol z \rightarrow \boldsymbol y$, it seems fair to assume that they do not mean that there is no common cause at all, but rather that the correlation between the measurement results are not only in virtue of a direct causal relation or common cause, as the common cause will surely contribute to the correlation to some extent. If this interpretation is correct, their view might best be represented by a structure similar to Fig. 3g.

In order to assess the position one would need more details about the kind of the non-causal relation and evidence why to assume it. Since Hausman and Woodward, however, do not provide these details, we move on to more explicit, elaborated versions of this kind of model (leaving open that they could have meant one or the other of the following models).

4.5.2 Making the models more explicit

The view that there is a non-causal, correlation producing, or at least correlation explaining, relation between the measurement outcomes is rather widespread in the debate about entanglement and Bell’s theorem. The strong correlation between the outcomes that persists even given the complete quantum state at the source (‘outcome dependence’) has been thought to establish some kind of non-causal connection between the outcomes and has been given different names, most prominently ‘passion at-a-distance’ (introduced by Shimony (1984) and adopted by others, e.g. Redhead (1986) and Jarrett (1989)). While the view emerged from the discussion about the more general Bell theorem, in the following we shall examine what we can say from a causal modelling perspective on the basis of the quantum mechanical formalism.

Since the connection is assumed to hold between ‘the measurement outcomes’, we should recall the discussion from Section 4.3.3 that there are different possible understandings of the term, which might either mean the states of the particles immediately after collapse, or the non-immediate states of the particles after collapse or the states of the humanly readable displays of the measurement apparatuses. Here as well, I think, it is obvious that when the claim about the connection between the outcomes is to make any sense, it should presume the first meaning. So the models we are considering here assume that the states immediately after collapse are connected by a symmetric non-causal relation of some kind.

How could one justify a connection? I emphasize that in the present context it would be question begging to argue that there must be some kind of connection between the outcomes because the CMC (or GMC) requires it in order to explain the strong correlation. Since the question here is whether there are genuine ICC structures violating the CMC, one cannot just assume that the CMC holds without giving further reasons; rather, independent reasons for the existence of a connection would be required, and here we examine whether the quantum mechanical formalism provides evidence for a connection.¹⁸ In order to establish a connection we need a correlate in the formalism. There are four prima facie possible candidates: interactions, the relation of non-separability, the collapse and conservation laws.

4.5.3 Interactions

It is well-known that usual interaction potentials (that appear in the Hamiltonian) cannot connect the outcomes. Consider, for instance, that the experiment involves two electrons, which due to their charge would clearly interact electromagnetically with each other. But, first, this is not the general case, since one could have particles emerging from an entangled state that do not interact at all, say two photons; and second, even if one has an interaction, such interactions do not propagate faster than the speed of light.

4.5.4 Non-separability

One might think that the non-causal relation between the outcomes just is a holistic relation of non-separability. However, while it is clear that the entangled state is non-separable, the view that the measurement outcomes are non-separable is implausible: By the quantum mechanical formalism, the measurement outcomes occur after collapse, i.e. entanglement has ceased to exist and the post-collapse product state we are about to describe is explicitly separable.

4.5.5 Collapse

Another, more serious candidate for a connection between the outcomes is the collapse of the entangled state. Being instantaneous, it can in principle connect space-like events. Nevertheless, the collapse does not seem to be appropriately described as an influence from the one outcome to the other for two main reasons.

First, the collapse is an instantaneous process which describes the transition from the entangled state (5), the first stage of the process, to the product state (6), the final stage of the process.¹⁹ It is in this sense, maybe somewhat imprecisely, that we have said that the outcomes are the quantum states immediately after collapse. But if the product state is the final stage of the process called ‘collapse’, then the collapse cannot be a connection between the components of the product state, which are the outcomes.

Second, rather than describing a positive, physical connection between the objects, the collapse describes the breaking of such a connection: The collapse describes the transition from the entangled state, according to which the distant objects are connected by a relation of non-separability, to the product state, according to which each object has its own separate state. So the collapse for entangled systems describes the collapse of the relation of non-separability, and its result is the absence of that formerly existing connection, described by the separate outcomes. According to the quantum mechanical formalism, the outcomes x and y are just components of a separable product state and there is no connection between the two.

Again the analogy with the case of dividing a piece of twine might help to push intuitions here, the collapse being analogous to the cut: Before the cut the pieces making up the twine are physically connected, and the cut leads to two unconnected pieces. It would be absurd to say that the cut connects the pieces. The strong correlations between the pieces after the cut (they always add up to the original length) cannot be explained by a connection between them.

I conclude that the collapse is not a suitable correlate in the formalism for grounding a connection between the outcomes. The collapse rather seems to be appropriately understood as a process from a common cause to its effects (and the effects are not connected, at least not by the collapse).

4.5.6 Conservation laws

It has some prima facie appeal to think that the connection between the outcomes might be given by conservation laws, since the collapse of paradigmatic entangled states like the singlet state

$$ |\psi_{1}\rangle=(|\uparrow\downarrow\rangle-|\downarrow\uparrow\rangle) /\sqrt{2} $$

(7)

seems to conserve the total spin direction $S_{z}^{AB}$ (the single spin directions sum to zero before and after measurement).

Gebharter and Retzlaff (2020) have recently formulated a view along these lines in the context of causal modelling. They argue that in cases of purported ICCs and especially in EPR experiments the effects of the common cause are connected by a kind of non-causal dependence that ‘arises due to background assumptions which rule how quantities, properties, or parts are distributed among different objects or places if the common cause occurs.’ (p. 1468f.) They hold that in the EPR case the relevant background assumptions or ‘distribution conditions’ (p. 1479) as they also call them, are conservation laws.

Pairs of entangled photons can, for example, be produced by splitting a photon beam with a non-linear crystal obeying energy and momentum conservation. So there seem to be laws of nature (i.e., the principles of energy and momentum conservation) ruling how quantities are distributed that are responsible for the fact that [x] and [y] are dependent conditional on [the entangled state and the polarizer settings].                                 (Gebharter & Retzlaff, 2020, 1480)

They then rule out causal relations (due to the space-like separation of the outcomes) and conclude that the connection between the outcomes established by the conservation laws is non-causal.

I would like to mention two worries that I have with this proposal. First, the proposal seems to amount to the claim that a conservation law determines how the conserved quantities in question are ‘distributed’ among the two outcomes, such that the outcomes are correlated. We then have the following dilemma: Either, in a literal reading, the conserved quantities are distributed, as the connection indicates, between the outcomes. Then, however, since the outcomes are space-like separated that would involve some kind of superluminal propagation of conserved quantities, in tension with relativity. It does not help for consistency with relativity to just say that the connection is non-causal when a space-like flow of conserved quantities is involved. Alternatively, in a non-literal reading, the conserved quantities are distributed in the preceding process from the non-local entangled state to the outcomes. Then, however, it would be inappropriate to regard the connection as holding between the outcomes, because the distribution has already occurred when the outcomes emerge.

A second worry is this. On the one hand, it is true that conservation laws play a central role in typical generation processes for entangled states. In the case of the decaying molecule, for instance, it is momentum conservation, which restricts the entangled state to only involve terms with opposite momenta. On the other hand, when talking about the correlations of the measurement outcomes given the entangled state, we are not concerned with the generation but with the measurement of entangled states, i.e. the existence of an entangled state is presupposed and the measured correlations between the outcomes need to be explained. There is, however, no conservation law for measurements: The non-unitary collapse that occurs at measurement in general neither preserves probability distributions nor expectation values of physical quantities. By collapsing all terms in the superposition but one, both the probability distributions and expectation values generally change. Typical conservation laws in quantum physics therefore rather refer to the unitary Hamilton dynamics that can, given certain symmetries, preserve the expectation value of certain quantities.

Let me shortly illustrate the claim. On the one hand, one can be easily deceived by the singlet state, according to which conservation holds: The probability distribution for the relevant variable, the total spin direction $S_z^{AB}$, is $P(S_z^{AB}=0)=1$ before measurement, and it remains unchanged after measurement for each of the states $|{}\uparrow \downarrow \rangle$ or $|{}\downarrow \uparrow \rangle$. Consequently, the expectation value of the total spin direction remains unchanged as well. ²⁰ On the other hand, the expectation value, and hence the probability distribtion, does change for other entangled states like $|\psi _{2}\rangle =\frac {1}{\sqrt {2}}(|{}\uparrow \uparrow \rangle +|{}\downarrow \downarrow \rangle )$.²¹ So the conservation of the probability distribution and the expectation value of the total spin direction given the singlet state cannot be law-like; it is an accidental fact that is due to the symmetry of the state, i.e. the initial conditions, not due to the symmetry of the dynamics.

In sum, at the measurement of entangled states there are no relevant conservation laws involved that a proponent of a connection between the outcomes could refer to.

4.5.7 Result

All prima facie plausible candidates for a connection between the outcomes in the quantum mechanical formalism have turned out to be inappropriate for justifying a connection. I conclude that there is no connection between the measurement outcomes.

One might wonder then, how the strong correlations between the outcomes can occur when the outcomes are not connected. Does not Bell’s theorem show that there must be a non-local connection? Of course there is a non-local connection, namely the non-separability of the entangled state. However, there need not be an additional connection between the outcomes, because the correlations observed between the outcomes are already present in the entangled state. Have a look at Eq. (5): All possible combinations of outcomes are already contained in the entangled state and all are perfectly correlated. The collapse then just eliminates all possible combinations of outcomes but one, the emerging product state, which then is strongly correlated. In order to secure the correlation, there neither needs to be a conservation law working at collapse and the collapse does not need to connect the outcomes.

Similarly with the twine: The pieces of twine emerging after the cut do not need to be connected in order to be perfectly correlated (by adding up to the original length). The connected pieces of twine before the cut just continue to exist after they have been separated by the cut, and then it is not magic that afterwards they add up to the original length. (In order to see the analogy to the entangled state more clearly, one might think of the twine as having the disposition to be separable at infinitely many points, resulting in correlated lengths of the pieces. And if one wants complete analogy in the sense that the division of the twine also violates the CMC, one needs to think of the twine not as being separated externally by scissors but by being in an unstable state such that it divides indeterministically into two separate pieces of a certain length; i.e. before the decay happens, it is undetermined how long the resulting pieces will be, although it is certain that the two pieces will add up to the original length.)

5 Generalization to continuous collapse theories

In our analysis of the quantum mechanical formalism we have presumed a theory of discrete collapse, i.e. a theory according to which the weights $\sqrt {q}$ and $\sqrt {1-q}$ of the superposition terms in an entangled state (5) instantaneously change to 0 or 1, respectively, when the state collapses. Continuous dynamical collapse theories, in contrast, require a continuous and hence temporally extended dynamics for the weights of superpositions, the most prominent being the theory of continuous spontaneous localization (CSL; Pearle, 1989; Ghirardi et al., 1990). The theory assumes that the squared weights change by a fair random walk, while their sum remains constant equal to 1 (so when one squared weight decreases due to the random walk, the other accordingly increases). The collapse process comes to an end when one of the squared weights reaches the value 1 (then, the other squared weight has the value 0).²² Do such dynamical collapse theories involve ICCs as well?

Say one of a pair of entangled particles hits a measurement device at t₀, such that the collapse process speeds up, the weights perform their random walk in a short interval of time, and the collapse finishes at t₁, when one of the weights reaches the value 1. Then, at all times before t₁, and even when the collapse process has already started, we still have an entangled state, so (by our reasoning in Section 4.1) we need to represent the state before t₁ as one variable. Only at t₁ a product state emerges, which we represent by two separate variables (cf. Section 4.3). Hence, the crucial step, where a common cause operates, is only the last step of the collapse process from an entangled state (5) with weights $\sqrt {1-\epsilon }$ and $\sqrt {\epsilon }$, where 𝜖 is infinitesimally small, to a state with weights 1 and 0, i.e. a product state.

Despite the fact that the last entangled state is only infinitesimally entangled, it is an ICC – which can be seen as follows. The collapse process is a fair random walk, assigning probability $\frac {1}{2}$ to raise or lower each weight in each step of the process, so in particular also for the last step. Consequently, the relevant probabilities for the last step of the continuous process are:

$$ \begin{array}{@{}rcl@{}} P(x_{0} y_{0}|z_{1})=\frac{1}{2}, \quad P(x_{0}|z_{1})=\frac{1}{2}, \quad P(y_{0}|z_{1})=\frac{1}{2}. \end{array} $$

(8)

Then, it is obvious that the common cause z₁, the last entangled state, does not screen off the two states x₀ and y₀ that form the product state, $P(x_{0} y_{0}|z_{1})=\frac {1}{2}\neq \frac {1}{4}=P(x_{0}|z_{1})P(y_{0}|z_{1})$.

In sum, continuous collapse theories involve ICCs (in the instantaneous last step of the continuous process) as discrete collapse theories do (where the whole process is instantaneous).

6 Discussion of other interpretations

We have seen that genuine ICCs follow for the measurement of entangled systems when an objective collapse theory is true, i.e. when (i) quantum states are understood to provide a realistic and complete description (see condition (i) in Section 1) and (ii) the indeterministic collapse at measurement represents the correct dynamics (whether continuous or discrete; see condition (ii) in Section 1). Since there are many interpretations of quantum theory that are inconsistent with these assumptions, I here sketch roughly what a failure of one of these conditions implies for the existence of genuine ICCs.

In the case that the indeterministic collapse is only an effective description (¬ii), and the true dynamics is deterministic, there cannot be genuine ICCs because indeterminism, as we have seen, is a necessary condition for ICCs. One example for this case is the de Broglie–Bohm theory, which assumes that every quantum object has a definite position at any time (i.e. there are hidden variables, ¬(1)) and that these positions jointly with the wave function determine the dynamics. However, since one can never know exactly both the particle positions and the wave function, it appears as if there were an indeterministic collapse on the level of the empirically available data, producing apparent ICCs on this level.

Similarly with Everett interpretations: The fundamental dynamics is deterministic, so there cannot be genuine ICCs (while quantum states are realistic and complete, i.e. (i) holds); however, for any observer who only has data from a branch or world, there seems to be an indeterministic collapse and ICCs; but these, again, are not genuine.

Finally, consider the case that the wave function is denied a realistic interpretation in the sense that it does not describe features of physical systems (¬i). Quantum Bayesianism (QBism; Caves et al., 2002), for instance, assumes that the wave function describes subjective states of agents, that the probabilities from Born’s rule are subjective probabilities and that measurements should be described by an indeterministic collapse, representing a sudden change in the agent’s state of belief. Hence the collapse is not an ontic process, so condition (ii) fails as well. In this case, of course, there is no question that the theory does not describe genuine ICCs in an ontological sense since the theory’s scope is purely epistemic. Involving an indeterministic collapse, however, very similar arguments to the ones I have presented above for realistic theories will lead to the conclusion that there are irreducible ICCs in the causal description of these belief states, violating the CMC. In this sense the theory implies ICCs on an epistemic level (and similarly for related views such as Friederich, 2011).

7 Conclusion

(1) In sum, the quantum mechanical description in a dynamic collapse interpretation yields a causal model according to which the entangled state z is a proper common cause of the distinct and unconnected collapsed states x and y. Since according to this model z does not screen off the correlation between its effects, the quantum mechanical formalism incorporates genuine ICCs, violating the CMC. If x and y denote the immediate quantum states after collapse (rather than the detector states indicating the measurement results), the model also violates modularity and IF. The arguments presented here provide detailed evidence for Cartwright’s claim that there are genuine ICCs if a dynamic collapse interpretation of quantum mechanics is true.

There were two main rival proposals to avoid an anomaly by redescribing the models with quantum ICCs: One is to describe the product state immediately after collapse as one variable xy; the other assumes a connection (of some kind) between the separate variables x and y. Against Hausman and Woodward and others I have argued that these suggestions to redescribe ICCs are implausible when one understands the quantum mechanical formalism realistically.

(2) Rejecting the misdescription thesis argues against a natural reaction of many philosophers of causation that reaches back until when the very first examples were raised by Salmon and others. As long as ICCs could be redescribed to usual causal models, they are no genuine threat to the principles of causal modelling. Only when the misdescription thesis is well supported, as I have tried to argue here, one has to take them and their unusual properties seriously.

It is worth stressing that the aim of this paper was just to reject the misdescription thesis, and the resulting claim is that there are genuine ICCs; i.e. there is a causal anomaly that has the structure of an ICC. Especially, the aim of the paper was not to say how to deal with such genuine ICCs or how to explain the unusual correlations it involves.

(3) I should mention that it is consistent with the results of this paper that one can avoid the existence of ICCs, if one claims that quantum theory in a dynamic collapse interpretation is not a realistic description of the micro processes in our world. One might, for instance, assume that there are hidden variables u that characterize quantum systems more precisely than the entangled quantum state z does, yielding one of the structures in Fig. 3b–c. The de Broglie–Bohm theory is the most prominent example for such a theory; since its dynamics is deterministic, all common causes trivially screen off.

(4) Once the redescription of ICCs is implausible and their existence is substantiated, further questions about ICCs (see Q2–Q6 above) come into focus, upon which I could not touch in this paper. Most importantly, we have seen that systems with ICCs violate usual principles of causal modelling: By definition the CMC does not hold in such systems, and, as a matter of fact, modularity and independent fixability fail as well. While a violation of the CMC directly violates causal Bayes nets modelling, a failure of IF and modularity threatens interventionist theories of causation as defended by Woodward.

There are two main strategies to defend causal modelling against the challenge of ICCs: Either one can assume that entangled quantum systems are not causal just because they violate usual causal principles (van Fraassen, 1982a; Spohn, 2001). Or, if one considers entangled quantum systems to require causal explanations, systems with ICCs are a counterexample to the mentioned principles, which then need to be revised (Näger, 2014; a very similar proposal in Schurz, 2017). Both options are live. Whether one chooses the one or the other, it is clear that once the existence of ICCs is established by suitable evidence, as I have argued here, it has substantive consequences.