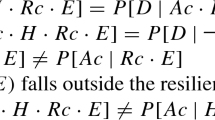Abstract
This paper poses a problem for Lewis’ Principal Principle in a subjective Bayesian framework: we show that, where chances inform degrees of belief, subjective Bayesianism fails to validate normal informal standards of what is reasonable. This problem points to a tension between the Principal Principle and the claim that conditional degrees of belief are conditional probabilities. However, one version of objective Bayesianism has a straightforward resolution to this problem, because it avoids this latter claim. The problem, then, offers some support to this version of objective Bayesianism.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
We show in Section 1 that standard subjective Bayesianism has a problem in accommodating David Lewis’ Principal Principle. In Section 2, we see that the problem does not beset a recent version of objective Bayesianism. In Section 3, we consider three possible ways in which a subjectivist might try to avoid the problem but we argue that none of these suggestions succeed. We conclude that the problem favours objective Bayesianism over subjective Bayesianism (Section 4). In Section 4 we also compare our results to some other lines of recent work.
1 The problem
Let the belief function B specify the degrees of belief of a particular agent: BE(A) is the degree to which she believes A, supposing only E, for all propositions A and E. One key commitment of standard subjective Bayesianism is the claim that rationality requires that these conditional degrees of belief are conditional probabilities:
- CBCP. :
-
A rational belief function B is a conditional probability function, i.e., there is some probability function P such that for all A and E, BE(A) = P(A|E).
The agent’s unique probability function P is sometimes called her prior probability function. Note that CBCP is a static principle: it governs conditional degrees of belief in the prior probability function, not changes to degree of belief. The dynamics of belief are captured as follows. When the agent’s evidence consists just of E, BE(A) = P(A|E) is taken as expressing her current degree of belief in A. Changes to her degrees of belief can then be determined by reapplying CBCP to changes in evidence: e.g., on learning new evidence F, BEF(A) = P(A|EF). (The dynamic principle is usually known as Bayesian Conditionalisation.) The key question for the Bayesian is: what constraints must the prior function P satisfy?
The Principal Principle, put forward by Lewis (1986), uses chances to constrain prior probabilities:
- Principal Principle. :
-
P(A|XE) = x, where X says that the chance at time t of proposition A is x and E is any proposition that is compatible with X and admissible at time t.
In the context of CBCP and Bayesian Conditionalisation, the Principal Principle implies that at time t, if one’s evidence includes the proposition that the current chance of A is x then one should believe A to degree x, as long as one’s other evidence E does not include anything that defeats this ascription of rational belief. If x < 1 and E logically entails A then E is a defeater, for instance, since by the laws of probability, P(A|XE) = 1≠x. On the other hand, if E is a proposition entirely about matters of fact no later than time t then as a rule E is admissible and not a defeater (Lewis 1986, pp. 92–96).Footnote 1
Suppose, for example, that E is a proposition about matters of fact no later than the present, A says that it will rain tomorrow in Abergwyngregyn, and X says that the present chance of A is 0.7. The Principal Principle implies that:
C1: P(A|XE) = 0.7.
We shall show that a problem arises for subjective Bayesianism when A has the same truth value as another proposition F, for which there is less compelling evidence. Suppose, for instance, that A, E and X are as above, F says that Fred’s fibrosarcoma will recur, E provides evidence for F that is less compelling than the present chance of F, and that:
C2: P(F|XE) = 0.3
is a permissible assignment of degree of belief. Perhaps E contains no information pertinent to F, for example, or perhaps there is evidence that a competent expert believes F to degree 0.3. E is less compelling evidence for F than the present chance of F in the following sense: if Y is the proposition that the present chance of F is y≠ 0.3, then Y is compatible with XE. Note that by the Principal Principle, P(F|XY E) = y≠ 0.3, since XE is a proposition determined by matters of fact no later than the present and so admissible with respect to this application of the Principal Principle. The chance claim trumps less compelling evidence.
Next, consider a situation in which we condition on the proposition F in addition to XE, and suppose that E contains no evidence connecting A and F. Plausibly, it is at least permissible that:
C3: P(A|XEF) = 0.7.
Although this is a small step from C1, we do not have enough information to tell whether the Principal Principle forces a credence of 0.7 in A because we do not know whether EF is admissible with respect to proposition A. Lewis did say that matters of fact up to t (in our example, up to the present time) are admissible. However, the truth of F is not (we assume) determined by matters of fact up to the present. Lewis did not specify whether F is admissible with respect to A in such a situation; he simply said, ‘There may be sorts of admissible propositions besides those I have considered’ (Lewis 1986, p. 96). Nevertheless, there is no conflict between X and EF here—indeed, we have assumed that E provides no information about any connection between A and F. In such a situation it would be perverse to deem it impermissible to continue to believe A to degree 0.7, even if such a degree of belief is not obligatory.
Finally, consider the case in which we condition on XE(A ⇔ F) instead of XEF. In this case, a conflict arises: A ⇔ F says that A and F have the same truth value, so one cannot coherently have both a credence of 0.7 in A and a credence of 0.3 in F. Again, the question remains open as to whether E(A ⇔ F) is admissible with respect to A, because the truth of A ⇔ F cannot be determined by matters of fact up to the present.
As discussed above, however, we do know that there is something special about chance that makes it the stronger influence in cases where there is a conflict with credences based on less compelling evidence. It is plausible, then, that it should be at least permissible that the chance is the stronger influence in this case. Thus, if the chance of rain in Abergwyngregyn is 0.7, one believes Fred’s fibrosarcoma will recur to degree 0.3, the two propositions have the same truth value and E is admissible, then it is at least permissible that one’s degree of belief in rain in Abergwyngregyn is closer to the chance of rain in Abergwyngregyn than to one’s prior degree of belief that Fred’s fibrosarcoma will recur:
C4: P(A|XE(A ⇔ F)) > 0.5.
Indeed, to maintain otherwise—i.e., to maintain that one’s degree of belief in rain in Abergwyngregyn ought to be influenced at least as much by one’s prior degree of belief that Fred’s fibrosarcoma will recur as by the chance of rain in Abergwyngregyn—would clearly violate normal informal standards of what is reasonable.
Note that cases in which an agent receives reports from multiple experts of differing competence are quite common. The literature on probabilistic opinion pooling is replete with proposals for determining rational credences in such situations (see, e.g., Genest and Zidek 1986, Dietrich and List 2017). Most often, the resulting credence is a weighted average of the individual expert opinions. In this context, the weights given to experts are interpreted as measures of the relative competence of the experts (Bradley 2018; Dietrich and List 2017): higher epistemic weight is given to opinions of more competent experts. Such procedures will always satisfy C4, where the chance 0.7 plays the role of the credence of an ideally competent expert and the credence 0.3 might be obtained by deference to a less competent expert.
Interestingly, C1–3 lead to a form of non-linear pooling when determining P(A|XE(A ⇔ F)). This can be seen from the following result, if we let G be XE, x = 0.7 and y = 0.3:
Theorem 1
Suppose P(A ⇔ F|G) > 0, P(A|G) = P(A|FG) = x and P(F|G) = y. Then,
Proof
□
This form of non-linear pooling poses a problem in our context:
Corollary 1
C1–4 are inconsistent.
Proof
Set G to be XE. C4 presupposes that P(A|XE(A ⇔ F)) is well defined. Moreover,
so the denominator P(A ⇔ F|G) > 0. C1–3 ensure that the other conditions of Theorem 1 are satisfied. Applying Theorem 1, then, we infer that
which contradicts C4.□
This inconsistency is a problem for standard subjective Bayesianism, because it shows that standard subjective Bayesianism cannot accommodate C1–4, yet the assignments C1–4 merely explicate normal informal standards of what is reasonable. C1 is a straightforward application of the Principal Principle. C2 is merely a permissible assignment of belief in an unrelated proposition. C3 captures the seemingly unobjectionable idea that it is at least permissible to retain a credence that has been set by the Principal Principle on learning an apparently irrelevant proposition. C4 is an application of the claim that is it permissible for a credence to be more strongly influenced by the relevant chance than by a prior belief based on less compelling evidence.
It is apparent, then, that standard subjective Bayesianism does not provide a satisfactory framework for Lewis’ Principal Principle. We will explore various ways in which the subjectivist might try to resist this problem in Section 3. Before that, we briefly sketch how one version of objective Bayesianism can avoid the problem entirely.
2 An objective Bayesian resolution
While the Principal Principle uses evidence to constrain rational degrees of belief, objective Bayesianism goes further in also employing principles that use a lack of evidence to constrain rational degrees of belief. Examples of such principles include the Principle of Indifference and the Maximum Entropy Principle. These principles deem it unreasonable to adopt committal degrees of belief (i.e., credences close to 1 or 0) unless one has evidence which forces such extreme degrees of belief. Objective Bayesians hold that in the absence of such evidence, degrees of belief should be more equivocal.
Objective Bayesians, in common with subjective Bayesians, endorse the view that, at any point in time, rational degrees of belief are probabilities, BE(⋅) = PE(⋅) for some probability function PE. As we noted above, subjective Bayesians go further by endorsing CBCP: BE(A) = P(A|E). While some objective Bayesians also employ CBCP (e.g., Jaynes 2003), not all do. Indeed, Williamson (2010) develops an account of objective Bayesianism in which the Maximum Entropy Principle is used to update degrees of belief when evidence changes, instead of Bayesian Conditionalisation. While credences updated by reapplying the Maximum Entropy Principle often coincide with those updated by applying CBCP to new evidence, there are situations in which the two approaches can come apart. Williamson (2010, Chapter 4) argues that where they do come apart, the objective Bayesian approach—i.e., updating via the Maximum Entropy Principle—should be preferred.
By avoiding CBCP, this version of objective Bayesianism is immune to the problem developed in Section 1. Under this objective Bayesian approach, the Principal Principle can be formulated as claiming that PXE(A) = x, where X says that the chance at time t of proposition A is x and E is any proposition that is compatible with X and admissible at time t. This is a constraint on conditional degrees of belief but not on conditional probabilities. The problem of inconsistency no longer arises. It is trivial to satisfy analogues of C1–4, namely PXE(A) = 0.7; PXE(F) = 0.3; PXEF(A) = 0.7, PXE(A⇔F)(A) > 0.5, because these expressions invoke three different probability functions, PXE, PXEF and PXE(A⇔F), rather than a single conditional probability function P.
In more detail, here is how a version of objective Bayesianism along the lines of Williamson (2010) and Williamson (2019, Subsections 3.1, 3.2) can tackle the example of Section 1. This version of objective Bayesianism can invoke the following variant of the Principal Principle (where we suppose, for simplicity, that the domain of the present chance function is the same as that of the belief functions):
- Chance Calibration.:
-
If, according to G, the present chance function P∗ lies within some set ℙ∗ of probability functions, P∗∈ ℙ∗, then the belief function PG should lie within the convex hull 〈ℙ∗〉 of that set, PG ∈〈ℙ∗〉, as long as everything else in G is admissible with respect to the chance claim P∗∈ ℙ∗.Footnote 2
Suppose first that G = XE. Then ℙ∗⊆{P ∈ ℙ : P(A) = 0.7}, where ℙ is the set of all probability functions. Chance Calibration then implies that PXE ∈{P ∈ ℙ : P(A) = 0.7}, i.e.,
C1*: PXE(A) = 0.7.
Suppose next that the following assignment of credence is rationally permissible:
C2*: PXE(F) = 0.3.
Perhaps E contains evidence that Fred’s clinical consultant reasonably believes that his fibrosarcoma will recur to degree 0.3, for example, and this version of objective Bayesianism deems it rationally permissible to defeasibly defer to the credences of a competent expert in the absence of other relevant information. Next, let us suppose that this version of objective Bayesianism deems EF to be admissible with respect to X for Chance Calibration. Then,
C3*: PXEF(A) = 0.7.
(Note that this invokes a different probability function, PXEF rather than PXE.) Finally, let us suppose that E(A ⇔ F) is also deemed to be admissible with respect to X for Chance Calibration. Then,
which implies:
C4*: PXE(A⇔F)(A) > 0.5.
(Again, this refers to a different probability function.) We see, then, that analogues of C1–4 can all be satisfied in the objective Bayesian framework.
In sum, the objective Bayesian can avoid the problem of Section 1 rather straightforwardly, by revoking CBCP. This is possible because objective Bayesianism can appeal to other strong principles (such as the Maximum Entropy Principle) that do work analogous to that done by CBCP, i.e., that determine how degrees of belief should respond to changes in evidence. Note that the above resolution of the problem of Section 1 did not need to apply the Maximum Entropy Principle in order to satisfy C1*–C4*: here, Chance Calibration and deference to expert credence deliver point-valued probabilities that satisfy these conditions. However, it is by appealing to the Maximum Entropy Principle that this version of objective Bayesianism can do without CBCP.
To give an example in which the Maximum Entropy Principle does some work, consider a proposition A ∨ B, where B is some contingent atomic proposition about which G = XE(A ⇔ F) provides no information. The Maximum Entropy Principle says that, supposing G constrains the rational belief function PG to lie in the set 〈ℙ∗〉, as required by Chance Calibration, PG should be the function in that set that has maximum entropy, if there is such a function. The entropy of probability function P is defined as
where Ω is the set of basic possibilities over which the belief function is defined. Here we can take Ω = {±A±F±B}. Note that, by the axioms of probability, PG(A ∨ B) ≥ PG(A). So Eq. 1 yields the constraint PXE(A⇔F)(A ∨ B) ∈ [0.7,1]. The Maximum Entropy Principle will then set PXE(A⇔F)(A ∨ B) = 0.85.Footnote 3
While objective Bayesianism can do without CBCP, CBCP is a principle that is core to standard subjective Bayesianism. It is hard to see what a version of subjective Bayesianism that did not conform to CBCP would look like. One might suggest that credences should be updated not by reapplying CBCP but by choosing the probability function, from all those that satisfy the current evidence, that is closest to the prior function in terms of Kullback-Leibler divergence,
However, this makes no difference in our example: as Williams (1980) points out, the resulting credences still conform to CBCP wherever evidence is representable as a proposition E in the domain of the belief function. Thus the problem of Section 1 still arises for such an approach.
Here, then, we have two normative epistemological frameworks, objective and subjective Bayesianism, one of which validates normal informal standards of what is reasonable and the other of which does not. This offers support for the framework that does accommodate the standards, i.e., for a version of objective Bayesianism that employs the Maximum Entropy Principle instead of CBCP.
3 Any way out?
In this section we consider and reject three strategies for avoiding the problem for subjectivism outlined in Section 1. One strategy is to attack the conditions C2–4 head on (Section 3.1); a second is to reformulate the Principal Principle (Section 3.2); and a third is to move to the framework of imprecise probability (Section 3.3).
3.1 Attack the conditions
One might try to take issue with one of the key conditions C1–4. Note first that one cannot attack C1 without revoking Lewis’ Principal Principle. We consider modifying the Principal Principle in Section 3.2, so we set this strategy aside here, focussing on the other conditions.
Rejecting C2 would deem it to be impermissible to believe F to degree 0.3, given XE. This is not an option that sits well with subjective Bayesianism. If E contains no evidence for F, a subjectivist would normally say that a wide range of degrees of belief in F are rationally permissible, including 0.3. It is precisely this feature that distinguishes subjective from objective Bayesianism, after all. On the other hand, if E contains evidence that a competent expert believes F to degree 0.3, but no other evidence for F, then it would be odd for any Bayesian to maintain that it is rationally impermissible to believe F to degree 0.3. Perhaps one should not fully defer to an expert’s credence in the way that one should fully defer to a chance value, e.g., one should give F credence greater than 0.3. So suppose P(F|XE) = 0.4 instead. Then simply consider another proposition A′ that has chance 0.6; our problem resurfaces. More generally, a sequence of such propositions whose chances converge to 0.5 would show that the only value of P(F|XE) that avoids the problem is 0.5. But to insist that P(F|XE) = 0.5 in the absence of evidence of F is an objective Bayesian move, not a subjectivist requirement. We see, then, that it is hard for the subjectivist to deny C2, whether or not E contains evidence pertinent to F.
Rejecting C3 would not only violate normal informal standards of what is reasonable, it would in any case be of no help to the subjectivist. This is because C1, C2 and C4 turn out to be sufficient on their own to generate an inconsistency, by the following argument. By C1 and C2, P(¬F|XE) = 0.7 = P(A|XE) so P(A¬F|XE) + P(¬A¬F|XE) = P(AF|XE) + P(A¬F|XE) and hence P(¬A¬F|XE) = P(AF|XE). Then,
contradicting C4. Consequently, denying C3 would not help the subjectivist seeking to avoid the problem posed by the fact that C1–4 are inconsistent.Footnote 4
Lastly, one might try to attack C4. One might try to resist the intuition behind C4 on the grounds that conditioning on a biconditional is somewhat counterintuitive (Hart and Titelbaum 2015; Titelbaum and Hart 2018). Whether or not this is so, the question remains as to what one should do in our scenario when one supposes that two propositions have the same truth value. There are two options. One is to hold that it is permissible to be swayed more by chance than by less compelling evidence (C4). The other is to hold that it is rationally required that less compelling evidence should influence one’s degree of belief to exactly the same extent as chance (denying C4). It seems that the latter option is the stronger claim about conditioning on a biconditional, and more counterintuitive because it fails to do justice to the special role that chance has in informing belief. Thus denying C4 is not an appealing option for someone who finds biconditionals puzzling.
Alternatively, one might object to C4 by reasoning as follows. By C3 and the equally well motivated claim that P(A|XE¬F) = 0.7, A and F are probabilistically independent conditional on XE. Hence, the probability that A and F are both true is 0.7 × 0.3 = 0.21 and the probability that they are both false is 0.3 × 0.7 = 0.21. So AF and ¬A¬F are equally probable. The supposition A ⇔ F merely serves to rule out A¬F and ¬AF, not to change the relative probability of AF and ¬A¬F. Hence, under the supposition A ⇔ F, one should believe each of AF and ¬A¬F to degree 12. Consequently one should believe A to degree 12, since A is logically equivalent to AF under the supposition A ⇔ F. This refutes the permissibility of C4.
In response to this objection, it suffices to note that the second step of the argument—i.e., the inference that AF and ¬A¬F must remain equally believed on the assumption that A and F are both true or both false—simply presumes CBCP, and it is precisely CBCP that is at stake here.
Indeed, this sort of objection to C4 mistakes the dialectic. We have already seen that C1–3 (in fact, C1 and C2 on their own) imply the negation of C4—that is not at issue. The key issue is what this implies about rational belief. We reject any inference to the claim that, given XE(A ⇔ F), it is impermissible to believe A to degree greater than 12, on the grounds that this claim erroneously discounts the influence of chance on rational degree of belief. To reject this inference is to reject the interpretation of the conditional probability P(A|XE(A ⇔ F)) = 0.5 as a conditional belief—i.e., to reject CBCP as a universal rule. So, to undermine C4, the subjectivist needs to explain without appeal to CBCP why less compelling evidence should exert as strong an influence on degree of belief as chance.
3.2 Advocate a conditional principal principle
Instead of attacking C2–4 head on, one might try an alternative formulation of the Principal Principle. Following Hall (1994, 2004), one might reformulate the Principal Principle as requiring deference to conditional chance, rather than chance simpliciter:
- CPP. :
-
P(A|XE) = x, where X says that the chance at time t of proposition A, conditional on E, is x.
This move is rather unappealing from an epistemological point of view, because one does not tend to be presented with chances that are conditional on one’s own evidence. But more importantly this move offers no help here, because an analogue of the problem of Section 1 can be developed in this new framework by changing the interpretation of X but keeping the other propositions fixed. We shall say that the chance of A is robustlyx at time t if the chance at t of A is x and remains x when conditioning on any fact determined by time t. Now suppose X says that the present chance of A is robustly 0.7. Then C1–4 all still hold: C1 is a straightforward application of the conditional Principal Principle CPP, because the chance of A is 0.7 conditional on E; C2 is permissible given the evidence for F (or lack of it) in E; C3 is still intuitively permissible given that F is apparently irrelevant to A; and C4 is still intuitively permissible given the fact that chance has such a strong influence on credence. Moreover, Theorem 1 still holds and an inconsistency is generated, as in Corollary 1.Footnote 5 Therefore, the strategy of employing a conditional Principal Principle fails to avoid the fundamental problem of Section 1.
In response, the proponent of CPP might try to deny C4 by insisting that X says nothing about the chance of A conditional on E(A ⇔ F) and so X should not influence the value of P(A|XE(A ⇔ F)). Instead, one should perhaps view CPP as merely providing the following constraint. If Ww says that the chance of A conditional on E(A ⇔ F) is w, then by applying the law of total probability with the fact that C1 and C2 imply that P(A|XE(A ⇔ F)) = 0.5 (see Eq. 2 above), one can argue that CPP requires:
Thus one might view CPP as merely providing a constraint on the prior probabilities P(Ww|XE(A ⇔ F)).
But the suggestion that X must not influence P(A|XE(A ⇔ F)) is no more viable here than it was in the case of the unconditional Principal Principle considered in Section 1, which was also a scenario in which there was not enough information to determine P(A|XE(A ⇔ F)) via the Principal Principle. X says that the unconditional chance of rain tomorrow in Abergwyngregyn is 0.7 and that this chance is robust. To suggest, on a subjectivist account of belief, that one is rationally compelled to ignore this robust chance when evaluating how strongly to believe that it will rain tomorrow in Abergwyngregyn under the further information that A and F have the same truth value, is bizarre. Any subjectivist who advocates a version of the Principal Principle should want to say that, to the extent that one is not forced to adopt a credence of 0.7 in A by that principle, it is at least permissible to be more strongly influenced by robust chances that are relevant to A than by less compelling evidence.
3.3 Move to imprecise probability
Finally, one might propose abandoning standard subjective Bayesianism in favour of subjectivist imprecise probability. This would offer a third strategy for avoiding the problem of Section 1 yet retaining a broadly subjectivist framework. In this framework, a rational agent has a credal state consisting of a set of initial belief functions P, rather than a single such function. Each of these functions is a probability function and is standardly taken to conform to CBCP.
Unfortunately, this strategy will not work, for the following reason: subjectivist imprecise probability is a generalisation of standard subjective Bayesianism. This means that standard, precise subjectivist assignments of credence are also coherent assignments of credence on the imprecise account. Therefore, C1–4 are well-motivated assignments of credence in the imprecise probability framework. C1 is a straightforward application of the Principal Principle, even in an imprecise framework. C2, C3 and C4 are merely permissible credences that no subjectivist would be entirely happy to rule out as irrational.
The imprecise probabilist might counter that, with respect to C4, credence in A conditional on XE(A ⇔ F) must be represented by a set of values, rather than a single value, given uncertainty about whether or not A ⇔ F is admissible with respect to the Principal Principle. But this is a curious form of uncertainty to take into account. Either A ⇔ F is admissible or it isn’t. If it is, then the Principal Principle applies and a credence of 0.7 in A, given XE(A ⇔ F), is the only reasonable option and C4 holds. Otherwise—if A ⇔ F is inadmissible—then the subjectivist will presumably want to say that a variety of credal states are permissible. In particular, any credal state whose members all give probability greater than 0.5 to A, given XE(A ⇔ F), is surely permissible, given that chance has such an important influence on credence. Either way, C1–4 remain plausible for all members of the credal state; these are inconsistent, so the imprecise account is not viable, after all.
The imprecise probabilist might suggest in response that if A ⇔ F is inadmissible then one ought to adopt the whole interval [0.3,0,7] as one’s credence in A, given XE(A ⇔ F). However, there are two problems with this suggestion. First, this is an objectivist constraint: it is motivated by the thought that one ought to equivocate between credences when there is no evidence to prefer some values over the others. Thus this suggestion offers little succour to the subjectivist.Footnote 6 The second problem with this suggestion is that Corollary 1 shows that the only functions P that satisfy C1–3 together with the constraint that P(A|XE(A ⇔ F)) ∈ [0.3,0.7] are such that P(A|XE(A ⇔ F)) = 0.5. Thus there is no credal state that attaches the whole interval [0.3,0.7] to A, given XE(A ⇔ F). Therefore, this suggestion cannot be implemented in the standard framework for imprecise probability.
While the subjectivist approach considered here is a standard version of imprecise probability (Joyce 2010), there are other versions. Indeed, one might defend an objectivist version which denies CBCP, takes as the credal state the whole set of probability functions that are not ruled out by evidence, and uses the Maximum Entropy Principle as a means of selecting an appropriate belief function to use as the basis for decision making. While this version may be able to solve the problem of Section 1, it is operationally equivalent to objective Bayesianism as outlined in Section 2, so it is of no help to the subjectivist. It is far from clear whether there is some other version of imprecise probability that can both solve the problem of Section 1 and retain a central role for subjectivism and CBCP.
4 Conclusion
That C1–4 are inconsistent poses a problem for subjective Bayesianism, which is unable to capture normal informal standards of what is reasonable when applying the Principal Principle. We considered three possible strategies for avoiding this problem in Section 3, but argued that none of these strategies is ultimately successful.
On the other hand, we saw in Section 2 that a version of objective Bayesianism is not susceptible to this problem and can accommodate the Principal Principle perfectly well. This is because the problem can be attributed to CBCP, which is a principle that subjective Bayesianism endorses but objective Bayesianism need not endorse. Thus, the considerations put forward here provide grounds for moving to an objective Bayesian framework, rather than holding out for subjectivism. A full assessment of the relative merits of subjective and objective Bayesianism is beyond the scope of this paper, but, we suggest, any such assessment should take this problem into account.
Along the way, we saw that the problem developed in this paper also shows that one shouldn’t in general set one’s credences to a linear combination of values to which one might defer: supposing that C2 is a result of deference to expert opinion, Theorem 1 shows that C1–3 force a particular kind of geometric pooling. On the other hand, C1–3 contradict C4 (by Corollary 1), so even this geometric pooling method can be considered problematic. Thus this paper poses a challenge for various forms of pooling as well as for CBCP, the central dogma of subjective Bayesianism.
Related work
We close by pointing out some connections to other recent work.
The problem posed here is related to, and in some respects more troublesome than, that of Hawthorne et al. (2017), who also argue that subjective Bayesianism cannot properly accommodate Lewis’ Principal Principle. Their argument appeals to auxiliary admissibility principles which, although intuitively plausible, go beyond Lewis’ original discussion of admissibility. In contrast, the problem presented here does not assume these auxiliary principles—our problem occurs even under Lewis’ rather minimal claims about admissibility. Furthermore, the problem presented in this paper has more substantial consequences: it can be viewed as a problem for a core Bayesian dogma, namely that conditional rational degrees of belief are conditional probabilities. Only by rejecting this dogma can one successfully capture normal informal standards of what is reasonable.
The problem developed in this paper is also related to, but more troublesome than, a problem for subjective Bayesianism identified by Gallow (2018).Footnote 7 Recall that if C2 is obtained by deference to a competent expert, the problem of Section 1 can be thought of as a pooling problem. Gallow shows that a problem arises if one defers to the forecasts of two different experts, where one is not certain that they will issue the same forecast and where one would adopt a linear combination of the two forecasts should they differ. The problem presented here is more troublesome because it does not presume that experts’ forecasts should be pooled linearly, which is a contentious assumption (e.g., Steele 2012; Easwaran et al. 2016; Bradley 2018). Note in particular that linear pooling conflicts with Theorem 1; this provides another reason for thinking that linear pooling is untenable. In addition, Gallow focusses on deference to incompatible forecasts with respect to the same proposition, while we show that a problem arises even when considering different propositions. There are some other differences between the two arguments. For example, our argument stems from an asymmetry between beliefs calibrated to chances and beliefs formed on the basis of less compelling evidence, which ensures that chances are the more important influence on degrees of belief, while Gallow’s argument considers two agents of equal influence. Finally, Gallow poses a problem for deference principles, while we also present a diagnosis (CBCP) and a solution (a version of objective Bayesianism) for the problem that we identify.
There has also been an interesting discussion of higher-order evidence in recent years. Higher-order evidence ‘rationalizes a change of belief precisely because it indicates that my former beliefs were rationally sub-par’ (Christensen 2010, p. 185). In contrast to first-order evidence, higher-order evidence is not directly about the subject matter of the belief. Note that the problem of Section 1 is not a case of higher-order evidence. The evidential connection between the chance claim X and the proposition A remains intact when conditioning on F or A ⇔ F. Such propositions do not indicate that former beliefs were rationally sub-par.
Some other strands of recent work serve to strengthen the case against CBCP. For example, Wallmann and Hawthorne (2018) highlight a possible conflict between CBCP and the Principal Principle. They consider several cases that involve credences based on differing amounts of evidence. These cases include logically complex propositions, competing chance claims and non-resilient chance claims. The authors remain divided over what these cases show, but they can be taken as undermining a version of Bayesianism that employs both CBCP and the Principal Principle.
Other authors have also claimed that Bayesianism and the Principal Principle are incompatible, in the context of CBCP. Nissan-Rozen (2018b) considers an interesting puzzle that relies on the fact that CBCP leads to an implausible kind of evidential symmetry. Since a chance claim X screens off a certain piece of evidence E from the proposition the chance claim is referring to A, A is evidentially irrelevant to E given X. Nissan Rozen argues that this is implausible in certain cases. Kyburg (1977) formulates a similar example, as well as many others. He shows that in the context of CBCP, since a chance claim X is highly relevant to a proposition A, the proposition A needs to be highly relevant to the chance claim X. He then argues that this evidential symmetry clashes with core intuitions on evidential support. All these arguments support the case against CBCP. Our result contributes to this body of evidence by providing a new and especially disturbing problem for CBCP, involving permissible degrees of belief rather than evidential symmetries.
Notes
Nissan-Rozen (2018a) suggests that a proposition about matters of fact prior to t that explains A might be a defeater. This is somewhat doubtful: the truth of a proposition that explains A might raise the chance of A, but is hard to see how it could provide grounds for believing A to some degree other than the chance of A. In any case, we set this suggestion aside here because none of the propositions we consider here are explanations.
The convex hull of a set of probability functions is the set of convex combinations of pairs of probability functions, i.e., 〈ℙ∗〉 = df{λP + (1 − λ)Q : P,Q ∈ℙ∗,λ ∈ [0, 1]}.
Briefly, given A ⇔ F, PG(A∨B) = PG(AFB) + PG(AF¬B) + PG(¬A¬FB) = PG(A) + PG(¬A¬FB) = 0.7 + PG(¬A¬FB), by Eq. 1. The Maximum Entropy Principle divides the remaining probability 0.3 equally between the two states ¬A¬FB and ¬A¬F¬B, so sets PG(¬A¬FB) = 0.15. Thus PG(A ∨ B) = 0.7 + 0.15 = 0.85. See Williamson (2017, Chapter 6) for a more detailed overview of this sort of calculation.
Recall that C3 is not strictly necessary to generate an inconsistency.
This problem would beset a similiar attempt to deny C2 and C3.
See also Bradley (2018, Section 4.2), who makes similar points.
References
Bradley, R. (2018). Learning from others: conditioning versus averaging. Theory and Decision, 85(1), 5–20.
Christensen, D. (2010). Higher-order evidence 1. Philosophy and Phenomenological Research, 81(1), 185–215.
Dietrich, F., & List, C. (2017). Probabilistic opinion pooling. In Hájek, A., & Hitchcock, C. (Eds.) The Oxford Handbook of Probability and Philosophy (pp. 519–542): Oxford University Press.
Easwaran, K., Fenton-Glynn, L., Hitchcock, C., Velasco, J.D. (2016). Updating on the credences of others: disagreement, agreement, and synergy. Philosophers’ Imprint, 16(11), 1–39.
Gallow, J.D. (2018). No one can serve two epistemic masters. Philosophical Studies, 175(10), 2389–2398.
Genest, C., & Zidek, J.V. (1986). Combining probability distributions: a critique and an annotated bibliography. Statistical Science, 1(1), 114–135.
Hall, N. (1994). Correcting the guide to objective chance. Mind, 103(412), 505–518.
Hall, N. (2004). Two mistakes about credence and chance. Australasian Journal of Philosophy, 82(1), 93–111.
Hart, C., & Titelbaum, M.G. (2015). Intuitive dilation? Thought: A Journal of Philosophy, 4(4), 252–262.
Hawthorne, J., Landes, J., Wallmann, C., Williamson, J. (2017). The Principal Principle implies the Principle of Indifference. British Journal for the Philosophy of Science, 68, 123–131.
Jaynes, E.T. (2003). Probability theory: the logic of science. Cambridge: Cambridge University Press.
Joyce, J.M. (2010). A defense of imprecise credences in inference and decision making. Philosophical Perspectives, 24(1), 281–323.
Kyburg, H.E. (1977). Randomness and the right reference class. The Journal of Philosophy, 74(9), 501–521.
Lewis, D.K. (1986). A subjectivist’s guide to objective chance. In Philosophical papers. With postscripts, (Vol. 2 pp. 83–132). Oxford: Oxford University Press.
Nissan-Rozen, I. (2018a). On the inadmissibility of some historical information. Philosophy and Phenomenological Research, 97(2), 479–493.
Nissan-Rozen, I. (2018b). A puzzle about experts, evidential screening-off and conditionalization. Episteme. https://doi.org/10.1017/epi.2018.17.
Steele, K. (2012). Testimony as evidence: More problems for linear pooling. Journal of Philosophical Logic, 41(6), 983–999.
Titelbaum, M.G., & Hart, C. (2018). The principal principle does not imply the principle of indifference, because conditioning on biconditionals is counterintuitive. British Journal for the Philosophy of Science. https://doi.org/10.1093/bjps/axy011.
Wallmann, C., & Hawthorne, J. (2018). Admissibility troubles for Bayesian direct inference principles. Erkenntnis. https://doi.org/10.1007/s10670-018-0070-0.
Williams, P.M. (1980). Bayesian conditionalisation and the principle of minimum information. British Journal for the Philosophy of Science, 31, 131–144.
Williamson, J. (2010). In defence of objective Bayesianism. Oxford: Oxford University Press.
Williamson, J. (2017). Lectures on inductive logic. Oxford: Oxford University Press.
Williamson, J. (2019). Calibration for epistemic causality. Erkenntnis, published online. https://doi.org/10.1007/s10670-019-00139-w.
Acknowledgments
We are very grateful to the anonymous referees for many helpful comments and to Richard Pettigrew for helpful discussions. We are also grateful to the Austrian Federal Ministry for Digital and Economic Affairs; the Austrian National Foundation for Research, Technology and Development; the German DFG; the Leverhulme Trust and the UK Arts and Humanities Research Council for supporting this research.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wallmann, C., Williamson, J. The Principal Principle and subjective Bayesianism. Euro Jnl Phil Sci 10, 3 (2020). https://doi.org/10.1007/s13194-019-0266-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13194-019-0266-4