The Infinity from Nothing paradox and the Immovable Object meets the Irresistible Force

Abstract

In this paper I present a novel supertask in a Newtonian universe that destroys and creates infinite masses and energies, showing thereby that we can have infinite indeterminism. Previous supertasks have managed only to destroy or create finite masses and energies, thereby giving cases of only finite indeterminism. In the Nothing from Infinity paradox we will see an infinitude of finite masses and an infinitude of energy disappear entirely, and do so despite the conservation of energy in all collisions. I then show how this leads to the Infinity from Nothing paradox, in which we have the spontaneous eruption of infinite mass and energy out of nothing. I conclude by showing how our supertask models at least something of an old conundrum, the question of what happens when the immovable object meets the irresistible force.

1 Introduction

Since Zeno, supertasks, tasks that involve infinite actions or interactions, have had an important role as objects of philosophical contemplation. Each encapsulates a vivid and intriguing challenge to our metaphysical theory.¹ Zeno’s paradoxes themselves pose serious problems for our understanding of space and time and it is thought Zeno intended them as a proof of monism.² Achilles and the Tortoise, for example, takes as a premiss that space and time are infinitely divisible and the putative impossibility of Achilles catching up with the tortoise is a reductio of that premiss. The Stadium takes as a premiss that space and time are finitely divisible and the conclusion that half the time equals twice the time is a similar reductio. Whether modern analysis³ fully resolves these challenges has continued to be debated by philosophers.⁴

More recently we have supertasks such as Benardete’s Paradox of the Gods,

A man decides to walk one mile from A to B. A god waits in readiness to throw up a wall blocking the man’s further advance when the man has travelled ½ a mile. A second god (unknown to the first) waits in readiness to throw up a wall of his own blocking the man’s further advance when the man has travelled ¼ mile. A third god … etc. ad infinitum. (Benardete 1964, pp. 259-60)

Since for any place after A, a wall would have stopped him reaching it, the traveller cannot move from A. The gods have kept him still without ever raising a wall. Yet how could they cause him to stay still without causally interacting with him? Only a wall can stop him and no wall is ever raised, since for each wall he must reach it for it to be raised but he would have been stopped at an earlier wall. So he can move from A.⁵

Supertasks can be set up in Newtonian universes of point particles with classical dynamics (hereafter, Newtonian universes) in which actual infinities of particles are permitted but each must have a finite speed.⁶ So, for example, consider Benardete’s Spaceship Paradox (1964), in which a space ship doubles its speed in the first ½ hour, doubles it again in the next ¼ hour and so on. Where has it got to one hour after it started? Infinitely far from its starting place? But there is no such place. It has gone out of existence. Yet how can mere increase in speed result in non-existence? Perez Laraudogoitia (1997) has shown how this can be modelled in a Newtonian universe by arranging an infinitude of particles to successively collide with a single particle, doubling its speed on each collision.

Perez-Laraudogoitia also created the Beautiful Supertask within a Newtonian universe. Since this last was the original inspiration for this paper and we make partial use of it I shall outline it briefly. In the Beautiful Supertask we have a one dimensional space in which we take one point to be the reference frame zero and an infinitude of point particles such that the ith particle is positioned at 1/2ⁱ, for all i in the natural numbers (i.e. at ½, ¼, 1/8…and so on). Approaching from the right is a single particle with velocity −1. It will collide with the 1st particle and thereby stop, imparting its velocity to the 1st particle, which in turn will collide with the 2nd particle and thereby stop, imparting its velocity to the 3rd particle...and so on (1996:81). For every i, within one unit of time from the first collision, the ith particle has collided with the i + 1th particle and stopped. Hence after one unit of time all the particles are stationary, thereby showing how

the total initial energy of the system of particles… can disappear by means of an infinitely denumerable number of elastic collisions, in each one of which the energy is conserved (1996:82)

Some people reject altogether the application of classical Newtonian mechanics to actually infinite systems. Even if they are admitted, one may also raise questions about the initial conditions that are posited for these supertasks, such as how they could ever come about, or whether their possibility doesn’t depend on some mysterious creation by a god. More broadly, for those who are skeptical of metaphysics that is not very severely disciplined by our current best physics, a position most recently advanced by Ladyman and Ross (2007), such applications may have no interest.

In response, it may be said that metaphysical possibility is very broad, broader than mere physical possibility, and broad enough to include Newtonian universes of all varieties. Granted the possibility of infinite duration for the universes there is little to object to the initial conditions posited: they are merely the conditions convenient to start with and the entire history of the universe leading to those conditions could easily be given if necessary.⁷ Newtonian supertasks in the literature are of this type. They have no need of a creator nor instant of creation but are just the possible worlds with a certain specifiable history that leads to the moment from which we start our explorations. That being said, there are also possible worlds that have an initial instant⁸ and such include Newtonian universes with various distributions of particles at that instant.

These are all issues about Newtonian universes that can be contended but for reasons of space they are not contended here.⁹ This paper is in the tradition of previous papers that have treated such systems on the assumption that exploring the metaphysical possibilities of Newtonian universes, and in that way testing the metaphysical principles manifested therein, has philosophical significance.

Previous supertasks in Newtonian universes have managed only to destroy or create finite masses and energies, thereby giving cases of only finite indeterminism. They have usually offered only a single argument to their paradoxical conclusions, making them vulnerable to single rebuttals. In this paper I present a novel supertask that destroys and creates infinite masses and energies, showing thereby that we can have infinite indeterminism. In the Nothing from Infinity paradox we will see an infinitude of finite masses and an infinitude of energy disappear entirely, and do so despite the conservation of energy in all collisions. Furthermore, the paradox can be based on each of four different continuity principles and as a result there are four independent arguments to the paradoxical conclusion. Consequently it raises significant challenges to the metaphysical principles on which it rests, with a special robustness because there is no single path to its resolution. I then show how this leads to the Infinity from Nothing paradox, in which we have the spontaneous eruption of infinite mass and energy out of nothing. I conclude by showing how our supertask models at least something of an old conundrum, the question of what happens when the immovable object meets the irresistible force. This has often been thought to be simply contradictory and therefore a weak paradox, and we shall see a question arises over the exact relation of our model to the paradox that our ancestors had in mind. Nevertheless, the fact that a version of it can be given a formal model shows the easy dismissal may be too quick.

2 The Nothing from Infinity paradox

Our supertask is set in a one-dimensional Newtonian universe without gravity, containing point particles with unit mass. Nothing turns on it being one-dimensional, but all the action happens in one dimension so it might as well be. Space and time are continuous and we use a reference frame with a spatial x-axis and a temporal t-axis. Particles have continuous paths; have inertia, so they continue at uniform velocity unless and until colliding with another; are impenetrable, so if a particle is on one side of another it can never reach the other side. Collisions are perfectly elastic so result in particles exchanging velocities.

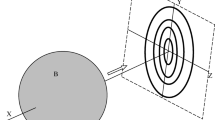
We have two countably infinite pluralities of particles, which I shall call the Ms and the Fs. The Ms are motionless at time t = 0 and at that time, for all n∈ℕ,¹⁰ the nth particle, m_n, is positioned at x = 1/n, i.e. m₁ is at 1, m₂ is at ½, m₃ is at 1/3 and so on . The Fs are in motion at time t = 0 and at that time, for all n∈ℕ\{1}, the nth particle, f_n, is positioned at x = n with velocity v_n = −n, i.e. f₂ (there is no f₁ for notational convenience) is at 2 with velocity − 2, f₃ is at 3 with velocity − 3 and so on. We will call the state of our universe at time t = 0 the initial condition.

I give here a picture that I hope is an aid to the reader. This and the later pictures use blue for Ms and purple for Fs, arrows to represent velocity, and are not to scale (Fig. 1):

Fig. 1

The Ms and the Fs

2.1 Possibility of the initial condition

Before we turn to what happens after t = 0 let us consider the question of co-existence of the Ms and Fs. The Ms comprise particles in an arrangement similar to the infinity of stationary particles in Perez Laraudogoitia’s Beautiful Supertask (1996). The Fs comprise particles in an arrangement similar to the infinity of moving particles in Perez Laraudogoitia’s (1997) version of the aforementioned Benardete’s Spaceship Paradox (1964). So our initial condition is based on well known examples in the literature investigating puzzling phenomena in classical particle dynamics. Individually, then, the Ms and Fs are possible. Can they co-exist?

Consider another universe containing Ms and F⁺s where the F⁺s are exactly like the Fs except their velocities are positive rather than negative. The Ms and F⁺s will never meet and their future is straightforward.¹¹ This shows that there is nothing objectionable per se about a universe in which an infinitude of stationary particles coexists with an infinitude of particles in motion nor need such coexistence imply obscurity about the future of that universe. Granted the cases in the literature, this other universe seems also possible and that alone proves the possible co-existence of a pair of pluralities like the Ms and Fs. The mere reversal of velocities cannot make the initial co-existence of the Ms and Fs impossible when the Ms and F⁺s are possible.

Finally, we should note that there is nothing special about the initial condition of our Ms and Fs being initial. It is merely the state of our universe at t = 0 and given that state we know the prior history of the universe for all t in (−∞, 0]. It just happens to be convenient to start our exploration at t = 0. So the initial condition is possible.

2.2 What happens when the Ms and Fs meet

The consequence of the initial condition is that the Ms and Fs will undergo a series of collisions, which for brevity I will call the meeting of the Ms and Fs. What happens when the Ms and Fs meet? For a start, less us consider a similar universe consisting of the Ms with a single particle, p, at position x = 2 at time t = −1 with velocity v = −1. This results in a chain of collisions. Particle p hits particle m₁ at t = 0 and stops, imparting its velocity of −1 to m₁. In general particle m_n hits particle m_n + 1 at time t = 1–1/(n + 1) and stops, passing on its velocity. Consequently for all n, the nth particle will have stopped at time t = 1–1/(n + 1). So every particle has stopped at some definite moment before t = 1 so at t = 1 every particle is at rest. This should seem familiar, since it is a version of the aforementioned Beautiful Supertask.

It will be useful if we can refer to the chain of collisions in the Ms initiated by the collision of p with m₁ as the wave w_p. The kth collision in the wave takes place at x = 1/k and the wave travels at the same velocity as p did before the first impact. Because Ms are confined to the interval (0,1] so too is w_p. The effect of the wave is for p to take the original position of particle m₁ and in general for particle m_n to take the original position of particle m_n + 1. Although p starts out with a velocity adequate to reach x = 0 at t = 1, nothing ever reaches x = 0.

When the Ms and Fs meet, the meeting is constituted by an extended series of collisions. Each f_n arrives at x = 1 at t = 1–1/n.¹² So f₂ hits particle m₁ and stops, imparting its velocity of −2 to m₁. In general at t = 1–1/n each f_n hits particle f_n-1 and stops, imparting its velocity of –n to f_n-1.

It looks as if the collisions constituting the meeting of the Ms and Fs are very complex, since each particle will be struck infinitely often by the particle to its right and will then move until it strikes the particle to its left. In fact we can see what is going on by considering the waves of collisions that constitute the meeting of the Ms and Fs.

The wave w_n is the chain of collisions started by the impact of f_n at x = 1 at t = 1–1/n.¹³ It may appear that one wave can catch another, i.e. that collisions in w_n and w_m might happen at the same time and place but I have arranged for that not to be possible. Since the wave travels with the velocity of its initiating particle v_n = −n the position of the wave w_n is w_n(t) = n(1-t). So coincidence would require a time t such that n(1-t) = m(1-t) which can only occur if t = 1 or n = m. What this means is that if collisions in w_n and w_m coincide for t < 1 then w_n is w_m.

What happens at t = 1 is going to require some discussion. At t = 1, w_n(t) = 0. It is worth noting that there is no particle at x = 0 with which to have a collision. Wave w_n has its first collision with m₁ at x = 1/(n-1), after which its remaining collisions all occur within the Ms. Since the Ms are constituted by a sequence of particles with order type ω and every wave passes through the Ms before ceasing to be, no wave can have a final collision. Since we know the waves do not catch up prior to t = 1 we also know that all the waves have their kth collision at x = 1/k. Consequently the waves are confined to the interval (0,1] and so do not exist at time t = 1.

We haven’t got to the bottom of what happens at t = 1 yet. Intuitively it may look as if all the particles have to be at x = 0 at t = 1 and it may be unclear what to make of the case. Certainly it is easy to construct a proof that if the particles are anywhere at t = 1, then they are at x = 0. But we cannot simply assume that the particles must be somewhere, i.e. assume that they cannot go out of existence. I am now going to show how, at least in the general case, this is misleading, thereby showing that the mere coincidence of infinitely many particles may not be an essential feature of the puzzle that the Ms and Fs meeting sets us.

What gives rise to the apparent problem at t = 1 is that for the heuristic benefits of mathematical simplicity I arranged the velocities of the Fs so that they all (in the absence of the Ms) would arrive at x = 0 at t = 1. Since each wave w_n has the velocity of its initiating particle, this is why each wave would arrive at x = 0 at t = 1. If I have made the general pattern of the case clear you can see that at the cost of more complicated equations of motion I could have arranged the coincidence of the Fs (in the absence of the Ms) to occur at, say, x = −10, that is to say, at a place well displaced from the whole meeting of the Ms and Fs. So in that case there would be no temptation to think some part of the meeting was constituted by all the waves of collisions catching up at the same time and place since clearly they would have gone out of existence well to the right of where their equations of motion are equal.

So now having got clear of the essential features of the case and the way in which the meeting of the Ms and Fs can be understood in terms of thinking about infinitely many waves of collisions which cannot catch up with each other, we can leave behind mere mathematical detail.

Since waves do not catch up we can see that a universe consisting of an initial segment of the Fs, Fs|_n,¹⁴ meeting Ms would be like an n-fold repetition of the Beautiful Supertask.¹⁵ There is no obvious fallacy of composition involved in taking an n-fold repetition to have the same outcome as the Beautiful Supertask. At t = 1 the original Ms now occupy (0,1/(n + 1)] and the Ms have absorbed the n particles of the Fs|_n and nothing ever reaches x = 0.

If we assume that no fallacy of composition is involved in taking the meeting of the Ms and Fs to be constituted by an infinite repetition of the Beautiful Supertask then nothing gets to x = 0 and the entire infinite energy of the Fs has been absorbed by the Ms. Can this be right?

If we can assume a continuity principle, then the meeting of the Ms and Fs is the limit as n tends to infinity of the Fs|_n meeting the Ms. In general continuity is a matter of the outcome being determined by nearby outcomes whereas discontinuity allows an outcome to be nothing like nearby outcomes.¹⁶ Here the nearby outcomes to the meeting of the Ms and Fs are the meetings of the Fs|_n and Ms. If we take it that these nearby outcomes determine the outcome of the meeting of the Ms and Fs, so that it is the same as the limit as n→∞ of the meetings of the Fs|_n and Ms, then we are making a continuity assumption about the relation of the meeting of the Ms and Fs to the meetings of the Fs|_n and Ms. So we assume the universe under consideration and nearby possible worlds are continuous in this way. (A similar argument can be formulated in terms of a within-world continuity principle instead.¹⁷) Each composition of Fs|_n and Ms is in a separate world and we are making a topological assumption about the structure of possible worlds, that nearby worlds are similar to one another in a special way that grounds the continuity assumption about the relation of the world containing the Ms and Fs and the nearby worlds of Fs|_n and Ms. Since for all nearby worlds no particle is at x = 0 at t = 0, for any particle to be at x = 0 at t = 1 in our universe would be a discontinuity and that is ruled out by continuity. Hence for our universe, there is no particle is at x = 0 at t = 0.¹⁸

We can now prove that there is no position at which any of the Ms can be. First, nothing gets to 0 so they can’t be there nor, therefore, further left by the fact of continuous paths for particles. Second, the Ms are confined to the limit as n tends to infinity of (0,1/(n + 1)] = the open interval (0, 0) = the empty set, so there is no point in the space at which they can be. To labour the point, since the Ms are confined to the limit as n tends to infinity of (0,1/(n + 1)], for any x > 0 there is an n∈ℕ such that 1/(n + 1) < x and so no constituent of the Ms can be at x. To have proved that there is no position at which any Ms can be appears to be sufficient proof that the Ms have gone out of existence. If there is some doubt we may appeal to Alper et al.’s principle:

(P5) A particle P_i has disappeared by time t* if for any position a, the assertion x_i (t*) = a leads to a contradiction. (Alper et al. 2002:175)

Since we have proved that for t = 1, for all m_i in the Ms and for all x in ℝ, m_i is not at x, asserting that m_i is at x leads to a contradiction and hence m_i has gone out of existence.¹⁹²⁰

What has happened to the Fs? Consider first a universe consisting of Fs|_n + k, meeting Ms. The situation at the time the nth constituent²¹ of Fs|_n + k reaches x = 1 and stops, awaiting being struck in turn by the next of the Fs is when we are now ready for the n + 1th repetition of the Beautiful Supertask, with the particles in the interval (0,1] consisting of the particles in the Ms followed by f₂, f₃,…., f_n, f_n + 1: call them the M*s (Fig. 2).

Fig. 2

Partial meeting for n = 3

So the forthcoming k-fold repetition of the supertask that starts from here will, by t = 1, compress the M*s to the interval (0,1/(k + 1)]. So in the limit as k tends to infinity, by the argument just applied for the Ms we can prove for each n that the first n constituents of the Fs have gone out of existence. And this argument applies for any n so we have proved that at t = 1 all the Fs have gone out of existence as well.

I cannot think of a simple reason why we are committing a fallacy of composition in the infinite case and I can think of a case which in which the Ms and Fs meet where the suspicion doesn’t arise. Consider now a two-dimensional universe where each particle in the Ms has initial x and y coordinates equal to the x coordinate in the original case. So m₁ is at (1,1), m₂ is at (½,½) and in general m_n is at (1/n,1/n). Each particle of the Fs has velocities as before and we arrange initial coordinates to match them individually with the constituents of the Ms thus: f₂ is at (2,1), f₃ is at (3, ½) and in general f_n at (n, 1/(n-1)) (Fig. 3).

Fig. 3

The Ms and Fs in a two-dimensional universe

Now m₁ and f₂ exchange velocities at t = 1/2 and in general m_n-1 and f_n exchange velocities at t = 1–1/n(n-1). What happens to the Ms and Fs is the composition of these infinitely many exchanges and the upshot is that the Ms and Fs have changed roles: the Fs are now a stationary plurality and the Ms are a plurality in motion (Fig. 4).

Fig. 4

After the Ms and Fs have met in the two-dimensional universe

This is plainly a case in which continuity holds, since what happens to the Ms and Fs just is what happens at the limit of the interactions of the Fs|_n and Ms. Furthermore, that continuity holds here supports our assumption that it holds for our supertask.

We needed the continuity assumption to conduct the critical parts of the immediately foregoing arguments. I cannot think of a simple reason why that assumption may be false. It seems reasonable but I would concede that it would require further investigation and defence. We shall now consider some lines of analysis that do not depend on it.

If we give up the assumption of continuity but retain the assumption that the meeting of the Ms and Fs is constituted by an infinite repetition of the Beautiful Supertask then we have another argument for the inexistence of the Ms and Fs from the paths of particles being continuous. For any x > 0 we can prove for each particle there is a time < 1 for which it is to the left of x and since all velocities are to the left and paths are continuous, for t > 1 no particle is at x > 0. It would be arbitrary to assume that what is constituted of an infinite repetition of the Beautiful Supertask could achieve what no individual or finite repetitions can.²² So nothing passes through x = 0. Since they all started to the right of zero and particles have continuous paths, they can’t be positioned to the left of zero without passing through 0. So no constituent of the Ms and Fs can be anywhere for t > 1 so the Ms and Fs no longer exist.

If we give up the assumption of infinite constitution the proof that no particle can be at any x > 0 at t = 1 still holds. We can also prove that for each particle x = 0 is the limit of their path at t = 1 and if they still exist, given continuous paths they would coalesce at x = 0 at t = 1. Coalescence cannot be ruled out in particle mechanics: it happens at every collision. However, if we consider the average velocity²³ of each particle over intervals of time bounded by t = 1 above and take the limit, it is unbounded below.²⁴ This amounts to a different appeal to continuity: not that the meeting of Fs and Ms is the limit as n tends to infinity of Fs|_n meeting Ms, but only that the velocity of each particle at an instant is the limiting average velocity. Taking the velocity of a particle at an instant to be the limiting average velocity is the definition of instantaneous velocity. If the particles exist at t = 1 they have an instantaneous velocity, which, by the definition of instantaneous velocity is the limiting average velocity, and so they all simultaneously reach universe escape velocity at t = 1, which amounts to going out of existence for all t > 1.

There is a way to raise a doubt for our case. We might worry about an apparent conflict between the sequence of average velocities being unbounded and the sequence of velocities from the starts and stops of each particle, which sequence is divergent by alternation as opposed to being unbounded.

In fact, this brings into view two further arguments for non-existence. First, we assume that the alternating sequence is among the proper ones determining the limiting average velocity. We then have two conflicting sequences resulting in the instantaneous velocity at t = 1 of the particles being indeterminate, which is incompatible with their existence. Also we find here an analogy to Thompson’s lamp (Thomson 1954:5) in which a lamp is alternately switched on and off at times t = 1/n for all n. Is the light on or off at t = 1?

It cannot be on, because I did not ever turn it on without at once turning it off. It cannot be off, because I did in the first place turn it on, and thereafter I never turned it off without at once turning it on. But the lamp must be either on or off. This is a contradiction. (Thomson 1954:5)

Each of the infinitely many particles in the Ms are started and stopped, and those in the Fs are stopped and started, infinitely many times prior to t = 1. Assuming they exist at t = 1 gives us the analogous contradiction. So we have another paradox here that is interesting in its own right.

There is widespread agreement that Thompson’s original argument is invalid because it falsely assumes that the alternating ‘ons’ and ‘offs’ prior to t = 1 sets the state of the lamp at t = 1 (Benacerraf 1962; Thomson 1970). The import of Benacerraf’s point for us is that just as the sequence of ons and offs need not determine what happens at the limit for the lamp, so the mere fact of a sequence of stops and starts need not do so either and hence neither need the sequence of ‘oscillating velocities’ of those stops and starts. That is to say, the fact that the sequence of oscillating velocities does not itself converge does not mean that that failure to converge determines what the velocity is at t = 1. What we cannot ignore about the sequence of oscillating velocities is that, whilst they oscillate, they oscillate over ever shorter periods of time and so we can perfectly well consider the average velocity of particles during intervals that include such oscillations.

So our dialectic here is one of a dilemma. Either the oscillating velocities from the infinite sequence of starts and stops matter, in which case we have two further arguments for non-existence. Alternatively, the Benacerraf reply to Thompson shows the oscillating velocities from the infinite sequence of starts and stops don’t matter, in which case the limit of the average velocities shows non-existence.

We have now seen a variety of arguments to the effect that one unit of time after meeting, the Ms and the Fs all go out of existence. I do not say the arguments are conclusive since each depended on reasonable continuity principles that could nevertheless bear further examination. I have used four distinct continuity principles, the within-world principle, the across-worlds principle, the continuous paths principle and the instantaneous velocity principle; two of these (paths and velocity) are not really up for rejection, but there is room for debate on the other two. Nevertheless, each argument for disappearance based on a continuity principle is independent from the arguments based on the others so we have four independent arguments for disappearance and therefore four independent arguments for the Nothing from Infinity paradox. I shall now finish by drawing out their significance for indeterminism in classical particle mechanics. For it seems to me that our case gives us the most extreme example seen to date.

3 The Infinity from Nothing paradox

The laws of classical Newtonian mechanics are temporally symmetrical.²⁵ Perez Laraudogoitia pointed out the temporal inversion of the Beautiful Supertask amounted to a spontaneous self-excitation and resultant emission of a particle, giving us an important and elegant example of ‘the problem of indeterminism in classical particle mechanics’ (1996:83). In the Spaceship case temporal inversion results in the appearance from nowhere of a decelerating Spaceship.

These latter are cases in which finite objects disappear or are absorbed, so in temporal inversion something of finite mass and energy appears from nowhere, or is emitted from some particles. We however, don’t have a spaceship or a particle disappearing: we have an infinity of particles with infinite energy disappearing. So in the temporal inversion we have infinitely many particles instantaneously coming into existence and arranging themselves into a stationary and a moving plurality by one second later. It could hardly be a more extreme case of indeterminism: we have the spontaneous eruption of infinite mass and energy out of nothing. This is the Infinity from Nothing paradox.

4 The paradox of the Immovable Object meeting the Irresistible Force

No object can resist an irresistible force. No force can move an immovable object. So if an immovable object meets an irresistible force it will move and not move.²⁶ The premisses seem to be necessary truths. Does this mean ‘it is impossible for an irresistible force to meet an immovable objects’, or that ‘it is contradictory to say they co-exist’ (Sorensen 1992:154)? Maybe not! Admittedly, the ancient and medieval concepts in terms of which this paradox was originally formulated are perhaps obscure; they are at least grounded in views we now find potentially dubious, such as the idea of absolute rest or forces as being in some sense the possession of bodies.²⁷ So I do not wish to claim that what I am about to offer is in any straightforward sense capturing what concerned our ancestors. Nevertheless, given plausible interpretations of what immovability and irresistibility might mean for Newtonian universes, we can model their meeting in our supertask. The result is not a mere whimsy even if it is somewhat whimsical. It offers us a more fine grained view of the immovable meeting the irresistible, relates interestingly to a traditional view of the paradox and perhaps advances a new challenge to the metaphysical assumptions in play.

There is no difficulty in the notion of ‘an immovable object’: it is simply the concept of a physical object that cannot be moved, namely, that cannot have different positions at different times. The notion of ‘an irresistible force’ is not so clear. Certainly, the paradox can be understood in terms of the standard scientific concept of force, that is to say, the concept of a vector with scalar magnitude having the dimensions of Mass×Length÷Time squared.²⁸ Does the paradox does require us to understand it in that way? I think not. We should bear in mind Jammer’s point:

in the prescientific stage…. “force,” “strength,” “effort,” “power,” and “work” were synonymous, as they still are today in ordinary unsophisticated language. (Jammer 1957:17)

We should also bear in mind that understanding of the paradox which places it among the paradoxes of omnipotence. For example, we have Sorensen’s embedding this paradox in his argument against polytheism

However, if there were two omnipotent beings and they were to have a shoving match, an irresistible force would meet an immovable object. (For one would have the power to move anything and the other would have the power to resist any movement.) (Sorensen 1992:153–4)

We can countenance these points by taking off from an earlier remark of Jammer:

As to the concept of force, taken originally in analogy to human will power, spiritual influence, or muscular effort, the concept became projected into inanimate objects as a power dwelling in physical things. (Jammer 1957:7)

I would suggest that in the paradox ‘force’ should be understood to stand for a wide class of powers ‘dwelling in physical things’ that can somehow or other bring about motion, where here the concept of power is the metaphysician’s one. Then, what is meant by ‘an irresistible force’ is a power had by an object, when that object interacts with another object in the way suitable for that power to bring about motion, to overcome any resistance to motion, however great, that the second object may offer. In these terms, an irresistible force is really an irresistible power.

So I think the paradox hopes to pose a more general problem than merely one that arises solely in terms of the scientific concept of force, the problem of the conflict between an immovable object and any irresistible power to cause motion. One variety of the paradox would be given in terms of the scientific concept of force, and perhaps all when spelt out scientifically would entail the exertion of irresistible force (scientifically understood) in the causal chain, but others may be given in other terms.

Under this interpretation, the paradox as originally presented and as standardly promulgated deploys the informal concept of force which, when analysed, amounts to a power of an object to bring about the motion of another object. The meeting of an immovable object and an irresistible force is then the occasion of the exercise or manifestation of that power on an immovable object.

This interpretation seems essentially correct to me but I can see that some might think it amounts to substituting the paradox of the immovable object meeting the irresistible power to cause motion for the original paradox. Supposing that objection to be correct, it is still evident that any irresistible power to cause motion entails, when manifested, an irresistible force and hence any paradox of the immovable object meeting the irresistible power to cause motion has embedded in it the paradox of the immovable object meeting the irresistible force (this is essentially the embedding that Sorensen exploits above). Consequently, I take it that if I exhibit a model of the paradox of an immovable object meeting an irresistible power to cause motion I have, if only implicitly, exhibited a model of the paradox of the immovable object meeting the irresistible force.

For these reasons, then, I think I am free to embed, ground or originate an irresistible force, in scientific terms, in something that suits our universe and captures the basic idea of an irresistible power to cause motion. Something that has that power will manifest its power in part by exerting force but it itself need not be a force. In the encounter with something with this power one will be subjected to an irresistible force in the standard scientific sense of force. So when I locate the irresistible power to cause motion as a power dwelling in an object having infinite momentum or infinite energy, I have not changed the subject. Whenever we need to we can return to distinguishing the object as the possessor of the power, the power itself and the irresistible force as what is manifested by it in the interaction of the possessor with other objects.

In a Newtonian universe, since any force, however small, can accelerate any finite mass, however large, an immovable object must have infinite mass. In point particle collision dynamics, the only dynamics of our universe, force is exerted by the changes of momentum in particles that collide. Such collisions result in instantaneous changes of momentum but instantaneous changes in momentum entail infinite forces. Force applied over a distance does work, which is energy, thereby changing momentum. In instantaneous collisions the energy transmitted remains finite but the distance is zero so the force goes to infinity.²⁹ Hence we can’t take an irresistible force to be simply an infinite force. For when a particle collides with an infinitely massive object, even though it exerts an infinite force the object does not move (since that would require the transmission of infinite energy, which the particle does not have) and so an infinite force can be resisted. Instead of dealing directly with forces we can deal with them indirectly, avoiding awkward and potentially misleading infinities, by considering the carriers and effects of force in the universe, namely momentum and changes in momentum, or alternatively, energies and changes in energies. In our universe the power to overcome any resistance to motion is not merely an infinite force such as that which manifests in any instantaneous collision, but is the power of an object with infinite momentum or infinite kinetic energy. The irresistible force is what is manifested by such an object when encountering other objects and is what those objects are subjected to as a result of the encounter.

With these thoughts in mind, and granted a mereological fusion principle that for a plurality of particles there is an object that is their fusion, the model is evident.³⁰ Our immovable object, IO, is the fusion of the Ms and our possessor of irresistible power that exerts irresistible force, IF, is the fusion of the Fs.

The main obstacle in the way of accepting this model is the question of whether IO is, strictly speaking, immovable.³¹ My suggestion is that although there is a strict notion of immovability that might rule out IO from being an immovable object on the grounds of compression, growth and internal motion, there is also a perfectly good notion that permits them and requires instead displacement of the whole from its location.³² Consequently it is at least defensible that none of these grounds impugns IO’s immovability.

Consider again the upshot of a one particle collision of p with IO.³³ It could be argued that this shows IO to be movable after all since its original constituents are now confined to the interval (0,1/2]. Does this compression alone impugn the immovability? Perhaps not. In general when we are considering whether an object has moved we are looking for the whole object to be displaced rather than merely compressed. When I lean against a concrete block it compresses very slightly but we don’t say it has moved. If we found part of IO outside of the interval it originally occupied that would clearly be a case of it moving, but that is not what we have here. So whilst strict immovability might rule out compression there does seem a perfectly good sense of immovability that allows compression provided displacement is lacking.

We could reject the claim that IO has been compressed. The argument to compression must assume that IO cannot acquire new parts but IO is a fusion of the particles, not a set of particles. Nothing in our fusion principle rules out IO absorbing additional particles³⁴ and nothing about immovability entails that an immovable object cannot acquire new parts. Neither mass nor particle number help determine identity conditions for IO, since both are infinite, so spatial boundary may be the better criterion for identity.³⁵ In that case and granted that we accept objects can increase by accumulating new matter IO has absorbed p as a new constituent that occupies the original position of m₁. As a consequence, although its original constituents are confined to (0,1/2], IO itself has not been compressed.³⁶ The possibility of growth is a central part of our common-sense mereological beliefs so it is not an unreasonable assumption. What is required to show IO to be movable is to displace it but, on this assumption, IO has not been displaced. It is exactly where it was before. Admittedly that assumption faces the deep and interesting difficulties of the paradox of increase (e.g. see Olson 2006).³⁷

The final ground would be that the motion of the constituents of IO shows it to be movable. There is a strict notion of immovability that requires not only the object itself to stay put but also rules out any internal motion. Yet we do not say that the salt crystal on my desk is moving just because its internal atoms are. We require the salt crystal itself to move and that requires displacement of the whole, not the jiggling and internal migration of its parts. So there is a sense of immovability that allows internal motion provided displacement is lacking.

My earlier defence of the initial condition of the supertask suffices, granted our fusion principle, to show the possible initial co-existence of IO and IF. This alone proves the possible co-existence of an immovable object and an irresistible power to cause motion. The consequence of that initial condition is that IO and IF will meet and the outcome of their meeting will depend on the outcome of the meeting of the Ms and Fs. Granted the correctness of the earlier arguments, what happens when IO and IF meet?

We considered first an argument that the Ms absorbed the energy of the Fs. This would amount to the entire energy grounding the irresistible force being absorbed by the immovable object, which, if right, would seem to be a triumph for the immovable object.

We can reject this triumph by considering in detail what happened to the Ms under various continuity assumptions. We proved that there was no place at which any of them could be and thereby proved they had gone out of existence. Unless IO came to be composed by something else that would prove IO itself to have gone out of existence, which would look like a triumph for the irresistible force.

We can reject that triumph by considering what happened to the Fs. We proved that they too went out of existence and again, unless IF came to be composed by something else that would prove that IF went out of existence. Finally, since we proved that all of the Ms and the Fs went out of existence, there was nothing left for IO or IF to become composed by, and hence we can conclude the result of the immovable object meeting the irresistible force is both going out of existence.

What then is the interest of this model? The paradox of the immovable object and the irresistible force has been generally regarded as a weak paradox (see my definition Shackel 2008:49), a thin and trivially illusory paradox of omnipotence.³⁸ The contradiction I started with is taken to prove that a possible world with one cannot have the other. Yet I have offered a model in which an immovable object and an irresistible force coexist and meet. We must grant, of course, that the obscurity of the ancient and medieval concepts means the exact relation of this model to their paradox is indeterminate. Nevertheless, I have shown what the relevant omnipotence concepts could mean when applied to Newtonian universes. The application of a simple mereological principle to our supertask gave two objects to which those concepts properly apply. The formality of the model allowed me to give a variety of precise and independent histories of their meeting (correlate to the variety and independence of continuity principles considered in the underlying supertask). Each history confirms one of the standard thoughts about the paradox, namely that if they coexist their meeting results in annihilation. So we now have an interpretation of the immovable object meeting the irresistible force in a Newtonian universe and we know what happens when they meet. It remains paradoxical because the annihilation of the infinite is absurd on its face.

5 Conclusion

In the Nothing from Infinity paradox we have seen an infinitude of finite masses and an infinitude of energy disappear entirely, and do so despite the conservation of energy in all collisions. This was provable with four independent arguments based on four different continuity principles, two at least of which are not available for rejection. The other two seem plausibly based on with-in world and between world similarity. So this paradox will not easily be rebutted. The temporal invertibility of Newtonian universes then allowed us to show the Infinity from Nothing paradox, in which we have the spontaneous eruption of infinite mass and energy out of nothing, thereby bringing into view the most extreme indeterminism for these universes yet demonstrated. We concluded by showing how a defensible interpretation of the concepts from the old paradox of the immovable object meeting the irresistible force allowed our supertask to model that paradox, raising a question over whether something about that paradox might have been too quickly dismissed.