Abstract
We call attention to an underappreciated way in which non-epistemic values influence evidence evaluation in science. Our argument draws upon some well-known features of scientific modeling. We show that, when scientific models stand in for background knowledge in Bayesian and other probabilistic methods for evidence evaluation, conclusions can be influenced by the non-epistemic values that shaped the setting of priorities in model development. Moreover, it is often infeasible to correct for this influence. We further suggest that, while this value influence is not particularly prone to the problem of wishful thinking, it could have problematic non-epistemic consequences in some cases.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
According to the value-free ideal, the internal workings of science, including the evaluation of evidence, should be kept free from the influence of social, ethical and political values as much as possible. A standard challenge to the value-free ideal stems from the risk of error in inferring conclusions – that is, inductive risk (e.g. Rudner 1953; Douglas 2009). In their classic forms, arguments from inductive risk focus on standards of evidence: these standards should be (and in practice often are) more demanding in cases in which erring in accepting a hypothesis can be expected to have serious negative consequences. For example, stronger evidence should be required before accepting the hypothesis that all parachutes in a batch will open when their release cords are pulled than before accepting, say, the hypothesis that a new design on a shampoo bottle will be more appealing to customers than the old one.
More recently, Douglas (2000, 2009) has developed an expanded argument from inductive risk, which pertains not just to standards of evidence but to methodological choices throughout the research process. According to her argument, it is appropriate for non-epistemic values to influence methodological choices when all three of the following conditions are met: there is substantial uncertainty about which methodological option would lead to the most accurate results; the available options have different inductive risk profiles; and erring in some ways can be foreseen to be particularly bad. For example, if it is unclear whether a tumor should be classified as malignant in the context of an investigation of the carcinogenicity of a particular chemical, a researcher might justifiably decide to classify such ambiguous tumors as malignant, because he judges that it would be worse to erroneously classify the chemical as safe – in which case it will end up being used widely and bring about additional cases of cancer – than it would be to erroneously classify the chemical as carcinogenic (see also Douglas 2000). Classifying the ambiguous tumors as malignant decreases the risk that the chemical will erroneously be considered safe.
One might try to resist these inductive risk arguments by adopting a Bayesian perspective. When it comes to classic inductive risk arguments focusing on standards of evidence, a Bayesian can deny that scientists need to accept or reject hypotheses in the first place; the scientist’s job is merely to assign probabilities to hypotheses (e.g. Jeffrey 1956). Such assignments, which represent degrees of belief in hypotheses, should be arrived at via an application of Bayes’ Rule, which does not require appeal to social, political or ethical values. For expanded inductive risk arguments encompassing other methodological choices, a similar strategy is open to the Bayesian: there may be different options available at a given methodological decision point, but the Bayesian’s analysis should determine the probability of the hypothesis being true given the outcome of the chosen methodology, taking into account that the methodology itself is prone to erring in particular ways.Footnote 1 Policymakers and other decision makers may employ non-epistemic values when it comes time to decide whether probabilities assigned to hypotheses are high enough to warrant some course of action – high enough, say, to warrant banning a chemical – but, the argument goes, scientists need not and indeed should not allow these values to have influence when evaluating how evidence bears on a hypothesis.
The Bayesian response is subject to various counter-replies. A standard one is that probability assignments – and more generally estimates of uncertainty – are also subject to inductive risk considerations (Rudner 1953; Douglas 2009). On this view, concluding that H’s probability is P is tantamount to accepting a hypothesis H’ about the probability of H. So, the argument goes, one has not escaped the need to decide whether evidence is strong enough to warrant accepting a hypothesis; it is just a different hypothesis, H’, for which the decision needs to be made. This argument assumes that an agent can be uncertain about the probability of a hypothesis in light of available information. Such an assumption would fail for ideal Bayesian agents, but for real-world epistemic agents it is not implausible.
Developing this sort of reply further, Steel (2015) contends that real-world agents often lack the precise degrees of belief needed as inputs to Bayesian analysis, i.e. the probabilities that serve as priors and likelihoods. Instead, real-world agents, including scientists, decide how to represent these probabilities, often using distributions that are uniform, binomial, Poisson, normal, etc. These decisions, like other methodological decisions in science, can be subject to inductive risk considerations. Thus, he concludes, in practice there is scope for the influence of non-epistemic values deep in the heart of Bayesian evaluations of the extent to which hypotheses are confirmed or disconfirmed by evidence.
In this paper, we provide a different argument for a similar conclusion. Our argument, which builds upon but generalizes beyond recent work focusing on values in climate modeling (Biddle and Winsberg 2009; Winsberg 2012; Parker 2014; Intemann 2015), focuses on the use of scientific models – especially mathematical models and computer simulation models – as surrogates for background knowledge in Bayesian and other studies that aim to assign probabilities to scientific hypotheses. Because these scientific models often deviate from background knowledge in ways that are in part dependent on non-epistemic values, the probabilities estimated via these studies also turn out to be dependent on non-epistemic values in the sense that, if the non-epistemic values had been different, so would have the estimated probabilities, even with the same background knowledge. Moreover, correcting for the differences between models and background knowledge, and thereby removing the model-based influence of non-epistemic values on the probabilities produced, is often infeasible. In this way, we argue, facts about scientific models, and about sciences that rely heavily on them, pose an underappreciated challenge to the view that evidence evaluation – even Bayesian evidence evaluation – can be kept free from the influence of non-epistemic values. Our argument differs from those discussed above not only in its focus on scientific models, but also in that the non-epistemic values that exert an influence are related not to a preference for producer or consumer risk; our argument appeals to preferences for accuracy in estimating some quantities over others, based on considerations of social and ethical importance.
In Section 2, we review some familiar ways in which non-epistemic values unproblematically influence choices in scientific model development. In Section 3, we show that this influence nevertheless creates trouble for the view that evidence evaluation, via Bayesian and other probabilistic methodologies, can be kept value free. We also explain why the value influence that we identify does not directly give rise to problems like ‘wishful thinking’, a standard motivation for the value-free ideal, though it could have problematic non-epistemic consequences in some cases. Section 4 identifies and responds to three possible objections to our argument. Section 5 considers whether the value influence that we identify can be dampened or escaped, either with the help of robustness analysis or by expressing the conclusions of evidence evaluation in terms other than precise probabilities. Finally, in Section 6, we offer some concluding remarks.
2 Models, priorities and values
In many cases, scientific models are constructed or selected with a set of purposes in mind, some of which are deemed a higher priority than others. For instance, a fisheries model might be constructed with the primary aim of making accurate short-term predictions of the sizes of key fish stocks, because these predictions will inform a set of management decisions that need to be made, and with the secondary aim of facilitating broad-brush understanding of why certain patterns occurred in the rise and fall of fish stocks in the past. Or a global weather forecasting model might be developed with the aim of producing accurate forecasts of rainfall and surface temperature, but with accuracy for one region – say, the country in which the model is located – considered a particularly high priority.
As the weather forecasting example suggests, purposes and priorities in modeling reflect interests. It is often because some things are deemed more important than others – the weather in our home country rather than in Antarctica, and rainfall and surface temperature rather than, say, precise wind speed high above the ground – that modeling activities prioritize some purposes over others. The interests shaping such prioritization decisions might be those of the modelers, a sponsor of the research (e.g. a national government funding a meteorological agency), a public community, etc. Such interests, in turn, reflect values. Importantly, these values typically are not just epistemic but also social. Weather forecasting is especially concerned with surface conditions because these conditions matter directly to people’s daily lives, having the potential to cause them hardship. This is not to deny that some modeling studies are motivated primarily by epistemic interests – simulations of the evolution of the early universe might be a good example – but the purposes and priorities of many modeling studies have far more practical underpinnings. Just to be clear: our claim is not that modeling studies do not have epistemic goals; clearly they do. Our point is merely that the epistemic goals of modeling studies often stem in part from non-epistemic interests and values.
The selection of purposes and priorities in turn can influence decisions in model construction and evaluation (Winsberg 2012; Elliott and McKaughan 2014; Intemann 2015). When it comes to model construction, for instance, purposes and priorities shape not just which entities and processes are represented in a model but also how they are represented, including which simplifications, idealizations and other distortions are more or less tolerable. For example, depending on the purposes for which a model of an ecosystem will be used, modelers might or might not decide to include a variable representing the population of a particular species. Likewise, in the fisheries example above, if there is reason to think that achieving accurate short-term predictions of key fish stocks requires that the model represent a relatively small number of processes with very high fidelity, then distortion in the representation of those processes (relative to background knowledge) might be unacceptable even if it would not undermine the model’s ability to facilitate the broad-brush understanding that is a secondary goal. Moreover, the numerical values assigned to uncertain parameters within the fisheries model might be tuned to ensure that the model’s output closely matches past observations of the variables for which accurate predictions are sought; if predictions of different variables in the model were a higher priority, then the parameter values chosen might well be different too.
When it comes to model evaluation, purposes and priorities can influence which modeling results scientists compare with observations and what counts as a good enough fit with those observations. For example, if the primary aim in a modeling study is to accurately simulate the rise and fall of a river level in response to rainfall in a region, then the fact that certain idealizations are made when representing vegetation in the region – idealizations that are not thought to make much difference to the rise and fall of the river level in the simulations – will not be seen as problematic; although the model’s representation of the vegetation fails to even approximately match observations of particular aspects of that vegetation, the fit may be deemed good enough, given the priorities at hand. It would not be acceptable, however, for the model’s results for river levels to fail to fit closely with observations of those levels.
In practice, of course, model construction and model evaluation are not neatly separable. Much informal evaluation occurs during the process of model construction, and what is learned via formal evaluation activities typically feeds back into the model construction process. For example, if results for a variable that significantly influences river level in our simulation are found to fit relatively poorly with observations, then adjusting the model to achieve better results for that variable may become a high priority. Such adjustment might involve increasing the fidelity with which a particular process is represented or including in the model a representation of a process that before had been omitted entirely.
In fact, it is not uncommon for some models, including complex computer simulation models, to be developed in this layered way, with the latest models obtained by adjusting and adding to existing ones. In such cases, purposes and priorities from earlier times can continue to exert an influence. Suppose process A was represented in the model in a particular way at an earlier time in the model’s development because of priorities at that time. That A was represented in that way might well have shaped how some other processes were subsequently represented in the model; perhaps process F was represented in a way that helps to compensate for some errors introduced by A’s representation. Or perhaps the way in which A was represented makes it impractical, or impossible, to represent F in an otherwise desirable way, because those two methods of representation do not work in harmony with each other. A decade later in the model’s development, priorities may have shifted somewhat, but modelers often will not bother to change the way A is represented, unless there is a good reason to do so. This is because they know that, were A to be given a different – even higher fidelity – representation now, the model might perform less well; such a change might upset the ‘balance of approximations’ that currently allows the model to successfully simulate some important features of the target system or phenomenon (see also e.g. Mauritsen et al. 2012, 14). Such interdependencies among errors are often fully expected, even though exactly what the dependencies are is often unclear, and so earlier layers of model development are left intact (see also Lenhard and Winsberg 2010).
The foregoing considerations suggest that, with different purposes and priorities, the models of a system or phenomenon that exist at any given time would be somewhat different and would give somewhat different results for some variables (if they included those variables at all). This is because, with different purposes and priorities, choices made in model development – including the simplifications, idealizations and other distortions relative to background knowledge that were considered tolerable – would be somewhat different. But since purposes and priorities in modeling often stem in part from non-epistemic values, and since different non-epistemic values would often give rise to different purposes and priorities, it follows that in many cases modeling results are dependent on non-epistemic values in the sense that, if those values had been different, then the modeling results would have been somewhat different too (if they had been produced at all), even given the same background knowledge.Footnote 2
This conclusion about modeling results is a variation on the familiar point that our current knowledge at any given time depends on (among other things) what we considered important enough to investigate, and thus on our interests and values. The argument developed in the next section, however, will hinge precisely on the fact that models typically are not straightforward embodiments of existing knowledge but rather include various simplifications and distortions relative to that knowledge.
3 Models, values and probabilities
According to the Bayesian view sketched earlier, the job of scientists is not to accept or reject hypotheses, but to determine the probabilities of those hypotheses in light of available information. This determination, on that view, can and should be done in a value-free way in accordance with Bayes’ Rule, which provides a formula for updating the probability assigned to H in light of each new piece of information, e: p(H|e) = p(H) x p(e|H) / p(e). This version of Bayes’ Rule leaves implicit that the probabilities assigned are always conditional on the agent’s background information B, i.e. on all of the information that the agent has obtained prior to the point of considering how obtaining e should affect her probability assignments. Making this explicit yields: p(H|e&B) = p(H|B) x p(e|H&B) / p(e|B).
In the discussion surrounding values in science, the Bayesian claim is not that the probability assigned to H will not depend in any way on non-epistemic values. After all, as noted at the end of the last section, the information that agents have at a given time, and hence the priors and likelihoods that they employ in Bayes’ Rule, depend on what they considered important enough to investigate in the past. The claim is rather that non-epistemic values need not and should not play a role in determining the extent to which, given B, the probability assigned to H should be increased or decreased in light of e. This change in probability should be determined in accordance with Bayes’ Rule.
For ideal Bayesian agents, following this advice would be no problem: these agents would have ample computing power, a precise probability assignment for any hypothesis that might be entertained, coherence among all of these assignments, awareness of all of the deductive consequences of B, etc. Real-world epistemic agents, however, often lack these luxuries. For instance, they often do not have all of the computing power they would like to have, they do not recognize all of the deductive consequences of B, and so on. Nevertheless, in some simple epistemic situations, even real-world agents are able to implement the Bayesian approach in a relatively straightforward way. But in the rest of this section we try to show why, in the more complex epistemic situations that often arise in scientific practice, scientists’ best attempts to implement a Bayesian approach – and thereby to estimate the extent to which e, in conjunction with B, supports H – often will be influenced by non-epistemic values.
We begin from the observation that, for actual scientists, computing p(H|e&B) explicitly is often practically infeasible, especially when the system or phenomenon under study is a complex one. It is infeasible because there is too much relevant background information to take into account and/or because available computational methods or computational power (or both) are insufficient. In such situations, scientists’ best attempts at estimating p(H|e&B) often involve computing or estimating p(H|e&B’) instead, where B’ (i) includes only a subset of claims in B – some relevant background information is not taken into account because it is not recognized as relevant or because doing so is simply too difficult given the time and resources available – and (ii) replaces some of the claims in B with one or more computationally tractable scientific models, M, of the system or phenomenon under investigation.Footnote 3 , Footnote 4
Examples are not difficult to find, especially in the environmental sciences. In hydrology, for instance, the “Bayesian Forecasting System” (BFS) methodology draws upon results from a hydrological simulation model to assign probabilities to hypotheses about future values of hydrological variables, e.g. river stage, discharge, runoff, etc. (Krzysztofowicz 1999, 2002). BFS combines a probability forecast that is based on results from the model with a ‘prior’ probability forecast based on past observations of the system. The simulation models used in BFS serve as a stand-in for relevant background theory; they are said to ‘embody’ ‘hydrological knowledge’ (Krzysztofowicz 1999), though they do so in an approximate way at best.
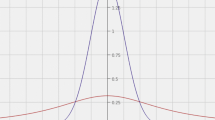
Similarly, in meteorology, computer simulation models of the atmosphere are at the heart of state-of-the-art Bayesian methods for estimating the probabilities that should be assigned to hypotheses about future weather conditions, given observations of recent conditions. The methodology known as Bayesian Model Averaging (BMA), for example, produces a probability density function (PDF) for the future value of a weather variable of interest – such as the temperature in a particular locale – as a function of a set of model-based forecasts (see e.g. Gneiting and Katzfuss 2014). More specifically, the predictive PDF produced in BMA is a weighted average of PDFs associated with different model-based forecasts (see Fig. 1), where the weights are Bayesian posterior probabilities that represent, for each model, the probability that its forecast will be the best of the bunch, given its performance in making similar forecasts in the recent past (see e.g. Raftery et al. 2005).
BMA predictive PDF (thick curve) and its five components (thin curves) for the 48-h surface temperature forecast at Packwood, WA, initialized at 0000 UTC on 12 Jun 2000. Also shown are the ensemble member forecasts (open circles) and range (solid horizontal line), the BMA 90% prediction interval (dotted lines), and the verifying observation (solid vertical line). After Raftery et al. 2005, Fig. 3
An even more elaborate Bayesian methodology involving complex simulation models can be found among recent efforts to assign probabilities to hypotheses about future climate change. The UK Climate Projections 2009 (UKCP09) project produced probabilistic projections of climate change at a fine-grained spatial scale for the UK through the end of the twenty-first century (Murphy et al. 2009). Describing the methodology in detail is beyond the scope of this paper (see ibid.; see also Harris et al. 2013), but roughly speaking it involved (i) identifying a set of uncertain parameters in a complex climate model and assigning prior distributions for these parameters, which represent uncertainty about which parameter values will give the most accurate climate simulations, (ii) updating these distributions in light of how well the model performs against past data when it is run with different combinations of parameter values sampled from these distributions, and (iii) weighting the model’s projections of future climate change according to these updated probabilities about which parameter values will give the most accurate results, while accounting for the fact that even the most accurate results are likely to be imperfect; the latter is done by including a (probabilistic) estimate of the remaining error, where this estimate is informed by the spread among climate models from other modeling centers.
For our purposes here, most of the technical details of BFS, BMA, UKCP09, etc. are unimportant. What matters is that these are state-of-the-art attempts at implementing a Bayesian approach in scientific practice and that their results are a function of forecasts produced by scientific models that serve as a stand-in for background theoretical and other knowledge (from hydrology, meteorology, climate science, etc.). The assumptions of these models – in these cases computer simulation models – deviate from this background knowledge in various ways, and these deviations reflect, at least to some extent, the fact that predictive accuracy with regard to some variables was considered more important – for non-epistemic reasons – during model development. Nevertheless, these models are the best tools available to scientists for applying available theoretical knowledge to determine the probabilities that should be assigned to hypotheses of interest about future conditions.
Our argument is now coming into focus. In practice, scientists’ best attempts at estimating p(H|e&B) sometimes involve estimating p(H|e&B’) instead, where B’ includes only a subset of the claims in B and replaces some of these with a computationally tractable scientific model, M. But, per Section 2, the distortions relative to B that scientists are willing to tolerate when developing M will depend in part on the purposes and priorities of their investigations, as well as the purposes and priorities that shaped any earlier layers of the model’s development. Often, these purposes and priorities stem in part from non-epistemic values in such a way that, with different values, some of the ways in which available models deviate from B would be different too; scientists would be working with somewhat different models, M’. In that case, the estimate of p(H|e&B) produced would be somewhat different as well, as illustrated schematically in Fig. 2. Thus, in practice, scientists’ best attempts to implement a Bayesian approach are sometimes such that non-epistemic values do influence their evaluation of the extent to which, given B, the probability assigned to H should be increased or decreased in light of e.
Schematic illustration of the influence of non-epistemic values in model-based Bayesian evidence evaluation. With different non-epistemic values, different models and modeling results might be produced, giving rise to different estimates of p(H|e&B). Except by coincidence, p(H|e&B’) ≠ p(H|e&B”) ≠ p(H|e&B”’) ≠ p(H|e&B’’’’)
Furthermore, while BFS, BMA and related methodologies nicely illustrate how scientists’ attempts to implement a Bayesian approach to evidence evaluation can be influenced by non-epistemic values via modeling purposes and priorities, it would be hasty to assume that such influence occurs only when scientists employ mechanical methods for estimating probabilities. There are, in fact, other methods for estimating p(H|e&B) that lean more heavily on the subjective judgment of experts, such as expert elicitation methods in which priors and likelihoods are obtained by asking scientists for their degrees of belief in various hypotheses (see e.g. Morgan 2014). Imagining that these estimates of p(H|e&B) are free from the model-based value influence that we have identified, however, overlooks the fact that the judgments of experts can be shaped significantly by their experience working with particular models and by their awareness of particular modeling results. Indeed, models are used in the study of complex systems in part because it can be very difficult to reason (accurately) about such systems without them. We would argue that, for sciences in which complex, non-linear models play a prominent role, it is naïve to think that scientists can typically reach conclusions about p(H|e&B) that are both adequately well-informed and independent of the set of models that happens to be available to them at any particular time.
Finally, before turning to possible objections to our argument, we consider whether the model-based value influence that we have identified is a source of bias in scientific findings or has other worrisome consequences. A key question seems to be whether there is some systematic link between, on the one hand, the non-epistemic values that motivate the selection of high-priority variables and, on the other hand, the probabilities assigned to hypotheses with the help of those models; such a link might give rise to problems like ‘wishful thinking’, where methodologies are biased toward conclusions that scientists wish to be true. However, no such link seems present here: the value influence that we have identified makes the probability assigned to H in light of e different from what it would have been if full background information B could have been employed in the analysis, and different from what it would have been if different values had exerted an influence, but it does not drive the analysis toward some particular conclusion about H’s probability (or about H more generally). Consider, for example, the hypothesis that it will rain tomorrow in Hamburg. The past decision of a German meteorological agency to prioritize accurate simulation of rainfall in Germany in its global weather prediction models would not on its own drive the probability estimated for H (with the help of those models) toward any particular value, nor would it make it more likely that the probability would deviate in some particular direction from the probability that would be assigned to H if full background information B were used in the analysis.
That said, the value influence that we identified does have the potential for problematic consequences. One reason is simply that the influence operates via distortions in modeling assumptions, and such distortions can artificially limit what types of data are considered relevant and what the space of possible outcomes looks like, among other things (see also Steel 2015, p.85). This can have significant practical implications. For example, suppose that a simplification in an ecosystem model involves lumping together several different species who play similar predator/prey roles, even as other species are represented individually. The model will then say nothing about how possible interventions on the ecosystem (e.g. associated with different proposed policies) might affect the relative proportions of the different species that have been lumped together. Suppose that, unbeknownst to the model builders, there is a group of people whose food supply depends upon the abundance of one of those lumped species. Then, if modeling is the primary means by which people can learn about the likely effects of the proposed policy interventions, then that group of people may be less able to identify – and thus advocate for – the policy that best serves their interests.Footnote 5
Problematic consequences can emerge in a similar way via prioritization decisions. In model development, scientists work harder to minimize distortions (relative to background information B) in modeling assumptions when those distortions will lead to inaccuracies in high-priority variables than when they will lead to inaccuracies in low-priority variables. While there is no guarantee that p(H|e&B’) more closely approximates p(H|e&B) when H concerns a high-priority variable than when it concerns a low-priority variable, it does seem that, ceteris paribus, we should be more suspect of results for p(H|e&B’) for hypotheses concerning lower-priority variables, since less effort has been made to ensure that the modeling results informing those probability estimates are accurate.Footnote 6 In cases where p(H|e&B’) does approximate p(H|e&B) much more closely when H concerns high-priority variables than when it concerns low-priority variables, then those people whose interests and values shaped priorities in model development may be better informed about the questions that interest them – and thus perhaps also in a better position to identify, prepare for and respond to risks – compared to those people who didn’t have a say in priority-setting.Footnote 7 To give a simple but stark example, if some African countries only have access to model-based global weather forecasts produced in North American and Western European countries, none of which considers accurate simulation of rainfall in those African countries to be a high priority, and if people in those African countries consequently receive forecasts of the probability of rainfall that are less skillful due to this inattention, then this may disadvantage them, compared to people living in North American and Western Europe, when it comes to identifying and responding to e.g. flood risks, droughts, etc. In this way, the value influence that we identified could in some cases be complicit in perpetuating certain kinds of power imbalances and injustices. In the extreme, high-priority variables might be selected with this very aim in mind.
Thus, while the value influence that we have identified is not particularly prone to the problem of wishful thinking, it does have the potential for problematic non-epistemic consequences. The extent to which such consequences actually occur, of course, varies from case to case.
4 Objections and replies
In this section, we present and respond to three possible objections to our argument: that it relies on a misguided understanding of what Bayesian probabilities are; that the true Bayesian would just correct for the value influence we have identified; and that the value influence we have identified is of negligible magnitude and thus unimportant.
First, one might object that, given what Bayesian probabilities are, it makes no sense to speak of “estimating” these probabilities: they are subjective degrees of belief that agents just have. Bayes’ rule simply represents how an ideal epistemic agent’s degrees of belief would change in light of new pieces of information. In response, we grant that this is one way to think of Bayesian probabilities, but we find good reason to adopt an alternative view. In particular, we see good reason to treat Bayesian probabilities as personal probabilities that can be objects of acceptance (Cohen 1992; Steel 2015), rather than as subjective degrees of belief, especially in scientific contexts. Steel (2015) notes that real-world epistemic agents often have degrees of belief that are vague (i.e. imprecise), incomplete (i.e. missing entirely for some hypotheses) or unreasonable (i.e. not apportioned to their available information, based on unreliable heuristics, subject to implicit bias, etc.). In addition, we would point to scientific practice, where explicit Bayesian analyses are sometimes performed and where the probabilities that serve as inputs are not obtained by introspection or by engaging in hypothetical betting games but rather through careful and time-consuming efforts to work out the implications of available information. On the view that Bayesian probabilities should be treated as subjective degrees of belief that agents involuntarily and already have, it is hard to make sense these aspects of scientific practice.Footnote 8 By contrast, they are easy to explain if Bayesian probabilities are viewed as personal probabilities that are objects of acceptance: scientists recognize that the degrees of belief that they happen to have in hypotheses – to the extent that they have them at all – might not be warranted by the information available to them; the careful scientist uses whatever aids to reasoning are at her disposal to try to arrive at probabilities that are warranted by available information.
Second, one might object that, even if non-epistemic values do influence evidence evaluation via modeling as we have argued, the true Bayesian scientist would just correct for that influence. That is, the scientist would apply corrections so that the probabilities match those that would be produced by conditionalizing on full background information, B. To this our reply is: easier said than done. To the extent that the scientific model or models involved are complex, nonlinear, motley, the product of many layers of model development, and the product of a wide array of disciplinary areas of expertise, it becomes nearly impossible for today’s experts to know what such corrections should be. For one thing, it may not be clear to a given group of scientists what all of the distortions of M relative to existing knowledge B are, much less what the effects of these distortions are on M’s results; this could be because they didn’t build the model or because the model is complicated enough that not all effects of choices are easy to anticipate, or both.Footnote 9 This is the situation when it comes to the weather forecasting models discussed in the last section and even more so for their cousins, global climate models (see also Biddle and Winsberg 2009; Winsberg 2012). In practice, it is often infeasible to adjust model-based estimates to arrive at confident and precise assignments for p(H|e&B).
A third possible objection is that the model-based influence of non-epistemic values that we have identified is unimportant because, if all goes well, its contribution to any difference between p(H|e&B’) and p(H|e&B) will be negligible. It will be negligible because scientists will choose models that are suited to the purposes at hand; these models will be constructed such that the ways in which their assumptions deviate from background knowledge make little difference to the results of interest. As suggested in Section 2, distortions in modeling assumptions relative to background knowledge are considered acceptable only if they have a relatively small impact on high-priority results.
To this objection we have two replies. First, we note that it is not always possible to choose modeling assumptions whose deviations from background knowledge make little difference to results produced. While we agree that this is typically the goal, we would argue that scientific models, especially complex mathematical and computational models, often fall noticeably short of this goal, despite scientists’ best efforts. Thus, in practice the difference between p(H|e&B’) and p(H|e&B) due to reliance on models is certainly not always small. Second, we note that scientists typically do not have at their disposal, for each purpose of interest, a model that has been constructed or tuned with that purpose as a top priority. Instead, a single model often ends up being used for some range of purposes, not all of which were high priorities during model construction. The same weather forecasting model or climate model, for instance, might be used to produce probabilistic forecasts both for high-priority and lower-priority variables. It is practically infeasible to do otherwise, given the tremendous amount of work that goes into constructing a single model – they are often developed and refined over many years, by teams of scientists. Given that inaccuracies in modeling results for lower-priority variables are often tolerated in model development for the sake of computational tractability, efficiency, etc., it cannot be presumed that the difference between p(H|e&B’) and p(H|e&B) is small for hypotheses associated with these variables.
5 Escaping the influence of values?
We claimed above that it is often infeasible for scientists to apply corrections to their results for p(H|e&B’) in such a way that they can be confident that they have arrived at a probability that closely approximates p(H|e&B). Are there other ways that scientists might try to escape or circumvent the model-based value influence that we have identified? In this section, we discuss two possible approaches, though in the end neither seems to offer a straightforward escape.
First, it might be thought that robustness analysis, or considerations of robustness, could help. Suppose scientists were to find that several different estimates of p(H|e&B), obtained with the help of a different model (or models) in each case, were in close agreement. Would this indicate that any value influence, via modeling purposes and priorities, had only a negligible effect on the estimated probability? Not necessarily. It is possible that the models were developed with similar purposes and priorities in mind and that they consequently incorporate some of the same idealizations and simplifications relative to B; a case would need to be made that the agreement among estimates of p(H|e&B) did not reflect the models’ shared deviations from B. Moreover, it is worth emphasizing that close agreement on estimates of p(H|e&B) may be rather rare to begin with, because probabilistic estimates can be highly sensitive even to small changes in modeling assumptions. For an illustration, consider the BMA weather forecasting example in Fig. 1: the individual probabilistic forecasts (represented by the small, component PDFs), which come from very similar models, differ quite markedly in the probabilities that they assign to future temperature values; BMA is employed precisely because such disagreement among results from state-of-the-art models is not uncommon.Footnote 10
A second possible approach to escaping or dampening the model-based value influence that we have identified involves reporting the conclusions of evidence evaluation in terms other than single-valued probabilities. Conclusions might be expressed instead using imprecise probabilities (i.e. probability intervals) or in even more hedged terms, e.g. ‘H is plausible.’ Arguably, this would be more appropriate anyway when scientists do not know how to apply corrections to model-based estimates of p(H|e&B’) to account for the difference between B’ and B; their actual uncertainty about H is ‘deeper’ than precise probabilities would imply.Footnote 11 , Footnote 12 We explore this second approach in the remainder of this section.
First, we note that methods that use probability intervals to express conclusions about H, given e, are not necessarily less sensitive to value-influence than methods that use single-valued probabilities. If a method assigns probability intervals in such a way that, for each possible modeling result (or set of results), a different probability interval will be assigned, then the method is just as sensitive as standard methods (like BFS, BMA, etc.) that assign a different single-valued probability for each possible modeling result (or set of results). If, however, the method uses a limited number of probability intervals to express conclusions, then the method will be less value-sensitive, relative to standard, precise-probabilistic methods, in the sense that some differences in modeling results would not make a difference to the conclusion reached (see also Parker 2014). Ceteris paribus, the fewer the intervals from which the method chooses, the greater the reduction in value-sensitivity.Footnote 13
It is helpful to have a concrete illustration. The Intergovernmental Panel on Climate Change (IPCC), tasked with evaluating available evidence related to climate change, often reports conclusions using a limited set of probability intervals, which are paired with specific terminology (see Table 1). In their most recent assessment, IPCC scientists considered – among many other things – whether global mean surface temperature would rise by more than 2 °C by 2100 (relative to the 1850–1900 average) under different greenhouse gas emission scenarios.Footnote 14 They concluded that a temperature change greater than 2 °C was ‘unlikely’ (i.e. probability <33%) under a low emission scenario known as RCP2.6 but ‘likely’ (i.e. probability >66%) under higher emission scenarios RCP6.0 and RCP8.5 (see Table 2). Though it is unclear exactly how these conclusions were arrived at in the course of the IPCC expert assessment, it seems clear that the percentage of climate model projections that exceeded 2 °C for each of the different emission scenarios (also shown in Table 2) played an important role, as these percentages were highlighted in the report (see Collins et al. 2013, Section 12.4). Yet if the IPCC scientists were using only the probability intervals in Table 1 to report conclusions, then clearly some differences in these percentages (i.e. the percentage of models indicating greater than 2 °C warming) would not have made a difference to the conclusions reached. This is simply because there are fewer probability intervals in Table 1 than possible percentages, given the number of models used.Footnote 15 It seems likely, for example, that even if only 96% of model projections (rather than 100%) showed greater than 2 °C warming for RCP6.0, such warming still would have been deemed ‘likely’ (i.e. probability >66%).
It should be clearer now how the influence of non-epistemic values, via modeling, might be dampened by moving from single-valued probabilities to interval probabilities. Single-valued probabilities, if generated as a function of modeling results (e.g. as in BMA), are maximally sensitive to changes in those results: except by coincidence the conclusions reached (i.e. the probabilities) would be at least somewhat different if the modeling results were somewhat different. This need not be the case when coarser uncertainty depictions, such as a limited number of probability intervals, are employed; even if the modeling results were somewhat different, the conclusion reached might well be the same.
It is important to recognize, however, that even when conclusions are to be expressed using a limited number of probability intervals, scientists still face a significant reasoning task: they must reason, in a coarse-grained way at least, about the plausible effects of idealizations and simplifications in modeling assumptions, as well as about the implications of information in B that was not accounted for at all in the modeling process. While Parker (2014) suggests that in some cases this might be possible, it is unclear just how often scientists can perform this reasoning in a way that is not unduly influenced by their experience with a particular set of models and modeling results. As noted earlier, models are used in the study of complex systems in part because it can be very difficult to reason about such systems without them. In considering how different a set of modeling results might be if, say, a particular physical process were represented with high fidelity (relative to B), a scientist’s thinking might be strongly influenced by her observation of how much difference it made when, in existing models, the process was given a medium fidelity representation instead of a low fidelity one. Even when conclusions are expressed in very hedged terms (Betz 2013, 2015), it is not always easy to move beyond one’s experience working with a particular set of models; conclusions about what is plausible, for instance, may be strongly shaped by the range of results observed to have been produced by available models. So even with a move from single-valued probabilities to coarser conclusions, it is unclear how ‘escapable’ the model-based influence of non-epistemic values that we have identified ultimately is.
6 Concluding remarks
We have argued that, in practice, it is sometimes infeasible for scientists to evaluate evidence in a value-free manner along the lines envisioned by the Bayesian response to arguments from inductive risk. It is infeasible because scientists’ best attempts at implementing a Bayesian approach involve using scientific models as surrogates for background knowledge, and those models deviate from background knowledge in ways that are dependent on non-epistemic values and that are difficult to correct for. We further argued that, while this value influence is not particularly prone to the problem of wishful thinking, it does have the potential for problematic non-epistemic consequences.
We have not addressed the question of whether non-epistemic values ought to have various other roles to play in modeling or in science more generally, e.g. in guiding uncertain methodological choices when those choices can be foreseen to affect the balance of inductive risk in significant ways (Douglas 2009). We do, however, have two related observations to make. The first is that, at least in those fields of science that rely heavily on complex, non-linear models, it is often not foreseeable how methodological choices in model development will shape modeling results in the long run, because of the layered ways in which those models are developed and the fact that later choices in model development can ‘undo’ the effects of earlier ones. The second is that there is a close connection between this unforeseeability and limits to the extent to which science in such fields can, in practice, be value-free: it is in part because it is difficult to know some of the ways in which past methodological choices have shaped today’s modeling results that the Bayesian response ceases to be a reply to which the defender of the value-free ideal can appeal.
Finally, we note that the model-based value influence that we have identified is not limited to Bayesian evidence evaluation. There are non-Bayesian model-based methodologies for assigning probabilities to hypotheses, including some varieties of ‘ensemble methods’ (e.g. Giorgi and Mearns 2003; see also Parker 2013), that exhibit the same sort of value-dependence that we have highlighted for Bayesian methods. Moreover, in many fields, scientific models serve as an important aid to reasoning in general, not just in the process of evidence evaluation. The significance of our argument thus lies not just in the challenge it provides to the Bayesian response to inductive risk arguments, but in its identification of an underappreciated and subtle route by which non-epistemic values exert an influence in scientific practice, namely, by shaping – via the setting of epistemic priorities – the development of scientific models that subsequently aid scientific reasoning in various ways.
Notes
In Douglas’s tumor classification example, for instance, the Bayesian scientist would calculate the probability of the chemical being carcinogenic conditional on both the outcome of her classifications and the fact that a particular classification strategy (i.e. liberal or conservative) was used.
This value-dependence of modeling results is independent of standard inductive risk considerations, so long as the purposes of the modeling study do not have risk preferences ‘built in’. For example, if the purpose of a study is to produce results for variable X that include a large ‘margin of safety’ or that we can consider a ‘worst-case scenario’, then the model-based value influence that we have identified is not independent of inductive risk considerations. But it is independent for more typical modeling purposes that call for producing accurate results for a quantity X, without specifying that any particular inaccuracy with regard to X is to be avoided.
In many places, we talk about p(H|e&B’) as an estimate of p(H|e&B). One might worry that this assumes that there is a true, uniquely correct p(H|e&B). This, in turn, would require a commitment not only to a kind of objective Bayesianism, but also to the proposition that everyone in the relevant epistemic community shares the same B. We would prefer not to commit ourselves to either of these, though we also don’t assume that it is impossible for there to be a shared or common B. When we say that p(H|e&B’) is an estimate of p(H|e&B), we mean that it is an estimate of the value of p(H|e&B) that some particular agent who accepts B -- an agent who is attempting to assign a probability to H with the help of models -- would assign if s/he were logically omniscient. In some situations, this value might reasonably be different for two different agents who accept the same B. In other cases, even if different agents accept different Bs and different likelihoods, etc., there still might be some single estimate, p(H|E&B’), that approximates p(H|e&B) for each of them reasonably well.
A referee noted that this is reminiscent of Harsanyi’s (1985) suggestion that it is not unusual (nor unreasonable) to accept, as part of one’s background information, statements that – while not strictly true – will simplify one’s decision problems without distorting one’s reasoning too much; this simplification-without-distortion is certainly the goal here, though often the distortions in fact turn out to be significant, as we emphasize in Section 4 below.
The point we wish to make is not that the ecosystem model ought, on social or ethical grounds, to have been constructed differently – we do not take up that question here – but just that choices made in model construction, including choices about what sorts of simplifications and idealizations are made, can have significant non-epistemic consequences when probabilities estimated with the help of those models will help to inform practical decisions. For a broader perspective, see also Proctor and Schiebinger 2008 on why we remain ignorant about some things and how this sometimes has harmful consequences.
There is no guarantee for numerous reasons. One reason is that, even though scientists prioritize accurate results for some variables, it is not always clear how to achieve such accuracy; it is possible that the choices made in model development in fact lead to more accurate results for lower-priority variables. Moreover, as noted earlier, scientific models sometimes undergo multiple layers of development over long periods, during which modeling purposes and priorities can shift. In the long run, a model may or may not give more accurate results for variables that were once a high priority, since choices made in the service of those priorities can be ‘undone’ by later choices in model development; in complex models, there is no simple additive formula for the compound effect of multiple modeling choices. Indeed, the long run and overall effects on modeling results of a series of choices in model development may be very difficult to identify (Lenhard and Winsberg 2010).
Moreover, those who had no role in shaping modeling priorities might be the least well informed about which variables were high/low priority.
As Steel (2015) points out, however, once we move from a picture in which Bayesian probabilities are degrees of belief that an agent involuntarily has, to one in which they are personal probabilities that an agent chooses to accept, we seem to have opened the door to inductive risk arguments, as suggested by Rudner (1953) and Douglas (2009).
de Melo-Martin and Intemann (2016) make a similar point in reply to the suggestion that, if scientists communicate the non-epistemic values that influenced methodological choices on inductive risk grounds, then policy makers can consider how conclusions reached in a study might have been different if different values were employed. They note that it is doubtful that policy makers and other stakeholders can do this. We are suggesting here that it is sometimes infeasible for scientists as well, especially when conclusions are expressed in terms of precise probabilities.
In fact, the implementation of BMA shown in Figure 1 uses the same simulation model to make the various forecasts; the model is run from different initial conditions each time, where the alternative initial conditions are estimated with the help of other weather forecasting models. Each run is then associated with one these other models.
The same is true if scientists determine that available information simply does not warrant assigning a single-valued probability to H. This might happen, for instance, if H pertains to the value of variable X, and the mechanisms that control the value of X are thought to be very poorly understood.
Of course, this is not the same thing as having low credence in H.
Interestingly, Steele (2012) argues that, when the structure of beliefs of scientists does not neatly match any of a limited set of options that they are constrained to choose among when reporting conclusions, then “scientists cannot avoid making value judgments, at least implicitly, when deciding how to match their beliefs to the required” options (see p.899). So the same limitation of options that can dampen the model-based value influence that is the focus of our discussion can – according to Steele – also open the door to value influence via inductive risk considerations.
Such questions are of interest in the international policy arena, where avoiding ‘dangerous’ climate change is often operationalized to mean keeping global temperature change under 2 °C.
There were between 25 and 42 simulations used for each of the scenarios. Thus, even for the scenario with the smallest number of simulations (25), there were 26 possible outcomes in terms of percentage values (i.e. 0%, 4%, 8%, … 100%) but only 9 probability intervals in Table 1.
References
Betz, G. (2013). In defense of the value-free ideal. European Journal for Philosophy of Science, 3(2), 207–220.
Betz, G. (2015). Are climate models credible worlds? Prospects and limitations of possibilistic climate prediction. European Journal for Philosophy of Science, 5, 191–215.
Biddle, J., & Winsberg, E. (2009). Value judgments and the estimation of uncertainty in climate modeling. In P. D. Magnus & J. Busch (Eds.), New waves in the Philosophy of science (pp. 172–197). New York: Palgrave MacMillan.
Cohen, L. J. (1992). An essay on belief and acceptance. Oxford: Clarendon Press.
Collins, M., Knutti, R., Arblaster, J., et al. (2013). Long-term climate change: Projections, commitments and irreversibility. In T. F. Stocker et al. (Eds.), Climate change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge: Cambridge University Press.
de Melo-Martin, I., & Intemann, K. (2016). The risk of using inductive risk to challenge the value-free ideal. Philosophy of Science, 83(4), 500–520.
Douglas, H. (2000). Inductive risk and values in science. Philosophy of Science, 67, 559–579.
Douglas, H. (2009). Science, policy, and the value-free ideal. Pittsburgh: Pittsburgh University Press.
Elliott, K., & McKaughan, D. (2014). Nonepistemic values and the multiple goals of science. Philosophy of Science, 81, 1–21.
Giorgi, F., & Mearns, L. O. (2003). Probability of regional climate change based on the reliability ensemble averaging (REA) method. Geophysical Research Letters, 30(12), 1629.
Gneiting, T., & Katzfuss, M. (2014). Probabilistic forecasting. Annual Review of Statistics and its Application, 1, 125–151.
Harris, G. R., Sexton, D. M. H., Booth, B. B. B., et al. (2013). Probabilistic projections of transient climate change. Climate Dynamics, 40(11–12), 2937–2972. doi:10.1007/s00382-012-1647-y.
Harsanyi, J. C. (1985). Acceptance of empirical statements: A Bayesian theory without cognitive utilities. Theory and Decision, 18, 1–30.
Intemann, K. (2015). Distinguishing between legitimate and illegitimate values in climate modeling. European Journal for Philosophy of Science, 5, 217–232.
Jeffrey, R. (1956). Valuation and acceptance of scientific hypotheses. Philosophy of Science, 22, 237–246.
Krzysztofowicz, R. (1999). Bayesian theory of probabilistic forecasting via deterministic hydrologic model. Water Resources Research, 35(9), 2739–2750.
Krzysztofowicz, R. (2002). Bayesian system for probabilistic river stage forecasting. Journal of Hydrology, 268, 16–40.
Lenhard, J., & Winsberg, E. (2010). Holism, entrenchment and the future of climate model pluralism. Studies in History and Philosophy of Science Part B, 41(3), 253–262.
Mastrandrea, M. D., Field, C. B., Stocker, T. F., et al. (2010). Guidance note for lead authors of the IPCC fifth assessment report on consistent treatment of uncertainties. Intergovernmental Panel on Climate Change (IPCC). Available at http://ww1w.ipcc.ch.
Mauritsen, T., Stevens, B., Roeckner, E., et al. (2012). Tuning the climate of a global model. Journal of Advances in Modeling Earth Systems, 4, M00A01. doi:10.1029/2012MS000154.
Morgan, M. G. (2014). Use (and abuse) of expert elicitation in support of decision making for public policy. PNAS, 111(20), 7176–7184.
Murphy, J. M., Sexton, D. M. H., Jenkins, G. J., et al. (2009). UK climate projections science report: Climate change projections. Exeter: Met Office Hadley Centre.
Parker, W. (2013). Ensemble modeling, uncertainty and robust predictions. Wiley Interdisciplinary Reviews: Climate Change, 4(3), 213–223.
Parker, W. (2014). Values and uncertainties in climate prediction, revisited. Studies in History and Philosophy of Science Part A, 46, 24–30.
Proctor, R. N., & Schiebinger, L. (Eds.). (2008). Agntology: the making and unmaking of ignorance. Stanford: Stanford University Press.
Raftery, A. E., Gneiting, T., Balabdaoui, F., et al. (2005). Using Bayesian model averaging to calibrate forecast ensembles. Monthly Weather Review, 133, 1155–1174.
Rudner, R. (1953). The scientist qua scientist makes value judgments. Philosophy of Science, 20(1), 1–6.
Steel, D. (2015). Acceptance, values and probability. Studies in History and Philosophy of Science, 53, 81–88.
Steele, K. (2012). The scientist qua policy advisor makes value judgments. Philosophy of Science, 79, 893–904.
Winsberg, E. (2012). Values and uncertainties in the predictions of global climate models. Kennedy Institute of Ethics Journal, 22(2), 111–137.
Acknowledgements
Audiences at the London School of Economics, the University of Leeds and Durham University’s Centre for Humanities Engaging Science and Society (CHESS) provided helpful feedback on earlier versions of this paper. We are also grateful for the suggestions made by the paper’s referees.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Parker, W.S., Winsberg, E. Values and evidence: how models make a difference. Euro Jnl Phil Sci 8, 125–142 (2018). https://doi.org/10.1007/s13194-017-0180-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13194-017-0180-6