1 Introduction

Traffic anomalies are common during disasters. In this study, a model to detect traffic anomalies during heavy rainfall events was developed, and its versatility was evaluated. To mitigate the effects of a disaster, understanding traffic anomalies following a disaster and devising countermeasures is necessary. Therefore, traffic-anomaly detection is important. Currently, road administrators assess damage in the event of a disaster through onsite inspections (visual confirmation) and CCTV cameras. Access to a disaster site may be limited owing to traffic restrictions and congestion caused by evacuation. In addition, the number of locations where CCTV cameras can be installed is limited, and some areas may not be monitored. In the event of a heavy rainfall disaster, characterized by simultaneous damage, efficient and prompt detection of hazardous areas is necessary. Previously, we analyzed traffic anomaly and proposed an anomaly detection method in the event of heavy rainfall, snowfall, and earthquakes [1,2,3,4,5,6]. During heavy rainfall, a vehicle moving in traffic may make a U-turn in front of a damaged area after noticing a disaster-struck area (e.g., flooded roads). If such traffic anomalies can be detected automatically, they are expected to contribute to (1) the early detection of hazardous areas and (2) the prioritization of areas for field surveys (e.g., surveys in areas where traffic anomalies occur).

A method for detecting the U-turn behavior (traffic anomaly) of vehicles during heavy rainfall using probe-vehicle data is proposed in this paper. The proposed method was used to developed a calibration method for model parameters. Finally, the generality (transferability) of the model was evaluated by applying it to other disasters.

2 Previous Research

In this section, previous studies from two perspectives (understanding the actual traffic situation during a disaster and detecting traffic obstacles) are summarized. This section is concluded by describing the contributions of this research based on previous studies.

2.1 Traffic State Analysis during Disasters

Zhu et al. [7] analyzed the changes in traffic patterns after the collapse of the I-35W bridge using vehicle detectors, bus user statistics, and questionnaires. A temporary change in the traffic pattern on the highway near the I-35W bridge was observed, and the traffic demand did not change significantly after the collapse. The actual traffic conditions in the entire road network could not be determined owing to limited the observation points of the vehicle detectors. Moreover, the results of questionnaire surveys are not always accurate as they are based on memory of a subject, and obtaining a large sample is difficult since surveys are time-consuming.

Probe vehicle data collected from cell phones and car navigation systems can provide detailed information on the routes and speeds of trips across an entire road network. Several researchers analyzed traffic during disasters using probe vehicle data [7,8,9,10]. For example, Hara et al. [10] quantitatively analyzed a long traffic jam (the so-called gridlock) caused by evacuation during the Great East Japan Earthquake in March 2011. The tsunami that hit traffic in the gridlock caused extensive damage.

Probe vehicle data have been extensively utilized to understand traffic conditions during disasters and can help understand vehicle behavior over a wide area, even in the event of a disaster. Therefore, probe vehicle data is effective for detecting traffic anomalies during heavy rainfall events.

2.2 Traffic Anomaly Detection

Cullip and Hall [11] and Kawasaki et al. [12] attempted to detect traffic anomalies using vehicle detectors installed as sensors. The differences between normal and abnormal conditions in terms of traffic volume, occupancy, and lane-wise speed were analyzed using vehicle detectors, and thresholds were set to discriminate between these conditions. Subsequently, traffic disturbances were detected by determining whether the newly obtained vehicle detector data were normal according to threshold values.

Asakura et al. [13] obtained a shock wave surface connecting the inflection points of a vehicle trajectory in two dimensions (time × distance traveled) as a function of time and distance traveled at the time of traffic disturbance. Cai et al. [14] defined “abnormal behavior” as wobble or lane departure at the entry section of an intersection on a public road in the event of a traffic disturbance. The time and location of the traffic disturbances were estimated using only the probe trajectory data near the intersection (plane). We attempted to detect abnormal behavior using only the probe trajectory data of the vicinity of an intersection (flat surface). Based on the speed and direction of travel obtained from the probe trajectory data, clusters of vehicle trajectories indicating normal and abnormal behaviors were constructed in advance. When a newly obtained trajectory was classified into a cluster of abnormal behavior, the trajectory was detected as abnormal behavior (occurrence of traffic disturbance). However, if the entire obtained trajectory for the entire road network is statistically processed, the computational load increases significantly. In addition, even if a vehicle is classified into a cluster of abnormal behaviors, determining whether it is classified into a cluster owing to a unique vehicle behavior during a disaster is not possible. Therefore, constructing a model based on the abnormal behavior of vehicles during disasters is necessary. Hirata et al. [15] used probe vehicle data corresponding to a heavy rainfall event to determine 1) whether traffic anomalies similar to those observed in previous disasters could be identified (Is there a generality in traffic anomalies?); (2) the common characteristics of traffic anomalies across multiple cities; 3) the quantitative analysis results of the traffic anomalies in front of the affected area. Events similar to those observed during previous disasters were determined. The results showed that vehicles exhibited U-turn behavior in front of damaged areas in the event of heavy rainfall in several cities. This behavior can be characterized by the location and speed of the U-turn. In this study, a U-turn detection method was developed based on the U-turn characteristics identified in the aforementioned studies.

2.3 Contribution of this Study

The contributions of this study, based on the previous studies, described in Sections 2.1 and 2.2, are given below:

  1. 1)

    Proposal of anomaly detection method: A U-turn in front of a damaged area in the event of heavy rainfall was defined as a traffic anomaly. We proposed a simple and fast U-turn detection method that uses only probe vehicle data.

  2. 2)

    Parameter calibration method: The parameters of the detection model must be calibrated to detect U-turns. In this study, we proposed a method for calibrating parameters using historical data corresponding to heavy rainfall disasters.

  3. 3)

    Generalizability of the anomaly-detection model: We applied the calibrated anomaly-detection model to typhoon data of multiple cities and evaluated its accuracy. This model can accurately detect traffic anomalies (U-turns). Hence, the proposed model can be applied (extended) to various scenarios, such as newly occurring disasters.

3 Methodology

In this section, an overview of the data used in this study is provided, and the U-turn detection algorithm based on the probe data is described.

3.1 Data

An overview of the data is provided in this section. First, meteorological and disaster-related data for heavy rainfall events were obtained. Data related to Typhoon No. 19, which hit Fukushima Prefecture, Japan in 2019, were analyzed. The typhoon hit the city on Saturday, October 12, resulting in the highest amount of precipitation recorded in October. This heavy rainfall caused levee failure and overtopping on Sunday, October 13. In this study, the period from 0:00 to 12:00 on October 13, 2019, corresponding to the consequent inundation, was considered for analysis. Meteorological data related to Typhoon No. 19 were obtained from the Japan Meteorological Agency [16]. Data on areas inundated (flooded roads) by typhoon were obtained from open-source hazard maps [17, 18] collected by each municipality. Hazard maps were used to confirm the correct data for U-turns in the event of a disaster (i.e., whether U-turns were made before the flood zone) and to narrow down the U-turn detection area.

The probe data are described below. In this study, we used probe data collected by ETC2.0 [19], a system that enables collaborative links between vehicles and roads of a variety of services. Vehicles equipped with ETC2.0 service compliant OBUs accumulate travel and behavior histories in a privacy-protected format. This information is collected as probe data when the vehicles pass through an RSU. The travel history is recorded every 200 m. In this study, we used point-sequence data from the probe data without aggregation. The penetration rate of the ETC2.0 onboard units was 30.1% in Japan as of February 2023 [22]. RSU were installed at more than 1,800 locations on expressways and 2,400 locations on national roads in Japan (as of April 2023). Therefore, notably, data may not be obtained for locations where RSUs were not installed (e.g., narrow streets). However, we believe that this system can monitor a wider area than a CCTV camera owing to the following reasons:

  1. 1)

    Rapid detection of traffic anomalies is necessary to support mobility during disasters. Therefore, the data processing time was reduced by omitting the map-matching process.

  2. 2)

    The accuracy of map matching depends on the state of road network data. Traffic anomalies may occur even on narrow streets where network data are unavailable. Therefore, we developed a traffic anomaly detection method that is independent of the network data.

3.2 U-Turn Detection Algorithm

We defined the U-turn behavior during heavy rainfall as a traffic anomaly and proposed an algorithm for its detection using probe data. This algorithm is intended to be executed in the event of a heavy rainfall warning (or rainfall restriction).

First, the U-turn behavior during heavy rainfall was defined as follows:

  • 1) A U-turn is made on a single road (route) (i.e., when a vehicle moves into an oncoming lane) within the same road (route).

  • 2) U-turns were made before the flooding (or within the flooded area).

In this study, U-turns that met these conditions were defined as disaster-caused U-turns. In a previous study [15], based on the above definition, U-turns during Typhoon No. 19 were classified by visually checking the probe trajectory data.

  1. 1)

    Location of occurrence: U-turns are frequent near bridges and rivers.

  2. 2)

    Speed transition before and after a U-turn: A vehicle decelerates before the U-turn and then further decelerates during the U-turn, after which the vehicle recovers (increases) its speed.

  3. 3)

    U-turn angle: All U-turns were made at sharp angles.

Figure 1 shows the latitude and longitude of a U-turn; as shown, U-turns were detected using GPS data at three points (Nos. 1–3). The corresponding velocities were defined as \({v}_{1},{v}_{2}\), and \({v}_{3}\), and the angles at Points 1–3 were defined as \({X}_{\mathrm{1,2},3}\). The thresholds of the velocities were defined as \({v}_{1}^{th},{v}_{2}^{th},{v}_{3}^{th}\), and the thresholds of the angles were defined as \({X}_{\mathrm{1,2},3}^{th}\).

Fig. 1
figure 1

Definition of a U-turn

Full size image

The following procedures were proposed to detect U-turns using probe data:

  • Step 1: Establishment of candidate locations

    U-turns are routinely made in parking lots and turnarounds. However, these U-turns are beyond the scope of this study. To improve the accuracy of U-turn detection in the event of heavy rainfall, the locations where U-turns were detected were narrowed down in advance. Based on a previous study [15], we targeted locations near riverbanks. The specific method is described as follows.

  • Step 2: Detection of candidate U-turn locations

    Speed changes were detected at Points 1–3, as shown in Fig. 1.

    1. 1:

      The vehicle is traveling at a speed higher than speed \({v}_{1}^{th}\) before the start of the U-turn. Next, the point where the vehicle is moving normally immediately after decelerating to make a U-turn (i.e., the point where the vehicle is moving at a speed of \({v}_{1}^{th}\) or less immediately after decelerating to a speed ≤ \({v}_{1}^{th}\)).

    2. 2:

      The point where the vehicle appears to have made a U-turn (the point where the vehicle decelerates to a speed ≤ \({v}_{2}^{th}\)).

    3. 3:

      The point at which the vehicle appears to have started moving after the U-turn (the point where the vehicle accelerates to a speed of ≤\({v}_{3}^{th}\) after (2)).

  • Step 3: Calculation and evaluation of U-turn angle

    Using the angle \({X}^{(\mathrm{1,2},3)}\) between the three points detected in Step 2, we can determine if the vehicle has made a U-turn or simply decelerated and proceeded (without making a U-turn). Specifically, if \({X}_{\mathrm{1,2},3}<{X}_{\mathrm{1,2},3}^{th}\)(the angle threshold), a vehicle is considered to have made a U-turn.

\({v}_{1}^{th},{v}_{2}^{th},{v}_{3}^{th}\), and \({X}_{\mathrm{1,2},3}^{th}\) are the parameters of the U-turn behavior detection. Based on the above procedure, an algorithm for U-turn detection was established. The notation used in this algorithm are listed in Table 1. Figures 2 and 3 show the U-turn detection algorithm for a single vehicle based on these notations. Figure 2 shows the algorithm for Step 2, which extracts Points 1–3 where the speed changes. Figure 3 shows the algorithm for Step 3, which passes the information of the three points and determines whether a U-turn is made based on the angle.

Table 1 Notation of variables
Full size table
Fig. 2
figure 2

Algorithm for Step 2

Full size image
Fig. 3
figure 3

Algorithm for Step 3

Full size image

4 Parameter Calibration

In this section, a method for calibrating the parameters of the U-turn detection method described in Section 3 is proposed, and the calibration results are summarized. The data used for the parameter calibration were obtained from Koriyama City, Fukushima Prefecture, Japan, during Typhoon No. 19.

4.1 Data for Parameter Calibration

The data used in parameter calibration are described in this section. The data were related to vehicles that made a U-turn (traffic anomaly) owing to heavy rainfall in Koriyama City, Fukushima Prefecture (correct U-turn data). The correct were organized according to the definition of U-turn (Section 3.2), using the following procedure: First, vehicle trajectory and inundated area data were visualized in GIS. The individual vehicle trajectories were visually confirmed, and the data that met the definition of a U-turn were organized as “correct data.” For details on the method for creating correct data, please refer to [15]. Owing to human errors (e.g., oversight), not all U-turns could be detected as the data were collected by visual inspection. Figure 4 shows the visually detected U-turn locations. The red star indicates the U-turn point. This figure shows that U-turns were frequently made near crossing areas and rivers. The distribution of U-turns differs significantly between the east and west sides of the river, as shown in Figure. A large number of U-turns on the west side of the river can be attributed to the 1) lower level of the west side of the river, 2) wider undrivable road caused by inundation, and 3) higher population (automobiles) than the eastern area of the river.

Fig. 4
figure 4

Visualization of U-turn locations (correct data only)

Full size image

4.2 Parameter Calibration Procedure

The parameter-calibration procedure is described in this section.

  1. (1)

    A mesh was set up for U-turn detection and accuracy verification (see below for details).

  2. (2)

    Multiple parameter candidates were enumerated.

  3. (3)

    The accuracy of the U-turn detection for each parameter was evaluated. The high-frequency value of the top pattern with the highest accuracy was used as the calibration value.

We did not use the calibration result with the highest accuracy, instead, used a multifrequency pattern, as in (3). The results showed no significant differences in the top U-turn detection accuracy, and the parameter set patterns were diverse (details are described later).

In the following section, the mesh setting of the U-turn detection location in (1) is described. According to a previous study [15], U-turns are frequently made near river banks. Therefore, we set the detection locations to units of the GSI regional mesh [20]. Two meshes, tertiary (1 km × 1 km) and quaternary (500 m × 500 m), were selected as candidates, and their accuracies were compared. Using hazard maps, the location of the mesh for U-turn detection was determined to be within the expected inundation area near rivers (where many U-turns are expected to occur in the event of a disaster). The reasons for setting GSI regional mesh are as follows: 1) The regional mesh is organized with GIS information such as elevation, which enables analysis of environmental factors that cause traffic anomalies such as U-turns; and 2) the regional mesh is defined with similar definitions (e.g., size) in each region. Therefore, we considered that the regional mesh could be used as a standard for matching the spatial resolution to compare the accuracy of U-turn detection among regions.

Next, we defined the indices to evaluate the accuracy of U-turn detection in (2): Precision (fit rate), Recall (recall rate), and F-value. The Recall indicates the extent of inclusion of all matched data in the search results. The harmonic mean of the Precision and Recall is the F-value. Typically, Precision and Recall have a tradeoff relationship. A high F-value implies that the model performs well [21]. In this study, Precision, Recall, and F-value were defined as follows: First, the relationship between the actual and model-estimated traffic congestions was defined, as summarized in Table 2. True positives (TP), false positives (FP), false negatives (FN), and true negatives (TN) in the table represent the number of cases (counts) that correspond to each value. For example, if the model can detect a U-turn at the location where the U-turn actually occurs, the TP is counted (+ 1). Precision, Recall, and F-value are defined as follows:

Table 2 Relationship between model and actual data
Full size table
$$Precision=\frac{TP}{TP+FP}$$
(1)
$$Recall=\frac{TP}{TP+FN}$$
(2)
$$F-value=\frac{2\times Precision\times Recall}{Precision+Recall}$$
(3)

The locations where U-turns are not observed disasters are infinite; therefore, the TN in Table 2 cannot be counted. Instead of using TN as an indicator (e.g., accuracy), we used Precision, Recall, and F-value as evaluation indicators.

4.3 Parameter Calibration Results

4.3.1 Setting of Conditions

In this section, the parameter calibration setup is described.

First, we described the mesh setup for the U-turn detection and accuracy verification. Figure 5 shows the fourth mesh (red frame) used for the validation of Koriyama City, Fukushima Prefecture, including a mesh containing the river.

Fig. 5
figure 5

Visualization of U-turn locations (correct data and model)

Full size image

Next, we described the parameter set (\({v}_{1}^{th},{v}_{2}^{th},{v}_{3}^{th}\), and \({X}_{\mathrm{1,2},3}^{th}\))of the model. The parameter patterns are listed in Table 3. The speeds were set to five to six patterns with values up to the regulated speed (60 km/h), and the angles were set to six patterns with values up to 90°, similar to the right and left turns. Thus, the number of patterns in the parameter set was 1,080.

Table 3 Parameter patterns
Full size table

4.3.2 Candidate Mesh Settings

In this section, the results of setting up a mesh to detect U-turns are discussed. Figure 6 shows a scatter plot of the precision and recall according to the mesh pattern, where the horizontal and vertical axes represent Recall and Precision, respectively. The values for each pattern were plotted; the Precision tended to be lower, and the Recall was higher. Recall is crucial for preventing anomalies from being missed. However, a higher recall rate increases the coverage of true U-turns and the number of FPs. For example, the points in Fig. 6 where the Recall = 1.0 (diamonds and squares) indicate low precision ranging from 0.05 0.08. As an abnormality detection system should reduce false alarms (strikeouts), a higher Precision is desirable compared with the Recall. As the correct data in this study were detected visually by an analyst, some of the data were likely to be overlooked owing to human error. Therefore, the precision was assumed to be lower than that of the true correct answer owing to the fewer validation data than true correct answer data. A method for creating the correct dataset is an issue that should be addressed in future research. Figure 6 shows a comparison of the accuracies of the tertiary and quaternary meshes. A quadratic mesh produces higher accuracy than a tertiary mesh in terms of the mean points. This was presumably owing to the improved accuracy of the quaternary mesh caused by the narrowing of the target area, which excluded roads outside the inundation zone, thereby reducing the number of FPs. Therefore, we set candidate locations for U-turn detection on a quaternary mesh.

Fig. 6
figure 6

Distributions of the precision and recall

Full size image

4.3.3 Parameter Settings

The parameter calibration results are described in this section. Figure 7 shows a descending graph of the F-values for each parameter pattern, including the Precision and Recall values for each F-value. The Recall was significantly larger than the Precision. From the viewpoint of the administrator, overlooking an anomaly is undesirable, and focusing on Recall is preferable. However, in terms of the efficiency of abnormality detection (i.e., reduction of false alarms), Precision should also be evaluated. Therefore, in this study, we mainly evaluated the F-value by considering both Precision and Recall. No significant differences were observed in the top F-values. The pattern with the highest F-value exhibited variation (lack of regularity) in Recall. In contrast, Precision did not exhibit significant variation and tended to decrease gradually with decreasing F-value. The parameters in the top F-value range were diverse although no significant difference in the F-value was observed. We considered simply adopting a parameter pattern with the highest F-value as inappropriate. Therefore, we searched for appropriate parameters by analyzing the trends in their patterns in the top 5% of the F-values. We used the most frequently occurring parameter values (\({v}_{1}^{th},{v}_{2}^{th},{v}_{3}^{th}\), and \({X}_{\mathrm{1,2},3}^{th}\)). Figure 8 shows a parallel coordinate plot of the top 5% of F-value parameters. For \({v}_{1}^{th}\), the most frequent value was 40 km/h, followed by 60 km/h. A previous study [15] showed that the speed at which U-turns are made during a disaster tends to be lower than normal, \({v}_{1}^{th}=40\) km/h; \({v}_{2}^{th}\) was 10 km/h in most cases, followed by 20 km/h. However, the ETC2.0 probe can only acquire GPS data while driving, and acquiring data in the low-speed range is challenging (Since data corresponding to < 5 km/h can be missing, and a threshold value of 10 km/h may result in additional missing data). The pattern with \({v}_{2}^{th}\)=20 km/h also contained a first-place Recall. As mentioned above, from the perspective of an administrator, Recall should be emphasized to prevent misses. Therefore, we set \({v}_{2}^{th}=20\) km/h in this study; most common was \({v}_{3}^{th}=\) 60 km/h, followed by 20 km/h, which tends to be higher than the other speeds. Based on this, we set \({v}_{3}^{th}=60\) km/h. Finally, \({X}_{\mathrm{1,2},3}^{th}\) was set; the most common values for \({X}_{\mathrm{1,2},3}^{th}\) were 20° and 10°. The large number of sharp-angle patterns may be due to the fact that the U-turns in this study were limited to those performed on the same road. Based on this, \({X}_{\mathrm{1,2},3}^{th}\) was set to 20°. After the calibration, the parameters were set as follows:

  • \({v}_{1}^{th}=40\) km/h

  • \({v}_{2}^{th}=20\) km/h

  • \({v}_{3}^{th}=60\) km/h

  • \({X}_{\mathrm{1,2},3}^{th}=20\)°

Fig. 7
figure 7

Descending-order graph of the F-value

Full size image
Fig. 8
figure 8

Parallel coordinate plot of the parameter

Full size image

As mentioned above, the optimal parameters could not be determined based only on the F-value; therefore, the parameter patterns with the highest F-values were analyzed in this study. For practical implementation, easy and systematic determination of the parameters is desirable. Construction of a systematic parameter calibration method will be considered in future studies.

4.3.4 Discussion

In this section, the limitations (issues) of the model are discussed. First, the normal conditions (0:00–12:00 on October 8, 2019) and disaster conditions were compared. Figure 9 shows the locations of the U-turns detected by the model under normal conditions. The figure shows that the proposed model captured U-turns under normal conditions. Normal conditions are characterized by change in the course to reach a destination (e.g., a U-turn at an intersection) or parking (e.g., a U-turn in a parking lot). However, few U-turns are made in the vicinity of bridge sections during normal times (Fig. 9). However, during a disaster (Fig. 4), many U-turns are made near bridge sections. Thus, the distribution of U-turns differs between the normal and disaster situations. ETC2.0 probe data processing alone cannot prevent false detection of U-turns (e.g., U-turns in parking lots) under normal conditions. Therefore, in the event of a disaster, narrowing down the U-turn detection points in advance is necessary, as described in Section 3.2. The limitations of the proposed model are discussed below. As shown in Fig. 4 and 9, the proposed method can detect U-turn behavior using only ETC2.0 probe data. However, the ETC2.0 probe data has the following problems: 1) The data is sample data; therefore, entire data cannot be identified; and 2) the locations of ITS spots (data transmission and reception points) are biased. Therefore, focusing on the interpretation of U-turn locations is necessary. Notably, statistical processing such as normalization by the number of probes is not possible owing to this issue.

Fig. 9
figure 9

Visualization of U-turn locations (normal condition)

Full size image

Consider the reasons for the occurrence of FP. FP means the model detects U-turns even where there is no correct U-turn data. While this could be a false positive in the model, we believe it is an effect of insufficient true correct data. Although U-turns were actually occurring at the time of the disaster, all U-turns could not be detected because the correct data was manually generated, and the FP increased due to this effect, which is thought to have lowered Precision. The method of generating true correct data is considered a future issue.

5 Validation: Applicability of model in other Cities

The validity of the model for Koriyama City was verified using calibrated parameters, and its applicability to other cities was evaluated. We also present validation results for Iwaki City, Fukushima Prefecture, during Typhoon No. 19. Koriyama (located inland) and Iwaki (located in the coast) are 90 km apart and have different topographies and climates.

5.1 Validation Results for Koriyama City

In this section, the accuracy of U-turn detection in Koriyama City using post-calibration parameters is described. In Fig. 5, the U-turns detected by the proposed method, correct answers, and fourth meshes set up for detection are indicated by green dots, red stars, and red boxes, respectively. Note that the total number of meshes used for detection was 37, and the figure shows only some of them.

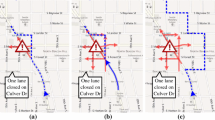
Next, we discuss accuracy: Precision = 0.128, Recall = 0.888, and F-value = 0.223. The Recall value indicated that the model covered approximately 90% of all U-turns. Figure 10 shows the U-turn detection status in the target mesh for 0:00–12:00. No significant decrease was observed in the detection accuracy during this period. Figure 11 shows two examples of the visualization of traffic control and U-turn detection points attributed to the disaster. In these cases, U-turns were detected in areas other than the restricted areas. In particular, a U-turn was detected in a flooded hazardous area near a bridge; however, traffic control was not implemented. Thissuggests that improving the detection accuracy of U-turns may contribute to quicker identification of uncontrolled areas.

Fig. 10
figure 10

Detection of U-turns by time of day in Koriyama City

Full size image
Fig. 11
figure 11

Traffic restrictions and U-turn detection points due to heavy rains

Full size image

Finally, to identify areas for improvement in the model, data for which U-turns could not be detected (i.e., FP and FN) were analyzed. The analysis results indicate the following cases in which U-turns could not be detected: 1) U-turns made at high speeds (no deceleration before and after the U-turn) and 2) the behavior before and after the U-turn consisting of multiple points (four or more). However, their Precision and F-values were insufficient to detect U-turns at high speeds. However, detecting U-turns at high speeds is difficult while maintaining accuracy within the framework of the proposed model, as the Precision and F-value are low. Next, we considered the possibility of improving the model for 2). Figure 12 shows an example of a U-turn that could not be detected by the proposed model. As shown in the figure, the positions before and after a U-turn consisted of multiple points. The points (locations) where the steering wheel maneuvers, which are made several times when making a careful U-turn, are recorded. Such U-turns cannot be detected as they do not satisfy the assumption of U-turn behavior, as shown in Fig. 1. In case of presence of multiple candidates near the deceleration point at the time of a U-turn, only the data of the deceleration point with the lowest speed should be extracted and used, a situation in which the vector of the vehicle trajectory changes significantly as a U-turn should be detected, or a situation in which the vehicle trajectory vector changes significantly as a U-turn should be detected. This model improvement is an issue that needs to be addressed in the future.

Fig. 12
figure 12

Examples of U-turns that could not be detected

Full size image

5.2 Validation Results for Iwaki City

In this section, the verification results for Iwaki City are described.

First, the damage caused by Typhoon No. 19 in Iwaki was studied. Similar to Koriyama City, Iwaki City was confirmed to have been inundated by Typhoon No. 19, which resulted in a large number of U-turns. In Iwaki City, as in Koriyama City, U-turn detection points were set using a fourth mesh. The target mesh in Iwaki City was 31, which was identical to the number of meshes as that in Koriyama City. The number of confirmed U-turns was only 45, as the total number of trips was lower than that observed in Koriyama City. The characteristics of the U-turns were similar to those observed in Koriyama City, such as the concentration of U-turns near rivers. For more details, please refer to data provided in a previous study [15].

Figure 13 shows the data related to the correct U-turns taken in Iwaki City and the U-turn detection results obtained by the model. Clearly, the model can detect U-turns near the riverbanks. Figure 14 shows the accuracy of the U-turn detection for Koriyama and Iwaki. Figure 14 shows that the Precision, Recall, and F-values of Iwaki City were not significantly different from those of Koriyama City, implying that the same level of accuracy can be guaranteed. Figure 15 shows the U-turn detection status in the target mesh over time (0:00–12:00). U-turns during the nighttime (0:00–6:00) were generally detected with good accuracy.

Fig. 13
figure 13

Visualization of U-turn locations

Full size image
Fig. 14
figure 14

U-turn detection accuracy by city

Full size image
Fig. 15
figure 15

Detection of U-turns by time of day in Iwaki City

Full size image

6 Conclusions

In this study, a model for detecting traffic anomalies during heavy rainfall events was developed, and its versatility was evaluated. The model was constructed using the speed transition before and after considering the U-turn and U-turn angles as parameters. The model parameters were calibrated using disaster-related data. The calibrated model was applied to a heavy rainfall disaster in Koriyama City, and it could detect U-turns with high accuracy. When applied to a heavy rainfall disaster in Iwaki City, it exhibited similar accuracy. This suggests that the proposed model can be extended to other cities.

Directions for future research:

  1. 1)

    Expansion of cases: We targeted only two cities, Koriyama and Iwaki. Further case studies are required to verify the applicability of the proposed method.

  2. 2)

    Verification of applicability to other types of disasters: The U-turn event defined in this study can occur if road damage occurs. Therefore, verifying the applicability of this model to other types of disasters, such as earthquakes is necessary.

  3. 3)

    Consideration of how to generate true correct data: The correct data used in validation does not cover all true U-turns (Section 4.3.4). Therefore, accurate accuracy verification is not possible. Future issues include a study of how to generate correct data.

  4. 4)

    Model improvement: As described in Section 5.1, the proposed model cannot detect cases in which multiple points exist before and after a U-turn (as shown in Fig. 11). Therefore, essentially, the model can be improved by extracting and using only the data of the deceleration point with the lowest speed in the presence of multiple candidates at the deceleration point at the time of a U-turn, detecting a situation in which the vector of the vehicle trajectory changes significantly as a U-turn, or detecting a situation in which the vehicle trajectory vector changes significantly as a U-turn is considered necessary.

  5. 5)

    Model improvement: In this study, we focused on the U-turn behavior of vehicles in front of a damaged area as an example of a traffic anomaly. However, in the event of an actual disaster, various traffic anomalies, such as detours and sudden decelerations, are likely to occur. Therefore, the model must be improved to detect various traffic anomalies in a flexible and versatile manner. For example, the model can be modified to switch between various models, depending on the situation.