On smooth functions with two critical values

Abstract

We prove that every smooth closed connected manifold admits a smooth real-valued function with only two critical values such that the set of minima (or maxima) can be arbitrarily prescribed, as soon as this set is a finite subcomplex of the manifold (we call a function of this type a Reeb function). In analogy with Reeb’s Sphere Theorem, we use such functions to study the topology of the underlying manifold. In dimension 3, we give a characterization of manifolds having a Heegaard splitting of genus g in terms of the existence of certain Reeb functions. Similar results are proved in dimension $n\ge 5$.

1 Introduction

In 1946 Reeb [12] proved the following result.

Reeb’s Sphere Theorem   Let M be a smooth closed manifold of dimension n. Suppose that there is a smooth function $f \,{:}\; M \rightarrow {\mathbb {R}}$ with only two critical points, which are also non-degenerate. Then M is homeomorphic to the n-sphere.

Subsequently, Milnor [10] improved the theorem by relaxing the non-degeneracy assumption for the two critical points.

In the present article we study smooth functions on closed manifolds having two critical values (instead of two critical points), which are then the minimum and the maximum, respectively. Such functions (which are defined below, see Definition 3) will be called Reeb functions. Moreover, we will be able to keep some control on the critical subset of a Reeb function. Some examples of Reeb functions are provided at the beginning of Sect. 2.

It is a natural question to understand to what extent the knowledge of the set $X_0$ of minima and $X_1$ of maxima of a Reeb function $f\,{:}\; M\rightarrow {\mathbb {R}}$ determines the manifold M (at least up to homeomorphisms). This problem is already interesting when $X_0, X_1$ are smooth submanifolds of M and, to our knowledge, it does not seem to have been investigated in the literature. In order to address this question, in this paper, we will consider Reeb functions whose critical sets $X_0$ and $X_1$ are finite subcomplexes of M. Notice this requirement imposes restrictions only on the structure of the critical set, and not the behaviour of the function near it (i.e., we allow f to assume the minimum and the maximum values with arbitrary order of degeneracy). Similar results are known when the function has more structure. An example is [3], where Gelbukh studied Morse-Bott functions with two critical values and classified the surfaces that admit such functions.

To start with, we prove that every smooth closed manifold M admits a Reeb function, even with a prescribed set of minima (or maxima).

Theorem 1

Let M be a smooth closed manifold, and let $X \subsetneq M$ be a finite subcomplex. Then there exists a $C^{\infty }$ Reeb function $f\,{:}\; M \rightarrow [0,1]$, having 0 and 1 as extrema, such that $f^{-1}(0)= X$.

The homology of maxima and minima of a Reeb function satisfy some “duality” relation, see Remark 12. For example, if $M=S^n$ then the homology of $X_0$ is isomorphic to the homology of $X_1$, with reversed indices. Moreover, as one could expect, $M\setminus X_1$ deformation retracts to $X_0$ and viceversa, see Lemma 11.

We can restate Reeb’s Sphere Theorem using the language of Reeb functions as follows: a smooth closed manifold of dimension n admits a smooth Reeb function with two points as extrema, if and only if it is homeomorphic to an n-sphere. What happens if the set of minima and maxima are finite subcomplexes? In dimension $n=3$ we prove the following result.

Theorem 2

Let M be a smooth closed connected 3-manifold. Then the following conditions are equivalent:

• (1) there exists a Reeb function $f :M \rightarrow [0,1]$ having connected 1-dimensional finite subcomplexes of the same Euler characteristic $\chi$ as extrema, for some $\chi \le 1$;

• (2) the Heegaard genus of M is at most $1-\chi$ in the orientable case and $2-2\chi$ in the non-orientable case.

Results in the same spirit as of Theorem 2 can be proved in higher dimensions using cobordism theory, see Corollary 16.

2 Reeb’s functions

In the following, smooth means $C^\infty$, and diffeomorphisms between smooth manifolds are $C^\infty$ unless otherwise stated.

We recall that every smooth manifold has a compatible PL structure, and therefore a triangulation which turns out to be unique up to smooth ambient isotopy and subdivisions. This makes available all the concepts and tools of PL topology in the smooth category. In particular we can consider subcomplexes of smooth manifolds, and a subcomplex is finite if and only if it is compact.

A subcomplex X of a smooth manifold M has regular neighborhoods in the PL sense, namely closed neighborhoods of X in M that are PL submanifolds which can be PL collapsed onto X. According to Hirsch [7] we call smooth regular neighborhood of X in M a regular neighborhood whose boundary is a smooth codimension-1 submanifold of M.

A subcomplex X of a smooth manifold M is a spine for M if M can be PL collapsed onto X, namely if M is a regular neighborhood of X. Spines always exist, see Matveev [9]. The reader is also referred to the classical book by Rourke and Sanderson [13] for generalities on PL topology, triangulations, regular neighborhoods and collapsing.

Definition 3

Let M be a smooth closed manifold and let $f\,{:}\; M \rightarrow [a,b]$ be a $C^k$ function, with $k\ge 2$ and $a<b$. We say that f is a Reeb function on M if f has a and b as the only critical values (the extrema of f). The subsets $f^{-1}(a)$ and $f^{-1}(b)$ are the critical levels of f.

Without loss of generality, we assume throughout the paper that $a=0$ and $b=1$. The simplest example of a Reeb function is a function on $S^n$ with only two critical points. Below we give some other examples.

Example 4

Let M be a smooth manifold and $g\,{:}\; S^n\rightarrow [0,1]$ be a smooth function with only two critical points $p_0, p_1\in S^n$. Then the function $f\,{:}\; M \times S^n\rightarrow [0,1]$ defined by $f(x, y) =g(y)$ is a Reeb function with $X_0=M \times \{p_0\}$ and $X_1=M \times \{p_1\}.$

Example 5

Let ${\mathbb {K}}\!=\!{\mathbb {R}}, {\mathbb {C}}, {\mathbb {H}}$ and denote by ${\mathbb {K}}\textrm{P}^n$ the n-dimensional projective space over ${\mathbb {K}}$ with homogeneous coordinates $[x_0, \ldots , x_n]$. Let $X_0\!=\!\{x_i=0 \mid i\le k\}\cong {\mathbb {K}}\textrm{P}^{n-k-1}$ and $X_1=\{x_i=0 \mid i> k\}\cong {\mathbb {K}}\textrm{P}^k$. The function $f\,{:}\; {\mathbb {K}}\textrm{P}^n\rightarrow [0,1]$ defined by

$$\begin{aligned} f(x)=\frac{|x_0|^2+\cdots +|x_k|^2}{|x_0|^2+\cdots +|x_n|^2} \end{aligned}$$

is a Reeb function (in fact, also a Morse–Bott function).

Example 6

Let $M\subset {\mathbb {R}}^n$ be a smooth semialgebraic set and $X\subset M$ be a basic semialgebraic set (relative to M). There is an explicit way to define a Reeb function $f\,{:}\; M\rightarrow {\mathbb {R}}$ with $f^{-1}(0)=X$. In fact, assuming that

$$\begin{aligned} X = \{x \in {\mathbb {R}}^n \,|\, g_1(x)\ge 0, \ldots , g_s(x)\ge 0\}\cap M \end{aligned}$$

where $g_i \in {\mathbb {R}}[x_1,\ldots ,x_n]$ for every $i=1,\ldots ,s$, the function f can be constructed as follows. First consider the functions $f_i\,{:}\; {\mathbb {R}}^n \rightarrow {\mathbb {R}}$ such that

$$\begin{aligned} f_i (x) = {\left\{ \begin{array}{ll} 0 &{} g_i(x) \ge 0, \\ e^{\frac{1}{g_i(x)}} &{} g_i(x) < 0. \end{array}\right. } \end{aligned}$$

Then set $f= \sum _{i=1}^s f_i|_{M}$. This example is also connected to the theory developed by Durfee [1] and Dutertre [2].

Example 7

If $f:M\rightarrow [0,1]$ is a Reeb function, then for every integer $n>0$ the function $f^n$ is also Reeb, with the same critical set of f but with a higher order of degeneracy at zero. More generally, if $g:I\rightarrow I$ is a smooth map such that $g'(t)\ne 0$ for all $t\in (0,1)$, then $g\circ f:M\rightarrow [0,1]$ is still a Reeb function.

Throughout the paper, we make use of the following notation. Given a function $f \,{:}\; M \rightarrow {\mathbb {R}}$ we set

$$\begin{aligned} A_{\varepsilon }(f)&= \{x\in M \mid f(x)\ge \varepsilon \}{} & {} \text {(the}\ \varepsilon -\text {superlevel of}\ f)\\ B_{\varepsilon }(f)&= \{x\in M \mid f(x)\le \varepsilon \}{} & {} \text {(the}\ \varepsilon \text {-sublevel of}\ f). \end{aligned}$$

We recall the following well-known fact, which we state without proof (the reader may refer to Lee [8] for a proof).

Lemma 8

Let $M_0$, $M_1$ be two smooth m-manifolds with non-empty boundary, and suppose that there is a diffeomorphism $\varphi \,{:}\; \partial M_0 \rightarrow \partial M_1$ between their boundaries. Let $f_0 \,{:}\; M_0 \rightarrow [a,b]$ and $f_1 \,{:}\; M_1 \rightarrow [b,c]$ be $C^k$ functions, $1\le k \le \infty$, such that $f_0^{-1}(b) = \partial M_0$ and $f_1^{-1}(b) = \partial M_1$. Furthermore, we assume that $\nabla f_0$ is non-vanishing and pointing outwards along $\partial M_0$, and $\nabla f_1$ is non-vanishing and pointing inwards along $\partial M_1$, with respect to certain Riemannian metrics on $M_0$ and $M_1$. Then, the manifolds $M_0$ and $M_1$, as well as the functions $f_0$ and $f_1$, can be glued together by $\varphi$ yielding a smooth manifold $M= M_0\cup _\varphi M_1$ and a $C^k$ function $f = f_0 \cup _\varphi f_1 \,{:}\; M \rightarrow [a,c]$. Moreover, this construction is unique up to $C^k$ diffeomorphisms of M.

For the proof of Theorem 1 we will need the following two technical lemmas.

Lemma 9

(Existence of arbitrarily flat functions)Let $\{c_k\}_{k\in {\mathbb {N}}}$ be a sequence of positive real numbers. There exists a smooth function $\gamma \,{:}\; [0, 1]\rightarrow {\mathbb {R}}$ such that $\gamma (0)=0$, $\gamma (1)>0$, $\gamma '(t)>0$ for $t\in (0,1]$ and for every $k\in {\mathbb {N}}$

$$\begin{aligned} \sum _{j=0}^k|\gamma ^{(j)}(t)|\le c_k\quad \forall t\le \frac{1}{k}.\end{aligned}$$

Proof

Without loss of generality, we assume that the sequence $\{c_k\}_{k\in {\mathbb {N}}}$ is monotone decreasing with $c_0<1$. Consider the smooth function $\varphi \,{:}\; [0, 1]\rightarrow [0,1]$ defined by:

$$\begin{aligned}\varphi (x)= \frac{e^{\frac{-1}{x}}}{e^{\frac{-1}{x}}+e^{\frac{-1}{1-x}}}, \quad \text {for } 0<x< 1, \end{aligned}$$

$\varphi (0)=0$ and $\varphi (1)=1$. This is a monotone function on [0, 1] with $\varphi ^{(r)}(0)=0=\varphi ^{(r)}(1)$ for all $r> 0.$ For every $k\ge 1$ let us define the function $\varphi _k\,{:}\; [\frac{1}{k+1}, \frac{1}{k}]\rightarrow {\mathbb {R}}$ by

$$\begin{aligned} \varphi _k(x)=a_k\varphi (k(k+1)x-k), \end{aligned}$$

where the sequence $\{a_k>0\}_{k\ge 1}$ is chosen in such a way that

$$\begin{aligned} \sup _{t\in [\frac{1}{k+1},\frac{1}{k}]}\sum _{j=0}^{k-2}|\varphi _k^{(j)}(t)|\le \frac{c_{k}}{3}. \end{aligned}$$

(2.1)

By replacing $a_k$ with a possibly smaller positive number, we can assume that:

• (1) $\{a_k\}_{k\ge 1}$ is monotone decreasing and that $\sum _{k\ge 1}a_k=A<1.$

• (2) for every $k\ge 1$ we have $\sum _{j\ge k+1}a_j\le \frac{c_k}{3}$;

• (3) denoting by $\sigma =(\sum _{j}\frac{1}{j^4})^{1/2}$, for every $k\ge 1$ we have $(\sum _{j\ge k}a_j^2)^{1/2}\le \frac{c_k}{3\sigma }.$

Pick now the sequence $\{b_k\}_{k\ge 1}$ defined by $b_k=b_{k-1}-a_k$ and $b_1=1-a_1$, and define $f\,{:}\; [0, 1]\rightarrow {\mathbb {R}}$ to be the function

$$\begin{aligned} f(t)=\left( \sum _{k\ge 1}(\varphi _k(t)+b_k)\chi _{[\frac{1}{k+1}, \frac{1}{k}]}(t)\right) -(1-A), \end{aligned}$$

where $\chi _S$ is the characteristic function of a subset S. The function f is smooth. In fact, for every $k>1$ we have

$$\begin{aligned} f|_{(\frac{1}{k+1}, \frac{1}{k})}(t)=\varphi _k(t)+b_k-1+A\quad \text {and}\quad f|_{(\frac{1}{k}, \frac{1}{k-1})}(t)=\varphi _{k-1}(t)+b_{k-1}-1+A. \end{aligned}$$

Therefore

$$\begin{aligned} f\left( \left( \frac{1}{k}\right) ^{\!\!-}\right)&=a_k\varphi (1)+b_k-1+A\nonumber \\&=a_k+b_k-1+A \end{aligned}$$

(2.2)

and

$$\begin{aligned} f\left( \left( \frac{1}{k}\right) ^{\!\!+}\right)&=a_{k-1}\varphi (0)+b_{k-1}-1+A\nonumber \\&=b_{k-1}-1+A. \end{aligned}$$

(2.3)

Since, by definition, $b_{k}+a_k=b_{k-1}$, then (2.2) and (2.3) imply that

$$\begin{aligned} f\left( \left( \frac{1}{k}\right) ^{\!\!-}\right) =f\left( \left( \frac{1}{k}\right) ^{\!\!+}\right) . \end{aligned}$$

This tells that f is continuous at the points of the form $t=\tfrac{1}{k}.$ Moreover, since all derivatives of $\varphi$ vanish at 0 and 1, then for every $j\ge 1$

$$\begin{aligned} f^{(j)}\left( \left( \frac{1}{k}\right) ^{\!\!-}\right) =0=f^{(j)}\left( \left( \frac{1}{k}\right) ^{\!\!+}\right) . \end{aligned}$$

This proves that f is smooth on (0, 1]. Since $f(0)=0$ and for every $j\ge 1$ we have

$$\begin{aligned} \lim _{t\rightarrow 0} f^{(j)}(t)=0, \end{aligned}$$

then f is smooth on [0, 1]. Note also that $f(1)=b_1-(1-A)=A-a_1>0$.

Finally, we define $\gamma$ by:

$$\begin{aligned} \gamma (t)=\int _{0}^t\!\!\int _{0}^s f(x)\, dx\, ds. \end{aligned}$$

Then, $\gamma (0)=0$ and $\gamma (1)>0$. Moreover for every $t\in (0,1)$

$$\begin{aligned} \gamma '(t)=\int _{0}^t f(x)\, dx>0, \end{aligned}$$

since the integrand is non-negative and non-zero on any interval (0, t).

For $t\le \frac{1}{k}$ we have the following estimate for $|\gamma (t)|$:

$$\begin{aligned} \begin{aligned} |\gamma (t)|&\le \int _{0}^{\frac{1}{k}}\!\!\!\int _{0}^{\frac{1}{k}}|f(x)|\, dx\, ds\le \frac{1}{k^2} \sup _{t\le \frac{1}{k}} |f(t)| =\frac{1}{k^2}\! \sup _{\frac{1}{k+1}\le t\le \frac{1}{k}} \! |f(t)|\\&\le -1+A+(1-a_1-\cdots -a_k) = A-a_1-\cdots -a_k\\&= \sum _{j\ge k+1} a_j\le \frac{c_k}{3}. \end{aligned} \end{aligned}$$

(2.4)

Notice that, since f is monotone, from the previous computation it also follows that

$$\begin{aligned} \sup _{t\in [0, \frac{1}{k}]}|f(t)|=\sup _{t\in [\frac{1}{k+1}, \frac{1}{k}]}|f(t)|\le \frac{c_k}{3}. \end{aligned}$$

Therefore, for $t\le \frac{1}{k}$ we have the following estimate for the derivative $|\gamma '(t)|$:

$$\begin{aligned} |\gamma '(t)|&\le \int _{0}^{\frac{1}{k}}|f(x)|\, dx\le \frac{1}{k}\frac{c_k}{3}\le \frac{c_k}{3}. \end{aligned}$$

(2.5)

Moreover, for $t\le \frac{1}{k}$ we have the following estimate for $\sum _{j=2}^k|\gamma ^{(j)}(t)|$:

$$\begin{aligned} \begin{aligned} \sum _{j=2}^k |\gamma ^{(j)}(t)|&= \sum _{j=0}^{k-2}|f^{(j)}(t)| \le \sup _{i\ge k}\sup _{t\in [\frac{1}{i+1}, \frac{1}{i}]}\sum _{j=0}^{k-2}|\varphi _i^{(j)}(t)|\\&= \sup _{t\in [\frac{1}{k+1}, \frac{1}{k}]}\sum _{j=0}^{k-2}|\varphi _k^{(j)}(t)|\le \frac{c_k}{3}, \end{aligned} \end{aligned}$$

(2.6)

where in the last step we have used (2.1). Combining (2.4), (2.5) and (2.6) we get:

$$\begin{aligned} \sum _{j=0}^k|\gamma ^{(j)}(t)|\le c_k\quad \hbox { for } t\le \frac{1}{k}. \end{aligned}$$

$\square$

Lemma 10

Let M be a smooth manifold, and let $X \subsetneq {{\,\textrm{Int}\,}}(M)$ be a finite subcomplex. Let also U be a compact, smooth regular neighborhood of X. Then there exists a $C^{\infty }$ function $\alpha \,{:}\; U \rightarrow [0,1]$ such that:

• (1) $\alpha ^{-1}(0)= X$ and $\alpha ^{-1}(1)=\partial U$;

• (2) $\alpha$ has no critical values in (0, 1);

• (3) the sublevels $B_{\varepsilon }(\alpha )$ are smooth regular neighborhoods of X for every $\varepsilon \in (0,1]$.

Proof

There is a triangulation of M such that the star ${{\,\textrm{st}\,}}(X, M)$ of X is a regular neighborhood of X in M. We set ${{\widetilde{U}}} = {{\,\textrm{st}\,}}(X, M)$. Let us also consider the function ${\widetilde{f}} \,{:}\; {\widetilde{U}} \rightarrow [0,2]$ which is affine-linear on every simplex and which takes value zero on X and value 2 on $\partial {\widetilde{U}}$. Observe that this function is piecewise smooth, and hence Lipschitz. Let ${\widetilde{v}}$ be the Lipschitz vector field on ${\widetilde{U}}$ constructed as in [6, Lemma 2.3]. It follows from [7] that there exists a fundamental system of neighborhoods $\{U_n\}_{n\ge 1}$ of X in M such that

• (1) $U_1\subset {\widetilde{U}}$ and $U_{n+1}\subset {{\,\textrm{Int}\,}}(U_n)$ for every $n\ge 1$;

• (2) $X_n=\partial U_n$ is a smooth embedded submanifold of M of codimension one;

• (3) the vector field ${\widetilde{v}}$ is transversal to $X_n$ for every $n\ge 1$;

• (4) $U_n\setminus {{\,\textrm{Int}\,}}(U_{n+1})$ is PL diffeomorphic to $X_n\times [\frac{1}{n+1}, \frac{1}{n}]$.

For every $n\ge 1$ let now $v_n$ be a smooth vector field on $U_n\setminus {{\,\textrm{Int}\,}}(U_{n+1})$ which is sufficiently close to ${\widetilde{v}}$ in order to guarantee that the flow lines of $v_n$ give a diffeomorphism

$$\begin{aligned} \varphi _n\,{:}\; X_n\times \left[ \frac{1}{n+1}, \frac{1}{n}\right] \rightarrow U_n\setminus {{\,\textrm{Int}\,}}(U_{n+1}). \end{aligned}$$

All these diffeomorphisms can be glued together to give a diffeomorphism

$$\begin{aligned} \varphi \,{:}\; X_1\times (0, 1]\rightarrow U_1\setminus X. \end{aligned}$$

Let $\pi _2$ be the projection of $X_1\times (0,1]$ on the second factor. Notice that, by the uniqueness up to smooth isotopies of regular neighborhoods, we can assume $U=U_1$ and define the map $\alpha \,{:}\; U \rightarrow [0,1]$ such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha \big \vert _{U\setminus X} = \gamma \circ \pi _2 \circ \varphi ^{-1} \\ \alpha \big \vert _{X} \equiv 0, \end{array}\right. } \end{aligned}$$

where $\gamma \,{:}\; [0,1] \rightarrow [0,1]$ is an appropriate smooth function that we will now construct. Such function will be monotone, with nonzero derivative on (0, 1] and with derivatives that go to zero sufficiently fast at zero, in such a way that $\alpha$ will be smooth and with no critical points in U other than the points in X.

For the construction of $\gamma$, denote $\beta =\pi _2\circ \varphi ^{-1}$ and fix fiberwise norms on the jet bundles $J^k(U, {\mathbb {R}})$ and $J^k({\mathbb {R}}, {\mathbb {R}})$. We denote both these norms by $\Vert \cdot \Vert$. Denoting by $j_p^kf\in J_p(X, M)$ the k-th jet of a smooth map $f\,{:}\; X\rightarrow M$, we claim that for every $k\ge 0$ there exists $p(k)>0$ such that every $p\in U\setminus X$ and for every smooth function $\gamma \,{:}\; [0,1]\rightarrow {\mathbb {R}}$, we have

$$\begin{aligned} \Vert j_p^k(\gamma \circ \beta )\Vert \le C(k)\cdot \Vert j_{\beta (p)}^k\gamma \Vert \cdot \Vert j_p^k\beta \Vert ^k, \end{aligned}$$

(2.7)

for some $C(k)>0$. Denoting by $(x_1, \ldots , x_n)$ coordinates on $U_1$, Faá di Bruno’s formula reads:

$$\begin{aligned} \frac{\partial ^k(\gamma \circ \beta )}{\partial x_1\cdots \partial x_{k}}(x(p))=\sum _{\pi \in {\mathcal {P}}_k}\gamma ^{(|\pi |)}(\beta ({ p}))\cdot \prod _{b\in \pi }\frac{\partial ^{|b|}\beta }{\partial x_{i_1}\cdots \partial x_{i_{b}}}(x(p)), \end{aligned}$$

where ${\mathcal {P}}_k$ denotes the set of all partitions $\pi$ of the set $\{1, \ldots , k\}$ and “$b\in \pi$” means that the variable b runs through the list of all of the blocks of the partition $\pi$. In particular, from this formula we deduce that:

$$\begin{aligned} \Vert j_p^k(\gamma \circ \beta )\Vert&\le C_1(k)\left( \sup _{j=0, \ldots , k}|\gamma ^{(j)}(\beta (p))|\right) \sum _{\pi \in {\mathcal {P}}_k} \prod _{b\in \pi }\left| \frac{\partial ^{|b|}\beta }{\partial x_{i_1}\cdots \partial x_{i_{b}}}(x(p))\right| \\&\le C_2(k)\left( \sup _{j=0, \ldots , k}|\gamma ^{(j)}(\beta (p))|\right) \sum _{\pi \in {\mathcal {P}}_k} \Vert j_p^{k}\beta \Vert ^{|b|}\\&\le C_3(k)\Vert j_{\beta (p)}^k\gamma \Vert \cdot (\#{\mathcal {P}}_k)\cdot \Vert j_p^k\beta \Vert ^k\\&\le C(k)\cdot \Vert j_{\beta (p)}^k\gamma \Vert \cdot \Vert j_p^k\beta \Vert ^k, \end{aligned}$$

which is (2.7). For every $k\ge 0$ set now

$$\begin{aligned} {\tilde{c}}_k:=C(k)\sup _{p\in \varphi (X_1\times [\frac{1}{k+1}, 1])}\Vert j_p^{k}\beta \Vert ^k. \end{aligned}$$

From Lemma 9 (applied with the choice $\{c_k=({\tilde{c}}_kk)^{-1}\}$) we get a smooth function ${\tilde{\gamma }}\,{:}\; [0,1]\rightarrow {\mathbb {R}}$ such that ${\tilde{\gamma }}(0)=0$, ${\tilde{\gamma }}(1)>0$, ${\tilde{\gamma }}'(t)>0$ on (0, 1] and $\sum _{j\le k}|{\tilde{\gamma }}^{(j)}(t)|\le \frac{1}{k{\tilde{c}}_k}$ for all $t\le \frac{1}{k}.$

We define our function as $\gamma :={\tilde{\gamma }}/{\tilde{\gamma }}(1),$ so that $\gamma (1)=1$. We claim that for every $\ell \ge 0$ and for every $\varepsilon >0$ there exists $m\ge 0$ such that $\Vert j_p^\ell (\gamma \circ \beta )\Vert \le \varepsilon$ for all $p\in \beta ^{-1}([0, \frac{1}{m}])$. This means that for every $\ell \ge 0$ the $\ell$-th jet of $\gamma \circ \beta$ goes uniformly to zero as p approaches X. Hence, the extension of $\gamma \circ \beta$ to zero on X is smooth on $U_1$.

In order to prove the claim, let $\ell \ge 0$, $\varepsilon >0$ and pick $m\ge 0$ such that

$$\begin{aligned} \frac{1}{m} \le \min \left\{ \frac{1}{\ell },\varepsilon {\tilde{\gamma }}(1)\right\} . \end{aligned}$$

Let $p=\varphi (x, t)$ be a point with $t=\beta (p)\le \frac{1}{m}$ and choose $k\ge m$ such that $\frac{1}{k+1}\le t\le \frac{1}{k}$. Then:

$$\begin{aligned} \Vert j_{p}^\ell (\gamma \circ \beta )\Vert&\le \Vert j_{p}^{k}(\gamma \circ \beta )\Vert \\&\le C(k)\cdot \Vert j_{\beta (p)}^k\gamma \Vert \cdot \Vert j_p^k\beta \Vert ^k\\&=\frac{C(k)}{{\tilde{\gamma }}(1)}\Vert j_{\beta (p)}^k{\tilde{\gamma }}\Vert \cdot \Vert j_p^k\beta \Vert ^k\\&=\frac{C(k)}{{\tilde{\gamma }}(1)}\left( \sum _{j=0}^k|{\tilde{\gamma }}^{(j)}(\beta (p))|\right) \cdot \Vert j_p^k\beta \Vert ^k\\&\le \frac{C(k)}{{\tilde{\gamma }}(1)}\frac{1}{k{\tilde{c}}_k}\cdot \Vert j_p^k\beta \Vert ^k\\&\le \frac{1}{k{\tilde{\gamma }}(1)}\le \frac{1}{m{\tilde{\gamma }}(1)}\le \varepsilon , \end{aligned}$$

which is what we wanted. Since ${\tilde{\gamma }}'(t)>0$ on (0, 1], the same is true for $\gamma '(t)$ and therefore $\alpha$ has no critical points other than the points in X. $\square$

Proof of Theorem 1

Without loss of generality we may assume that M is connected, since we can construct the Reeb function independently on each connected component. Let $\alpha \,{:}\; U\rightarrow [0,1]$ be given by Lemma 10, where U is a smooth regular neighborhood of X in M. Let now $V=M\setminus {{\,\textrm{Int}\,}}(U)$ and consider a spine Y for V. Using Lemma 10 we get a smooth regular neighborhood $V'$ of Y in M and a function $\alpha '\,{:}\; V'\rightarrow [0,1]$ with the set of minima Y; using the uniqueness of regular neighborhoods, V is diffeomorphic to $V'$ and hence the function $\alpha '$ can be defined on V itself. Set $\beta =1-\alpha '$. We can glue the functions $\alpha$ and $\beta$ along the common boundary $\partial U = \partial V$, using Lemma 8. The result is a Reeb function f on M with extrema X and Y, as desired. $\square$

2.1 Relation between maxima and minima

Lemma 11

Let M be a smooth, connected, compact manifold and let $f\,{:}\; M\rightarrow [0,1]$ be a Reeb function such that $X_0=f^{-1}(0)$ is a finite subcomplex. For every $\varepsilon \in (0,1)$ there exists a smooth regular neighborhood T of $X_0$ in M such that $T\subset {{\,\textrm{Int}\,}}(B_\varepsilon (f))$ and $W=B_\varepsilon (f){\setminus } {{\,\textrm{Int}\,}}(T)$ is an h-cobordism between $\partial T$ and $f^{-1}(\varepsilon )=\partial B_\varepsilon (f).$ In particular $M{\setminus } f^{-1}(1)$ deformation retracts to $X_0$.

Proof

Without loss of generality we assume that $X_0$ is connected; the non-connected case can be treated analogously, working separately on every connected component.

We observe first that the sublevels $B_{\varepsilon }(f)$ are also connected. In fact, suppose by contradiction that there exists $0<a<1$ such that $B_{a}(f)$ is not connected. Denote by C a connected component of $B_{a}(f)$ that does not contain $X_0$. Let

$$\begin{aligned} b = \min _{x\in C} f(x) \end{aligned}$$

and fix ${\bar{x}}\in C$ such that $f({\bar{x}}) = b$. This is a critical point for f that is not in $X_0$ or $X_1$, so we get the contradiction.

Moreover the family of sublevels $\{ B_{\varepsilon }(f) \}_{\varepsilon >0}$ is a fundamental system of neighborhoods. In fact let V be a closed regular neighborhood of $X_0$ and take

$$\begin{aligned} s = \min _{x\in \partial V} f(x). \end{aligned}$$

If we assume that $B_{\frac{s}{2}}(f) \nsubseteq {{\,\textrm{Int}\,}}V$, then we can separate it as

$$\begin{aligned} \left( B_{\frac{s}{2}}(f) \cap {{\,\textrm{Int}\,}}V \right) \sqcup \left( B_{\frac{s}{2}}(f) \cap (M\setminus V) \right) , \end{aligned}$$

which leads to a contradiction, since $B_{\frac{s}{2}}(f)$ is connected.

Let $\alpha \,{:}\; U\rightarrow [0,1]$ be given by Lemma 10 and consider the family $\{B_{\varepsilon }(\alpha ) \}_{0<\varepsilon \le 1}$ of smooth regular neighborhoods of $X_0$ (recall that $U=B_1(\alpha )$). Let $0<\varepsilon _3<\varepsilon _2<\varepsilon _1<\varepsilon$ be such that

$$\begin{aligned} B_{\varepsilon _3}(\alpha )\subset {{\,\textrm{Int}\,}}(B_{\varepsilon _2}(f))\subset B_{\varepsilon _2}(f)\subset {{\,\textrm{Int}\,}}(B_{\varepsilon _1}(\alpha ))\subset B_{\varepsilon _1}(\alpha )\subset {{\,\textrm{Int}\,}}(B_\varepsilon (f)). \end{aligned}$$

We set $T=B_{\varepsilon _3}(\alpha )$ and fix a Riemannian metric on M, so that we can consider the gradients of f and $\alpha$ (and their flows). We can write $W=W'\cup f^{-1}([\varepsilon _2, \varepsilon ])$ with $W'=B_{\varepsilon _2}(f)\setminus {{\,\textrm{Int}\,}}(T).$ Following the flow of $-\nabla f$ one first deformation retracts W onto $W'$. Since $W'\subset \alpha ^{-1}([\varepsilon _3, \varepsilon _1])\subset W$, we can restrict to $W'$ the deformation retraction of $\alpha ^{-1}([\varepsilon _3, \varepsilon _1])$ onto $\partial T=\alpha ^{-1}(\varepsilon _3)$, given by the flow of $-\nabla \alpha$. This gives a deformation retraction of W onto $\partial T$. A similar reasoning, exchanging the roles of $\alpha$ and f and using their gradients, yields a deformation retraction of W onto $f^{-1}(\varepsilon )$. This proves the first part of the lemma, since the inclusions $\partial T \hookrightarrow W$, $f^{-1}(\varepsilon ) \hookrightarrow W$ are in particular homotopy equivalences.

The second part of the lemma follows easily: $M\setminus f^{-1}(1)$ deformation retracts to $B_\varepsilon (f)$ using the flow of $-\nabla f$; $B_\varepsilon (f)=W\cup T$ deformation retracts to T (by the previous part) and T deformation retracts to $X_0$, since it is a regular neighborhood. $\square$

Remark 12

Suppose that M is a closed oriented n-manifold and let $f \,{:}\; M \rightarrow [0,1]$ be a Reeb function having as extrema two finite subcomplexes $X_0, X_1 \subset M$. There are isomorphisms $H_i(M,X_1) \cong H_i(M, M-X_0)\cong H^{n-i}(X_0)$, for all $i \ge 0$, the former being induced by inclusion and using Lemma 11, while the latter is a well-known duality (see for example [4, Proposition 3.46]). Then, the long exact sequence of the pair $(M, X_1)$ yields the following long exact sequence

$$\begin{aligned} \cdots \rightarrow H_i(X_1) \rightarrow H_i(M) \rightarrow H^{n-i}(X_0) \rightarrow H_{i-1}(X_1) \rightarrow \cdots . \end{aligned}$$

In the non-orientable case an analogous long exact sequence holds with ${\mathbb {Z}}_2$ coefficients.

This means that the image of the inclusion $H_{i} \left( X_1 \right) \rightarrow H_i \left( M \right)$ lies in the orthogonal complement of the restriction $H^{n-i} \left( M \right) \rightarrow H^{n-i}\left( X_0 \right)$. This gives a necessary condition for two finite subcomplexes of M to be the extrema of a Reeb function.

In the particular case of $M= S^n$ we can notice something more. Alexander duality in fact states that ${\widetilde{H}}_i(S^n {\setminus } X_0) \cong {\widetilde{H}}^{n-i-1}(X_0)$ and therefore

$$\begin{aligned} {\widetilde{H}}_i(X_1) \cong {\widetilde{H}}^{n-i-1}(X_0). \end{aligned}$$

This implies for example that the sum of the Betti numbers of $X_0$ must coincide with the sum of the Betti numbers of $X_1$.

3 Dimension 3

We prove now Theorem 2 from Sect. 1, whose statement we recall here for the reader’s convenience.

Theorem 2

Let M be a smooth closed connected 3-manifold. Then the following conditions are equivalent:

• (1) there exists a Reeb function $f :M \rightarrow [0,1]$ having connected 1-dimensional finite subcomplexes of the same Euler characteristic $\chi$ as extrema, for some $\chi \le 1$;

• (2) the Heegaard genus of M is at most $1-\chi$ in the orientable case and $2-2\chi$ in the non-orientable case.

Proof

$(1)\Rightarrow (2)$. Given $\varepsilon >0$, by Lemma 11 there exists a regular neighborhood T of $X_0$ such that $T\subset {{\,\textrm{Int}\,}}(B_\varepsilon (f))$ and $W=B_{\varepsilon }(f){\setminus } {{\,\textrm{Int}\,}}(T)$ is an h-cobordism. By [5, Theorem 10.2], it follows that this cobordism is a product, that is $W\cong \partial T\times [0,1]$. Since T is a genus-g handlebody, with $g=1-\chi$ in the orientable case and $g=2-2\chi$ in the non-orientable case, it follows that $B_\varepsilon (f)=T\cup W$ is a genus-g handlebody. Similarly, the superlevel $A_{\varepsilon }(f)$ is a genus-g handlebody and the Heegaard genus of $M=B_{\varepsilon }(f)\cup _{\partial }A_{\varepsilon }(f)$ is at most g.

$(2)\Rightarrow (1)$. Consider a genus g Heegaard splitting of $M=P\cup _\partial Q$, where P and Q are 3-dimensional handlebodies of genus g, with $g=1-\chi$ in the orientable case and $g=2-2\chi$ in the non-orientable case. Then there are connected graphs $X_0\subset P$ and $X_1\subset Q$ with Euler characteristic $\chi$, such that P is a regular neighborhood of $X_0$ and Q is a regular neighborhood of $X_1$. The proof of the claim follows immediately from Lemma 10 and the uniqueness of regular neihgborhoods, as in the proof of Theorem 1. $\square$

Remark 13

In the proof of the first implication of the previous theorem we used [5, Theorem 10.2]. The application of this result does not need the Poincaré Conjecture because the sublevel $B_{\varepsilon }(f)$ can be embedded into a handlebody (hence in ${\mathbb {R}}^3$) following the flow of $-\nabla f$. In particular $B_\varepsilon (f)$ does not contain fake 3-cells.

Remark 14

If M is a closed, orientable 3-manifold and $f\,{:}\; M\rightarrow [0,1]$ is a Reeb function such that $X_0\cong X_1\cong S^k$ are smoothly embedded k-spheres, then one can prove that for $k = 0$, and hence $X_0\cong X_1\cong \{-1,1\}$, we have $M\cong S^3\sqcup S^3$. This case follows from Milnor’s version of Reeb’s Sphere Theorem, by looking at the two connected components one by one. For $k = 2$, following the same lines as in Proposition 15 below, and using the fact that the h-cobordism holds true also in dimension $n=3$, being equivalent to the Poincaré Conjecture, one proves that $M\cong S^1\times S^2$.

4 Higher dimensions

Consider a manifold M of dimension n and a Reeb function with two smoothly embedded copies of $S^k$, $k<n$, as extrema. If we restrict to $n\ge 6$, we may use cobordism techniques and prove the following statements.

Proposition 15

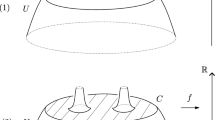
Let M be a smooth closed connected orientable manifold of dimension $n\ge 6$. Suppose that there exists a Reeb function $f :M \rightarrow [0,1]$ whose extrema are finite subcomplexes with fundamental group having trivial Whitehead group. Then $B_\varepsilon (f)$ and $A_\varepsilon (f)$ are smooth regular neighborhoods of $X_0$ and $X_1$, respectively.

Proof

As in the proof of Theorem 2, for $\varepsilon >0$, by Lemma 11 there exists a regular neighborhood $T_0$ of $X_0$ such that $T_0\subset {{\,\textrm{Int}\,}}(B_\varepsilon (f))$, and $W_0=B_{\varepsilon }(f)\setminus {{\,\textrm{Int}\,}}(T_0)$ is an h-cobordism. Since $X_0$ has trivial Whitehead group, by the s-cobordism Theorem [11, Sect. 10] we conclude that $W_0$ is trivial, hence $W_0\cong \partial T_0\times [0,1]$. The same holds for a regular neighborhood $T_1$ of $X_1$, because of the triviality of the Whitehead group of $X_1$. Hence, $B_\varepsilon (f)$ and $A_\varepsilon (f)$ themselves are smooth regular neighborhoods of the respective subcomplex. $\square$

From this result, we can then deduce the following corollary.

Corollary 16

Let M be a smooth closed connected orientable manifold of dimension $n\ge 6$ and let $1 \le k < n$. Then the following conditions are equivalent:

• (1) there exists a Reeb function $f\,{:}\; M\rightarrow [0,1]$ with two smoothly embedded k-spheres as extrema, with trivial normal bundle;

• (2) M is obtained by gluing two copies of $S^k\times D^{n-k}$ along their boundaries with a diffeomorphism of $S^k\times S^{n-k-1}=\partial (S^k\times D^{n-k})$.

Proof

$(1)\Rightarrow (2)$. Since the preimages $X_0, X_1$ of the two critical values are spheres, their Whitehead group is trivial. Then, $B_\varepsilon (f)$ and $A_\varepsilon (f)$ are diffeomorphic to the normal bundle $S^k \times D^{n-k}$, by Proposition 15. The claim follows.

$(2)\Rightarrow (1)$. This direction is trivial. $\square$

Notice in particular that for $k=n-1$, M is diffeomorphic to $S^{n-1}\times S^1$.

5 Concluding remarks and open questions

Remark 17

The s-cobordism theorem still holds true in dimension 5 topologically, so Proposition 15 and Corollary 16 can be extended to dimension 5 up to homeomorphisms instead of diffeomorphisms. However 5-dimensional s-cobordism theorem fails in the smooth category. Indeed, any two homeomorphic but not diffeomorphic closed smooth simply connected 4-manifolds are known to be smoothly h-cobordant.

In dimension 4, the h-cobordism theorem holds topologically in the simply connected case, while in the smooth category it is equivalent to the 4-dimensional Smooth Poincaré Conjecture, which is still open. It would be intriguing to investigate an analogous to Corollary 16 in dimension 4, in the smooth category.

Remark 18

If $f\,{:}\; M \rightarrow [0,1]$ is a Reeb function with extrema $X_0, X_1 \subset M$, the flow of $\nabla f$, with respect to a fixed Riemannian metric, yields a diffeomorphism

$$\begin{aligned} M \setminus (X_0\cup X_1) \cong f^{-1}(\varepsilon ) \times {\mathbb {R}}, \end{aligned}$$

for any $\varepsilon \in (0,1)$, and $f^{-1}(\varepsilon )$ is a smooth closed hypersurface in M. In particular, $M \setminus (X_0\cup X_1)$ has finitely many ends, because the connected components of $X_0\cup X_1$ can be identified with the end points of $M \setminus (X_0\cup X_1)$, which, in turn, correspond to the connected components of $f^{-1}(\varepsilon )$. Moreover, if M is connected and $X_0$ and $X_1$ have topological dimension at most $\dim M -2$, then they do not disconnect M and hence they must be connected. Therefore, certain subspaces of M (for example, a Cantor set) cannot occur as extrema of a Reeb function.

So, the following question arises naturally.

Question 19

Which subspaces of a closed manifold can be realized as one of the extrema of a certain Reeb function?

Another question is motivated by our constructions in Lemma 10 and in Theorem 1, which produce Reeb functions admitting a collapsing pseudo-gradient vector field v, that is, the flow lines of v (resp. $-v$) give a collapsing of $M\setminus X_0$ to $X_1$ (resp. of $M\setminus X_1$ to $X_0$).

Question 20

Does there exist a closed manifold M with a Reeb function $f\,{:}\; M \rightarrow [0,1]$ with no collapsing pseudo-gradient vector field?