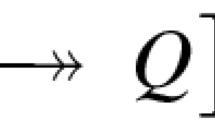Comparison of Poisson structures on moduli spaces

Abstract

Let X be a complex irreducible smooth projective curve, and let ${{\mathbb {L}}}$ be an algebraic line bundle on X with a nonzero section $\sigma _0$. Let ${\mathcal {M}}$ denote the moduli space of stable Hitchin pairs $(E,\, \theta )$, where E is an algebraic vector bundle on X of fixed rank r and degree $\delta$, and $\theta \, \in \, H^0(X,\, {\mathcal {E}nd}(E)\otimes K_X\otimes {{\mathbb {L}}})$. Associating to every stable Hitchin pair its spectral data, an isomorphism of ${\mathcal {M}}$ with a moduli space ${\mathcal {P}}$ of stable sheaves of pure dimension one on the total space of $K_X\otimes {{\mathbb {L}}}$ is obtained. Both the moduli spaces ${\mathcal {P}}$ and ${\mathcal {M}}$ are equipped with algebraic Poisson structures, which are constructed using $\sigma _0$. Here we prove that the above isomorphism between ${\mathcal {P}}$ and ${\mathcal {M}}$ preserves the Poisson structures.

1 Introduction

Let X be a complex irreducible smooth projective curve of genus g. Take an algebraic line bundle N on X such that $N\otimes K^{-1}_X$ admits a nonzero section, where $K_X$ is the canonical bundle of X; fix a section $\sigma _0\,\in \, H^0(X,\, N\otimes K^{-1}_X) {\setminus }\{0\}$. Fix integers r and $\delta$. Let ${\mathcal {M}}$ denote the moduli space of stable pairs of the form $(E,\,\theta )$, where E is an algebraic vector bundle on X of rank r and degree $\delta$, and $\theta \, \in \, H^0(X,\, {\mathcal {E}nd}(E) \otimes N)$. These are called Hitchin pairs; when $N\,=\, K_X$, they are called Higgs bundles. The moduli space ${\mathcal {M}}$ is nonempty if one of the following four assumptions hold (cf. [13, Remark 3.4]):

• (1) the genus g of X is at least 2;

• (2) $g \,=\, 1$, $N \,=\, K_X$ and $\gcd (r,\,\delta ) \,= \,1$;

• (3) $g \,= \,1$ and $\deg (N \otimes K_X^{-1}) \,>\, 0$; and

• (4) $g = 0$ and $\deg (N \otimes K_X^{-1}) \,\ge \, 3$.

We assume that one of these four conditions hold. This moduli space ${\mathcal {M}}$ has a natural algebraic Poisson structure [4, 13], which is constructed using $\sigma _0$.

In the special case where $N\,=\, K_X$ and $\sigma _0$ is the constant function 1, this ${\mathcal {M}}$ is a moduli space of Higgs bundles. In that case, the Poisson structure is nondegenerate, meaning it is a symplectic structure; this symplectic structure was constructed earlier in [8, 9]. Furthermore, there is a natural algebraic 1–form on ${\mathcal {M}}$ such that the symplectic form is the exterior derivative of it.

Let S denote the smooth complex quasi-projective surface defined by the total space of the line bundle N. Given any Hitchin pair $(E,\,\theta )\,\in \, {\mathcal {M}}$, there is a subscheme $Y_{(E,\theta )} \, \subset \, S$ of dimension one associated to it. Furthermore, associated to the pair $(E,\,\theta )$ there is a coherent sheaf ${{\mathcal {L}}}_{(E,\theta )}$ on $Y_{(E,\theta )}$ which is pure of dimension one. This pair $(Y_{(E,\theta )},\, {{\mathcal {L}}}_{(E,\theta )})$ is known as the spectral datum associated to $(E,\,\theta )$. This construction produces an algebraic map

$$\begin{aligned} \Phi \, :\, {\mathcal {M}}\, \longrightarrow \, {\mathcal {P}}\, , \end{aligned}$$

(1.1)

where ${\mathcal {P}}$ is a moduli space of stable sheaves of pure dimension one on S. This construction is reversible, and $\Phi$ is in fact an isomorphism (see [1, 8, 9, 17]).

The earlier mentioned section $\sigma _0$ of $N\otimes K^{-1}_X$ produces a Poisson structure on the surface S. An algebraic Poisson structure on ${\mathcal {P}}$ is constructed using this Poisson structure on S [5, 18].

It may be mentioned that when $N\,=\, K_X$ and $\sigma _0$ is the constant function 1, the Poisson structure on S is the canonical symplectic form on the cotangent bundle $K_X$ of X. In that case the Poisson structure on ${\mathcal {P}}$ coincides with the symplectic structure on ${\mathcal {P}}$ constructed by Mukai in [14]. Also, in this case there is a natural algebraic 1–form on ${\mathcal {P}}$ such that the symplectic form is the exterior derivative of it.

In this continuation of the papers [4, 5] of the second author, our aim is to prove the following (see Theorem 4.6):

Theorem 1.1

The isomorphism $\Phi$ in (1.1) takes the Poisson structure on ${\mathcal {M}}$ to the Poisson structure on ${\mathcal {P}}$.

When $N\,=\, K_X$, related results can be found in [2, 7, 10]; there the symplectic form on a moduli space of Higgs bundles is compared with the symplectic form on the Hilbert scheme of zero dimensional subschemes of fixed length of the total space of $K_X$ (Mukai had shown that this Hilbert scheme has a symplectic structure).

2 Hitchin pairs and spectral data

Let X be an irreducible smooth complex projective curve of genus g, and let N be a fixed algebraic line bundle on X. A Hitchin pair $(E,\,\theta )$ is an algebraic vector bundle E on X together with a morphism $\theta \,:\,E\,\longrightarrow \,E\otimes N$ of ${\mathcal {O}}_X$-modules [8, 15].

A Hitchin pair $(E,\,\theta )$ is stable (respectively, semistable) if

$$\begin{aligned} \frac{\deg F}{{\text {rk}}F} \,< \,\frac{\deg E}{{\text {rk}}E} \ \ \ \text {(respectively,}\ \frac{\deg F}{{\text {rk}}F} \, \le \,\frac{\deg E}{{\text {rk}}E}\text {)} \end{aligned}$$

for all subbundles $0\, \not =\, F\,\subsetneq \, E$ for which $\theta (F)\, \subset \, F\otimes N$.

Let ${\overline{{\mathcal {M}}}}$ denote the moduli space of all S-equivalence classes of semistable Hitchin pairs (constructed in [15]; see [15, Definition 4.2] for definition of S-equivalence) of fixed rank r and degree $\delta$. Let

$$\begin{aligned} {\mathcal {M}}\,\subset \, {\overline{{\mathcal {M}}}} \end{aligned}$$

be the open subset of stable Hitchin pairs. We remark that the S-equivalence class of a stable Hitchin pair is the same thing as its isomorphism class, so this moduli space parametrizes isomorphism classes of objects.

Lemma 2.1

The moduli space ${\mathcal {M}}$ of stable Hitchin pairs $(E,\theta : E\rightarrow E\otimes N)$, with $\deg (E)=\delta$, ${\text {rk}}(E)=r$, and $N = K_X(D)$ for an effective divisor $D\ge 0$, is smooth.

Proof

This is well-known, but since we did not find a reference, we include a sketch of the proof. Fix a line bundle $\Delta \in {\text {Pic}}^\delta (X)$ on X of degree $\delta$, and let ${\mathcal {M}}_{\Delta }$ be the moduli space of stable Hitchin pairs with fixed determinant $\det (E)\cong \Delta$ and $\mathrm{tr}(\theta )=0$. Consider the determinant morphism

$$\begin{aligned} \det :{\mathcal {M}}\longrightarrow {\text {Pic}}^\delta (X) \times H^0(N) \end{aligned}$$

(2.1)

sending $(E,\theta )$ to $(\det (E),\mathrm{tr}(\theta ))$. This morphism is surjective, and the target is smooth, so to prove smoothness of ${\mathcal {M}}$ it is enough to show that the morphism is flat and the fibers are smooth. Note that the fiber over a point $(L,\alpha )$ is isomorphic to the moduli space ${\mathcal {M}}_{\Delta }$. Indeed, let $\eta \in J(X)$ such that $\eta ^r=L\otimes \Delta ^{-1}$, and send $(E,\theta )\in {\mathcal {M}}_{\Delta }$ to $(E\otimes \eta , \theta + \frac{1}{r}\alpha )$. We can choose a root $\eta$ in an étale neighbourhood of $\Delta$, so the determinant morphism is étale locally trivial, and in particular it is flat. Therefore, it only remains to prove that ${\mathcal {M}}_\Delta$ is smooth.

The deformation theory of the moduli space ${\mathcal {M}}$ of Hitchin pairs of fixed degree is governed by the complex (in degrees 0 and 1)

$$\begin{aligned} C^{\bullet }_{{\mathcal {E}nd}}:{\mathcal {E}nd}(E) {\mathop {\longrightarrow }\limits ^{[\cdot ,\theta ]}}{\mathcal {E}nd}(E)\otimes N \end{aligned}$$

This is proved in [3]. In particular, the infinitesimal deformations are given by $\mathbb {H}^1(C^{\bullet }_{{\mathcal {E}nd}})$, and $\mathbb {H}^2(C^{\bullet }_{{\mathcal {E}nd}})$ is the obstruction space. Furthermore, the exact sequence of complexes

$$\begin{aligned} 0 \longrightarrow {\mathcal {E}nd}(E)\otimes N[-1] \longrightarrow C^{\bullet }_{{\mathcal {E}nd}} \longrightarrow {\mathcal {E}nd}(E) \longrightarrow 0 \end{aligned}$$

($[-1]$ means that the sheaf is placed in degree 1) gives an exact sequence

$$\begin{aligned} 0 \longrightarrow \mathbb {H}^0\left( C^{\bullet }_{{\mathcal {E}nd}}\right) \longrightarrow H^0({\mathcal {E}nd}(E)) {\mathop {\longrightarrow }\limits ^{[\cdot ,\theta ]}}H^0({\mathcal {E}nd}(E)\otimes N) \end{aligned}$$

(2.2)

and then $\mathbb {H}^0(C^{\bullet }_{{\mathcal {E}nd}})$ represents the endomorphisms of $(E,\theta )$ in the category of Hitchin pairs, i.e., endomorphisms of E which commute with $\theta$.

On the other hand, the deformation theory of the moduli space ${\mathcal {M}}_\Delta$ of stable Hitchin pairs of fixed determinant is given by the complex

$$\begin{aligned} C^{\bullet }_{ad}:ad(E) {\mathop {\longrightarrow }\limits ^{[\cdot ,\theta ]}}ad(E)\otimes N \end{aligned}$$

This can be checked by a straightforward modification of the proofs in [3], requiring at each step that the deformation of E does not change its determinant, and that the deformation of $\theta$ preserves the vanishing of its trace.

It is well-known that if E is a stable vector bundle, then its only endomorphisms are given by scalar multiplication (cf. [11, Proposition 1.2.7 and Corollary 1.2.8]). A straightforward modification of the usual argument for vector bundles shows that this is also true in the category of Hitchin pairs, i.e., if $(E,\theta )$ is stable as a Hitchin pair, and $\varphi :E\rightarrow E$ is a homomorphism which commutes with $\theta$, then $\varphi$ is the multiplication by a scalar. Therefore, using (2.2) we have

$$\begin{aligned} \mathbb {H}^0\left( C^{\bullet }_{{\mathcal {E}nd}}\right) =\mathbb {C}\cdot {\text {id}}_E \end{aligned}$$

Using the exact sequence

$$\begin{aligned} 0 \longrightarrow \mathbb {H}^0\left( C^{\bullet }_{ad}\right) \longrightarrow H^0(ad(E)) {\mathop {\longrightarrow }\limits ^{[\cdot ,\theta ]}}H^0(ad(E)\otimes N) \end{aligned}$$

we obtain

$$\begin{aligned} \mathbb {H}^0(C^{\bullet }_{ad})=0 \end{aligned}$$

(2.3)

because this cohomology is given by the endomorphisms of E which are traceless and commute with $\theta$.

We claim that $\mathbb {H}^2(C^{\bullet }_{ad})$ vanishes. Indeed, this group is dual to

$$\begin{aligned} \mathbb {H}^0(ad(E)\otimes N^{-1}\otimes K_X \longrightarrow ad(E)\otimes K_X) \end{aligned}$$

(2.4)

If $N\cong K_X$, then this is just $\mathbb {H}^0(C^{\bullet }_{ad})$, which we have just seen that it is zero (2.3). On the other hand, if $N\cong K_X(D)$ with $D>0$ an effective, nonzero divisor, then note that the complex which appears in (2.4) is just $C^{\bullet }_{ad}\otimes {\mathcal {O}}_X(-D)$. We have an exact sequence of complexes

$$\begin{aligned} 0 \longrightarrow C^{\bullet }_{ad}\otimes {\mathcal {O}}_X(-D) \longrightarrow C^{\bullet }_{ad} \longrightarrow C^{\bullet }_{ad}\otimes {\mathcal {O}}_D \longrightarrow 0 \end{aligned}$$

The associated long exact cohomology sequence starts as

$$\begin{aligned} 0 \longrightarrow \mathbb {H}^0\left( C^{\bullet }_{ad}\otimes {\mathcal {O}}_X(-D)\right) \longrightarrow \mathbb {H}^0\left( C^{\bullet }_{ad}\right) \longrightarrow \mathbb {H}^0\left( C^{\bullet }_{ad}|_D\right) \end{aligned}$$

The vanishing of $\mathbb {H}^0(C^{\bullet }_{ad})$ (2.3) implies the vanishing of $\mathbb {H}^0(C^{\bullet }_{ad}\otimes {\mathcal {O}}_X(-D))$. So we have proved that the obstruction space $\mathbb {H}^2(C^{\bullet }_{ad})$ vanishes.

Summing up, there are no infinitesimal isomorphisms, and the obstruction space vanishes, so ${\mathcal {M}}_\Delta$ is smooth, and then the smoothness of ${\text {Pic}}^\delta (X)$ implies the smoothness of ${\mathcal {M}}$. $\square$

In the sequel we assume that one of the following four assumptions hold:

• (1) $g \,\ge \, 2$;

• (2) $g \,=\, 1$, $N\, =\, K_X$ and $\gcd (r,\,\delta )\, =\, 1$;

• (3) $g \,=\, 1$ and $\deg (N \otimes K_X^{-1}) \,>\, 0$;

• (4) $g \,=\, 0$ and $\deg (N \otimes K_X^{-1}) \,\ge \, 3$.

This assumption implies the existence of stable Hitchin pairs [13, Remark 3.4], and hence ${\mathcal {M}}$ is nonempty.

We will now recall the spectral construction, which is a bijective correspondence between Hitchin pairs $(E,\,\theta )$ and certain sheaves ${\mathcal {L}}$ on the total space

$$\begin{aligned} p\, :\, S\, :=\,\mathbb {V}(N)\, \longrightarrow \, X \end{aligned}$$

(2.5)

of the line bundle N. This construction is in [9, § 5] for smooth spectral curves, [1, p. 173–174, Proposition 3.6] for integral spectral curves, and [17, p. 18, Lemma 6.8] in general (see also [1, p. 173–174, Remark 3.7] and [16]).

Consider the projection p in (2.5). Let x denote the tautological section of $p^*N$ on $S\,=\,\mathbb {V}(N)$. For a Hitchin pair $(E,\,E{\mathop {\longrightarrow }\limits ^{\theta }} E\otimes N)$, we define the associated sheaf ${\mathcal {L}}$ using the following short exact sequence of coherent sheaves on S

$$\begin{aligned} 0 \,\longrightarrow \, p^*\left( E\otimes N^\vee \right) \,{\mathop {\longrightarrow }\limits ^{h}}\, p^* E \,\longrightarrow \, {\mathcal {L}}\,\longrightarrow \, 0\, , \end{aligned}$$

(2.6)

where p is the projection in (2.5) and $h\, :=\,p^*\theta - x$, with x being the tensor product with the above mentioned tautological section x; the homomorphism $E\otimes N^\vee \, \longrightarrow \, E$ given by $\theta$ is denoted here by $\theta$ also. Throughout, the dual will be denoted by the superscript “$\vee$”. The homomorphism h in (2.6) is injective (it is an isomorphism over the generic point of S), so (2.6) is indeed a short exact sequence of coherent sheaves. The spectral curve

$$\begin{aligned} Y\,\subset \, S \end{aligned}$$

for $(E,\, \theta )$ is the subscheme defined by the characteristic polynomial

$$\begin{aligned} \det (p^* \theta -x) \,=\,0\, . \end{aligned}$$

Equivalently, the spectral curve Y is the subscheme defined by the 0–th Fitting ideal sheaf

$$\begin{aligned} \mathrm{Fitt}_0({\mathcal {L}})\,\subset \, {\mathcal {O}}_S\, . \end{aligned}$$

To see this equivalence, note that (2.6) gives a presentation of ${\mathcal {L}}$, and, by definition, the 0–th Fitting ideal is the ideal generated by the codimension zero minors of the morphism h in (2.6). Since the ranks of the source and target of h are equal, we only have one minor which is the determinant $\det (h)\,=\,\det (p^* \theta -x)$, in other words the characteristic polynomial of $\theta$. We have the following diagram

(2.7)

The spectral curve Y is given as the zero of $\det (h)$, which is a section of $p^*N^r$, and it is proper over X, of degree r. Note that ${\mathcal {L}}$ is pure of dimension 1 because $p_*{\mathcal {L}}=E$ is torsion free. The Euler characteristic of ${\mathcal {L}}$ is $\chi ({\mathcal {L}})=\chi (E)=\deg (E)+r(1-g)$. We collect all these properties in the following definition.

Definition 2.2

A spectral sheaf ${\mathcal {L}}$ on S, with invariants r and $\delta$, is a coherent sheaf such that:

• (1) ${\mathcal {L}}$ is pure of dimension 1.

• (2) The subscheme $Y\subset S$ defined by its 0-th Fitting ideal is in the divisor class given by $p^*N^r$.

• (3) The projection $Y\longrightarrow X$ is proper, finite of degree r.

• (4) $\chi ({\mathcal {L}})=\delta +r(1-g)$.

If the spectral curve $Y\subset S$ associated to a spectral sheaf ${\mathcal {L}}$ is smooth, then there is a line bundle L on Y such that ${\mathcal {L}}\,=\,i_* L$, where i is the map in (2.7) ( [1, p. 173–174, Remarks 3.7 and 3.8]).

Conversely, let ${\mathcal {L}}$ be a spectral sheaf on S. The push-forward

$$\begin{aligned} E\,=\,p_*{\mathcal {L}}\end{aligned}$$

(2.8)

is then a torsion free coherent sheaf, of rank r and degree $\delta$. Define the Hitchin pair $(E,\, \theta )$ by setting $\theta \,=\,p_*x$, where p is the projection in (2.7). More explicitly, consider the multiplication by the tautological section x of $p^* N$

$$\begin{aligned} {\mathcal {L}}\,{\mathop {\longrightarrow }\limits ^{x}}\, {\mathcal {L}}\otimes p^* N \end{aligned}$$

and then $\theta \,=\,p_* x$ is defined as the push-forward of this homomorphism, using the projection formula

$$\begin{aligned} \theta \,:\,E \,=\, p_*{\mathcal {L}}\,\longrightarrow \, p_*\left( {\mathcal {L}}\otimes p^* N\right) \,=\, \left( p_*{\mathcal {L}}\right) \otimes N \,=\,E\otimes N \end{aligned}$$

[see (2.8)]. The above reversible construction gives a correspondence between the Hitchin pairs $(E,\,\theta )$ and the spectral sheaves ${\mathcal {L}}$ on S

Note that the push-forward $p_*{\mathcal {L}}$ is coherent if and only if the projection $Y \longrightarrow X$ is proper, and this holds if and only if the closure of Y in ${\overline{S}}\,=\,\mathbb {P}(N\oplus {\mathcal {O}}_X)$ lies in S ( [17, p. 18, Lemma 6.8]).

We shall now recall the definition of stability given by Simpson ([17]) for a spectral sheaf ${\mathcal {L}}$. Let

$$\begin{aligned} P({\mathcal {L}},m)\,=\,\chi \left( {\mathcal {L}}\otimes p^*{\mathcal {O}}_X(m)\right) \end{aligned}$$

be its Hilbert polynomial. Its degree d is equal to the dimension of the support of ${\mathcal {L}}$, and the leading coefficient is $a m^d/d!$, where $a\,=\,a({\mathcal {L}})$ is an integer which we call the rank of ${\mathcal {L}}$. We say that ${\mathcal {L}}$ is stable (respectively, semistable) if for all proper subsheaves $0\, \not =\, {\mathcal {L}}'\,\subset \, {\mathcal {L}}$,

$$\begin{aligned} a({\mathcal {L}}) P({\mathcal {L}}',m) \,<\, a({\mathcal {L}}') P({\mathcal {L}},m)\ \ \ \text { (respectively, }\,\ a({\mathcal {L}}) P({\mathcal {L}}',m) \,\le \, a({\mathcal {L}}')P({\mathcal {L}},m)\text {)} \end{aligned}$$

It is easy to see that if ${\mathcal {L}}$ is semistable, then it has pure dimension, i.e., the dimension of the support of every nonzero subsheaf is the same as the dimension of the support of ${\mathcal {L}}$. Note that, in the spectral construction, the condition that ${\mathcal {L}}'$ is a subsheaf of ${\mathcal {L}}$ translates into the condition that the subbundle

$$\begin{aligned} E'\,:=\,p_*{\mathcal {L}}'\,\subset \,E\,:=\,p_*{\mathcal {L}}\end{aligned}$$

satisfies the condition $\theta (E')\, \subset \, E'\otimes N$. It follows that a Hitchin pair is stable (respectively, semistable) if and only if the corresponding spectral sheaf on S is stable (respectively, semistable) [17, p. 19, Corollary 6.9].

The spectral construction can be carried out for families, so we get an isomorphism between the moduli functors. Since the stability conditions coincide, we get an isomorphism between the moduli space of stable Hitchin pairs ${\mathcal {M}}$ or rank r and degree $\delta$ and the moduli space ${\mathcal {P}}$ of stable spectral sheaves with invariants r and $\delta$

$$\begin{aligned} \Phi \,:\,{\mathcal {M}}\,\longrightarrow \, {\mathcal {P}}\, . \end{aligned}$$

(2.9)

In particular, both moduli spaces, ${\mathcal {M}}$ and ${\mathcal {P}}$, are smooth (Lemma 2.1).

We are interested in calculating the differential of the isomorphism $\Phi$ in (2.9). More generally, we will give an isomorphism between the infinitesimal deformation space of a Hitchin pair $(E,\,\theta )$ and the infinitesimal deformation space of the corresponding sheaf ${\mathcal {L}}$ on S.

3 Poisson structure on the moduli spaces

The infinitesimal deformation space of a spectral sheaf (Definition 2.2) ${\mathcal {L}}$ is given by

$$\begin{aligned} {\text {Ext}}^1({\mathcal {L}},\,{\mathcal {L}}) \end{aligned}$$

(3.1)

[5, p. 425, (3.1)]. To calculate the dual of this vector space we will use Serre duality. Recall that ${\mathcal {L}}$ is a coherent sheaf on the surface $S\,=\,\mathbb {V}(N)$ in (2.5) which is not projective. However, it has a projective compactification

$$\begin{aligned} j\,:\,S \,\longrightarrow \, {\overline{S}}\,=\,\mathbb {P}(N\oplus {\mathcal {O}}_X) \, ; \end{aligned}$$

furthermore, the direct image $j_*{\mathcal {L}}$ is a coherent sheaf on ${\overline{S}}$, because the closure, in ${\overline{S}}$, of the support of ${\mathcal {L}}$ does not meet the boundary ${\overline{S}}{\setminus } S$ (this argument is in [17, p. 18, Lemma 6.8]). We have

$$\begin{aligned} {\text {Ext}}^1({\mathcal {L}},\,{\mathcal {L}})^\vee= & {} {\text {Ext}}^1_{{\mathcal {O}}_{{\overline{S}}}}\left( j_*{\mathcal {L}},\,j_*{\mathcal {L}}\right) ^\vee \,\cong \, {\text {Ext}}^1_{{\mathcal {O}}_{{\overline{S}}}}\left( j_*{\mathcal {L}},\,j_*{\mathcal {L}}\otimes K_{{\overline{S}}}\right) \nonumber \\ {}= & {} {\text {Ext}}^1\left( {\mathcal {L}},\,{\mathcal {L}}\otimes K_S\right) \, , \end{aligned}$$

(3.2)

where the second isomorphism is Serre duality on the projective surface ${\overline{S}}$.

Let ${\mathcal {P}}$ be the moduli space of stable spectral sheaves on S (cf. (2.9)). The tangent space $T_{[{\mathcal {L}}]}{\mathcal {P}}$ at the point corresponding to ${\mathcal {L}}$ is canonically identified with ${\text {Ext}}^1({\mathcal {L}},\,{\mathcal {L}})$, and the cotangent space $T^\vee _{[{\mathcal {L}}]}{\mathcal {P}}$ is canonically identified with ${\text {Ext}}^1({\mathcal {L}},\,{\mathcal {L}}\otimes K_S)$ (see (3.2)).

Henceforth assume that the line bundle $N\otimes K^{-1}_X$ on X admits a nonzero section. We fix a nonzero section

$$\begin{aligned} \sigma _0\, \in \, H^0\left( X,\, N\otimes K^{-1}_X\right) {\setminus } \{0\}\, . \end{aligned}$$

(3.3)

Since the anticanonical line bundle $K_S^\vee$ of the surface S in (2.5) is identified with $p^* (N\otimes K^{-1}_X)$, where p is the projection in (2.5), we have

$$\begin{aligned} s\, :=\, p^* \sigma _0\, \in \, H^0\left( S,\, K_S^\vee \right) \, , \end{aligned}$$

(3.4)

where $\sigma _0$ is the section in (3.3). This s produces an algebraic Poisson structure on ${\mathcal {P}}$

$$\begin{aligned} B\,:\,T^\vee {\mathcal {P}}\,\longrightarrow \, T{\mathcal {P}}\end{aligned}$$

(3.5)

[5, 18]. We will recall below the fiberwise construction of B.

Tensoring with the section s produces a homomorphism ${\mathcal {L}}\otimes K_S\, \longrightarrow \, {\mathcal {L}}$. Consequently, we obtain a homomorphism

$$\begin{aligned} T^\vee _{[{\mathcal {L}}]} {\mathcal {P}}\,\cong \, {\text {Ext}}^1({\mathcal {L}},\,{\mathcal {L}}\otimes K_S)\,\longrightarrow \, {\text {Ext}}^1({\mathcal {L}},\,{\mathcal {L}})\,\cong \, T_{[{\mathcal {L}}]}{\mathcal {P}}\, . \end{aligned}$$

(3.6)

The isomorphism ${\text {Ext}}^1({\mathcal {L}},\,{\mathcal {L}})\,\cong \, T_{[{\mathcal {L}}]}{\mathcal {P}}$ is a consequence of the fact that the infinitesimal deformations of ${\mathcal {L}}$ are parametrized by ${\text {Ext}}^1({\mathcal {L}},\,{\mathcal {L}})$, while the isomorphism $T^\vee _{[{\mathcal {L}}]} {\mathcal {P}}\,\cong \, {\text {Ext}}^1({\mathcal {L}},\,{\mathcal {L}}\otimes K_S)$ follows from (3.2). Let $B([{\mathcal {L}}])$ be the restriction to the fiber over the point $[{\mathcal {L}}]$ of the bundle map B in (3.5). This homomorphism $B([{\mathcal {L}}])$ coincides with the one in (3.6) (see [5, p. 428, Formula (4.4)]).

On the other hand, the infinitesimal deformation space of a Hitchin pair $(E,\, \theta )$ is given by the first hypercohomology of a complex

$$\begin{aligned} \mathbb {H}^1\left( E^\vee \otimes E \,{\mathop {\longrightarrow }\limits ^{[\cdot ,\,\theta ]}}\, E^\vee \otimes E \otimes N \right) \end{aligned}$$

(3.7)

(see [4, p. 399, Proposition 3.1.2], [13, p. 271, Proposition 7.1], [3, p. 220, Theorem 2.3]). The dual vector space

$$\begin{aligned} \mathbb {H}^1\left( E^\vee \otimes E \,{\mathop {\longrightarrow }\limits ^{[\cdot ,\,\theta ]}}\, E^\vee \otimes E \otimes N \right) ^\vee \end{aligned}$$

is calculated using Serre duality for hypercohomologies. Denote by $A^\bullet$ the complex

$$\begin{aligned} A^\bullet \,:\, \quad E^\vee \otimes E \,{\mathop {\longrightarrow }\limits ^{[\cdot ,\,\theta ]}}\, E^\vee \otimes E \otimes N \end{aligned}$$

concentrated in degrees 0 and 1. Serre duality gives an isomorphism

$$\begin{aligned} \mathbb {H}^1 \left( A^\bullet \right) ^\vee {\mathop {\longrightarrow }\limits ^{\cong }} \mathbb {H}^{-1}\left( A^\bullet {}^\vee [1] \otimes K_X\right) = \mathbb {H}^1\left( A^\bullet {}^\vee [-1]\otimes K_X\right) \end{aligned}$$

[12, p. 67, Theorem 3.12]. The dual complex

$$\begin{aligned} A^\bullet {}^\vee \,: \quad E \otimes E^\vee \otimes N^\vee \,{\mathop {\longrightarrow }\limits ^{[\cdot ,\,\theta ]^{t}}} \, E \otimes E^\vee \end{aligned}$$

is concentrated in degrees $-1$ and 0. We identify $E \otimes E^\vee$ and $E^\vee \otimes E$ by switching the factors; then the morphism $[\cdot ,\,\theta ]^{t}$ becomes $[\theta ,\,\cdot ]$, so

$$\begin{aligned} A^\bullet {}^\vee \,: \quad E^\vee \otimes E \otimes N^\vee \,{\mathop {\longrightarrow }\limits ^{[\theta ,\,\cdot ]}} \, E^\vee \otimes E\, . \end{aligned}$$

(3.8)

Finally we shift the complex in (3.8) by $[-1]$. Recall that, when we shift a complex by one unit, we multiply by $-1$ all the differentials [12, p. 28, Definition 2.4], so we get the complex, concentrated in degrees 0 and 1

$$\begin{aligned} A^\bullet {}^\vee [-1]\otimes K_X\,: \quad E^\vee \otimes E \otimes N^\vee \otimes K_X \,{\mathop {\longrightarrow }\limits ^{[\cdot ,\,\theta ]}} \,E^\vee \otimes E\otimes K_X\, . \end{aligned}$$

(3.9)

Remark 3.1

In [4, p. 402, Proposition 3.1.10] the morphism is actually $[\theta ,\,\cdot ]$ instead of the homomorphism $[\cdot ,\, \theta ]$ in (3.7). Of course there is an isomorphism between the two complexes (multiplication by $-1$ in one term and $+1$ in the other).

As in (2.9), let ${\mathcal {M}}$ be a moduli space of stable Hitchin pairs such that the rank and degree of the vector bundle underlying a Hitchin pair are r and $\delta$ respectively. Using the section $\sigma _0$ in (3.3) an algebraic Poisson structure

$$\begin{aligned} B^H\, :\, T^\vee {\mathcal {M}}\,\longrightarrow \, T{\mathcal {M}}\end{aligned}$$

(3.10)

on ${\mathcal {M}}$ is constructed [4, § 4.3], [13, p. 278, Corollary 7.15]. We recall below a fiberwise construction of the homomorphism $B^H$ in (3.10).

Tensoring with the section $\sigma _0$ in (3.3) induces homomorphisms $N^\vee \otimes K_X\, \longrightarrow \, {{\mathcal {O}}}_X$ and $K_X\, \longrightarrow \, N$. Using these we obtain a homomorphism of complexes

(3.11)

The morphism of complexes in (3.11) gives a morphism of cohomologies

$$\begin{aligned}&\mathbb {H}^1\left( E^\vee \otimes E \otimes N^\vee \otimes K_X \quad \,{\mathop {\longrightarrow }\limits ^{[\cdot ,\,\theta ] }}\, E^\vee \otimes E \otimes K_X \right) \nonumber \\&\quad \longrightarrow \,\mathbb {H}^1\left( E^\vee \otimes E \quad {\mathop {\longrightarrow }\limits ^{[\cdot ,\,\theta ]}}E^\vee \otimes E \otimes N\right) \, . \end{aligned}$$

(3.12)

We have $T_{[(E,\theta )]}{\mathcal {M}}\,=\, \mathbb {H}^1( E^\vee \otimes E {\mathop {\longrightarrow }\limits ^{[\cdot ,\,\theta ]}}E^\vee \otimes E\otimes N)$, because the infinitesimal deformations of $(E,\, \theta )$ are parametrized by $\mathbb {H}^1(E^\vee \otimes E {\mathop {\longrightarrow }\limits ^{[\cdot ,\,\theta ]}}E^\vee \otimes E\otimes N)$ (see (3.7)); this and (3.9) together imply that

$$\begin{aligned} T^\vee _{[(E,\theta )]}{\mathcal {M}}\,=\, \mathbb {H}^1\left( E^\vee \otimes E \otimes N^\vee \otimes K_X \,{\mathop {\longrightarrow }\limits ^{[\cdot ,\,\theta ] }}\, E^\vee \otimes E \otimes K_X\right) \, . \end{aligned}$$

(3.13)

Using (3.13) and (3.7), the homomorphism in (3.12) becomes a homomorphism

$$\begin{aligned} T^\vee _{[(E,\theta )]} {\mathcal {M}}\,\longrightarrow \, T_{[(E,\theta )]}{\mathcal {M}}\, . \end{aligned}$$

This homomorphism coincides with $B^H([(E,\theta )])$ in (3.10) [4, § 4.3], [13, p. 278, Corollary 7.15].

Remark 3.2

If we compare (3.11) with the commutative diagram in [4, Remark 1.3.3], we see that the sign is changed in the vertical left arrow and in one of the horizontal arrows (there is $[\theta ,\,\cdot ]$ in [4, Remark 1.3.3] as opposed to $[\cdot ,\,\theta ]$ here).

4 Comparison of Poisson structures

We shall compare the Poisson structures B and $B^H$, constructed in (2.9) and (3.10) respectively, using the isomorphism $\Phi$ in (2.9).

We first recall that the global Ext can be calculated using locally free resolutions and hypercohomology.

Lemma 4.1

( [6, Corollary 2 to Theorem 4.2.1]). Let V and W be coherent sheaves on a scheme T. Let

$$\begin{aligned} \cdots \,\longrightarrow \, L^{-3} \,\longrightarrow \, L^{-2} \,\longrightarrow \, L^{-1} \,\longrightarrow \, L^{0} \,\longrightarrow \, V \,\longrightarrow \, 0 \end{aligned}$$

be a resolution of V by finitely generated locally free sheaves. Then there is an isomorphism

$$\begin{aligned} {\text {Ext}}^i(V,\,W) \,\cong \, \mathbb {H}^i\left( {\mathcal {H}om}\left( L^\bullet ,\,W\right) \right) \end{aligned}$$

which is functorial on W.

Proposition 4.2

Let W be a coherent sheaf on the surface S in (2.5). Let $x\,:\,W\,\longrightarrow \, W\otimes p^*N$ be multiplication by the tautological section of $p^* N$ on S, where p is the projection in (2.5). Then for any $(E,\, \theta )\, \in \, {\mathcal {M}}$ [see (2.9)] there is an isomorphism

$$\begin{aligned} \varphi _W\,\,\,:\,\,\, {\text {Ext}}^1({\mathcal {L}},\,W) \,{\mathop {\longrightarrow }\limits ^{\cong }}\, \mathbb {H}^1\left( E^\vee \otimes p_*W \,{\mathop {\longrightarrow }\limits ^{f_W}}\, E^\vee \otimes N\otimes p_*W\right) \, , \end{aligned}$$

where ${\mathcal {L}}\, =\, \Phi ((E,\, \theta ))$ [see (2.9)], $f_W\,=\,\theta ^\vee \otimes 1 - 1 \otimes p_*x$, and $f_W$ is seen as a complex concentrated in degrees 0 and 1. This isomorphism is functorial on W, meaning a homomorphism $V\,\longrightarrow \, W$ of coherent sheaves on S induces a commutative diagram

Proof

The short exact sequence in (2.6) gives a locally free resolution $L^\bullet$ of ${\mathcal {L}}$ (concentrated on degrees $-1$ and 0)

$$\begin{aligned} L^\bullet \,:\quad p^*\left( E\otimes N^\vee \right) \,{\mathop {\longrightarrow }\limits ^{h}}\, p^* E\,. \end{aligned}$$

For any sheaf W on S, Lemma 4.1 gives an isomorphism functorial for W

$$\begin{aligned} {\text {Ext}}^1({\mathcal {L}},\,W)\,=\,\mathbb {H}^1\left( {\mathcal {H}om}\left( L^\bullet ,\,W\right) \right) \, . \end{aligned}$$

(4.1)

Consider the diagram

where f and $\gamma$ are the structure morphisms. Note that the hypercohomology of any complex $D^\bullet$ on S can be calculated as the cohomology of the complex $Rf_*D^\bullet$ (where $Rf_*$ is the derived functor between the derived categories). We have

$$\begin{aligned} Rf_*\,=\, R\left( \gamma _* \circ p_*\right) \,{\mathop {\longrightarrow }\limits ^{\cong }}\, R\gamma _* \circ Rp_*\, . \end{aligned}$$

The morphism p is affine, hence $p_*$ is exact and then $Rp_*\,=\,p_*$. If we apply this observation to the complex ${\mathcal {H}om}(L^\bullet ,W)$, we get

$$\begin{aligned} \mathbb {H}^1\left( {\mathcal {H}om}\left( L^\bullet ,\,W\right) \right) \,{\mathop {\longrightarrow }\limits ^{\cong }} \,\mathbb {H}^1\left( p_* {\mathcal {H}om}\left( L^\bullet ,\, W\right) \right) \, . \end{aligned}$$

(4.2)

In view of (4.1) and (4.2), to finish the proof, it only remains to show that the complex $p_*{\mathcal {H}om}(L^\bullet ,W)$ is equal to the complex $f_W$ in the statement of the proposition.

Applying ${\mathcal {H}om}(\cdot ,\,W)$ to the complex $L^\bullet$ we obtain a complex concentrated in degrees 0 and 1

$$\begin{aligned} {\mathcal {H}om}\left( L^\bullet ,\,W\right) \,:\quad p^* E^\vee \otimes W \,{\mathop {\longrightarrow }\limits ^{h'}}\, p^* E^\vee \otimes p^* N \otimes W\, , \end{aligned}$$

(4.3)

where $h'\, :=\, p^* \theta ^\vee \otimes 1 - 1\otimes x$. By the projection formula, $p_*{\mathcal {H}om}(L^\bullet ,W)$ is

$$\begin{aligned} E^\vee \otimes p_*W= p_*\left( p^* E^\vee \otimes W\right) \,{\mathop {\longrightarrow }\limits ^{p_*h'}}\, p_*\left( p^* E^\vee \otimes p^* N \otimes W\right) = E^\vee \otimes N\otimes p_*W\, , \end{aligned}$$

where $p_*h'\,=\,\theta ^\vee \otimes 1 - 1\otimes p_*x$, and the proposition follows. $\square$

Remark 4.3

In the proof of Proposition 4.2, the main step is the isomorphism in (4.2), because it facilitates the passage of objects defined on S to objects defined on X. Note that this isomorphism is induced by the push-forward $p_*$ using p.

Let

$$\begin{aligned} d\Phi \, :\, T{\mathcal {M}}\, \longrightarrow \, \Phi ^*T{\mathcal {P}}\end{aligned}$$

(4.4)

be the differential of the isomorphism $\Phi$ in (2.9).

Lemma 4.4

Let

$$\begin{aligned} \varphi \,\,\,:\,\,\, {\text {Ext}}^1({\mathcal {L}},\,{\mathcal {L}}) \,{\mathop {\longrightarrow }\limits ^{\cong }}\, \mathbb {H}^1(E^\vee \otimes E \,{\mathop {\longrightarrow }\limits ^{f_{{\mathcal {L}}}}}\, E^\vee \otimes N\otimes E) \end{aligned}$$

be the homomorphism given by Proposition 4.2 for $W\,=\,{\mathcal {L}}$ [see (2.8)]. Then the following diagram is commutative

where $\alpha$ and $\beta$ are the infinitesimal deformation maps in (3.1) and (3.7) respectively, and $d\Phi (\Phi ^{-1}([{\mathcal {L}}]))$ is the homomorphism in (4.4) at $\Phi ^{-1}([{\mathcal {L}}])\, \in \, {\mathcal {M}}$.

Proof

Consider an infinitesimal deformation ${\mathcal {L}}_\epsilon$ of ${\mathcal {L}}$, i.e., a sheaf on $S \times {\text {Spec}}(\mathbb {C}[\epsilon ]/(\epsilon ^2))$ flat over ${\text {Spec}}(\mathbb {C}[\epsilon ]/(\epsilon ^2))$, that fits in a short exact sequence

$$\begin{aligned} 0 \,\longrightarrow \, {\mathcal {L}}\,{\mathop {\longrightarrow }\limits ^{\epsilon }}\, {\mathcal {L}}_\epsilon \,{\mathop {\longrightarrow }\limits ^{\mathrm{mod}\,\epsilon }}\, {\mathcal {L}}\,\longrightarrow \, 0\, . \end{aligned}$$

(4.5)

By applying the functor ${\text {Hom}}({\mathcal {L}},\, \cdot )$ to this short exact sequence we obtain a long exact sequence

$$\begin{aligned} \cdots \, \longrightarrow \, {\text {Hom}}({\mathcal {L}},\,{\mathcal {L}}_\epsilon ) \,\longrightarrow \, {\text {Hom}}({\mathcal {L}},\,{\mathcal {L}}) \,{\mathop {\longrightarrow }\limits ^{\delta }}\, {\text {Ext}}^1({\mathcal {L}},\,{\mathcal {L}}) \,\longrightarrow \, \cdots \, ; \end{aligned}$$

the element of ${\text {Ext}}^1({\mathcal {L}},\, {\mathcal {L}})$ that corresponds to the infinitesimal deformation ${\mathcal {L}}_\epsilon$ is $\delta ({\text {id}})$, the image of the identity ${\text {id}}\,\in \, {\text {Hom}}({\mathcal {L}},\, {\mathcal {L}})$ by the connecting homomorphism $\delta$.

If we set $W\,=\,{\mathcal {L}}$ in Proposition 4.2, we have $p_*W\,=\,E$ and $p_*x\,=\,\theta$; then $f_W\,=\,[\cdot ,\,\theta ]$, and Proposition 4.2 produces the isomorphism $\varphi$.

The element

$$\begin{aligned} \beta \circ \varphi \circ \alpha ({\mathcal {L}}_\epsilon )\, \in \, T_{[(E,\theta )]}{\mathcal {M}}\, , \end{aligned}$$

(4.6)

where ${\mathcal {L}}_\epsilon \, \in \, T_{[{\mathcal {L}}]}{\mathcal {P}}$ is the element in (4.5), has the following description.

Consider the short exact sequence (4.5). Applying $p_*$ to it, we obtain an exact sequence of complexes

$$\begin{aligned} 0 \,\longrightarrow \, K^\bullet \,{\mathop {\longrightarrow }\limits ^{\epsilon }}\, K^\bullet _\epsilon \,{\mathop {\longrightarrow }\limits ^{\mathrm{mod}\,\epsilon }}\, K^\bullet \,\longrightarrow \, 0\, , \end{aligned}$$

(4.7)

where $K^\bullet$ denotes the complex $0 \,\longrightarrow \, E \,{\mathop {\longrightarrow }\limits ^{\theta }}\, E \otimes N \,\longrightarrow \, 0$. Since $K^\bullet _\epsilon$ in (4.7) is a family of Hitchin pairs on X parametrized by ${\text {Spec}}(\mathbb {C}[\epsilon ]/(\epsilon ^2))$, it corresponds to an element of $T_{[(E,\theta )]}{\mathcal {M}}$. This element of $T_{[(E,\theta )]}{\mathcal {M}}$ coincides with the one in (4.6). Now from the construction of the map $\Phi$ it follows that

$$\begin{aligned} d\Phi \left( \Phi ^{-1}([{\mathcal {L}}])\right) (\beta \circ \varphi \circ \alpha ({\mathcal {L}}_\epsilon ))\, \in \, T_{[{\mathcal {L}}]}{\mathcal {P}}\end{aligned}$$

coincides with ${\mathcal {L}}_\epsilon \,\in \, T_{[{\mathcal {L}}]}{\mathcal {P}}$. $\square$

We remark that the key to the commutativity of the diagram in the statement of Lemma 4.4 is that both $\varphi$ and $\Phi ^{-1}$ are induced by the push-forward $p_*$.

Lemma 4.5

Consider

$$\begin{aligned} \varphi _1:= & {} (\varphi _{{\mathcal {L}}\otimes K_S})^{-1} \, :\,{\mathbb {H}^1(E^\vee \otimes E \otimes K_X\otimes N^\vee {\mathop {\longrightarrow }\limits ^{[\cdot ,\,\theta ]}}E^\vee \otimes E \otimes K_X )}\\\longrightarrow & {} {\text {Ext}}^1({\mathcal {L}},\,{\mathcal {L}}\otimes K_S), \end{aligned}$$

where $\varphi _{{\mathcal {L}}\otimes K_S}$ is the isomorphism in Proposition 4.2 for $W\,=\,{\mathcal {L}}\otimes K_S$. Let $(d\Phi )^\vee ([{\mathcal {L}}])$ be dual of the differential of the isomorphism $\Phi$ at $[{\mathcal {L}}]$. Then the following diagram is commutative

where $\alpha ^\vee$ and $\beta ^\vee$ are the natural isomorphisms obtained from (3.2) and (3.9) respectively, and $(d\Phi )^\vee$ is the dual of the homomorphism in (4.4).

Proof

Consider the homomorphism $\varphi$ in Lemma 4.4. For any

$$\begin{aligned} \omega \, \in \, {\mathbb {H}^1(E^\vee \otimes E \otimes K_X\otimes N^\vee {\mathop {\longrightarrow }\limits ^{[\cdot ,\,\theta ]}}E^\vee \otimes E \otimes K_X )} \end{aligned}$$

and $v\, \in \, {\text {Ext}}^1({\mathcal {L}},\,{\mathcal {L}})$, we have

$$\begin{aligned} \varphi _1(\omega )(v)\, =\, \omega (\varphi (v))\, \in \, {{\mathbb {C}}}\, ; \end{aligned}$$

(4.8)

recall that

$$\begin{aligned} \mathbb {H}^1(E^\vee \otimes E \otimes K_X\otimes N^\vee {\mathop {\longrightarrow }\limits ^{[\cdot ,\,\theta ]}}E^\vee \otimes E \otimes K_X )\!=\! \mathbb {H}^1(E^\vee \otimes E \,{\mathop {\longrightarrow }\limits ^{[\cdot ,\,\theta ]}}\, E^\vee \otimes E\otimes N)^\vee \end{aligned}$$

[see (3.13) and (3.7)], and

$$\begin{aligned} {\text {Ext}}^1({\mathcal {L}},\,{\mathcal {L}}\otimes K_S)\,=\, {\text {Ext}}^1({\mathcal {L}},\,{\mathcal {L}})^\vee \end{aligned}$$

[see (3.2)]. From (4.8) it follows immediately that $\varphi _1$ coincides with the dual homomorphism $\varphi ^\vee$.

Therefore, every homomorphism in the diagram in this lemma is the dual of the corresponding homomorphism in the diagram in Lemma 4.4. Hence the lemma follows from Lemma 4.4. $\square$

The homomorphism B in (3.5) gives an algebraic section

$$\begin{aligned} B\, \in \, H^0({\mathcal {P}},\, \bigwedge \nolimits ^2 T{\mathcal {P}})\, , \end{aligned}$$

(4.9)

and the homomorphism $B^H$ in (3.10) gives an algebraic section

$$\begin{aligned} B^H\, \in \, H^0({\mathcal {M}},\, \bigwedge \nolimits ^2 T{\mathcal {M}})\, . \end{aligned}$$

Consider the homomorphism $d\Phi$ in (4.4). We note that

$$\begin{aligned} \Phi _* B^H\, :=\, (\bigwedge \nolimits ^2 d\Phi ) (B^H)\, \in \, H^0({\mathcal {P}},\, \bigwedge \nolimits ^2 T{\mathcal {P}}) \end{aligned}$$

(4.10)

is a Poisson structure on ${\mathcal {P}}$.

Theorem 4.6

The isomorphism $\Phi$ in (2.9) satisfies the condition

$$\begin{aligned} \Phi _* B^H\,=\, B\, , \end{aligned}$$

where $\Phi _* B^H$ and B are the sections in (4.10) and (4.9) respectively.

Proof

The section $\sigma _0\,\in \, H^0(X,\, N\otimes K^\vee _X)$ gives a section s of $K_S^\vee \,=\,p^*(N\otimes K^\vee _X)$, and hence it produces a homomorphism ${\mathcal {L}}\otimes K_S\,\longrightarrow \, {\mathcal {L}}$. We apply Proposition 4.2 to this homomorphism and get the following commutative diagram:

(4.11)

where the left vertical homomorphism is the one in (3.6) and the right vertical homomorphism is the one in (3.12).

Lemma 4.5 shows that the top horizontal homomorphism $\varphi '$ in (4.11) coincides with $(d\Phi )^\vee ([{\mathcal {L}}])$. We note that $\varphi '\,=\, (\varphi _1)^{-1}$, where $\varphi _1$ is the homomorphism in Lemma 4.5. On the other hand, Lemma 4.4 shows that the bottom horizontal homomorphism in (4.11) coincides with $d\Phi ^{-1}([{\mathcal {L}}])$. The left vertical homomorphism in (4.11) gives $B([{\mathcal {L}}])$, the Poisson structure on ${\mathcal {P}}$, while the right vertical homomorphism in (4.11) gives $B^H([(E,\theta )])\,=\, B^H(\Phi ^{-1}([{\mathcal {L}}]))$, the Poisson structure on ${\mathcal {M}}$. Consequently, the theorem follows from the commutativity of the diagram in (4.11). $\square$