Another computer-assisted proof of unimodality of solutions for Proudman–Johnson equation

Abstract

This paper presents a computer-assisted proof of the existence and unimodality of steady-state solutions for the Proudman–Johnson equation which is representative of two-dimensional fluid flow. The proposed approach is based on an infinite-dimensional fixed-point theorem with interval arithmetic, and is another proof by Miyaji and Okamoto (Jpn J Ind Appl Math 36:287–298, 2019). Verification results show the validity of both proofs.

1 Introduction

Consider the following fourth-order nonlinear differential equation:

$$\begin{aligned} \left\{ \begin{array}{l} u'''' = f(u) \qquad \text {in} \ \ \varOmega :=(0,\pi ), \\[.25em] u(0)=u(\pi )= u''(0)=u''(\pi )=0, \end{array} \right. \end{aligned}$$

(1)

where

$$\begin{aligned} f(u):= R ( u u''' - u' u'' ) + \sin (kx), \end{aligned}$$

(2)

$R>0$, and k is a given positive integer. The aim of the present paper is to prove, in a computer-assisted manner, that there exists a solution u satisfying (1) and that this solution has a strict extremum at one and only one point in $\varOmega$. The proof of the existence and extremum of the solution of (1) implies unimodality of the solution for the Proudman–Johnson equation:

$$\begin{aligned} u_{txx} + uu_{xxx} - u_x u_{xx} = \dfrac{1}{R}( u_{xxxx} - \sin (kx)), \quad -\pi< x < \pi , \quad t>0, \end{aligned}$$

(3)

which is derived from the two-dimensional Navier–Stokes equations. For more details about the Proudman–Johnson equation and the unimodality of the solution, see the references [2,3,4] and references therein. In a previous paper, one of the authors proved the existence and unimodality for (1) in a rigorously mathematical manner via the multiple shooting method and multiple-precision interval arithmetic for $R \le 5000$ [4]. In the present paper, we apply a verification algorithm FN-Int [5], which is based on an infinite-dimensional fixed-point Newton-like formulation, and prove the solution has a unique extremum in $\varOmega$. The procedure does not need multiple-precision interval arithmetic and for readers interested in the details of our computer program, the source code is available for downloading from the first author’s web page. Our proposed approach is another computer-assisted proof of unimodality of the solution for the Proudman–Johnson equation. We do not describe in detail the relative merits of the two approaches in the present paper but would like to point out a couple relative merits as follows . The method described in [4] is applicable mainly to ordinary differential equations, and the authors of [4] reported that there is a unimodal solution for $k=10$, as well as other values k. The approach presented herein is potentially applicable to more direct multi-dimensional problems, and, for $k=2$, we successfully prove the existence of a unimodal solution for $R \le 10000$, which is a wider range than reported in [4].

This paper is organized as follows. Section 2 describes a fixed-point formulation using an approximate solution and verification procedure. Section 3 is devoted to details of the verification procedure. In Sect. 4, we report an enclosing result for the solution of (1). The final section reports on verification results of unimodality.

2 Fixed-point formulation and verification procedure

From the imposed boundary conditions, $u(0)=u(\pi )= u''(0)=u''(\pi )=0$, we will find the solutions of (1) in the function spaces $X^l$ ($l \ge 0$) by the closure in $H^l(\varOmega )$ of the linear hull of all functions: $\sin (mx)$, $m \in {\mathbb {N}}_+ := \{1,2,\dots \}$. In particular, because our aim is to enclose the weak solutions of (1), we set $X:=X^3$. We note that

$$\begin{aligned} {(\,\sin (m x),\sin (nx)\,)_{L^2}} = \left\{ \begin{array}{cl} \displaystyle \frac{\pi }{2}, &{} \quad \text {if }\ m=n, \\ 0, &{} \quad \text {otherwise} \end{array} \right. \end{aligned}$$

holds for any $[m,n]^T \in {\mathbb {N}}_+^2$, where ${(\,\cdot ,\cdot \,)_{L^2}}$ is the usual $L^2$-inner product in $\varOmega$. For $\phi _m:= \sin (m x)$, let $X_N := \text {span} \{ \phi _m \}_{m=1}^N$ be a finite-dimensional approximation subspace of X that depends on a positive integer parameter N which is not less than k. The subspace $X_N$ is the N-th truncation of the Fourier series of X. Let $X_*$ be the orthogonal complement of $X_N$ in X such that $X=X_N \oplus X_*$. Because of $\{ {\Vert \phi \Vert _{L^2}}, {\Vert \phi '\Vert _{L^2}}, {\Vert \phi ''\Vert _{L^2}} \} \le {\Vert \phi '''\Vert _{L^2}}$ for $\phi \in X$ (see proofs in Lemma 1), we define the norm of X as ${\Vert \phi \Vert _X}:= {\Vert \phi '''\Vert _{L^2}}$ by ${\Vert \phi \Vert ^2_{L^2}}={(\,\phi ,\phi \,)_{L^2}}$.

Next, we define a bilinear form B by

$$\begin{aligned} B(u,v):= u v''' - u' v'':\ X\times X \rightarrow X^0. \end{aligned}$$

(4)

Note that ${\hat{u}}=\sin (kx)/k^4$ is a solution of (1) for each R and k because $B({\hat{u}},{\hat{u}}) =0$. For each $u, v \in X$ such that

$$\begin{aligned} u = \sum _{m=1}^\infty A_m \phi _m, \qquad v = \sum _{n=1}^\infty D_n \phi _n, \qquad A_m, D_n \in {\mathrm{I\hspace{-0.22em}R}}, \end{aligned}$$

we can find the following:

$$\begin{aligned} B(u,v) =&\dfrac{1}{2} \sum _{\begin{array}{c} m \ge 1\\ n \ge 1 \end{array}} n^2 A_m D_n \left[ (m-n) \phi _{m+n} - (m+n) \phi _{m-n} \right] , \end{aligned}$$

(5)

$$\begin{aligned} f(u) =&\dfrac{R}{2} \sum _{\begin{array}{c} m \ge 1\\ n \ge 1 \end{array}} n^2 A_m A_n \left[ (m-n) \phi _{m+n} - (m+n) \phi _{m-n} \right] + \phi _k, \end{aligned}$$

(6)

$$\begin{aligned} f'[u]v =&R ( B(u,v) + B(v,u) ) \nonumber \\ =&\dfrac{R}{2} \sum _{\begin{array}{c} m \ge 1\\ n \ge 1 \end{array}} A_m D_n (m^2-n^2) \left[ (-m+n) \phi _{m+n} + (m+n) \phi _{m-n} \right] . \end{aligned}$$

(7)

By using $\phi _0=0$ and $\phi _{-m}=-\phi _m$ for $m \ge 1$, each B(u, v), f(u), and $f'[u]v$ can be expanded by $\{\phi _m\}_{m=1}^\infty$ as an element in $X^0$.

Now, using the standard Newton–Raphson method, we compute $u_N \in X_N$ satisfying

$$\begin{aligned} {(\,u_N'',\phi _i''\,)_{L^2}} = {(\,f(u_N),\phi _i\,)_{L^2}}, \quad 1 \le i \le N \end{aligned}$$

(8)

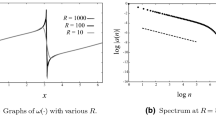
approximately. We note that $u_N$ need not to be the exact solution of (8). Fig. 1 shows plots of the approximate solution $u_N = \sum _{m=1}^N (u_N)_m \phi _m$ and its derivatives of (8) for $R=5000$, $N=400$, and $k=2$. The principal coefficients of the Fourier expansion are as follows:

$$\begin{aligned} (u_N)_1&= 1.999270784802591, \quad&(u_N)_2 = 4.444486852702385 \times 10^{-5}, \\ (u_N)_3&=-6.247933780811187 \times 10^{-6}, \quad&(u_N)_4 = 1.776479376506378 \times 10^{-6}, \\ (u_N)_5&=-6.935979514533375 \times 10^{-7}. \end{aligned}$$

Fig. 1

Plots of approximate solution and its derivatives

Remark 1

If $u(x)=\sum _{m=1}^\infty A_m \phi _m(x)$ is a solution of (1) in $\varOmega$, then from (6), $\tilde{u}(x):=\sum _{m=1}^\infty (-1)^m A_m \phi _m(x)$ also satisfies (1) in the same interval $\varOmega$. Therefore, below, we concentrate on the “maximum” type convex-upward solution, such as in Fig. 1.

Now we find the norm estimations in the following lemma.

Lemma 1

For each $\psi _* \in X_*$, it is true that

$$\begin{aligned} {\Vert \psi _*\Vert _X}&\le C_* {\Vert \psi _*''''\Vert _{L^2}} \quad \text {if} \quad \psi _*'''' \in {L^2(\varOmega )}, \end{aligned}$$

(9)

$$\begin{aligned} {\Vert \psi _*''\Vert _{L^2}}&\le C_* {\Vert \psi _*\Vert _X}, \end{aligned}$$

(10)

$$\begin{aligned} {\Vert \psi _*'\Vert _{L^2}}&\le C_*^2 {\Vert \psi _*\Vert _X}, \end{aligned}$$

(11)

$$\begin{aligned} {\Vert \psi _*\Vert _{L^2}}&\le C_*^3 {\Vert \psi _*\Vert _X}, \end{aligned}$$

(12)

$$\begin{aligned} {\Vert \psi _*\Vert _{L^\infty (\varOmega )}}&\le C_{*0} {\Vert \psi _*\Vert _X}, \end{aligned}$$

(13)

$$\begin{aligned} {\Vert \psi _*'\Vert _{L^\infty (\varOmega )}}&\le C_{*1} {\Vert \psi _*\Vert _X}, \end{aligned}$$

(14)

$$\begin{aligned} {\Vert \psi _*''\Vert _{L^\infty (\varOmega )}}&\le C_{*2} {\Vert \psi _*\Vert _X}, \end{aligned}$$

(15)

where

$$\begin{aligned} C_* = \displaystyle \dfrac{1}{N+1}, \qquad C_{*0} = \displaystyle \sqrt{\dfrac{2}{5\pi N^5}}, \qquad C_{*1} = \displaystyle \sqrt{\dfrac{2}{3\pi N^3}}, \qquad C_{*2} = \displaystyle \sqrt{\dfrac{2}{\pi N}}. \end{aligned}$$

Proof

Below, we represent each element $\psi _* \in X_*$ by $\psi _* = \displaystyle \sum _{m={N+1}}^\infty A_m \phi _m \in X_*$, with $A_m \in {\mathrm{I\hspace{-0.22em}R}}$.

• Proof of (9):

  $$\begin{aligned} {\Vert \psi _*\Vert _X^2}&= \dfrac{\pi }{2} \sum _{m=N+1}^\infty m^6 A_m^2 \le \max _{N+1 \le m \le \infty } \dfrac{1}{m^2} \times {\Vert \psi _*''''\Vert ^2_{L^2}} \le \dfrac{1}{(N+1)^2} \times {\Vert \psi _*''''\Vert ^2_{L^2}}. \end{aligned}$$

• Proof of (10):

  $$\begin{aligned} {\Vert \psi _*''\Vert ^2_{L^2}} = \dfrac{\pi }{2} \sum _{m=N+1}^\infty m^4 A_m^2 \le \max _{N+1 \le m \le \infty } \dfrac{1}{m^2} \times {\Vert \psi _*\Vert _X^2} \le \dfrac{1}{(N+1)^2} \times {\Vert \psi _*\Vert _X^2}. \end{aligned}$$

• Proof of (11):

  $$\begin{aligned} {\Vert \psi _*'\Vert ^2_{L^2}} = \dfrac{\pi }{2} \sum _{m=N+1}^\infty m^2 A_m^2 \le \max _{N+1 \le m \le \infty } \dfrac{1}{m^4} \times {\Vert \psi _*\Vert _X^2} \le \dfrac{1}{(N+1)^4} \times {\Vert \psi _*\Vert _X^2}. \end{aligned}$$

• Proof of (12):

  $$\begin{aligned} {\Vert \psi _*\Vert ^2_{L^2}} = \dfrac{\pi }{2} \sum _{m=N+1}^\infty A_m^2 \le \max _{N+1 \le m \le \infty } \dfrac{1}{m^6} \times {\Vert \psi _*\Vert _X^2} \le \dfrac{1}{(N+1)^6} \times {\Vert \psi _*\Vert _X^2}. \end{aligned}$$

• Proof of (13): From the Cauchy–Schwarz inequality, we have

  $$\begin{aligned} {\Vert \psi _*\Vert _{L^\infty (\varOmega )}}&= \max _{x \in \varOmega } \left| \sum _{m=N+1}^\infty A_m \sin (mx) \right| \le \sum _{m=N+1}^\infty |A_m| = \sum _{m=N+1}^\infty m^3 |A_m| \dfrac{1}{m^3} \\&\le \left( \dfrac{2}{\pi }\sum _{m=N+1}^\infty \dfrac{1}{m^6} \right) ^{1/2} \left( \dfrac{\pi }{2} \sum _{m=N+1}^\infty A_m^2 m^6 \right) ^{1/2}\\&= \left( \dfrac{2}{\pi }\sum _{m=N+1}^\infty \dfrac{1}{m^6} \right) ^{1/2} {\Vert \psi _*\Vert _X}; \end{aligned}$$

  then from

  $$\begin{aligned} \sum _{m=N+1}^\infty \dfrac{1}{m^6} \le \int _N^\infty t^{-6} \, dt = \dfrac{1}{5N^5}, \end{aligned}$$

  we obtain the conclusion.

• Proof of (14): Because

  $$\begin{aligned} {\Vert \psi _*'\Vert _{L^\infty (\varOmega )}}&= \max _{x \in \varOmega } \left| \sum _{m=N+1}^\infty m A_m \sin (mx) \right| \le \sum _{m=N+1}^\infty m|A_m| = \sum _{m=N+1}^\infty m^3 |A_m| \dfrac{1}{m^2} \\&\le \left( \dfrac{2}{\pi }\sum _{m=N+1}^\infty \dfrac{1}{m^4} \right) ^{1/2} \left( \dfrac{\pi }{2} \sum _{m=N+1}^\infty A_m^2 m^6 \right) ^{1/2} \\&= \left( \dfrac{2}{\pi }\sum _{m=N+1}^\infty \dfrac{1}{m^4} \right) ^{1/2} {\Vert \psi _*\Vert _X}, \end{aligned}$$

  and

  $$\begin{aligned} \sum _{m=N+1}^\infty \dfrac{1}{m^4} \le \int _N^\infty t^{-4} \, dt = \dfrac{1}{3N^3}, \end{aligned}$$

  we have the conclusion.

• Proof of (15): Because

  $$\begin{aligned} {\Vert \psi _*''\Vert _{L^\infty (\varOmega )}}&= \max _{x \in \varOmega } \left| \sum _{m=N+1}^\infty m^2 A_m \sin (mx) \right| \le \sum _{m=N+1}^\infty m^2|A_m| = \sum _{m=N+1}^\infty m^3 |A_m| \dfrac{1}{m} \\&\le \left( \dfrac{2}{\pi }\sum _{m=N+1}^\infty \dfrac{1}{m^2} \right) ^{1/2} \left( \dfrac{\pi }{2} \sum _{m=N+1}^\infty A_m^2 m^6 \right) ^{1/2}\\&= \left( \dfrac{2}{\pi }\sum _{m=N+1}^\infty \dfrac{1}{m^2} \right) ^{1/2} {\Vert \psi _*\Vert _X}, \end{aligned}$$

  and

  $$\begin{aligned} \sum _{m=N+1}^\infty \dfrac{1}{m^2} \le \int _N^\infty t^{-2} \, dt = \dfrac{1}{N}, \end{aligned}$$

  we have the conclusion.

$\square$

Now we apply the verification procedure FN-Int [5, Sect. 2.1], where the name “FN-Int” comes from “Finite,” “Newton,” and “Interval.” For the sake of self-containedness of the manuscript, we give a detailed formulation for problem (1).

By setting

$$\begin{aligned} w:= & {} u - u_N, \end{aligned}$$

(16)

$$\begin{aligned} r_{2N}:= & {} -u_N'''' + f(u_N) \in X_{2N}, \end{aligned}$$

(17)

and

$$\begin{aligned} g(w):= R \, \left( B(w,w) + B(u_N,w) + B(w,u_N) \right) + r_{2N}: \quad X \rightarrow X^0, \end{aligned}$$

(18)

problem (1) can be rewritten as an equivalent residual form in order to find $w \in X$ satisfying

$$\begin{aligned} w'''' = g(w) \ \ \text {in} \ \ \varOmega \end{aligned}$$

(19)

in a weak sense. The term $r_{2N}$ in (18) is the defect of the approximate solution $u_N$ and can be re-expanded as an element of $X_{2N}$. Therefore, we can compute its inner product with $\{\phi _i\}_{i=1}^N$ and the $L^2$-norm by interval arithmetic [7]. It is expected that, if $u_N$ is an accurate approximation, some norms of w satisfying (19) are small.

By virtue of the property regarding B, the map g from X to $X^0$ is bounded and continuous. Moreover, it can be shown that for all $\psi \in X^0$, the linear problem $\xi '''' = \psi$ has a unique solution $\xi \in X^4$ (the proof follows the same procedure as in [1]). If we denote this map as $\varDelta ^{-2}$, then $\varDelta ^{-2}: X^0 \rightarrow X$ becomes a compact map because of the compactness of the embedding $H^4(\varOmega ) \hookrightarrow H^3(\varOmega )$. Therefore, (19) can be rewritten as the fixed-point equation

$$\begin{aligned} w = F(w) \end{aligned}$$

(20)

for the compact operator $F:=\varDelta ^{-2} g$ on X.

Next, for $u = \sum _{m=1}^\infty A_m \phi _m \in X^0$, we define $P_N: X^0 \rightarrow X_N$ as the truncation $P_N u = \sum _{m=1}^N A_m \phi _m \in X_N$. Note that $P_N|_X$ coincides with the $H^2_0$-projection such that

$$\begin{aligned} {(\,(u-P_N|_Xu)'',v_N''\,)_{L^2}}=0, \qquad \forall v_N \in X_N, \end{aligned}$$

(21)

and from (9) of Lemma 1, we can find that

$$\begin{aligned} {\Vert (I-P_N)u\Vert _X} \le C_* {\Vert (I-P_N)u''''\Vert _{L^2}}, \qquad u \in X \quad \text {and} \quad u'''' \in X^0. \end{aligned}$$

Now, we apply a Newton-like method to the fixed-point equation (20). Using the projection $P_N$, the fixed-point problem $w = F(w)$ can be uniquely decomposed as a finite-dimensional (projection) part $X_N$ and an infinite-dimensional (error) part $X_*$ as follows:

$$\begin{aligned} \left\{ \begin{array}{rcl} P_N w &{}=&{} P_N F(w), \\ (I-P_N) w &{}=&{} (I-P_N) F(w). \end{array} \right. \end{aligned}$$

(22)

Here I stands for the identity map on X. Suppose that the restriction of the operator $P_N(I-F'[0]): X \rightarrow X_N$ to $X_N$ has an inverse

$$\begin{aligned}{}[I-F'[0]]_N^{-1}: X_N \rightarrow X_N, \end{aligned}$$

(23)

where $F'[w]$ denotes the Fréchet derivative of F at w. Note that this assumption is equivalent to the invertibility of a matrix, and it can be checked numerically for actual verified computations [6].

We now define a Newton-like operator $\mathcal{N}: X \rightarrow X_N$ by

$$\begin{aligned} \mathcal{N}(w):= P_N w -[I-F'[0]]_N^{-1} P_N(w-F(w)), \end{aligned}$$

(24)

and a compact map $T: X \rightarrow X$ by

$$\begin{aligned} T(w):=\mathcal{N}(w) + (I-P_N)F(w). \end{aligned}$$

(25)

We find that, if $[I-F'[0]]_N^{-1}$ exists, then the two fixed-point problems,

$$\begin{aligned} w = T(w) \end{aligned}$$

(26)

and (20), are equivalent. If the approximate solution $u_N$ is sufficiently accurate, then the operator $\mathcal{N}(w)$ for the finite-dimensional part of T will possibly be a retraction. On the other hand, because of (9) in Lemma 1, the magnitude of the infinite-dimensional part of T is expected to be small when the truncation numbers of $X_N$ are taken to be sufficiently large.

We must now consider how to find a solution of (26) in a set $W \subset X$, which is referred to as a candidate set. For $n \ge 1$, an interval vector ${\textbf{c}} = [\underline{{\textbf{c}}}, \overline{{\textbf{c}}}]$ for $\underline{{\textbf{c}}}, \overline{{\textbf{c}}} \in {\mathrm{I\hspace{-0.22em}R}}^n$ is defined by

$$\begin{aligned} {\textbf{c}} = \{ {\textbf{v}} \in {\mathrm{I\hspace{-0.22em}R}}^n \ | \ \underline{{\textbf{c}}} \le {\textbf{v}} \le \overline{{\textbf{c}}} \} \end{aligned}$$

(see [6, part 1, chapter 9]). Let ${\mathbb{I}\mathbb{R}}^N$ be the set of N-dimensional interval vectors, and let $[B_i] \in {\mathbb{I}\mathbb{R}}^N$. Because $N=\dim X_N$, we introduce a finite-dimensional set $W_N \subset X_N$ which is a set of linear combinations of base functions in $X_N$ with interval coefficients $\{B_i\}_{1\le i \le N}$ as follows:

$$\begin{aligned} W_N:= \left\{ \left. \sum _{i=1}^N \, b_i \phi _i \in X_N \ \right| \ b_i \in {\mathrm{I\hspace{-0.22em}R}}, \ b_i \in B_i, \ 1 \le i \le N \right\} . \end{aligned}$$

(27)

For $\alpha >0$, an infinite-dimensional set $W_* \subset X_*$ and a candidate set $W \subset X$ are taken to be

$$\begin{aligned} W_*&:= \{w_* \in X_* \ | \ {\Vert w_*\Vert _X} \le \alpha \}, \end{aligned}$$

(28)

$$\begin{aligned} W&:= W_N + W_* . \end{aligned}$$

(29)

Now, by defining an $N \times N$ matrix $G=[G_{ij}]$ by

$$\begin{aligned} G_{ij}:= {(\,\phi _j'',\phi _i''\,)_{L^2}} - {(\,g'[0]\phi _j,\phi _i\,)_{L^2}}, \quad 1 \le i,j \le N, \end{aligned}$$

(30)

we obtain a verification condition.

Theorem 1

For the candidate set $W \subset X$ defined by (29), let any element $w \in W$ be represented by

$$\begin{aligned} w=w_N+w_*, \qquad w_N \in W_N, \quad w_* \in W_*. \end{aligned}$$

Let ${\textbf{d}}=[d_i] \in {\mathbb{I}\mathbb{R}}^N$ denote an interval enclosure of the set whose i-th component consists of

$$\begin{aligned} \{ \, {(\,g(w)-g'[0]w_N,\phi _i\,)_{L^2}} \in {\mathrm{I\hspace{-0.22em}R}}\ | \ w \in W \, \}, \qquad 1 \le i \le N. \end{aligned}$$

(31)

If, for an interval vector ${\textbf{v}}=[v_i] \in {\mathbb{I}\mathbb{R}}^N$ enclosing the solution ${\textbf{x}} \subset {\mathbb{I}\mathbb{R}}^N$ for the linear equation

$$\begin{aligned} G {\textbf{x}} = {\textbf{d}}, \end{aligned}$$

(32)

the conditions

$$\begin{aligned} v_i \subset B_i, \qquad 1 \le i \le N, \end{aligned}$$

(33)

and

$$\begin{aligned} \sup _{w \in W} {\Vert (I-P_N)F(w)\Vert _X} \le \alpha \end{aligned}$$

(34)

hold, then there exists a fixed point of F in W.

Proof

For each $w=w_N + w_* \in W$, since

$$\begin{aligned} \mathcal{N}(w)&= w_N - [ I - F'[0] ]_N^{-1} ( w_N - P_N F(w) ) \\&= [ I - F'[0]]^{-1}_N P_N( F(w) - F'[0]w_N), \end{aligned}$$

by setting

$$\begin{aligned} v_N:= \mathcal{N}(w) = \sum _{i=1}^N (v_N)_i \phi _i, \qquad {\textbf{v}}:=[(v_N)_i] \in {\mathrm{I\hspace{-0.22em}R}}^N, \end{aligned}$$

we obtain

$$\begin{aligned} P_N (I-F'[0]) v_N = P_N( F(w) - F'[0]w_N). \end{aligned}$$

(35)

From the definition of $P_N$, equation (35) is equivalent to

$$\begin{aligned} \sum _{i=1}^N \left\{ {(\,\phi _i'',\phi _j''\,)_{L^2}} -{(\,g'[0]\phi _i,\phi _j\,)_{L^2}} \right\} v_i = {(\,g(w)-g'[0]w_N,\phi _j\,)_{L^2}}, \quad 1 \le j \le N.\nonumber \\ \end{aligned}$$

(36)

Then, condition (33) ensures that $\mathcal{N}(w) \in W_N$. Condition (34) also shows that $(I-P_N)F(w) \in W_*$, so we obtain $T(W) \subset W$, which, by the Schauder fixed-point theorem, ensures the existence of a fixed point of T in the candidate set W. $\square$

Remark 2

Note that for all of the computation procedures in Theorem 1, we should consider the effects of rounding errors.

Remark 3

If we obtain a fixed point $w \in X$ by Theorem 1, we can also assure the existence of a nontrivial solution $u = u_N + w \in X$ for (1) with the error bound

$$\begin{aligned} {\Vert u-u_N\Vert _X} \le {\Vert W_N\Vert _X} + \alpha . \end{aligned}$$

Moreover, since w can be written as $w = w_N + w_*, w_N\in W_N, w_* \in W_*$, the estimation (13) in Lemma 1 provides an $L^\infty$-error estimate:

$$\begin{aligned} {\Vert u-u_N\Vert _{L^\infty (\varOmega )}} \le {\Vert W_N\Vert _{L^\infty (\varOmega )}}+ C_{*0} \alpha . \end{aligned}$$

(37)

3 Details of verification procedure

3.1 Finite-dimensional part

This subsection is devoted to the detailed estimation that satisfies (31). For each $w \in W$, setting $w=w_N+w_* \in W_N + W_*$ and $v_N = u_N+w_N \in X_N$, we have

$$\begin{aligned} g(w)-g'[0]w_N&= R \left( B(u_N,w_*) + B(w_*,u_N) + B(w,w) \right) + r_{2N} \nonumber \\&= R \left( B(v_N,w_*) + B(w_*,v_N) + B(w_N,w_N) + B(w_*,w_*) \right) + r_{2N} \end{aligned}$$

(38)

from (18). We note that it is important to reduce the number of differentiations of infinite-dimensional error part $w_*$ because we only know its norm and cannot treat $w_*$ directly in computers. In order to do so, we use the following property regarding B.

Lemma 2

For each $u,v,w \in X$, it holds that

$$\begin{aligned} {(\,B(u,v)+B(v,u),w\,)_{L^2}} = -{(\,4u''w'+4u'w''+uw''',v\,)_{L^2}}. \end{aligned}$$

(39)

Proof

Because $v''$, $u'w$, $uw'$, and v have zeros at 0 and $\pi$, applying partial integration, we have

$$\begin{aligned} \begin{array}{l} {(\,B(u,v)+B(v,u),w\,)_{L^2}} = {(\,uv'''-u'v''+vu'''-v'u'',w\,)_{L^2}} \\ \quad = {(\,uv''',w\,)_{L^2}}-{(\,u'v'',w\,)_{L^2}}+{(\,vu''',w\,)_{L^2}}-{(\,v'u'',w\,)_{L^2}} \\ \quad = {(\,v''',uw\,)_{L^2}}-{(\,v'',u'w\,)_{L^2}}+{(\,u'''w,v\,)_{L^2}}-{(\,v',u''w\,)_{L^2}} \\ \quad = -{(\,v'',u'w\,)_{L^2}}-{(\,v'',uw'\,)_{L^2}} -{(\,v'',u'w\,)_{L^2}}+{(\,u'''w,v\,)_{L^2}}-{(\,v',u''w\,)_{L^2}} \\ \quad = -2{(\,v'',u'w\,)_{L^2}}-{(\,v'',uw'\,)_{L^2}} +{(\,u'''w,v\,)_{L^2}}-{(\,v',u''w\,)_{L^2}} \\ \quad = 2{(\,v',u''w\,)_{L^2}} + 2{(\,v',u'w'\,)_{L^2}} +{(\,v',u'w'\,)_{L^2}} +{(\,v',uw''\,)_{L^2}} +{(\,u'''w,v\,)_{L^2}}\\ \qquad -{(\,v',u''w\,)_{L^2}} \\ \quad = {(\,v',u''w\,)_{L^2}} + 3{(\,v',u'w'\,)_{L^2}} +{(\,v',uw''\,)_{L^2}} +{(\,u'''w,v\,)_{L^2}} \\ \quad = -{(\,v,u'''w\,)_{L^2}}-{(\,v,u''w'\,)_{L^2}} - 3{(\,v,u''w'\,)_{L^2}} - 3{(\,v,u'w''\,)_{L^2}}\\ \qquad -{(\,v,u'w''\,)_{L^2}} -{(\,v,uw'''\,)_{L^2}} +{(\,u'''w,v\,)_{L^2}} \\ \quad = -4{(\,v,u''w'\,)_{L^2}} - 4{(\,v,u'w''\,)_{L^2}} -{(\,v,uw'''\,)_{L^2}} \\ \quad = -{(\,4u''w'+4u'w''+uw''',v\,)_{L^2}}. \end{array} \end{aligned}$$

$\square$

By using Lemma 2, the orthogonality of $P_N$, the Cauchy–Schwarz inequality, and (12) in Lemma 1, the inner product with $\phi _i$ of $B(v_N,w_*) + B(w_*,v_N)$ in (38) can be bounded as

$$\begin{aligned}&{(\,B(v_N,w_*) + B(w_*,v_N),\phi _i\,)_{L^2}} \\&\quad = -{(\,4v_N''\phi _i'+4v_N'\phi _i''+v_N\phi _i''',w_*\,)_{L^2}} \\&\quad = -{(\,(I-P_N)(4v_N''\phi _i'+4v_N'\phi _i''+v_N\phi _i'''),w_*\,)_{L^2}} \\&\quad \in [-1,1] \times {\Vert (I-P_N)(4v_N''\phi _i'+4v_N'\phi _i''+v_N\phi _i''')\Vert _{L^2}}{\Vert w_*\Vert _{L^2}} \\&\quad \subset [-1,1] \times {\Vert (I-P_N)(4v_N''\phi _i'+4v_N'\phi _i''+v_N\phi _i''')\Vert _{L^2}} C_*^3 \alpha \\&\quad \subset [-1,1] \times (z_1)_i \, C_*^3 \alpha , \end{aligned}$$

where ${\textbf{z}}_1=[(z_1)_i] \in {\mathrm{I\hspace{-0.22em}R}}^N$ satisfies

$$\begin{aligned} {\Vert (I-P_N)(4v_N''\phi _i'+4v_N'\phi _i''+v_N\phi _i''')\Vert _{L^2}} \le (z_1)_i, \qquad 1 \le i \le N. \end{aligned}$$

(40)

The inner product with $\phi _i$ of $B(w_N,w_N)$ in (38) can be enclosed by ${\textbf{z}}_2=[(z_2)_i] \in {\mathbb{I}\mathbb{R}}^N$ as

$$\begin{aligned} {(\,B(w_N,w_N),\phi _i\,)_{L^2}} \in (z_2)_i \qquad 1 \le i \le N \end{aligned}$$

(41)

(see Sect. 3.3.2). Additionally, the inner product between $\phi _i$ and $B(w_*,w_*)$ in (38) is evaluated as

$$\begin{aligned} {(\,B(w_*,w_*),\phi _i\,)_{L^2}}&= {(\,w_* w_*''' - w_*' w_*'',\phi _i\,)_{L^2}} = {(\,w_*,\phi _i w_*'''\,)_{L^2}} - {(\, w_*',\phi _i w_*''\,)_{L^2}} \\&\in [-1,1] \left( {\Vert w_*\Vert _{L^2}} {\Vert \phi _i w_*'''\Vert _{L^2}} + {\Vert w_*'\Vert _{L^2}} {\Vert \phi _i w_*''\Vert _{L^2}} \right) \\&\subset [-1,1] \left( {\Vert w_*\Vert _{L^2}} {\Vert w_*'''\Vert _{L^2}} + {\Vert w_*'\Vert _{L^2}} {\Vert w_*''\Vert _{L^2}} \right) \\&\subset [-1,1] \left( C_*^3 \alpha \alpha + C_*^2 \alpha C_* \alpha \right) \\&\subset [-2,2] C_*^3 \alpha ^2 \end{aligned}$$

by using ${\Vert \phi _i\Vert _{L^\infty (\varOmega )}}=1$, (10), (11), and (12).

Consequently, setting ${\textbf{z}}_3 = [(z_3)_i] \in {\mathbb{I}\mathbb{R}}^N$ by

$$\begin{aligned} {(\,r_{2N},\phi _i\,)_{L^2}} \subset (z_3)_i, \qquad 1 \le i \le N, \end{aligned}$$

(42)

the interval enclosure $d_i$ ($1 \le i \le N$) for (31) in Theorem 1 can be computed to satisfy

$$\begin{aligned} R \, \left( [-1,1] (z_1)_i C_*^3 \alpha + (z_2)_i + [-2,2] C_*^3 \alpha ^2 \right) + (z_3)_i \subset d_i \qquad 1 \le i \le N. \end{aligned}$$

3.2 Infinite-dimensional part

This subsection is devoted to the detailed estimation that satisfies (34). For each $w \in W$, since $g(w) \in X^0$ and $P_N$ is the truncation of the Fourier series, we have

$$\begin{aligned} (I-P_N) F(w)= & {} (I-P_N) \varDelta ^{-2} g(w) = \varDelta ^{-2} (I-P_N) g(w) \\= & {} (I-P_N) \varDelta ^{-2} (I-P_N) g(w). \end{aligned}$$

Thus, (9) in Lemma 1 gives us

$$\begin{aligned} {\Vert (I-P_N)F(w)\Vert _X} \le C_* {\Vert (I-P_N) g(w)\Vert _{L^2}}. \end{aligned}$$

(43)

We note that, for a practical verification, to keep overestimation as low as possible, removing the $X_N$ part of g(w) is important. From (18), we obtain

$$\begin{aligned} {\Vert (I-P_N)g(w)\Vert _{L^2}}\le & {} R {\Vert (I-P_N) \left( B(w,w) + B(u_N,w) + B(w,u_N) \right) \Vert _{L^2}} \nonumber \\{} & {} + {\Vert (I-P_N)r_{2N}\Vert _{L^2}}. \end{aligned}$$

(44)

The $L^2$-norm ${\Vert (I-P_N)r_{2N}\Vert _{L^2}}$ in (44) can be bounded by using interval arithmetic with the fixed approximate solution $u_N$. We take a bound $z_9>0$ of the defect satisfying

$$\begin{aligned} {\Vert (I-P_N)r_{2N}\Vert _{L^2}} \le z_9. \end{aligned}$$

(45)

Next, let us consider the first $L^2$-norm in (44). Setting $w=w_N+w_* \in W_N + W_*$ and $v_N = u_N + w_N \in X_N$, we obtain

$$\begin{aligned} \begin{array}{l} B(w,w) + B(u_N,w) + B(w,u_N) \\ \quad = B(u_N+w_N,w_N) + B(w_N,u_N) + B(u_N+w_N,w_*) + B(w_*,u_N+w_N) \\ \qquad + B(w_*,w_*)\\ \quad = B(v_N,w_N) + B(w_N,u_N) + B(v_N,w_*) + B(w_*,v_N) + B(w_*,w_*), \end{array} \end{aligned}$$

and thus

$$\begin{aligned} \begin{array}{l} {\Vert (I-P_N) \left( B(w,w) + B(u_N,w) + B(w,u_N) \right) \Vert _{L^2}} \\ \qquad \le \underbrace{{\Vert (I-P_N)\left( B(v_N,w_N) + B(w_N,u_N) \right) \Vert _{L^2}}}_{(a)} + \underbrace{{\Vert B(v_N,w_*)\Vert _{L^2}}}_{(b)}\\ \qquad \qquad + \underbrace{{\Vert B(w_*,v_N)\Vert _{L^2}}}_{(c)} + \underbrace{{\Vert B(w_*,w_*)\Vert _{L^2}}}_{(d)}. \end{array} \end{aligned}$$

(46)

The upper bound for part (a) on the right-hand side of (46) can be computed by interval arithmetic. We define $z_4>0$ satisfying

$$\begin{aligned} {\Vert (I-P_N) \left( B(v_N,w_N) + B(w_N,u_N) \right) \Vert _{L^2}} \le z_4. \end{aligned}$$

(47)

By using Lemma 1 and (28), and setting positive values $z_k>0$ for $k=5,6,7,8$ satisfying

$$\begin{aligned} {\Vert v_N\Vert _{L^\infty (\varOmega )}}&\le z_5, \end{aligned}$$

(48)

$$\begin{aligned} {\Vert v_N'\Vert _{L^\infty (\varOmega )}}&\le z_6, \end{aligned}$$

(49)

$$\begin{aligned} {\Vert v_N''\Vert _{L^\infty (\varOmega )}}&\le z_7, \end{aligned}$$

(50)

$$\begin{aligned} {\Vert v_N'''\Vert _{L^\infty (\varOmega )}}&\le z_8, \end{aligned}$$

(51)

we find that the rest of the $L^2$-norm terms are bounded as

$$\begin{aligned} (b) \quad {\Vert B(v_N,w_*)\Vert _{L^2}}&\le {\Vert v_N\Vert _{L^\infty (\varOmega )}} {\Vert w_*'''\Vert _{L^2}} + {\Vert v_N'\Vert _{L^\infty (\varOmega )}} {\Vert w_*''\Vert _{L^2}} \\&\le z_5 {\Vert w_*\Vert _X} + z_6 C_* {\Vert w_*\Vert _X} \\&\le \alpha ( z_5 + z_6 C_* ), \end{aligned}$$

$$\begin{aligned} (c) \quad {\Vert B(w_*,v_N)\Vert _{L^2}}&\le {\Vert w_*\Vert _{L^2}} {\Vert v_N'''\Vert _{L^\infty (\varOmega )}} + {\Vert w_*'\Vert _{L^2}} {\Vert v_N''\Vert _{L^\infty (\varOmega )}} \\&\le C_*^3 {\Vert w_*\Vert _X} z_8 + C_*^2 {\Vert w_*\Vert _X} z_7 \\&\le \alpha C_*^2 ( z_8 C_* + z_7 ), \end{aligned}$$

$$\begin{aligned} (d) \quad {\Vert B(w_*,w_*)\Vert _{L^2}}&\le {\Vert w_*\Vert _{L^\infty (\varOmega )}} {\Vert w_*'''\Vert _{L^2}} + {\Vert w_*'\Vert _{L^\infty (\varOmega )}} {\Vert w_*''\Vert _{L^2}} \\&\le C_{*0} {\Vert w_*\Vert _X} {\Vert w_*\Vert _X} + C_{*1} {\Vert w_*\Vert _X} C_* {\Vert w_*\Vert _X} \\&\le \alpha ^2 ( C_{*0} + C_{*1}C_* ). \end{aligned}$$

Consequently, the infinite-dimensional part of (34) can be computed as

$$\begin{aligned} \begin{array}{l} \displaystyle \sup _{w \in W} {\Vert (I-P_N)F(w)\Vert _{L^2}} \\ \qquad \le C_* \left\{ R ( z_4 + \alpha (z_5 + z_6 C_*) + \alpha C_*^2 (z_8 C_* + z_7) + \alpha ^2 ( C_{*0} + C_{*1}C_* )) + z_9 \right\} . \end{array} \end{aligned}$$

In our algorithm, when the Reynolds number is large, the truncation number N should be larger, because each $d_i$ and ${\Vert (I-P_N)F(w)\Vert _{L^2}}$ are proportional to R.

3.3 ${\mathbf {z_k}}$ ($1 \le k \le 3$) and $z_k$ ($4 \le k \le 9$)

In this subsection, we describe detailed computations for ${\mathbf {z_1}} \in {\mathrm{I\hspace{-0.22em}R}}^N$, ${\mathbf {z_2}}, {\mathbf {z_3}} \in {\mathbb{I}\mathbb{R}}^N$, and $z_k \in {\mathrm{I\hspace{-0.22em}R}}$ ($4 \le k \le 9$) introduced in previous subsections.

Below, using $(u_N)_m, (w_N)_m, (v_N)_m \in {\mathrm{I\hspace{-0.22em}R}}$ ($1 \le m \le N$), we express $u_N \in X_N$ of (8), any element $w_N \in W_N$ ($W_N$ is defined by (27)), and $v_N = u_N+w_N \in X_N$ as

$$\begin{aligned} u_N = \sum _{m=1}^N (u_N)_m \phi _m, \qquad w_N = \sum _{m=1}^N (w_N)_m \phi _m, \qquad v_N = \sum _{m=1}^N (v_N)_m \phi _m, \end{aligned}$$

respectively. Here, note that $(w_N)_m \in B_m$, $(v_N)_m \in (u_N)_m + B_m$ for $1 \le m \le N$. We also use the same symbols $E_{2N}$ and $e_m$ throughout the calculations, redefining them as necessary.

3.3.1 ${\mathbf {z_1}}=[(z_1)_i]$

For each i ($1 \le i \le N$), setting $\xi _m = \cos (m x)$, we re-expand

$$\begin{aligned} E_{2N}^i&:= 4v_N''\phi _i'+4v_N'\phi _i''+v_N\phi _i''' \\&= -4 \sum _{m=1}^N m^2 i (v_N)_m \phi _m \xi _i -4 \sum _{m=1}^N m i^2 (v_N)_m \xi _m \phi _i - \sum _{m=1}^N i^3 (v_N)_m \phi _m \xi _i \\&= -\sum _{m=1}^N \left[ i(4 m^2 + i^2) \phi _m \xi _i + 4 m i^2 \phi _i \xi _m \right] (v_N)_m \\&= -\dfrac{1}{2}\sum _{m=1}^N \left[ i(4 m^2 + i^2) ( \phi _{m+i} + \phi _{m-i} ) + 4 m i^2 ( \phi _{m+i} + \underbrace{\phi _{i-m}}_{-\phi _{m-i}} ) \right] (v_N)_m \\&= -\dfrac{i}{2}\sum _{m=1}^N \left[ (i + 2m)^2 \phi _{m+i} + (i - 2m)^2 \phi _{m-i} \right] (v_N)_m \in X_{2N}. \end{aligned}$$

Then, by using the interval $(u_N)_m + B_m \in {\mathbb{I}\mathbb{R}}$ enclosing $(v_N)_m$ for $1 \le m \le N$, we can compute $e_m^i \in {\mathbb{I}\mathbb{R}}$ ($1 \le m \le 2N$) satisfying

$$\begin{aligned} E^i_{2N} \in \sum _{m=1}^{2N} e_m^i \phi _m \subset X_{2N}. \end{aligned}$$

Therefore, $(z_1)_i \ge 0$ ($1 \le i \le N$) for (40) can be taken to satisfy

$$\begin{aligned} {\Vert (I-P_N) E_{2N}^i \Vert _{L^2}} \le \left\| \sum _{m=N+1}^{2N} e_m^i \phi _m \right\| _{L^2} = \sqrt{\dfrac{\pi }{2}} \cdot \sqrt{\sum _{m=N+1}^{2N} (e_m^i)^2} \le (z_1)_i, \end{aligned}$$

which is an upper bound for all $w_N \in W_N$.

3.3.2 ${\mathbf {z_2}}=[(z_2)_i]$

The equation (5) implies

$$\begin{aligned} B(w_N,w_N) = \dfrac{1}{2} \sum _{m=1}^N \sum _{n=1}^N n^2 (w_N)_m (w_N)_n \left[ (m-n) \phi _{m+n} - (m+n) \phi _{m-n} \right] \in X_{2N}. \end{aligned}$$

Then, by using the interval $B_m \in {\mathbb{I}\mathbb{R}}$ enclosing $(w_N)_m$ for $1 \le m \le N$, we can compute $e_m \in {\mathbb{I}\mathbb{R}}$ ($1 \le m \le 2N$) satisfying

$$\begin{aligned} B(w_N,w_N) \in \sum _{m=1}^{2N} e_m \phi _m \subset X_{2N}. \end{aligned}$$

Therefore, for each i such that $1 \le i \le N$, we can take $(z_2)_i$ of (41) to satisfy

$$\begin{aligned} {(\,B(w_N,w_N),\phi _i\,)_{L^2}} \in \dfrac{\pi }{2} e_i \subset (z_2)_i, \end{aligned}$$

which holds for all $w_N \in W_N$.

3.3.3 ${\mathbf {z_3}}=[(z_3)_i]$ and $z_9$

Using (6), the defect $r_{2N} \in X_{2N}$ of (17) can be expanded as

$$\begin{aligned} r_{2N} =&\; -\sum _{m=1}^N m^4 (u_N)_m \phi _m\nonumber \\ {}&\quad + \dfrac{R}{2} \sum _{\begin{array}{c} m \ge 1\\ n \ge 1 \end{array}} n^2 (u_N)_m (u_N)_n \left[ (m-n) \phi _{m+n} - (m+n) \phi _{m-n} \right] + \phi _k. \end{aligned}$$

(52)

Then, interval arithmetic gives $e_m \in {\mathbb{I}\mathbb{R}}$ ($1 \le m \le 2N$) satisfying

$$\begin{aligned} r_{2N} = -u_N'''' + f(u_N) \in \sum _{m=1}^{2N} e_m \phi _m. \end{aligned}$$

In the actual computations for the right-hand side of (52), each $(u_N)_m \in {\mathrm{I\hspace{-0.22em}R}}$ ($1 \le m \le N$) is translated to an interval that includes $(u_N)_m$.

Therefore, the interval vector ${\textbf{z}}_3=[(z_3)_i] \in {\mathbb{I}\mathbb{R}}^N$ for (42) and the positive value $z_9$ for (45) can be obtained to satisfy

$$\begin{aligned} \dfrac{\pi }{2} e_i \subset (z_3)_i, \qquad 1 \le i \le N \end{aligned}$$

and

$$\begin{aligned} \sqrt{\dfrac{\pi }{2}} \times \sqrt{\sum _{m=N+1}^{2N} e_m^2} \le z_9. \end{aligned}$$

3.3.4 $z_4$

From (5), it holds that

$$\begin{aligned} \begin{array}{rl} E_{2N} &{}:= B(v_N,w_N) + B(w_N,u_N) \\ &{}= \dfrac{1}{2} \displaystyle \sum _{m=1}^N \sum _{n=1}^N n^2 (v_N)_m (w_N)_n \left[ (m-n) \phi _{m+n} - (m+n) \phi _{m-n} \right] \\ &{}\qquad + \dfrac{1}{2} \displaystyle \sum _{m=1}^N \sum _{n=1}^N n^2 (w_N)_m (u_N)_n \left[ (m-n) \phi _{m+n} - (m+n) \phi _{m-n} \right] \\ &{} = \dfrac{1}{2} \displaystyle \sum _{m=1}^N \sum _{n=1}^N \left[ n^2 ( (v_N)_m (w_N)_n + (w_N)_m (u_N)_n ) \times (m-n) \phi _{m+n} \right. \\ &{} \qquad \qquad \left. - n^2 ( (v_N)_m (w_N)_n + (w_N)_m (u_N)_n) \times (m+n) \phi _{m-n} \right] \in X_{2N}. \end{array} \end{aligned}$$

Then, by using $B_m \in {\mathbb{I}\mathbb{R}}$ with $(w_N)_m \in B_m$ and $(u_N)_m + B_m \in {\mathbb{I}\mathbb{R}}$ enclosing $(v_N)_m$ for $1 \le m \le N$, we can compute $e_m \in {\mathbb{I}\mathbb{R}}$ ($1 \le m \le 2N$) satisfying

$$\begin{aligned} E_{2N} \in \sum _{m=1}^{2N} e_m \phi _m \subset X_{2N}. \end{aligned}$$

Therefore, $(z_4)_i \ge 0$ ($1 \le i \le N$) for (47) can be taken to satisfy

$$\begin{aligned} {\Vert (I-P_N) E_{2N} \Vert _{L^2}} \le \left\| \sum _{m=N+1}^{2N} e_m \phi _m \right\| _{L^2} \le \sqrt{\dfrac{\pi }{2}} \cdot \sqrt{\sum _{m=N+1}^{2N} e_m^2} \le z_4, \end{aligned}$$

which is an upper bound for all $w_N \in W_N$.

3.3.5 $z_5$, $z_6$, $z_7$, $z_8$

For each $v_N = u_N + w_N \in u_N + W_N$, it is true that

$$\begin{aligned} {\Vert v_N\Vert _{L^\infty (\varOmega )}}&= \max _{x \in \varOmega } \left| \sum _{m=1}^N (v_N)_m \sin (mx) \right| \le \sum _{m=1}^N \left| (v_N)_m \right| , \\ {\Vert v_N'\Vert _{L^\infty (\varOmega )}}&= \max _{x \in \varOmega } \left| \sum _{m=1}^N m (v_N)_m \cos (mx) \right| \le \sum _{m=1}^N \left| m (v_N)_m \right| ,\\ {\Vert v_N''\Vert _{L^\infty (\varOmega )}}&= \max _{x \in \varOmega } \left| - \sum _{m=1}^N m^2 (v_N)_m \sin (mx) \right| \le \sum _{m=1}^N \left| m^2 (v_N)_m \right| ,\\ {\Vert v_N'''\Vert _{L^\infty (\varOmega )}}&= \max _{x \in \varOmega } \left| - \sum _{m=1}^N m^3 (v_N)_m \cos (mx) \right| \le \sum _{m=1}^N \left| m^3 (v_N)_m \right| . \end{aligned}$$

Then, by using the interval $(u_N)_m + B_m \in {\mathbb{I}\mathbb{R}}$ enclosing $(v_N)_m$ for $1 \le m \le N$, we can compute $z_5$, $z_6$, $z_7$, and $z_8$ for (48)–(51) by interval arithmetic, which holds for all $w_N \in W_N$.

4 Enclosing results

This section reports on several computer-assisted results of (1) obtained by Theorem 1. All computations were carried out on the Fujitsu PRIMERGY CX2570 M4; Intel Xeon Gold 6140 (Skylake-SP); 2.3 GHz (Turbo 3.7 GHz) by using INTerval LABoratory Version 11, a toolbox in MATLAB R2019a (9.7.0.1261785) 64-bit (glnxa64) developed by Rump [7] for self-validating algorithms. Therefore, all numerical values in these tables are verified data in the sense of strict rounding error control in the mathematical sense (see [6, part 1, chapter 3]).

Table 1 shows some verification results for $k=2$. In the table, $|B_i|:=\max \{|b| \ | \ b \in B_i \}$ is obtained by the INTLAB function mag.

Table 1 Enclosing result of solutions of (1)

5 Verification of unimodality

In the final section, we prove the unimodality of enclosed solutions in the previous section. Let $u \in X$ be a verified solution of (1). Then the following conditions assure the unimodality of u [4, Lemma 3.2].

• 1. h is a real number such that $0< h < \pi /2$,

• 2. $0 \notin u'([0,h]) \cup u'([\pi -h,\pi ])$,

• 3. $\text {sgn}(u'([0,h]) \ne \text {sgn}(u'([\pi -h,\pi ]))$,

• 4. $0 \notin u''([h,\pi -h])$.

The verified solution of (1) by FN-Int can be enclosed in the set as follows:

$$\begin{aligned} u \in u_N + W_N + W_*, \qquad u_N \in X_N, \quad W_N \subset X_N, \quad W_* \subset X_*, \quad \sup _{w_* \in X_*}\Vert w_*\Vert _X \le \alpha . \end{aligned}$$

Setting

$$\begin{aligned} u_N + W_N = \sum _{m=1}^N V_m \phi _m, \quad V_m \in {\mathbb{I}\mathbb{R}}, \end{aligned}$$

there exist $v_N \in u_N + W_N$ and $v_* \in W_*$ such that $u = v_N + v_*$. Then, for each $x \in \varOmega$, (14) and (15) imply

$$\begin{aligned} u'(x)&= v_N'(x) + v_*'(x) \\&\in v_N'(x) + [-1,1] \times {\Vert v_*'\Vert _{L^\infty (\varOmega )}} \\&\subset \sum _{m=1}^N V_m m \cos (mx) + [-1,1] \times C_{*1} \alpha , \end{aligned}$$

and

$$\begin{aligned} u''(x)&= v_N''(x) + v_*''(x) \\&\in v_N''(x) + [-1,1] \times {\Vert v_*''\Vert _{L^\infty (\varOmega )}} \\&\subset -\sum _{m=1}^N V_m m^2 \sin (mx) + [-1,1] \times C_{*2} \alpha . \end{aligned}$$

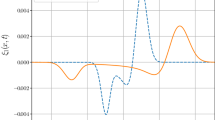
Therefore, for a subinterval J of $\varOmega =(0,\pi )$, we can enclose the ranges $u'(J)$ and $u''(J)$ by interval arithmetic. Fig. 2 shows enclosing ranges of $u'(J)$ (black) and $u''(J)$ (blue dots) in each J. Using this procedure, we can validate the unimodality of all solutions in Table 1 with $h=2\pi /5$.

Fig. 2

Enclosing ranges of $u'(J)$ (black) and $u''(J)$ (blue dots) in each subinterval J (color figure online)