Abstract
Every polyhedron can be decomposed into a Minkowski sum (or vector sum) of a bounded polyhedron and a polyhedral cone. This paper establishes similar statements for some classes of discrete sets in discrete convex analysis, such as integrally convex sets, \(\hbox {L}^{\natural }\)-convex sets, and \(\hbox {M}^{\natural }\)-convex sets.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
As is well known, every polyhedron can be decomposed into a Minkowski sum (or vector sum) of a bounded polyhedron and a polyhedral cone. The objective of this paper is to establish similar decomposition theorems with additional features of integrality and discrete convexity using concepts from discrete convex analysis [3, 8,9,10,11]. Emphasis is laid on integrally convex sets. This notion in discrete convex analysis is equivalent, via convex hull, to that of box-integer polyhedra in the theory of polyhedra [19, 20] (see Proposition 2.2 for the precise statement).
Integral convexity is a fundamental concept introduced by Favati–Tardella [2] for functions on the integer lattice \({{\mathbb {Z}}}^{n}\), and integrally convex sets are defined in [9, Section 3.4] as the set version of integral convexity; see Sect. 2.2 for the precise definition. Integral convexity encompasses almost all kinds of discrete convexity proposed so far, such as \(\hbox {L}^{\natural }\)-convexity, \(\hbox {M}^{\natural }\)-convexity, \(\hbox {M}^{\natural }_{2}\)-convexity, and multimodularity [9]. A discrete fixed point theorem was formulated by Iimura–Murota–Tamura [4] in terms of integrally convex sets (see also [10, Section 11.9], [11, Section 13.1] for expositions). Mathematical properties of integrally convex sets and functions have been clarified in recent studies (Moriguchi–Murota [5], Moriguchi–Murota–Tamura–Tardella [7], Murota–Tamura [15, 16]). The reader is referred to Murota–Tamura [17] for a recent comprehensive survey on integral convexity.
For any sets \(S_{1}\), \(S_{2} \subseteq {{\mathbb {R}}}^{n}\), we denote their Minkowski sum (or vector sum) by \(S_{1}+S_{2}\), that is,
Let \(P \subseteq {{\mathbb {R}}}^{n}\) be a polyhedron. A fundamental fact in the theory of polyhedra says that it can be represented as \(P= Q + C\) with a bounded polyhedron Q and a polyhedral cone C (see Sect. 2.1 for details). In this decomposition, the cone C is uniquely determined from P, coinciding with the characteristic (or recession) cone of P, whereas there is some degree of freedom in the choice of Q. We are interested in integrality and discrete convexity in this decomposition, and our contribution consists of two phases.
In the first phase we consider a box-integer polyhedron P and impose an additional condition that Q and C be box-integer polyhedra. Our first main result, Theorem 3.3, states that this is indeed possible. Furthermore, it is shown in Theorem 3.4 that if P is an \(\hbox {L}^{\natural }\)-convex (resp., \(\hbox {M}^{\natural }\)-convex) polyhedron, then we can impose that Q and C be \(\hbox {L}^{\natural }\)-convex (resp., \(\hbox {M}^{\natural }\)-convex). A technical challenge in establishing Theorem 3.3 for box-integer polyhedra stems from the lack of ‘outer description’ of box-integer polyhedra in terms of inequality systems. In contrast, inequality systems are available for \(\hbox {L}^{\natural }\)-convex and \(\hbox {M}^{\natural }\)-convex polyhedra, which makes the proof of Theorem 3.4 shorter and more transparent.
In the second phase we are concerned with discrete sets \(S \subseteq {{\mathbb {Z}}}^{n}\). Our second main result, Theorem 3.6, states that an integrally convex set S can be represented as \(S= T + G\) with a bounded integrally convex set T and a ‘conic’ integrally convex set G. Furthermore, it is shown in Theorem 3.7 that if S is an \(\hbox {L}^{\natural }\)-convex (resp., \(\hbox {M}^{\natural }\)-convex) set, then we can impose that T and G be \(\hbox {L}^{\natural }\)-convex (resp., \(\hbox {M}^{\natural }\)-convex). A technical challenge in the second phase is to overcome the well-known difficulty of discreteness in the Minkowski summation. Namely, for discrete sets \(S_{1}, S_{2} \subseteq {{\mathbb {Z}}}^{n}\), the Minkowski sum \(S_{1} + S_{2}\) may possibly be different from \((\overline{S_{1}} + \overline{S_{2}}) \cap {{\mathbb {Z}}}^{n}\) (see Fig. 1, Example 2.1 for a concrete example). The possibility of \((\overline{S_{1}} + \overline{S_{2}}) \cap {{\mathbb {Z}}}^{n} \ne S_{1} + S_{2}\) prevents us to derive the decomposition theorem for integrally convex sets as a corollary of Theorem 3.3 for box-integer polyhedra.
This paper is organized as follows. Section 2 is devoted to preliminaries on polyhedra and integrally convex sets. The main results are described in Sect. 3. Section 3.1 deals with subsets of \({{\mathbb {R}}}^{n}\) such as box-integer polyhedra, \(\hbox {L}^{\natural }\)-convex polyhedra, and \(\hbox {M}^{\natural }\)-convex polyhedra, while Sect. 3.2 treats subsets of \({{\mathbb {Z}}}^{n}\) such as integrally convex sets, \(\hbox {L}^{\natural }\)-convex sets, and \(\hbox {M}^{\natural }\)-convex sets. The proofs are given in Sect. 4, and Sect. 5 concludes the paper.
2 Preliminaries
2.1 Polyhedra
A subset P of \({{\mathbb {R}}}^{n}\) is called a polyhedron if it is described by a finite number of linear inequalities, that is, \(P = \{ x \mid Ax \le b \}\) for some matrix A and a vector b. In this paper we always assume that a polyhedron is nonempty. A subset Q of \({{\mathbb {R}}}^{n}\) is called a polytope if it is the convex hull of a finite number of points, that is, \(Q = {\overline{S}}\) for a finite subset S of \({{\mathbb {R}}}^{n}\), where \({\overline{S}}\) denotes the convex hull of S. It is known that a polytope is nothing but a bounded polyhedron. A subset C of \({{\mathbb {R}}}^{n}\) is called a cone if \(d \in C\) implies \(\lambda d \in C\) for all \(\lambda \ge 0\). We follow [19, 20] for terminology about polyhedra.
Let P be a polyhedron. The characteristic cone of P, denoted by \(\mathrm{char.cone}\, P\), is the polyhedral cone given by
The characteristic cone is also called the recession cone. The following are basic facts about the characteristic cone:
The following is a fundamental theorem, stating that a polyhedron can be decomposed into a Minkowski sum of a polytope and a cone.
Proposition 2.1
(Decomposition theorem for polyhedra)
(1) Every polyhedron P can be represented as \(P= Q + C\) with some polytope Q and polyhedral cone C.
(2) If \(P = Q + C\), with Q a polytope and C a polyhedral cone, then P is a polyhedron and \(C= \mathrm{char.cone}\, P\).
It is emphasized that the choice of the polytope Q in \(P= Q + C\) is not unique, while C is uniquely determined by P as stated in (2).
A polyhedron is said to be rational if it is described by a finite number of linear inequalities with rational coefficients. A polyhedron P is an integer polyhedron if \(P=\overline{P \cap {{\mathbb {Z}}}^{n}}\), i.e., if it coincides with the convex hull of the integer points contained in it, or equivalently, if P is rational and each face of P contains an integer vector. A polyhedron P is called box-integer if \(P \cap \{ x \in {{\mathbb {R}}}^{n} \mid l \le x \le u \}\) is an integer polyhedron for each choice of integer vectors \(l, u \in {{\mathbb {Z}}}^{n}\) with \(l \le u\) ( [20, Section 5.15]). We call a subset B of \({{\mathbb {R}}}^{n}\) an integral box if \(B = \{ x \in {{\mathbb {R}}}^{n} \mid l \le x \le u \}\) for some integer vectors \(l, u \in {{\mathbb {Z}}}^{n}\) with \(l \le u\).
2.2 Integrally convex sets
In this section we introduce the concept of integrally convex sets, as defined in [9, Section 3.4], and discuss subtleties related to the Minkowski sum of integrally convex sets. The reader is referred to Murota–Tamura [17] for technical details of integral convexity including the most recent results.
For \(x \in {{\mathbb {R}}}^{n}\) the integral neighborhood of x is defined by
It is noted that strict inequality “ < ” is used in this definition and N(x) admits an alternative expression
where, for \(t \in {{\mathbb {R}}}\) in general, \(\left\lfloor t \right\rfloor \) denotes the largest integer not larger than t (rounding-down to the nearest integer) and \(\lceil t \rceil \) is the smallest integer not smaller than t (rounding-up to the nearest integer). That is, N(x) consists of all integer vectors z between \(\lfloor x \rfloor =( \lfloor x_{1} \rfloor ,\lfloor x_{2} \rfloor , \ldots , \lfloor x_{n} \rfloor )\) and \(\lceil x \rceil = ( \lceil x_{1} \rceil , \lceil x_{2} \rceil , \ldots , \lceil x_{n} \rceil )\).
Let S be a subset of \({{\mathbb {Z}}}^{n}\) and recall that \({\overline{S}}\) denotes the convex hull of S. As is well known, \({\overline{S}}\) coincides with the set of all convex combinations of (finitely many) elements of S. For any real vector \(x \in {{\mathbb {R}}}^{n}\), we call the convex hull of \(S \cap N(x)\) the local convex hull of S around x. A nonempty set \(S \subseteq {{\mathbb {Z}}}^{n}\) is said to be integrally convex if the union of the local convex hulls \(\overline{S \cap N(x)}\) over \(x \in {{\mathbb {R}}}^{n}\) is convex. In other words, a set \(S \subseteq {{\mathbb {Z}}}^{n}\) is called integrally convex if
This condition is equivalent to saying that every point x in the convex hull of S is contained in the convex hull of \(S \cap N(x)\), i.e.,
Obviously, every subset of \(\{ 0, 1\}^{n}\) is integrally convex.
We say that a set \(S \subseteq {{\mathbb {Z}}}^{n}\) is hole-free if
It is known that an integrally convex set is hole-free; see [17, Proposition 2.2] for a formal proof. It is also known that the convex hull of an integrally convex set is a polyhedron (Murota–Tamura [15, Section 4.1]). However, no characterization is known about the inequality systems to describe integrally convex sets.
The concept of integrally convex sets is closely related (or essentially equivalent) to that of box-integer polyhedra as follows.
Proposition 2.2
([13, Section 2.2]) If a set \(S \subseteq {{\mathbb {Z}}}^{n}\) is integrally convex, then its convex hull \({\overline{S}}\) is a box-integer polyhedron and \(S = {\overline{S}} \cap {{\mathbb {Z}}}^{n}\). Conversely, if P is a box-integer polyhedron, then \(P \cap {{\mathbb {Z}}}^{n}\) is an integrally convex set and \(P = \overline{P \cap {{\mathbb {Z}}}^{n}}\).
Minkowski summation is an intriguing operation in discrete setting. For two (discrete) sets \(S_{1}, S_{2} \subseteq {{\mathbb {Z}}}^{n}\), in general, we have
(see, e.g., [9, Proposition 3.17(4)]). In contrast, the naive looking relation
is not always true, as Example 2.1 below shows.
Example 2.1
([9, Example 3.15]) The Minkowski sum of \(S_{1} = \{ (0,0), (1,1) \}\) and \(S_{2} = \{ (1,0), (0,1) \}\) is equal to \(S_{1}+S_{2} = \{ (1,0), (0,1), (2,1), (1,2) \}\), for which \((1,1) \in (\overline{S_{1}+S_{2}}) {\setminus } (S_{1}+S_{2})\). That is, the Minkowski sum \(S_{1}+S_{2}\) has a ‘hole’ at (1, 1). See Fig. 1.
It may be said that if (2.12) is true for some class of discrete convex sets, this equality captures a certain essence of the discrete convexity in question. For example, (2.12) is true for two \(\hbox {M}^{\natural }\)-convex sets, since the Minkowski sum of two \(\hbox {M}^{\natural }\)-convex sets remains to be \(\hbox {M}^{\natural }\)-convex ( [9, Section 4.6], [12, Section 3.5]). The identity (2.12) also holds for two \(\hbox {L}^{\natural }\)-convex sets, since the Minkowski sum of two \(\hbox {L}^{\natural }\)-convex sets is integrally convex [9, Theorem 8.42], although it is not necessarily \(\hbox {L}^{\natural }\)-convex.
For the Minkowski sum of integrally convex sets \(S_{1}\) and \(S_{2}\), we observe the following.
-
\(S_{1} + S_{2}\) may have a ‘hole’, that is, (2.12) may fail (see Example 2.1).
-
\(S_{1} + S_{2}\) may not be integrally convex (see Example 2.1).
-
\(\overline{(S_{1} + S_{2})} \cap {{\mathbb {Z}}}^{n}\) may not be integrally convex (see Example 2.2 below).
Example 2.2
Consider \(S_{1} = \{ (1,0,0), (0,1,0), (0,0,1) \}\) and \(S_{2} = \{ (0,0,0), (1,1,1) \}\). Their Minkowski sum is given by \(S_{1}+S_{2} = \{ (1,0,0), (0,1,0), (0,0,1), (2,1,1), (1,2,1), (1,1,2) \}\). Let \(S = \overline{(S_{1} + S_{2})} \cap {{\mathbb {Z}}}^{3}\) and consider \(x = [ (1,0,0) + (1,1,2) ] /2 = (1, 1/2, 1)\) belonging to \({\overline{S}}\). We have \(N(x) = \{ (1,0,1), (1,1,1) \}\), \(N(x) \cap S = \{ (1,1,1) \}\), and \(x \notin \overline{N(x) \cap S}\). Thus the condition (2.9) for integral convexity of S is violated. This example also shows that the Minkowski sum of box-integer polyhedra is not necessarily box-integer; see also Remark 3.1.
Discrepancy between \(S_{1}+S_{2}\) and \(\overline{S_{1}+ S_{2}}\) has attracted considerable attention in (ordinary) convex analysis, leading to the Shapley–Folkman theorem, which has applications in economics, optimization, etc. A recent paper [18] of the present authors shows a Shapley–Folkman-type theorem for integrally convex sets.
3 Results
3.1 Decomposition of box-integer polyhedra
In this section we describe our first main result (Theorem 3.3), a decomposition theorem for box-integer polyhedra. The proof of this theorem relies on the following technical results (in their equivalent reformulations in Propositions 4.1 and 4.4; see Fig. 3 in Sect. 4).
Proposition 3.1
The characteristic cone of a box-integer polyhedron is generated by \(\{ -1,0, +1 \}\)-vectors.
Proposition 3.2
The characteristic cone of a box-integer polyhedron is box-integer.
The proofs of these propositions are quite long and involved, probably because no characterization is known about inequality systems to describe box-integer polyhedra. The proofs of Propositions 3.1 and 3.2 are given in Sects. 4.1 and 4.2, respectively. Our decomposition theorem for box-integer polyhedra is as follows.
Theorem 3.3
Every box-integer polyhedron P can be represented as
with a bounded box-integer polyhedron Q and a box-integer polyhedral cone C.
Proof
By Proposition 2.1, we can decompose P as \(P = {\hat{Q}} + C\), where \({\hat{Q}}\) is a polytope and C is the characteristic cone of P. The cone C is box-integer by Proposition 3.2. Take a bounded integral box B containing \({\hat{Q}}\) and define \(Q:= P \cap B\), which is a bounded box-integer polyhedron. Since
we obtain
The reverse inclusion \(Q + C \subseteq P\) follows from \(Q \subseteq P\) and \(P + C = P\) in (2.4) as \(Q + C \subseteq P + C = P\). \(\square \)
Remark 3.1
In view of Proposition 2.1(2) we may be tempted to imagine that if Q is a bounded box-integer polyhedron and C is a box-integer polyhedral cone, then \(Q + C\) is a box-integer polyhedron. But this is not the case. A counterexample can be constructed from Example 2.2. Let Q be the convex hull of \(S_{1} = \{ (1,0,0), (0,1,0), (0,0,1) \}\) and C be the polyhedral cone generated by \(S'_{2} = \{ (1,1,1) \}\), that is, \(C = \{ \lambda (1,1,1) \mid \lambda \ge 0 \}\). Both Q and C are box-integer, but \(Q + C\) is not. Indeed, \(T = (Q + C) \cap {{\mathbb {Z}}}^{3}\) is not integrally convex, because \(x = [ (1,0,0) + (0,0,1) ] /2 + (1,1,1)/2 = (1, 1/2, 1) \in {\overline{T}}\), \(N(x) = \{ (1,0,1), (1,1,1) \}\), \(N(x) \cap T = \{ (1,1,1) \}\), and \(x \notin \overline{N(x) \cap T}\).
Remark 3.2
By Proposition 3.1, a box-integer cone is generated by \(\{ -1,0, +1 \}\)-vectors, but the latter property does not characterize a box-integer cone. Consider the cone C generated by (1, 1, 0, 1), (0, 1, 1, 1), (1, 0, 1, 1), that is,
For \(\alpha _1 = \alpha _2 = \alpha _3 = 1/2\), we have \(x = (1,1,1,3/2)\) and \(N(x) = \{ (1,1,1,2), (1,1,1,1) \} \). But \( (1,1,1,2) \notin C\) and \((1,1,1,1) \notin C\), and hence \(N(x) \cap C = \emptyset \). This shows that \(C \cap {{\mathbb {Z}}}^4\) is not integrally convex, and hence C is not box-integer.
Theorem 3.3 can be adapted to some classes of integer polyhedra treated in discrete convex analysis, such as \(\hbox {L}^{\natural }\)-convex and \(\hbox {M}^{\natural }\)-convex polyhedra. An \(\hbox {L}^{\natural }\)-convex polyhedron is, by definition, an integer polyhedron obtained as the convex hull of an \(\hbox {L}^{\natural }\)-convex set. It is known that an \(\hbox {L}^{\natural }\)-convex polyhedron P can be described as
for some \(I, J \subseteq \{ 1,2,\ldots , n\}\), \(E \subseteq \{ 1,2,\ldots , n\} \times \{ 1,2,\ldots , n\}\), \(l_{i} \in {{\mathbb {Z}}}\) \((i \in I)\), \(u_{j} \in {{\mathbb {Z}}}\) \((j \in J)\), and \(d_{ij} \in {{\mathbb {Z}}}\) \(((i,j) \in E)\), and the converse is also true. An \(\hbox {L}^{\natural }\)-convex cone means an \(\hbox {L}^{\natural }\)-convex polyhedron that is a cone. An \(\hbox {M}^{\natural }\)-convex polyhedron is a synonym of an integral generalized polymatroid, and hence an \(\hbox {M}^{\natural }\)-convex polyhedron P is described as
where \(x(X) = \sum _{i \in X} x_{i}\), for a (strong or paramodular) pair of an integer-valued supermodular function \(\mu \) and an integer-valued submodular function \(\rho \) (cf., [3, Section 3.5(a)], [9, Section 4.7]); \(\mu \) and \(\rho \) are allowed to take \(-\infty \) and \(+\infty \), respectively. An \(\hbox {M}^{\natural }\)-convex cone is defined in an obvious manner. Other kinds of polyhedra (such as \(\hbox {L}^{\natural }_{2}\)-convex polyhedron, \(\hbox {M}^{\natural }_{2}\)-convex polyhedron, and multimodular polyhedron) are defined similarly from the corresponding notions for sets of integer vectors. More precisely, an \(\hbox {L}^{\natural }_{2}\)-convex set is defined as the Minkowski sum of two \(\hbox {L}^{\natural }\)-convex sets and an \(\hbox {L}^{\natural }_{2}\)-convex polyhedron is the convex hull of an \(\hbox {L}^{\natural }_{2}\)-convex set, implying that an \(\hbox {L}^{\natural }_{2}\)-convex polyhedron can also be defined as the Minkowski sum of two \(\hbox {L}^{\natural }\)-convex polyhedra. Similarly, an \(\hbox {M}^{\natural }_{2}\)-convex set is defined as the intersection of two \(\hbox {M}^{\natural }\)-convex sets and an \(\hbox {M}^{\natural }_{2}\)-convex polyhedron is the convex hull of an \(\hbox {M}^{\natural }_{2}\)-convex set; then it is known (cf., e.g., [9, Theorem 4.22]) that an \(\hbox {M}^{\natural }_{2}\)-convex polyhedron can also be defined as the intersection of two \(\hbox {M}^{\natural }\)-convex polyhedra.
The adaptation of Theorem 3.3 to specific classes is given in Theorem 3.4 below. It should be clear that, although \(\hbox {L}^{\natural }\)-convex polyhedra, etc., constitute subclasses of box-integer polyhedra, Theorem 3.3 does not imply the corresponding statements for these subclasses. It is worth noting that the proofs for these special cases do not rely on Theorem 3.3 and that they are shorter and simpler because of the inequality descriptions known for these special cases (see Murota [9], Moriguchi–Murota [6, Table 1], Murota–Tamura [17, Table 1]).
Theorem 3.4
(1) Every \(\hbox {L}^{\natural }\)-convex polyhedron P can be represented as \(P= Q + C\) with a bounded \(\hbox {L}^{\natural }\)-convex polyhedron Q and an \(\hbox {L}^{\natural }\)-convex cone C.
(2) Every \(\hbox {L}^{\natural }_{2}\)-convex polyhedron P can be represented as \(P= Q + C\) with a bounded \(\hbox {L}^{\natural }_{2}\)-convex polyhedron Q and an \(\hbox {L}^{\natural }_{2}\)-convex cone C.
(3) Every \(\hbox {M}^{\natural }\)-convex polyhedron P can be represented as \(P= Q + C\) with a bounded \(\hbox {M}^{\natural }\)-convex polyhedron Q and an \(\hbox {M}^{\natural }\)-convex cone C. Similarly for an M-convex polyhedron P, with Q and C being M-convex.
(4) Every \(\hbox {M}^{\natural }_{2}\)-convex polyhedron P can be represented as \(P= Q + C\) with a bounded \(\hbox {M}^{\natural }_{2}\)-convex polyhedron Q and an \(\hbox {M}^{\natural }_{2}\)-convex cone C. Similarly for an \(\hbox {M}_{{2}}\)-convex polyhedron P, with Q and C being \(\hbox {M}_{{2}}\)-convex.
(5) Every multimodular polyhedron P can be represented as \(P= Q + C\) with a bounded multimodular polyhedron Q and a multimodular cone C.
Proof
(1) The proof of Theorem 3.3 can be adapted to an \(\hbox {L}^{\natural }\)-convex polyhedron on the basis of the following properties of an \(\hbox {L}^{\natural }\)-convex polyhedron.
-
1.
The characteristic cone of an \(\hbox {L}^{\natural }\)-convex polyhedron is \(\hbox {L}^{\natural }\)-convex.
-
2.
The intersection of an \(\hbox {L}^{\natural }\)-convex polyhedron with an integral box is \(\hbox {L}^{\natural }\)-convex.
We can prove the first statement by making use of the fact that an \(\hbox {L}^{\natural }\)-convex polyhedron \(P \subseteq {{\mathbb {R}}}^{n}\) is described as (3.2). It follows from (3.2) and (2.5) that the characteristic cone of P is given by \(C = \{ x \mid 0 \le x_{i} \ (i \in I), x_{j} \le 0 \ (j \in J), x_{j} - x_{i} \le 0 \ ((i,j) \in E) \}\), which is also an \(\hbox {L}^{\natural }\)-convex polyhedron. The second statement also follows from (3.2). We consider the decomposition \(P = {\hat{Q}} + C\) in Proposition 2.1, take a bounded integral box B containing \({\hat{Q}}\), and define \(Q:= P \cap B\), for which we can show \(P = Q + C\) as in the proof of Theorem 3.3.
(2)–(5) These cases are proved in Sect. 4.4 by using a unified proof scheme consistent with the case of (1). \(\square \)
Remark 3.3
Theorem 3.4(1) gives a decomposition of an \(\hbox {L}^{\natural }\)-convex polyhedron. However, we cannot obtain a similar statement for an L-convex polyhedron, simply because there is no bounded L-convex polyhedron. Note that an L-convex polyhedron P has the invariance in the direction of \(\textbf{1}= (1,1,\ldots ,1)\) in the sense that \(x \in P\) implies \(x + \lambda \textbf{1}\in P\) for all \(\lambda \in {{\mathbb {R}}}\). Similarly, there is no bounded \(\hbox {L}_{{2}}\)-convex polyhedron.
Remark 3.4
In each case of Theorem 3.4, the polyhedron P is necessarily an integer polyhedron. Recall that we have defined P to be an \(\hbox {L}^{\natural }\)-convex polyhedron if it is the convex hull of an \(\hbox {L}^{\natural }\)-convex set S \((\subseteq {{\mathbb {Z}}}^{n})\). In the literature of discrete convex analysis, the notion of \(\hbox {L}^{\natural }\)-convexity is generalized to non-integer polyhedra (Murota–Shioura [14]). An \(\hbox {L}^{\natural }\)-convex polyhedron (not necessarily integral) is described by (3.2) with \(l_{i} \in {{\mathbb {R}}}\) \((i \in I)\), \(u_{j} \in {{\mathbb {R}}}\) \((j \in J)\), and \(d_{ij} \in {{\mathbb {R}}}\) \(((i,j) \in E)\). For an \(\hbox {L}^{\natural }\)-convex polyhedron P in this generalized sense, we also obtain the decomposition \(P= Q + C\). Similar generalizations are possible for \(\hbox {M}^{\natural }\)-convex polyhedra, etc., in (2)–(5) of Theorem 3.4.
3.2 Decomposition of integrally convex sets
Theorem 3.3 for box-integer polyhedra can be rephrased for integrally convex sets as follows.
Corollary 3.5
The convex hull \({\overline{S}}\) of an integrally convex set S \((\subseteq {{\mathbb {Z}}}^{n})\) can be represented as
with a polytope Q and a polyhedral cone C such that \(Q \cap {{\mathbb {Z}}}^{n}\) and \(C \cap {{\mathbb {Z}}}^{n}\) are integrally convex.
Proof
Since S is integrally convex, \({\overline{S}}\) is a box-integer polyhedron by Proposition 2.2. By Theorem 3.3 applied to \({\overline{S}}\) we obtain the decomposition (3.4), where Q is a bounded box-integer polyhedron and C is a box-integer cone. Then \(Q \cap {{\mathbb {Z}}}^{n}\) and \(C \cap {{\mathbb {Z}}}^{n}\) are integrally convex by Proposition 2.2. \(\square \)
While the decomposition \({\overline{S}} = Q + C\) in (3.4) is defined via embedding of S into \({{\mathbb {R}}}^{n}\), our second main result (Theorem 3.6 below) establishes a decomposition of an integrally convex set S directly within \({{\mathbb {Z}}}^{n}\). We emphasize the difference between \({\overline{S}} = Q + C\) and
We can show “(3.5) \(\Rightarrow \) (3.4)” as
where \(\overline{ S_{1} + S_{2} } = \overline{ S_{1} } + \overline{ S_{2} }\) in (2.11) is used. However, the converse “(3.5) \(\Leftarrow \) (3.4)” is not always true (see Example 3.1 below). Thus, (3.5) is (strictly) stronger than (3.4).
To state the theorem we need to introduce a terminology. We call a set G \((\subseteq {{\mathbb {Z}}}^{n})\) a conic set if its convex hull \({\overline{G}}\) is a cone. An integrally convex set G is conic if and only if \(G = C \cap {{\mathbb {Z}}}^{n}\) for some box-integer cone C.
Theorem 3.6
Every integrally convex set S \((\subseteq {{\mathbb {Z}}}^{n})\) can be represented as
with a bounded integrally convex set T and a conic integrally convex set G.
Proof
The proof, to be given in Sect. 4.3, is based on propositions equivalent to Propositions 3.1 and 3.2. \(\square \)
Example 3.1
We compare the decompositions in Corollary 3.5 and Theorem 3.6 for a simple two-dimensional example. Let S be an infinite subset of \({{\mathbb {Z}}}^{2}\) depicted at the top left of Fig. 2, which can be described, e.g., as \(S = \{ x \in {{\mathbb {Z}}}^{2} \mid x_{1} + x_{2} \ge 1, \ | x_{1} - x_{2} | \le 1 \}\). This set S is integrally convex, and the convex hull \({\overline{S}}\) is a box-integer polyhedron described as \({\overline{S}} = \{ x \in {{\mathbb {R}}}^{2} \mid x_{1} + x_{2} \ge 1, \ | x_{1} - x_{2} | \le 1 \}\). Let Q be the line segment connecting (1, 0) and (0, 1) and C be the semi-infinite line starting at (0, 0) and emanating in the direction of (1, 1). Both Q and C are box-integer, and we obtain the decomposition \({\overline{S}} = Q + C\) in Corollary 3.5. The semi-infinite line C is, in fact, the characteristic cone of \({\overline{S}}\). Both \(Q\cap {{\mathbb {Z}}}^{2}\) and \(C \cap {{\mathbb {Z}}}^{2}\) are integrally convex, but the identity \(S = (Q\cap {{\mathbb {Z}}}^{2}) + (C \cap {{\mathbb {Z}}}^{2})\) in (3.5) fails, because of the ‘holes’ in \((Q\cap {{\mathbb {Z}}}^{2}) + (C \cap {{\mathbb {Z}}}^{2})\) at \(x = (t,t)\) for integers \(t \ge 1\). With the choice of \(T = (Q\cap {{\mathbb {Z}}}^{2}) \cup \{ (1,1) \} = \{ (1,0), (0,1), (1,1) \}\) and \(G = C \cap {{\mathbb {Z}}}^{2} = \{ (t,t) \mid t\ge 0, t \in {{\mathbb {Z}}}\}\), we obtain the decomposition \(S = T + G\) in Theorem 3.6. Here both T and G are integrally convex.
Theorem 3.6 can be adapted to some classes of discrete convex sets in discrete convex analysis, such as \(\hbox {L}^{\natural }\)-convex and \(\hbox {M}^{\natural }\)-convex sets (see Murota [9] for definitions of these concepts). The corresponding statements for these subclasses are given in Theorem 3.7 below. It is emphasized that Theorem 3.7 does not follow from Theorem 3.6 (for general integrally convex sets) nor from Theorem 3.4 (for \(\hbox {L}^{\natural }\)-convex polyhedra, etc.). Note that we have \(S, T, G \subseteq {{\mathbb {Z}}}^{n}\) in Theorem 3.7, whereas \(P, Q, C \subseteq {{\mathbb {R}}}^{n}\) in Theorem 3.4.
Theorem 3.7
(1) Every \(\hbox {L}^{\natural }\)-convex set S can be represented as \(S= T + G\) with a bounded \(\hbox {L}^{\natural }\)-convex set T and a conic \(\hbox {L}^{\natural }\)-convex set G.
(2) Every \(\hbox {L}^{\natural }_{2}\)-convex set S can be represented as \(S= T + G\) with a bounded \(\hbox {L}^{\natural }_{2}\)-convex set T and a conic \(\hbox {L}^{\natural }_{2}\)-convex set G.
(3) Every \(\hbox {M}^{\natural }\)-convex set S can be represented as \(S= T + G\) with a bounded \(\hbox {M}^{\natural }\)-convex set T and a conic \(\hbox {M}^{\natural }\)-convex set G. Similarly for an M-convex set S, with T and G being M-convex.
(4) Every \(\hbox {M}^{\natural }_{2}\)-convex set S can be represented as \(S= T + G\) with a bounded \(\hbox {M}^{\natural }_{2}\)-convex set T and a conic \(\hbox {M}^{\natural }_{2}\)-convex set G. Similarly for an \(\hbox {M}_{{2}}\)-convex set S, with T and G being \(\hbox {M}_{{2}}\)-convex.
(5) Every multimodular set S can be represented as \(S= T + G\) with a bounded multimodular set T and a conic multimodular set G.
Proof
The proof is given in Sect. 4.5. \(\square \)
4 Proofs
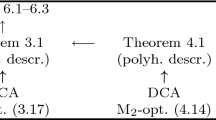
The structure of the proofs (dependence among propositions and theorems) is shown in the diagram in Fig. 3.
4.1 Proof of proposition 3.1
In this section we prove Proposition 3.1, stating that the characteristic cone of a box-integer polyhedron is generated by \(\{ -1,0, +1 \}\)-vectors. By Proposition 2.2, this statement can be rephrased (equivalently) in terms of integral convexity as follows.
Proposition 4.1
Let S \((\subseteq {{\mathbb {Z}}}^{n})\) be an integrally convex set. The characteristic cone C of its convex hull \({\overline{S}}\) is generated by vectors in \(\{ -1,0,+1 \}^{n}\). In particular, C is an integer polyhedron.
Proof
Take any \(d \in C\) with \(\Vert d \Vert _{\infty }=1\). Proposition 4.2 below shows that there exist \(d^{1}, d^{2}, \ldots , d^{h} \in N(d)\) such that \(d \in \overline{ \{ d^{1}, d^{2}, \ldots , d^{h} \} }\), where N(d) denotes the integral neighborhood of d defined in (2.6). We have \(N(d) \subseteq \{ -1,0,+1 \}^{n}\) since \(\Vert d \Vert _{\infty }=1\). \(\square \)
Proposition 4.2
Let S \((\subseteq {{\mathbb {Z}}}^{n})\) be an integrally convex set, \(x^{0} \in S\), and \(d \in {{\mathbb {R}}}^{n}\) with \(\Vert d \Vert _{\infty }=1\). If
there exist \(d^{1}, d^{2}, \ldots , d^{h} \in N(d) \) such that \(d \in \overline{ \{ d^{1}, d^{2}, \ldots , d^{h} \} }\) and
Necessity of integral convexity in Proposition 4.2
The condition (4.1) is equivalent to saying that d belongs to the characteristic cone of \({\overline{S}}\). The condition (4.2) implies that each \(d^{j}\) belongs to the characteristic cone of \({\overline{S}}\), but the converse is not true because (4.2) imposes an additional requirement of integrality. The role of integral convexity of S is illustrated in Fig. 4. In the left panel, the set S is integrally convex, while S is not integrally convex in the right, where \(d^{1}\) does not meet the condition in (4.2).
To prove Proposition 4.2, we need the following general lemma concerning a set of \(\{ 0,1 \}\)-vectors. Fig. 5 illustrates this lemma when \(X = \{ 0,1 \}^{2}\), where we think of R and B as sets of ‘red’ and ‘black’ points, respectively, which are disjoint by (4.3).
Lemma 4.3
Let \(X=\{ 0, 1 \}^{m}\). For any \(R \subseteq X\) and \(d \in {\overline{X}} {\setminus } {\overline{R}}\), there exists some \(B \subseteq X\) that satisfies the following conditions:
Moreover, the elements of B can be ordered as \(B = \{ d^{1}, d^{2}, \ldots , d^{l} \}\) (where \(l=|B|\)) so as to satisfy
Notations in Lemma 4.3
Proof
We first point out that (4.6) is a refinement of (4.5). Indeed, (4.6) for \(i = l\) reads \({\overline{B}} \cap \overline{ \{ d^{l} \} \cup (X {\setminus } B)} = \{ d^{l} \}\). Since \(d^{l} \notin \overline{X {\setminus } B}\), this implies \({\overline{B}} \cap (\overline{X {\setminus } B}) = \emptyset \) in (4.5).
In the (special) case where the given vector d belongs to X, d is an extreme point of \({\overline{X}}\) and hence we can take \(B = \{ d \}\) to meet the requirements (4.3), (4.4), and (4.6). In the following we assume \(d \notin X\).
The given subset R may be empty or nonempty. Suppose first that \(R \ne \emptyset \). Since \(d \notin {\overline{R}}\), the point d can be separated from \({\overline{R}}\) by a hyperplane. More precisely, there exists a hyperplane \(H = \{ x \mid a^{\top } x = \delta \}\), where \(\delta \in {{\mathbb {R}}}\), \(a \in {{\mathbb {R}}}^{n}\), and \(a^{\top } x = \sum _{i=1}^{n} a_{i} x_{i}\), such that the (open) half spaces \(H^{+}:= \{ x \mid a^{\top } x > \delta \}\) and \(H^{-}:= \{ x \mid a^{\top } x < \delta \}\) contain d and \({\overline{R}}\), respectively. It follows from \(d \in H^{+}\) and \({\overline{R}} \subseteq H^{-}\) that \(B:= H^{+} \cap X\) meets the requirements of (4.3) and (4.4). Indeed, \(B \subseteq X {\setminus } R\) in (4.3) follows from \(B \subseteq H^{+}\) and \(R \subseteq H^{-}\), and \(d \notin \overline{X {\setminus } B}\) in (4.4) follows from \(d \in H^{+}\) and \(X {\setminus } B \subseteq H^{-} \cup H\). To meet (4.6), we perturb the vector a so that \(a^{\top } x\) are distinct for \(x \in X \cup \{ d \}\), and number the elements of \(B = \{ d^{1}, d^{2}, \ldots , d^{l} \}\) so that \(a^{\top } d^{1}> a^{\top } d^{2}> \cdots > a^{\top } d^{l}\). In the remaining (rather exceptional) case where \(R = \emptyset \), we choose a vector a for which \(a^{\top } x\) are distinct for \(x \in X \cup \{ d \}\), and define \(\delta := a^{\top } d - \varepsilon \) with a sufficiently small positive \(\varepsilon \). Using such \((a, \delta )\) we define H, \(H^{+}\), \(H^{-}\), and \(B = H^{+} \cap X\). The rest of the argument is the same as in the case of \(R \ne \emptyset \). \(\square \)
We are ready to begin the proof of Proposition 4.2. Without loss of generality, we may assume \(d \ge \textbf{0}\), since integral convexity of S is preserved under coordinate inversions \(x_{i} \rightarrow -x_{i}\) for i in an arbitrary subset of \(\{ 1,2,\ldots ,n\}\).
Let \(X:= N(d)\). Then \(X \subseteq \{ 0,1 \}^{n}\) and \(d \in {\overline{X}}\). Up to a permutation of coordinates, X is equal to a set of the form \(\{ 1 \}^{p} \times \{ 0 \}^{q} \times \{ 0, 1 \}^{m}\) (\(p+q+m = n\); \(p,q,m \ge 0\)), so that we may identify X with \(\{ 0, 1 \}^{m}\). Define
or equivalently, \(R:= X \cap \mathrm{char.cone}\, {\overline{S}}\). Then we have \(d \in {\overline{R}}\) if and only if there exist \(d^{1}, d^{2}, \ldots , d^{h} \in N(d)\) satisfying \(d \in \overline{ \{ d^{1}, d^{2}, \ldots , d^{h} \} }\) and (4.2). That is, our goal is to show \(d \in {\overline{R}}\). To prove this by contradiction, we assume \(d \notin {\overline{R}}\).
We have \(R \subseteq X\) and \(d \in {\overline{X}} {\setminus } {\overline{R}}\), where X can be identified with \(\{ 0, 1 \}^{m}\). This allows us to use Lemma 4.3 to obtain \(B = \{ d^{1}, d^{2}, \ldots , d^{l} \}\) \((\subseteq X)\) satisfying (4.3)–(4.6). Let \(j^{*} \in \{ 0,1,\ldots , l \}\) be the (uniquely determined) number such that
where \(j^{*} =0\) if \(x^{0} + d^{1} \in S\), and \(j^{*} =l\) if \(x^{0} + d^{i} \notin S\) for all \(i=1,2,\ldots ,l\). Using this index \(j^{*}\) we define \(B^{*} = \{ d^{1}, d^{2}, \ldots , d^{j^{*}} \}\). Note that \(B^{*} = \emptyset \) if \(j^{*} =0\), and \(B^{*} = B\) if \(j^{*} =l\).
Let \(y:= x^{0} + d\). By the assumption (4.1), namely, \(d \in \mathrm{char.cone}\, {\overline{S}}\), we have \(y \in {\overline{S}}\), which, in turn, implies \(y \in \overline{N(y) \cap S}\) by integral convexity of S. It follows from \(N(d) = X\) and the definition of \(B^{*}\) thatFootnote 1
Hence \(y \in \overline{N(y) \cap S}\subseteq x^{0} + \overline{X {\setminus } B^{*}}\), that is, \(d \in \overline{X {\setminus } B^{*}}\). On the other hand, \(d \notin \overline{X \setminus B}\) as shown in (4.4). Thus we obtain
If \(B^{*} = B\), these two assertion contradict each other, and we are done. If \(B^{*}\) is a proper subset of B, we cannot derive a contradiction from (4.9).
We overcome this difficulty as follows. Although the definition of R in (4.7) refers to \(x^{0}\), it is, in fact, independent of the initial point \(x^{0}\), as seen from the alternative expression \(R = X \cap \mathrm{char.cone}\, {\overline{S}}\). The set B is also independent of \(x^{0}\), whereas \(B^{*}\), defined via (4.8), varies with \(x^{0}\), that is, \(B^{*}= B^{*}(x^{0})\). Our strategy is to show that, if \(B^{*}(x^{0}) \ne B\), we can choose another initial point \(x^{1}\) satisfying \(B^{*}(x^{0}) \subsetneqq B^{*}(x^{1})\). By repeating this process, we can increase \(B^{*}\) until \(B^{*} = B\). Then we obtain a contradiction from (4.9), to complete the proof of Proposition 4.2.
Since \(d^{j^{*}+1} \in B\) and \(R \cap B = \emptyset \) (cf. (4.3)), we have \(d^{j^{*}+1} \notin R\), while \(x^{0} + d^{j^{*}+1} \in S\) by (4.8). Therefore, there exists a positive integer \(k^{*} \ge 1\) such that
This integer \(k^{*}\) represents the maximum number of steps from \(x^{0}\) toward \(d^{j^{*}+1}\) to stay in S. We define \(x^{1}:= x^{0} + k^{*} d^{j^{*}+1}\), which is a point in S. We shall show \(B^{*}(x^{0}) \subsetneqq B^{*}(x^{1})\) by proving
The second property (4.12) is easy to prove. Namely,
using the definition of \(k^{*}\) in (4.10). To prove (4.11), we consider a sequence of intermediate points, say, \(x', x'', \ldots \) between \(x^{0}\) and \(x^{1}\), where \(x':= x^{0} + d^{j^{*}+1}\), \(x'':= x^{0} + 2 d^{j^{*}+1}\), etc.
Claim 4.1
For \(x' = x^{0} + d^{j^{*}+1}\) we have \(x' \in S\) and
Proof
First, we see \(x' \in S\) from (4.10). To prove (4.13), fix i \((1 \le i \le j^{*})\) and define \({{\hat{d}}}:= (d^{j^{*}+1} + d^{i})/2\). We have
Since \({{\hat{d}}} \ne d^{j^{*}+1}\) (which is equivalent to \(d^{i} \ne d^{j^{*}+1}\)) and
by (4.6), we have
On the other hand, it follows from the definition of \(B^{*}\) that
Combining (4.14) and (4.15) we obtain
If \(x' + d^{i} \in S\) were true, we would obtain
which is a contradiction to (4.16), since S is integrally convex. Therefore, we must have \(x' + d^{i} \notin S\), proving (4.13). \(\square \)
For the second intermediate point \(x''= x^{0} + 2 d^{j^{*}+1} = x' + d^{j^{*}+1}\), we can prove
in a similar manner, by replacing \((x^{0},x')\) in the proof of Claim 4.1 by \((x',x'')\). Continuing in this way, we can show the statement (4.11) at the new initial point \(x^{1}\) where \(B^{*}(x^{1})\) is strictly larger than \(B^{*}(x^{0})\).
If \(B^{*}(x^{1}) = B\), we are done, with a contradiction from (4.9). Otherwise, we repeat the same procedure to obtain a (finite) sequence \(x^0, x^1, \ldots x^s\) of initial points such that the associated \(B^{*}\) increases to B, i.e., \(B^{*}(x^{0}) \subsetneqq B^{*}(x^{1}) \cdots \subsetneqq B^{*}(x^{s}) = B\). This completes the proof of Proposition 4.2.
4.2 Proof of Proposition 3.2
In this section we prove Proposition 3.2, stating that the characteristic cone of a box-integer polyhedron is box-integer. By Proposition 2.2, this statement can be rephrased (equivalently) in terms of integral convexity as follows.
Proposition 4.4
Let S \((\subseteq {{\mathbb {Z}}}^{n})\) be an integrally convex set. The characteristic cone C of its convex hull \({\overline{S}}\) has the property that \(C \cap {{\mathbb {Z}}}^{n}\) is integrally convex.
We begin the proof of Proposition 4.4 by observing that the convex hull \({\overline{S}}\) can be represented as \({\overline{S}} = Q + C\) with a bounded box-integer polyhedron Q and a polyhedral cone C. Indeed, by Proposition 2.1, we can decompose \({\overline{S}}\) as \({\overline{S}} = {\hat{Q}} + C\), where \({\hat{Q}}\) is a polytope and C is the characteristic cone of \({\overline{S}}\). Take a bounded integral box B containing \({\hat{Q}}\) and define \(Q:= {\overline{S}} \cap B\), which is a bounded box-integer polyhedron. Since \(Q = {\overline{S}} \cap B = ({\hat{Q}} + C) \cap B \supseteq {\hat{Q}} \cap B = {\hat{Q}}\), we obtain \(Q + C \supseteq {\hat{Q}} + C = {\overline{S}}\). The reverse inclusion \(Q + C \subseteq {\overline{S}}\) follows from \(Q \subseteq {\overline{S}}\) and \({\overline{S}} + C = {\overline{S}}\) (cf. (2.4)) as \(Q + C \subseteq {\overline{S}} + C = {\overline{S}}\).
We prove Proposition 4.4 by contradiction. Namely, we assume that \(C \cap {{\mathbb {Z}}}^{n}\) is not integrally convex and derive a contradiction to the integral convexity of S. We shall construct a point \(y^{*} \in {\overline{S}}\) with the property \(y^{*} \notin \overline{N(y^{*}) \cap S }\). We start with an arbitrary \(x^{0} \in Q \cap {{\mathbb {Z}}}^{n}\) and find a point \(y^{0} \in x^{0} + C\) with some properties (Claim 4.2 below). We consider a system of inequalities describing \(x^{0} + C\). With reference to the inequalities tight at \(y^{0}\), we find a vertex \(x^{*}\) of Q. Then the point \(y^{*}\) is constructed as \(y^{*} = y^{0} + (x^{*} - x^{0})\) in (4.29) below.
Recalling that Q is a nonempty integer polyhedron, take any \(x^{0} \in Q \cap {{\mathbb {Z}}}^{n}\) and define
By Proposition 4.1, C is an integer polyhedron, which implies that D is an integer polyhedron and \(D = \overline{D_{I}}\). The set \(D_I\) is not integrally convex as a consequence of the assumption that \(C \cap {{\mathbb {Z}}}^{n}\) is not integrally convex.
Claim 4.2
There exists \(y^{0} \in D\) that satisfies the following conditions:
Proof
Since \(D_I\) is not integrally convex, there exists \(z \in \overline{D_{I}}\) such that \(z \notin \overline{N(z) \cap D_{I}}\). Take such z with the smallest dimension of \(\overline{N(z)}\). Note that \(\overline{N(z)}\) is an integral box of the form \(\{ x \in {{\mathbb {R}}}^{n} \mid l \le x \le u \}\) for some \(l, u \in {{\mathbb {Z}}}^{n}\) with \(\Vert u - l \, \Vert _{\infty } \le 1\) and the dimension of \(\overline{N(z)}\) is equal to the number of indices i satisfying \(u_{i} - l_{i} = 1\).
Notations in the proof of Claim 4.2 (The square represents \(\overline{N(z)}\) and the triangle is \(\overline{N(z)} \cap D\))
The set \(\overline{N(z)} \cap D\) is a bounded polyhedron, and \(( \overline{N(z)} \cap D ) {\setminus } \overline{N(z) \cap D_{I}} \ne \emptyset \) since \(z \in ( \overline{N(z)} \cap D ) {\setminus } \overline{N(z) \cap D_{I}}\). Hence there is a vertex v of \(\overline{N(z)} \cap D\) not contained in \(\overline{N(z) \cap D_{I}}\) (see Figure 6). The vertex v is a relative interior point of \(\overline{N(z)}\), because, otherwise, we would have \(\dim \overline{N(v)} < \dim \overline{N(z)}\) while \(v \notin \overline{N(v) \cap D_{I}}\) from \(v \notin \overline{N(z) \cap D_{I}} \supseteq \overline{N(v) \cap D_{I}}\), a contradiction to our choice of z. Since v is a relative interior point of \(\overline{N(z)}\), we have \(N(v) = N(z)\). Let \(y^{0}:=v\), which satisfies the three conditions (4.18)–(4.20). \(\square \)
Consider a (non-redundant) system of inequalities describing D. Since \(y^{0}\) is a vertex of \(\overline{N(y^{0})} \cap D\) lying in the relative interior of \(\overline{N(y^{0})}\), at least one inequality is tight (i.e., satisfied in equality). Enumerate all such inequalities as
where \(k \ge 1\). By definition we have \(a_{i}^{\top } y^{0} = \beta _{i}\) for \(i=1,2,\ldots ,k\). Since \(D = x^{0} +C\) and C is a cone, all the inequalities in (4.21) are also tight at \(x^{0}\), that is, \(a_{i}^{\top } x^{0} = \beta _{i}\) for \(i=1,2,\ldots ,k\).
Claim 4.3
There exist some positive coefficients \(\mu _{1}, \mu _{2}, \ldots , \mu _{k} > 0\) such that \(a = \sum _{i=1}^{k} \mu _{i} a_{i}\) and \(\beta = \sum _{i=1}^{k} \mu _{i} \beta _{i}\) satisfy
Proof
(4.22)–(4.24) hold for any \(\mu _{1}, \mu _{2}, \ldots , \mu _{k} >0\). (4.22) is immediate from the tightness \(a_{i}^{\top } x^{0} = a_{i}^{\top } y^{0} = \beta _{i}\) for \(i=1,2,\ldots ,k\). (4.23) holds since the inequalities in (4.21) are valid for D. (4.24) follows from (4.22) and (4.23) because \(D=x^{0}+C\) and C is a cone. (4.25) can be shown as follows. Since \(y^{0}\) is a vertex, the intersection of \(\overline{N(y^{0})}\) and the hyperplanes \(a_{i}^{\top } x = \beta _{i}\) \((i=1,2,\ldots ,k)\) consists of a single vector \(y^{0}\), that is, for \(x \in \overline{N(y^{0})}\), we have \(a_{i}^{\top } x = \beta _{i}\) for all \(i=1,2,\ldots ,k\) if and only if \(x = y^{0}\). Therefore, for each \(x \in N(y^{0}) {\setminus } D_{I}\), there is some i with \(a_{i}^{\top } x \ne \beta _{i}\). It then follows that (4.25) holds for randomly chosen \(\mu _{1}, \mu _{2}, \ldots , \mu _{k} > 0\). \(\square \)
Claim 4.4
Proof
Recall from (4.23) that \(\{ x \in {{\mathbb {Z}}}^{n} \mid a^{\top } x \le \beta \} \supseteq D_{I}\). Using notation \(E:= \{ x \in {{\mathbb {Z}}}^{n} \mid a^{\top } x \le \beta \} {\setminus } D_{I}\), we can rewrite (4.26) as
We have \(y^{0} \notin \overline{N(y^{0}) \cap D_{I} }\) in (4.18) and \(a^{\top } y^{0} = \beta \) in (4.22), whereas \(a^{\top } x < \beta \) for all \(x \in N(y^{0}) \cap E\) by (4.25). Then (4.27) follows. \(\square \)
Let \(\beta ^{*}\) denote the maximum value of \(a^{\top } x \) over Q, that is,
Since Q is a bounded integer polyhedron, we may assume that this maximum is attained by an integer vector \(x^{*} \in Q \cap {{\mathbb {Z}}}^{n}\). Define \(y^{*} \in {{\mathbb {R}}}^{n}\) by
We have \(y^{*} \in {\overline{S}}\), since \(y^{*} = x^{*} + (y^{0} - x^{0}) \in Q + (D - x^{0}) = Q+C ={\overline{S}}\).
Claim 4.5
Proof
Recall from (4.26) that
By adding \(x^{*} - x^{0}\) to the left-hand side, we obtain \(y^{*} = y^{0} + (x^{*} - x^{0})\). On the right-hand side, we have \(N(y^{0}) + (x^{*} - x^{0}) = N(y^{0} + x^{*} - x^{0}) = N(y^{*})\), where the first equality is true by \(x^{*} - x^{0} \in {{\mathbb {Z}}}^{n}\). Since \(a^{\top } x^{*} = \beta ^{*}\) by the definition of \(x^{*}\) and \(a^{\top } x^{0} = \beta \) by (4.22), we also have
Thus we obtain (4.30). \(\square \)
Claim 4.6
Proof
We have \(Q \subseteq \{ x \mid a^{\top } x \le \beta ^{*} \}\) by the definition (4.28) of \(\beta ^{*}\), whereas \(C \subseteq \{ x \mid a^{\top } x \le 0 \}\) by (4.24). Therefore, every \(x \in {\overline{S}} = Q + C\) satisfies \(a^{\top } x \le \beta ^{*}\). \(\square \)
It follows from (4.30) and (4.31) that \(y^{*} \notin \overline{N(y^{*}) \cap S }\), whereas \(y^{*} \in {\overline{S}}\). This is a contradiction to the integral convexity of S, completing the proof of Proposition 4.4.
4.3 Proof of Theorem 3.6
In this section we prove Theorem 3.6, stating that every integrally convex set S \((\subseteq {{\mathbb {Z}}}^{n})\) can be represented as \(S = T + G\) with a bounded integrally convex set T and a conic integrally convex set G.
By Proposition 2.1, the convex hull \({\overline{S}}\) of S can be represented as
with a polytope \({\hat{Q}}\) and the characteristic cone C of \({\overline{S}}\). By Proposition 4.4, \(C \cap {{\mathbb {Z}}}^{n}\) is integrally convex. With reference to the polytope \({\hat{Q}}\), define
for \(i=1,2,\ldots ,n\). The numbers \(l_{i}, u_{i}\) are (finite) integers with \(l_{i} \le u_{i}\), since \({\hat{Q}}\) is a nonempty and bounded polyhedron.
Let \(\{ d^{1}, d^{2}, \ldots , d^{L} \}\) be a generating set of cone C, where we may assume \(d^{j} \in \{ -1,0,+1 \}^{n}\) by Proposition 4.1. With reference to the number L of the generators of C, define a bounded integral box B by
and put \(Q:= {\overline{S}} \cap B\), which is a bounded box-integer polyhedron containing \({\hat{Q}}\). We have \({\overline{S}} = Q + C\), since \({\overline{S}} = {\hat{Q}} + C \subseteq Q + C \subseteq {\overline{S}} + C = {\overline{S}}\).
Define
which are, respectively, a bounded integrally convex set and a conic integrally convex set. In the following we show \(S = T + G\) by a sequence of claims.
Claim 4.7
\(S \supseteq T + G\).
Proof
For two (discrete) sets \(S_{1}, S_{2} \subseteq {{\mathbb {Z}}}^{n}\), in general, we have
Using this for \((S_{1}, S_{2}) = (T,G)\) as well as \({\overline{S}} = Q + C = {\overline{T}} + {\overline{G}}\), we obtain
\(\square \)
To show the reverse inclusion \(S \subseteq T + G\), take any \(z \in S\). By \({\overline{S}} = {\hat{Q}} + C\) in (4.32), there exist real vectors \({\hat{x}} \in {\hat{Q}}\) and \({{\hat{d}}} \in C\) satisfying
The vector \({{\hat{d}}}\) can be represented as a nonnegative combination of the generators \(\{ d^{1}, d^{2}, \ldots , d^{L} \}\) of C as
With reference to this expression, define vectors \(d^{*}\) and \(x^{*}\) by
for which we have
Claim 4.8
\(d^{*} \in G\).
Proof
(4.34) shows \(d^{*} \in C\). We also have \(d^{*} \in {{\mathbb {Z}}}^{n}\), since \(\lfloor \lambda _{j} \rfloor \in {{\mathbb {Z}}}\) and \(d^{j} \in \{ -1,0,+1 \}^{n}\) for \(j=1,2,\ldots , L\) by Proposition 4.1. Therefore, \(d^{*} \in C \cap {{\mathbb {Z}}}^{n} = G\). \(\square \)
Claim 4.9
\(x^{*} \in T\).
Proof
Since \(T = {\overline{S}} \cap B \cap {{\mathbb {Z}}}^{n}\) (see (4.33)), it suffices to show (i) \(x^{*} \in {{\mathbb {Z}}}^{n}\), (ii) \(x^{*} \in {\overline{S}}\), and (iii) \(x^{*} \in B\). We have \(x^{*} \in {{\mathbb {Z}}}^{n}\), since \(z \in {{\mathbb {Z}}}^{n}\), \(d^{*} \in {{\mathbb {Z}}}^{n}\), and \(x^{*} = z - d^{*}\) by (4.36). We have \(x^{*} \in {\overline{S}}\), since \(x^{*} \in {\hat{Q}} + C\) by (4.35) and \({\hat{Q}} + C = {\overline{S}}\) by (4.32). Finally, we show \(x^{*} \in B\). For the first term \({\hat{x}}\) on the right-hand side of (4.35), we have \(l \le {\hat{x}} \le u\) since \({\hat{x}} \in {\hat{Q}}\). Each component of the second term \( \sum _{j=1}^{L} (\lambda _{j} - \lfloor \lambda _{j} \rfloor ) \ d^{j}\) lies between \(-L\) and \(+L\), since \(0 \le \lambda _{j} - \lfloor \lambda _{j} \rfloor < 1\) and \(d^{j} \in \{ -1,0,+1 \}^{n}\) for \(j=1,2,\ldots , L\) by Proposition 4.1. Therefore, \(x^{*} \in B\). \(\square \)
The inclusion \(S \subseteq T + G\) follows from Claims 4.8 and 4.9, while \(S \supseteq T + G\) is already shown in Claim 4.7. This completes the proof of Theorem 3.6.
4.4 Proof of Theorem 3.4
In this section we prove Theorem 3.4 for polyhedra P \((\subseteq {{\mathbb {R}}}^{n})\) with particular discrete convexities such as \(\hbox {L}^{\natural }\)-convexity, \(\hbox {M}^{\natural }\)-convexity, etc. The proof for the case (1) of \(\hbox {L}^{\natural }\)-convex polyhedra has already been given in Sect. 3.1, right after Theorem 3.4. Here we present a unified proof scheme for all cases including \(\hbox {L}^{\natural }\)-convex polyhedra. We use a generic name “A-convex” to mean any of \(\hbox {L}^{\natural }\)-convex, \(\hbox {L}^{\natural }_{2}\)-convex, \(\hbox {M}^{\natural }\)-convex, M-convex, \(\hbox {M}^{\natural }_{2}\)-convex, \(\hbox {M}_{{2}}\)-convex, and multimodular.
The unified proof scheme is as follows. Let P be an A-convex polyhedron. By Proposition 2.1, we can decompose P as \(P = {\hat{Q}} + C\), where \({\hat{Q}}\) is a polytope and C is the characteristic cone of P. We assume that
By \({\hat{Q}} \subseteq Q \subseteq P\) in (4.38), we have \(P = {\hat{Q}} + C \subseteq Q + C \subseteq P + C = P\). This shows \(P = Q + C\), where Q is a bounded A-convex polyhedron by (4.38) and C is an A-convex cone by (4.37).
The first assumption (4.37) is met by each discrete convexity in (1)–(5). Indeed, a polyhedron P with such discrete convexity can be described as \(P = \{ x \mid Ax \le b \}\), where a necessary and sufficient condition on (A, b) for that discrete convexity of P is known. For example, an \(\hbox {L}^{\natural }\)-convex polyhedron is described by (3.2) and an \(\hbox {M}^{\natural }\)-convex polyhedron by (3.3); see Murota [9], Moriguchi–Murota [6, Table 1], and Murota–Tamura [17, Table 1] for other cases. This enables us to prove that the characteristic cone \(C = \{ d \mid A d \le 0 \}\) is also endowed with the same kind of discrete convexity.
For the second assumption (4.38), we consider \(Q:= P \cap B\) for a bounded integral box B containing \({\hat{Q}}\), expecting that Q is endowed with A-convexity as a consequence of the assumed A-convexity of P. This construction is indeed valid for all discrete convexities in question, with the exception of \(\hbox {L}^{\natural }_{2}\)-convexity in (2) (see Remark 4.1 below).
In Case (2) of an \(\hbox {L}^{\natural }_{2}\)-convex polyhedron P, we construct an \(\hbox {L}^{\natural }_{2}\)-convex (integer) polyhedron Q as follows. Let \(P = P_{1} + P_{2}\) with two \(\hbox {L}^{\natural }\)-convex polyhedra \(P_{1}\) and \(P_{2}\). Enumerate all vertices of the polytope \({\hat{Q}}\) as \(\{ z^{1},z^{2},\ldots ,z^{m} \}\), where \(z^{j} \in {{\mathbb {R}}}^{n}\) for \(j=1,2,\ldots ,m\). By \(z^{j} \in {\hat{Q}} \subseteq P_{1} + P_{2}\), each \(z^{j}\) can be expressed as \(z^{j} = x^{j} + y^{j}\) with \(x^{j} \in P_{1}\) and \(y^{j} \in P_{2}\). Take integral boxes \(B_{1}\) and \(B_{2}\) satisfying \(\{ x^{1},x^{2},\ldots ,x^{m} \} \subseteq B_{1}\) and \(\{ y^{1},y^{2},\ldots ,y^{m} \} \subseteq B_{2}\), respectively, and define \(Q_{1}:= P_{1} \cap B_{1}\), \(Q_{2}:= P_{2} \cap B_{2}\), and \(Q:= Q_{1} + Q_{2}\). Then \(Q_{1}\) and \(Q_{2}\) are \(\hbox {L}^{\natural }\)-convex (integer) polyhedra, and hence Q is an \(\hbox {L}^{\natural }_{2}\)-convex (integer) polyhedron. Then we have
and \(Q = Q_{1} + Q_{2} \subseteq P_{1} + P_{2} = P\). Thus we obtain \({\hat{Q}} \subseteq Q \subseteq P\).
This completes the proof of Theorem 3.4.
Remark 4.1
The intersection of an \(\hbox {L}^{\natural }_{2}\)-convex polyhedron with an integral box is not necessarily \(\hbox {L}^{\natural }_{2}\)-convex. For example, let \(P_{1}\) be the line segment connecting (0, 0, 0) and (1, 1, 0) and \(P_{2}\) be the one connecting (0, 0, 0) and (0, 1, 1). Then \(P = P_{1} + P_{2}\) \((\subseteq {{\mathbb {R}}}^{3})\) is an \(\hbox {L}^{\natural }_{2}\)-convex polyhedron, which is a parallelogram lying on the plane \(x_{1} - x_{2} + x_{3} =0\) in \({{\mathbb {R}}}^{3}\). For the unit box \(B = \{ x \mid 0 \le x_{i} \le 1 \ (i=1,2,3) \}\), the intersection \(P \cap B\) is a triangle with vertices at (0, 0, 0), (0, 1, 1), and (1, 1, 0). This triangle is not \(\hbox {L}^{\natural }_{2}\)-convex.
Remark 4.2
Here is an alternative proof of Theorem 3.4(2) that relies on (1) for an \(\hbox {L}^{\natural }\)-convex polyhedron. Let \(P = P_{1} + P_{2}\) with \(\hbox {L}^{\natural }\)-convex polyhedra \(P_{1}\) and \(P_{2}\). By (1) we have \(P_{i} = Q_{i} + C_{i}\) with a bounded \(\hbox {L}^{\natural }\)-convex polyhedron \(Q_i\) and an \(\hbox {L}^{\natural }\)-convex cone \(C_{i}\), where \(i=1,2\). Then \(P = (Q_{1} + Q_{2}) + (C_{1} + C_{2})\), where \(Q_{1} + Q_{2}\) is a bounded \(\hbox {L}^{\natural }_{2}\)-convex polyhedron and \(C_{1} + C_{2}\) is an \(\hbox {L}^{\natural }_{2}\)-convex cone.
4.5 Proof of Theorem 3.7
In this section we prove Theorem 3.7 for discrete sets S \((\subseteq {{\mathbb {Z}}}^{n})\) with particular discrete convexities such as \(\hbox {L}^{\natural }\)-convexity, \(\hbox {M}^{\natural }\)-convexity, etc. The proof relies on Theorem 3.6 for integrally convex sets. Just as in Sect. 4.4, we present a unified proof scheme by using a generic name “A-convex” to mean any of \(\hbox {L}^{\natural }\)-convex, \(\hbox {L}^{\natural }_{2}\)-convex, \(\hbox {M}^{\natural }\)-convex, M-convex, \(\hbox {M}^{\natural }_{2}\)-convex, \(\hbox {M}_{{2}}\)-convex, and multimodular.
The unified proof scheme is as follows. Let S be an A-convex set. This implies that S is an integrally convex set. By Theorem 3.6 we can decompose S as \(S = {\hat{T}} + G\), where \({\hat{T}}\) is a bounded integrally convex set and G is a conic integrally convex set. We have \(G = C \cap {{\mathbb {Z}}}^{n}\) for the characteristic cone C of the convex hull \({\overline{S}}\) of S, where \({\overline{S}}\) is an A-convex polyhedron. We assume that
By \({\hat{T}} \subseteq T \subseteq S\) in (4.40), we have \(S = {\hat{T}} + G \subseteq T + G \subseteq S + G \subseteq S\), where the last inclusion follows from \( \overline{S + G} = {\overline{S}} + {\overline{G}} = {\overline{S}} + C = {\overline{S}}\), \(S + G \subseteq \overline{S + G} \cap {{\mathbb {Z}}}^{n}\), and \({\overline{S}} \cap {{\mathbb {Z}}}^{n} = S\). Therefore, \(S = T + G\), where T is a bounded A-convex set by (4.40) and G is a conic A-convex set by (4.39).
The first assumption (4.39), which is the same as (4.37), is met by each discrete convexity in (1)–(5), as explained in the proof of Theorem 3.4 in Sect. 4.4. Recall that the inequality representations are used here.
For the second assumption (4.40), we consider \(T:= S\cap B\) for a bounded integral box B containing \({\hat{T}}\), expecting that T is endowed with A-convexity as a consequence of the assumed A-convexity of S. This construction is indeed valid for all discrete convexities in question (see [9, 12]), with the exception of \(\hbox {L}^{\natural }_{2}\)-convexity in (2) (see Remark 4.3 below).
In Case (2) of an \(\hbox {L}^{\natural }_{2}\)-convex set S, we construct T as follows. Represent S as \(S = S_{1} + S_{2}\) with two \(\hbox {L}^{\natural }\)-convex sets \(S_{1}\) and \(S_{2}\). Enumerate all members of the finite set \({\hat{T}}\) as \({\hat{T}} = \{ z^{1},z^{2},\ldots ,z^{m} \}\). Each \(z^{j} \in {\hat{T}} \subseteq S = S_{1} + S_{2}\) can be expressed as \(z^{j} = x^{j} + y^{j}\) with \(x^{j} \in S_{1}\) and \(y^{j} \in S_{2}\). Take integral boxes \(B_{1}\) and \(B_{2}\) satisfying \(\{ x^{1},x^{2},\ldots ,x^{m} \} \subseteq B_{1}\) and \(\{ y^{1},y^{2},\ldots ,y^{m} \} \subseteq B_{2}\), respectively, and define \(T_{1}:= S_{1} \cap B_{1}\), \(T_{2}:= S_{2} \cap B_{2}\), and \(T:= T_{1} + T_{2}\). Then \(T_{1}\) and \(T_{2}\) are \(\hbox {L}^{\natural }\)-convex, and hence T is \(\hbox {L}^{\natural }_{2}\)-convex. We have \({\hat{T}} \subseteq T\), since \(x^{j} \in S_{1} \cap B_{1}\) and \(y^{j} \in S_{2} \cap B_{2}\) imply that \(z^{j} = x^{j} + y^{j} \in (S_{1} \cap B_{1} ) + (S_{2} \cap B_{2}) = T_{1} + T_{2} = T\). Finally we note \(T = T_{1} + T_{2} \subseteq S_{1} + S_{2} = S\), to obtain \({\hat{T}} \subseteq T \subseteq S\).
This completes the proof of Theorem 3.7.
Remark 4.3
The intersection of an \(\hbox {L}^{\natural }_{2}\)-convex set with an integral box is not necessarily \(\hbox {L}^{\natural }_{2}\)-convex. For example, consider an \(\hbox {L}^{\natural }_{2}\)-convex set \(S = S_{1} + S_{2}\) given by two \(\hbox {L}^{\natural }\)-convex sets \(S_{1} = \{(0, 0, 0), (1, 1, 0)\}\) and \(S_{2} = \{(0, 0, 0)\), \((0, 1, 1)\}\). That is, \(S = S_{1} + S_{2} = \{(0, 0, 0), \ (0, 1, 1), \ (1, 1, 0), \ (1, 2, 1)\}\). For \(B = \{ x \mid 0 \le x_{i} \le 1 \ (i=1,2,3) \}\) we have \(S \cap B = \{(0, 0, 0), \ (0, 1, 1), \ (1, 1, 0) \}\), which is not \(\hbox {L}^{\natural }_{2}\)-convex.
Remark 4.4
Here is an alternative proof of Theorem 3.7(2) that relies on (1) for an \(\hbox {L}^{\natural }\)-convex set. Let \(S = S_{1} + S_{2}\) with \(\hbox {L}^{\natural }\)-convex sets \(S_{1}\) and \(S_{2}\). By (1) we have \(S_{i} = T_{i} + G_{i}\) with a bounded \(\hbox {L}^{\natural }\)-convex set \(T_i\) and a conic \(\hbox {L}^{\natural }\)-convex set \(G_{i}\), where \(i=1,2\). Then \(S = (T_{1} + T_{2}) + (G_{1} + G_{2})\), where \(T_{1} + T_{2}\) is a bounded \(\hbox {L}^{\natural }_{2}\)-convex set and \(G_{1} + G_{2}\) is a conic \(\hbox {L}^{\natural }_{2}\)-convex set. Note that \(\overline{G_{1} + G_{2}} = \overline{G_{1}} + \overline{G_{2}}\) is a cone.
5 Conclusion
Our proofs given in Sects. 4.1–4.3 are long and primitive based on the very definition of integral convexity. On the other hand, it is known (Chervet–Grappe–Robert [1]) that a polyhedral cone is box-integer if and only if it is box-TDI. It is left for future investigation to find shorter or more transparent proofs, possibly making use of this equivalence.
Data availability
Not applicable
Notes
For any vector x and set Y, we use abbreviation \(x + Y\) for \(\{ x \} + Y\).
References
Chervet, P., Grappe, R., Robert, L.-H.: Box-total dual integrality, box-integrality, and equimodular matrices. Mathematical Programming. Ser. A 188, 319–349 (2021)
Favati, P., Tardella, F.: Convexity in nonlinear integer programming. Ricerca Operativa 53, 3–44 (1990)
Fujishige, S.: Submodular Functions and Optimization. Annals of Discrete Mathematics 58, 2nd edn. Elsevier, Amsterdam (2005)
Iimura, T., Murota, K., Tamura, A.: Discrete fixed point theorem reconsidered. J Math Econ 41, 1030–1036 (2005)
Moriguchi, S., Murota, K.: Projection and convolution operations for integrally convex functions. Discrete Appl Math 255, 283–298 (2019)
Moriguchi, S., Murota, K.: Note on the polyhedral description of the Minkowski sum of two L-convex sets. Japan J Indust Appl Math 40, 223–263 (2023)
Moriguchi, S., Murota, K., Tamura, A., Tardella, F.: Scaling, proximity, and optimization of integrally convex functions. Math Program 175, 119–154 (2019)
Murota, K.: Discrete convex analysis. Math Program 83, 313–371 (1998)
Murota, K.: Discrete Convex Analysis. Society for Industrial and Applied Mathematics, Philadelphia (2003)
Murota, K.: Recent developments in discrete convex analysis. In: Cook, W., Lovász, L., Vygen, J. (eds.) Research Trends in Combinatorial Optimization, Chapter 11, pp. 219–260. Springer, Berlin (2009)
Murota, K.: Discrete convex analysis: A tool for economics and game theory. J Mechan Inst Design 1, 151–273 (2016)
Murota, K.: A survey of fundamental operations on discrete convex functions of various kinds. Optimiz Method Softw 36, 472–518 (2021)
Murota, K.: On basic operations related to network induction of discrete convex functions. Optimiz Methods Softw 36, 519–559 (2021)
Murota, K., Shioura, A.: Extension of M-convexity and L-convexity to polyhedral convex functions. Adv Appl Math 25, 352–427 (2000)
Murota, K., Tamura, A.: Integrality of subgradients and biconjugates of integrally convex functions. Optimiz Lett 14, 195–208 (2020)
Murota, K., Tamura, A.: Discrete Fenchel duality for a pair of integrally convex and separable convex functions. Japan J Indust Appl Math 39, 599–630 (2022)
Murota, K., Tamura, A.: Recent progress on integrally convex functions. Japan J Indust Appl Math 40, 1445–1499 (2023)
Murota, K., Tamura, A.: Shapley–Folkman-type theorem for integrally convex sets. arXiv:2305.15125 (2023)
Schrijver, A.: Theory of Linear and Integer Programming. Wiley, New York (1986)
Schrijver, A.: Combinatorial Optimization—Polyhedra and Efficiency. Springer, Heidelberg (2003)
Acknowledgements
The authors are grateful to the anonymous referees for helpful comments. This work was supported by JSPS/MEXT KAKENHI JP23K11001 and JP21H04979.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Kazuo Murota and Akihisa Tamura are on the Editorial Board of Japan Journal of Industrial and Applied Mathematics. On behalf of all authors, the corresponding author states there are no other conflicts of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Murota, K., Tamura, A. Decomposition of an integrally convex set into a Minkowski sum of bounded and conic integrally convex sets. Japan J. Indust. Appl. Math. 41, 987–1011 (2024). https://doi.org/10.1007/s13160-023-00635-1
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13160-023-00635-1