Characterization and algorithm for bivariate multi-unit assignment valuations

Abstract

A multi-unit assignment valuation is a function represented by a weighted bipartite graph. In this paper, we provide a characterization of such a function in terms of maximizer sets of perturbed functions. We then present an algorithm that checks whether a given bivariate function is a multi-unit assignment valuation, and if the answer is “yes,” computes a weighted bipartite graph representing the function.

1 Introduction

A valuation function is a function that for a given set of goods, returns the value of the set. This paper deals with multi-unit valuation functions defined on non-negative integral vectors ${{\mathbb {Z}}}^n_+$, in which a vector $x \in {{\mathbb {Z}}}^n_+$ represents a multiset of n discrete goods. We consider a class of multi-unit valuation functions that are represented by weighted bipartite graphs, which are referred to as multi-unit assignment valuation functions.

Given a complete bipartite graph $G=(V,N; V\times N)$ with a weight function $w: V\times N \rightarrow {{\mathbb {R}}}$ and a supply function $\varphi : V \rightarrow {{\mathbb {Z}}}_{++}$, a multi-unit assignment valuation function $f: T_\Phi \rightarrow {{\mathbb {R}}}$ is defined by

$$\begin{aligned} f(x)&= \max \bigg \{\sum _{(i,j)\in V \times N} w(i,j)y(i,j) \ \bigg |\ \sum _{i \in V}y(i,j) = x(j) \ (j \in N), \nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \sum _{j \in N} y(i,j) \le \varphi (i) \ (i \in V),\nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad y(i,j) \in {{\mathbb {Z}}}_+\ (i \in V, j \in N) \bigg \} \qquad (x \in T_\Phi ), \end{aligned}$$

where

$$\begin{aligned} N=\{1,2,\ldots ,n\}, \qquad \Phi = \sum _{i \in V} \varphi (i), \qquad T_\Phi = \Big \{x \in {{\mathbb {Z}}}^n_+ \ \Big |\ \sum _{j\in N} x(j) \le \Phi \Big \}. \end{aligned}$$

In the case where the domain of function f is restricted to zero–one vectors, f is nothing but an assignment valuation [16], which often appears in the literature of auction theory. In the following, we simply refer to function f as an assignment valuation when no confusion arises.

It is known that the class of assignment valuations is a proper subclass of strong-substitutes valuations (see, e.g., [13, 14, 17]). The strong-substitutes condition for a multi-unit valuation [10] is a natural generalization of the gross-substitutes condition for a single-unit valuation due to Kelso and Crawford [8] (see also Gul and Stacchetti [6, 7]), and the former condition inherits various nice properties of the latter condition. In particular, strong-substitutes condition for bidders’ valuations implies the existence of Walrasian equilibrium in the auction market with multiple units of indivisible goods. Also, strong-substitutes valuations are known to be equivalent to M$^\natural$-concave functions in discrete convex analysis [4, 15] (see also [13, 14, 17]). This fact implies that an assignment valuation also enjoys nice properties as a discrete concave function.

We are interested in a special case of assignment valuations with $N=\{1,2\}$, motivated by the “product-mix” auction used in Bank of England [9] (see also [1,2,3]). The auction in Bank of England deals with two kinds of multiple discrete goods. Each bidder of the auction expresses its demand to the goods by using a set of “weighted bid vectors;” a weighted bid vector is a pair $(b, \omega )$ of a bidding price vector $b \in {{\mathbb {R}}}^2$ and its weight $\omega \in {{\mathbb {Z}}}_{++}$. It turns out that sets of weighted bid vectors have a natural one-to-one correspondence with assignment valuations, and the demand information represented by a set of weighted bid vectors is the same as the one represented by the corresponding assignment valuation; see Remark 4.1 in Sect. 4 for more details on this relationship.

Suppose that a bidder wants to participate the product-mix auction with its own valuation function. In such a situation a bidder wants to know whether its valuation can be represented as an assignment valuation, and if it is an assignment valuation, the bidder also wants to know the representation by a weighted bipartite graph. This motivates us to consider the following Bivariate Assignment Valuation Checking Problem (BAVCP):

given a bivariate valuation function $f: T_\Phi \rightarrow {{\mathbb {R}}}$ with some positive integer $\Phi$, which is not necessarily an assignment valuation, answer whether f is an assignment valuation, and if the answer is “yes,” then find a weighted bipartite graph representing f.

Our goal in this paper is to propose an efficient algorithm for solving this problem.

To develop an algorithm for the problem (BAVCP), we first provide a characterization of assignment valuations in terms of maximizer sets. For a bivariate function $f: T_\Phi \rightarrow {{\mathbb {R}}}$ and a vector $p \in {{\mathbb {R}}}^2$, we define a set

$$\begin{aligned} D_f(p) = \{x \in T_\Phi \mid f(x) - p^\top x \ge f(y) - p^\top y\ (y \in T_\Phi ) \}, \end{aligned}$$

which is called a maximizer set (also called a demand set). As mentioned above, every assignment valuation is an M$^\natural$-concave function, for which the following characterization in terms of maximizer sets is known; definitions of M$^\natural$-concave function and M$^\natural$-convex set will be given in Sect. 2.

Theorem 1.1

(cf. [11, 12]) A bivariate function $f: T_\Phi \rightarrow {{\mathbb {R}}}_+$ is M$^\natural$-concave if and only if for every $p \in {{\mathbb {R}}}^2$ the maximizer set $D_f(p)$ is an M$^\natural$-convex set.

Since an assignment valuation is an M$^\natural$-concave function, its maximizer set is an M$^\natural$-convex set, which is (the set of integral vectors in) a hexagon. We classify M$^\natural$-convex sets into three types based on the length of six edges: positive-type, zero-type, and negative-type (see Sect. 2.2 for precise definitions), and show that an assignment valuation can be characterized by a stronger property for maximizer sets.

Theorem 1.2

A bivariate function $f: T_\Phi \rightarrow {{\mathbb {R}}}$ with $f(0,0)=0$ is an assignment valuation if and only if for every $p \in {{\mathbb {R}}}^2$ the maximizer set $D_f(p)$ is an M$^\natural$-convex set of positive-type or zero-type.

We will also show that for an assignment valuation f, the information about its representation can be obtained from maximizer sets of f that are M$^\natural$-convex sets of positive-type. Based on the results, we propose an algorithm for the problem (BAVCP) that runs in $\textrm{O}(\Phi ^2)$ time, under the assumption that the value oracle for f is available; given a vector x, the value oracle returns the value f(x).

Finally, we note that a closely related problem is discussed by Goldberg, Lock, and Marmolejo-Cossío [5]. In our terminology, their problem is described as follows: the input is an n-variate multi-unit assignment valuation $f: T_\Phi \rightarrow {{\mathbb {R}}}$, represented by a demand oracle, and the output is a weighted bipartite graph representing f; given a vector $p \in {{\mathbb {R}}}^n$, the demand oracle returns a vector in the maximizer set $D_f(p)$. The algorithm proposed in [5] runs in $\textrm{O}(n |V| \log W)$ time with $W = \max \{w(i,j) \mid i \in V,\ j \in N\}$. It is known (see, e.g., [13]) that a demand oracle can be realized by using a value oracle in $\textrm{O}(n^3 \log (\Phi /n))$ time. Hence, if the value oracle is available, then the algorithm in [5] runs in $\textrm{O}(n^4 |V| \log W\log (\Phi /n))$ time. In particular, if $n = 2$ (i.e., f is a bivariate function), then the algorithm runs in $\textrm{O}(|V| \log W\log {\Phi })$ time, which is incomparable to the running time $\textrm{O}(\Phi ^2)$ of our algorithm since $|V| \le \Phi$ and the parameter W does not appear in ours. Also, it should be noted that our algorithm checks whether a given function is an assignment valuation or not, while the algorithm in [5] does not.

2 Preliminaries

In this paper, we denote by ${{\mathbb {Z}}}_+$ (resp., ${{\mathbb {Z}}}_{++}$) the set of non-negative (resp., positive) integers.

2.1 Multi-unit assignment valuation and M$^\natural$-concave function

A bivariate assignment valuation $f: T_\Phi \rightarrow {{\mathbb {R}}}$ is defined as follows by using a complete bipartite graph $G=(V,\{1,2\}; V\times \{1,2\})$ with weight function $w: V\times \{1,2\} \rightarrow {{\mathbb {R}}}$ and supply function $\varphi : V \rightarrow {{\mathbb {Z}}}_{++}$:

$$\begin{aligned}f(x) = \max \bigg \{\sum _{i\in V}(w(i,1)y(i,1)+w(i,2)y(i,2)) \ \bigg |\ & \sum _{i \in V}y(i,j) = x(j) \ (j =1,2), \nonumber \\& y(i,1)+y(i,2) \le \varphi (i) \ (i \in V),\ \nonumber \\& y(i,j) \in {{\mathbb {Z}}}_+\ (i \in V,\ j=1,2) \bigg \} \quad (x \in T_\Phi ), \end{aligned}$$

(2.1)

where

$$\begin{aligned} \Phi = \sum _{i \in V}\varphi (i), \qquad T_\Phi = \{x \in {{\mathbb {Z}}}_+^2 \ \mid x(1)+x(2) \le \Phi \}. \end{aligned}$$

We may assume, without loss of generality, that

$$\begin{aligned} \forall i, i' \in V \hbox { with } i \ne i',\ w(i,1)\ne w(i',1) \hbox { or } w(i,2) \ne w(i',2) \hbox { (or both)}; \end{aligned}$$

(2.2)

if there exist distinct $i, i' \in V$ with $w(i,1)= w(i',1)$ and $w(i,2) = w(i',2)$, then we can replace $\varphi (i)$ with $\varphi (i)+\varphi (i')$ and delete the vertex $i'$, which results in the same assignment valuation.

It is known that a (not necessarily bivariate) assignment valuation has a nice discrete structure called M$^\natural$-concavity (see, e,g., [13]).

Proposition 2.1

A (bivariate) assignment valuation is an M$^\natural$-concave function.

A bivariate function $f: T_\Phi \rightarrow {{\mathbb {R}}}$ is said to be M$^\natural$ -concave if it satisfies the following exchange property for every $x, y \in T_\Phi$:

(M$^\natural$ -EXC) for each $i \in N=\{1,2\}$ with $x(i)>y(i)$, we have either (i), (ii), or both:

(i) $y(N) < \Phi$ and $f(x)+f(y) \le f(x - \chi _i)+ f(y + \chi _i)$,

(ii) there exists some $i' \in N$ with $x(i')<y(i')$ such that

$$\begin{aligned} f(x)+f(y) \le f(x - \chi _i+ \chi _{i'})+ f(y + \chi _i- \chi _{i'}), \end{aligned}$$

where $\chi _i \in \{0,1\}^2$ denotes the characteristic vector of $i \in \{1,2\}$, i.e., $\chi _1 = (1,0)$ and $\chi _2 = (0,1)$. Note that $x - \chi _i, y + \chi _i \in T_\Phi$ holds in the case of (i), and $x - \chi _i+ \chi _{i'},\ y + \chi _i- \chi _{i'} \in T_\Phi$ holds in the case of (ii).

M$^\natural$-concave functions can be characterized by a local exchange property: f is M$^\natural$-concave if and only if (M$^\natural$-EXC) holds for every $x, y \in T_\Phi$ with $\Vert x-y\Vert _1 \le 4$. This local exchange property can be specialized for bivariate functions f as follows:

$$\begin{aligned}&f(k,h)+f(k+1,h+1) \le f(k+1,h)+f(k,h+1) \quad ((k, h) \in {{\mathbb {Z}}}^2_+,\ k+h +2 \le \Phi ), \end{aligned}$$

(2.3)

$$\begin{aligned}&f(k,h+1)+f(k+2,h) \le f(k+1,h+1)+f(k+1,h) \quad ((k, h) \in {{\mathbb {Z}}}^2_+,\ k+h+2 \le \Phi ), \end{aligned}$$

(2.4)

$$\begin{aligned}&f(k+1,h)+f(k,h+2) \le f(k+1,h+1)+f(k,h+1) \quad ((k, h) \in {{\mathbb {Z}}}^2_+,\ k+h+2 \le \Phi ). \end{aligned}$$

(2.5)

Proposition 2.2

A bivariate function $f: T_\Phi \rightarrow {{\mathbb {R}}}$ is M$^\natural$-concave if and only if it satisfies the conditions (2.3), (2.4), and (2.5).

The conditions (2.3), (2.4), and (2.5) can be understood in terms of “triangles.” For $k, h \in {{\mathbb {Z}}}$, we define an upper-right triangle $T_{\textrm{ur}}(k, h) \subseteq {{\mathbb {Z}}}^2$ and a lower-left triangle $T_{\textrm{ll}}(k, h) \subseteq {{\mathbb {Z}}}^2$ by

$$\begin{aligned} T_{\textrm{ur}}(k, h)&= \{(k, h), (k-1, h), (k, h-1)\},\\ T_{\textrm{ll}}(k, h)&= \{(k, h), (k+1, h), (k, h+1)\}. \end{aligned}$$

The condition (2.3) means that the function f bends upward on $T_{\textrm{ur}}(k+1, h+1) \cup T_{\textrm{ll}}(k, h)$. Similarly, (2.4) (resp., (2.5)) means that that f bends upward on $T_{\textrm{ur}}(k+1, h+1) \cup T_{\textrm{ll}}(k+1, h)$ (resp. $T_{\textrm{ur}}(k+1, h+1) \cup T_{\textrm{ll}}(k, h+1)$).

2.2 M$^\natural$-convex set and its properties

We also define M$^\natural$-convexity for a set $S \subseteq {{\mathbb {Z}}}^2$ as follows. For a non-empty set $S \subseteq {{\mathbb {Z}}}^2$, we say that S is an M$^\natural$ -convex set if it satisfies the following exchange property for every $x, y \in S$:

for each $i \in N=\{1,2\}$ with $x(i)>y(i)$, at least one of (i) and (ii) holds:

(i) $x - \chi _i, y + \chi _i \in S$,

(ii) $x - \chi _i+ \chi _{i'},\ y + \chi _i- \chi _{i'} \in S$ for some $i' \in N$ with $x(i')<y(i')$.

We present some properties on polyhedral structure of M$^\natural$-convex sets in ${{\mathbb {Z}}}^2$. M$^\natural$-convex sets can be described by simple inequalities.

Proposition 2.3

A bounded set $S \subseteq {{\mathbb {Z}}}^2$ is an M$^\natural$-convex set if and only if it can be represented by the following system of inequalities:

$$\begin{aligned} S=\{(x(1),x(2)) \in {{\mathbb {Z}}}^2 \mid \lambda _1 \le x(1) \le \mu _1,\ \lambda _2 \le x(2) \le \mu _2,\ \lambda _{0} \le x(1)+x(2) \le \mu _{0} \}.\end{aligned}$$

(2.6)

We may assume that all inequalities in (2.6) are tight, i.e., it holds that

$$\begin{aligned}&\lambda _i = \min \{x(i) \mid x\in S\}, \quad \mu _i = \max \{x(i) \mid x\in S\} \quad (i=1,2),\\&\lambda _0 = \min \{x(1)+x(2) \mid x\in S\}, \quad \mu _0 = \max \{x(1)+x(2) \mid x\in S\}. \end{aligned}$$

We see from the representation (2.6) that every bounded two-dimensional (2-d, for short) M$^\natural$-convex set S can be represented as a union of upper-right triangles $T_\textrm{ur}(k, h)$ and lower-left triangles $T_{\textrm{ll}}(k, h)$.

Let $S \subseteq {{\mathbb {Z}}}^2$ be a bounded 2-d M$^\natural$-convex set. We denote by ${\overline{S}} \subseteq {{\mathbb {R}}}^2$ the convex hull of S. Proposition 2.3 implies that the convex hull ${\overline{S}}$ is represented by the same set of inequalities in (2.6) and satisfies ${\overline{S}}\cap {{\mathbb {Z}}}^2 = S$. In addition, ${\overline{S}}$ is a convex hull of the six integral vertices given (in clockwise order) as

$$\begin{aligned} (\lambda _1, \mu _2),\ (\mu _0-\mu _2, \mu _2), \ (\mu _1, \mu _0-\mu _1),\ (\mu _1, \lambda _2), \ (\lambda _0 - \lambda _2, \lambda _2),\ (\lambda _1, \lambda _0 - \lambda _1); \end{aligned}$$

(2.7)

this shows that ${\overline{S}}$ is a hexagon in general, while some vertices may coincide and some edges may have zero length in a degenerate case.

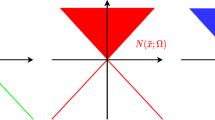
This observation shows that an M$^\natural$-convex set S can be identified with its convex hull ${\overline{S}}$. Hence, we can define an edge of S as the set of integral vectors in an edge of ${\overline{S}}$. Since the convex hull ${\overline{S}}$ is a hexagon with six edges in general, we can define upper-horizontal (UH) edge, lower-horizontal (LH) edge, left-vertical (LV) edge, right-vertical (RV) edge, upper-right-diagonal (URD) edge, and lower-left-diagonal (LLD) edge (see Fig. 1).

Fig. 1

Six edges of an M$^\natural$-convex set

We also define the length of an edge in an M$^\natural$-convex set S by the length of the corresponding edge in the convex hull ${\overline{S}}$. We denote by

$$\begin{aligned} \ell _{\textrm{UH}}(S), \quad \ell _{\textrm{LH}}(S), \quad \ell _{\textrm{LV}}(S), \quad \ell _{\textrm{RV}}(S), \quad \ell _{\textrm{URD}}(S), \quad \ell _{\textrm{LLD}}(S) \end{aligned}$$

the length of UH-edge, LH-edge, LV-edge, RV-edge, URD-edge, and LLD-edge; it is possible that some edges may have length zero.

By using six vertices in (2.7), the length of six edges are given as

$$\begin{aligned} \left. \begin{array}{ll} \ell _{\textrm{UH}}(S) &{}= (\mu _0-\mu _2)-\lambda _1, \\ \ell _{\textrm{LH}}(S) &{}= \mu _1 - (\lambda _0 - \lambda _2),\\ \ell _{\textrm{LV}}(S) &{}= \mu _2 - (\lambda _0 - \lambda _1), \\ \ell _{\textrm{RV}}(S) &{}= (\mu _0-\mu _1)-\lambda _2, \\ \ell _{\textrm{URD}}(S) &{}= \sqrt{2}(\mu _1 - (\mu _0-\mu _2)) = \sqrt{2}(\mu _2 - (\mu _0-\mu _1)), \\ \ell _{\textrm{LLD}}(S) &{}= \sqrt{2}((\lambda _0-\lambda _2)-\lambda _1) = \sqrt{2}((\lambda _0-\lambda _1)- \lambda _2). \end{array} \right\} \end{aligned}$$

(2.8)

This immediately implies the following relations for the six edge lengths.

Proposition 2.4

For a two-dimensional M$^\natural$-convex set $D \subseteq {{\mathbb {Z}}}^2$, it holds that

$$\begin{aligned} \ell _{\textrm{LH}}(D) - \ell _{\textrm{UH}}(D) = \ell _{\textrm{LV}}(D) -\ell _{\textrm{RV}}(D) = \frac{1}{\sqrt{2}}(\ell _{\textrm{URD}}(D) - \ell _{\textrm{LLD}}(D)). \end{aligned}$$

Using the edge length, we classify bounded 2-d M$^\natural$-convex sets. We say that a bounded M$^\natural$-convex set $D \subseteq {{\mathbb {Z}}}^2$ is positive-type (resp., negative-type) if $\ell _{\textrm{LH}}(D) - \ell _{\textrm{UH}}(D) > 0$ (resp. $\ell _{\textrm{LH}}(D) - \ell _{\textrm{UH}}(D) < 0$), and zero-type otherwise (i.e., D is not two-dimensional or satisfies $\ell _{\textrm{LH}}(D) - \ell _{\textrm{UH}}(D) = 0$). See Figs. 2, 3, and 4 for examples.

Fig. 2

M$^\natural$-convex sets of positive-type

Fig. 3

M$^\natural$-convex sets of zero-type

Fig. 4

M$^\natural$-convex sets of negative-type

2.3 Properties of M$^\natural$-concave functions

We present some properties of M$^\natural$-concave functions used in this paper. See [13] for more accounts on M$^\natural$-concave functions.

For a bivariate function $f: T_\Phi \rightarrow {{\mathbb {R}}}$ and a vector $p \in {{\mathbb {R}}}^2$, the maximizer set $D_f(p) \subseteq T_\Phi$ is defined as

$$\begin{aligned} D_f(p) = \{x \in T_\Phi \mid f(x) - p^\top x \ge f(y) - p^\top y\ (y \in T_\Phi ) \}; \end{aligned}$$

$D_f(p)$ is often referred to as a demand set in the context of auction, where f is regarded as a valuation for multisets of goods. If $D \subseteq T_\Phi$ is a two-dimensional maximizer set, then there exists a unique $p \in {{\mathbb {R}}}^2$ such that $D = D_f(p)$; we call such p the slope vector of D.

M$^\natural$-concavity of a function can be characterized in terms of maximizer sets.

Proposition 2.5

A bivariate function $f: T_\Phi \rightarrow {{\mathbb {R}}}$ is M$^\natural$-concave if and only if $D_f(p)$ is an M$^\natural$-convex set for every $p \in {{\mathbb {R}}}^2$.

An M$^\natural$-concave function can be extended to a polyhedral concave function. For a function $f: T_\Phi \rightarrow {{\mathbb {R}}}$, the concave closure ${\bar{f}}: {\overline{T_\Phi }} \rightarrow {{\mathbb {R}}}$ is defined as

$$\begin{aligned} {\bar{f}}(y) = \inf \{ p^\top y+ \eta \mid p \in {{\mathbb {R}}}^2,\ \eta \in {{\mathbb {R}}},\ p^\top x+ \eta \ge f(x)\ (x \in T_\Phi ) \} \qquad (y \in {\overline{T_\Phi }}). \end{aligned}$$

By definition, ${\bar{f}}$ is a polyhedral concave function satisfying ${\bar{f}}(x) \ge f(x)$ for all $x \in T_\Phi$.

Proposition 2.6

For a function $f: T_\Phi \rightarrow {{\mathbb {R}}}$, if f is M$^\natural$-concave, then ${\bar{f}}(x) = f(x)$ holds for every $x \in T_\Phi$.

Let $f: T_\Phi \rightarrow {{\mathbb {R}}}$ be a bivariate M$^\natural$-concave function. It follows from Proposition 2.6 that for every $p \in {{\mathbb {R}}}^2$, the convex hull $\overline{D_f(p)}$ of the maximizer set of f coincides with a maximizer set

$$\begin{aligned} \{x \in {\overline{T_\Phi }} \mid {\bar{f}}(x) - p^\top x \ge {\bar{f}}(y) - p^\top y\ (y \in {\overline{T_\Phi }}) \} \end{aligned}$$

of the concave closure ${\bar{f}}$. It is also known that a polyhedral subdivision of the polytope ${\overline{T_\Phi }}$ can be obtained from the family $\{\overline{D_f(p)} \mid p \in {{\mathbb {R}}}^2\}$ of convex hulls of maximizer sets. These facts imply that the information about the set of 2-d maximizer sets uniquely determines the function values of f. For two 2-d maximizer sets D and $D'$ of f, we say that D and $D'$ are adjacent if they share an edge of positive length.

Proposition 2.7

Let $f: T_\Phi \rightarrow {{\mathbb {R}}}$ be a bivariate M$^\natural$-concave function with $f(0,0)=0$. Then, the function values f(x) $(x \in T_\Phi )$ are uniquely determined by the following information:

• the family $\mathcal{D}=\{D_i \mid i \in V\}$ of two-dimensional maximizer sets of f, where V is an appropriately chosen index set.

• the adjacency relation among maximizer sets in $\mathcal{D}$,

• the slope vector $p_i \in {{\mathbb {R}}}^2$ of $D_i$ for $i \in V$,

• lengths $\ell _{\textrm{LH}}(D_i),\, \ell _{\textrm{UH}}(D_i),\, \ell _{\textrm{LV}}(D_i),\, \ell _{\textrm{RV}}(D_i),\, \ell _{\textrm{URD}}(D_i),\, \ell _{\textrm{LLD}}(D_i)$ of six edges for $i \in V$.

3 Characterization of multi-unit assignment valuations and algorithm

Main results of this paper are presented in this section. We first provide a characterization of bivariate assignment valuations by using the following condition for maximizer sets:

(MS $\ge$) every maximizer set of f is an M$^\natural$-convex set of positive-type or zero-type;

recall that every maximizer set of an M$^\natural$-concave function f is an M$^\natural$-convex set. In the following, we may simply say that a maximizer set of a bivariate M$^\natural$-concave function is of positive-type (resp. zero-type) if it is an M$^\natural$-convex set of positive-type (resp., zero-type).

We denote by $\mathcal{M}$ the family of bivariate M$^\natural$-concave functions $f: T_\Phi \rightarrow {{\mathbb {R}}}$ with $f(0,0)=0$ satisfying the condition (MS$\ge$). We denote by $\mathcal{A}$ the family of bivariate assignment valuations defined on $T_\Phi$. That is,

$$\begin{aligned} \mathcal{M}&= \{f: T_\Phi \rightarrow {{\mathbb {R}}}\mid f(0,0)=0,\ f\hbox { is an } \hbox {M}^\natural \hbox { -concave function satisfying (MS}\ge ) \}, \\ \mathcal{A}&= \{f: T_\Phi \rightarrow {{\mathbb {R}}}\mid f\hbox { is an assignment valuation in }(2.1) \}. \end{aligned}$$

We show that every bivariate assignment valuation satisfies the condition (MS$\ge$), i.e., $\mathcal{A}\subseteq \mathcal{M}$ holds.

Theorem 3.1

(necessary condition) Let $f: T_\Phi \rightarrow {{\mathbb {R}}}$ be an assignment valuation in (2.1), and assume that weight function w satisfies the condition (2.2). For every vector $p \in {{\mathbb {R}}}^2$, the maximizer set $D_f(p)$ is an M$^\natural$-convex set of positive-type or zero-type.

Theorem  3.1 follows immediately from the following properties of assignment valuations. It should be noted that the condition (2.2) for the weight function w implies that if a vector $p \in {{\mathbb {R}}}^2$ satisfies $p = (w(i,1),w(i,2))$ for some $i \in V$, then such i is uniquely determined.

Lemma 3.2

Let $f: T_\Phi \rightarrow {{\mathbb {R}}}$ be an assignment valuation in (2.1), and assume that weight function w satisfies the condition (2.2). Also, let $p \in {{\mathbb {R}}}^2$ be a vector such that the maximizer set $D_f(p)$ is two-dimensional.

• (i) If $p \ne (w(i,1),w(i,2))$ for all $i \in V$, then $D_f(p)$ is of zero-type.

• (ii) If $p = (w(i,1),w(i,2))$ holds for some $i \in V$, then $D_f(p)$ is of positive-type and satisfies $\ell _{\textrm{LH}}(D_f(p)) - \ell _{\textrm{UH}}(D_f(p)) = \varphi (i_p)$ with the (unique) vertex $i_p \in V$ such that $p = (w(i_p,1),w(i_p,2))$.

Proof of Lemma 3.2 is given in Sect. 4.

We then show that the inclusion $\mathcal{A}\subseteq \mathcal{M}$ holds with equality. For $f \in \mathcal{M}$, denote by $\mathcal{D}^+(f)$ the family of positive-type maximizer sets of f, and by $P^+(f)$ the set of slope vectors for maximizer sets in $\mathcal{D}^+(f)$. The definitions imply the equation $\mathcal{D}^+(f) = \{D_f(p) \mid p \in P^+(f)\}$.

Theorem 3.3

(sufficient condition) Let $f: T_\Phi \rightarrow {{\mathbb {R}}}_+$ be an M$^\natural$-concave function with ${f(0,0)=0}$ satisfying the condition (MS$\ge$). Then, f is an assignment valuation. Moreover, if $P^+(f)$ is given as $\{p_i \mid i \in V\}$ with an appropriately chosen index set V, then f is represented by the complete bipartite graph with vertex set $V \cup \{1,2\}$, weight function $w: V \times \{1,2\} \rightarrow {{\mathbb {R}}}$, and capacity function $\varphi : V \rightarrow {{\mathbb {Z}}}_{++}$ given by

$$\begin{aligned}&w(i,j) = p_i(j)\qquad (i \in V,\ j=1,2), \end{aligned}$$

(3.1)

$$\begin{aligned}&\varphi (i) = \ell _{\textrm{LH}}(D_f(p_i)) - \ell _{\textrm{UH}}(D_f(p_i))\ (>0) \qquad (i \in V). \end{aligned}$$

(3.2)

Note that the weight function w given by (3.1) satisfies the condition (2.2) since slope vectors in $P^+(f)$ are all different.

Theorem 3.3 is proved by using the following key lemma, stating that every function $f \in \mathcal{M}$ is uniquely determined by the information about positive-type maximizer sets of f.

Lemma 3.4

For functions $f,g \in \mathcal{M}$, we have $f=g$ if the following conditions hold:

$$\begin{aligned} P^+(f)=P^+(g), \qquad \ell _{\textrm{LH}}(D_f(p)) - \ell _{\textrm{UH}}(D_f(p)) = \ell _{\textrm{LH}}(D_g(p)) - \ell _{\textrm{UH}}(D_g(p)) \ (p \in P^+(f)). \end{aligned}$$

Proof of Lemma 3.4 is given in Sect. 5.

Proof of Theorem 3.3

Given a function $f \in \mathcal{M}$, let us consider the assignment valuation g represented by the weighted complete bipartite graph in the latter statement of Theorem 3.3, i.e., the assignment valuation $g: T_\Phi \rightarrow {{\mathbb {R}}}$ is obtained from the complete bipartite graph with vertex set $V \cup \{1,2\}$, weight function $w: V \times \{1,2\} \rightarrow {{\mathbb {R}}}$ in (3.1), and capacity function $\varphi : V \rightarrow {{\mathbb {Z}}}_{++}$ in (3.2). By Lemma 3.2 applied to g and the definition of g and w, we have $P^+(g) = \{p_i \mid i \in V\} = P^+(f)$. It follows from Lemma 3.2 (ii) that

$$\begin{aligned} \ell _{\textrm{LH}}(D_g(p_i)) - \ell _{\textrm{UH}}(D_g(p_i)) = \varphi (i) = \ell _{\textrm{LH}}(D_f(p_i)) - \ell _{\textrm{UH}}(D_f(p_i)) \qquad (i \in V). \end{aligned}$$

Hence, we have $f=g$ by Lemma 3.4. $\square$

The following characterization of bivariate assignment valuations can be obtained immediately from Theorems 3.1 and 3.3.

Corollary 3.5

An M$^\natural$-concave function $f: T_\Phi \rightarrow {{\mathbb {R}}}$ with ${f(0,0)=0}$ is an assignment valuation if and only if it satisfies the condition (MS$\ge$).

Based on the characterization of assignment valuations (Theorem 3.3, in particular), we propose an algorithm that determines whether a given function $f: T_\Phi \rightarrow {{\mathbb {R}}}$ is an assignment valuation or not, and if the answer is “yes,” computes its representation.

Algorithm for Checking Assignment Valuation

• Step 1: [Check M$^\natural$-concavity] Check whether f satisfies $f(0,0)=0$ and the conditions (2.3), (2.4), and (2.5). If f satisfies these conditions, then go to Step 2; otherwise, assert that f is not an assignment valuation.

• Step 2: [Check assignment valuation] For each 2-d maximizer set D of f, compute the length of edges $\ell _{\textrm{LH}}(D)$ and $\ell _{\textrm{UH}}(D)$. If there exists some D with $\ell _{\textrm{LH}}(D) < \ell _{\textrm{UH}}(D)$, (i.e., D is of negative-type), then assert that f is not an assignment valuation; otherwise, go to Step 3.

• Step 3: [Compute a weighted bipartite graph] Let $\{p_i \mid i \in V\}$ be the set of slope vectors for positive-type maximizer sets of f with an appropriately chosen index set V. Output the complete bipartite graph with vertex sets $V \cup \{1,2\}$, weight function $w: V \times \{1,2\}\rightarrow {{\mathbb {R}}}$ given by (3.1), and capacity function $u: V \rightarrow {{\mathbb {Z}}}_{++}$ given by (3.2).

We analyze the running time of the algorithm. Checking the conditions (2.3), (2.4), and (2.5) in Step 1 can be done in $\textrm{O}(\Phi ^2)$ time by using the value oracle for f. For a bivariate M$^\natural$-concave function f, all 2-d maximizer sets and their slope vectors can be computed in $\textrm{O}(\Phi ^2)$ time, as explained below. Once we obtain all 2-d maximizer sets, it is not difficult to compute their edge lengths in $\textrm{O}(\Phi ^2)$ time. Hence, Step 2 requires $\textrm{O}(\Phi ^2)$ time. It is easy to see that Step 3 can be done in $\textrm{O}(V) = \textrm{O}(\Phi ^2)$ time. Therefore, our algorithm runs in $\textrm{O}(\Phi ^2)$ time in total.

Theorem 3.6

Given a bivariate function $f: T_\Phi \rightarrow {{\mathbb {R}}}$, we can determine whether f is an assignment valuation or not in $\textrm{O}(\Phi ^2)$ time. Moreover, if f is an assignment valuation, we can compute the complete bipartite graph with vertex sets $V \cup \{1,2\}$, weight function $w: V \times \{1,2\} \rightarrow {{\mathbb {R}}}$, and capacity function $u: V \rightarrow {{\mathbb {Z}}}_{++}$ representing f in $\textrm{O}(\Phi ^2)$ time.

We explain how to compute in $\textrm{O}(\Phi ^2)$ time all 2-d maximizer sets and their slope vectors of a bivariate M$^\natural$-concave function f, where we use the fact that every 2-d M$^\natural$-convex set is given as the union of triangles ${T}_{\textrm{ur}}(k, h)$ and ${T}_{\textrm{ll}}(k, h)$.

Algorithm for Computing All 2-d Maximizer Sets

• Step 1: Let $\mathcal{T}$ be the set of triangles contained in $T_\Phi$, i.e.,

  $$\begin{aligned} \mathcal{T}:= &\{T_{\textrm{ur}}(k, h) \mid k \ge 1,\ h \ge 1,\ k+h \le \Phi \}\\ & \cup \{T_{\textrm{ll}}(k, h) \mid k \ge 0,\ h \ge 0,\ k+h \le \Phi -1\}. \end{aligned}$$

  For each $T \in \mathcal{T}$, set its slope vector $p_T \in {{\mathbb {R}}}^2$ by

  $$\begin{aligned} p_T = {\left\{ \begin{array}{ll} (f(k,h)-f(k-1,h),\, f(k,h)-f(k,h-1)) &{} \mbox {if } T=T_{\textrm{ur}}(k, h),\\ (f(k+1,h)-f(k,h),\, f(k,h+1)-f(k,h)) &{} \mbox {if } T=T_{\textrm{ll}}(k, h). \end{array}\right. } \end{aligned}$$

• Step 2: If there exists no distinct $T, T' \in \mathcal{T}$ with $p_T = p_{T'}$, then stop. Otherwise, go to Step 3.

• Step 3: Select any distinct $T, T' \in \mathcal{T}$ with $p_T = p_{T'}$, delete T and $T'$ from $\mathcal{T}$, and insert $T \cup T'$, where we set $p_{T \cup T'} = p_T$. Go to Step 3.

Step 1 can be done in $\textrm{O}(\Phi ^2)$ time. Since a bivariate M$^\natural$-concave function can be extended to a polyhedral concave function, any two triangles contained in $T_\Phi$ with the same slope vectors are adjacent. By using this fact, Steps 2 and 3 can be also done in $\textrm{O}(\Phi ^2)$ time.

4 Proof of Lemma 3.2

We give a proof of Lemma 3.2. Let $f: T_\Phi \rightarrow {{\mathbb {R}}}$ be an assignment valuation in (2.1), and assume that weight function w satisfies the condition (2.2). Also, let $p \in {{\mathbb {R}}}^2$ be a vector such that the maximizer set $D_f(p)$ is two-dimensional.

By the formula (2.1) for f, the value

$$\begin{aligned} \max \{f(k,h) - p(1)k- p(2)h \mid (k,h) \in T_\Phi \} \end{aligned}$$

is equal to the optimal value of the following optimization problem:

$$\begin{aligned} \begin{array}{lll} \hbox {(P)} &{} \hbox {Maximize } &{} \displaystyle \sum _{i\in V} (w(i,1)- p(1))y(i,1) + \sum _{i\in V} (w(i,2)- p(2))y(i,2) \\ &{} \hbox {subject to } &{} y(i,1)+y(i,2) \le \varphi (i) \ (i \in V),\\ &{} &{} y(i,j) \in {{\mathbb {Z}}}_+\ (i \in V,\ j =1,2), \end{array} \end{aligned}$$

and the set $D_f(p)$ is represented by using optimal solutions of (P) as follows:

$$\begin{aligned} D_f(p) = \bigg \{x \in {{\mathbb {Z}}}^2_+ \ \bigg | \ x(j) = \sum _{(i,j)\in V} y(i,j) \ (j=1,2),\ y\hbox { is an optimal solution of (P)} \bigg \}. \end{aligned}$$

(4.1)

The problem (P) can be decomposed into |V| independent problems (P$_i$) $(i \in V)$ given as

$$\begin{aligned} \begin{array}{lll} \hbox {(P}_i) &{} \hbox {Maximize } &{} \displaystyle w^p(i,1) y(i,1) + w^p(i,2) y(i,2) \\ &{} \hbox {subject to } &{} y(i,1)+y(i,2) \le \varphi (i),\ y(i,j) \in {{\mathbb {Z}}}_+\ (j =1,2) \end{array} \end{aligned}$$

with $w^p(i,j) = w(i,j)- p(j) \ (j=1,2)$. Denote by $Y_i^* \subseteq {{\mathbb {Z}}}^2_+$ the set of optimal solutions of (P$_i$), which is given as

$$\begin{aligned} Y_i^* = \left\{ x \in {{\mathbb {Z}}}^2_+ \ \left| \ \begin{array}{ll} x(1) + x(2) \le \varphi (i),\\ x(1) + x(2) = \varphi (i) \quad \hbox {if } 0< \max (w^p(i,1), w^p(i,2)),\\ x(1) = 0 \quad \hbox {if } w^p(i,1)< \max (0, w^p(i,2)),\\ x(2) = 0 \quad \hbox {if } w^p(i,2) < \max (0, w^p(i,1)) \end{array} \right. \right\} . \end{aligned}$$

(4.2)

That is, $Y_i^*$ is the set of vectors $x \in {{\mathbb {Z}}}_+^2$ satisfying

$$\begin{aligned} \begin{array}{ll} x(1) = \varphi (i), \quad x(2)=0 \quad &{} \hbox {if }i \in V_{+1} \equiv \{i' \in V \mid w^p(i',1)> \max (0, w^p(i',2))\},\\ x(1) =0,\quad x(2) = \varphi (i) &{} \hbox {if }i \in V_{+2}\equiv \{i' \in V \mid w^p(i',2)> \max (0, w^p(i',1))\},\\ x(1)+x(2) = \varphi (i) &{} \hbox {if }i \in V_{+=}\equiv \{i' \in V \mid w^p(i',1) =w^p(i',2) > 0\},\\ x(1)+x(2) \le \varphi (i) &{} \hbox {if }i \in V_{00} \equiv \{i' \in V \mid w^p(i',1) = w^p(i',2) = 0\},\\ x(1) = 0,\quad x(2) \le \varphi (i) &{} \hbox {if }i \in V_{-0} \equiv \{i' \in V \mid w^p(i',1)<0,\ w^p(i',2) = 0\},\\ x(1) \le \varphi (i),\quad x(2) = 0 &{} \hbox {if }i \in V_{0-}\equiv \{i' \in V \mid w^p(i',1) =0,\ w^p(i',2)< 0\},\\ x(1) = x(2) = 0 &{} \hbox {if }i \in V_{--}\equiv \{i' \in V \mid w^p(i',1)<0,\ w^p(i',2) < 0\}. \end{array} \end{aligned}$$

We see that y is an optimal solutions of (P) if and only if $(y(i,1), y(i,2)) \in Y_i^*$ holds for every $i \in V$. This relation and (4.1) imply that the set $D_f(p)$ is given as the Minkowski sum of $Y^*_i$ as follows:

$$\begin{aligned} D_f(p)&= \bigg \{x \in {{\mathbb {Z}}}^2_+ \ \bigg | \ x(j) = \sum _{(i,j)\in V} y(i,j) \ (j=1,2),\ (y(i,1), y(i,2)) \in Y_i^*\ (i \in V) \bigg \} =\bigoplus _{i \in V}Y^*_i \nonumber \\&= \{(x(1),x(2)) \in {{\mathbb {Z}}}^2 \mid \lambda _1 \le x(1) \le \mu _1,\ \lambda _2 \le x(2) \le \mu _2,\ \lambda _{0} \le x(1)+x(2) \le \mu _{0} \} \end{aligned}$$

(4.3)

with

$$\begin{aligned}&\lambda _1 = \varphi (V_{+1}), \qquad \mu _1 = \varphi (V_{+1} \cup V_{+=}\cup V_{00} \cup V_{0-}), \\&\lambda _2 = \varphi (V_{+2}), \qquad \mu _2 = \varphi (V_{+2} \cup V_{+=}\cup V_{00} \cup V_{-0}), \\&\lambda _0 = \varphi (V_{+1} \cup V_{+2}\cup V_{+=}), \qquad \mu _0 = \varphi (V \setminus V_{--}). \end{aligned}$$

Here, we denote $\varphi (V') = \sum _{i \in V'}\varphi (i)$ for $V' \subseteq V$.

It follows from (2.8) that

$$\begin{aligned}&\ell _{\textrm{LH}}(D_f(p)) - \ell _{\textrm{UH}}(D_f(p)) \nonumber \\&= \mu _1 + \mu _2 - \mu _0 +\lambda _1 +\lambda _2 - \lambda _0 \nonumber \\&= \varphi (V_{+1} \cup V_{+=}\cup V_{00} \cup V_{0-}) + \varphi (V_{+2} \cup V_{+=}\cup V_{00} \cup V_{-0}) - \varphi (V \setminus V_{--}) \nonumber \\&\quad + \varphi (V_{+1})+ \varphi (V_{+2}) - \varphi (V_{+1} \cup V_{+2}\cup V_{+=}) \nonumber \\&= \varphi (V_{+=}\cup V_{00}) - \varphi (V_{+=}) = \varphi (V_{00}). \end{aligned}$$

(4.4)

Suppose that $p \ne (w(i,1),w(i,2))$ for all $i \in V$. Then, we have $V_{00} = \emptyset$, which, together with (4.4), implies $\ell _{\textrm{LH}}(D_f(p)) - \ell _{\textrm{UH}}(D_f(p)) = 0$, i.e., $D_f(p)$ is of zero-type.

We then suppose that $p = (w(i,1),w(i,2))$ holds for some $i \in V$. Then, such $i = i_p \in V$ is uniquely determined by the condition (2.2) for the weight function w. Hence, we have $V_{00} =\{i_p\}$, which, together with (4.4), implies $\ell _{\textrm{LH}}(D_f(p)) - \ell _{\textrm{UH}}(D_f(p)) = \varphi (i_p) > 0$, i.e., $D_f(p)$ is of positive-type. This concludes the proof of Lemma 3.2.

Remark 4.1

As mentioned in Introduction, the demand information of a bidder in the product-mix auction in Bank of England is represented by a set of weighted bid vectors [9]. We observe below that sets of weighted bid vectors and assignment valuations can represent the same sets of bidders’ demand information. Moreover, we show that sets of weighted bid vectors and assignment valuations have a natural one-to-one correspondence.

A weighted bid vector is a pair $(b, \omega )$ of a bid $b \in {{\mathbb {R}}}^2$ and its weight $\omega \in {{\mathbb {Z}}}_{++}$. With a weighted bid vector $(b, \omega )$, a demand set $D(p;b,\omega )$ is defined as

$$\begin{aligned} D(p;b,\omega ) = \left\{ x \in {{\mathbb {Z}}}^2_+ \ \left| \ \begin{array}{ll} x(1) + x(2) \le \omega ,\\ x(1) + y(2) = \omega \quad \hbox {if } 0< \max (b(1)-p(1), b(2)-p(2)),\\ x(1) = 0 \quad \hbox {if } b(1)-p(1)< \max (0, b(2)-p(2)),\\ x(2) = 0 \quad \hbox {if } b(2)-p(2) < \max (0, b(1)-p(1)) \end{array} \right. \right\} . \end{aligned}$$

(4.5)

Using a set of weighted bid vectors $\mathcal{B}= \{(b_i, \omega (i)) \mid i \in V\}$ with an appropriately chosen index set V, we represent a demand set $D^{\mathcal{B}}(p)$ given as the Minkowski sum of $D(p;b_i, \omega (i))$:

$$\begin{aligned} D^{\mathcal{B}}(p)= \bigoplus _{i \in V} D(p;b_i, \omega (i)). \end{aligned}$$

(4.6)

We see from (4.2), (4.3), (4.5), and (4.6) that sets of weighted bid vectors can represent the same sets of bidders’ demand information as assignment valuations. Indeed, for a set of weighted bid vectors $\mathcal{B}= \{(b_i, \omega (i)) \mid i \in V\}$, define a complete bipartite graph $G=(V,\{1,2\}; V\times \{1,2\})$ with weight function $w: V\times \{1,2\} \rightarrow {{\mathbb {R}}}$ and supply function $\varphi : V \rightarrow {{\mathbb {Z}}}_{++}$ given as

$$\begin{aligned} w(i,j)=b_i(j)\quad (i \in V,\ j=1,2),\qquad \varphi (i)= \omega (i)\quad (i\in V), \end{aligned}$$

and let $f: T_\Phi \rightarrow {{\mathbb {R}}}$ be the associated assignment valuation. Then, it follows from (4.2), (4.3), (4.5), and (4.6) that $D^{\mathcal{B}}(p) = D_f(p)$ for every $p \in {{\mathbb {R}}}^2$. This shows that sets of weighted bid vectors have a natural one-to-one correspondence with weighted complete bipartite graphs representing assignment valuations. $\square$

5 Proof of Lemma 3.4

To prove Lemma 3.4, we show that for each function $f \in \mathcal{M}$, its function values are uniquely determined by the set $P^+(f)$ and the values $\ell _{\textrm{LH}}(D(p)) - \ell _{\textrm{UH}}(D(p))$ for $p \in P^+(f)$. To show this, we first investigate the structure of functions in $\mathcal{M}$.

Let $f \in \mathcal{M}$, and denote by $\mathcal{D}$ the family of 2-d maximizer sets of f. Then, every $D \in \mathcal{D}$ is an M$^\natural$-convex set of positive-type or zero-type by the definition of $\mathcal{M}$. Also, denote by $\mathcal{D}^+ \subseteq \mathcal{D}$ the family of positive-type maximizer sets of f. Recall that every $D \in \mathcal{D}$ is an M$^\natural$-convex set and therefore ${\overline{D}} \cap {{\mathbb {Z}}}^2 = D$ holds.

We classify maximizer sets in $\mathcal{D}$ according to their slopes. Denote by $D(\alpha , \beta )$ the maximizer set $D_f(p)$ with $p= (\alpha , \beta )$. For $\alpha , \beta , \gamma \in {{\mathbb {R}}}$, define

$$\begin{aligned} \mathcal{D}_{\textrm{H}}(\alpha )&= \{D \in \mathcal{D}\mid \ell _{\textrm{LH}}(D)> 0,\ D=D(\alpha , \beta ') \hbox { for some }\beta ' \in {{\mathbb {R}}}\}, \\ \mathcal{D}_{\textrm{V}}(\beta )&= \{D \in \mathcal{D}\mid \ell _{\textrm{LV}}(D)> 0,\ D=D(\alpha ', \beta ) \hbox { for some }\alpha ' \in {{\mathbb {R}}}\}, \\ \mathcal{D}_{\textrm{D}}(\gamma )&= \{D \in \mathcal{D}\mid \ell _{\textrm{URD}}(D) > 0,\ D=D(\alpha ', \alpha ' - \gamma ) \hbox { for some }\alpha ' \in {{\mathbb {R}}}\}. \end{aligned}$$

Also, define

$$\begin{aligned} \mathcal{B}_{\textrm{H}}&= \{D \in \mathcal{D}\mid \hbox {LH-edge of }D \hbox { has positive length}\\ & \qquad\qquad\qquad \mbox{and is contained in the horizontal edge of}\; T_\Phi \}, \\ \mathcal{B}_{\textrm{V}}&= \{D \in \mathcal{D}\mid \hbox {LV-edge of }D \hbox { has positive length}\\ & \qquad\qquad\qquad \mbox{ and is contained in the vertical edge of }T_\Phi \}, \\ \mathcal{B}_{\textrm{D}}&= \{D \in \mathcal{D}\mid \hbox {URD-edge of }D \hbox { has positive length}\\ & \qquad\qquad\qquad \mbox{ and is contained in the diagonal edge of } T_\Phi \}. \end{aligned}$$

That is, $\mathcal{B}_{\textrm{H}} \cup \mathcal{B}_{\textrm{V}} \cup \mathcal{B}_{\textrm{D}}$ is the family of 2-d maximizer sets that touch the boundary of the domain $T_\Phi$ of f.

We observe that $\mathcal{B}_{\textrm{H}}$ contains at most one maximizer set in $\mathcal{D}_{\textrm{H}}(\alpha )$ for every $\alpha \in {{\mathbb {R}}}$. For $D \in \mathcal{D}$ and $\alpha \in {{\mathbb {R}}}$, we say that $\alpha$ is the slope of D in the $(+1,0)$-direction if $D = D(\alpha , \beta )$ for some $\beta \in {{\mathbb {R}}}$.

Proposition 5.1

Let $D, D'$ be distinct maximizer sets in $\mathcal{B}_{\textrm{H}}$, and $\alpha$ (resp., $\alpha '$) be the slope of D (resp., $D'$) in the $(+1,0)$-direction. Then, we have $\alpha \ne \alpha '$; moreover, D is closer to the origin than $D'$ if and only if $\alpha > \alpha '$.

Proof

This follows from the fact that f can be extended to a polyhedral concave function ${\bar{f}}$, and that the convex hull of a 2-d maximizer set of f corresponds to a facet of the epigraph of ${\bar{f}}$. $\square$

For a sequence $D_0, D_1,\ldots , D_t$ of distinct 2-d maximizer sets of f, we say that it is

• an H-sequence if $D_{s}$ and $D_{s+1}$ share a horizontal edge of positive length for $s=0,1,\ldots , t-1$ (i.e., LH-edge of $D_{s}$ is the same as UH-edge of $D_{s+1}$, or UH-edge of $D_{s}$ is the same as LH-edge of $D_{s+1}$),

• a V-sequence if $D_{s}$ and $D_{s+1}$ share a vertical edge of positive length for $s=0,1,\ldots , t-1$.

• a D-sequence if $D_{s}$ and $D_{s+1}$ share a diagonal edge of positive length for $s=0,1,\ldots , t-1$.

See Fig. 5 for an example of H-sequence.

Fig. 5

An example of H-sequence. The dotted triangle represents the set $T_\Phi$

We show that there exists a unique H-sequence consisting of all maximizer sets in $\mathcal{D}_{\textrm{H}}(\alpha )$.

Proposition 5.2

For every $\alpha \in {{\mathbb {R}}}$ with $\mathcal{D}_{\textrm{H}}(\alpha ) \ne \emptyset$, there exists a unique H-sequence $D_0, D_1, \ldots , D_t$ of all 2-d maximizer sets in $\mathcal{D}_{\textrm{H}}(\alpha )$ satisfying the following conditions:

• (a) $D_0 \in \mathcal{D}^+$ and its UH-edge has length zero,

• (b) For $s=0,1,\ldots , t-1$, LH-edge of $D_s$ is the same as UH-edge of $D_{s+1}$,

• (c) $\mathcal{D}_{\textrm{H}}(\alpha ) \cap \mathcal{B}_{\textrm{H}} = \{D_t \}$,

• (d) $D_s = D(\alpha , \beta _s)$ $(s=0,1,\ldots , t)$ holds with some real numbers $\beta _0< \beta _1< \cdots < \beta _t$.

Moreover, for $s =0,1,\ldots , t$, the length $\ell _{\textrm{LH}}(D_s)$ of LH-edge in $D_s$ is equal to

$$\begin{aligned} \ell _{\textrm{LH}}(D_s) = \sum \{ \ell _{\textrm{LH}}(D_{s'})- \ell _{\textrm{UH}}(D_{s'}) \mid 0 \le s' \le s,\ D_{s'} \in \mathcal{D}^+ \}. \end{aligned}$$

(5.1)

Figure 5 shows an example of H-sequence satisfying the conditions (a), (b), (c), and (d). Since $D_0, D_2 \in \mathcal{D}^+$ and $D_1, D_3 \notin \mathcal{D}^+$, (5.1) implies that

$$\begin{aligned} \ell _{\textrm{LH}}(D_3)&= \ell _{\textrm{LH}}(D_2) = ( \ell _{\textrm{LH}}(D_{2})- \ell _{\textrm{UH}}(D_{2}))+( \ell _{\textrm{LH}}(D_{0})- \ell _{\textrm{UH}}(D_{0})) = 1+1 = 2,\\ \ell _{\textrm{LH}}(D_1)&= \ell _{\textrm{LH}}(D_0) = \ell _{\textrm{LH}}(D_{0})- \ell _{\textrm{UH}}(D_{0}) = 1. \end{aligned}$$

Proof of Proposition 5.2

We prove this proposition by using the following properties of 2-d maximizer sets.

Claim 1

Let $\beta \in {{\mathbb {R}}}$ be a real number with $D(\alpha , \beta ) \in \mathcal{D}_{\textrm{H}}(\alpha )$.

• (i) If $D(\alpha , \beta ) \notin \mathcal{B}_{\textrm{H}}$ and its LH-edge has positive length, then there exists a unique real number $\beta '$ with $\beta ' > \beta$ such that $D(\alpha , \beta ') \in \mathcal{D}_\textrm{H}(\alpha )$ and UH-edge of $D(\alpha , \beta ')$ is the same as LH-edge of $D(\alpha , \beta )$.

• (ii) If UH-edge of $D(\alpha , \beta )$ has positive length, then there exists a unique real number $\beta ''$ with $\beta '' < \beta$ such that $D(\alpha , \beta '')\in \mathcal{D}_{\textrm{H}}(\alpha )$ and LH-edge of $D(\alpha , \beta '')$ is the same as UH-edge of $D(\alpha , \beta )$.

[Proof of Claim 1]    We prove (i) only since (ii) can be proved in a similar way. Since $D(\alpha , \beta )$ is a 2-d maximizer set, there exists a unique $p \in {{\mathbb {R}}}^2$ such that $D_f(p)$ is a 2-d maximizer set and UH-edge of $D_f(p)$ is the same as LH-edge of $D(\alpha , \beta )$. Since $D_f(p) \cap D(\alpha , \beta )$ is a horizontal edge, we have $p(1)= \alpha$. Since f can be extended to a polyhedral concave function, we have $p(2) > \beta$. $\square$

Let $D_0$ be a maximizer set in $\mathcal{D}_{\textrm{H}}(\alpha )$ such that LH-edge of $D_0$ is the highest (i.e., farthest from the horizontal edge of $T_\Phi$); recall that $\ell _{\textrm{LH}}(D) > 0$ holds for every $D \in \mathcal{D}_{\textrm{H}}(\alpha )$.

We show that $D_0$ satisfies the condition (a). Assume, to the contrary, that $\ell _{\textrm{UH}}(D_0) > 0$. Then, Claim 1 (ii) implies that there exists some maximizer set $D \in \mathcal{D}_{\textrm{H}}(\alpha )$ such that UH-edge of $D_0$ is equal to LH-edge of D. This, however, is a contradiction to the choice of $D_0$. Hence, we have $\ell _{\textrm{UH}}(D_0) = 0$. Since LH-edge of $D_0$ has positive length, we have $\ell _{\textrm{LH}}(D_0) - \ell _{\textrm{UH}}(D_0)>0$, i.e., $D_0 \in \mathcal{D}^+$, implying the condition (a).

Let $D_0, D_1, \ldots , D_t$ be a maximal sequence of (not necessarily all) maximizer sets in $\mathcal{D}_{\textrm{H}}(\alpha )$ satisfying the conditions (a) and (b). It follows from Claim 1 that the sequence satisfies the condition (d).

We prove that the maximizer set $D_t$ satisfies the condition (c). Assume, to the contrary, that $D_t \not \in \mathcal{B}_{\textrm{H}}$. Since $\ell _{\textrm{LH}}(D_t) > 0$, Claim 1 (i) implies that there exists some maximizer set $D \in \mathcal{D}_{\textrm{H}}(\alpha )$ such that LH-edge of $D_t$ coincides with UH-edge of D. This, however, is a contradiction to the maximality of the sequence. Hence, we have $D_t \in \mathcal{B}_{\textrm{H}}$, which, together with Proposition 5.1, that $\mathcal{D}_{\textrm{H}}(\alpha ) \cap \mathcal{B}_{\textrm{H}} = \{D_t\}$, i.e., the condition (c) holds.

We next prove that the sequence $D_0, D_1, \ldots , D_t$ contains all maximizer sets in $\mathcal{D}_{\textrm{H}}(\alpha )$. Assume, to the contrary, that there exists some $D' \in \mathcal{D}_{\textrm{H}}(\alpha )$ that is not in $\{D_0, D_1, \ldots , D_t\}$; this implies $D' \not \in \mathcal{B}_{\textrm{H}}$ by the condition (c). We further assume that LH-edge of $D'$ is the lowest (i.e., nearest to the horizontal edge of $T_\Phi$) among all such maximizer sets.

Since $D' \notin \mathcal{B}_{\textrm{H}}$, Claim 1 (i) implies that there exists a maximizer set $D'' \in \mathcal{D}_{\textrm{H}}(\alpha )$ such that UH-edge of $D''$ is the same as LH-edge of $D'$. Since $D''$ is lower than $D'$, the choice of $D'$ implies that $D''$ is contained in the sequence $D_0, D_1, \ldots , D_t$. Since UH-edge of $D''$ has positive length, we have $D'' \ne D_0$ by the condition (a). Hence, we have $D'' = D_s$ for some $s > 0$, implying that $D'$ is the same as $D_{s-1}$ by Claim 1 (ii), a contradiction to the assumption that $D' \notin \{D_0, D_1, \ldots , D_t\}$. Therefore, the sequence contains all maximizer sets in $\mathcal{D}_{\textrm{H}}(\alpha )$. This concludes the proof for the first half of the proposition.

We finally prove the equation (5.1) by induction on s. Since $D_0 \in \mathcal{D}^+$ and $\ell _{\textrm{UH}}(D_0)=0$ by the condition (a), the equation (5.1) holds if $s=0$.

We then consider the case with $s > 0$. It holds that

$$\begin{aligned} \ell _{\textrm{LH}}(D_s)&= (\ell _{\textrm{LH}}(D_s) - \ell _{\textrm{UH}}(D_s)) + \ell _{\textrm{UH}}(D_s)\\&= (\ell _{\textrm{LH}}(D_s) - \ell _{\textrm{UH}}(D_s)) + \ell _{\textrm{LH}}(D_{s-1})\\&= (\ell _{\textrm{LH}}(D_s) - \ell _{\textrm{UH}}(D_s)) +\sum \{\ell _{\textrm{LH}}(D_{s'})- \ell _{\textrm{UH}}(D_{s'}) \mid 0 \le s' \le s-1,\ D_{s'} \in \mathcal{D}^+ \}\\&= \sum \{\ell _{\textrm{LH}}(D_{s'})- \ell _{\textrm{UH}}(D_{s'}) \mid 0 \le s' \le s,\ D_{s'} \in \mathcal{D}^+ \}, \end{aligned}$$

where the second equality is by the condition (b), the third by the induction hypothesis, and the last by the fact that if $D_{s} \notin \mathcal{D}^+$ then $D_s$ is of zero-type and $\ell _{\textrm{LH}}(D_s) = \ell _{\textrm{UH}}(D_s)$ holds. Hence, (5.1) holds. $\square$

We can also prove the following properties of $\mathcal{D}_{\textrm{V}}(\beta )$ and $\mathcal{D}_{\textrm{D}}(\gamma )$ in a similar way as in Proposition 5.2. It should be noted that the two equations (5.2) and (5.3) for the length of LV-edges and URD-edges given below are described in terms of the length of LH-edges and UH-edges, where we use the equation

$$ \begin{aligned} & \ell _{\textrm{LH}}(D_{s})- \ell _{\textrm{UH}}(D_{s}) = \ell _{\textrm{LV}}(D_{s})- \ell _{\textrm{RV}}(D_{s}) = \frac{1}{\sqrt{2}}(\ell _{\textrm{URD}}(D_{s})- \ell _{\textrm{LLD}}(D_{s}))\\&\qquad\qquad\qquad\qquad \qquad \qquad \qquad \qquad\qquad \qquad (s = 0,1,\ldots , t). \end{aligned} $$

Proposition 5.3

For every $\beta \in {{\mathbb {R}}}$ with $\mathcal{D}_{\textrm{V}}(\beta ) \ne \emptyset$, there exists a unique V-sequence $D_0, D_1, \ldots , D_t$ of all 2-d maximizer sets in $\mathcal{D}_{\textrm{V}}(\beta )$ satisfying the following conditions:

• (a) $D_0 \in \mathcal{D}^+$ and its RV-edge has length zero.

• (b) For $s=0,1,\ldots , t-1$, LV-edge of $D_s$ coincides with RV-edge of $D_{s+1}$.

• (c) $\mathcal{D}_{\textrm{V}}(\beta ) \cap \mathcal{B}_{\textrm{V}} = \{D_t\}$.

• (d) $D_s = D(\alpha _s, \beta )$ $(s=0,1,\ldots , t)$ holds with some real numbers $\alpha _0< \alpha _1< \cdots < \alpha _t$.

Moreover, for $s =0,1,\ldots , t$, the length $\ell _{\textrm{LV}}(D_s)$ of LV-edge in $D_s$ is given as

$$\begin{aligned} \ell _{\textrm{LV}}(D_s) = \sum \{\ell _{\textrm{LH}}(D_{s'})- \ell _{\textrm{UH}}(D_{s'}) \mid 1 \le s' \le s,\ D_{s'} \in \mathcal{D}^+ \}. \end{aligned}$$

(5.2)

Proposition 5.4

For every $\gamma \in {{\mathbb {R}}}$ with $\mathcal{D}_{\textrm{D}}(\gamma ) \ne \emptyset$, there exists a unique D-sequence $D_0, D_1, \ldots , D_t$ of all 2-d maximizer set in $\mathcal{D}_{\textrm{D}}(\gamma )$ satisfying the following conditions:

• (a) $D_0 \in \mathcal{D}^+$ and its LLD-edge has length zero.

• (b) For $s=0,1,\ldots , t-1$, URD-edge of $D_s$ coincides with LLD-edge of $D_{s+1}$.

• (c) $\mathcal{D}_{\textrm{D}}(\gamma ) \cap \mathcal{B}_{\textrm{D}} = \{D_t \}$.

• (d) $D_s = D_\varphi (\alpha _s, \alpha _s -\gamma )$ $(s=0,1,\ldots , t)$ holds with some real numbers $\alpha _0> \alpha _1> \cdots > \alpha _t$.

Moreover, for $s =0,1,\ldots , t$, the length $\ell _{\textrm{URD}}(D_s)$ of URD-edge in $D_s$ is given as

$$\begin{aligned} \ell _{\textrm{URD}}(D_s) = \sqrt{2}\cdot \sum \{\ell _{\textrm{LH}}(D_{s'})- \ell _{\textrm{UH}}(D_{s'}) \mid 1 \le s' \le s,\ D_{s'} \in \mathcal{D}^+ \}. \end{aligned}$$

(5.3)

Recall that $P^+(f)$ denotes the set of slope vectors for all positive-type maximizer sets. We show that vectors in $P^+(f)$ can be used to compute slope vectors of all 2-d maximizer sets, including those of zero-type.

Proposition 5.5

For $p \in {{\mathbb {R}}}^2$, $D_f(p)$ is a 2-d maximizer set of zero-type if and only if $p \in P^0_{\textrm{HV}} \cup P^0_{\textrm{HD}} \cup P^0_{\textrm{VD}} {\setminus } P^+(f)$ with

$$\begin{aligned}&P^0_{\textrm{HV}} = \{(q(1), q'(2))\mid q, q' \in P^{+}(f),\ q(1) > q'(1),\ q(2)< q'(2)\},\nonumber \\&P^0_{\textrm{HD}} = \{(q(1), q(1) - q'(1)+q'(2)) \mid q, q' \in P^{+}(f),\ 0< q'(1)-q(1)< q'(2)-q(2)\},\nonumber \\&P^0_{\textrm{VD}} = \{(q(2)-q'(2)+q'(1), q(2)) \mid q, q' \in P^{+}(f),\ 0< q'(2)-q(2) < q'(1)-q(1)\}. \end{aligned}$$

Proof

We denote $D_p = D_f(p)$ in the following.

[Proof of “only if” part]    Suppose that $D_p$ is a 2-d maximizer set of zero-type. Then, we have

$$\begin{aligned} \ell _{\textrm{LH}}(D_p) = \ell _{\textrm{UH}}(D_p),\quad \ell _{\textrm{LV}}(D_p) = \ell _{\textrm{RV}}(D_p),\quad \ell _{\textrm{URD}}(D_p) = \ell _{\textrm{LLD}}(D_p) \end{aligned}$$

by definition of zero-type. These equations, together with the fact that $D_p$ is a two-dimensional set, imply that at least two of the edge lengths $\ell _{\textrm{LH}}(D_p)$, $\ell _{\textrm{LV}}(D_p)$, and $\ell _{\textrm{URD}}(D_p)$ are positive. Moreover, Propositions 5.2, 5.3, and 5.4 (condition (a), in particular) imply that

• if $\ell _{\textrm{LH}}(D_p)>0$, then there exists some $q \in P^+(f)$ such that $q(1)=p(1)$ and $q(2) < p(2)$.

• if $\ell _{\textrm{LV}}(D_p)> 0$, then there exists some $q' \in P^+(f)$ such that $q'(1)<p(1)$ and $q'(2) = p(2)$.

• if $\ell _{\textrm{URD}}(D_p) > 0$, then there exists some $q'' \in P^+(f)$ such that $q''(1)-q''(2)=p(1)-p(2)$, $q''(1)> p(1)$, and $q''(2)> p(2)$.

If $\ell _{\textrm{LH}}(D_p)>0$ and $\ell _{\textrm{LV}}(D_p)> 0$ hold, then we have

$$\begin{aligned} q(1)=p(1) > q'(1), \qquad q(2) < p(2) = q'(2), \end{aligned}$$

implying that $p \in P^0_{\textrm{HV}}$. If $\ell _{\textrm{LH}}(D_p)>0$ and $\ell _{\textrm{URD}}(D_p) > 0$ hold, then we have

$$\begin{aligned} q(1)=p(1) < q''(1), \qquad q(1) - q(2) > p(1)-p(2)= q''(1)-q''(2), \end{aligned}$$

implying that

$$\begin{aligned} p(2) = p(1)- q''(1)+q''(2), \qquad q''(2) - q(2)> q''(1)-q(1) > 0, \end{aligned}$$

i.e., $p \in P^0_{\textrm{HD}}$ holds. Similarly, if $\ell _{\textrm{LV}}(D_p)> 0$ and $\ell _{\textrm{URD}}(D_p) > 0$, then we have $p \in P^0_{\textrm{VD}}$.

[Proof of “if” part]    We assume $p \in (P^0_{\textrm{HV}} \cup P^0_{\textrm{HD}} \cup P^0_{\textrm{VD}}) {\setminus } P^+(f)$, and show that $D_p$ is a 2-d maximizer set. In the following, we consider the case $p \in P^0_{\textrm{HV}}$ only since the remaining cases can be proven similarly.

By the definition of $P^0_{\textrm{HV}}$, there exist some $q, q' \in P^{+}(f)$ such that $p(1)=q(1) > q'(1)$ and $q(2) <q'(2)=p(2)$. Propositions 5.2 and 5.3 imply that there exist two sequences of 2-d maximizer sets

$$\begin{aligned} D_0, D_1, \ldots , D_{t-1}, D_t, D_{t+1}, \ldots , D_{t^*-1}, D_{t^*}, \qquad C_0, C_1, \ldots , C_{s-1}, C_{s}, C_{s+1}, \ldots , C_{s^*-1}, C_{s^*} \end{aligned}$$

with $D_t = D_f(q)$ and $C_s = D_f(q')$ satisfying the following conditions (see Fig. 6 for illustration):

Fig. 6

Illustration of the two sequences $D_0, D_1, \ldots , D_{t^*}$ and $C_0, C_1, \ldots , C_{s^*}$. Here, $D_3= D_f(q)$, $C_1= D_f(q')$, and $D_1 = C_3 = D_f(p)$ hold. The dotted triangle represents the set $T_\Phi$. $D_0,D_1,D_2,D_3$ and $C_0, C_1$ are H-sequences, while $D_3, D_4, D_5$ and $C_1, C_2, C_3, C_4, C_5$ are V-sequences

• $D_0, D_1, \ldots , D_{t-1}, D_t$ is the H-sequence from the unique maximizer set $D_0$ in $\mathcal{D}_{\textrm{H}}(q(1)) \cap \mathcal{B}_{\textrm{H}}$ to $D_t$,

• $D_t, D_{t+1}, \ldots , D_{t^*-1}, D_{t^*}$ is the V-sequence from $D_t$ to the unique maximizer set $D_{t^*}$ in $\mathcal{D}_{\textrm{V}}(q(2)) \cap \mathcal{B}_{\textrm{V}}$,

• $C_0, C_1, \ldots , C_{s-1}, C_{s}$ is the H-sequence from the unique maximizer set $C_0$ in $\mathcal{D}_{\textrm{H}}(q'(1)) \cap \mathcal{B}_{\textrm{H}}$ to $C_{s}$,

• $C_{s}, C_{s+1}, \ldots , C_{s^*-1}, C_{s^*}$ is the V-sequence from $C_{s}$ to the unique maximizer set $C_{s^*}$ in $\mathcal{D}_\textrm{V}(q'(2)) \cap \mathcal{B}_{\textrm{V}}$.

We show that $D_{t'} = C_{s'}$ holds for some $t'$ and $s'$ with $0 \le t' \le t$ and $s \le s' \le s^*$; such a 2-d maximizer set satisfies $D_{t'} = C_{s'} = D_p$ since $D_{t'} \in \mathcal{D}_\textrm{H}(p(1))$ and $C_{s'} \in \mathcal{D}_{\textrm{V}}(p(2))$. To show this, we use the following properties on the geometry of the two sequences.

Claim 1

• (i) H-sequence $D_0, D_1, \ldots , D_t$ is closer to the origin than H-sequence $C_0, C_1, \ldots , C_{s}$.

• (ii) V-sequence $C_{s}, C_{s+1}, \ldots , C_{s^*}$ is closer to the origin than V-sequence $D_t, D_{t+1}, \ldots , D_{t^*}$.

Proof of Claim 1

We prove (i) only. Since $D_0 \in \mathcal{D}_{\textrm{H}}(q(1))$, $C_0 \in \mathcal{D}_{\textrm{H}}(q'(1))$, and $q(1) > q'(1)$, Proposition 5.1 implies that the maximizer set $D_0$ is closer to the origin than $C_0$. Hence, the statement of the claim follows since the H-sequence $D_0, D_1, \ldots , D_{t-1}, D_t$ starts from $D_0$, the H-sequence $C_0, C_1, \ldots , C_{s-1}, C_{s}$ starts from $C_0$, and the two H-sequences are disjoint. $\square$

We see that maximizer sets $C_0, C_1, \ldots , C_{s^*}$ are connected, and two sets $C_0$ and $C_{s^*}$ are on the boundary of $T_\Phi$. This means that the sequence $C_0, C_1, \ldots , C_{s^*}$ separates $T_\Phi$ into two region, the one containing the origin and another one not containing the origin. Moreover, $D_0, C_0 \in \mathcal{B}_{\textrm{H}}$, $D_{t^*}, C_{s^*} \in \mathcal{B}_{\textrm{V}}$, $D_0$ is closer to the origin than $C_0$, and $D_{t^*}$ is farther from the origin than $C_{s^*}$. This observation and Claim 1 imply that

$$\begin{aligned} \{D_0, D_1, \ldots , D_t\} \cap \{C_s, C_{s+1}, \ldots , C_{s^*}\} \ne \emptyset , \end{aligned}$$

i.e., $D_{t'} = C_{s'}$ holds for some $t'$ and $s'$ with $0 \le t' \le t$ and $s \le s' \le s^*$. This concludes the proof for “if” part of Proposition 5.5. $\square$

We now give a proof of Lemma 3.4. Proposition 5.5 implies that the set P(f) of slope vectors of all 2-d maximizer sets for function f is uniquely determined by the set $P^+(f)$. Using the set P(f) and the values $\ell _{\textrm{LH}}(D(p)) - \ell _{\textrm{UH}}(D(p))$ for $p \in P^+(f)$, we can compute the lengths of six edges of all 2-d maximizer sets with the aid of the equations (5.1), (5.2), and (5.3) in Propositions 5.2, 5.3, and 5.4. We can also obtain the information on the adjacency relationship among 2-d maximizer sets of f by Propositions 5.2, 5.3, and 5.4. Hence, the function values of f at all points in $T_\Phi$ are uniquely determined by Proposition 2.7. This concludes the proof of Lemma 3.4.