1 Introduction

Bénard convection in a horizontal layer of a single fluid is one of the fundamental problems in fluid mechanics, and it has provided the basis for models and examples of linear and nonlinear phenomena of dynamical systems. The onset of convection is described by linearly unstable modes of a stationary state, and is followed by several types of bifurcations of solutions that have been clarified in extensive studies both theoretically and experimentally. However, the assumption of a single fluid does not necessarily hold in real convection phenomena, including the mantle of the Earth [14, 17], the plasma inside a nuclear fusion reactor [22], or molten materials in industrial applications [13], where the thermal convection is considered to take place not in a single fluid layer but in two or more layers of different fluids.

In multi-layer thermal convection systems, we have to distinguish two cases depending on whether the fluids are immiscible or miscible. For immiscible fluids, such as water and oil, a definite interface remains between the different fluids, and several traditional approaches of linear [7, 9,10,11,12, 14,15,16,17] and nonlinear [2, 8, 16] theories have been applied to the thermal convection. In contrast, in the case of miscible fluids, such as saline and fresh water, a definite interface, even if it exists initially, becomes less clear as time goes on, due to the effect of diffusion. Temperature and concentration (e.g. salinity) are then both diffusive, and the convection in this double diffusive system has been theoretically discussed mostly for a stationary continuous (vertically linear) distribution of both the temperature and the concentration, in relation to, for example, salt fingers and interleaving in the ocean [21].

In this paper we are interested in thermal convection in two horizontal layers of miscible fluids, with an initial state in which the fluids are at rest and the temperature has a linear continuous vertical distribution, but the concentration takes different constant values in each layer and is thus not in a stationary state. This configuration is similar to that of the original Bénard convection problem, but the initial state is not a stationary solution of the system. In this configuration two kinds of convection states and a transition between these states were observed (e.g. [23]).Footnote 1 The convection states can be classified by the directions of velocity in the cells in the upper and lower layers (Fig. 1). In the “viscous coupling” state, the direction of velocity in the upper cell is opposite to that in the cell just below it, while in the “thermal coupling” state, the direction of velocity is the same in the upper cell and the cell just below it.

This interesting phenomenon has been studied so far in the framework of linear stability theory by assuming that the interface between the two fluids has an infinitesimal width, but only the viscous coupling convection pattern was obtained [9, 22].

The theoretical method generally used for bifurcation problems in fluid mechanics is not very suitable for describing this change in the convection pattern in miscible fluids, because no stationary state which should be taken as a starting state for analysis is available, and all phenomena are transient. Especially the interface, that is, the transitional layer between the fluids, is not stationary but grows over time, even if it has infinitesimal width initially. This is a major obstacle to analysis. Thus, in this paper, we propose a new model system that inherits most characteristic properties of miscible convection but keeps the transitional layer and its horizontally averaged (nonzero) width constant over time.

In the following we first describe the original problem of miscible convection and its governing equations, our numerical experiments and their results. We then introduce a model system of thermal convection in which the horizontally averaged width of the transitional layer between the upper and lower fluids is constant over time, by modifying the concentration part of the governing equations. Suppressing the expansion of the transitional layer in an averaged sense, allows us to analyze the thermal convection with the transitional layer of constant average width, while the concentration itself is unstationary. In other words, this model system provides a snapshot of the transient phenomena arising in the convection of miscible fluids. This snapshot opens the system to standard theoretical methods, and we investigated the linear instability of a stationary solution of the model to find the most unstable modes for several widths of the transitional layer. The results correspond well to the phenomena in the original miscible convection. Finally, we studied the nonlinear stage of this instability and its attractors, the results of which show that two different attractors arise corresponding to the viscous coupling and the thermal coupling states. In the real convection problem of miscible fluids, however, both convection patterns are transient over time, and attractors cannot exist. However the similarities of phenomena between the real convection and the model convection suggest that the real system also has a trace of the attractors, which is similar to the attractors but are not invariant sets and have a saddle-like structure.

Fig. 1
figure 1

Sketch of two typical patterns of convection in two-layer system: a viscous coupling and b thermal coupling

Full size image

2 Original system and solutions

2.1 Governing equations and boundary and initial conditions

Fig. 2
figure 2

Initial configuration of a two-dimensional system of double diffusive thermal convection in two horizontal layers of miscible fluids under downward gravity. The fluid in the upper layer has lower concentration than the fluid in the lower layer. No concentration fluxes are assumed at the boundaries \(z=\pm 1\), where the temperatures are held constant in a way that makes the bottom hotter than the top

Full size image

We consider a two dimensional double diffusive thermal convection in two horizontal layers of miscible fluids which initially have the same depth, one lying on top of the other, under downward gravity (Fig. 2). We apply Boussinesq approximation to the system. The physical properties of the fluids, such as basic density, viscosity and thermal diffusivity, are assumed to be the same and constant. We take the x and z axes in the horizontal and vertical directions, respectively. Let \(z = 0\) be the initial boundary between the two fluids, which are definitely separated at \(t = 0\).

To non-dimensionalize the equations, we take the initial depth of each fluid layer h as the length scale, \(h^2 / D_T\) as the time scale(where \(D_T\) is a thermal diffusion coefficient), the temperature difference between the top and bottom boundaries \(\varDelta T\) as the temperature scale, and the initial concentration difference between the upper and lower layers \(\varDelta S\) as the concentration scale. Then the non-dimensional equations are,

$$\partial _{t} {\varvec{u}} + ({\varvec{u}} \cdot \nabla ) {\varvec{u}} = - \nabla p + {\text{Ra}} {\text{Pr}} (T - B S) {\varvec{k}} + {\text{Pr}} \nabla ^{2} {\varvec{u}}, $$
(1)
$$\begin{aligned}&\nabla \cdot {\varvec{u}} = 0, \nonumber \\&\partial _{t} T + ({\varvec{u}} \cdot \nabla ) T = \nabla ^{2} T, \nonumber \\&\partial _{t} S + ({\varvec{u}} \cdot \nabla ) S = \dfrac{1}{{\text{Le}}} \nabla ^{2} S{,} \end{aligned}$$
(2)

where \({\varvec{u}}=(u_x,u_z)\), T, S and p are non-dimensionalized velocity, temperature, concentration and pressure, respectively, and \({\varvec{k}}\) is the unit vector in the z direction. The operator \(\nabla \) is defined as \((\partial _x,\partial _z)\). The Rayleigh number Ra, Prandtl number Pr, buoyancy number B and Lewis number Le in the equations are non-dimensional quantities defined by

$$\begin{aligned} {\text{Ra}}&= \dfrac{\alpha _T g h^3 \varDelta T}{D_T \nu }, \quad {\text{Pr}} = \dfrac{\nu }{D_T}, \\ B&= \dfrac{\alpha _S \varDelta S}{\alpha _T \varDelta T}, \quad {\text{Le}} = \dfrac{D_T}{D_S}{,} \end{aligned}$$

where \(\nu \) is the kinematic viscosity, g is gravitational acceleration, \(\alpha _T\) and \(\alpha _S\) are thermal and compositional expansion coefficients, respectively, and \(D_S\) is the compositional diffusion coefficient.

The horizontal boundary condition is periodic. The boundary conditions at the top and bottom boundaries are non-slip with fixed temperatures and null concentration fluxes as follows.

$$\begin{aligned}&{\varvec{u}} (x, \pm 1, t) = 0, \end{aligned}$$
(3)
$$\begin{aligned}&T(x, 1, t) = 0, \quad T(x, - 1, t) = 1, \end{aligned}$$
(4)
$$\begin{aligned}&\partial _z S(x, 1, t) = 0, \quad \partial _z S(x, - 1, t) = {0.} \end{aligned}$$
(5)

We introduce a stream function \(\psi (x, z, t)\) that satisfies

$$\begin{aligned} u_{x} = \partial _{z} \psi , \quad u_{z} = - \partial _{x} \psi , \end{aligned}$$

because of the incompressibility condition (2). By assuming no net horizontal flow and choosing a proper additive constant, we can rewrite the non-slip condition (3) as the boundary condition of the stream function at the top and bottom boundaries

$$\begin{aligned} \psi (x, \pm 1, t) = \partial _{z} \psi (x, \pm 1, t) = 0. \end{aligned}$$
(6)

Taking the curl of (1) and rewriting non-linear terms using the Jacobian \(J(a, b) = (\partial _{z} a) (\partial _{x} b) - (\partial _{x} a) (\partial _{z} b)\), we can deduce the evolution equations as

$$\begin{aligned}&\partial _{t} \nabla ^{2} \psi + J(\psi , \nabla ^{2} \psi ) = - {\text{Ra}} {\text{Pr}} \partial _{x} (T - B S) + {\text{Pr}} \nabla ^{2} \nabla ^{2} \psi , \end{aligned}$$
(7)
$$\begin{aligned}&\partial _{t} T + J(\psi , T) = \nabla ^{2} T, \end{aligned}$$
(8)
$$\begin{aligned}&\partial _{t} S + J(\psi , S) = \dfrac{1}{{\text{Le}}} \nabla ^{2} S. \end{aligned}$$
(9)

2.2 Experimental setup

The vorticity-streamfunction method was used for time integration. The stream function, temperature and concentration were spatially discretized by the Fourier spectral method in the x direction, and by the finite difference method in the z direction. The horizontal system size was \(L_{x} = 4 \pi / 2.6 \approx 4.83\) while the vertical size of each layer was 1. We set the equally spaced grid points as \(192 \times 101\) in the x and z directions, respectively, and the truncation number 64 in the x direction, eliminating aliasing errors by the 1/3-rule. We used the Crank–Nicolson scheme for linear terms, and the modified Euler scheme for nonlinear terms.

We explored a set of parameters that included the horizontal extent of the domain in which we can clearly observe the viscous coupling and thermal coupling patterns (Fig. 1) and the transition between these states. We chose the non-dimensional physical parameters as

$$\begin{aligned} {\text{Ra}} = 3200, \quad {\text{Pr}} = 10, \quad {\text{Le}} = 10^{4}, \quad B = 10. \end{aligned}$$
(10)

The initial conditions for the temperature and concentration were

$$\begin{aligned} T(x, z, 0) = \dfrac{1}{2} (1 - z), \quad S(x, z, 0) = {\left\{ \begin{array}{ll} 0 &{}\quad (z > 0) \\ 1 &{}\quad (z < 0) \end{array}\right. }. \end{aligned}$$
(11)

We took some non-zero initial conditions of \(\psi \), one of which is in the following form:

$$\begin{aligned} \psi (x, z)=\left\{ \sin ^{2}\left[ \frac{\pi (z-1)}{2}\right] +\sin ^{3}\left[ \pi (z-1)\right] \right\} \exp \left\{ \sin \left( \frac{2\pi x}{L_{x}}\right) \right\} , \end{aligned}$$
(12)

while the numerical results for other initial conditions did not affect our analysis described below.

2.3 Results of numerical experiment

Figure 3 shows the stream function \(\psi \) and the temperature deviation \(\varTheta \equiv T - T|_{t = 0}\) in their early stage (\(t=0.7\)). Here, we observe two streets of vortex array: the upper vortices rotate in the direction opposite to the lower vortices just below them (Fig. 3a), and similarly the sign of the temperature deviation \(\varTheta \) is also opposite in the upper and lower vortices (Fig. 3b). We call the state with this convection pattern viscous coupling.

Fig. 3
figure 3

Snapshots of a the stream function \(\psi \) and b the temperature deviation \(\varTheta \) at \(t = 0.70\). This convection pattern is identified as ‘viscous coupling’

Full size image
Fig. 4
figure 4

Snapshots of the stream function \(\psi \) at a \(t = 1.0\), b 1.4, c 1.6 and d 2.3

Full size image
Fig. 5
figure 5

Temperature deviation \(\varTheta \) at \(t = 2.3\). The sign is the same between the upper and lower layers

Full size image

During \(1.0 \lesssim t \lesssim 2.3\), however, the viscous coupling pattern disappears and a different convection pattern appears as seen in Fig. 4, which shows the stream function \(\psi \) during \(1.0 \le t \le 2.3\). In the lower layer, the convection decays during \(1.0 \lesssim t \lesssim 1.4\), and a new convection in the opposite direction grows during \(1.4 \lesssim t \lesssim 2.3\), while the convection in the upper layer does not decay completely, and regrows for \(1.6 \lesssim t \lesssim 2.3\). Then two streets of vortex array are formed at \(t = 2.3\), in which the convection in the upper and lower layers rotates in the same direction. The sign of the temperature deviation \(\varTheta \) is also the same between the upper and lower vortices (Fig. 5). We call the state of this convection pattern thermal coupling.

Fig. 6
figure 6

Snapshots of the stream function \(\psi \) at a \(t = 4.6\), b 5.5 and c 6.0. The convection decays during \(4.6 \lesssim t \lesssim 5.5\), and convection in the opposite direction grows during \(5.5 \lesssim t \lesssim 6.0\)

Full size image
Fig. 7
figure 7

Stream function \(\psi \) at \(t = 15.0\). The remnants of thermal coupling are observed. The amplitude of the convection is lower than that at \(t = 2.3\) (Fig. 4d) by two digits

Full size image

The convection continues for some time, gradually decreasing in amplitude, and finally almost stops. Then the convection rotating in the opposite direction grows. This process takes place in parallel in both layers. This periodic oscillation continues but is gradually damped, and after a long time integration, the convection finally loses its clear pattern. The remnants of thermal coupling are observed at \(t = 15.0\) (Fig. 7), but the amplitude of the convection is lower than that at \(t = 2.3\) by two digits.

Fig. 8
figure 8

Horizontally averaged concentration \(\langle S \rangle _{x}\) at \(t = 0.7, 2.3, 6.0\) and 15.0 and \(z=-0.5\) to 0.5. The horizontal average of the transitional layer gradually increases with time

Full size image

It can be seen from Figs. 3a, 4d, 6c, 7 that, as time develops, the vertical scales of the convection vortices gradually decreases and the convection cells in the upper and lower layers become separated. This causes a decrease of the effective Rayleigh number for the convection and a decline of its amplitude. The horizontal averages of the concentration field \(\langle S \rangle _{x}\) at \(t = 0.7, 2.3, 6.0\) and 15.0 are shown in Fig. 8, where \(\langle \cdot \rangle _{x}\) stands for the horizontal average. The figure shows that the horizontal average of the transitional layer of the concentration is not steady, but gradually expands. For this reason, it is difficult to apply the standard techniques of dynamical systems such as linear stability analysis of equilibrium points or periodic orbits.

3 Model analysis of the convection of the miscible fluids

3.1 Model with a fixed transitional layer

Because the transitional layer of miscible fluids continues to expand, the phenomena are transient through the time development. To apply standard procedures based on stationary states, we introduce an artificial model whose transitional layer has a constant width in the horizontal average through modification of the evolution equation of the concentration.

We decompose S into two parts:

$$\begin{aligned} S(x, z, t) = S_{\delta }(z) + \varSigma (x, z, t), \end{aligned}$$
(13)

where

$$\begin{aligned} S_{\delta }(z) \equiv \dfrac{1}{2} \, {\mathrm {erfc}} \left( \dfrac{z}{\delta } \right) , \quad \delta \equiv 2 \sqrt{{\text{Le}}^{-1} t}, \end{aligned}$$

where \(S_{\delta }\) corresponds to the time development of S when \(\psi = 0\).

Here we devise a model system of equations to understand the transient behavior of the thermal convection of miscible fluids. A theoretical difficulty comes from the unstationary nature of the transient behavior where the width of the transient layer becomes larger over the course of time development. Therefore we propose a model system in which the width of the horizontally averaged transient layer is kept constant.

For this purpose, a simple way may be to assume \(S=S(z)\) independent of t. However this does not work because the effect of S(z) is then absorbed in the pressure as seen in (1). Therefore, we need to retain the concentration disturbance field \(\varSigma \) and instead choose to eliminate the eddy transport of concentration \(J(\psi , \varSigma )\) after substituting (13) into (9). This elimination would be justified if \(J(\psi ,\varSigma )\) were a much smaller quantity than the other terms. But this does not necessarily hold in our numerical experiment in Sect. 2.3. Although no asymptotic justification is yet available, the numerical results of this model (given below) show qualitative similarity to those of the original system, and we adopt

$$\begin{aligned} \partial _{t} \varSigma + J(\psi , S_{\delta }) = \dfrac{1}{{\text{Le}}} \nabla ^{2} \varSigma \end{aligned}$$
(14)

instead of (9), for the purpose of qualitatively understanding the structure of the change in the convection patterns observed in the original system. \(\langle \varSigma \rangle _{x} = 0\) always holds if it is satisfied at the initial time, and so we obtain \(\langle S \rangle _{x} = S_{\delta }\) for any t. In the following, we treat \(\delta \) as a time-independent fixed parameter, and consider a model system of (7), (8), (13) and (14) under the boundary conditions (4), (5) and (6). In this model, the width of the horizontally averaged transitional layer is constant for several values of \(\delta \), and we have a stationary state \(\psi =0\), \(T=T_0(z)=(1/2)(1-z)\), \(\varSigma =0\) (\(S=S_\delta (z))\). Hereafter, we employ the parameter values in (10) and also the initial conditions (11) and (12) for the model study, unless otherwise specified.

3.2 Linear stability problem of the stationary state

Because the coefficients appearing in the linearized equations (7), (8) and (14) do not depend on x and t, we can seek solutions in the following form:

$$\begin{aligned} \begin{aligned} \psi (x, z, t)&= 0&+ \tilde{\varPsi }(z) e^{i k x + \sigma t}, \\ T(x, z, t)&= T_{0}(z)&+ \tilde{\varTheta }(z) e^{i k x + \sigma t}, \\ \varSigma (x, z, t)&= 0&+ \tilde{\varSigma }(z) e^{i k x + \sigma t}, \end{aligned} \end{aligned}$$

where \(\sigma = r - i \omega \) is a complex constant, in which r and \(\omega \) are the growth rate and the frequency, respectively. The linearized equations become

$$\begin{aligned}&\sigma (D^{2} - k^{2}) \tilde{\varPsi } = - {\text{Ra}} {\text{Pr}} i k (\tilde{\varTheta } - B \tilde{\varSigma }) + {\text{Pr}} (D^{2} - k^{2})^{2} \tilde{\varPsi }, \end{aligned}$$
(15)
$$\begin{aligned}&\sigma \tilde{\varTheta } = i k (D T_{0}) \tilde{\varPsi } + (D^{2} - k^{2}) \tilde{\varTheta }, \end{aligned}$$
(16)
$$\begin{aligned}&\sigma \tilde{\varSigma } = i k (D S_{\delta }) \tilde{\varPsi } + \dfrac{1}{{\text{Le}}} (D^{2} - k^{2}) \tilde{\varSigma }, \end{aligned}$$
(17)

where \(D = \frac{d}{d z}\). The boundary conditions of \(\tilde{\varPsi }\), \(\tilde{\varTheta }\) and \(\tilde{\varSigma }\) derived from (4), (5), and (6) are written as

$$\begin{aligned} \tilde{\varPsi }(\pm 1) = D \tilde{\varPsi }(\pm 1) = \tilde{\varTheta }(\pm 1) = D \tilde{\varSigma }(\pm 1) = 0. \end{aligned}$$
(18)

Let \(\tilde{\varTheta }' \equiv i \tilde{\varTheta }\) and \(\tilde{\varSigma }' \equiv i \tilde{\varSigma }\), then by substituting them into (15), (16), and (17) we obtain

$$\begin{aligned} \sigma \begin{pmatrix} D^{2} - k^{2} &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \end{pmatrix} \begin{bmatrix} \tilde{\varPsi } \\ \tilde{\varTheta }' \\ \tilde{\varSigma }' \end{bmatrix} = \begin{pmatrix} {\text{Pr}} (D^{2} - k^{2})^{2} &{}\quad - {\text{Ra}} {\text{Pr}} k &{}\quad {\text{Ra}} {\text{Pr}} B k \\ - k (D T_{0}) &{}\quad D^{2} - k^{2} &{}\quad 0 \\ - k (D S_{\delta }) &{}\quad 0 &{}\quad \dfrac{1}{{\text{Le}}} (D^{2} - k^{2}) \end{pmatrix} \begin{bmatrix} \tilde{\varPsi } \\ \tilde{\varTheta }' \\ \tilde{\varSigma }' \end{bmatrix}. \end{aligned}$$
(19)

The boundary conditions (18) become

$$\begin{aligned} \tilde{\varPsi }(\pm 1) = D \tilde{\varPsi }(\pm 1) = \tilde{\varTheta }'(\pm 1) = D \tilde{\varSigma }'(\pm 1) = 0. \end{aligned}$$
(20)

For the given Ra, Le, Pr, B, k and \(\delta \), (19) and (20) setup a generalized eigenvalue problem of a linear operator with respect to an eigenvalue \(\sigma \) and an eigenstate \([\tilde{\varPsi }, \tilde{\varTheta }', \tilde{\varSigma }']^{T}\). Note that the eigenvalues of (19) and (20) are real, or pairs of complex conjugates with complex conjugate eigen functions, because the coefficients of the equations are all real.

The variables \(\tilde{\varPsi }(z)\), \(\tilde{\varTheta }'(z)\) and \(\tilde{\varSigma }'(z)\) are discretized by the finite difference method, using 1001 equally spaced grid points. The generalized eigenvalue problem of (19) and (20) is solved by LAPACK (http://www.netlib.org/lapack/). We adopt the same parameter values for Pr, Le, and B as in (10) in most of this section, except in a part of Sect. 3.4, where B is varied over the range \(1 \le B \le 10\). We seek neutral curves by solving the equation \(r = 0\) using the binary search method, changing the wave number k from 1 to 4 in steps of 0.05.

3.3 Neutral modes

Fig. 9
figure 9

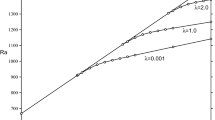
Neutral curves and frequency at \(\delta = 0.01\) (red solid curve), 0.02 (green solid curve), 0.03 (blue solid curve), and 0.06 (magenta solid curve). The critical wave number and Rayleigh number \((k_{c}, {\text{Ra}}_{c})\) are (2.65, 2290.47) at \(\delta = 0.01\), (2.60, 2578.97) at \(\delta = 0.02\), (2.55, 2675.78) at \(\delta = 0.03\), and (2.50, 3102.34) at \(\delta = 0.06\). The critical points are under the line of \({\text{Ra}} = 3200\) (cyan dashed line), as adopted in Sect. 2.3, when \(\delta \lesssim 0.06\) (color figure online)

Full size image

Neutral curves at \(\delta = 0.01\), 0.02, 0.03, and 0.06 are shown in the left panel of Fig. 9. The curves move upward and the critical wave number decreases as the width of the transient layer \(\delta \) increases. All the neutral modes obtained here are oscillatory (\(\omega \ne 0\)) as shown in the right panel of Fig. 9. Staircase variations observed in the frequency graphs for \(\delta =0.01\) and 0.02 are due to replacement of the viscous and thermal coupling modes. The larger frequency is for the viscous coupling mode. The line of the Rayleigh number (\({\text{Ra}}=3200\)) adopted in Sect. 2.3 is also drawn in the left panel of Fig. 9. The critical Rayleigh numbers are lower than 3200 when \(\delta \lesssim 0.06\). This implies that the stationary state is unstable with respect to infinitesimal disturbances when \({\text{Ra}} = 3200\) and \(\delta \lesssim 0.06\).

Fig. 10
figure 10

Critical mode at \(\delta = 0.02\): a the stream function and b the temperature deviation. This convection pattern is identified as viscous coupling. The critical frequency \(\omega _{c}\) is \(- 3.736\), and the propagation velocity is \(\omega _{c}/k_{c} = - 1.44\)

Full size image

Figure 10 shows the critical mode at \(\delta = 0.02\) with negative \(\omega \). Vortices at the same horizontal position are observed to rotate in the direction opposite to each other in Fig. 10a. The disturbance of the temperature shown in Fig. 10b has different signs in the upper and lower layers, indicating that the convection pattern is viscous coupling. The critical frequency \({\omega _c}\) is \(- 3.736\), and the propagation velocity is \({\omega _c}/{k_c} = - 1.44\). There exists another critical mode with \({\omega _c}=3.736\) arising from the reflection symmetry (\(x \leftrightarrow -x\)). Note that the horizontal propagation is an artifact not observed in the original system.

We can see from Fig. 10 that the critical mode has the symmetry of

$$\begin{aligned} \begin{bmatrix} \tilde{\varPsi }(- z) \\ \tilde{\varTheta }(- z) \\ \tilde{\varSigma }(- z) \end{bmatrix} = - \begin{bmatrix} \tilde{\varPsi }(z) \\ \tilde{\varTheta }(z) \\ \tilde{\varSigma }(z) \end{bmatrix}. \end{aligned}$$
(21)

This symmetry property is consistent with the linearized equations (15), (16), and (17) and the boundary conditions (18). In this paper, we call (21) the “symmetry of viscous coupling”, and the mode accompanying it the “viscous coupling mode”.

Fig. 11
figure 11

The critical mode at \(\delta = 0.03\): a the stream function and b the temperature deviation. This convection pattern is identified as thermal coupling. The critical frequency \(\omega _{c}\) is \(- 0.529\), and the propagation velocity is \(\omega _{c}/k_{c} = - 0.21\), which is much slower than that of the critical mode at \(\delta = 0.02\)

Full size image

Figure 11 shows the critical mode at \(\delta = 0.03\) with negative \(\omega \). Vortices at the same horizontal position are observed to rotate in the same direction in Fig. 11a. The disturbance of the temperature displayed in Fig. 11b has the same signs in the upper and lower layers. This convection pattern is thermal coupling. The critical frequency of this mode \(\omega _{c}\) is \(- 0.529\), and the propagation velocity is \(\omega _{c}/k_{c} = - 0.21\), which is much slower than that of the critical mode at \(\delta = 0.02\). In this case another critical mode arising from the reflection symmetry (\(x \leftrightarrow -x\)) exists with \({\omega _c}=0.529\).

We can see from Fig. 11 that the critical mode has the symmetry of

$$\begin{aligned} \begin{bmatrix} \tilde{\varPsi }(- z) \\ \tilde{\varTheta }(- z) \\ \tilde{\varSigma }(- z) \end{bmatrix} = \begin{bmatrix} \tilde{\varPsi }(z) \\ \tilde{\varTheta }(z) \\ \tilde{\varSigma }(z) \end{bmatrix}. \end{aligned}$$
(22)

This symmetry property is also consistent with the linearized equations (15), (16), (17), and the boundary conditions (18). We call (22) the “symmetry of thermal coupling”, and the mode accompanying it the “thermal coupling mode”.

At other values of \(\delta \le 0.1\), the critical modes have the symmetry of viscous coupling when \(\delta \lesssim 0.02\), while the critical modes have the symmetry of thermal coupling when \(\delta \gtrsim 0.02\). Therefore the symmetry of the critical mode changes at \(\delta \approx 0.02\).

Rasenat et al. [14] and Le Bars and Davaille [9] performed linear stability analysis of the infinitesimal transition layer, and found only the viscous coupling mode at criticality when the vertical lengths of the layers and the physical properties of the fluids in the two layers were the same, except for the densities. Our analysis found that the viscous coupling mode remains as a critical mode when the transitional layer has a finite width less than about 0.02. This implies that the width of the transitional layer is crucial for determining the structure of convection in two layer miscible fluids.

3.4 Unstable modes at \({\text{Ra}} = 3200\)

Here, we investigate unstable modes at \({\text{Ra}} = 3200\), which is the value used in Sect. 2.3, and discuss the behavior found in Sect. 2.3 using linear instability.

Fig. 12
figure 12

Growth rate and frequency of unstable thermal coupling modes (red solid curve) and of viscous coupling modes (blue dashed curve) for three values of \(\delta \) at \({\text{Ra}} = 3200\). The step width of the wave number k is 0.05 (color figure online)

Full size image

The growth rate and frequency of unstable modes at several values of \(\delta \) are shown in Fig. 12, where the wave number k varies in steps of 0.05. When \(\delta = 0.015\), the most unstable viscous coupling mode, whose wave number is \(k = 2.85\) and is non-oscillatory, has a higher growth rate than that of the most unstable thermal coupling mode, whose wave number is \(k = 2.9\) and is oscillatory (top row of Fig. 12). At \(\delta = 0.02\), unstable oscillatory viscous coupling modes and non-oscillatory thermal coupling modes exist, but the growth rate of the most unstable viscous coupling mode at \(k = 2.75\) is less than that of the most unstable thermal coupling mode at \(k = 2.85\) (middle row of Fig. 12). Thus the most unstable mode changes from viscous coupling to thermal coupling at \(0.015< \delta < 0.02\). At \(\delta = 0.03\), all viscous coupling modes are stable, while unstable thermal coupling modes exist (bottom row of Fig. 12). All viscous coupling modes and thermal coupling modes are found to be stable when \(\delta = 0.07\) (not shown).

Fig. 13
figure 13

Growth rate and frequency of unstable thermal coupling modes (red solid curve) and viscous coupling modes (blue dashed curve) at \(k = 2.60\) and \({\text{Ra}} = 3200\). The step width of \(\delta \) is 0.0005 (color figure online)

Full size image

Next, we consider the dependence of the growth rate and the frequency on the width of the transition layer, \(\delta \), taking fixed values of \(k=2.60\), \({\text{Ra}}=3200\), and \(L_{x} = \dfrac{4 \pi }{2.60}\), which were adopted in Sect. 2.3. The growth rate and frequency of unstable modes are shown in Fig. 13. Unstable thermal coupling modes exist for \(\delta < 0.064\), and unstable viscous coupling modes exist for \(\delta < 0.03\). Thermal coupling modes have two growth rates for \(\delta < 0.044\), while only a single growth rate is found for \(\delta > 0.044\). The thermal coupling modes for \(\delta < 0.044\) are stationary modes, that is, \(\omega = 0\), while those for \(\delta > 0.044\) are oscillatory modes, that is, \(\omega \ne 0\). A similar behavior of viscous coupling modes is found at \(\delta = 0.016\). The viscous coupling modes for \(\delta < 0.016\) are stationary modes, while those for \(\delta > 0.016\) are oscillatory modes. The most unstable mode changes at \(\delta = 0.017\): the most unstable mode is the viscous coupling mode for \(\delta < 0.017\) while the most unstable mode is the thermal coupling mode for \(\delta > 0.017\). The frequency values of the oscillations before and after \(t=2.0\) in the numerical experiment shown in Sect. 2.3 are 4.6 and 2.5, respectively. These are comparable to the frequencies of the oscillatory viscous and thermal coupling mode at \(\delta > 0.02\) and \(\delta > 0.044\), respectively.

Fig. 14
figure 14

Types of the most unstable modes for \(0.01 \le \delta \le 0.1\) and \(1 \le B \le 10\): stable modes (black crosses), thermal coupling modes (red solid and open squares) and viscous coupling modes (blue solid and open circles). Filled symbols represent oscillatory modes, and hollow ones represent stationary convections (color figure online)

Full size image

Figure 14 shows the symmetry (viscous/thermal coupling) and the time dependence (stationary/oscillatory) of the most unstable mode of the buoyancy number, B (\(1 \le B \le 10\)), which expresses the density contrast, and the transitional layer width \(\delta \) (\(0.01 \le \delta \le 0.1\)) with \(k = 2.60\) and \({\text{Ra}} = 3200\). As \(\delta \) increases from 0.01 to 0.10 for \(B > 2\), the most unstable mode changes from stationary viscous coupling mode to oscillatory viscous coupling mode, stationary thermal coupling mode, oscillatory thermal coupling mode, and stable mode in that order.

In the nonlinear simulation described in Sect. 2.3, the convection starts in the form of the viscous coupling pattern as long as the width of the transitional layer \(\delta \) is small. However, as time proceeds, the width of transitional layer \(\delta \) gradually increases while the mixing effect of convection is not strong enough to appreciably change the density contrast between the upper and lower layers. According to Fig. 14, the increase of \(\delta \) corresponds to the transition of the convection pattern from viscous coupling to thermal coupling. Actually, this pattern transition is observed in the numerical experiment described in Sect. 2.3, consistent with Fig. 14.

3.5 Asymptotic behavior of nonlinear states after a long time integration

In all cases in our numerical study, the numerical solutions up to \(t=100\) are observed to approach time periodic solutions asymptotically.

Fig. 15
figure 15

Snapshots of a time periodic asymptotic state at \(t = 100\) for \(\delta = 0.015\); a the stream function \(\psi \), b the temperature deviation \(\varTheta \) and c, d the concentration deviation, where d is made by enlarging \(- 0.1 \le z \le 0.1\) of c. The convection is identified as viscous coupling

Full size image

Figure 15 shows the stream function \(\psi \), the temperature deviation \(\varTheta \) and the concentration deviation \(\varSigma \), numerically obtained in the nonlinear simulation of the model at \(t = 100\) for \(\delta = 0.015\). Two streets of vortex array are observed, where the vortices in the upper street rotate in the direction opposite to that of the lower vortices just below them. Similar to the numerical simulations discussed in Sect. 2.3, the signs of the temperature deviation are opposite in the upper and lower vortices. The convection is therefore viscous coupling. This convection pattern moves in the negative x direction, with the two arrays of the convection pattern remaining unchanged. This solution is thus a traveling wave with a velocity of about \(- 1.51\). The model system as well as the original system has a reflection symmetry with respect to the vertical axis at \(x = 0\), and therefore the traveling wave solution in the positive x direction also exists. The initial condition determines which traveling wave is actually observed. Over the course of time development from the initial condition, the convection maintains itself for some time, and decreases gradually to an almost quiescent state, and again starts rotation in the direction opposite to the initial convection pattern. This process continues in parallel in both layers. After the repeated reversal of the convection direction, the convection finally converges to the traveling wave moving in the negative x direction with a velocity of about \(-1.51\).

From Fig. 15, we observe that the system is invariant to the transformation \({\mathscr {F}}_{{\mathrm {vis}}}\) defined by

$$\begin{aligned} {\mathscr {F}}_{{\mathrm {vis}}} \begin{bmatrix} \psi (x, z) \\ \varTheta (x, z) \\ \varSigma (x, z) \end{bmatrix} = \begin{bmatrix} - \psi (x, - z) \\ - \varTheta (x, - z) \\ - \varSigma (x, - z) \end{bmatrix}{,} \end{aligned}$$

which we call the “viscous coupling transformation”. Actually, this may give a formal definition of the “viscous coupling” solution.

Fig. 16
figure 16

Snapshots of a time periodic asymptotic state at \(t = 100\) for \(\delta = 0.02\): a the stream function \(\psi \), b the temperature deviation \(\varTheta \) and c, d the concentration deviation, where d is made by enlarging \(- 0.1 \le z \le 0.1\) of c. The convection is identified as thermal coupling

Full size image

In contrast, Fig. 16 shows the asymptotic state for a slightly larger transitional layer width \(\delta = 0.02\) where the upper and lower vortices are observed to rotate in the same direction, and the signs of the temperature deviation and the concentration deviation are observed to be the same in the upper and lower vortices. Thus the convection is thermal coupling. As time proceeds, this thermal coupling convection experiences a process similar to that of viscous coupling convection, and finally converges to a traveling wave moving in the positive x direction with a velocity of about 0.59.

Similar to Fig. 15, the solution of the thermal coupling state shown in Fig. 16 is observed to be invariant to the transformation \({\mathscr {F}}_{{\mathrm {therm}}}\) defined by

$$\begin{aligned} {\mathscr {F}}_{{\mathrm {therm}}} \begin{bmatrix} \psi (x, z) \\ \varTheta (x, z) \\ \varSigma (x, z) \end{bmatrix} = \begin{bmatrix} - \psi \left( x - \dfrac{L_{x}}{4}, - z \right) \\ - \varTheta \left( x - \dfrac{L_{x}}{4}, - z \right) \\ - \varSigma \left( x - \dfrac{L_{x}}{4}, - z \right) \end{bmatrix}{,} \end{aligned}$$

which we call the “thermal coupling transformation”. Note that, we use the horizontal translation of \(\dfrac{L_{x}}{4}\) because, in our simulation, four convection cells were observed in the computation domain, and that these symmetries with respect to \({\mathscr {F}}_{{\mathrm {vis}}}\) and \({\mathscr {F}}_{{\mathrm {therm}}}\) are conserved respectively in the time development of (7), (8), and (14) and the boundary conditions (4), (5), and (6). This transformation may provide a formal definition of the “thermal coupling” solution, similar to the viscous coupling case.

In each case of \(\delta = 0.03, 0.04, 0.05\), and 0.06, the asymptotic state is observed to be a traveling wave with thermal coupling symmetry, while the flow decays to the quiescent state for \(\delta = 0.07\).

In summary, the time periodic asymptotic state of viscous coupling is observed for \(\delta \lesssim 0.015\), and that of thermal coupling is observed for \(\delta \gtrsim 0.02\).

3.6 Projections to viscous coupling and thermal coupling function spaces

We now define projection operators for viscous coupling and thermal coupling function spaces. We introduce an inner product of \([\psi _1(x,z), \varTheta _1(x,z), \varSigma _1(x,z)]^{T}\) and \([\psi _2(x,z), \varTheta _2(x,z), \varSigma _2(x,z)]^{T}\) as

$$\begin{aligned} \left( \begin{bmatrix} \psi _1 \\ \varTheta _1 \\ \varSigma _1 \end{bmatrix}, \begin{bmatrix} \psi _2 \\ \varTheta _2 \\ \varSigma _2 \end{bmatrix} \right) = \int _0^{L_x}\int _{-1}^{1} ( \psi _1\psi _2 + \varTheta _1\varTheta _2+\varSigma _1\varSigma _2) dzdx, \end{aligned}$$

where we assume a real Hilbert space as \(\psi \), \(\varTheta \), and \(\varSigma \) are real variables. For a thermal convection \([\psi (x, z), \varTheta (x, z), \varSigma (x, z)]^{T}\), the orthogonal projection operator to the viscous coupling space is defined as

$$\begin{aligned} {\mathscr {P}}_{{\mathrm {vis}}} \begin{bmatrix} \psi (x, z) \\ \varTheta (x, z) \\ \varSigma (x, z) \end{bmatrix} = \begin{bmatrix} \dfrac{1}{2} \left( \psi (x, z) - \psi (x, - z) \right) \\ \dfrac{1}{2} \left( \varTheta (x, z) - \varTheta (x, - z) \right) \\ \dfrac{1}{2} \left( \varSigma (x, z) - \varSigma (x, - z) \right) \end{bmatrix}, \end{aligned}$$

which clearly leaves the viscous coupling convection invariant. Also, the projection operator orthogonal to the thermal coupling space is given by

$$\begin{aligned}&{\mathscr {P}}_{{\mathrm {therm}}} \begin{bmatrix} \psi (x, z) \\ \varTheta (x, z) \\ \varSigma (x, z) \end{bmatrix} \\&\quad = \begin{bmatrix} \dfrac{1}{4} \left( \psi (x, z) - \psi \left( x + \dfrac{L_{x}}{4}, - z \right) + \psi \left( x + \dfrac{2 L_{x}}{4}, z \right) - \psi \left( x + \dfrac{3 L_{x}}{4}, - z \right) \right) \\ \dfrac{1}{4} \left( \varTheta (x, z) - \varTheta \left( x + \dfrac{L_{x}}{4}, - z \right) + \varTheta \left( x + \dfrac{2 L_{x}}{4}, z \right) - \varTheta \left( x + \dfrac{3 L_{x}}{4}, - z \right) \right) \\ \dfrac{1}{4} \left( \varSigma (x, z) - \varSigma \left( x + \dfrac{L_{x}}{4}, - z \right) + \varSigma \left( x + \dfrac{2 L_{x}}{4}, z \right) - \varSigma \left( x + \dfrac{3 L_{x}}{4}, - z \right) \right) \end{bmatrix}, \end{aligned}$$

which also keeps the thermal coupling convection invariant. We call the ranges of these operators, \({\mathscr {P}}_{{\mathrm {vis}}}\) and \({\mathscr {P}}_{{\mathrm {therm}}}\), the viscous coupling space and the thermal coupling space, respectively. Note that these spaces are positively invariant under nonlinear time development. The viscous coupling and the thermal coupling spaces are not orthogonal to each other, because their intersection includes a nontrivial linear space. However, if we take the orthogonal complements of the linear space respectively in the viscous coupling space and the thermal coupling space, these orthogonal complements are mutually orthogonal. This observation enables us to classify the solution attractors into viscous coupling and thermal coupling attractors in the next section.

3.7 Time integration of viscous coupling and thermal coupling convections

When the convection field is in the viscous coupling or thermal coupling spaces, it remains so as time passes. We found that these two types of convections are realized in the numerical simulations shown in Sect. 2.3, and they are considered to be typical convection states that may exhibit attractor-like behavior in the solution space. Therefore, we now search for the solutions in these spaces in some detail.

We stress that we should then suppress the instability that makes the solution escape from these spaces. To do so, we project the solution to the relevant space at each time step of the numerical integration.

Fig. 17
figure 17

Time series of the kinetic energy \(\epsilon \) per unit volume for the case of viscous coupling for \(\delta = 0.015, 0.02\), and 0.03

Full size image

The kinetic energy \(\epsilon \) per unit volume for the case of the viscous coupling for \(\delta = 0.015, 0.02\) and 0.03 is shown in Fig. 17, where \(\epsilon \) is defined by

$$\begin{aligned} \epsilon (t) \equiv \dfrac{1}{2 L_{x}} \int _{0}^{L_{x}} \int _{- 1}^{1} \dfrac{1}{2} | {\varvec{u}} (x, z, t) |^{2} \, {d z d x}. \end{aligned}$$

In all cases, the kinetic energy converges fairly well to a constant value.

The convection pattern is found to approach the traveling wave for \(\delta = 0.015\) and 0.02, and it decays to the quiescent state for \(\delta = 0.03\).

Fig. 18
figure 18

Time series of the kinetic energy \(\epsilon \) per volume for the case of thermal coupling for a \(\delta = 0.015, 0.02, 0.03, 0.04, 0.05\) and 0.06 until \(t = 100\), and b \(\delta = 0.015\) and 0.06 until \(t = 200\)

Full size image

In the case of thermal coupling symmetry, the kinetic energies \(\epsilon \) per unit volume for \(0.015 \le \delta \le 0.06\) are shown in Fig. 18a. We plot longer time integrations until \(t = 200\) for the cases of \(\delta = 0.015\) and 0.06 in Fig. 18b. In all cases, the kinetic energy converges fairly well to a constant value, and we see that the convections are found to converge to the traveling waves.

Therefore, the asymptotic states with the viscous coupling and thermal coupling symmetries are found to coexist for \(\delta = 0.015\) and 0.02.

However, as discussed at the end of Sect. 3.6, the function spaces of viscous coupling and thermal coupling have a nontrivial intersection. Now, we define subspaces of these spaces that are orthogonal to each other, to confirm that the attracting set (which may be attractors) of the viscous coupling solutions contain a subset that is not in the attracting set of the thermal coupling solutions, and vice versa.

For a convection \([\psi , \varTheta , \varSigma ]^{T}\), we define \(\psi _{{\mathrm {vis}}}\), \(\varTheta _{{\mathrm {vis}}}\) and \(\varSigma _{{\mathrm {vis}}}\) by

$$\begin{aligned} \begin{bmatrix} \psi _{{\mathrm {vis}}} \\ \varTheta _{{\mathrm {vis}}} \\ \varSigma _{{\mathrm {vis}}} \end{bmatrix} = ({\mathscr {P}}_{{\mathrm {vis}}} - {\mathscr {P}}_{{\mathrm {vis}}} {\mathscr {P}}_{{\mathrm {therm}}}) \begin{bmatrix} \psi \\ \varTheta \\ \varSigma \end{bmatrix}. \end{aligned}$$

Similarly, we define \(\psi _{{\mathrm {therm}}}\), \(\varTheta _{{\mathrm {therm}}}\) and \(\varSigma _{{\mathrm {therm}}}\) by

$$\begin{aligned} \begin{bmatrix} \psi _{{\mathrm {therm}}} \\ \varTheta _{{\mathrm {therm}}} \\ \varSigma _{{\mathrm {therm}}} \end{bmatrix} = ({\mathscr {P}}_{{\mathrm {therm}}} - {\mathscr {P}}_{{\mathrm {vis}}} {\mathscr {P}}_{{\mathrm {therm}}} ) \begin{bmatrix} \psi \\ \varTheta \\ \varSigma \end{bmatrix}. \end{aligned}$$

Then, \((\psi _{{\mathrm {vis}}}, \varTheta _{{\mathrm {vis}}}, \varSigma _{{\mathrm {vis}}})\) and \((\psi _{{\mathrm {therm}}}, \varTheta _{{\mathrm {therm}}}, \varSigma _{{\mathrm {therm}}})\) respectively belong to the viscous coupling and thermal coupling spaces, and they are both orthogonal to the intersection of the two spaces.

Now, we define two kinds of kinetic energy as

$$\begin{aligned} \epsilon _{{\mathrm {vis}}}(t)&\equiv \dfrac{1}{2 L_{x}} \int _{0}^{L_{x}} \int _{- 1}^{1} \dfrac{1}{2} | {\varvec{u}}_{{\mathrm {vis}}}(x, z, t) |^{2} \, d z d x, \\ \epsilon _{{\mathrm {therm}}}(t)&\equiv \dfrac{1}{2 L_{x}} \int _{0}^{L_{x}} \int _{- 1}^{1} \dfrac{1}{2} | {\varvec{u}}_{{\mathrm {therm}}}(x, z, t) |^{2} \, d z d x, \end{aligned}$$

where

$$\begin{aligned} {\varvec{u}}_{{\mathrm {vis}}} = \begin{pmatrix} \partial _{z} \psi _{{\mathrm {vis}}} \\ - \partial _{x} \psi _{{\mathrm {vis}}} \end{pmatrix} , \quad {\varvec{u}}_{{\mathrm {therm}}} = \begin{pmatrix} \partial _{z} \psi _{{\mathrm {therm}}} \\ - \partial _{x} \psi _{{\mathrm {therm}}} \end{pmatrix}. \end{aligned}$$

Then \(\epsilon _{{\mathrm {therm}}} = 0\) holds if the convection pattern has the symmetry of the viscous coupling, and \(\epsilon _{{\mathrm {vis}}} = 0\) holds when the convection pattern has the symmetry of the thermal coupling.

Fig. 19
figure 19

Time series of the kinetic energy \(\epsilon _{{\mathrm {vis}}}\) and \(\epsilon _{{\mathrm {therm}}}\) for \(\delta = 0.02\). a, b are two realizations under different initial conditions: a corresponds to the case shown in Fig. 16, and b is a case with an initial condition different from that of a

Full size image

The time series of the kinetic energy \(\epsilon _{{\mathrm {vis}}}\) and \(\epsilon _{{\mathrm {therm}}}\) for \(\delta = 0.02\) under two different initial conditions are shown in Fig. 19, where a corresponds to the flow shown in Fig. 16, and b is a case with an initial condition different from that of a. In the case of a, \(\epsilon _{{\mathrm {therm}}} \gg \epsilon _{{\mathrm {vis}}} \approx 0\) holds and so the asymptotic state is thermal coupling and has a non-viscous coupling component, which is consistent with Fig. 16. Conversely, \(\epsilon _{{\mathrm {vis}}} \gg \epsilon _{{\mathrm {therm}}} \approx 0\) holds in the case of b and so the asymptotic state is viscous coupling and has a non-thermal coupling component. Therefore, an asymptotic state with either symmetry can be realized depending on the initial conditions. In other words, attractors with viscous coupling and thermal coupling convection patterns coexist at \(\delta = 0.02\).

In summary, the attractors behave as follows:

  1. (a)

    For sufficiently small \(\delta \), \(0 < \delta \lesssim 0.02\), attractors exist with both viscous coupling and thermal coupling convection patterns.

  2. (b)

    For a larger \(\delta \), \(0.03 \lesssim \delta \lesssim 0.06\), only attractors with the thermal coupling convection pattern exist.

  3. (c)

    For a sufficiently large \(\delta \), \(0.07 \lesssim \delta \), all the fluid motion decays to the quiescent state.

Therefore, the change of convection patterns observed in numerical simulations in Sect. 2.3 may correspond to the disappearance of the attractor of viscous coupling in the model system.

4 Discussion and conclusions

In this paper, we reported our study of the transient behavior of double diffusive convection where the upper and lower fluids are miscible with each other. Numerical experiments showed two patterns of convection, namely viscous coupling and thermal coupling. Viscous coupling took place in the initial convection stage, and was replaced by thermal coupling as the width of the transitional layer increased. We introduced a model in which the width of the transitional layer between the upper and lower layers (\(\delta \)) is kept constant in the horizontal average, to describe a possible mechanism of the change in convection patterns. Both the linear stability of a stationary state of the model and nonlinear time periodic solutions implied that viscous coupling is preferred when the width of the transitional layer \(\delta \) is small, and thermal coupling is preferred when \(\delta \) is large. Furthermore the transition from viscous coupling to thermal coupling was observed at \(\delta \approx 0.02\) in all cases.

First, we investigated the linear stability of a stationary state of the model. In our calculation, the critical Rayleigh number \({\text{Ra}}_{c}\) varied from 2290 (\(\delta = 0.01\)) to 3102 (\(\delta = 0.06\)). The convection pattern of the critical mode was observed to be viscous coupling when \(\delta \) was small, and thermal coupling when \(\delta \) was large. The convection pattern of the most unstable mode at \({\text{Ra}} = 3200\) also changed from viscous coupling for small \(\delta \) to thermal coupling for large \(\delta \). This property was also observed for different concentration contrasts between the two layers except when the concentration difference was very small.

Rasenat et al. [14] performed linear stability analysis of the steady state of a two-layer thermal convection system of immiscible fluids (thus with an infinitesimal transitional layer), and showed that the viscous coupling mode is preferred when fluid properties in both layers are nearly equal. Le Bars and Davaille [9] experimentally and analytically studied the cases of immiscible fluids with different density contrasts between the two layers. They studied the linear stability of the stationary state under the assumption of an infinitesimal transitional layer and found only the viscous coupling mode for the marginal mode.

In our linear stability analysis, which focused on density contrast \(B > 1\), the viscous coupling mode is preferred when the width of the transitional layer is small, while the thermal coupling mode is preferred in the large width case. The model proposed in this paper not only reproduces the emergence of the viscous coupling convection for small transitional layer widths, but also shows the transition from viscous coupling to thermal coupling convection when the transitional layer width increases. This implies that the width of the transitional layer crucially affects the convection structure in two layer miscible fluids. Note that, to our knowledge, the previous theoretical studies treated only the case of a transitional layer with infinitesimal thickness (e.g. [9, 11]).

Oscillatory modes were found by Rasenat et al. [14], but they were not the critical modes. Nepomnyanshchy et al. [12] found oscillatory critical modes by introducing the thermo-capillary effect of the interface. In the present model study, oscillatory critical modes also arise when the transitional layer has a finite width. Eventually, numerical simulations of the original system of equations showed that the convection becomes oscillatory or time-dependent when the transitional layer width gradually increases.

In the linear stability analysis in the model system, we found that viscous coupling transitions to thermal coupling as the width of the transitional layer increases at various density contrasts between the two layers. In contrast, a transition from the thermal coupling state to the viscous coupling state was observed in a laboratory experiment [23]. This may be explained by the thickness of the transition layer around the interface between the upper and lower layers. It has been reported that the observed boundary layer around the interface is fairly thick in the thermal coupling state, while in the viscous coupling state, the boundary layer becomes thinner than that in the thermal coupling state. If we interpret the thickness of the boundary layer as the thickness of the transition layer of the horizontally averaged density profile \(\delta \), these characteristics are consistent with our linear stability analyses where viscous (thermal) coupling becomes dominant at small (large) \(\delta \).

Next, in long time integrations of the model we found that in the case of the small width of the transitional layer the flow approaches a time periodic convection whose pattern is viscous coupling, while in the case of the large width it approaches the time periodic thermal coupling convection. These model results are consistent with the numerical observation in the original system where the viscous coupling convection is realized when the width of the transitional layer is small, and the thermal coupling convection emerges when the width becomes large. Furthermore, time periodic solutions whose convection patterns were viscous coupling and thermal coupling were found to coexist when the width of the transitional layer was neither very large nor zero.

We have proposed a model study for thermal convection of miscible fluids, where in reality the width of the transitional layer grows in time and the convection pattern drastically changes when the width reaches a certain value. The model system inherits most of the time-dependent properties of the original system, but discards the growth of the horizontally averaged width of the transitional layer between the miscible fluids. This artificial model system permits us to perform a systematic analysis of the pattern transition of the convection. We expect similar modelling approaches to be useful for understanding non-steady pattern transitions in complex systems.