Anisotropic interpolation error estimates using a new geometric parameter

Abstract

We present precise anisotropic interpolation error estimates for smooth functions using a new geometric parameter and derive inverse inequalities on anisotropic meshes. In our theory, the interpolation error is bounded in terms of the diameter of a simplex and the geometric parameter. Imposing additional assumptions makes it possible to obtain anisotropic error estimates. This paper also includes corrections to an error in Theorem 2 of our previous paper, “General theory of interpolation error estimates on anisotropic meshes” (Japan Journal of Industrial and Applied Mathematics, 38 (2021) 163–191).

1 Introduction

Analyzing the errors of interpolations on d-simplices is an important subject in numerical analysis. It is particularly crucial for finite element error analysis. Let us briefly outline the problems considered in this paper using the Lagrange interpolation operator.

Let $d \in \{ 1,2,3\}$. Let $\widehat{T} \subset {\mathbb {R}}^d$ and $T_0 \subset {\mathbb {R}}^d$ be a reference element and a simplex, respectively, that are affine equivalent. Let us consider two Lagrange finite elements $\{ \widehat{T},\widehat{P} :={\mathcal {P}}^k, \widehat{\varSigma } \}$ and $\{ {T}_0,{P} :={\mathcal {P}}^k, {\varSigma } \}$ with associated normed vector spaces $V(\widehat{T}) := {\mathcal {C}}(\widehat{T})$ and $V(T_0) :={\mathcal {C}}(T_0)$ with $k \in {\mathbb {N}}$, where ${\mathcal {P}}^m$ is the space of polynomials with degree at most $m \in {\mathbb {N}}_0 := {\mathbb {N}} \cup \{ 0 \}$. For $\hat{\varphi } \in V(\widehat{T})$, we use the correspondences

$$\begin{aligned} (\varphi _0:T_0 \rightarrow {\mathbb {R}}) \rightarrow (\hat{\varphi } := {\varphi }_0 \circ {\varPhi }:\widehat{T} \rightarrow {\mathbb {R}}), \end{aligned}$$

where $\varPhi$ is an affine mapping. Let $I_{\widehat{T}}^k: V(\widehat{T}) \rightarrow {\mathcal {P}}^k$ and $I_{{T}_0}^k: V({T}_0) \rightarrow {\mathcal {P}}^k$ be the corresponding Lagrange interpolation operators. Details can be found in Sect. 2.3.

We first consider the case in which $d=1$. Let $\varOmega := (0,1) \subset {\mathbb {R}}$. For $N \in {\mathbb {N}}$, let ${\mathbb {T}}_h = \{ 0 = x_0< x_1< \cdots< x_N < x_{N+1} = 1 \}$ be a mesh of $\overline{\varOmega }$ such as

$$\begin{aligned} \overline{\varOmega } := \bigcup _{i=1}^N T_0^i, \quad {\mathrm{int}}T_0^i \cap {\mathrm{int}}T_0^j = \emptyset \quad {\text {for}}\ i \ne j, \end{aligned}$$

where $T_0^i := [x_i , x_{i+1}]$ for $0 \le i \le N$. We denote $h_i := x_{i+1} - x_i$ for $0 \le i \le N$. If we set $x_j := \frac{j}{N+1}$ for $j=0,1,\ldots ,N,N+1$, the mesh ${\mathbb {T}}_h$ is said to be the uniform mesh. If we set $x_j := g \left( \frac{j}{N+1} \right)$ for $j=1,\ldots ,N,N+1$ with a grading function g, the mesh ${\mathbb {T}}_h$ is said to be the graded mesh with respect to $x=0$; see [5]. In particular, when $g(y) := y^{\varepsilon }$ ($\varepsilon > 0$), the mesh is called the radical mesh. To obtain the Lagrange interpolation error estimates, we impose standard assumptions and specify that $\ell , m \in {\mathbb {N}}_0$ and $p , q \in [1,\infty ]$ such that

$$\begin{aligned} 0 \le m \le \ell + 1: \quad W^{\ell +1,p}(\widehat{T}) \hookrightarrow W^{m,q} (\widehat{T}). \end{aligned}$$

(1)

Under these assumptions, the following holds for any $\varphi _0 \in W^{\ell +1,p}(T_0^i)$ with $\hat{\varphi } = \varphi _0 \circ \varPhi$:

$$\begin{aligned} |\varphi _0 - {I}_{T_0^i}^k \varphi _0 |_{W^{m,q}(T_0^i)} \le c h_{i}^{\frac{1}{q} - \frac{1}{p} + \ell +1-m} | \varphi _0 |_{W^{\ell +1,p}(T_0^i)}. \end{aligned}$$

(2)

The proof of this statement is standard; see [12]. When $p = q$, it is possible to obtain optimal error estimates even if the scale is different for each element. When $q > p$, the order of convergence of the interpolation operator may deteriorate.

We now consider the cases in which $d=2,3$. Let $\varOmega \subset {\mathbb {R}}^d$ be a bounded polyhedral domain. Let ${\mathbb {T}}_h = \{ T_0 \}$ be a simplicial mesh of $\overline{\varOmega }$ made up of closed d-simplices, such as

$$\begin{aligned} \overline{\varOmega } = \bigcup _{T_0 \in {\mathbb {T}}_h} T_0 \end{aligned}$$

with $h := \max _{T_0 \in {\mathbb {T}}_h} h_{T_0}$, where $h_{T_0} := {\mathrm{diam}}(T_0)$. For simplicity, we assume that ${\mathbb {T}}_h$ is conformal. That is, ${\mathbb {T}}_h$ is a simplicial mesh of $\overline{\varOmega }$ without hanging nodes. Let $\widehat{T} \subset {\mathbb {R}}^d$ be the reference element defined in Sect. 2 and $\varPhi$ be the affine mapping defined in Eq. (13). For any $T_0 \in {\mathbb {T}}_h$, it holds that $T_0 = \varPhi (\widehat{T})$. Under the standard assumptions and Eq. (1), the following holds for any $\varphi _0 \in W^{\ell +1,p}(T_0)$ with $\hat{\varphi } = \varphi _0 \circ \varPhi$:

$$\begin{aligned} |\varphi _0 - {I}_{T_0}^k \varphi _0 |_{W^{m,q}(T_0)} \le c |T_0|^{\frac{1}{q} - \frac{1}{p}} \left( \frac{\alpha _{\max }}{\alpha _{\min }} \right) ^m \left( \frac{H_{T_0}}{h_{T_0}} \right) ^m h_{T_0}^{\ell +1-m} | \varphi _0 |_{W^{\ell +1,p}(T_0)}, \end{aligned}$$

(3)

where $|T_0|$ is the measure of $T_0$, the parameters $\alpha _{\max }$ and $\alpha _{\min }$ are defined in Eq. (50), and the parameter $H_{T_0}$ is as proposed in a recent paper [16]; see Sect. 2.4 for a definition. The proof of estimate (3) can be found in Sect. 5. Compared with the one-dimensional case, the quantities $\alpha _{\max }/\alpha _{\min }$ and $H_{T_0}/h_{T_0}$ negatively affect the order of convergence and do not appear in Eq.(2). The two quantities $\alpha _{\max }/\alpha _{\min }$ and $H_{T_0}/h_{T_0}$ are considered in Sect. 7.1. As a mesh condition, the shape-regularity condition is widely used and well known. This condition states that there exists a constant $\gamma > 0$ such that

$$\begin{aligned} \rho _{T_0} \ge \gamma h_{T_0} \quad \forall {\mathbb {T}}_h \in \{ {\mathbb {T}}_h \}, \quad \forall T_0 \in {\mathbb {T}}_h, \end{aligned}$$

(4)

where $\rho _{T_0}$ is the radius of the inscribed ball of $T_0$. Under this condition, it holds that

$$\begin{aligned} |\varphi _0 - {I}_{T_0}^k \varphi _0 |_{W^{m,q}(T_0)} \le c |T_0|^{\frac{1}{q} - \frac{1}{p}} h_{T_0}^{\ell +1-m} | \varphi _0 |_{W^{\ell +1,p}(T_0)}; \end{aligned}$$

(5)

see Sect. 7.1.1. If condition (4) is violated (i.e., the simplex becomes too flat as $h_{T_0} \rightarrow 0$), the quantity

$$\begin{aligned} \left( \frac{\alpha _{\max }}{\alpha _{\min }} \right) ^m \left( \frac{H_{T_0}}{h_{T_0}} \right) ^m h_{T_0}^{\ell +1-m} \end{aligned}$$

may diverge even when $p=q$. The effect of the quantity $|T_0|^{\frac{1}{q} - \frac{1}{p}}$ on the interpolation error estimates is considered in Sect. 7.2.

In some cases, it is not necessary for condition (4) to hold to obtain Eq. (5). The shape-regularity condition can be relaxed to the maximum-angle condition, as stated in Eqs. (20) and (21), for both two-dimensional [4] and three-dimensional cases [20]. Anisotropic interpolation theory has also been developed [1, 2, 8]. The idea of Apel et al. is to construct a set of functionals satisfying conditions (54), (55), and (56). The introduction of these functionals makes it possible to remove the quantity $\alpha _{\max }/\alpha _{\min }$. Under the conditions of the maximum angle and coordinate system, anisotropic interpolation error estimates can then be deduced (e.g., see [1]).

In contrast, this paper proposes anisotropic interpolation error estimates using the new parameter under conditions (54), (55), and (56) and Assumption 1; i.e., we derive the following anisotropic error estimate (Theorem B, in particular, Corollary 1):

$$\begin{aligned}&| {\varphi }_0 - I_{{T}_0}^k {\varphi }_0 |_{W^{m,q}({T}_0)} \nonumber \\&\quad \le c |T_0|^{\frac{1}{q} - \frac{1}{p}} \left( \frac{H_{T_0}}{h_{T_0}} \right) ^m \sum _{|\gamma | = \ell -m} {\mathscr {H}}^{\gamma } | \partial ^{\gamma } {(\varphi _0 \circ \varPhi _{T_0})} |_{W^{ m ,p}(\varPhi _{T_0}^{-1}(T_0))}, \end{aligned}$$

(6)

where $\varPhi _{T_0}$ is defined in Eq. (12), $\gamma := (\gamma _1 , \ldots , \gamma _d) \in {\mathbb {N}}_0^d$ is a multi-index, and ${\mathscr {H}}^{\gamma }$ is specified in Definition 3. Theorem B applies to interpolations other than the Lagrange interpolation, and the basis for the proof of Theorem B is the scaling argument described in Sect. 3.

Because the new geometric parameter is used in the interpolation error analysis, the coefficient c used in the error estimation is independent of the geometry of the simplices, and the error estimations obtained may therefore be applied to arbitrary meshes, including very “flat” or anisotropic simplices. Furthermore, we are naturally able to consider the following geometric condition as being sufficient to obtain optimal order estimates (when $p=q$): there exists $\gamma _0 > 0$ such that

$$\begin{aligned} \frac{H_{T_0}}{h_{T_0}} \le \gamma _0 \quad \forall {\mathbb {T}}_h \in \{ {\mathbb {T}}_h \}, \quad \forall T_0 \in {\mathbb {T}}_h. \end{aligned}$$

(7)

Condition (7) appears to be simpler than the maximum-angle condition. Furthermore, the quantity $H_{T_0} / h_{T_0}$ can be easily calculated in the numerical process of finite element methods. Therefore, the new condition may be useful. A recent paper [18] showed that the new condition is satisfied if and only if the maximum-angle condition holds. We expect the new mesh condition to become an alternative to the maximum-angle condition.

Furthermore, under Assumption 1, component-wise inverse inequalities can be deduced as (see Sect. 7.3):

$$\begin{aligned} \Vert \partial ^{\gamma } \varphi _h \Vert _{L^q(T)} \le C^{IVC} |T|^{\frac{1}{q} - \frac{1}{p}} {\mathscr {H}}^{- \gamma } \Vert {\varphi }_h \Vert _{L^p({T})}. \end{aligned}$$

In a previous paper [16], the present authors developed new interpolation error estimations in a general framework and derived Raviart–Thomas interpolations on d-simplices. However, the statement of Theorem 2 in [16] includes a mistake. That is, under standard assumptions, the quantity $\alpha _{\max }/\alpha _{\min }$ cannot be removed. We need to modify the statement of this theorem to correct this error. The current paper presents Theorems A (see Sect. 5) and B (see Sect. 6), which replace Theorem 2 of [16]. In Sect. 4, we explain the inaccuracies in the proof of Theorem 2 in [16] and describe how the results can be recovered using our Theorems A and B. Furthermore, the Babuška and Aziz technique is generally not applicable on anisotropic meshes in the proof of Theorem 3 in [16]. Details will be discussed in a coming paper [14].

When there is no ambiguity, we use the notation and definitions given in [16]. Throughout this paper, c denotes a constant independent of h (defined later), unless specified otherwise. These values may change in each context. ${\mathbb {R}}_+$ is the set of positive real numbers.

2 Strategy for constructing anisotropic interpolation theory

In standard interpolation theory, one introduces an affine mapping that connects the reference element to the mesh element. However, on anisotropic meshes, the interpolation errors may be overestimated. Therefore, our strategy is to divide the transformation into three affine mappings.

2.1 Standard positions of simplices

We recall [16, Section 3]. Let us first define a diagonal matrix $\widehat{A}^{(d)}$ as

$$\begin{aligned} \widehat{A}^{(d)} := {\mathrm{diag}}(\alpha _1,\ldots ,\alpha _d), \quad \alpha _i \in {\mathbb {R}}_+ \quad \forall i. \end{aligned}$$

(8)

2.1.1 Two-dimensional case

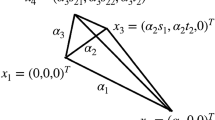
Let $\widehat{T} \subset {\mathbb {R}}^2$ be the reference triangle with vertices $\hat{x}_1 := (0,0)^T$, $\hat{x}_2 := (1,0)^T$, and $\hat{x}_3 := (0,1)^T$.

Let $\widetilde{{\mathfrak {T}}}^{(2)}$ be the family of triangles

$$\begin{aligned} \widetilde{T} = \widehat{A}^{(2)} (\widehat{T}) \end{aligned}$$

with vertices $\tilde{x}_1 := (0,0)^T$, $\tilde{x}_2 :=(\alpha _1,0)^T$, and $\tilde{x}_3 := (0,\alpha _2)^T$.

We next define the regular matrices $\widetilde{A} \in {\mathbb {R}}^{2 \times 2}$ by

$$\begin{aligned} \widetilde{A} :=\begin{pmatrix} 1 &{} \quad s \\ 0 &{}\quad t \\ \end{pmatrix}, \end{aligned}$$

(9)

with parameters

$$\begin{aligned} s^2 + t^2 = 1, \quad t > 0. \end{aligned}$$

For $\widetilde{T} \in \widetilde{{\mathfrak {T}}}^{(2)}$, let ${\mathfrak {T}}^{(2)}$ be the family of triangles

$$\begin{aligned} T = \widetilde{A} (\widetilde{T}) \end{aligned}$$

with vertices $x_1 := (0,0)^T, \ x_2 := (\alpha _1,0)^T, \ x_3 :=(\alpha _2 s , \alpha _2 t)^T$. We then have that $\alpha _1 = |x_1 -x_2| > 0$ and $\alpha _2 = |x_1 - x_3| > 0$.

2.1.2 Three-dimensional case

Let $\widehat{T}_1$ and $\widehat{T}_2$ be reference tetrahedra with the following vertices:

• (i) $\widehat{T}_1$ has the vertices $\hat{x}_1 := (0,0,0)^T$, $\hat{x}_2 := (1,0,0)^T$, $\hat{x}_3 := (0,1,0)^T$, $\hat{x}_4 := (0,0,1)^T$;

• (ii) $\widehat{T}_2$ has the vertices $\hat{x}_1 := (0,0,0)^T$, $\hat{x}_2 := (1,0,0)^T$, $\hat{x}_3 := (1,1,0)^T$, $\hat{x}_4 := (0,0,1)^T$.

Let $\widetilde{{\mathfrak {T}}}_i^{(3)}$, $i=1,2$, be the family of triangles

$$\begin{aligned} \widetilde{T}_i = \widehat{A}^{(3)} (\widehat{T}_i), \quad i=1,2, \end{aligned}$$

with vertices

• (i) $\tilde{x}_1 := (0,0,0)^T$, $\tilde{x}_2 := (\alpha _1,0,0)^T$, $\tilde{x}_3 := (0,\alpha _2,0)^T$, and $\tilde{x}_4 := (0,0,\alpha _3)^T$;

• (ii) $\tilde{x}_1 := (0,0,0)^T$, $\tilde{x}_2 := (\alpha _1,0,0)^T$, $\tilde{x}_3 := (\alpha _1,\alpha _2,0)^T$, and $\tilde{x}_4 := (0,0,\alpha _3)^T$.

We next define the regular matrices $\widetilde{A}_1, \widetilde{A}_2 \in {\mathbb {R}}^{3 \times 3}$ by

$$\begin{aligned} \widetilde{A}_1 :=\begin{pmatrix} 1 &{}\quad s_1 &{}\quad s_{21} \\ 0 &{}\quad t_1 &{}\quad s_{22}\\ 0 &{}\quad 0 &{}\quad t_2\\ \end{pmatrix}, \quad \widetilde{A}_2 :=\begin{pmatrix} 1 &{}\quad - s_1 &{}\quad s_{21} \\ 0 &{}\quad t_1 &{}\quad s_{22}\\ 0 &{}\quad 0 &{}\quad t_2\\ \end{pmatrix} \end{aligned}$$

(10)

with parameters

$$\begin{aligned} {\left\{ \begin{array}{ll} s_1^2 + t_1^2 = 1, \quad s_1> 0, \quad t_1> 0, \quad \alpha _2 s_1 \le \alpha _1 / 2, \\ s_{21}^2 + s_{22}^2 + t_2^2 = 1, \quad t_2 > 0, \quad \alpha _3 s_{21} \le \alpha _1 / 2. \end{array}\right. } \end{aligned}$$

For $\widetilde{T}_i \in \widetilde{{\mathfrak {T}}}_i^{(3)}$, $i=1,2$, let ${\mathfrak {T}}_i^{(3)}$, $i=1,2$, be the family of tetrahedra

$$\begin{aligned} T_i = \widetilde{A}_i (\widetilde{T}_i), \quad i=1,2, \end{aligned}$$

with vertices

$$\begin{aligned}&x_1 := (0,0,0)^T, \ x_2 := (\alpha _1,0,0)^T, \ x_4 := (\alpha _3 s_{21}, \alpha _3 s_{22}, \alpha _3 t_2)^T, \\&{\left\{ \begin{array}{ll} x_3 := (\alpha _2 s_1 , \alpha _2 t_1 , 0)^T \quad {\text {for case (i)}}, \\ x_3 := (\alpha _1 - \alpha _2 s_1, \alpha _2 t_1,0)^T \quad {\text {for case (ii)}}. \end{array}\right. } \end{aligned}$$

We then have $\alpha _1 = |x_1 - x_2| > 0$, $\alpha _3 = |x_1 - x_4| > 0$, and

$$\begin{aligned} \alpha _2 = {\left\{ \begin{array}{ll} |x_1 - x_3|> 0 \quad {\text {for case (i)}}, \\ |x_2 - x_3| > 0 \quad {\text {for case (ii)}}. \end{array}\right. } \end{aligned}$$

In the following, we impose conditions for $T \in {\mathfrak {T}}^{(2)}$ in the two-dimensional case and $T \in {\mathfrak {T}}_1^{(3)} \cup {\mathfrak {T}}_2^{(3)} =:{\mathfrak {T}}^{(3)}$ in the three-dimensional case.

Condition 1

(Case in which $d=2$) Let $T \in {\mathfrak {T}}^{(2)}$ with the vertices $x_i$ ($i=1,\ldots ,3$) introduced in Sect. 2.1.1. We assume that $\overline{x_2 x_3}$ is the longest edge of T; i.e., $h_T := |x_2 - x_ 3|$. Recall that $\alpha _1 = |x_1 - x_2|$ and $\alpha _2 = |x_1 - x_3|$. We then assume that $\alpha _2 \le \alpha _1$. Note that $\alpha _1 = {\mathcal {O}}(h_T)$.

Condition 2

(Case in which $d=3$) Let $T \in {\mathfrak {T}}^{(3)}$ with the vertices $x_i$ ($i=1,\ldots ,4$) introduced in Sect. 2.1.2. Let $L_i$ ($1 \le i \le 6$) be the edges of T. We denote by $L_{\min }$ the edge of T that has the minimum length; i.e., $|L_{\min }| =\min _{1 \le i \le 6} |L_i|$. We set $\alpha _2 := |L_{\min }|$ and assume that

$$\begin{aligned} {\text {the end points of}}\ L_{\min }\ {\text {are either}} \ \{ x_1 , x_3\}\ {\text {or}}\ \{ x_2 , x_3\}. \end{aligned}$$

Among the four edges that share an end point with $L_{\min }$, we take the longest edge $L^{({\min })}_{\max }$. Let $x_1$ and $x_2$ be the end points of edge $L^{({\min })}_{\max }$. Thus, we have that

$$\begin{aligned} \alpha _1 = |L^{(\min )}_{\max }| = |x_1 - x_2|. \end{aligned}$$

Consider cutting ${\mathbb {R}}^3$ with the plane that contains the midpoint of edge $L^{(\min )}_{\max }$ and is perpendicular to the vector $x_1 - x_2$. We then have two cases:

• (Type i) $x_3$ and $x_4$ belong to the same half-space;

• (Type ii) $x_3$ and $x_4$ belong to different half-spaces.

In each respective case, we set

• (Type i) $x_1$ and $x_3$ as the end points of $L_{\min }$, that is, $\alpha _2 = |x_1 - x_3|$;

• (Type ii) $x_2$ and $x_3$ as the end points of $L_{\min }$, that is, $\alpha _2 = |x_2 - x_3|$.

Finally, we set $\alpha _3 = |x_1 - x_4|$. Note that we implicitly assume that $x_1$ and $x_4$ belong to the same half-space. In addition, note that $\alpha _1 = {\mathcal {O}}(h_T)$.

Remark 1

Let ${\mathbb {T}}_h$ be a conformal mesh. We assume that any simplex $T_0 \in {\mathbb {T}}_h$ is transformed into $T_1 \in {\mathfrak {T}}^{(2)}$ such that Condition 1 is satisfied (in the two-dimensional case) or $T_i \in {\mathfrak {T}}_i^{(3)}$, $i=1,2$, such that Condition 2 is satisfied (in the three-dimensional case) through appropriate rotation, translation, and mirror imaging. Note that none of the lengths of the edges of a simplex or the measure of the simplex is changed by the transformation.

Assumption 1

In anisotropic interpolation error analysis, we may impose the following geometric conditions for the simplex T:

• 1. If $d=2$, there are no additional conditions;

• 2. If $d=3$, there exists a positive constant M, independent of $h_T$, such that $|s_{22}| \le M \frac{\alpha _2 t_1}{\alpha _3}$. Note that if $s_{22} \ne 0$, this condition means that the order with respect to $h_T$ of $\alpha _3$ coincides with the order of $\alpha _2$, whereas if $s_{22} = 0$, the order of $\alpha _3$ may be different from that of $\alpha _2$.

2.2 Affine mappings

In our strategy, we adopt the following affine mappings.

Definition 1

(Affine mappings) Let $\widetilde{T}, \widehat{T} \subset {\mathbb {R}}^d$ be the simplices defined in Sects. 2.1.1 and 2.1.2. That is,

$$\begin{aligned} \widetilde{T} = \widehat{\varPhi } (\widehat{T}), \quad {T} = \widetilde{\varPhi } (\widetilde{T}) \quad {\text {with}} \quad \tilde{x} := \widehat{\varPhi }(\hat{x}) := \widehat{{A}}^{(d)} \hat{x}, \quad x := \widetilde{\varPhi }(\tilde{x}) := \widetilde{{A}} \tilde{x}. \end{aligned}$$

We then define an affine mapping $\varPhi _T: \widehat{T} \rightarrow T$ as

$$\begin{aligned} \varPhi _T := \widetilde{\varPhi } \circ \widehat{\varPhi }: \widehat{T} \rightarrow T, \ {x} :={\varPhi }_T(\hat{x}) := {{A}}_T \hat{x}, \quad {A}_T := \widetilde{{A}} \widehat{{A}}^{(d)}. \end{aligned}$$

(11)

Furthermore, let $\varPhi _{T_0}$ be an affine mapping defined as

$$\begin{aligned} \varPhi _{T_0}: T \ni x \mapsto {A}_{T_0} x + b_{T_0} \in T_0, \end{aligned}$$

(12)

where $b_{T_0} \in {\mathbb {R}}^d$ and ${A}_{T_0} \in O(d)$ is a rotation and mirror imaging matrix. We then define an affine mapping $\varPhi : \widehat{T} \rightarrow T_0$ as

$$\begin{aligned} \varPhi := {\varPhi }_{T_0} \circ {\varPhi }_T: \widehat{T} \rightarrow T_0, \ x^{(0)} := \varPhi (\hat{x}) = ({\varPhi }_{T_0} \circ {\varPhi }_T)(\hat{x}) = {A} \hat{x} + b_{T_0}, \end{aligned}$$

(13)

where ${A} := {A}_{T_0} {A}_T$.

2.3 Finite element generation

We follow the procedure described in [12, Section 1.4.1 and 1.2.1]; see also [16, Section 3.5].

For the reference element $\widehat{T}$ defined in Sects. 2.1.1 and 2.1.2, let $\{\widehat{T} , \widehat{{P}} , \widehat{\varSigma } \}$ be a fixed reference finite element, where $\widehat{{P}}$ is a vector space of functions $\hat{p}: \widehat{T} \rightarrow {\mathbb {R}}^n$ for some positive integer n (typically $n=1$ or $n=d$) and $\widehat{\varSigma }$ is a set of $n_{0}$ linear forms $\{\hat{\chi }_1, \ldots , \hat{\chi }_{n_0} \}$ such that

$$\begin{aligned} \widehat{{P}} \ni \hat{p} \mapsto (\hat{\chi }_1(\hat{p}) , \ldots , \hat{\chi }_{n_0}(\hat{p}))^T \in {\mathbb {R}}^{n_0} \end{aligned}$$

is bijective; i.e., $\widehat{\varSigma }$ is a basis for ${\mathcal {L}}(\widehat{P};{\mathbb {R}})$. Further, we denote by $\{\hat{\theta }_1 , \ldots , \hat{\theta }_{n_0} \}$ in $\widehat{{P}}$ the local (${\mathbb {R}}^n$-valued) shape functions such that

$$\begin{aligned} \hat{\chi }_i(\hat{\theta }_j) = \delta _{ij}, \quad 1 \le i,j \le n_0. \end{aligned}$$

Let $V(\widehat{T})$ be a normed vector space of functions $\hat{\varphi }: \widehat{T} \rightarrow {\mathbb {R}}^n$ such that $\widehat{P} \subset V(\widehat{T})$ and the linear forms $\{\hat{\chi }_1 , \ldots , \hat{\chi }_{n_0} \}$ can be extended to $V(\widehat{T})^{\prime }$. The local interpolation operator ${I}_{\widehat{T}}$ is then defined by

$$\begin{aligned} {I}_{\widehat{T}} : V(\widehat{T}) \ni \hat{\varphi } \mapsto \sum _{i=1}^{n_0} \hat{\chi }_i (\hat{\varphi }) \hat{\theta }_i \in \widehat{{P}}. \end{aligned}$$

(14)

It is obvious that

$$\begin{aligned}&\hat{\chi }_i ({I}_{\widehat{T}} \hat{\varphi }) =\hat{\chi }_i (\hat{\varphi }) \quad \forall \hat{\varphi } \in V(\widehat{T}), \quad i=1,\ldots ,n_0, \end{aligned}$$

(15)

$$\begin{aligned}&I_{\widehat{T}} \hat{p} = \hat{p} \quad \forall \hat{p} \in \widehat{P}. \end{aligned}$$

(16)

Let ${\varPhi }$ be the affine mapping defined in Eq. (13). For $T_0 = {\varPhi } (\widehat{T})$, we first define a Banach space $V(T_0)$ of ${\mathbb {R}}^n$-valued functions that is the counterpart of $V(\widehat{T})$ and define a linear bijection mapping by

$$\begin{aligned} \psi := \psi _{\widehat{T}} \circ \psi _{\widetilde{T}} \circ \psi _{T} : V(T_0) \ni \varphi \mapsto \hat{\varphi } := \psi (\varphi ) := \varphi \circ \varPhi \in V(\widehat{T}) \end{aligned}$$

with the three linear bijection mappings

$$\begin{aligned}&\psi _{{T}} : V({T}_0) \ni \varphi _0 \mapsto {\varphi } := \psi _{{T}}(\varphi _0) := \varphi _0 \circ {\varPhi }_{T_0} \in V({T}), \\&\psi _{\widetilde{T}} : V({T}) \ni \varphi \mapsto \tilde{\varphi } := \psi _{\widetilde{T}}(\varphi ) := \varphi \circ \widetilde{\varPhi } \in V(\widetilde{T}), \\&\psi _{\widehat{T}} : V(\widetilde{T}) \ni \tilde{\varphi } \mapsto \hat{\varphi } := \psi _{\widehat{T}} (\tilde{\varphi }) := \tilde{\varphi } \circ \widehat{\varPhi } \in V(\widehat{T}). \end{aligned}$$

The triple $\{ \widetilde{T} , \widetilde{P} , \widetilde{\varSigma }\}$ is defined as

$$\begin{aligned} {\left\{ \begin{array}{ll} \widetilde{T} = \widehat{\varPhi }(\widehat{T}); \\ \widetilde{P} = \{ \psi _{\widehat{T}}^{-1}(\hat{p}) ; \ \hat{p} \in \widehat{{P}}\}; \\ \widetilde{\varSigma } = \{ \{ \tilde{\chi }_{i} \}_{1 \le i \le n_0}; \ \tilde{\chi }_{i} = \hat{\chi }_i (\psi _{\widehat{T}}(\tilde{p})), \forall \tilde{p} \in \widetilde{P}, \hat{\chi }_i \in \widehat{\varSigma } \}. \end{array}\right. } \end{aligned}$$

The triples $\{ {T} , {P} , {\varSigma } \}$ and $\{ {T}_0 , {P}_0 , {\varSigma }_0 \}$ are similarly defined. These triples are finite elements and the local shape functions are $\tilde{\theta }_{i} = \psi _{\widehat{T}}^{-1}(\hat{\theta }_i)$, $\theta _{i} = \psi _{\widetilde{T}}^{-1}(\tilde{\theta }_i)$, and $\theta _{0,i} := \psi _{T}^{-1} (\theta _i)$ for $1 \le i \le n_0$, and the associated local interpolation operators are respectively defined by

$$\begin{aligned} {I}_{\widetilde{T}} : V(\widetilde{T}) \ni \tilde{\varphi } \mapsto {I}_{\widetilde{T}} \tilde{\varphi }&:= \sum _{i=1}^{n_0} \tilde{\chi }_{i}(\tilde{\varphi }) \tilde{\theta }_{i} \in \widetilde{P}, \end{aligned}$$

(17)

$$\begin{aligned} {I}_{T} : V(T) \ni \varphi \mapsto {I}_{T} \varphi&:= \sum _{i=1}^{n_0} \chi _{i}(\varphi ) \theta _{i} \in {P}, \end{aligned}$$

(18)

$$\begin{aligned} {I}_{T_0} : V(T_0) \ni \varphi _0 \mapsto {I}_{T_0} \varphi _0&:= \sum _{i=1}^{n_0} \chi _{0,i}(\varphi _0) \theta _{i} \in {P}_0. \end{aligned}$$

(19)

Proposition 1

The diagrams

commute.

Proof

See, for example [12, Proposition 1.62]. □

2.4 New parameters

In a previous paper [16], we proposed two geometric parameters,

Definition 2

The parameter $H_T$ is defined as

$$\begin{aligned} H_T := \frac{\prod _{i=1}^d \alpha _i}{|T|} h_T, \end{aligned}$$

and the parameter $H_{T_0}$ is defined as

$$\begin{aligned} H_{T_0} := \frac{h_{T_0}^2}{|T_0|} \min _{1 \le i \le 3} |L_i| \quad {\text {if}}\ d=2, \quad H_{T_0} := \frac{h_{T_0}^2}{|T_0|} \min _{1 \le i , j \le 6, i \ne j} |L_i| |L_j| \quad {\text {if}}\ d=3 \end{aligned}$$

where $L_i$ denotes the edges of the simplex $T_0 \subset {\mathbb {R}}^d$.

The following lemma shows the equivalence between $H_T$ and $H_{T_0}$.

Lemma 1

It holds that

$$\begin{aligned} \frac{1}{2} H_{T_0}< H_T < 2 H_{T_0}. \end{aligned}$$

Furthermore, in the two-dimensional case, $H_{T_0}$ is equivalent to the circumradius $R_2$ of $T_0$.

Proof

The proof can be found in [16, Lemma 3]. □

Remark 2

We set

$$\begin{aligned} H(h) := \max _{T_0 \in {\mathbb {T}}_h} H_{T_0}. \end{aligned}$$

As we stated in the Introduction, if the maximum-angle condition is violated, the parameter H(h) may diverge as $h \rightarrow 0$ on anisotropic meshes. Therefore, imposing the maximum-angle condition for mesh partitions guarantees the convergence of finite element methods [3]. Reference [4] studied cases in which the finite element solution may not converge to the exact solution.

We now state the following theorem concerning the new condition.

Theorem 1

Condition (7) holds if and only if there exist $0<\gamma _1, \gamma _2 < \pi$ such that

$$\begin{aligned} d=2: \quad \theta _{T_0,\max } \le \gamma _1 \quad \forall {\mathbb {T}}_h \in \{ {\mathbb {T}}_h \}, \quad \forall T_0 \in {\mathbb {T}}_h, \end{aligned}$$

(20)

where $\theta _{T_0,\max }$ is the maximum angle of $T_0$, and

$$\begin{aligned} d=3: \quad \theta _{T_0, \max } \le \gamma _2, \quad \psi _{T_0, \max } \le \gamma _2 \quad \forall {\mathbb {T}}_h \in \{ {\mathbb {T}}_h \}, \quad \forall T_0 \in {\mathbb {T}}_h, \end{aligned}$$

(21)

where $\theta _{T_0, \max }$ is the maximum angle of all triangular faces of the tetrahedron $T_0$ and $\psi _{T_0, \max }$ is the maximum dihedral angle of $T_0$. Conditions (20) and (21) together constitute the maximum-angle condition.

Proof

In the case of $d=2$, we use the previous result presented in [19]; i.e., there exists a constant $\gamma _3 > 0$ such that

$$\begin{aligned} \frac{R_2}{h_{T_0}} \le \gamma _3 \quad \forall {\mathbb {T}}_h \in \{ {\mathbb {T}}_h \}, \quad \forall T_0 \in {\mathbb {T}}_h, \end{aligned}$$

if and only if condition (20) is satisfied. Combining this result with $H_{T_0}$ being equivalent to the circumradius $R_2$ of $T_0$, we have the desired conclusion. In the case of $d=3$, the proof can be found in a recent paper [18]. □

Lemma 2

It holds that

$$\begin{aligned} \Vert \widehat{{A}}^{(d)} \Vert _2&\le h_{T}, \quad \Vert \widehat{{A}}^{(d)} \Vert _2 \Vert (\widehat{{A}}^{(d)})^{-1} \Vert _2 =\frac{\max \{\alpha _1 , \ldots , \alpha _d \}}{\min \{\alpha _1 , \ldots , \alpha _d \}}, \end{aligned}$$

(22a)

$$\begin{aligned} \Vert \widetilde{{A}} \Vert _2&\le {\left\{ \begin{array}{ll} \sqrt{2} \quad {\text {if}}\ d=2, \\ 2 \quad {\text {if}}\ d=3, \end{array}\right. } \quad \Vert \widetilde{{A}} \Vert _2 \Vert \widetilde{{A}}^{-1} \Vert _2 \le {\left\{ \begin{array}{ll} \frac{\alpha _1 \alpha _2}{|T|} = \frac{H_{T}}{h_{T}} \quad {\text {if}}\ d=2, \\ \frac{2}{3} \frac{\alpha _1 \alpha _2 \alpha _3}{|T|} = \frac{2}{3} \frac{H_{T}}{h_{T}} \quad {\text {if}}\ d=3, \end{array}\right. } \end{aligned}$$

(22b)

$$\begin{aligned} \Vert A_{T_0} \Vert _2&= 1, \quad \Vert A_{T_0}^{-1} \Vert _2 = 1. \end{aligned}$$

(22c)

Furthermore, we have

$$\begin{aligned} | \det ({A}_T) | = | \det (\widetilde{{A}}) | | \det (\widehat{{A}}^{(d)}) | = d ! |T |, \quad | \det ({A}_{T_0}) | = 1. \end{aligned}$$

(23)

Proof

The proof of (22b) can be found in [16, (4.4), (4.5), (4.6), and (4.7)]. The inequality (22a) is easily proved. Because $A_{T_0} \in O(d)$, one easily finds that $A_{T_0}^{-1} \in O(d)$ and recovers Eq. (22c). The proof of equality (23) is standard. □

For matrix $A \in {\mathbb {R}}^{d \times d}$, we denote by $[{A}]_{ij}$ the (i, j)-component of A. We set $\Vert A \Vert _{\max } := \max _{1 \le i,j \le d} | [{A}]_{ij} |$. Furthermore, we use the inequality

$$\begin{aligned} \Vert {A} \Vert _{\max } \le \Vert {A} \Vert _2. \end{aligned}$$

(24)

3 Scaling argument

This section gives estimates related to a scaling argument corresponding to [12, Lemma 1.101]. The estimates play major roles in our analysis. Furthermore, we use the following inequality (see [12, Exercise 1.20]). Let $0 < r \le s$ and $a_i \ge 0$, $i=1,2,\ldots ,n$ ($n \in {\mathbb {N}}$), be real numbers. Then, we have that

$$\begin{aligned} \left( \sum _{i=1}^n a_i^s \right) ^{1/s} \le \left( \sum _{i=1}^n a_i^r \right) ^{1/r}. \end{aligned}$$

(25)

Lemma 3

Let $s \ge 0$ and $1 \le p \le \infty$. There exist positive constants $c_1$ and $c_2$ such that, for all $T_0 \in {\mathbb {T}}_h$ and $\varphi _0 \in W^{s,p}(T_0)$,

$$\begin{aligned} c_1 |\varphi _0 |_{W^{s,p}(T_0)} \le |\varphi |_{W^{s,p}(T)} \le c_ 2 | \varphi _0 |_{W^{s,p}(T_0)} \end{aligned}$$

(26)

with $\varphi = \varphi _0 \circ {\varPhi }_{T_0}$.

Proof

The following inequalities can be found in [12, Lemma 1.101]. There exists a positive constant c such that, for all $T_0 \in {\mathbb {T}}_h$ and $\varphi _0 \in W^{s,p}(T_0)$,

$$\begin{aligned} |\varphi |_{W^{s,p}(T)}&\le c \Vert {A}_{T_0} \Vert _2^s |\det ({A}_{T_0})|^{ - \frac{1}{p}} |\varphi _0 |_{W^{s,p}(T_0)}, \end{aligned}$$

(27)

$$\begin{aligned} |\varphi _0 |_{W^{s,p}(T_0)}&\le c \Vert {A}_{T_0}^{-1} \Vert _2^s | \det ({A}_{T_0})|^{ \frac{1}{p}} |\varphi |_{W^{s,p}(T)} \end{aligned}$$

(28)

with $\varphi = \varphi _0 \circ {\varPhi }_{T_0}$. Using Eqs. (27) and (28) together with Eqs. (22c) and (23) yields Eq. (26). □

Lemma 4

Let $m \in {\mathbb {N}}_0$ and $p \in [0,\infty )$. Let $\beta := (\beta _1,\ldots ,\beta _d) \in {\mathbb {N}}_0^d$ be a multi-index with $|\beta | = m$. Then, for any $\hat{\varphi } \in W^{m,p}(\widehat{T})$ with $\tilde{\varphi } = \hat{\varphi } \circ \widehat{\varPhi }^{-1}$ and ${\varphi } = \tilde{\varphi } \circ \widetilde{\varPhi }^{-1}$, it holds that

$$\begin{aligned} |{\varphi }|_{W^{m,p}({T})} \le C_1^{SA} |\det (A_T)|^{\frac{1}{p}} \Vert \widetilde{A}^{-1} \Vert ^m_2 \left( \sum _{|\beta | = m} (\alpha ^{- \beta } )^p \Vert \partial ^{\beta } \hat{\varphi } \Vert ^p_{L^p(\widehat{T})} \right) ^{1/p}, \end{aligned}$$

(29)

where $C_1^{SA}$ is a constant that is independent of T and $\widetilde{T}$. When $p = \infty$, for any $\hat{\varphi } \in W^{m,\infty }(\widehat{T})$ with $\tilde{\varphi } = \hat{\varphi } \circ \widehat{\varPhi }^{-1}$ and ${\varphi } = \tilde{\varphi } \circ \widetilde{\varPhi }^{-1}$, it holds that

$$\begin{aligned} |{\varphi }|_{W^{m,\infty }({T})} \le C_1^{SA,\infty } \Vert \widetilde{A}^{-1} \Vert ^m_2 \max _{|\beta | = m} \left( \alpha ^{- \beta } \Vert \partial ^{\beta } \hat{\varphi } \Vert _{L^{\infty }(\widehat{T})} \right) , \end{aligned}$$

(30)

where $C_1^{SA,\infty }$ is a constant that is independent of T and $\widetilde{T}$.

Proof

Let $p \in [1,\infty )$. Because the space ${\mathcal {C}}^{m}(\widehat{T})$ is dense in the space ${W}^{m,p}(\widehat{T})$, we show that Eq. (29) holds for $\hat{\varphi } \in {\mathcal {C}}^{m}(\widehat{T})$ with $\tilde{\varphi } = \hat{\varphi } \circ \widehat{\varPhi }^{-1}$ and ${\varphi } = \tilde{\varphi } \circ \widetilde{\varPhi }^{-1}$. From $\hat{x}_j = \alpha _j^{-1} \tilde{x}_j$, we have that, for any multi-index $\beta$,

$$\begin{aligned} \partial ^{\beta } \tilde{\varphi } = \alpha _{1}^{- \beta _1} \cdots \alpha _{d}^{- \beta _d} \partial ^{\beta } \hat{\varphi } = \alpha ^{- \beta } \partial ^{\beta } \hat{\varphi }. \end{aligned}$$

(31)

Through a change of variable, we obtain

$$\begin{aligned} |\tilde{\varphi }|_{W^{m,p}(\widetilde{T})}^p = \sum _{|\beta | = m} \Vert \partial ^{\beta } \tilde{\varphi } \Vert ^p_{L^p(\widetilde{T})} = | \det (\widehat{A}^{(d)}) | \sum _{|\beta | = m} (\alpha ^{- \beta } )^p \Vert \partial ^{\beta } \hat{\varphi } \Vert ^p_{L^p(\widehat{T})}. \end{aligned}$$

(32)

From the standard estimate in [12, Lemma 1.101], we have

$$\begin{aligned} |{\varphi }|_{W^{m,p}({T})} \le C_1^{SA} |\det (\widetilde{A})|^{\frac{1}{p}} \Vert \widetilde{A}^{-1} \Vert ^m_2 |\tilde{\varphi }|_{W^{m,p}(\widetilde{T})}. \end{aligned}$$

(33)

Inequality (29) follows from Eqs. (32) and (33) with Eq. (23).

We consider the case in which $p = \infty$. A function $\hat{\varphi } \in W^{m,\infty }(\widehat{T})$ belongs to the space $W^{m,p}(\widehat{T})$ for any $p \in [1,\infty )$. Therefore, it holds that $\tilde{\varphi } \in W^{m,p}(\widetilde{T})$ for any $p \in [1,\infty )$ and, from Eq. (25), we obtain

$$\begin{aligned} \Vert \partial ^{\gamma } \tilde{ \varphi } \Vert _{L^{p}(\widetilde{T})}&\le | \tilde{\varphi }|_{W^{|\gamma |,p}(\widetilde{T})} \nonumber \\&= |\det ( \widehat{A}^{(d)})|^{\frac{1}{p}} \left( \sum _{|\beta | = |\gamma |} ( \alpha ^{- \beta } )^p \Vert \partial ^{\beta } \hat{\varphi } \Vert ^p_{L^p(\widehat{T})} \right) ^{1/p} \nonumber \\&\le \left( \sup _{1 \le p} |\det (\widehat{A}^{(d)})|^{\frac{1}{p}} \right) \sum _{|\beta | = |\gamma |} \alpha ^{- \beta } \Vert \partial ^{\beta } \hat{\varphi } \Vert _{L^p(\widehat{T})} \nonumber \\&\le c \left( \sup _{1 \le p} |\det (\widehat{A}^{(d)})|^{\frac{1}{p}} \right) \sum _{|\beta | = |\gamma |} \alpha ^{- \beta } \Vert \partial ^{\beta } \hat{\varphi } \Vert _{L^{\infty }(\widehat{T})} < \infty \end{aligned}$$

(34)

for the multi-index $\gamma \in {\mathbb {N}}_0^d$ with $|\gamma | \le m$. This implies that the function $\partial ^{\gamma } \tilde{\varphi }$ is in the space $L^{\infty }(\widetilde{T})$ for each $|\gamma | \le m$. Therefore, we have that $\tilde{\varphi } \in W^{m,\infty }(\widetilde{T})$. Taking the limit $p \rightarrow \infty$ in Eq. (34) and using $\lim _{p \rightarrow \infty } \Vert \cdot \Vert _{L^p(\widetilde{T})} = \Vert \cdot \Vert _{L^{\infty }(\widetilde{T})}$, we have

$$\begin{aligned} | \tilde{\varphi } |_{W^{m,\infty }(\widetilde{T})} \le c \max _{|\beta | = m} \left( \alpha ^{- \beta } \Vert \partial ^{\beta } \hat{\varphi } \Vert _{L^{\infty }(\widehat{T})} \right) . \end{aligned}$$

(35)

From the standard estimate in [12, Lemma 1.101], we have

$$\begin{aligned} |{\varphi }|_{W^{m,\infty }({T})} \le c \Vert \widetilde{A}^{-1} \Vert ^m_2 |\tilde{\varphi }|_{W^{m,\infty }(\widetilde{T})}. \end{aligned}$$

(36)

Inequality (30) follows from Eqs. (35) and (36). □

We now introduce the following new notation.

Definition 3

We define a parameter ${\mathscr {H}}_i$, $i=1,\ldots ,d$, as

$$\begin{aligned} {\left\{ \begin{array}{ll} {\mathscr {H}}_1 := \alpha _1, \quad {\mathscr {H}}_2 := \alpha _2 t \quad {\text {if}}\ d=2, \\ {\mathscr {H}}_1 := \alpha _1, \quad {\mathscr {H}}_2 := \alpha _2 t_1, \quad {\mathscr {H}}_3 := \alpha _3 t_2 \quad {\text {if}}\ d=3. \end{array}\right. } \end{aligned}$$

For a multi-index $\beta = (\beta _1,\ldots ,\beta _d) \in {\mathbb {N}}_0^d$, we use the notation

$$\begin{aligned} {\mathscr {H}}^{\beta } := {\mathscr {H}}_1^{\beta _1} \cdots {\mathscr {H}}_d^{\beta _d}, \quad {\mathscr {H}}^{- \beta } := {\mathscr {H}}_1^{- \beta _1} \cdots {\mathscr {H}}_d^{- \beta _d}. \end{aligned}$$

We also define $\alpha ^{\beta } := \alpha _{1}^{\beta _1} \cdots \alpha _{d}^{\beta _d}$ and $\alpha ^{- \beta } := \alpha _{1}^{- \beta _1} \cdots \alpha _{d}^{- \beta _d}$.

Definition 4

We define vectors $r_n \in {\mathbb {R}}^d$, $n=1,\ldots ,d$, as follows. If $d=2$,

$$\begin{aligned} r_1 := (1 , 0)^T, \quad r_2 := (s,t)^T, \end{aligned}$$

and if $d=3$,

$$\begin{aligned}&r_1 := (1 , 0,0)^T, \quad r_3 := ( s_{21}, s_{22} , t_2)^T, \\&{\left\{ \begin{array}{ll} r_2 := ( s_1 , t_1 , 0)^T &{}\quad {\text {for case (i)}}, \\ r_2 := (- s_1, t_1,0)^T&{} \quad {\text {for case (ii)}}. \end{array}\right. } \end{aligned}$$

Furthermore, we define a directional derivative as

$$\begin{aligned} \frac{\partial }{\partial {r_i}^{(0)}} := (A_{T_0} r_i) \cdot \nabla _{x^{(0)}} = \sum _{j_0=1}^d (A_{T_0} r_i)_{j_0} \frac{\partial }{\partial x_{j_0}^{(0)}}, \quad i \in \{ 1 : d \}, \end{aligned}$$

where ${A}_{T_0} \in O(d)$ is the orthogonal matrix defined in Eq. (12). For a multi-index $\beta = (\beta _1,\ldots ,\beta _d) \in {\mathbb {N}}_0^d$, we use the notation

$$\begin{aligned} \partial ^{\beta }_{r^{(0)}} := \frac{\partial ^{|\beta |}}{ (\partial r_1^{(0)})^{\beta _1} \ldots (\partial r_d^{(0)})^{\beta _d}}. \end{aligned}$$

Note 1

Recall that

$$\begin{aligned} \begin{array}{ll} |s| \le 1, \quad \alpha _2 \le \alpha _1 &{}\quad {\text {if}}\ d=2,\\ |s_1|\le 1, \quad |s_{21}| \le 1, \ \alpha _2 \le \alpha _3 \le \alpha _1 &{}\quad {\text {if}}\ d=3. \end{array} \end{aligned}$$

When $d=3$, if Assumption 1 is imposed, there exists a positive constant M, independent of $h_T$, such that $|s_{22}| \le M \frac{\alpha _2 t_1}{\alpha _3}$. Thus, if $d=2$, we have

$$\begin{aligned} \alpha _1 | [\widetilde{A}]_{j1} | \le {\mathscr {H}}_j, \quad \alpha _2 | [\widetilde{A}]_{j2} | \le {\mathscr {H}}_j, \quad j=1,2, \end{aligned}$$

and if $d=3$, for $\widetilde{A} \in \{ \widetilde{A}_1 , \widetilde{A}_2 \}$ and $j=1,2,3$, we have

$$\begin{aligned} \alpha _1 | [\widetilde{A}]_{j1} | \le {\mathscr {H}}_j, \quad \alpha _2 | [\widetilde{A}]_{j2} | \le {\mathscr {H}}_j, \quad \alpha _3 | [\widetilde{A}]_{j3} | \le \max \{ 1,M\} {\mathscr {H}}_j, \quad j=1,2,3. \end{aligned}$$

Note 2

We use the following calculations in Lemma 5. For any multi-indices $\beta$ and $\gamma$, we have

$$\begin{aligned} \partial ^{\beta + \gamma }_{\hat{x}}&= \frac{\partial ^{|\beta | + |\gamma |}}{\partial \hat{x}_1^{\beta _1} \cdots \partial \hat{x}_d^{\beta _d} \partial \hat{x}_1^{\gamma _1} \cdots \partial \hat{x}_d^{\gamma _d}}\\&= \underbrace{\sum _{i_1^{(1)} = 1}^d \alpha _1 [\widetilde{A}]_{i_1^{(1)} 1} \cdots \sum _{i_{\beta _1}^{(1)} = 1}^d \alpha _1 [\widetilde{A}]_{i_{\beta _1}^{(1)} 1}}_{\beta _1 {\text {times}}} \cdots \underbrace{ \sum _{i_1^{(d)} = 1}^d \alpha _d [\widetilde{A}]_{i_1^{(d)} d} \cdots \sum _{i_{\beta _d}^{(d)} = 1}^d \alpha _d [\widetilde{A}]_{i_{\beta _d}^{(d)} d}}_{\beta _d {\text {times}}}\\&\quad \underbrace{\sum _{j_1^{(1)} = 1}^d \alpha _1 [\widetilde{A}]_{j_1^{(1)} 1} \cdots \sum _{j_{\gamma _1}^{(1)}= 1}^d \alpha _1 [\widetilde{A}]_{j_{\gamma _1}^{(1)} 1} }_{\gamma _1 {\text {times}}} \cdots \underbrace{\sum _{j_1^{(d)} = 1}^d \alpha _d [\widetilde{A}]_{j_1^{(d)} d} \cdots \sum _{j_{\gamma _d}^{(d)} = 1}^d \alpha _d [\widetilde{A}]_{j_{\gamma _d}^{(d)} d} }_{\gamma _d {\text {times}}} \\&\quad \underbrace{\frac{\partial ^{\beta _1}}{\partial {x}_{i_1^{1)}} \cdots \partial {x}_{i_{\beta _1}^{(1)}}}}_{\beta _1 {\text {times}}} \cdots \underbrace{\frac{\partial ^{\beta _d}}{\partial {x}_{i_1^{(d)}} \cdots \partial {x}_{i_{\beta _d}^{(d)}}}}_{\beta _d {\text {times}}} \underbrace{ \frac{\partial ^{\gamma _1}}{ \partial {x}_{j_1^{(1)}} \cdots \partial {x}_{j_{\gamma _1}^{(1)}} } }_{\gamma _1 {\text {times}}} \cdots \underbrace{\frac{\partial ^{\gamma _d}}{ \partial {x}_{j_1^{(d)}} \cdots \partial {x}_{j_{\gamma _d}^{(d)}} }}_{\gamma _d {\text {times}}}. \end{aligned}$$

Let $\hat{\varphi } \in {\mathcal {C}}^{\ell }(\widehat{T})$ with $\tilde{\varphi } = \hat{\varphi } \circ \widehat{\varPhi }^{-1}$ and ${\varphi } = \tilde{\varphi } \circ \widetilde{\varPhi }^{-1}$. Then, for $1 \le i \le d$,

$$\begin{aligned} \left| \frac{\partial \hat{\varphi }}{\partial \hat{x}_i } \right| \le \sum _{i_1^{(1)}=1}^d \alpha _i \left| [\widetilde{A}]_{i_1^{(1)} i}\right| \left| \frac{\partial \varphi }{\partial x_{i_1^{(1)}}} \right| \le {\left\{ \begin{array}{ll} \alpha _i \Vert \widetilde{A}\Vert _{\max } \sum _{i_1^{(1)}=1}^d \left| \frac{\partial \varphi }{\partial x_{i_1^{(1)}}} \right| \quad {\text {or}},\\ c \sum _{i_1^{(1)}=1}^d {\mathscr {H}}_{i_1^{(1)}} \left| \frac{\partial \varphi }{\partial x_{i_1^{(1)}}} \right| , \end{array}\right. } \end{aligned}$$

and for $1 \le i,j \le d$,

$$\begin{aligned} \left| \frac{\partial ^2 \hat{\varphi }}{\partial \hat{x}_i \partial \hat{x}_j } \right|&= \left| \sum _{i_1^{(1)}, j_1^{(1)}=1}^d \alpha _i \alpha _j [\widetilde{A}]_{i_1^{(1)} i} [\widetilde{A}]_{j_1^{(1)} j} \frac{\partial ^2 \varphi }{\partial x_{i_1^{(1)}} \partial x_{j_1^{(1)}}} \right| \\&\le {\left\{ \begin{array}{ll} \alpha _i \alpha _j \Vert \widetilde{A}\Vert _{\max }^2 \sum _{i_1^{(1)}, j_1^{(1)}=1}^d \left| \frac{\partial ^2 \varphi }{\partial x_{i_1^{(1)}} \partial x_{j_1^{(1)}}} \right| \quad {\text {or}}, \\ \alpha _j \sum _{j_1^{(1)}=1}^d |[\widetilde{A}]_{j_1^{(1)} j}| \left| \sum _{i_1^{(1)} = 1}^d \alpha _i [\widetilde{A}]_{i_1^{(1)} i} \frac{\partial ^2 \varphi }{\partial x_{i_1^{(1)}} \partial x_{j_1^{(1)}}} \right| \\ \quad \le c \alpha _j \Vert \widetilde{A} \Vert _{\max } \sum _{j_1^{(1)}=1}^d \sum _{i_1^{(1)} = 1}^d {\mathscr {H}}_{i_1^{(1)}} \left| \frac{\partial ^2 \varphi }{\partial x_{i_1^{(1)}} \partial x_{j_1^{(1)}}} \right| \quad {\text {or}}, \\ c \sum _{i_1^{(1)} = 1}^d \sum _{j_1^{(1)}=1}^d {\mathscr {H}}_{i_1^{(1)}} {\mathscr {H}}_{j_1^{(1)}} \left| \frac{\partial ^2 \varphi }{\partial x_{i_1^{(1)}} \partial x_{j_1^{(1)}}} \right| . \end{array}\right. } \end{aligned}$$

Lemma 5

Suppose that Assumption 1 is imposed. Let $m \in {\mathbb {N}}_0$, $\ell \in {\mathbb {N}}_0$ with $\ell \ge m$ and $p \in [0,\infty ]$. Let $\beta := (\beta _1,\ldots ,\beta _d) \in {\mathbb {N}}_0^d$ and $\gamma := (\gamma _1,\ldots ,\gamma _d) \in {\mathbb {N}}_0^d$ be multi-indices with $|\beta | = m$ and $|\gamma | = \ell - m$. Then, for any $\hat{\varphi } \in W^{\ell ,p}(\widehat{T})$ with $\tilde{\varphi } = \hat{\varphi } \circ \widehat{\varPhi }^{-1}$ and ${\varphi } = \tilde{\varphi } \circ \widetilde{\varPhi }^{-1}$, it holds that

$$\begin{aligned} \Vert \partial ^{\beta } \partial ^{\gamma } \hat{\varphi } \Vert _{L^p(\widehat{T})} \le C_2^{SA} |\det ({A}_T)|^{-\frac{1}{p}} \Vert \widetilde{A} \Vert ^m_2 \alpha ^{\beta } \sum _{|\epsilon | = |\gamma |} {\mathscr {H}}^{\varepsilon } | \partial ^{\epsilon } \varphi |_{W^{m,p}(T)}, \end{aligned}$$

(37)

where $C_2^{SA}$ is a constant that is independent of T and $\widetilde{T}$. Here, for $p = \infty$ and any positive real x, $x^{- \frac{1}{p}} = 1$.

Proof

Let $\varepsilon = (\varepsilon _1,\ldots ,\varepsilon _d) \in {\mathbb {N}}_0^d$ and $\delta = (\delta _1,\ldots ,\delta _d) \in {\mathbb {N}}_0^d$ be multi-indies with $|\varepsilon | = |\gamma |$ and $|\delta | = |\beta |$. Let $p \in [1,\infty )$. Because the space ${\mathcal {C}}^{\ell }(\widehat{T})$ is dense in the space ${W}^{\ell ,p}(\widehat{T})$, we show that Eq. (37) holds for $\hat{\varphi } \in {\mathcal {C}}^{\ell }(\widehat{T})$ with $\tilde{\varphi } = \hat{\varphi } \circ \widehat{\varPhi }^{-1}$ and ${\varphi } = \tilde{\varphi } \circ \widetilde{\varPhi }^{-1}$. Through a simple calculation, we obtain

$$\begin{aligned} |\partial ^{\beta + \gamma } \hat{\varphi } |&= \left| \frac{\partial ^{\ell } \hat{ \varphi }}{\partial \hat{x}_1^{\beta _1} \cdots \partial \hat{x}_d^{\beta _d} \partial \hat{x}_1^{\gamma _1} \cdots \partial \hat{x}_d^{\gamma _d}} \right| \\&\le c \alpha ^{\beta } \Vert \widetilde{A} \Vert _{\max }^{|\beta |} \underbrace{\sum _{i_1^{(1)} = 1}^d \cdots \sum _{i_{\beta _1}^{(1)} = 1}^d }_{\beta _1 {\text {times}}} \cdots \underbrace{ \sum _{i_1^{(d)} = 1}^d \cdots \sum _{i_{\beta _d}^{(d)} = 1}^d }_{\beta _d {\text {times}}} \underbrace{\sum _{j_1^{(1)} = 1}^d \cdots \sum _{j_{\gamma _1}^{(1)} = 1}^d}_{\gamma _1 {\text {times}}} \cdots \underbrace{\sum _{j_1^{(d)} = 1}^d \cdots \sum _{j_{\gamma _d}^{(d)} = 1}^d }_{\gamma _d {\text {times}}} \\&\quad \underbrace{{\mathscr {H}}_{j_1^{(1)}} \cdots {\mathscr {H}}_{j_{\varepsilon _1}^{(1)}}}_{\gamma _1 {\text {times}}} \cdots \underbrace{ {\mathscr {H}}_{j_1^{(d)}} \cdots {\mathscr {H}}_{j_{\varepsilon _d}^{(d)}}}_{\gamma _d {\text {times}}}\\&\quad \left| \underbrace{\frac{\partial ^{\beta _1}}{\partial {x}_{i_1^{1)}} \cdots \partial {x}_{i_{\beta _1}^{(1)}}}}_{\beta _1 {\text {times}}} \cdots \underbrace{\frac{\partial ^{\beta _d}}{\partial {x}_{i_1^{(d)}} \cdots \partial {x}_{i_{\beta _d}^{(d)}}}}_{\beta _d {\text {times}}} \underbrace{ \frac{\partial ^{\gamma _1}}{ \partial {x}_{j_1^{(1)}} \cdots \partial {x}_{j_{\gamma _1}^{(1)}} } }_{\gamma _1 {\text {times}}} \cdots \underbrace{\frac{\partial ^{\gamma _d}}{ \partial {x}_{j_1^{(d)}} \cdots \partial {x}_{j_{\gamma _d}^{(d)}} }}_{\gamma _d {\text {times}}} \varphi \right| \\&\le c \alpha ^{\beta } \Vert \widetilde{A} \Vert _{\max }^{|\beta |} \sum _{|\delta | = |\beta |} \sum _{|\varepsilon | = |\gamma |} {\mathscr {H}}^{\varepsilon } | { \partial ^{\delta } \partial ^{\varepsilon }\varphi }|. \end{aligned}$$

Using Eq. (24), we then have that

$$\begin{aligned} \int _{\widehat{T}} | \partial ^{\beta } \partial ^{ \gamma } \hat{\varphi }|^p d \hat{x}&\le c \Vert \widetilde{A} \Vert _2^{mp} \alpha ^{\beta p} \sum _{|\delta | = |\beta |} \sum _{|\epsilon | = |\gamma |} {\mathscr {H}}^{\varepsilon p} \int _{\widehat{T}} | { \partial ^{\delta } \partial ^{\varepsilon } \varphi } |^p d \hat{x} \\&= c |\det (A_T)|^{-1} \Vert \widetilde{A} \Vert _2^{mp} \alpha ^{\beta p} \sum _{|\delta | = |\beta |} \sum _{|\epsilon | = |\gamma |} {\mathscr {H}}^{\varepsilon p} \int _{{T}} |{\partial ^{\delta } \partial ^{\varepsilon } \varphi } |^p d {x}. \end{aligned}$$

Therefore, using (25), we obtain

$$\begin{aligned} \Vert \partial ^{\beta } \partial ^{\gamma } \hat{\varphi }\Vert _{L^p(\widehat{T})} \le c |\det (A_T)|^{-\frac{1}{p}} \Vert \widetilde{A} \Vert _2^{m} \alpha ^{\beta } \sum _{|\epsilon | = |\gamma |} {\mathscr {H}}^{\varepsilon } | \partial ^{\epsilon } \varphi |_{W^{m,p}(T)}, \end{aligned}$$

which recovers Eq. (37).

We consider the case in which $p = \infty$. A function $\varphi \in W^{\ell ,\infty }(T)$ belongs to the space $W^{\ell ,p}(T)$ for any $p \in [1,\infty )$. Therefore, it holds that $\hat{\varphi } \in W^{\ell ,p}(\widehat{T})$ for any $p \in [1,\infty )$, and thus,

$$\begin{aligned} \Vert \partial ^{\beta } \partial ^{\gamma } \hat{\varphi }\Vert _{L^p(\widehat{T})}&\le c |\det (A_T)|^{-\frac{1}{p}} \Vert \widetilde{A} \Vert _2^{m} \alpha ^{\beta } \sum _{|\epsilon | = |\gamma |} {\mathscr {H}}^{\varepsilon } | \partial ^{\epsilon } \varphi |_{W^{m,p}(T)} \nonumber \\&\le c \Vert \widetilde{A} \Vert _2^{m} \alpha ^{\beta } \sum _{|\epsilon | = |\gamma |} {\mathscr {H}}^{\varepsilon } | \partial ^{\epsilon } \varphi |_{W^{m,\infty }(T)} < \infty . \end{aligned}$$

(38)

This implies that the function $\partial ^{\beta } \partial ^{\gamma } \hat{\varphi }$ is in the space $L^{\infty }(\widehat{T})$. Inequality (37) for $p=\infty$ is obtained by taking the limit $p \rightarrow \infty$ in Eq. (38) on the basis that $\lim _{p \rightarrow \infty } \Vert \cdot \Vert _{L^p(\widehat{T})} =\Vert \cdot \Vert _{L^{\infty }(\widehat{T})}$. □

Remark 3

In inequality (37), it is possible to obtain the estimates in $T_0$ by specifically determining the matrix $A_{T_0}$.

Let $\ell =2$, $m=1$, and $p=q=2$. Recall that

$$\begin{aligned} \varPhi _{T_0}: T \ni x \mapsto x^{(0)} := {A}_{T_0} x + b_{T_0} \in T_0. \end{aligned}$$

For ${\varphi } \in {\mathcal {C}}^{2}({T})$ with $\varphi _0 = \varphi \circ \varPhi _{T_0}^{-1}$ and $1 \le i,j \le d$, we have

$$\begin{aligned} \left| \frac{\partial ^2 {\varphi }}{\partial {x}_i {\partial {x}_j}} ({x}) \right| = \left| \sum _{i_1^{(1)} , j_1^{(1)}=1}^2 [A_{T_0}]_{i_1^{(1)} i} [A_{T_0}]_{j_1^{(1)} j} \frac{\partial ^2 \varphi _0}{\partial x_{i_1^{(1)}}^{(0)} \partial x_{j_1^{(1)}}^{(0)}} (x) \right| . \end{aligned}$$

Let $d=2$. We define the matrix $A_{T_0}$ as

$$\begin{aligned} A_{T_0} := \begin{pmatrix} \cos \frac{\pi }{2} &{} \quad - \sin \frac{\pi }{2} \\ \sin \frac{\pi }{2} &{} \quad \cos \frac{\pi }{2} \end{pmatrix}. \end{aligned}$$

Because $\Vert A_{T_0} \Vert _{\max } = 1$, we have

$$\begin{aligned} \left| \frac{\partial ^2 {\varphi }}{\partial {x}_i {\partial {x}_j}} ({x}) \right| \le \left| \frac{\partial ^2 \varphi _0}{\partial x_{i+1}^{(0)} \partial x_{j+1}^{(0)}} (x) \right| , \end{aligned}$$

where the indices i, $i+1$ and j, $j+1$ must be evaluated modulo 2. Because $|\det (A_{T_0})| = 1$, it holds that

$$\begin{aligned} \left\| \frac{\partial ^2 {\varphi }}{\partial {x}_i {\partial {x}_j}} \right\| _{L^2(T)} \le \left\| \frac{\partial ^2 \varphi _0}{\partial x_{i_{i+1}}^{(0)} \partial x_{j+1}^{(0)}} \right\| _{L^2(T_0)}. \end{aligned}$$

We then have

$$\begin{aligned} \sum _{j = 1}^2 {\mathscr {H}}_j \left| \frac{\partial {\varphi }}{ {\partial {x}_j}} \right| _{H^1(T)} \le \sum _{j = 1}^2 {\mathscr {H}}_j \left| \frac{\partial \varphi _0}{ \partial x_{j+1}^{(0)}} \right| _{H^1(T_0)}, \end{aligned}$$

where the indices j, $j+1$ must be evaluated modulo 2.

We define the matrix $A_{T_0}$ as

$$\begin{aligned} A_{T_0} := \begin{pmatrix} \cos \frac{\pi }{4} &{} \quad - \sin \frac{\pi }{4} \\ \sin \frac{\pi }{4} &{} \quad \cos \frac{\pi }{4} \end{pmatrix}. \end{aligned}$$

We then have

$$\begin{aligned} \left| \frac{\partial ^2 {\varphi }}{\partial {x}_i {\partial {x}_j}} ({x}) \right| \le \frac{1}{\sqrt{2}} \sum _{i_1^{(1)} , j_1^{(1)}=1}^2 \left| \frac{\partial ^2 \varphi _0}{\partial x_{i_1^{(1)}}^{(0)} \partial x_{j_1^{(1)}}^{(0)}} (x) \right| , \end{aligned}$$

which leads to

$$\begin{aligned} \left\| \frac{\partial ^2 {\varphi }}{\partial {x}_i {\partial {x}_j}} \right\| _{L^2(T)}^2 \le c \sum _{i_1^{(1)} , j_1^{(1)}=1}^2 \left\| \frac{\partial ^2 \varphi _0}{\partial x_{i_1^{(1)}}^{(0)} \partial x_{j_1^{(1)}}^{(0)}} \right\| _{L^2(T_0)}^2 \le c |\varphi _0|^2_{H^2(T_0)}. \end{aligned}$$

Using (25), we than have that

$$\begin{aligned} \sum _{j = 1}^2 {\mathscr {H}}_j \left| \frac{\partial {\varphi }}{ {\partial {x}_j}} \right| _{H^1(T)} \le \sum _{j = 1}^2 {\mathscr {H}}_j |\varphi _0|_{H^2(T_0)} \le c h_{T_0} |\varphi _0|_{H^2(T_0)}. \end{aligned}$$

In this case, anisotropic interpolation error estimates cannot be obtained.

Note 3

We use the following calculations in Lemma 6. For any multi-indices $\beta$ and $\gamma$, we have

$$\begin{aligned} \partial ^{\beta + \gamma }_{\hat{x}}&= \frac{\partial ^{|\beta | + |\gamma |}}{\partial \hat{x}_1^{\beta _1} \cdots \partial \hat{x}_d^{\beta _d} \partial \hat{x}_1^{\gamma _1} \cdots \partial \hat{x}_d^{\gamma _d}} \\&= \underbrace{\sum _{i_1^{(1)},i_1^{(0,1)} = 1}^d \alpha _1 {[}\widetilde{A}]_{i_1^{(1)} 1} [A_{T_0}]_{i_1^{(0,1)} i_1^{(1)}} \cdots \sum _{i_{\beta _1}^{(1)},i_{\beta _1}^{(0,1)} = 1}^d \alpha _1 {[}\widetilde{A}]_{i_{\beta _1}^{(1)} 1} [A_{T_0}]_{i_{\beta _1}^{(0,1)} i_{\beta _1}^{(1)}} }_{\beta _1 {\text {times}}} \cdots \\&\quad \underbrace{ \sum _{i_1^{(d)} , i_1^{(0,d)} = 1}^d \alpha _d {[}\widetilde{A}]_{i_1^{(d)} d} [A_{T_0}]_{i_1^{(0,d)} i_1^{(d)}} \cdots \sum _{i_{\beta _d}^{(d)} , i_{\beta _d}^{(0,d)}= 1}^d \alpha _d {[}\widetilde{A}]_{i_{\beta _d}^{(d)} d} [A_{T_0}]_{i_{\beta _d}^{(0,d)} i_{\beta _d}^{(d)}} }_{\beta _d {\text {times}}} \\&\quad \underbrace{\sum _{j_1^{(1)} , j_1^{(0,1)} = 1}^d \alpha _1 {[}\widetilde{A}]_{j_1^{(1)} 1} [A_{T_0}]_{j_1^{(0,1)} j_1^{(1)}} \cdots \sum _{j_{\gamma _1}^{(1)} , j_{\gamma _1}^{(0,1)}= 1}^d \alpha _1 [\widetilde{A}]_{j_{\gamma _1}^{(1)} 1} {[}A_{T_0}]_{j_{\gamma _1}^{(0,1)} j_{\gamma _1}^{(1)}} }_{\gamma _1 {\text {times}}} \cdots \\&\quad \underbrace{\sum _{j_1^{(d)} , j_1^{(0,d)} = 1}^d \alpha _d {[}\widetilde{A}]_{j_1^{(d)} d} [A_{T_0}]_{j_1^{(0,d)} j_1^{(d)}} \cdots \sum _{j_{\gamma _d}^{(d)} , j_{\gamma _d}^{(0,d)}= 1}^d \alpha _d [\widetilde{A}]_{j_{\gamma _d}^{(d)} d} {[}A_{T_0}]_{j_{\gamma _d}^{(0,d)} j_{\gamma _d}^{(d)}} }_{\gamma _d{\text {times}}}\\&\quad \underbrace{\frac{\partial ^{\beta _1}}{\partial {x}_{i_1^{(0,1)}}^{(0)} \cdots \partial {x}_{i_{\beta _1}^{(0,1)}}^{(0)}}}_{\beta _1 {\text {times}}} \cdots \underbrace{\frac{\partial ^{\beta _d}}{\partial {x}_{i_1^{(0,d)}}^{(0)} \cdots \partial {x}_{i_{\beta _d}^{(0,d)}}^{(0)}}}_{\beta _d {\text {times}}} \underbrace{ \frac{\partial ^{\gamma _1}}{ \partial {x}_{j_1^{(0,1)}}^{(0)} \cdots \partial {x}_{j_{\gamma _1}^{(0,1)}}^{(0)} } }_{\gamma _1 {\text {times}}} \cdots \underbrace{\frac{\partial ^{\gamma _d}}{ \partial {x}_{j_1^{(0,d)}}^{(0)} \cdots \partial {x}_{j_{\gamma _d}^{(0,d)}}^{(0)} }}_{\gamma _d {\text {times}}}. \end{aligned}$$

Let $\hat{\varphi } \in {\mathcal {C}}^{\ell }(\widehat{T})$ with $\tilde{\varphi } = \hat{\varphi } \circ \widehat{\varPhi }^{-1}$, ${\varphi } = \tilde{\varphi } \circ \widetilde{\varPhi }^{-1}$ and $\varphi _0 = \varphi \circ \varPhi _{T_0}^{-1}$. Then, for $1 \le i \le d$,

$$\begin{aligned} \left| \frac{\partial \hat{\varphi }}{\partial \hat{x}_i } \right|&= \left| \sum _{i_1^{(1)}=1}^d \sum _{i_1^{(0,1)} =1}^d \alpha _i {[}\widetilde{A}]_{i_1^{(1)} i} [A_{T_0}]_{i_1^{(0,1)} i_1^{(1)}} \frac{\partial \varphi _0}{\partial x_{i_1^{(0,1)}}^{(0)}} \right| \\&= \alpha _i \left| \sum _{i_1^{(1)}=1}^d \sum _{i_1^{(0,1)}=1}^d {[}A_{T_0}]_{i_1^{(0,1)} i_1^{(1)}} (r_i)_{i_1^{(1)}} \frac{\partial \varphi _0}{\partial x_{i_1^{(0,1)}}^{(0)}} \right| = \alpha _i \left| \frac{\partial \varphi _0}{\partial r_{i}^{(0)}} \right| \\&\le \alpha _i \Vert \widetilde{A} \Vert _{\max } \Vert A_{T_0} \Vert _{\max } \sum _{i_1^{(1)}=1}^d \sum _{i_1^{(0,1)}=1}^d \left| \frac{\partial \varphi _0}{\partial x_{i_1^{(0,1)}}^{(0)}} \right| , \end{aligned}$$

and for $1 \le i,j \le d$,

$$\begin{aligned} \left| \frac{\partial ^2 \hat{\varphi }}{\partial \hat{x}_i \partial \hat{x}_j } \right|&= \left| \sum _{i_1^{(1)}, j_1^{(1)}=1}^d \sum _{i_1^{(0,1)}, j_1^{(0,1)}=1}^d \alpha _i \alpha _j [\widetilde{A}]_{i_1^{(1)} i} {[}\widetilde{A}]_{j_1^{(1)} j}\right. \\&\quad \left. [A_{T_0}]_{i_1^{(0,1)} i_1^{(1)}} [A_{T_0}]_{j_1^{(0,1)} j_1^{(1)}} \frac{\partial ^2 \varphi _0}{\partial x_{i_1^{(0,1)}}^{(0)} \partial x_{j_1^{(0,1)}}^{(0)}} \right| = \alpha _i \alpha _j \left| \frac{\partial ^2 \varphi _0}{\partial r_{i}^{(0)} \partial r_{j}^{(0)}} \right| \\&\le \alpha _i \alpha _j \sum _{j_1^{(1)} =1}^d | {[}\widetilde{A}]_{j_1^{(1)} j} | \left| \sum _{j_1^{(0,1)}=1}^d {[}A_{T_0}]_{j_1^{(0,1)} j_1^{(1)}} \frac{\partial ^2 \varphi _0}{\partial r_{i}^{(0)} \partial x_{j_1^{(0,1)}}^{(0)}}\right| \\&\le \alpha _i \alpha _j \Vert \widetilde{A} \Vert _{\max } \Vert {A}_{T_0} \Vert _{\max } \sum _{j_1^{(0,1)}=1}^d \left| \frac{\partial ^2 \varphi _0}{\partial r_{i}^{(0)} \partial x_{j_1^{(0,1)}}^{(0)}}\right| \\&\le \alpha _i \alpha _j \Vert \widetilde{A} \Vert _{\max }^2 \Vert {A}_{T_0} \Vert _{\max }^2 \sum _{i_1^{(0,1)}, j_1^{(0,1)}=1}^d \left| \frac{\partial ^2 \varphi _0}{\partial x_{i_1^{(0,1)}}^{(0)} \partial x_{j_1^{(0,1)}}^{(0)}} \right| . \end{aligned}$$

If Assumption 1 is not imposed, the estimates corresponding to Lemma 5 are as follows.

Lemma 6

Let $m \in {\mathbb {N}}_0$, $\ell \in {\mathbb {N}}_0$ with $\ell \ge m$, and $p \in [0,\infty ]$. Let $\beta := (\beta _1,\ldots ,\beta _d) \in {\mathbb {N}}_0^d$ and $\gamma := (\gamma _1,\ldots ,\gamma _d) \in {\mathbb {N}}_0^d$ be multi-indices with $|\beta | = m$ and $|\gamma | = \ell - m$. Then, for any $\hat{\varphi } \in W^{\ell ,p}(\widehat{T})$ with $\tilde{\varphi } = \hat{\varphi } \circ \widehat{\varPhi }^{-1}$, ${\varphi } = \tilde{\varphi } \circ \widetilde{\varPhi }^{-1}$, and $\varphi _0 = \varphi \circ \varPhi _{T_0}^{-1}$, it holds that

$$\begin{aligned} \Vert \partial ^{\beta } \partial ^{\gamma } \hat{\varphi }\Vert _{L^p(\widehat{T})} \le C_3^{SA} |\det ({A}_T)|^{-\frac{1}{p}} \Vert \widetilde{{A}} \Vert _2^{m} \alpha ^{\beta } \sum _{|\epsilon | = |\gamma |} {\alpha }^{\varepsilon } | \partial _{r^{(0)}}^{\epsilon } \varphi _0 |_{W^{m,p}(T_0)}, \end{aligned}$$

(39)

where $C_3^{SA}$ is a constant that is independent of $T_0$ and $\widetilde{T}$. Here, for $p = \infty$ and any positive real x, $x^{- \frac{1}{p}} = 1$.

Proof

We follow the proof of Lemma 5. Let $p \in {[}1,\infty )$. Because the space ${\mathcal {C}}^{\ell }(\widehat{T})$ is dense in the space ${W}^{\ell ,p}(\widehat{T})$, we show that Eq. (39) holds for $\hat{\varphi } \in {\mathcal {C}}^{\ell }(\widehat{T})$ with $\tilde{\varphi } =\hat{\varphi } \circ \widehat{\varPhi }^{-1}$, ${\varphi } =\tilde{\varphi } \circ \widetilde{\varPhi }^{-1}$, and $\varphi _0 =\varphi \circ \varPhi _{T_0}^{-1}$. For $1 \le i,k \le d$,

$$\begin{aligned} \left| \partial ^{\beta + \gamma } \hat{\varphi } \right| \le c \alpha ^{\beta } \Vert \widetilde{A} \Vert _{\max }^{|\beta |} \Vert {A}_{T_0} \Vert _{\max }^{|\beta |} \sum _{|\delta | = |\beta |} \sum _{|\varepsilon | = |\gamma |} \alpha ^{\varepsilon } \left| \partial ^{\delta } \partial _{r^{(0)}}^{\varepsilon } \varphi _0 \right| . \end{aligned}$$

Using Eqs. (22c) and (24), we obtain Eq. (39) for $p \in [1,\infty ]$ by an argument analogous to that used for Lemma 5. □

4 Remarks on anisotropic interpolation analysis

We use the following Bramble–Hilbert-type lemma on anisotropic meshes proposed in [1, Lemma 2.1].

Lemma 7

Let $D \subset {\mathbb {R}}^d$ with $d \in \{ 2,3\}$ be a connected open set that is star-shaped with respect to a ball B. Let $\gamma$ be a multi-index with $m := |\gamma |$ and $\varphi \in L^1(D)$ be a function with $\partial ^{\gamma } \varphi \in W^{\ell -m,p}(D)$, where $\ell \in {\mathbb {N}}$, $m \in {\mathbb {N}}_0$, $0 \le m \le \ell$, and $p \in [1,\infty ]$. Then, it holds that

$$\begin{aligned} \Vert \partial ^{\gamma } (\varphi - Q^{(\ell )} \varphi ) \Vert _{W^{\ell -m,p}(D)} \le C^{BH} |\partial ^{\gamma } \varphi |_{W^{\ell -m,p}(D)}, \end{aligned}$$

(40)

where $C^{BH}$ depends only on d, $\ell$, ${\mathrm{diam}}D$, and ${\mathrm{diam}}B$, and $Q^{(\ell )} \varphi$ is defined as

$$\begin{aligned} (Q^{(\ell )} \varphi )(x) := \sum _{|\delta | \le \ell -1} \int _B \eta (y) (\partial ^{\delta }\varphi )(y) \frac{(x-y)^{\delta }}{\delta !} dy \in {\mathcal {P}}^{\ell -1}, \end{aligned}$$

(41)

where $\eta \in {\mathcal {C}}_0^{\infty }(B)$ is a given function with $\int _B \eta dx = 1$.

As explained in the Introduction, there exist some mistakes in the proof of Theorem 2 of [16], and the statement is not valid in its original form. To clarify the following description, we explain the errors in the proof. Let $\widehat{T} \subset {\mathbb {R}}^2$ be the reference element defined in Sect. 2.1.1. We set $k = m = 1$, $\ell = 2$, and $p=2$. For $\hat{\varphi } \in H^2(\widehat{T})$, we set $\tilde{\varphi } := \hat{\varphi } \circ \widehat{\varPhi }^{-1}$ and ${\varphi } := \tilde{\varphi } \circ \widetilde{\varPhi }^{-1}$. Inequality (29) yields

$$\begin{aligned} |{\varphi } - I_T \varphi |_{H^{1}({T})} \le c |\det (A_T)|^{\frac{1}{2}} \Vert \widetilde{A}^{-1} \Vert _2 \left( \sum _{i=1}^2 \alpha ^{- 2}_i \Vert \partial _{\hat{x}_i} (\hat{\varphi } - I_{\widehat{T}} \hat{\varphi }) \Vert ^2_{L^2(\widehat{T})} \right) ^{\frac{1}{2}}. \end{aligned}$$

(42)

The coefficient $\alpha _i^{-2}$ appears on the right-hand side of Eq. (42). In [16, Theorem 2], we wrongly claimed that $\alpha _i^{-2}$ could be canceled out. In fact, a further assumption is required for this. Using Eq. (41) and the triangle inequality, we have

$$\begin{aligned} \Vert \partial _{\hat{x}_i} ( \hat{\varphi } - I_{\widehat{T}} \hat{\varphi } ) \Vert ^2_{L^2(\widehat{T})} \le 2 \Vert \partial _{\hat{x}_i} ( \hat{\varphi } - Q^{(2)} \hat{\varphi } ) \Vert ^2_{L^2(\widehat{T})} + 2 \Vert \partial _{\hat{x}_i} ( Q^{(2)} \hat{\varphi } - I_{\widehat{T}} \hat{\varphi } ) \Vert ^2_{L^2(\widehat{T})}. \end{aligned}$$

We use inequality (40) to obtain the target inequality [16, Theorem 2]. To this end, we have to show that

$$\begin{aligned} \Vert \partial _{\hat{x}_i} ( Q^{(2)} \hat{\varphi } - I_{\widehat{T}} \hat{\varphi } ) \Vert _{L^2(\widehat{T})} \le c \Vert \partial _{\hat{x}_i} ( \hat{\varphi } - Q^{(2)} \hat{\varphi } ) \Vert _{H^1(\widehat{T})}. \end{aligned}$$

(43)

However, this is unlikely to hold because Eqs. (14) and (16) yield

$$\begin{aligned} \Vert \partial _{\hat{x}_i} ( Q^{(2)} \hat{\varphi } - I_{\widehat{T}} \hat{\varphi } ) \Vert _{L^2(\widehat{T})}&= \Vert \partial _{\hat{x}_i} ( I_{\widehat{T}} (Q^{(2)} \hat{\varphi } ) - I_{\widehat{T}} \hat{\varphi } ) \Vert _{L^2(\widehat{T})} \\&\le c \Vert Q^{(2)} \hat{\varphi } - \hat{\varphi } \Vert _{H^2(\widehat{T})} \le c |\hat{\varphi }|_{H^2(\widehat{T})}. \end{aligned}$$

Using the classical scaling argument (see [12, Lemma 1.101]), we have

$$\begin{aligned} |\hat{\varphi }|_{H^2(\widehat{T})} \le c |\det (A_T)|^{-\frac{1}{2}} \Vert \widetilde{A} \Vert _2 |\varphi |_{H^2(T)}, \end{aligned}$$

which does not include the quantity $\alpha _i$. Therefore, the quantity $\alpha _i^{-1}$ in Eq. (42) remains. Thus, the proof of [16, Theorem 2] is incorrect.

To overcome this problem, we use some results from previous studies [1, 2]. That is, we assume that there exists a linear functional ${\mathscr {F}}_1$ such that

$$\begin{aligned}&{\mathscr {F}}_1 \in H^{1} (\widehat{T})^{\prime }, \\&{\mathscr {F}}_1 ( \partial _{\hat{x}_i} (\hat{\varphi } - I_{\widehat{T}} \hat{\varphi }) ) = 0 \quad i = 1,2, \quad \forall \hat{\varphi } \in {\mathcal {C}}({\widehat{T}}): \ \partial _{\hat{x}_i} \hat{\varphi } \in H^{1} (\widehat{T}), \\&\hat{\eta } \in {\mathcal {P}}^{1}, \quad {\mathscr {F}}_1(\partial _{\hat{x}_i} \hat{\eta }) = 0 \quad i = 1,2, \quad \Rightarrow \quad \partial _{\hat{x}_i} \hat{\eta } = 0. \end{aligned}$$

Because the polynomial spaces are finite-dimensional, all norms are equivalent; i.e., because $| {\mathscr {F}}_1( \partial _{\hat{x}_i} ( \hat{\eta } - I_{\widehat{T}} \hat{\varphi } ) )|$ ($i=1,2$) is a norm on ${\mathcal {P}}^{0}$, we have that, for $i=1,2$,

$$\begin{aligned} \Vert \partial _{\hat{x}_i} (\hat{\eta } - I_{\widehat{T}} \hat{\varphi }) \Vert _{L^2(\widehat{T})}&\le c | {\mathscr {F}}_1 (\partial _{\hat{x}_i} ( \hat{\eta } - I_{\widehat{T}} \hat{\varphi } ))| = c |{\mathscr {F}}_1 (\partial _{\hat{x}_i} ( \hat{\eta } - \hat{\varphi } ) )| \\&\le c \Vert \partial _{\hat{x}_i} ( \hat{\eta } - \hat{\varphi } ) \Vert _{H^1(\widehat{T})}. \end{aligned}$$

Setting $\hat{\eta } := Q^{(2)} \hat{\varphi }$, we obtain Eq. (43). Using inequality (40) yields

$$\begin{aligned} \Vert \partial _{\hat{x}_i} ( \hat{\varphi } - I_{\widehat{T}} \hat{\varphi } ) \Vert ^2_{L^2(\widehat{T})} \le c | \partial _{\hat{x}_i} \hat{\varphi } |^2_{H^1(\widehat{T})}, \end{aligned}$$

and so inequality (42) together with Eq. (25) can be written as

$$\begin{aligned} |{\varphi } - I_T \varphi |_{H^{1}({T})} \le c |\det (A_T)|^{\frac{1}{2}} \Vert \widetilde{A}^{-1} \Vert _2 \sum _{i,j=1}^2 \alpha ^{- 1}_i \Vert \partial _{\hat{x}_i} \partial _{\hat{x}_j} \hat{\varphi } \Vert _{L^2(\widehat{T})}. \end{aligned}$$

(44)

Inequality (37) yields

$$\begin{aligned} \Vert \partial _{\hat{x}_i} \partial _{\hat{x}_j} \hat{\varphi } \Vert _{L^2(\widehat{T})} \le c |\det ({A}_T)|^{-\frac{1}{2}} \Vert \widetilde{A} \Vert _2 \alpha _i \sum _{n=1}^2 {\mathscr {H}}_n \left| \frac{\partial \varphi }{\partial x_n} \right| _{H^{1}(T)}. \end{aligned}$$

(45)

Therefore, the quantity $\alpha _i^{-1}$ in Eq. (44) and the quantity $\alpha _i$ in Eq. (45) cancel out.

5 Classical interpolation error estimates

The following embedding results hold.

Theorem

Let $d \ge 2$, $s > 0$, and $p \in [1,\infty ]$. Let $D \subset {\mathbb {R}}^d$ be a bounded open subset of ${\mathbb {R}}^d$. If D is a Lipschitz set, we have that

$$\begin{aligned} W^{s,p}(D) \hookrightarrow {\left\{ \begin{array}{ll} L^q(D) \quad \forall q \in [p , \frac{pd}{d - sp}]\ {\text {if}}\ s p < d, \\ L^q(D) \quad \forall q \in [p,\infty ), {\text {if}}\ sp=d,\\ L^{\infty }(D) \cap {\mathcal {C}}^{0,\xi }(\overline{D}) \quad \xi = 1 - \frac{d}{s p}\ {\text {if}}\ sp > d. \end{array}\right. } \end{aligned}$$

(46)

Furthermore,

$$\begin{aligned} W^{s,p}(D) \hookrightarrow L^{\infty }(D) \cap {\mathcal {C}}^{0}(\overline{D}) \quad {\text {(case}}\ s=d\ {\text {and}}\ p=1{\text {)}}. \end{aligned}$$

(47)

Proof

See, for example, [12, Corollary B.43, Theorem B.40], [13, Theorem 2.31], and the references therein. □

Remark 4

Let $s > 0$ and $p \in [1,\infty ]$ be such that

$$\begin{aligned} s> \frac{d}{p} \quad {\text {if}}\ p>1, \quad s \ge d \quad {\text {if}}\ p=1. \end{aligned}$$

Then, it holds that $W^{s,p}(D) \hookrightarrow {\mathcal {C}}^0(\overline{D})$.

Using the new geometric parameter $H_{T_0}$, it is possible to deduce the classical interpolation error estimates; e.g., see [12, Theorem 1.103] and [13, Theorem 11.13].

Theorem A

Let $1 \le p \le \infty$ and assume that there exists a nonnegative integer k such that

$$\begin{aligned} {\mathcal {P}}^{k} \subset \widehat{{P}} \subset W^{k+1,p}(\widehat{T}) \subset V(\widehat{T}). \end{aligned}$$

Let $\ell$ ($0 \le \ell \le k$) be such that $W^{\ell +1,p}(\widehat{T}) \subset V(\widehat{T})$ with the continuous embedding. Furthermore, assume that $\ell , m \in {\mathbb {N}} \cup \{ 0 \}$ and $p , q \in [1,\infty ]$ such that $0 \le m \le \ell + 1$ and

$$\begin{aligned} W^{\ell +1,p}(\widehat{T}) \hookrightarrow W^{m,q} (\widehat{T}). \end{aligned}$$

(48)

Then, for any $\varphi _0 \in W^{\ell +1,p}(T_0)$, it holds that

$$\begin{aligned} |\varphi _0 - {I}_{T_0} \varphi _0 |_{W^{m,q}(T_0)} \le C_*^I |T_0|^{\frac{1}{q} - \frac{1}{p}} \left( \frac{\alpha _{\max }}{\alpha _{\min }} \right) ^m \left( \frac{H_{T_0}}{h_{T_0}} \right) ^m h_{T_0}^{\ell +1-m} | \varphi _0 |_{W^{\ell +1,p}(T_0)}, \end{aligned}$$

(49)

where $C_*^I$ is a positive constant that is independent of $h_T$ and $H_T$, and the parameters $\alpha _{\max }$ and $\alpha _{\min }$ are defined as

$$\begin{aligned} \alpha _{\max } := \max \{ \alpha _1 , \ldots , \alpha _d \}, \quad \alpha _{\min } := \min \{ \alpha _1 , \ldots , \alpha _d \}. \end{aligned}$$

(50)

Proof

Let $\hat{\varphi } \in W^{\ell +1,p}(\widehat{T})$. Because $0 \le \ell \le k$, ${\mathcal {P}}^{\ell } \subset {\mathcal {P}}^k \subset \widehat{{P}}$. Therefore, for any $\hat{\eta } \in {\mathcal {P}}^{\ell }$, we have $I_{\widehat{T}} \hat{\eta } = \hat{\eta }$. Using Eqs. (16) and (48), we obtain

$$\begin{aligned} | \tilde{\varphi } - I_{\widehat{T}} \hat{\varphi } |_{W^{m,q}(\widehat{T})}&\le | \tilde{\varphi } -\hat{\eta } |_{W^{m,q}(\widehat{T})} +|I_{\widehat{T}} ( \hat{\eta } - \hat{\varphi } ) |_{W^{m,q}(\widehat{T})} \\&\le c \Vert \tilde{\varphi } -\hat{\eta } \Vert _{W^{\ell +1,p}(\widehat{T})}, \end{aligned}$$

where we have used the stability of the interpolation operator $I_{\widehat{T}}$; i.e.,

$$\begin{aligned} |I_{\widehat{T}} ( \hat{\eta } - \hat{\varphi } ) |_{W^{m,q}(\widehat{T})} \le \sum _{i=1}^{n_0} |\hat{\chi }_i (\hat{\eta } - \hat{\varphi })| | \hat{\theta }_i|_{W^{m,q}(\widehat{T})} \le c \Vert \hat{\eta } - \tilde{\varphi } \Vert _{W^{\ell +1,p}(\widehat{T})}. \end{aligned}$$

Using the classic Bramble–Hilbert-type lemma (e.g., [7, Lemma 4.3.8]), we obtain

$$\begin{aligned} |\tilde{\varphi } - I_{\widehat{T}} \hat{\varphi } |_{W^{m,q}(\widehat{T})} \le c \inf _{\hat{\eta } \in {\mathcal {P}}^{\ell }} \Vert \hat{\eta } - \tilde{\varphi } \Vert _{W^{\ell +1,p}(\widehat{T})} \le c |\hat{\varphi }|_{W^{\ell +1,p}(\widehat{T})}. \end{aligned}$$

(51)

Inequalities (26), (29), (25), and (51) yield

$$\begin{aligned}&|\varphi _0 - {I}_{T_0} \varphi _0 |_{W^{m,q}({T}_0)} \le c | \varphi - {I}_T \varphi |_{W^{m,q}({T})} \nonumber \\&\quad \le c |\det ({A}_T)|^{\frac{1}{q}} \Vert \widetilde{A}^{-1} \Vert _2^m \left( \sum _{|\beta | = m} ( \alpha ^{- \beta } )^q \Vert \partial ^{\beta } (\hat{\varphi } - I_{\widehat{T}} \hat{\varphi } ) \Vert ^q_{L^q(\widehat{T})} \right) ^{1/q} \nonumber \\&\quad \le c |\det ({A}_T)|^{\frac{1}{q}} \Vert \widetilde{A}^{-1} \Vert _2^m \max \{ \alpha _1^{-1} , \ldots , \alpha _d^{-1} \}^{|\beta |} | \tilde{\varphi } - I_{\widehat{T}} \hat{\varphi } |_{W^{m,q}(\widehat{T})} \nonumber \\&\quad \le c |\det ({A}_T)|^{\frac{1}{q}} \Vert \widetilde{A}^{-1} \Vert _2^m \alpha _{\min }^{- |\beta |} |\hat{\varphi }|_{W^{\ell +1,p}(\widehat{T})}. \end{aligned}$$

(52)

Using inequalities (25) and (39) together with Eq. (22c), we have

$$\begin{aligned}&|\hat{\varphi }|_{W^{\ell +1,p}(\widehat{T})} \nonumber \\&\quad \le \sum _{|\gamma | = \ell + 1 -m} \sum _{|\beta | = m} \Vert \partial ^{\beta } \partial ^{\gamma } \hat{\varphi } \Vert _{L^{p}(\widehat{T})} \nonumber \\&\quad \le c |\det ({A}_T)|^{-\frac{1}{p}} \Vert \widetilde{{A}} \Vert _2^{m} \sum _{|\gamma | = \ell + 1 -m} \sum _{|\beta | = m} \alpha ^{\beta } \sum _{|\epsilon | = |\gamma |} {\alpha }^{\varepsilon } | \partial _{r^{(0)}}^{\epsilon } \varphi _0 |_{W^{m,p}(T_0)} \nonumber \\&\quad \le c |\det ({A}_T)|^{-\frac{1}{p}} \Vert \widetilde{{A}} \Vert _2^{m} \max \{ \alpha _1 , \ldots , \alpha _d \}^{|\beta |} h_{T_0}^{\ell +1-m} |\varphi _0|_{W^{\ell +1,p} (T_0)} \nonumber \\&\quad \le c |\det ({A}_T)|^{-\frac{1}{p}} \Vert \widetilde{{A}} \Vert _2^{m} \alpha _{\max }^{|\beta |} h_{T_0}^{\ell +1-m} |\varphi _0|_{W^{\ell +1,p} (T_0)}. \end{aligned}$$

(53)

From Eqs. (52) and (53) together with Eq. (23), we have the desired estimate (49). □

6 Anisotropic interpolation error estimates

6.1 Main theorem

Theorem A can be applied to standard isotropic elements as well as some classes of anisotropic elements. If we are concerned with anisotropic elements, it is desirable to remove the quantity $\alpha _{\max } / \alpha _{\min }$ from estimate (49). To this end, we employ the approach described in [1] and consider the case of a finite element with $V(\widehat{T}) := {\mathcal {C}}({\widehat{T}})$ and $\widehat{{P}} := {\mathcal {P}}^{k}(\widehat{T})$ (Theorem B). However, one needs stronger assumptions to obtain the optimal estimate. When using finite elements that do not satisfy the assumptions of Theorem B (e.g., ${\mathcal {P}}^1$-bubble finite element), we have to use Theorem A. In these cases, it may not be possible to obtain optimal order estimates if the shape-regularity condition is violated.

Theorem B

Let $\{ \widehat{T} , \widehat{{P}} , \widehat{\varSigma } \}$ be a finite element with the normed vector space $V(\widehat{T}) := {\mathcal {C}}({\widehat{T}})$ and $\widehat{{P}} := {\mathcal {P}}^{k}(\widehat{T})$ with $k \ge 1$. Let $I_{\widehat{T}} : V({\widehat{T}}) \rightarrow \widehat{{P}}$ be a linear operator. Fix $\ell \in {\mathbb {N}}$, $m \in {\mathbb {N}}_0$, and $p,q \in [1,\infty ]$ such that $0 \le m \le \ell \le k+1$, $\ell - m \ge 1$, and assume that the embeddings (46) and (47) with $s := \ell - m$ hold. Let $\beta$ be a multi-index with $|\beta | = m$. We set $j := \dim (\partial ^{\beta } {\mathcal {P}}^{k})$. Assume that there exist linear functionals ${\mathscr {F}}_i$, $i=1,\ldots ,j$, such that

$$\begin{aligned}&{\mathscr {F}}_i \in W^{\ell - m ,p} (\widehat{T})^{\prime },\quad \forall i = 1,\ldots ,j, \end{aligned}$$

(54)

$$\begin{aligned}&{\mathscr {F}}_i ( \partial ^{\beta } (\hat{\varphi } - I_{\widehat{T}} \hat{\varphi }) ) = 0 \quad \forall i = 1,\ldots ,j, \quad \forall \hat{\varphi } \in {\mathcal {C}}({\widehat{T}}): \ \partial ^{\beta } \hat{\varphi } \in W^{\ell - m , p} (\widehat{T}), \end{aligned}$$

(55)

$$\begin{aligned}&\hat{\eta } \in {\mathcal {P}}^{k}, \quad {\mathscr {F}}_i(\partial ^{\beta } \hat{\eta }) = 0 \quad \forall i = 1,\ldots ,j \quad \Rightarrow \quad \partial ^{\beta } \hat{\eta } = 0. \end{aligned}$$

(56)

For any $\hat{\varphi } \in W^{\ell , p} (\widehat{T}) \cap {\mathcal {C}}({\widehat{T}})$, we set ${\varphi }_0 := \hat{\varphi } \circ {\varPhi }^{-1}$. If Assumption 1 is imposed, it holds that

$$\begin{aligned}&| {\varphi }_0 - I_{{T}_0} {\varphi }_0 |_{W^{m,q}({T}_0)} \nonumber \\&\quad \le C_1^{TB} |T_0|^{\frac{1}{q} - \frac{1}{p}} \left( \frac{H_{T_0}}{h_{T_0}} \right) ^m \sum _{|\gamma | = \ell -m} {\mathscr {H}}^{\gamma } | \partial ^{\gamma } {(\varphi _0 \circ \varPhi _{T_0})} |_{W^{ m ,p}(\varPhi _{T_0}^{-1}(T_0))}, \end{aligned}$$

(57)

where $C_1^{TB}$ is a positive constant that is independent of $h_{T_0}$ and $H_{T_0}$. Furthermore, if Assumption 1 is not imposed, it holds that

$$\begin{aligned}&|{\varphi }_0 - I_{{T}_0} {\varphi }_0 |_{W^{m,q}({T}_0)} \nonumber \\&\quad \le C_2^{TB} |T_0|^{\frac{1}{q} - \frac{1}{p}} \left( \frac{H_{T_0}}{h_{T_0}} \right) ^m \sum _{|\gamma | = \ell -m} {\alpha }^{\gamma } | \partial _{r^{(0)}}^{\gamma } {\varphi _0} |_{W^{ m ,p}(T_0)}, \end{aligned}$$

(58)

where $C_2^{TB}$ is a positive constant that is independent of $h_{T_0}$ and $H_{T_0}$.

Proof

The introduction of the functionals ${\mathscr {F}}_i$ follows from [1]. In fact, under the same assumptions as made in Theorem B, we have (see [1, Lemma 2.2])

$$\begin{aligned} \Vert \partial ^{\beta } (\hat{\varphi } - I_{\widehat{T}} \hat{\varphi }) \Vert _{L^q(\widehat{T})} \le C^B | \partial ^{\beta } \hat{\varphi } |_{W^{\ell - m ,p}(\widehat{T})}, \end{aligned}$$

(59)

where $|\beta | = m$, $\hat{\varphi } \in {\mathcal {C}}({\widehat{T}})$, and $\partial ^{\beta } \hat{\varphi } \in W^{\ell - m , p} (\widehat{T})$.

Inequalities (26), (29), (25), and (59) yield

$$\begin{aligned}&|\varphi _0 - {I}_{T_0} \varphi _0 |_{W^{m,q}({T}_0)} \le c | \varphi - {I}_T \varphi |_{W^{m,q}({T})} \nonumber \\&\quad \le c |\det ({A}_T)|^{\frac{1}{q}} \Vert \widetilde{A}^{-1} \Vert _2^m \left( \sum _{|\beta | = m} ( \alpha ^{- \beta } )^q \Vert \partial ^{\beta } (\hat{\varphi } - I_{\widehat{T}} \hat{\varphi } ) \Vert ^q_{L^q(\widehat{T})} \right) ^{1/q} \nonumber \\&\quad \le c |\det ({A}_T)|^{\frac{1}{q}} \Vert \widetilde{A}^{-1} \Vert _2^m \sum _{|\beta | = m} ( \alpha ^{- \beta } ) \Vert \partial ^{\beta } (\hat{\varphi } - I_{\widehat{T}} \hat{\varphi } ) \Vert _{L^q(\widehat{T})} \nonumber \\&\quad \le c |\det ({A}_T)|^{\frac{1}{q}} \Vert \widetilde{A}^{-1} \Vert _2^m \sum _{|\beta | = m} ( \alpha ^{- \beta } ) | \partial ^{\beta } \hat{\varphi } |_{W^{\ell - m ,p}(\widehat{T})}. \end{aligned}$$

(60)

If Assumption 1 is imposed, then using inequalities (25) and (37) leads to

$$\begin{aligned}&\sum _{|\beta | = m} ( \alpha ^{- \beta } ) | \partial ^{\beta } \hat{\varphi } |_{W^{\ell - m ,p}(\widehat{T})} \nonumber \\&\quad \le \sum _{|\gamma | = \ell -m} \sum _{|\beta | = m} ( \alpha ^{- \beta } ) \Vert \partial ^{\beta + \gamma } \hat{\varphi } \Vert _{L^{p}(\widehat{T})} \nonumber \\&\quad \le c |\det ({A}_T)|^{-\frac{1}{p}} \Vert \widetilde{A} \Vert ^m_2 \sum _{|\gamma | = \ell -m} \sum _{|\beta | = m} ( \alpha ^{- \beta } ) \alpha ^{\beta } \sum _{|\epsilon | = |\gamma |} {\mathscr {H}}^{\varepsilon } | \partial ^{\epsilon } \varphi |_{W^{m,p}(T)} \nonumber \\&\quad \le c |\det ({A}_T)|^{-\frac{1}{p}} \Vert \widetilde{A} \Vert ^m_2 \sum _{|\epsilon | = \ell -m} {\mathscr {H}}^{\varepsilon } | \partial ^{\epsilon } \varphi |_{W^{m,p}(T)}. \end{aligned}$$

(61)

From Eqs. (60) and (61) together with Eqs. (22) and (23), we have the desired estimate (57) using $T = \varPhi _{T_0}^{-1}(T_0)$ and $\varphi = \varphi _0 \circ \varPhi _{T_0}$.

If Assumption 1 is not imposed, then an analogous argument using inequality (39) instead of (37) yields estimate (58). □

Example 1

Specific finite elements satisfying conditions (54), (55), and (56) are given in [2] and [1]; see also Sect. 6.2.

Remark 5

Finite elements that do not satisfy conditions (54), (55), and (56) can be found in [2, Table 3]; e.g., the ${\mathcal {P}}^1$-bubble finite element and the ${\mathcal {P}}^3$ Hermite finite element. In these cases, Theorem A can be applied.

6.2 Examples satisfying conditions (54), (55), and (56) in Theorem B

Corollary 1

Let $\{ \widehat{T} , \widehat{{P}} , \widehat{\varSigma } \}$ be the Lagrange finite element with $V(\widehat{T}) := {\mathcal {C}}({\widehat{T}})$ and $\widehat{{P}} := {\mathcal {P}}^{k}(\widehat{T})$ for $k \ge 1$. Let $I_T: V({T}) \rightarrow {{P}}$ be the corresponding local Lagrange interpolation operator. Let $m \in {\mathbb {N}}_0$, $\ell \in {\mathbb {N}}$, and $p \in {\mathbb {R}}$ be such that $0 \le m \le \ell \le k+1$ and

$$\begin{aligned}&d=2: \ {\left\{ \begin{array}{ll} p \in (2,\infty ] \quad {\text {if}}\ m=0, \ell = 1,\\ p \in [1,\infty ] \quad {\text {if}}\ m=0, \ell \ge 2\ {\text {or}} \ m \ge 1, \ell - m \ge 1, \end{array}\right. } \\&d=3: \ {\left\{ \begin{array}{ll} p \in \left( \frac{3}{\ell }, \infty \right] &{}\quad {\text {if}}\ m=0, \ell =1,2,\\ p \in (2,\infty ]&{} \quad {\text {if}}\ m \ge 1, \ell -m = 1, \\ p \in [1,\infty ] &{}\quad {\text {if}}\ m=0, \ell \ge 3\ {\text {or}} \ m \ge 1, \ell -m \ge 2. \end{array}\right. } \end{aligned}$$

We set $q \in [1,\infty ]$ such that $W^{\ell -m,p}(\widehat{T}) \hookrightarrow L^q(\widehat{T})$. Then, for all $\hat{\varphi } \in W^{\ell ,p}(\widehat{T})$ with ${\varphi }_0 := \hat{\varphi } \circ {\varPhi }^{-1}$, we recover Eq. (57) if Assumption 1 is imposed, and Eq. (58) holds.

Furthermore, for any $\hat{\varphi } \in {\mathcal {C}}(\widehat{T})$ with ${\varphi }_0 := \hat{\varphi } \circ {\varPhi }^{-1}$, it holds that

$$\begin{aligned} \Vert {\varphi }_0 - I_{{T}_0} {\varphi }_0 \Vert _{L^{\infty }({T}_0)} \le c \Vert {\varphi }_0 \Vert _{L^{\infty }(T_0)}. \end{aligned}$$

Proof

The existence of functionals satisfying Eqs. (54), (55), and (56) is shown in the proof of [1, Lemma 2.4] for $d=2$ and in the proof of [1, Lemma 2.6] for $d=3$. Inequality (59) then holds. This implies that estimates (57) and (58) hold. □

Setting $V(T) := {\mathcal {C}}({{T}})$, we define the nodal Crouzeix–Raviart interpolation operators as

$$\begin{aligned} I_{T}^{CR,S}: V(T) \ni \varphi \mapsto I_{T}^{CR,S} \varphi := \sum _{i=1}^{d+1} \varphi (x_{F_i}) \theta _i \in {\mathcal {P}}^1. \end{aligned}$$

Corollary 2

Let $\{ \widehat{T} , \widehat{{P}} , \widehat{\varSigma } \}$ be the Crouzeix–Raviart finite element with $V(\widehat{T}) := {\mathcal {C}}({\widehat{T}})$ and $\widehat{{P}} := {\mathcal {P}}^{1}(\widehat{T})$. Set $I_T ;= I_{T}^{CR,S}$. Let $m \in {\mathbb {N}}_0$, $\ell \in {\mathbb {N}}$, and $p \in {\mathbb {R}}$ be such that

$$\begin{aligned}&d=2: \ {\left\{ \begin{array}{ll} p \in (2,\infty ] &{}\quad {\text {if}}\ m=0, \ell = 1,\\ p \in [1,\infty ]&{} \quad {\text {if}}\ m=0, \ell = 2\ {\text {or}}\ m=1, \ell = 2, \end{array}\right. } \\&d=3: \ {\left\{ \begin{array}{ll} p \in \left( \frac{3}{\ell } , \infty \right] &{} \quad {\text {if}}\ m=0, \ell =1,2,\\ \displaystyle p \in (2,\infty ]&{} \quad {\text {if}}\ m=1, \ell = 2. \end{array}\right. } \end{aligned}$$

Set $q \in [1,\infty ]$ such that $W^{\ell -m,p}(\widehat{T}) \hookrightarrow L^q(\widehat{T})$. Then, for all $\hat{\varphi } \in W^{\ell ,p}(\widehat{T})$ with ${\varphi }_0 := \hat{\varphi } \circ {\varPhi }^{-1}$, we recover Eq. (57) if Assumption 1 is imposed, and Eq. (58) holds.

Furthermore, for any $\hat{\varphi } \in {\mathcal {C}}(\widehat{T})$ with ${\varphi }_0 := \hat{\varphi } \circ {\varPhi }^{-1}$, it holds that

$$\begin{aligned} \Vert {\varphi }_0 - I_{{T}_0} {\varphi }_0 \Vert _{L^{\infty }({T}_0)} \le c \Vert {\varphi }_0 \Vert _{L^{\infty }(T_0)}. \end{aligned}$$

Proof

For $k=1$, we only introduce functionals ${\mathscr {F}}_i$ satisfying Eqs. (54)–(56) in Theorem B for each $\ell$ and m.

Let $m=0$. From the Sobolev embedding theorem, we have $W^{\ell ,p}(\widehat{T}) \subset {\mathcal {C}}^0(\widehat{T})$ with $1 < p \le \infty$, $d < \ell p$ or $p=1$, $d \le \ell$. Under this condition, we use

$$\begin{aligned} {\mathscr {F}}_i(\hat{\varphi }) := \hat{\varphi } (\hat{x}_{\widehat{F}_i}), \quad \hat{\varphi } \in W^{\ell ,p}(\widehat{T}), \quad i=1,\ldots , d+1. \end{aligned}$$

Let $d=2$ and $m=1$ ($\ell = 2$). We set $\beta = (1,0)$. Then, we have that $j = \dim ( \partial ^{\beta } {\mathcal {P}}^1 ) = 1$. We consider a functional

$$\begin{aligned} {\mathscr {F}}_1(\hat{\varphi }) := \int _{0}^{\frac{1}{2}} \hat{\varphi }(\hat{x}_1,1/2) d \hat{x}_1, \quad \hat{\varphi } \in W^{2,p}(\widehat{T}). \end{aligned}$$

By an analogous argument, we can set a functional for the case $\beta = (0,1)$.

Let $d=3$ and $m=1$ ($\ell = 2$). We first consider Type (i) in Sect. 2.1.2. That is, the reference element is $\widehat{T} = {\mathrm{conv}}\{ 0,e_1, e_2,e_3 \}$. Here, $e_1, \ldots , e_3 \in {\mathbb {R}}^3$ form the canonical basis. We set $\beta = (1,0,0)$ and consider the functional

$$\begin{aligned} {\mathscr {F}}_1(\hat{\varphi }) := \int _{0}^{\frac{1}{3}} \hat{\varphi }(\hat{x}_1,1/3,1/3) d \hat{x}_1, \quad \hat{\varphi } \in W^{2,p}(\widehat{T}). \end{aligned}$$

We now consider Type (ii) in Sect. 2.1.2. That is, the reference element is $\widehat{T} = {\mathrm{conv}}\{ 0,e_1, e_1 + e_2 , e_3 \}$. We set $\beta = (1,0,0)$ and consider the functional

$$\begin{aligned} \varPhi _1(\hat{\varphi }) := \int _{\frac{1}{3}}^{\frac{2}{3}} \hat{\varphi }(\hat{x}_1,1/3,1/3) d \hat{x}_1, \quad \hat{\varphi } \in W^{2,p}(\widehat{T}). \end{aligned}$$

By an analogous argument, we can set functionals for cases $\beta = (0,1,0), (0,0,1)$.

When $m = \ell = 0$ and $p = \infty$, we can easily check that

$$\begin{aligned} \Vert \hat{\varphi } - I_{\widehat{T}}^{CR,S} \hat{\varphi } \Vert _{L^{\infty }(\widehat{T})} \le c \Vert \hat{\varphi } \Vert _{L^{\infty }(\widehat{T})}. \end{aligned}$$

□

7 Concluding remarks

As our concluding remarks, we identify several topics related to the results described in this paper.

7.1 Good elements or not for $d=2,3$?

In this subsection, we consider good elements on meshes. Here, we define “good elements” on meshes as those for which there exists some $\gamma _0 > 0$ satisfying Eq. (7). We treat a “Right-angled triangle,” “Blade,” and “Dagger” for $d=2$, and a “Spire,” “Spear,” “Spindle,” “Spike,” “Splinter,” and “Sliver” for $d=3$, as introduced in [9]. We present the quantities $\alpha _{\max } / \alpha _{\min }$ and $H_{T_0}/h_{T_0}$ for these elements.

7.1.1 Isotropic mesh

We consider the following condition. There exists a constant $\gamma _1 > 0$ such that, for any ${\mathbb {T}}_h \in \{ {\mathbb {T}}_h \}$ and any simplex $T_0 \in {\mathbb {T}}_h$, we have

$$\begin{aligned} |T_0| \ge \gamma _1 h_{T_0}^d. \end{aligned}$$

(62)

Condition (62) is equivalent to the shape-regularity condition; see [6, Theorem 1].

If geometric condition (62) is satisfied, it holds that

$$\begin{aligned} \frac{H_{T_0}}{h_{T_0}} \le \frac{h_{T_0}^d}{|T_0|} \le \frac{1}{\gamma _1}, \quad \frac{\alpha _{\max }}{\alpha _{\min }} \le c \frac{h_{T_0}}{\alpha _2} \le c \frac{h_{T_0}^d}{|T_0|} \le \frac{c}{\gamma _1}. \end{aligned}$$

If $p=q$ in Theorem A, one can obtain the optimal order $h_{T_0}^{\ell +1-m}$. In this case, elements satisfying geometric condition (62) are “good.”

7.1.2 Anisotropic mesh: two-dimensional case

Let $S_0 \subset {\mathbb {R}}^2$ be a triangle. Let $0 < s \ll 1$, $s \in {\mathbb {R}}$, and $\varepsilon ,\delta ,\gamma \in {\mathbb {R}}$. A dagger has one short edge and a blade has no short edge.

Example 2

(Right-angled triangle) Let $S_0 \subset {\mathbb {R}}^2$ be the simplex with vertices $x_1 := (0,0)^T$, $x_2 := (s,0)^T$, and $x_3 := (0,s^{\varepsilon })^T$ with $1 < \varepsilon$; see Fig. 1. Then, we have that $\alpha _1 = s$ and $\alpha _2 = s^{\varepsilon }$; i.e.,

$$\begin{aligned} \frac{\alpha _{\max }}{\alpha _{\min }}&\le s^{1 - \varepsilon } \rightarrow \infty \quad {\text {as}}\ s \rightarrow 0, \quad \frac{H_{S_0}}{h_{S_0}} =2. \end{aligned}$$

In this case, the element $S_0$ is “good.”

Fig. 1

Example 2: Right-angled triangle

Example 3

(Dagger) Let $S_0 \subset {\mathbb {R}}^2$ be the simplex with vertices $x_1 := (0,0)^T$, $x_2 := (s,0)^T$, and $x_3 := (s^{\delta },s^{\varepsilon })^T$ with $1< \varepsilon < \delta$, see Fig. 2. Then, we have that $\alpha _1 = \sqrt{(s - s^{\delta })^2 + s^{2 \varepsilon }}$ and $\alpha _2 = \sqrt{s^{2 \delta } + s^{2 \varepsilon }}$; i.e.,

$$\begin{aligned} \frac{\alpha _{\max }}{\alpha _{\min }}&= \frac{ \sqrt{(s - s^{\delta })^2 + s^{2 \varepsilon }}}{\sqrt{s^{2 \delta } + s^{2 \varepsilon }}} \le c s^{1 - \varepsilon } \rightarrow \infty \quad {\text {as}}\ s \rightarrow 0,\\ \frac{H_{S_0}}{h_{S_0}}&= \frac{ \sqrt{(s- s^{\delta })^2 + s^{2 \varepsilon }} \sqrt{s^{2 \delta } + s^{2 \varepsilon }}}{\frac{1}{2} s^{1 + \varepsilon }} \le c. \end{aligned}$$

In this case, the element $S_0$ is “good.”

Fig. 2

Examples 3 and 5: Dagger

Remark 6

In the above examples, $\alpha _2 \approx \alpha _2 t = {\mathscr {H}}_2$ holds. That is, the good element $S_0 \subset {\mathbb {R}}^2$ satisfies conditions such as $\alpha _2 \approx \alpha _2 t = {\mathscr {H}}_2$.

Example 4

(Blade) Let $S_0 \subset {\mathbb {R}}^2$ be the simplex with vertices $x_1 := (0,0)^T$, $x_2 := (2s,0)^T$, and $x_3 := (s ,s^{\varepsilon })^T$ with $1 < \varepsilon$; see Fig. 3. Then, we have that $\alpha _1 = \alpha _2 = \sqrt{s^{2} + s^{2 \varepsilon }}$; i.e.,

$$\begin{aligned} \frac{\alpha _{\max }}{\alpha _{\min }} = 1, \quad \frac{H_{S_0}}{h_{S_0}} = \frac{s^{2} + s^{2 \varepsilon }}{s^{1 + \varepsilon }} \rightarrow \infty \quad {\text {as}}\ s \rightarrow 0. \end{aligned}$$

In this case, the element $S_0$ is “not good.”

Fig. 3

Example 4: Blade

Example 5

(Dagger) Let $S_0 \subset {\mathbb {R}}^2$ be the simplex with vertices $x_1 := (0,0)^T$, $x_2 := (s,0)^T$, and $x_3 := (s^{\delta },s^{\varepsilon })^T$ with $1< \delta < \varepsilon$; see Fig. 2. Then, we have that $\alpha _1 = \sqrt{(s - s^{\delta })^2 + s^{2 \varepsilon }}$ and $\alpha _2 = \sqrt{s^{2 \delta } + s^{2 \varepsilon }}$; i.e.,

$$\begin{aligned} \frac{\alpha _{\max }}{\alpha _{\min }}&= \frac{ \sqrt{(s - s^{\delta })^2 + s^{2 \varepsilon }}}{\sqrt{s^{2 \delta } + s^{2 \varepsilon }}} \le c s^{1 - \delta } \rightarrow \infty \quad {\text {as}}\ s \rightarrow 0,\\ \frac{H_{S_0}}{h_{S_0}}&= \frac{ \sqrt{(s- s^{\delta })^2 + s^{2 \varepsilon }} \sqrt{s^{2 \delta } + s^{2 \varepsilon }}}{\frac{1}{2} s^{1 + \varepsilon }} \le c s^{\delta - \varepsilon } \rightarrow \infty \quad {\text {as}}\ s \rightarrow 0. \end{aligned}$$

In this case, the element $S_0$ is “not good.”

7.1.3 Anisotropic mesh: three-dimensional case

Example 6

Let $T_0 \subset {\mathbb {R}}^3$ be a tetrahedron. Let $S_0$ be the base of $T_0$; i.e., $S_0 = \triangle x_1 x_2 x_3$. Recall that

$$\begin{aligned} \frac{H_{T_0}}{h_{T_0}} = \frac{\alpha _1 \alpha _2 \alpha _3}{|T_0|} =\frac{\alpha _1 \alpha _2}{\frac{1}{2} \alpha _1 \alpha _2 t_1} \frac{\alpha _3}{\frac{1}{3} \alpha _3 t_2} \le \frac{H_{S_0}}{h_{S_0}} \frac{\alpha _3}{\frac{1}{3} {\mathscr {H}}_3}. \end{aligned}$$

(63)

If the triangle $S_0$ is “not good,” such as in Examples 4 and 5, the quantity in Eq. (63) may diverge. In the following, we consider the case in which the triangle $S_0$ is “good.”

Assume that there exists a positive constant M such that $\frac{H_{S_0}}{h_{S_0}} \le M$. For simplicity, we set $x_1 := (0,0,0)^T$, $x_2 := (2s,0,0)^T$, and $x_3 := (2s - \sqrt{4 s^2 - s^{2 \gamma }}, s^{\gamma },0)^T$ with $1 < \gamma$; see Fig. 4. Then,

$$\begin{aligned} \alpha _1 = 2s, \ \alpha _2 = \sqrt{\frac{4 s^{2 \gamma }}{2 + \sqrt{4 - s^{2 \gamma -2} }}}, \end{aligned}$$

and because $\alpha _{\max } \approx c s$,

$$\begin{aligned} \frac{\alpha _{\max }}{\alpha _{\min }} \le \frac{c s}{\alpha _2} \le c s^{1 - \gamma } \rightarrow \infty \quad {\text {as}}\ s \rightarrow 0. \end{aligned}$$

If we set $x_4 := (s,0,s^{\varepsilon })^T$ with $1 < \varepsilon$, the triangle $\triangle x_1 x_2 x_4$ is the blade (Example 4). Then,

$$\begin{aligned} \alpha _3 = \sqrt{s^2 + s^{2 \varepsilon }}. \end{aligned}$$

Thus, we have

$$\begin{aligned} \frac{H_{T_0}}{h_{T_0}} \le c \frac{s^{2s + \gamma }}{s^{1+\gamma +\varepsilon }} \le c s^{1-\varepsilon } \rightarrow \infty \quad {\text {as}}\ s \rightarrow 0. \end{aligned}$$

In this case, the element $T_0$ is “not good.”

If we set $x_4 := (s^{\delta },0,s^{\varepsilon })^T$ with $1< \delta< \varepsilon < \gamma$, the triangle $\triangle x_1 x_2 x_4$ is the dagger (Example 5). Then,

$$\begin{aligned} \alpha _3 = \sqrt{s^{2 \delta } + s^{2 \varepsilon }}. \end{aligned}$$

Thus, we have

$$\begin{aligned} \frac{H_{T_0}}{h_{T_0}} \le c \frac{s^{1+\gamma + \delta }}{s^{1+\gamma +\varepsilon }} \le c s^{\delta - \varepsilon } \rightarrow \infty \quad {\text {as}}\ s \rightarrow 0. \end{aligned}$$

In this case, the element $T_0$ is “not good.”

If we set $x_4 := (s^{\delta },0,s^{\varepsilon })^T$ with $1< \varepsilon< \delta < \gamma$, the triangle $\triangle x_1 x_2 x_4$ is the dagger (Example 3). Then,

$$\begin{aligned} \alpha _3 = \sqrt{s^{2 \delta } + s^{2 \varepsilon }}. \end{aligned}$$

Thus, we have

$$\begin{aligned} \frac{H_{T_0}}{h_{T_0}} \le c \frac{s^{1+\gamma + \varepsilon } }{ s^{1+\gamma +\varepsilon }} \le c. \end{aligned}$$

In this case, the element $T_0$ is “good” and $\alpha _3 \approx \alpha _3 t_2 = {\mathscr {H}}_3$ holds.

Fig. 4

Example 6

Example 7

In [9], the spire has a cycle of three daggers among its four triangles; see Fig. 5. The splinter has four daggers; see Fig. 9. The spear and spike have two daggers and two blades as triangles; see Figs. 6, 8. The spindle has four blades as triangles; see Fig. 7.

Fig. 5

Spire

Fig. 6

Spear

Fig. 7

Spindle

Fig. 8

Spike

Fig. 9

Splinter

Remark 7

The above examples reveal that the good element $T_0 \subset {\mathbb {R}}^3$ satisfies conditions such as $\alpha _2 \approx \alpha _2 t_1 = {\mathscr {H}}_2$ and $\alpha _3 \approx \alpha _3 t_2 = {\mathscr {H}}_3$.

Example 8

Using an element $T_0$ called a Sliver, we compare the three quantities $\frac{h_{T_0}^3}{|{T_0}|}$, $\frac{H_{T_0}}{h_{T_0}}$, and $\frac{R_3}{h_{T_0}}$, where the parameter $R_3$ denotes the circumradius of $T_0$.

Let $T_0 \subset {\mathbb {R}}^3$ be the simplex with vertices $x_1 := (s^{\varepsilon _2},0,0)^T$, $x_2 := (-s^{\varepsilon _2},0,0)^T$, $x_3 := (0,-s,s^{\varepsilon _1})^T$, and $x_4 := (0,s,s^{\varepsilon _1})^T$ ($\varepsilon _1, \varepsilon _2 > 1$), where $s := \frac{1}{N}$, $N \in {\mathbb {N}}$; see Fig. 10. Let $L_i$ ($1 \le i \le 6$) be the edges of $T_0$ with $\alpha _{\min } = L_1 \le L_2 \le \cdots \le L_6 = h_{T_0}$. Recall that $\alpha _{\max } \approx h_{T_0}$ and

$$\begin{aligned} \frac{\alpha _{\max }}{\alpha _{\min }} \le c \frac{L_6}{L_1}, \quad \frac{H_{T_0}}{h_{T_0}} = \frac{L_1 L_2}{|T_0|} h_{T_0}. \end{aligned}$$

In Table 1, the angle between $\triangle x_1 x_2 x_3$ and $\triangle x_1 x_2 x_4$ tends to $\pi$ as $s \rightarrow 0$, and the simplex $T_0$ is “not good.” In Table 2, the angle between $\triangle x_1 x_3 x_4$ and $\triangle x_2 x_3 x_4$ tends to 0 as $s \rightarrow 0$, and the simplex $T_0$ is “good.” In Table 3, from the numerical results, the simplex $T_0$ is “not good.”

Fig. 10

Example 8: Sliver

Table 1 $h_{T_0}^3/{|T_0|}$, $H_{T_0}/h_{T_0}$, and $R_3/h_{T_0}$ ($\varepsilon _1 = 1.5$, $\varepsilon _2 = 1.0$)

Table 2 $h_{T_0}^3/{|T_0|}$, $H_{T_0}/h_{T_0}$, and $R_3/h_{T_0}$ ($\varepsilon _1 = 1.0$, $\varepsilon _2 = 1.5$)

Table 3 $h_{T_0}^3/{|T_0|}$, $H_{T_0}/h_{T_0}$, and $R_3/h_{T_0}$ ($\varepsilon _1 = 1.5$, $\varepsilon _2 = 1.5$)

7.2 Effect of the quantity $|T_0|^{\frac{1}{q} - \frac{1}{p}}$ on the interpolation error estimates for $d = 2,3$

We now consider the effect of the factor $|T_0|^{\frac{1}{q} - \frac{1}{p}}$.

7.2.1 Case in which $q > p$

When $q > p$, the factor may affect the convergence order. In particular, the interpolation error estimate may diverge on anisotropic mesh partitions.

Let $T_0 \subset {\mathbb {R}}^2$ be the triangle with vertices $x_1 := (0,0)^T$, $x_2 := (s,0)^T$, $x_3 := (0, s^{\varepsilon })^T$ for $0 < s \ll 1$, $\varepsilon \ge 1$, $s \in {\mathbb {R}}$, and $\varepsilon \in {\mathbb {R}}$; see Fig. 1. Then,

$$\begin{aligned} \frac{\alpha _{\max }}{\alpha _{\min }} = s^{1 - \varepsilon }, \quad |T_0| = \frac{1}{2} s^{1 + \varepsilon }. \end{aligned}$$

Let $k=1$, $\ell = 2$, $m = 1$, $q = 2$, and $p \in (1,2)$. Then, $W^{1,p}({T}_0) \hookrightarrow L^2({T}_0)$ and Theorem B lead to

$$\begin{aligned} | {\varphi }_0 - I_{{T}_0} {\varphi }_0 |_{H^{1}({T}_0)} \le c s^{ - (1+\varepsilon )\frac{2 - p}{2p}} \left( s \left| \frac{\partial \varphi _0}{\partial x_1} \right| _{W^{1,p}({T}_0)} + s^{\varepsilon } \left| \frac{\partial \varphi _0}{\partial x_2} \right| _{W^{1,p}({T}_0)} \right) . \end{aligned}$$

When $\varepsilon = 1$ (i.e., an isotropic element), we obtain

$$\begin{aligned} | {\varphi }_0 - I_{{T}_0} {\varphi }_0 |_{H^{1}({T}_0)} \le c h_{T_0}^{ \frac{2(p-1)}{p}} |\varphi _0|_{W^{2,p}(T_0)}, \quad \frac{2(p-1)}{p} > 0. \end{aligned}$$

However, when $\varepsilon > 1$ (i.e., an anisotropic element), the estimate may diverge as $s \rightarrow 0$. Therefore, if $q > p$, the convergence order of the interpolation operator may deteriorate.

7.2.2 Case in which $q < p$

We consider Theorem B. Let $I_{T_0}^{L}: {\mathcal {C}}^0(T_0) \rightarrow {\mathcal {P}}^k$ ($k \in {\mathbb {N}}$) be the local Lagrange interpolation operator. Let ${\varphi }_0 \in W^{\ell ,\infty }(T_0)$ be such that $\ell \in {\mathbb {N}}$, $2 \le \ell \le k+1$. Then, for any $m \in \{ 0, \ldots ,\ell -1\}$ and $q \in [1,\infty ]$, it holds that

$$\begin{aligned} | {\varphi }_0 - I_{{T}_0}^L {\varphi }_0 |_{W^{m,q}({T}_0)} \le c |T_0|^{\frac{1}{q} } \left( \frac{H_{T_0}}{h_{T_0}} \right) ^m \sum _{|\gamma | = \ell -m} {\mathscr {H}}^{\gamma }| \partial ^{\gamma } {(\varphi _0 \circ \varPhi _{T_0})} |_{W^{ m ,\infty } (\varPhi _{T_0}^{-1}(T_0))}. \end{aligned}$$

(64)

Therefore, the convergence order is improved by $|T_0|^{\frac{1}{q}}$.

We can perform some numerical tests to confirm this. Let $k=1$ and

$$\begin{aligned} \varphi _0(x,y,z) := x^2 + \frac{1}{4} y^2 + z^2. \end{aligned}$$

• (I) Let $T_0 \subset {\mathbb {R}}^3$ be the simplex with vertices $x_1 := (0,0,0)^T$, $x_2 := (s,0,0)^T$, $x_3 := (0,s^{\varepsilon },0)^T$, and $x_4 := (0,0,s^{\delta })^T$ ($1 < \delta \le \varepsilon$), and $0 < s \ll 1$, $s \in {\mathbb {R}}$; see Fig. 11. Then, we have that $\alpha _1 = \sqrt{s^2 + s^{2 \varepsilon }}$, $\alpha _2 = s^{\varepsilon }$, and $\alpha _3 := \sqrt{s^{2 \varepsilon } + s^{2 \delta }}$; i.e.,

  $$\begin{aligned} \frac{\alpha _{\max }}{\alpha _{\min }} \le c s^{1 - \varepsilon }, \quad \frac{H_{T_0}}{h_{T_0}} \le c. \end{aligned}$$

  From Eq. (64) with $m=1$, $\ell = 2$, and $q=2$, because $|T_0| \approx s^{1+\varepsilon + \delta }$, we have the estimate

  $$\begin{aligned} | {\varphi }_0 - I_{{T}_0}^L {\varphi }_0 |_{H^{1}({T}_0)} \le c h_{T_0}^{\frac{3 + \varepsilon + \delta }{2}}. \end{aligned}$$

  Computational results for $\varepsilon = 3.0$ and $\delta = 2.0$ are presented in Table 4.

• (II) Let $T_0 \subset {\mathbb {R}}^3$ be the simplex with vertices $x_1 := (0,0,0)^T$, $x_2 := (s,0,0)^T$, $x_3 := (s/2,s^{\varepsilon },0)^T$, and $x_4 := (0,0,s)^T$ ($1 < \varepsilon \le 6$) and $0 < s \ll 1$, $s \in {\mathbb {R}}$; see Fig. 12. Then, we have that $\alpha _1 = s$, $\alpha _2 = \sqrt{ s^2/4 + s^{2 \varepsilon }}$, and $\alpha _3 := s$; i.e.,

  $$\begin{aligned} \frac{\alpha _{\max }}{\alpha _{\min }} = \frac{s}{\sqrt{ s^2/4 + s^{2 \varepsilon }}} \le c, \quad \frac{H_{T_0}}{h_{T_0}} \le c s^{1 - \varepsilon }. \end{aligned}$$

  From Eq. (64) with $m=1$, $\ell = 2$, and $q=2$, because $|T_0| \approx s^{2+\varepsilon }$, we have the estimate

  $$\begin{aligned} |{\varphi }_0 - I_{{T}_0}^L {\varphi }_0 |_{H^{1}({T}_0)} \le c h_{T_0}^{3 - \frac{\varepsilon }{2}}. \end{aligned}$$

  Computational results for $\varepsilon = 3.0,6.0$ are presented in Table 5.

Table 4 Error of the local interpolation operator ($\varepsilon = 3.0, \delta = 2.0$)

Fig. 11

Case in which $q < p$, Example (I)

Table 5 Error of the local interpolation operator ($\varepsilon = 3.0,6.0$)

Fig. 12

Case in which $q < p$, Example (II)

7.3 Inverse inequalities

This section presents some limited results for the inverse inequalities. The results are only stated; the proofs can be found in [15].

Lemma 8

Let $\widehat{P} := {\mathcal {P}}^k$ with $k \in {\mathbb {N}}$. If Assumption 1 is imposed, there exist positive constants $C_i^{IV,d}$, $i=1, \ldots ,d$, independent of $h_{T}$ and T, such that, for all ${\varphi }_h \in {P} = \{ \hat{\varphi }_h \circ {\varPhi }_{T}^{-1} ; \ \hat{\varphi }_h \in \widehat{P} \}$,

$$\begin{aligned} \left\| \frac{\partial \varphi _h}{\partial x_i} \right\| _{L^q(T)} \le C_i^{IV,d} |T|^{\frac{1}{q} - \frac{1}{p}} \frac{1}{{\mathscr {H}}_i} \Vert \varphi _h \Vert _{L^p(T)}. \quad i=1,\ldots ,d. \end{aligned}$$

(65)

Remark 8

If Assumption 1 is not imposed, estimate (65) for $i=3$ is

$$\begin{aligned} \left\| \frac{\partial \varphi _h}{\partial x_3} \right\| _{L^q(T)} \le C_{3}^{IV,3} |T|^{\frac{1}{q} - \frac{1}{p}} \frac{H_{T}}{h_{T}} \frac{1}{{\mathscr {H}}_2} \Vert \varphi _h \Vert _{L^p(T)}. \end{aligned}$$

(66)

This may not be sharp. We leave further arguments for future work.

Theorem D

Let $\widehat{P} := {\mathcal {P}}^k$ with $k \in {\mathbb {N}}_0$. Let $\gamma = (\gamma _1,\ldots ,\gamma _d) \in {\mathbb {N}}_0^d$ be a multi-index such that $0 \le |\gamma | \le k$. If Assumption 1 is imposed, there exists a positive constant $C^{IVC}$, independent of $h_{T}$ and T, such that, for all ${\varphi }_h \in {P} = \{ \hat{\varphi }_h \circ {\varPhi }_{T}^{-1} ; \ \hat{\varphi }_h \in \widehat{P} \}$,

$$\begin{aligned} \Vert \partial ^{\gamma } \varphi _h \Vert _{L^q(T)} \le C^{IVC} |T|^{\frac{1}{q} - \frac{1}{p}} {\mathscr {H}}^{- \gamma } \Vert {\varphi }_h \Vert _{L^p({T})}. \end{aligned}$$

(67)