A robust discontinuous Galerkin scheme on anisotropic meshes

Abstract

Discontinuous Galerkin (DG) methods are extensions of the usual Galerkin finite element methods. Although there are vast amount of studies on DG methods, most of them have assumed shape-regularity conditions on meshes for both theoretical error analysis and practical computations. In this paper, we present a new symmetric interior penalty DG scheme with a modified penalty term. We show that, without imposing the shape-regularity condition on the meshes, the new DG scheme inherits all of the good properties of standard DG methods, and is thus robust on anisotropic meshes. Numerical experiments confirm the theoretical error estimates obtained.

1 Introduction

Discontinuous Galerkin (DG) methods are extensions of the usual (continuous) Galerkin finite element methods. The idea of introducing penalty terms in finite element methods originated from Nitsche [16] and Babuška [3], while the idea of using discontinuous elements with an interior penalty was introduced by Wheeler [19]. Later, this approach was extended to the cases of nonlinear elliptic and parabolic problems by Arnold [1]. Since then, the DG methods have developed in many directions. For an account of the history of DG methods for elliptic problems, readers are referred to [2, Section 2]. Overall, the mathematical theory of DG methods is well established [4,5,6,7, 17]. In this paper, we consider the symmetric interior penalty (SIP) DG method, which is one of the most basic and well-known DG schemes.

The above mentioned papers and textbooks confirm that a shape-regularity condition has always been imposed on meshes for theoretical error analysis of DG methods. The shape-regularity condition requires that elements in the meshes must be neither very “flat” nor “degenerated” (see Definition 1). If a mesh contains very flat elements, it is said to be anisotropic. The simple numerical experiment described in Sect. 3.3 shows that the standard SIP-DG method is not robust on anisotropic meshes, and that the shape-regularity condition is crucial for practical computations.

The purpose of this paper is to introduce a new SIP-DG scheme that is robust on anisotropic meshes. To this end, we use the general trace inequality to define a new penalty term for the proposed SIP-DG scheme in Sect. 4. In Sect. 5, we show that the new scheme inherits all of the good properties of standard SIP-DG methods. That is, if the penalty parameter is sufficiently large, the new SIP-DG scheme is consistent, coercive, stable, and bounded on arbitrary (proper) meshes (Lemma $3^{new}$ and Lemma 8). Those properties immediately yield error estimations of the new SIP-DG scheme without imposing the shape-regularity condition (see Corollary 11). An immediate consequence is the error estimate of order ${\mathcal {O}}(h^k)$ under the maximum angle condition on meshes (see Corollary 12). In Sect. 6, we present the results of numerical experiments to confirm the theoretical results obtained. From the results, we conclude that the newly presented SIP-DG scheme is robust on anisotropic meshes.

2 Preliminaries

2.1 The model problem

Let $\varOmega \subset {\mathbb {R}}^d$, ($d = 2, 3$) be a bounded polyhedral domain. Let $L^2(\varOmega )$, $H^1(\varOmega )$, and $H_0^1(\varOmega )$ be the usual Lebesgue and Sobolev spaces (see Sect. 2.3 for notation of their (semi)norms and inner products). We consider the following Poisson problem: find $u \in H^1(\varOmega )$ such that

$$\begin{aligned} - \varDelta u = \phi \quad \text { in } \varOmega , \quad u = 0 \; \text { on } \partial \varOmega , \end{aligned}$$

(2.1)

where $\phi \in L^2(\varOmega )$ is a given function. The weak form of the model problem is as follows:

$$\begin{aligned} a(u,v) := \int _\varOmega \nabla u \cdot \nabla v \, \mathrm {d}{\mathbf {x}}= (\phi , v)_\varOmega , \quad \forall v \in H_0^1(\varOmega ). \end{aligned}$$

(2.2)

The model problem (2.1) is said to satisfy elliptic regularity if there exists a positive constant $C_{ell}$ such that the following a priori estimate holds for the exact solution u:

$$\begin{aligned} \Vert u\Vert _{2,\varOmega } \le C_{ell} \Vert \phi \Vert _{0,\varOmega }, \quad \forall \phi \in L^2(\varOmega ). \end{aligned}$$

(2.3)

It is well known that if $\varOmega$ is convex, then the model problem (2.1) satisfies elliptic regularity [8].

2.2 Meshes of $\varOmega$

Although DG methods allow elements with a variety of geometries, we consider only simplicial elements in this paper. Thus, we suppose that the domain $\varOmega$ is divided into a finite number of triangles ($d=2$) or tetrahedrons ($d=3$), which are assumed to be closed sets. A mesh (or triangulation) of $\varOmega$ is denoted by $\mathcal {T}_h$. That is, $\mathcal {T}_h$ is a finite set of triangles or tetrahedrons that has the following properties:

$$\begin{aligned} {\overline{\varOmega }} = \bigcup _{T \in \mathcal {T}_h} T, \quad {{\text {int}} T_1} \cap {{\text {int}} T_2} = \emptyset \; \text { if } \; T_1 \ne T_2, \end{aligned}$$

where ${\text {int}} T_i$ is the interior of $T_i$. For $T \in \mathcal {T}_h$, let ${\mathbf {n}}_T$ be the unit outer normal vector on $\partial T$.

In this paper, we assume that meshes are proper (or face-to-face). This means that, for $T_1, T_2 \in \mathcal {T}_h$, $T_1 \ne T_2$,

$$\begin{aligned} \text { if } T_1 \cap T_2 \ne \emptyset , \text { then } T_1 \cap T_2 \text { is an } r\text {-face of } T_i\; (i = 1, 2) \text { with } 0 \le r \le d-1. \end{aligned}$$

(2.4)

For a d-simplex T and its facet f, their Lebesgue and Hausdorff measures are denoted by $|T|$ and $|f|$, respectively.

For T, we define $h_T := {{\text {diam}} T}$. If $d=2$, $R_T$ is the circumradius of T. Note that $R_T = l_1l_2h_T/(4|T|)$, where $l_1 \le l_2 \le h_T$ are the lengths of the edges of T. If $d=3$, $R_T$ is defined by

$$\begin{aligned} R_T := \frac{l_1l_2}{|T|}h_T^2, \end{aligned}$$

(2.5)

where $l_1 \le l_2 \le \cdots \le h_T$ are the lengths of the edges of T. As has been seen in [10,11,12,13,14,15], $R_T$ is an important parameter in measuring interpolation errors on d-simplices. For example, the errors of Lagrange interpolation on T are bounded in terms of $R_T$, as presented by (5.10) and (5.11).

Remark

The best definition of $R_T$ for tetrahedrons remains an open problem. A simple example immediately rejects the idea that $R_T$ for a tetrahedron might be the radius of its circumsphere [14, p. 3]. The definition (2.5) is given in [10]. In [10], another parameter, denoted by $H_T$, is introduced, and it is shown that $R_T$ and $H_T$ are equivalent (see also [15]). In [14], the projected circumradius of T is defined for a tetrahedrons. It is conjectured that $R_T$ and the projected circumradius are equivalent.

Let $\mathcal {F}_h := \{f \mid f \text { is a facet of } T \in \mathcal {T}_h\}$. That is, $\mathcal {F}_h$ is the set of all edges ($d=2$) or faces ($d=3$) in $\mathcal {T}_h$. Then, let $\mathcal {F}_h^\partial := \{f \in \mathcal {F}_h \mid f \subset \partial \varOmega \}$ and $\mathcal {F}_h^o := \mathcal {F}_h \backslash \mathcal {F}_h^\partial$.

Suppose that we consider a (possibly infinite) family of meshes $\{\mathcal {T}_h\}_{h > 0}$ with $h \rightarrow 0$.

Definition 1

(1) The family of meshes $\{\mathcal {T}_h\}_{h > 0}$ is said to satisfy the shape-regularity condition with respect to $\sigma$ if there exists a positive constant $\sigma$ such that

$$\begin{aligned} \frac{h_T}{\rho _T} \le \sigma , \quad \forall T \in \mathcal {T}_h, \quad \forall h > 0, \end{aligned}$$

where $\rho _T$ is the diameter of the inscribed ball of T. We call $\sigma$ the shape-regular constant in this paper.

(2) The family of meshes $\{\mathcal {T}_h\}_{h > 0}$ is said to satisfy the maximum angle condition with respect to a constant $C_{max}$ $(\pi /3< C_{max} < \pi )$ if the following hold for all $T \in \mathcal {T}_h$ and for all $\mathcal {T}_h$:

• An arbitrary inner angle $\theta$ of T is $\theta \le C_{max}$ ($d=2$), or

• An arbitrary inner angle $\theta$ of any facet of T is $\theta \le C_{max}$, and an arbitrary dihedral angle $\eta$ of T is $\eta \le C_{max}$ ($d=3$).

(3) The family of meshes $\{\mathcal {T}_h\}_{h > 0}$ is said to satisfy the circumradius condition if the family satisfies

$$\begin{aligned} \lim _{h \rightarrow 0}\max _{T \in \mathcal {T}_h} R_T = 0. \end{aligned}$$

In this paper, we always assume that the family $\{\mathcal {T}_h\}_{h > 0}$ of meshes satisfies the circumradius condition.

Remark

If we deal with only a finite family of meshes $\{\mathcal {T}_h\}$ and we take a sufficiently large $\sigma > 0$, then the family satisfies the shape-regularity condition because $\{\mathcal {T}_h\}$ contains only a finite number of d-simplices. However, if $\sigma$ is too large (say, $\sigma \ge 10$), we commonly say that $\{\mathcal {T}_h\}$ is not shape-regular. In such a case, as mentioned in Sect. 1, $\{\mathcal {T}_h\}$ is said to be anisotropic.

2.3 Function spaces

Let $k \ge 1$ be a positive integer. We use the notation $L^2(\varOmega )$, $L^2(f)$ $(f \in \mathcal {F}_h)$, $H^k(\varOmega )$, $H_0^1(\varOmega )$ for the usual Lebesgue and Sobolev spaces. We denote their norms and semi-norms by, for example, $\Vert \cdot \Vert _{0,f}$, $|\cdot |_{1,\varOmega }$, and their inner products by $(\cdot ,\cdot )_f$, $(\cdot ,\cdot )_\varOmega$. Let $\mathcal {P}_k(K)$ be the set of all polynomials defined on the closed set K with degree less than or equal to a positive integer k.

As usual, we introduce the broken Sobolev and polynomial spaces by

$$\begin{aligned} \displaystyle H^k(\mathcal {T}_h)&:= \left\{ v \in L^2(\varOmega ) \bigm | v|_{T} \in H^k(T), \forall T \in \mathcal {T}_h \right\} , \\ \mathcal {P}_k(\mathcal {T}_h)&:= \left\{ v \in L^2(\varOmega ) \bigm | v|_{T} \in \mathcal {P}_k(T), \forall T \in \mathcal {T}_h \right\} . \end{aligned}$$

Finally, define $V := H_0^1(\varOmega )$, $V_* := H_0^1(\varOmega ) \cap H^2(\varOmega )$, $V_h := \mathcal {P}_k(\mathcal {T}_h)$, and $V_{*h} := V_* + V_h$.

2.4 Jump and mean of functions on $f \in \mathcal {F}_h$

For each interior facet $f \in \mathcal {F}_h^o$, there are two simplices that share f. We number those simplices as $T_{f}^{i} \in \mathcal {T}_h$ $(i=1,2)$ and fix the numbering once the mesh is obtained. Then, we have $f = T_{f}^{1} \cap T_{f}^{2}$. Recalling that ${\mathbf {n}}_T$ is the unit outer nomal vector on $\partial T$, define ${\mathbf {n}}_f := {\mathbf {n}}_{T_{f}^{1}}$. For $v \in H^2(\mathcal {T}_h)$, we set $v_1 := v|_{T_{f}^{1}}$ and $v_2 := v|_{T_{f}^{2}}$. We denote the trace operator on $T_f^i$ to f by $\gamma _f^i$ ($i=1,2$). Define

$$\begin{aligned}{}[v] := \gamma _f^1(v_1) - \gamma _f^2(v_2), \quad \{v\} := \frac{1}{2}\left( \gamma _f^1(v_1) + \gamma _f^2(v_2)\right) . \end{aligned}$$

The jump $[\nabla v]_f$ and average $\{\nabla v\}_f$ are defined in a similar way.

If $g \in \mathcal {F}_h^\partial$, then $g \subset \partial \varOmega$. Let $g \subset \partial T_g$ with $T_g \in \mathcal {T}_h$. Then, define

$$\begin{aligned}{}[v] = \{v\} := \gamma _g(v|_{T_{g}}). \end{aligned}$$

3 Standard SIP-DG scheme

3.1 Definition of SIP-DG scheme

In the SIP-DG scheme, the bilinear form a(u, v) in (2.2) is discretized as

$$\begin{aligned} a_h^{std}(v,w_h)&:= \sum _{T \in \mathcal {T}_h} \int _T \nabla v \cdot \nabla w_h \mathrm {d}{\mathbf {x}}- \sum _{f \in \mathcal {F}_h} \int _{f} [w_h] \{\nabla v\} \cdot {\mathbf {n}}_f \mathrm {d}s \\&\quad - \sum _{f \in \mathcal {F}_h} \int _{f} [v] \{\nabla w_h\} \cdot {\mathbf {n}}_f \mathrm {d}s + \eta \sum _{f \in \mathcal {F}_h} \frac{1}{h_f} \int _f [v][w_h]\mathrm {d}s \end{aligned}$$

for $v \in V_{*h}$ and $w_h \in V_h$, where $h_f := {{\text{diam}}\, f}$. Here, $\eta$ is a penalty parameter that is taken to be sufficiently large. To make the notation concise, we set

$$\begin{aligned} a_h^{(0)}(v,w_h)&:= \sum _{T \in \mathcal {T}_h} \int _T \nabla v \cdot \nabla w_h \, \mathrm {d}{\mathbf {x}}\nonumber \\ J_h(v,w_h)&:= \sum _{f \in \mathcal {F}_h} \int _{f} [w_h] \{\nabla v\} \cdot {\mathbf {n}}_f \, \mathrm {d}s + \sum _{f \in \mathcal {F}_h} \int _{f} [v] \{\nabla w_h\} \cdot {\mathbf {n}}_f \, \mathrm {d}s, \nonumber \\ P_h^{std}(v,w_h)&:= \eta \sum _{f \in \mathcal {F}_h} \frac{1}{h_f} \int _f [v][w_h] \, \mathrm {d}s. \end{aligned}$$

(3.1)

The terms $J_h(v,w_h)$ and $P_h^{std}(v,w_h)$ are called the jump term and penalty term, respectively. The discretized bilinear form $a_h^{std}(v,w_h)$ is written as

$$\begin{aligned} a_h^{std}(v,w_h) = a_h^{(0)}(v,w_h) - J_h(v,w_h) + P_h^{std}(v,w_h). \end{aligned}$$

Definition 2

The SIP-DG scheme for the model problem is defined as follows: find $u_h \in V_h$ such that

$$\begin{aligned} a_h^{std}(u_h, v_h) = (\phi , v_h)_\varOmega , \quad \forall v_h \in V_h. \end{aligned}$$

(3.2)

3.2 Properties of SIP-DG scheme and error analysis

In the following, we summarize the properties of the SIP-DG method. For their proofs, readers are referred to the standard textbooks [4, 6, 7, 17]. In this section, we mainly refer to [6].

Lemma 3

(Consistency) [6, Lemma 4.8] The exact solution $u \in V_*$ of the model problem (2.1) is consistent:

$$\begin{aligned} a_h^{std}(u,v_h) = (\phi , v_h)_\varOmega , \quad \forall v_h \in V_h. \end{aligned}$$

Therefore, the solution $u_h \in V_h$ of the SIP-DG method (3.2) satisfies the Galerkin orthogonality:

$$\begin{aligned} a_h^{std}(u - u_h,v_h) = 0, \quad \forall v_h \in V_h. \end{aligned}$$

We define the norms associated with the bilinear form $a_h^{std}$ as:

$$\begin{aligned} \Vert v\Vert _{\mathcal {DG}}&:= \left( a_h^{(0)}(v,v) + P_h^{std}(v,v) \right) ^{1/2}, \quad v \in V_{*h}, \\ \Vert v\Vert _{\mathcal {DG}*}&:= \left( \Vert v\Vert _{\mathcal {DG}}^2 + \eta ^{-1} \sum _{f \in \mathcal {F}_h} h_f \Vert \{\nabla v\}\cdot {\mathbf {n}}_f\Vert _{0,f}^2 \right) ^{1/2}. \end{aligned}$$

Lemma 4

Suppose that the mesh $\mathcal {T}_h$ is shape-regular with respect to a constant $\sigma > 0$ and the penalty parameter $\eta$ is sufficiently large. Then,

(1):

$(\mathbf {Discrete\; coercivity})$ [6, Lemma 4.12] The bilinear form $a_h^{std}$ is coercive in $V_h$ with respect to the norm $\Vert \cdot \Vert _{\mathcal {DG}}$:

$$\begin{aligned} a_h^{std}(w_h,w_h) \ge \frac{1}{2} \Vert w_h\Vert _{\mathcal {DG}}^2, \quad \forall w_h \in V_h. \end{aligned}$$

(2):

$(\mathbf {Discrete\; stability})$ The following inequality holds:

$$\begin{aligned} \frac{1}{2}\Vert v_h\Vert _{\mathcal {DG}} \le \sup _{w_h \in V_h} \frac{a_h^{std}(v_h,w_h)}{\Vert w_h\Vert _{\mathcal {DG}}}, \quad \forall v_h \in V_h. \end{aligned}$$

(3):

$(\mathbf {Boundedness})$ [6, Lemma 4.16] The following inequality holds:

$$\begin{aligned} a_h^{std}(v,w_h) \le C \Vert v\Vert _{\mathcal {DG}*}\Vert w_h\Vert _{\mathcal {DG}}, \quad \forall (v,w_h) \in V_{*h}\times V_h, \end{aligned}$$

where the constant $C := C(\eta ,\sigma )$ is independent of h.

Theorem 5

[6, Theorem 4.17] Suppose that the mesh $\mathcal {T}_h$ is shape-regular with respect to a constant $\sigma > 0$ and the penalty parameter $\eta$ is sufficiently large. Then, there exists a unique SIP-DG solution $u_h \in V_h$ of (3.2), and the following error estimate holds:

$$\begin{aligned} \Vert u - u_h\Vert _{\mathcal {DG}} \le C \inf _{y_h \in V_h} \Vert u - y_h\Vert _{\mathcal {DG}*}, \end{aligned}$$

where the constant C depends only on the penalty parameter $\eta$ and $\sigma$.

Corollary 6

[6, Corollary 4.18] Suppose that the assumptions of Theorem 5hold and that the exact solution u of the model problem (2.1) belongs to $H^2(\varOmega )$. Then, we have the following error estimate:

$$\begin{aligned} \Vert u-u_h\Vert _{\mathcal {DG}} \le C h |u|_{2,\varOmega }, \end{aligned}$$

where the constant C depends on $\eta$ and $\sigma$, but is independent of h.

3.3 Numerical experiments (part 1)

We consider a numerical experiment to examine how the shape-regular constant $\sigma$ affects the practical computations involved in the standard SIP-DG scheme.

Set $\varOmega :=(0,1)\times (0,1)$ and $\phi (x,y):= \pi ^2\sin (\pi x)\sin (\pi y)$ in the model problem (2.1). Then, the exact solution is $u(x,y)=\sin (\pi x)\sin (\pi y)/2$. Let n and m be positive integers. We divide the horizontal and vertical sides of $\varOmega$ into n and m equal segments, respectively. We then draw diagonal lines in each small rectangle to define the mesh, as depicted in Fig. 1.

Fig. 1

Mesh constructed in $\varOmega$. $n=10$, $m=20$

We fix $n=40$ and the penalty parameter $\eta = 10$. We apply the standard SIP-DG method to the model problem with various m. The conjugate gradient method with the incomplete Cholesky decomposition preconditioner (ICCG) is used for the linear solver. The successive over-relaxation (SOR) method is also used occasionally to check whether the obtained $u_h$ is reasonable. The results are summarized in Table 1.

Table 1 Errors produced by the SIP-DG method

Here, for $T \in \mathcal {T}_h$, $h={{\text {diam}}{T}}$, R is the circumradius of T, the “$L^2$-error” is $|u - u_h|_{L^2(\varOmega )}$, the “$H^1(\mathcal {T}_h)$-error” is $a_h^{(0)}(u - u_h,u-u_h)^{1/2}$, the “$P_h^{std}$-error” is $P_h^{std}(u-u_h,u-u_h)^{1/2}$, and the “DG-error” is $\Vert u-u_h\Vert _{\mathcal {DG}}$. We employ the 4-point Gauss quadrature of degree 3 on triangles to compute those errors. We see that the errors given by the SIP-DG method decrease as m increases until $m = 100$, which is consistent with the theoretical error estimates. However, the errors increase as m increases from $m=120$. The ICCG iterations do not converge for $m = 200$, while the SOR iterations give almost the same results until $m=160$. For $m=180, 200$, the SOR iterations converge quickly but the obtained $u_h$ are not reasonable.

We also examined the case $m=400$. In this case, we required $\eta =30$ to obtain reasonable $u_h$.

4 New penalty term and SIP-DG scheme

From the numerical experiments described in the previous section, we can conclude that the shape-regularity condition is crucial for the standard SIP-DG method with a fixed penalty parameter $\eta$. It is natural to wonder why this is the case.

The most important term in the SIP-DG scheme is the penalty term $P_h^{std}(v,w_h)$ defined by (3.1). The penalty term originates from the trace inequalities

$$\begin{aligned} \Vert v\Vert _{0,f}&\le \frac{C_1^{tr}}{h_f^{1/2}} \Vert v\Vert _{0,T}, \quad \Vert \nabla v\cdot {\mathbf {n}}\Vert _{0,f} \le \frac{C_2^{tr}}{h_f^{1/2}} \Vert \nabla v\Vert _{0,T}, \quad \forall v \in \mathcal {P}_k(T), \end{aligned}$$

(4.1)

where f is an arbitrary facet of $T \in \mathcal {T}_h$. Note that the constants $C_i^{tr}$ ($i=1,2$) strongly depend on the shape-regular constant $\sigma$.

To avoid imposing the shape-regularity condition, we adopt the general trace inequalities

$$\begin{aligned} \Vert v\Vert _{0,f}&\le C_3^{tr} \frac{|f|^{1/2}}{|T|^{1/2}} \Vert v\Vert _{0,T}, \quad \left\| \nabla v \cdot {\mathbf {n}}\right\| _{0,f} \le C_4^{tr} \frac{|f|^{1/2}}{|T|^{1/2}} \Vert \nabla v\Vert _{0,T}, \quad \forall v \in \mathcal {P}_k(T), \end{aligned}$$

(4.2)

which are valid on an arbitrary d-simplex T. Warburton and Hesthaven [18] presented explicit forms of the constants $C_i^{tr}$ ($i=3,4$) that are independent of the geometry of T. Note that (4.1) is a “simplified” version of (4.2) under the shape-regularity condition. We introduce a quantity on each $f \in \mathcal {F}_h$ below.

Let $f \in \mathcal {F}_h^o$. Then, there exist $T_f^{1}$, $T_f^{2} \in \mathcal {T}_h$ such that $f = T_f^{1} \cap T_f^{2}$. Let $\widetilde{T}_{f}^{i}$ be the d-simplex whose vertices are those of f and the barycenter of $T_{f}^{i}$ ($i=1,2$). Then, define

$$\begin{aligned} \left\{ \frac{|f|}{|\widetilde{T}_f|}\right\} := \frac{|f|}{|\widetilde{T}_{f}^{1}|} + \frac{|f|}{|\widetilde{T}_{f}^{2}|}. \end{aligned}$$

If $g \in \mathcal {F}_h^\partial$, then $g \subset \partial \varOmega$. Let $g \subset \partial T_g$ with $T_g \in \mathcal {T}_h$ and $\widetilde{T}_g$ be the d-simplex whose vertices are those of g and the barycenter of $T_g$. Define

$$\begin{aligned} \left\{ \frac{|g|}{|\widetilde{T}_g|}\right\} := \frac{|g|}{|\widetilde{T}_g|}. \end{aligned}$$

Note that

$$\begin{aligned} \left( \bigcup _{g \in \mathcal {F}_h^\partial }\widetilde{T}_g\right) \cup \left( \bigcup _{f \in \mathcal {F}_h^o} \widetilde{T}_{f}^{1}\cup \widetilde{T}_{f}^{2}\right) = {\overline{\varOmega }}. \end{aligned}$$

(4.3)

See Fig. 2. We remark that the only information we need for the simplex $\widetilde{T}_f^i$ is its measure $|\widetilde{T}_f^i| = |T_f^i|/(d+1)$.

Fig. 2

Domains for the new penalty terms

With the quantity $\left\{ \frac{|f|}{|\widetilde{T}_f|}\right\}$ defined for $f \in \mathcal {F}_h$, we (re)define the penalty term and SIP-DG bilinear form $a_h^{std}$ as

$$\begin{aligned} P_h^{new}(v,w_h)&:= \eta \sum _{f \in \mathcal {F}_h} \left\{ \frac{|f|}{|\widetilde{T}_f|}\right\} \int _f [v] [w_h] \mathrm {d}s, \end{aligned}$$

(4.4)

$$\begin{aligned} a_{h}^{new}(v,w_h)&:= a_h^{(0)}(v,w_h) - J_h(v,w_h) + P_h^{new}(v,w_h). \end{aligned}$$

(4.5)

Note that, if a mesh satisfies the shape-regularity condition, $\left\{ \frac{|f|}{|\widetilde{T}_f|}\right\} \approx \frac{1}{h_f}$ for any facet $f \in \mathcal {F}_h$, and $P_h^{new}$ becomes equivalent to the standard penalty term $P_h^{std}$.

Definition 7

The SIP-DG scheme for the model problem is redefined as follows: find $u_h \in V_h$ such that

$$\begin{aligned} a_{h}^{new}(u_h, v_h) = (\phi , v_h)_\varOmega , \quad \forall v_h \in V_h. \end{aligned}$$

(4.6)

Remark

To see the meaning of the new penalty terms (4.4), let us consider a small part of the mesh of Fig. 1, as shown in Fig. 3.

Fig. 3

Part of the mesh

The mesh consists of congruent right triangles. Let T be one of the right triangles, and $f_1$, $f_2$ be its edges as depicted in Fig. 3. Set $h = |f_1|$. Then, $|f_2| = \alpha h$, where $0< \alpha < 1$. Elementary geometry tells us that $\left\{ \frac{f_2}{|\widetilde{T}_{f_2}|}\right\} = 12/h$,

$$\begin{aligned} \left\{ \frac{|f_1|}{|\widetilde{T}_{f_1}|}\right\} = \frac{12}{\alpha h}, \quad \text { and }\quad \eta \left\{ \frac{|f_1|}{|\widetilde{T}_{f_1}|}\right\} \int _{f_1} [v][w_h] \mathrm {d}s = \frac{12\eta }{\alpha h} \int _{f_1} [v][w_h] \mathrm {d}s. \end{aligned}$$

(4.7)

Note that if T is becoming degenerated, the coefficient $12\eta /\alpha$ will increase. This means that we can interpret the coefficient $\eta \left\{ \frac{|f|}{|\widetilde{T}_f|}\right\}$ as an “improved” version of the standard penalty term coefficient $\frac{\eta }{h_f}$ with the “adaptive” parameter $\alpha$.

5 Properties of the new bilinear form $a_{h}^{new}$ and error estimates

In this section, we show that, without imposing the shape-regularity condition, the new SIP-DG scheme inherits all of the good properties from the standard SIP-DG scheme.

From the definitions, it is clear that Lemma 3 still holds for the new $a_{h}^{new}$:

Lemma 3$^{new}$ (Consistency) The exact solution $u \in V_*$ of the model problem (2.1) is consistent:

$$\begin{aligned} a_{h}^{new}(u,v_h) = (\phi ,v_h)_\varOmega , \quad \forall v_h \in V_h. \end{aligned}$$

Therefore, the solution $u_h \in V_h$ of SIP-DG method (3.2) satisfies the Galerkin orthogonality:

$$\begin{aligned} a_{h}^{new}(u - u_h,v_h) = 0, \quad \forall v_h \in V_h. \end{aligned}$$

We redefine the norms associated with the SIP-DG scheme:

$$\begin{aligned} \Vert v\Vert _{\mathcal {DG}}^{new}&:= \left( a_h^{(0)}(v,v) + P_h^{new}(v,v) \right) ^{1/2}, \quad v \in V_{*h}, \end{aligned}$$

(5.1)

$$\begin{aligned} \Vert v\Vert _{\mathcal {DG}*}^{new}&:= \left( {\left( \Vert v\Vert _{\mathcal {DG}}^{new}\right) ^2} + \eta ^{-1} \sum _{f \in \mathcal {F}_h} \left\{ \frac{|f|}{|\widetilde{T}_f|}\right\} ^{-1} \Vert \{\nabla v\}\cdot {\mathbf {n}}_f\Vert _{0,f}^2 \right) ^{1/2}. \end{aligned}$$

(5.2)

The following lemma holds. Its proof is quite similar to the standard proofs. Here, we loosely follow the proofs given by Di Pietro and Ern [6].

Lemma 8

Suppose that the penalty parameter $\eta$ is sufficiently large. Then,

(1):

$(\mathbf {Discrete\; coercivity})$ The bilinear form $a_{h}^{new}$ is coercive in $V_h$ with respect to the norm $\Vert \cdot \Vert _{\mathcal {DG}}^{new}$:

$$\begin{aligned} a_{h}^{new}(w_h,w_h) \ge \frac{1}{2} \left( \Vert w_h\Vert _{\mathcal {DG}}^{new}\right) ^2, \quad \forall w_h \in V_h. \end{aligned}$$

(2):

$(\mathbf {Discrete\; stability})$ The following inequality holds:

$$\begin{aligned} \frac{1}{2}\Vert v_h\Vert _{\mathcal {DG}}^{new} \le \sup _{w_h \in V_h} \frac{a_{h}^{new}(v_h,w_h)}{\Vert w_h\Vert _{\mathcal {DG}}^{new}}, \quad \forall v_h \in V_h. \end{aligned}$$

(3):

$(\mathbf {Boundedness})$ The following inequalities hold:

$$\begin{aligned} a_{h}^{new}(v,w_h)&\le C \Vert v\Vert _{\mathcal {DG}*}^{new}\Vert w_h\Vert _{\mathcal {DG}}^{new}, \quad \forall (v,w_h) \in V_{*h}\times V_h, \end{aligned}$$

(5.3)

$$\begin{aligned} a_{h}^{new}(v,w)&\le \Vert v\Vert _{\mathcal {DG}*}^{new}\Vert w\Vert _{\mathcal {DG}*}^{new}, \quad \forall (v,w) \in V_{*h}\times V_{*h}, \end{aligned}$$

(5.4)

where the constant $C := C(\eta , C_4^{tr})$ is independent of h and the geometry of elements in $\mathcal {T}_h$.

Proof

(1) Let $w_h \in V_h$. For $f \in \mathcal {F}_h^o$, there exist $T_f^{i} \in \mathcal {F}_h$ ($i=1,2$) with $f = T_f^{1} \cap T_f^{2}$. It follows from the trace inequality (4.2) that

$$\begin{aligned} \left\| \left\{ \nabla w_h \right\} \cdot {\mathbf {n}}_f \right\| _{0,f}&\le C_4^{tr} \frac{|f|^{1/2}}{2} \left( \frac{\Vert \nabla w_h\Vert _{0,\widetilde{T}_f^{1}}}{|\widetilde{T}_f^{1}|^{1/2}} + \frac{\Vert \nabla w_h\Vert _{0,\widetilde{T}_f^{2}}}{|\widetilde{T}_f^{2}|^{1/2}} \right) . \end{aligned}$$

Hence, we have

$$\begin{aligned} (\{\nabla w_h \} \cdot {\mathbf {n}}_f, [w_h])_f&\le \Vert \{\nabla w_h \} \cdot {\mathbf {n}}_f\Vert _{0,f}\Vert [w_h]\Vert _{0,f} \nonumber \\&\le \frac{C_4^{tr} |f|^{1/2}}{2} \left( \frac{\Vert \nabla w_h\Vert _{0,\widetilde{T}_f^{1}}}{|\widetilde{T}_f^{1}|^{1/2}} + \frac{\Vert \nabla w_h\Vert _{0,\widetilde{T}_f^{2}}}{|\widetilde{T}_f^{2}|^{1/2}} \right) \Vert [w_h]\Vert _{0,f} \nonumber \\&\le \frac{C_4^{tr}}{2} \left( \Vert \nabla w_h\Vert _{0,\widetilde{T}_f^{1}}^2 + \Vert \nabla w_h\Vert _{0,\widetilde{T}_f^{2}}^2 \right) ^{1/2} \left\{ \frac{|f|}{|\widetilde{T}_f|}\right\} ^{1/2} \Vert [w_h]\Vert _{0,f}. \end{aligned}$$

(5.5)

We also obtain a similar inequality for the case $f \in \mathcal {F}_h^{\partial }$.

Because of $J_h(w_h,w_h) = 2\sum _{f \in \mathcal {F}_h} (\{\nabla w_h \} \cdot {\mathbf {n}}_f, [w_h])_f$ and (4.3), we have that

$$\begin{aligned} J_h(w_h,w_h)&\le C_4^{tr} \left( \sum _{f \in \mathcal {F}_h} \left\{ \frac{|f|}{|\widetilde{T}_f|}\right\} \Vert [w_h]\Vert _{0,f}^2 \right) ^{1/2} \left( \sum _{T \in \mathcal {T}_h} \Vert \nabla w_h\Vert _{0,T}^2 \right) ^{1/2}. \end{aligned}$$

(5.6)

Thus, it follows from the arithmetic-geometric mean that

$$\begin{aligned} J_h(w_h,w_h)&\le \delta \sum _{T \in \mathcal {T}_h} \Vert \nabla w_h\Vert _{0,T}^2 + \frac{(C_4^{tr})^2}{\delta } \sum _{f \in \mathcal {F}_h} \left\{ \frac{|f|}{|\widetilde{T}_f|}\right\} \Vert [w_h]\Vert _{0,f}^2 \\&= \delta a_h^{(0)}(w_h,w_h) + \frac{(C_4^{tr})^2}{{4} \delta \eta } P_h^{new}(w_h,w_h) \end{aligned}$$

for some constant $\delta > 0$. Set $\delta := 1/2$, and let $\eta$ be sufficiently large so that $\eta \ge (C_4^{tr})^2$. Then, the following coercivity holds:

$$\begin{aligned} a_{h}^{new}(w_h,w_h)&= a_h^{(0)}(w_h,w_h) - J_h(w_h,w_h) + P_h^{new}(w_h,w_h) \\&\ge \frac{1}{2} a_h^{(0)}(w_h,w_h) + \frac{1}{2}P_h^{new}(w_h,w_h) = \frac{1}{2} (\Vert w_h\Vert _{\mathcal {DG}}^{new})^2. \end{aligned}$$

(2) For arbitrary $v_h \in V_h$, we have

$$\begin{aligned} \frac{1}{2}\Vert v_h\Vert _{\mathcal {DG}}^{new} \le \frac{a_{h}^{new}(v_h,v_h)}{\Vert v_h\Vert _{\mathcal {DG}}^{new}} \le \sup _{w_h \in V_h} \frac{a_{h}^{new}(v_h,w_h)}{\Vert w_h\Vert _{\mathcal {DG}}^{new}} \end{aligned}$$

because of the coercivity.

(3) By the Cauchy–Schwarz inequality, we see that

$$\begin{aligned} a_h^{(0)}(v,w_h)&\le \left( a_h^{(0)}(v,v)\right) ^{1/2} \left( a_h^{(0)}(w_h,w_h)\right) ^{1/2}, \\ P_h^{new}(v,w_h)&\le \left( P_h^{new}(v,v)\right) ^{1/2} \left( P_h^{new}(w_h,w_h)\right) ^{1/2}. \end{aligned}$$

Furthermore, we have that

$$\begin{aligned} \sum _{f \in \mathcal {F}_h} (\{\nabla v\}\cdot {\mathbf {n}}_f, [w_h])_f&\le \sum _{f \in \mathcal {F}_h} \eta ^{-1/2}\left\{ \frac{|f|}{|\widetilde{T}_f|}\right\} ^{-1/2} \Vert \\&\quad \times \{\nabla v\}\cdot {\mathbf {n}}_f\Vert _{0,f} \cdot \eta ^{1/2}\left\{ \frac{|f|}{|\widetilde{T}_f|}\right\} ^{1/2}\Vert [w_h]\Vert _{0,f} \\&\le \left( \eta ^{-1}\sum _{f \in \mathcal {F}_h} \left\{ \frac{|f|}{|\widetilde{T}_f|}\right\} ^{-1}\Vert \{\nabla v\}\cdot {\mathbf {n}}_f\Vert _{0,f}^2 \right) ^{1/2}\\&\quad \times \left( P_h^{new}(w_h,w_h)\right) ^{1/2}. \end{aligned}$$

It follows from (5.5) and (4.3) that

$$\begin{aligned} \sum _{f \in \mathcal {F}_h} (\{\nabla w_h\}\cdot {\mathbf {n}}_f, [v])_f&\le \frac{C_4^{tr}}{2} \sum _{f \in \mathcal {F}_h} \left( \Vert \nabla w_h\Vert _{0,T_1'}^2 + \Vert \nabla w_h\Vert _{0,T_2'}^2 \right) ^{1/2} \left\{ \frac{|f|}{|\widetilde{T}_f|}\right\} ^{1/2} \Vert [v]\Vert _{0,f} \\&\le \frac{C_4^{tr}}{2\eta } \left( \sum _{T \in \mathcal {T}_h} \Vert \nabla w_h\Vert _{0,T}^2 \right) ^{1/2} \left( P_h^{new}(v,v)\right) ^{1/2}. \end{aligned}$$

Therefore, we obtain

$$\begin{aligned} J_h(v,w_h)&= \sum _{f \in \mathcal {F}_h} (\{\nabla v\}\cdot {\mathbf {n}}_f, [w_h])_f + \sum _{f \in \mathcal {F}_h} (\{\nabla w_h\}\cdot {\mathbf {n}}_f, [v])_f \\&\le \left( \sum _{f \in \mathcal {F}_h} \eta ^{-1}\left\{ \frac{|f|}{|\widetilde{T}_f|}\right\} ^{-1}\Vert \{\nabla v\}\cdot {\mathbf {n}}_f\Vert _{0,f}^2 \right) ^{1/2}\left( P_h^{new}(w_h,w_h)\right) ^{1/2} \\&\quad + \frac{C_4^{tr}}{2\eta } \left( a_h^{(0)}(w_h,w_h)\right) ^{1/2} \left( P_h^{new}(v,v)\right) ^{1/2}. \end{aligned}$$

For $(v,w) \in V_{*h} \times V_{*h}$, we immediately obtain

$$\begin{aligned} J_h(v,w)&= \sum _{f \in \mathcal {F}_h} (\{\nabla v\}\cdot {\mathbf {n}}_f, [w])_f + \sum _{f \in \mathcal {F}_h} (\{\nabla w\}\cdot {\mathbf {n}}_f, [v])_f \\&\le \left( \sum _{f \in \mathcal {F}_h} \eta ^{-1}\left\{ \frac{|f|}{|\widetilde{T}_f|}\right\} ^{-1}\Vert \{\nabla v\}\cdot {\mathbf {n}}_f\Vert _{0,f}^2 \right) ^{1/2}\left( P_h^{new}(w,w)\right) ^{1/2} \\&\quad + \left( \sum _{f \in \mathcal {F}_h} \eta ^{-1}\left\{ \frac{|f|}{|\widetilde{T}_f|}\right\} ^{-1}\Vert \{\nabla w\}\cdot {\mathbf {n}}_f\Vert _{0,f}^2 \right) ^{1/2}\left( P_h^{new}(v,v)\right) ^{1/2}. \end{aligned}$$

Gathering these inequalities together, we conclude that (5.3) and (5.4) hold. $\square$

Theorem 9

For the exact solution $u \in V_{*h}$ of the model problem (2.1) and its SIP-DG solution $u_h \in V_h$ of (4.6), the following error estimate holds:

$$\begin{aligned} \Vert u - u_h\Vert _{\mathcal {DG}}^{new} \le C \inf _{y_h \in V_h} \Vert u - y_h\Vert _{\mathcal {DG}*}^{new}, \end{aligned}$$

(5.7)

where the constant $C=C(\eta ,C_4^{tr})$ is independent of h and the geometry of elements in $\mathcal {T}_h$.

Proof

By the consistency of $a_{h}^{new}$, we have

$$\begin{aligned} a_{h}^{new}(u - u_h, {w_h}) = 0, \quad \forall {w_h} \in V_h. \end{aligned}$$

Thus, the discrete coercivity and boundedness yield

$$\begin{aligned} \Vert u_h - y_h\Vert _{\mathcal {DG}}^{new}&\le 2 \sup _{w_h \in V_h} \frac{a_{h}^{new}(u_h - y_h,w_h)}{\Vert w_h\Vert _{\mathcal {DG}}^{new}} = 2 \sup _{w_h \in V_h} \frac{a_{h}^{new}(u - y_h,w_h)}{\Vert w_h\Vert _{\mathcal {DG}}^{new}} \\&\le 2 C\Vert u - y_h\Vert _{\mathcal {DG}*}^{new} \end{aligned}$$

for an arbitrary $y_h \in V_h$. Therefore, we obtain

$$\begin{aligned} \Vert u - u_h\Vert _{\mathcal {DG}}^{new} \le (1 + 2C) \Vert u - y_h\Vert _{\mathcal {DG}*}^{new}, \quad \forall y_h \in V_h. \end{aligned}$$

Taking the infimum for $y_h \in V_h$ and rewriting C, we conclude that (5.7) holds. $\square$

To derive a more practical error estimation, we prepare another general trace inequality. Let T be a d-simplex and f be a facet of T. The following inequality holds [17, p.24]:

$$\begin{aligned} \Vert \nabla v\cdot {\mathbf {n}}\Vert _{0,f}&\le C_5^{tr} \frac{|f|^{1/2}}{|T|^{1/2}} \left( |v|_{1,T} + h_T|v|_{2,T}\right) , \quad \forall v \in H^2(T). \end{aligned}$$

(5.8)

Now, let $\mathcal {I}_h^ku \in \mathcal {P}_k(\mathcal {T}_h)$ be an interpolation of u that satisfies

$$\begin{aligned} \left[ u - \mathcal {I}_h^k u\right] _f = 0 \quad \forall f \in \mathcal {F}_h. \end{aligned}$$

(5.9)

Note that the usual Lagrange interpolation satisfies (5.9). Insert $\mathcal {I}_h^k u$ into $y_h$ in (5.7), and set $U := u - \mathcal {I}_h^k u$. Then, $[U]_f = 0$ on any $f \in \mathcal {F}_h$, and $P_h^{new}(U,U) = 0$. Therefore, we see that

$$\begin{aligned} \Vert U\Vert _{\mathcal {DG}} = \left( \sum _{T \in \mathcal {T}_h} |U|_{1,T}^2\right) ^{1/2}. \end{aligned}$$

For a facet $f \in \mathcal {F}_h^o$, let $f = T_f^{1} \cap T_f^{2}$, $T_f^{i} \in \mathcal {T}_h$, and $U_i := U|_{T_f^{i}}$. The trace inequality (5.8) yields

$$\begin{aligned} \left\{ \frac{|f|}{|\widetilde{T}_f|}\right\} ^{-1} \Vert \{\nabla U\}\cdot {\mathbf {n}}_f\Vert _{0,f}^2&\le \frac{1}{2}\left\{ \frac{|f|}{|\widetilde{T}_f|}\right\} ^{-1} \left( \Vert \nabla U_1\cdot {\mathbf {n}}_f\Vert _{0,f}^2 + \Vert \nabla U_2\cdot {\mathbf {n}}_f\Vert _{0,f}^2 \right) \\&\le \frac{(C_5^{tr})^2}{2}\left\{ \frac{|f|}{|\widetilde{T}_f|}\right\} ^{-1} \Bigl ( \frac{|f|}{|\widetilde{T}_f^{1}|}(|U|_{1,\widetilde{T}_f^{1}} + h_{\widetilde{T}_f^1} |U|_{2,\widetilde{T}_f^{2}})^2 \\&\quad + \frac{|f|}{|\widetilde{T}_f^2|}(|U|_{1,\widetilde{T}_f^2} + h_{\widetilde{T}_f^2}|U|_{2,\widetilde{T}_f^2})^2 \Bigr ) \\&\le (C_5^{tr})^2 \left( |U|_{1,\widetilde{T}_f^1}^2 + |U|_{1,\widetilde{T}_f^2}^2 + h_{\widetilde{T}_f^1}^2 |U|_{2,\widetilde{T}_f^1}^2 + h_{\widetilde{T}_f^2}^2 |U|_{2,\widetilde{T}_f^2}^2 \right) , \end{aligned}$$

and thus

$$\begin{aligned} \sum _{f \in \mathcal {F}_h} \left\{ \frac{|f|}{|\widetilde{T}_f|}\right\} ^{-1} \Vert \{\nabla U\cdot {\mathbf {n}}\}\Vert _{0,f}^2 \le (C_5^{tr})^2 \sum _{T \in \mathcal {T}_h} \left( |U|_{1,T}^2 + h_T^2 |U|_{2,T}^2\right) . \end{aligned}$$

That is, the following theorem has been proved.

Theorem 10

Let $u \in V_{*h}$ be the exact solution of the model problem (2.1), and $u_h \in V_h$ be its SIP-DG solution (4.6). Then, we have the following error estimation:

$$\begin{aligned} \Vert u - u_h\Vert _{\mathcal {DG}}^{new} \le C \Vert u - \mathcal {I}_h^k u\Vert _{\mathcal {DG}*}^{new} \le C \sum _{T \in \mathcal {T}_h} \left( |u - \mathcal {I}_h^k u|_{1,T}^2 + h_T^2 |u - \mathcal {I}_h^k u|_{2,T}^2 \right) ^{1/2}, \end{aligned}$$

where $\mathcal {I}_h^k u$ is an interpolation that satisfies (5.9), and the constant $C = C(C_4^{tr}, C_5^{tr}, \eta )$ is independent of h and the geometry of elements in $\mathcal {T}_h$.

Let $\mathcal {I}_h^1 u$ be the usual Lagrange interpolation of u and let $R_T$ be the quantity defined in Sect. 2.2. Suppose that $k = 1$, $d = 2$ and $u \in H^2(\varOmega )$. Then, $|u - \mathcal {I}_h^1 u|_{2,T} = |u|_{2,T}$, and, from the results in [11, 13],

$$\begin{aligned} |u - \mathcal {I}_h^1 u|_{1,T} \le C_{L1} R_T |u|_{2,T}, \quad \forall u \in H^2(T), \end{aligned}$$

(5.10)

where the constant $C_{L1}$ is independent of the geometry of T. Thus, we find that

$$\begin{aligned} \Vert u - u_h\Vert _{\mathcal {DG}}^{new} \le \Vert u - \mathcal {I}_h^k u\Vert _{\mathcal {DG}*}^{new}&\le C \sum _{T \in \mathcal {T}_h} (R_T^2 + h_T^2)^{1/2} |u|_{2,T} \\&\le C \max _{T \in \mathcal {T}_h} (R_T^2 + h_T^2)^{1/2} |u|_{2,\varOmega } \le C (R^2 + h^2)^{1/2} |u|_{2,\varOmega }, \end{aligned}$$

where $R := \max _{T \in \mathcal {T}_h} R_T$ and $h := \max _{T \in \mathcal {T}_h} h_T$.

Suppose that $k \ge 2$, $d=2,3$, and $u \in H^{k+1}(\varOmega )$. Then, from [10, 13, 14],

$$\begin{aligned} |u - \mathcal {I}_h^1 u|_{1,T} \le C_{Lk} R_T h_T^{k-1} |u|_{k+1,T}, \quad |u - \mathcal {I}_h^1 u|_{2,T} \le C_{Lk} R_T^2 h_T^{k-3} |u|_{k+1,T}, \end{aligned}$$

(5.11)

and

$$\begin{aligned} \left( |u - \mathcal {I}_h^k u|_{1,\varOmega }^2 + \sum _{T \in \mathcal {T}_h} h_T^2 |u - \mathcal {I}_h^k u|_{2,T}^2 \right) ^{1/2} \le C \max _{T \in \mathcal {T}_h} \left[ R_T h_T^{k-2}\left( h_T^2 + R_T^2\right) ^{1/2} \right] |u|_{k+1,\varOmega }, \end{aligned}$$

where the constant $C_{Lk}$ is independent of the geometry of T. Therefore, we have obtained the following corollary.

Corollary 11

Let $u \in V_{*h}$ be the exact solution of the model problem (2.1), and $u_h \in V_h$ be its SIP-DG solution (4.6). Suppose that $u \in H^{k+1}(\varOmega )$. Then, we have the following error estimations:

$$\begin{aligned} \Vert u - u_h\Vert _{\mathcal {DG}}^{new}&\le C \max _{T \in \mathcal {T}_h} (R_T^2 + h_T^2)^{1/2} |u|_{2,\varOmega } \le C(R^2 + h^2)^{1/2}|u|_{2,\varOmega } \quad (k=1,d=2), \\ \Vert u - u_h\Vert _{\mathcal {DG}}^{new}&\le C \max _{T \in \mathcal {T}_h} \left[ R_T h_T^{k-2}(R_T^2 + h_T^2)^{1/2} \right] |u|_{k+1,\varOmega } \\&\le CRh^{k-2}(R^2 + h^2)^{1/2}|u|_{k+1,\varOmega } \quad (k\ge 2, d=2,3), \end{aligned}$$

where the constant $C = C(C_4^{tr}, C_5^{tr}, C_{Lk}, \eta )$ is independent of h, R, and the geometry of elements in $\mathcal {T}_h$.

Let $d=2$. In this case, elementary geometry (the law of sines) tells us that a mesh $\mathcal {T}_h$ satisfies the maximum angle condition if and only if there exists a constant $\sigma _2$ such that

$$\begin{aligned} \frac{R_T}{h_T} \le \sigma _2, \quad \forall T \in \mathcal {T}_h. \end{aligned}$$

(5.12)

Recently, it is reported that the same situation holds for tetrahedrons. That is, a tetrahedron satisfies the maximum angle condition if and only if (5.12) holds [9]. See also [15]. Hence, we have the following corollary.

Corollary 12

Suppose that $k \ge 1$ if $d = 2$, and $k \ge 2$ if $d = 3$. Let $u \in V_{*h}$ be the exact solution of the model problem (2.1), and $u_h \in V_h$ be its SIP-DG solution (4.6). Suppose that $u \in H^{k+1}(\varOmega )$ and $\mathcal {T}_h$ satisfies the maximum angle condition. Then, we have the following error estimation:

$$\begin{aligned} \Vert u - u_h\Vert _{\mathcal {DG}}^{new} \le C h^k |u|_{k+1,\varOmega }, \end{aligned}$$

where the constant C depends only on $C_4^{tr}$, $C_5^{tr}$, $C_{Lk}$, $\eta$, and $\sigma _2$.

For an $L^2$ error estimate, we have the following theorem, which is quite similar to the Aubin–Nitsche lemma.

Theorem 13

Let $d=2$. Let $u \in V_{*h}$ be the exact solution of the model problem (2.1), and $u_h \in V_h$ be its SIP-DG solution (4.6). Suppose that the model problem satisfies the elliptic regularity (2.3). Then, we have the following error estimation:

$$\begin{aligned} \Vert u - u_h\Vert _{0,\varOmega } \le C R \Vert u - u_h\Vert _{\mathcal {DG}*}^{new}, \end{aligned}$$

where $C = C(C_4^{tr}, C_5^{tr}, \eta , C_{ell}, C_{L1})$.

Proof

Setting $\phi := u - u_h$ in (2.2), we consider an auxiliary problem: find $\zeta \in H_0^1(\varOmega )$ such that

$$\begin{aligned} a(\zeta , v) = \int _\varOmega (u - u_h)v \mathrm {d}x, \quad \forall v \in H_0^1(\varOmega ). \end{aligned}$$

Because of the elliptic regularity (2.3), we have $\Vert \zeta \Vert _{2,\varOmega } \le C_{ell} \Vert u-u_h\Vert _{0,\varOmega }$. Because $\zeta \in H^2(\varOmega )$, we have $[\nabla \zeta ]\cdot {\mathbf {n}}_f = {\mathbf {0}}$ on any $f \in \mathcal {F}_h^o$, and $[\zeta ] = 0$ on any $f \in \mathcal {F}_h$. Hence, the definition of $a_{h}^{new}$ implies that

$$\begin{aligned} a_{h}^{new}(\zeta ,u-u_h)&= \sum _{T \in T_h} \int _T \nabla \zeta \cdot \nabla (u - u_h) \mathrm {d}{\mathbf {x}}- \sum _{f \in \mathcal {F}_h} \int _f [u - u_h]\nabla \zeta \cdot {\mathbf {n}}_f \mathrm {d}\\&= \int _{\varOmega }(- \varDelta \zeta )(u - u_h) \mathrm {d}{\mathbf {x}}= \Vert u - u_h\Vert _{0,\varOmega }^2. \end{aligned}$$

Let $\mathcal {I}_h^{1}\zeta$ be the piecewise linear Lagrange interpolation of $\zeta$ on $\mathcal {T}_h$. Because of the Galerkin orthogonality in Lemma $3^{new}$, we infer that

$$\begin{aligned} a_{h}^{new}(u-u_h,\mathcal {I}_h^{1}\zeta ) = 0. \end{aligned}$$

Therefore, it follows from (5.4) and (5.10) that

$$\begin{aligned} \Vert u - u_h\Vert _{0,\varOmega }^2&= a_{h}^{new}(\zeta ,u-u_h) = a_{h}^{new}(u-u_h, \zeta - \mathcal {I}_h^{1}\zeta ) \\&\le \Vert u-u_h\Vert _{\mathcal {DG}*}^{new} \Vert \zeta - \mathcal {I}_h^{1}\zeta \Vert _{\mathcal {DG}*}^{new} \\&\le C_{L1} R \Vert u-u_h\Vert _{\mathcal {DG}*}^{new} |\zeta |_{2,\varOmega } \\&\le C_{L1} C_{ell} R \Vert u-u_h\Vert _{\mathcal {DG}*}^{new}\Vert u - u_h\Vert _{0,\varOmega }. \end{aligned}$$

This completes the proof. $\square$

Corollary 14

Let $d = 2$. Let $u \in V_{*h}$ be the exact solution of the model problem (2.1), and $u_h \in V_h$ be its SIP-DG solution (4.6). Suppose that elliptic regularity holds, and $u \in H^{k+1}(\varOmega )$. Then, we have the following error estimation:

$$\begin{aligned} \Vert u - u_h\Vert _{0,\varOmega }&\le C R (R^2 + h^2)^{1/2}|u|_{2,\varOmega } \quad (k=1), \\ \Vert u - u_h\Vert _{0,\varOmega }&\le C R^2h^{k-2} (R^2 + h^2)^{1/2}|u|_{k+1,\varOmega } \quad (k\ge 2), \end{aligned}$$

where the constant $C = C(C_4^{tr}, C_5^{tr}, \eta , C_{ell}, C_{L1})$ is independent of h, R, and the geometry of elements in $\mathcal {T}_h$.

Remark

It is conjectured that Theorem 13 and Corollary 14 hold for $d = 3$. To show this conjecture, we need to use a different interpolation, such as the Crouzeix–Raviart interpolation, and analyze its error in terms of the $\Vert \cdot \Vert _{DG*}^{new}$ norm.

6 Numerical experiments for the new SIP-DG scheme

In this section, we report the results of numerical experiments to confirm the theoretical results obtained in the previous section. First, we consider the same numerical experiment as in Sect. 3.3 (the same domain $\varOmega$, same function $\phi$, and same meshes $\mathcal {T}_h$) with the new SIP-DG scheme. We fix $n=40$ and the penalty parameter $\eta = 0.8$.¹ Then, the new SIP-DG method is applied to the model problem (2.1) with various m. The results are summarized in Table 2.

Table 2 Errors produced using the new SIP-DG method

Note that the discretized solution $u_h$ is stable for all cases, and the errors decrease as m increases, which is consistent with the error estimations.

To see how $\eta$ affects the performance of the proposed SIP-DG scheme, we vary $\eta$ as 0.6, 0.5, 0.4, 0.3, 0.2, 0.1 in the cases $m=40$ and $m=120$. The proposed SIP-DG scheme is stable if $\eta \ge 0.4$. The scheme becomes unstable (more CPU time and less accuracy) if $\eta \le 0.3$. The ICCG method does not converge if $\eta = 0.1$.

For the next experiment, we set $\varOmega := (-1,1)\times (-1,1)$ and $f(x,y) := \pi ^2 \sin (\pi x) \sin (\pi y)$ in (2.1). In this case, the exact solution is again $u(x,y) = \sin (\pi x) \sin (\pi y)/2$. We introduce the following Schwarz–Peano-type meshes for $\varOmega$.

For a given positive integer N and $\alpha > 1$, we consider the isosceles triangle with base length $h:=2/N$ and height $2/\lfloor 2/h^\alpha \rfloor \approx h^\alpha$ (then, $R_T \approx h^\alpha /2 + h^{2-\alpha }/8$), as depicted in Fig. 4. We triangulate $\varOmega$ with this triangle as shown in Fig. 5. Note that if $h \rightarrow 0$, these meshes satisfy neither the shape-regularity condition nor the maximum angle condition. Furthermore, if $\alpha \ge 2.0$ and $h \rightarrow 0$, the meshes do not satisfy the circumradius condition. See Kobayashi–Tsuchiya [12].

Fig. 4

An isosceles triangle

Fig. 5

Schwarz–Peano-type mesh of $\varOmega$. $N=12$, $\alpha =1.6$

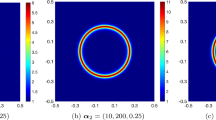
We compute the SIP-DG solutions on this mesh with $\alpha = 1.2$, 1.5, 1.8, 2.0, 2.1 and various N, and measure the errors. Figures 6 and 7 list the numerical results. Tables 3 and 4 contain concrete values of the numerical results for $\alpha =1.5$ and $\alpha =2.0$, respectively.

It seems that both errors behave similarly as $\alpha$ varies. Observing Figs. 6 and 7, we can infer that $a_h^{(0)}(u-u_h,u-u_h)^{1/2}$ and $P_h^{(0)}(u-u_h,u-u_h)^{1/2}$ are ${\mathcal {O}}(R)$, that is, the errors are governed by the parameter R, not h. For example, when $\alpha = 2.1$, the errors $a_h^{(0)}(u-u_h,u-u_h)^{1/2}$ and $P_h^{(0)}(u-u_h,u-u_h)^{1/2}$ increase as h decreases. However, the ratio $a_h^{(0)}(u-u_h,u-u_h)^{1/2}/R$ and $P_h^{(0)}(u-u_h,u-u_h)^{1/2}/R$ seem to be bounded by a constant.

Fig. 6

Behavior of the error $a_h^{(0)}(u-u_h,u-u_h)^{1/2}$ with respect to $\alpha$. The horizontal axis represents the maximum diameter (left) and the circumradius of the triangles (right), and the vertical axis represents the error. The legend indicates the value of $\alpha$ in each case

Fig. 7

Behavior of the error $P_h^{new}(u-u_h,u-u_h)^{1/2}$ with respect to $\alpha$. The horizontal axis represents the maximum diameter (left) and the circumradius of the triangles (right), and the vertical axis represents the error. The legend indicates the value of $\alpha$ in each case

Table 3 Errors given by the new SIP-DG method on the mesh in Fig. 5 with $\alpha = 1.5$

Table 4 Errors given by the new SIP-DG method on the mesh in Fig. 5 with $\alpha = 2.0$

7 Conclusion

Using the general trace inequality (4.2), we have presented a new penalty term (4.4) and a new SIP-DG scheme (4.5). We have established its error estimates without imposing the shape-regularity condition. From numerical experiments, we have confirmed that the new SIP-DG scheme is robust on anisotropic meshes.

The main idea in this paper is to use $\left\{ \frac{|f|}{|\widetilde{T}_f|}\right\}$ instead of the standard term $\frac{1}{h_f}$ in the penalty term. Because this idea is very simple, we expect that it can be extended in many directions and will be used in many DG schemes. In the following, we mention some directions that are immediately apparent.

• Application to many variants of DG methods.

• Application of the new SIP-DG scheme to non-proper meshes, and the establishment of error estimations for these cases.

• Investigation of the possibility of applying the proposed approach to hybridized DG methods.