1 Introduction

The goal of regional ensemble systems is the generation of reliable probabilistic forecasts, often in real-time, with special emphasis on mesoscale and synoptic phenomena relevant to a specific region. The Taiwan mesoscale ensemble prediction system (EPS) based on the Weather Research and Forecast model (WRF), also referred to as WEPS, is an example for such a mesoscale ensemble system. Taiwan is an island in East Asia; located some 180 km off the southeastern coast of China. Surrounded by the Pacific Ocean, its central mountains reach an altitude of almost 4000 m making the mesoscale forecast of heavy precipitation events an important regional focus. On the other hand, Taiwan is in the path of tropical cyclones approaching from the deep waters to the East which requires the synoptic-scale forecast of typhoon tracks.

While of central importance, accounting for initial-condition error is often insufficient for a full representation of forecast uncertainty (Palmer 2001; Berner et al. 2009; Leutbecher et al. 2017) and the WEPS is no exception to this (Li and Hong 2014). Hence different approaches for the representation of model-error were tested to obtain the optimal configuration of the Taiwan mesoscale ensemble prediction system (Li and Hong 2014). In particular, the benefits of using a different set of physics packages for each ensemble member were compared to that of using one or more stochastic parameterizations.

While multi-physics schemes have been very successful to generate the reliable probabilistic forecasts, especially for mesoscale prediction systems, they have several theoretical and practical disadvantages. The maintenance of different parameterizations is resource-intensive and will result in members with systematically different climatology and mean error, which poses difficulties for probabilistic interpretation and statistical post-processing. On the other hand, tropical storms are sensitive to details of the cumulus convection scheme (Vitart et al. 2001; Biswas et al. 2014), and parametrization sensitivity might play a bigger role than initial condition uncertainty in comparison to the mid-latitudes.

An alternative to the multi-physics approach is the representation of model-uncertainty by stochastic perturbation methods. When used together with a single set of parameterizations, this approach leads to statistically consistent ensemble distributions. Stochastic parameterizations can also be used in addition to multiple physics packages to further increase member diversity. In particular, two schemes are widely used: the Stochastic-Kinetic Energy Backscatter (SKEB; Shutts 2005) Scheme and the Stochastic Perturbation of Physics Tendencies (SPPT; Buizza et al. 1999, Palmer et al. 2009) scheme.

Leutbecher et al. (2017) investigated the impact of two stochastic schemes in the global model framework and they found that SPPT scheme was more beneficial to additional spread in the ensemble than SKEB scheme, irrespective of region, thereby reducing ensemble mean error. Berner et al. (2017) also showed that SPPT scheme could be effective in increasing spread and decreasing error. In terms of the operational viewpoint, we aware that the model performance highly depends on the model configuration, including the model resolution, domain coverage, and the model physics, etc. The performance is also weather regime dependent, for example the performance for typhoon and winter system could be very different. It is worth to systematically evaluate the model-error scheme over different region, for example the sub-tropical ocean and for the typhoon cases. We believe such a research could provide an independent results for reference, especially compared with the previous study.

Here, we report on the experiments conducted to obtain the optimal configuration of the Taiwanese mesoscale ensemble system, which has been applied to a number of typhoon and Meiyu rainfall events over the Taiwan area (Zhang et al. 2010; Fang et al. 2011; Xie and Zhang 2012; Hsiao et al. 2013; Hong et al. 2015; Su et al. 2016).

In particular, we address the following two questions: 1) Can a single-physics ensemble augmented with a suite of optimally tuned stochastic parameterization schemes provide forecasts of comparable skill to that of a multi-physics ensemble? 2) Can SKEB and/or SPPT further improve the probabilistic skill of the multi-physics ensemble?

The paper organized as follows: The experiment design and model-error representation are introduced in section 2. Section 3 summarizes the verification metrics used. The results are reported in section 4, for both standard verification metrics as well as some case-specific metrics. The final results are compared to that of other mesoscale ensemble systems in section 5.

2 Experiment Design and Model-Error Representations

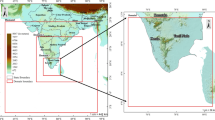
The Taiwan mesoscale ensemble prediction system is based on Weather Research and Forecasting (WRF) Model with the Advanced Research WRF dynamic solver (Skamarock et al. 2008). It is also referred to as WEPS for WRF ensemble prediction system. The model domain is centered on Taiwan, and covers the East-Asian region (Fig. 1), this domain cover from 5 S~43 N and 78 E~180 E. The model is integrated over a domain of 662 × 386 horizontal grid points with 15-km grid spacing. The ensemble uses 52 vertical levels, with the highest level at a pressure height of 20 hPa. The model is integrated with a time step of 60 s for a total of 72 h.

Fig. 1
figure 1

The model domain of Taiwan mesoscale ensemble prediction system

Full size image

2.1 Initial Condition and Lateral Boundary Condition Perturbations

Initial conditions were obtained by downscaling the NCEP Global Forecast system (GFS) and adding perturbations from an Ensemble Adjustment Kalman Filter (EAKF; Anderson 2001) to obtain a 20-member ensemble. The perturbations are computed as the difference between each member of the EAKF and the ensemble mean after a forecast time of 6 h. The lateral boundary conditions are taken from the 10 members of the NCEP Global Ensemble Forecast System (GEFS; Wei et al. 2008) and each LBC is used for two members.

The EAKF system is an ensemble data assimilation system from the National Center for Atmospheric Research (NCAR) Data Assimilation Research Testbed (DART; Anderson et al. 2009). The system uses 32 members to provide 6-h forecasts which provide the first-guess background for the next analysis as a continuously cycled analysis system. To counteract ensemble deflation in the assimilation system, the EAKF uses covariance inflation as well as stochastic perturbations from SKEB (see below) before the assimilation step. The assimilated observations are comprised of radiosondes, surface observations from ship and land stations, GPS radio occultation, aviation routine weather report, and aircraft reports.

2.2 Multi-Physics Configuration and Stochastic Parameterization Schemes

In its standard configuration, WEPS uses 20 different combinations of physics packages for parameterizing the microphysics, cumulus parameterization, planetary boundary layer, and surface layer (Table 1). This configuration was chosen by analyzing the results from 48 experiments combining a total of six different cumulus parameterization schemes, four planetary boundary layer schemes, and two microphysics schemes. It was found that the forecasts were most sensitive to the choice of the cumulus schemes, followed by the PBL scheme. To maximize ensemble diversity, all six cumulus schemes are approximately equally represented and combined with different PBL and micro-physics schemes.

Table 1 Physics packages for multi-physics ensemble
Full size table

To represent random model-error, we test two widely used stochastic parameterization schemes. SKEB is designed to represent the interactions between the resolved flow and unresolved subgrid-scale processes (Shutts 2005) and introduces random perturbations to streamfunction and potential temperature tendencies (Berner et al. 2011).

The SPPT scheme aims at representing uncertainty in the physical parameterization schemes by perturbing the total physical tendencies of temperature, zonal and meridional winds, and humidity (Buizza et al. 1999; Palmer et al. 2009). The perturbations are proportional to the deterministic tendency, so that they are large where the physical tendencies are large, and small where the tendencies are small .

Table 2 Experiments
Full size table

2.3 Ensemble Prediction Experiments

To quantify the performance of the Taiwanese ensemble system, probabilistic hindcasts with WRF V3.7.1. were performed for two weeks in summer and winter: August 1, 2015 - September 15, 2015 and December, 12,015 – January, 152,016, respectively.

We will demonstrate in this study, that the use of multiple physics packages is beneficial for the performance of the Taiwan ensemble prediction system. Hence, we comprehensively report on the results of four experiments: the control experiment MP uses multiple physics-packages for each ensemble member. Additional experiments combine MP with SPPT or SKEB. Finally, the experiment SKEB+SPPT+MP uses all three model-error representations (see Table2). Additional experiments – albeit for a shorter verification period - were conducted to determine the sensitivity on the settings and to see if the stochastic schemes could replace the multi-physics scheme. The results of these experiments together with the overall tuning strategy are discussed in section 4d. The final settings for the SPPT and SKEB schemes given in Table 3. In SKEB, the tot_backscat_psi represents the total backscattered dissipation rate for streamfunction, and it impacts the amplitude of rotational wind perturbations; and the tot_backscat_T is for potential temperature. In SPPT, gridpt_stddev_sppt defines standard deviation of random perturbation field, and stddev_cutoff_sppt cut off the perturbation pattern above the standard deviation. The lengthscale_sppt defines random perturbation length scale, and timescale_sppt defines temporal decorrelation of random field.

Table 3 Summary of namelist parameter settings for stochastic schemes
Full size table

3 Verification Methodology

3.1 Continuous Ranked Probability Score and Continuous Ranked Probability Skill Score

A probabilistic verification based on the Continuous Ranked Probability Score (CRPS, Hersbach 2000; Toth et al. 2003) is performed. The CRPS is based on the Brier score, but verifies the forecast over a range of thresholds rather than a single threshold. The Continuous Ranked Probability Skill Score (CRPSS) is constructed to measure forecast skill, where 0 means no skill over the reference forecast and 1 denotes perfect skill.

To determine if the improvements are significant, we obtain the empirical distribution of CRPSS differences by bootstrap sampling 30 times with replacement over all dates. A student t-test is used to get the p values which determines the significance. When the p value is smaller than 0.05, we reject the null-hypothesis that the two forecasts come from the same underlying distribution and say that the ensemble forecast is significantly different from the reference forecast with 95% confidence. Significant improvements over MP are denoted by solid circles.

3.2 Rank Histograms

Rank histograms(Hamill 2001;Toth et al. 2003) also known as Talagrand diagrams, are used to analyze ensemble spread. They are generated by ordering the forecast values of each ensemble members and at each gridpoint from smallest to largest. For an ensemble with J members, this results in J + 1 intervals. The first interval spans values smaller than any of the J member forecasts and the last interval spans values larger than any individual forecast. Then the rank of the interval of the verifying analysis is determined. This is repeated for all gridpoints and forecasts for a particular forecast lead time. An “U”-shaped rank histogram means that the verifying analysis tends to fall outside the range of member forecasts: The ensemble is under-dispersive. The rank histogram is “A”-shaped, if the verifying analysis rarely falls into the edge intervals, which signifies an over-dispersed ensemble system. Ideally, the rank histogram is “flat”, which means the verifying analysis falls equally in each forecast interval.

3.3 The Fractions Skill Score

The fractions skill score (FSS, Roberts and Lean 2008) evaluates the skill of a single forecasts as function of spatial scale. For each gridpoint, a neighborhood is defined by a radius of influence and a precipitation threshold is prescribed. Then the probability of the forecasts exceeding the threshold value is computed within each neighborhood. The Fractions Brier Score (FBS) is given by

$$ \mathrm{FBS}=\frac{1}{\mathrm{N}}{\sum}_{\mathrm{i}=1}^{\mathrm{N}}{\left[{\mathrm{N}\mathrm{P}}_{\mathrm{F}\left(\mathrm{i}\right)}-{\mathrm{N}\mathrm{P}}_{\mathrm{o}\left(\mathrm{i}\right)}\right]}^2, $$
(1)

Where NPF(i) and NPo(i) are the neighborhood probability at the i-th grid box in the model forecast and observation.

For ensemble systems, the FBS can be defined in a similar way (Schwartz et al. 2010). The “neighborhood ensemble probability” is computed as average over the all ensemble forecasts. A skill score can be defined with regard to a reference forecast. The worst possible FBS is achieved when there is no overlap of nonzero probabilities

$$ {\mathrm{F}\mathrm{BS}}_{\mathrm{worst}}=\frac{1}{\mathrm{N}}\left[{\sum}_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{N}\mathrm{P}}_{\mathrm{F}\left(\mathrm{i}\right)}^2+{\sum}_{\mathrm{i}=1}^{\mathrm{N}}{\mathrm{N}\mathrm{P}}_{\mathrm{o}\left(\mathrm{i}\right)}^2\right]. $$
(2)

The Fractions Skill Score is then defined as:

$$ \mathrm{FSS}=1-\frac{\mathrm{FBS}}{{\mathrm{FBS}}_{\mathrm{worst}}}. $$
(3)

4 Results

4.1 Probabilistic Verification of Dynamical Variables over East Asia

All forecasts are verified against ECMWF analyses. For our verification period, this analysis was produced with the IFS version CY41R1 which uses the 16 km horizontal resolution of T1279. To maximize significance, the verification is conducted over all winter and summer dates. Seasonal differences are discussed in section 4c.

Vertical profiles of the root-mean square error (RMSE) of the ensemble mean and the spread of the ensemble members around the ensemble mean were computed for geopotential height, temperature and zonal wind at a lead time of 72 h (Fig. 2). For geopotential height, the RMSE and spread have a minimum for heights around the 700 hPa pressure level, and are larger at the surface and in the free atmosphere. For temperature, the RMSE is largest near the surface, then decreases up to 700 hPa and remains roughly constant for heights above this pressure level. For zonal winds, the RMSE and spread increase as function of height.

Fig. 2
figure 2

Top figures are the spread (dashed) and RMSE (solid), and bottom figures are the spread-error ratio. a, d for geopotential height, b, e for temperature and c, f for zonal wind for four ensemble experiments over the East Asia domain. The different experiments are denoted by line colors: MP (black), SPPT+MP (red), SKEB+MP (green), and SKEB+SPPT+MP (blue). The different experiments are denoted by line colors: MP (black), SPPT+MP (red), SKEB+MP (green), and SKEB+SPPT+MP (blue)

Full size image

For a perfectly reliable ensemble system, spread and error should have the same amplitude and growth rate, so the spread-error ratio would be 1. Like many ensemble systems, the spread for this forecast lead time is too small in all verified variables. Overall, SKEB introduces most spread and combining SKEB and SPPT introduces more spread than a single model-error scheme alone. Consistent with previous work (Berner et al. 2011, 2015, 2017), SKEB increases the spread throughout the free atmosphere and for all variables, while SPPT is most effective in increasing the spread of temperature near the surface. Moreover, the impact of SKEB is more significant in typhoon track region, and it consistent with Berner et al. 2017. The perturbations from SKEB or SPPT would be different because of the weather systems, and lots of typhoons existed in this domain. Hence, the SKEB is more sensitive than SPPT in this study. The stochastic schemes neither deteriorate nor improve the RMS error of the ensemble mean. The spread-error ratio (Fig. 2(d)-(f)) is the best for the experiment SKEB+SPPT+MP, which combines the multi-physics approach with SKEB and SPPT.

To see if our findings hold for other lead times, we repeat the verification and report the results as function of forecast lead time for geopotential height at 500 hPa (Z500), temperature at 850 hPa (T850), and zonal wind at 850 hPa (U850). Spread and RMSE increase with forecast lead time, signifying increased uncertainty at larger lead times. For Z500 (Fig. 3a) the spread is larger than the error for lead time up to 36 h. However, the error grows faster than the spread so that the ensemble system is under-dispersive for forecast lead times of more than 36 h. For T850, the ensemble is under-dispersive at all forecast lead times. Interestingly, the RMSE in U850 is smaller than the spread, indicating over-dispersion in this variable.

Fig. 3
figure 3

RMSE of the ensemble mean (solid) and spread (dashed) of (a) Z at 500 hPa, (b) T and (c) U at 850 hPa for four ensemble experiments as a function of lead time. The different experiments are denoted by line colors: MP (black), SPPT+MP (red), SKEB+MP (green), and SKEB+SPPT+MP (blue)

Full size image

Overall, the conclusions drawn from the vertical profiles of spread and error at a lead time of 72 h carry over to other lead times: The stochastic schemes do not increase the RMS error of the ensemble mean and the experiments with stochastic parameterization - and in particular SKEB - introduce notably more spread, leading to a better spread/error consistency.

Ideally, any verification should include an estimate of observation error. However, the estimation of observation error is generally difficult, especially since it consists of representativeness error as well as instrument error. Because of these difficulties, we follow other studies focusing on short-range forecasts and neglect observation error at this point. We acknowledge that the inclusion of observation error would lead to an increase in the total spread, so that the ensemble system would be less under-dispersive and the impact of the model-error schemes less beneficial.

As measure of probabilistic skill, we compute the CRPSS with regard to two references as described in the next two paragraphs.

To assess the forecast skill of the ensemble system versus the deterministic forecast, the high-resolution forecast produced by the Central Weather Bureau (CWB) is used. CWB is the government meteorological research and forecasting institution of Taiwan. The skill scores are positive for all variables and forecast lead times (Fig. 4a-c), demonstrating that the ensemble forecast is more skillful than the deterministic forecast. For geopotential height and T850 the skill decreases as function of forecast lead time, which reflects that skill decreases for increased lead times. For T850 we observe a jump in skill at a lead time of 12 h, which could be related to ensemble spin-up and should be further investigated. Interestingly, the skill for U850 increases as function of lead time. Further work will investigate the reasons for this unusual signature.

Fig. 4
figure 4

CRPSS, top figures use deterministic forecast as reference, and bottom figures use MP as reference. a, d Z at 500 hPa, b, e T and c, f U at 850 hPa for four ensemble experiments as a function of lead time. The different experiments are denoted by line colors: MP (black), SPPT+MP (red), SKEB+MP (green), and SKEB+SPPT+MP (blue). The solid rounds are denoted it is significant improvements over MP

Full size image

To focus on the skill added by the stochastic parameterization schemes, this time the reference is the CRPSr of the MP ensemble. For Z500 and T850 the CRPSS is positive, indicating that adding stochastic perturbations improved the forecast skill. Moreover, some of these improvements are significant but not at all lead times and for all variables (see Fig.4d-f for significance of specific lead times). For U850, adding SPPT improves the system marginally for short forecast lead times, but SKEB deteriorates the skill. Given that SKEB is very efficient at introducing spread, this result is consistent with the over-dispersion of U850: by adding additional spread to an already over-dispersive variable, the skill is deteriorated. However, the CRPSS changes for U850 are not statistically significant, so that we conclude that this skill deterioration is small.

In summary, the ensemble is more skillful than the high-resolution forecast and combining different model-error scheme tends to produce the largest spread, which results in better probabilistic skill for variables that are under-dispersive. Tuning model-error schemes to an ensemble system that is under-dispersive for some variables but over-dispersive for others, is difficult.

4.2 Precipitation Verification over Taiwan

Rank histograms and the fractions skill score are used to verify the quantitative precipitation forecast over the Taiwanese region only. Precipitation verification is against estimates from the “Quantitative Precipitation Estimation and Segregation Using Multiple Sensor” (QPESUMS) system, which is developed by the Central Weather Bureau in Taiwan and the National Severe Storm Laboratory. It combines radar and rain gauge data to estimate quantitative precipitation rates.

Rank histograms of quantitative precipitation for a forecast lead time of 60–72 h are displayed in Fig. 5. The distributions are characterized by an inverted L-shape, signifying that the verifying QPESUMS data usually fall into the highest ranked forecast intervals. Such a rank distribution indicates that the predicted precipitation amounts are systematically less than observations. Since precipitation cannot be negative, this translates into insufficient ensemble spread in this variable. Adding stochastic perturbations hardly changes the rank histograms.

Fig. 5
figure 5

Rank histogram at 60–72 h. a to d are the spread of MP, SPPT+MP, SKEB+MP, SKEB+SPPT+MP respectively. The red dash line is the perfect frequency value at each intervals

Full size image

Figure 6 shows the FSS for thresholds of 0.5 mm, 20 mm and 100 mm. Because the FSS for ensemble is the average of FBS of all ensemble members, the skill of an ensemble system as function of spatial scale would be known by FSS. It is worth noting that the FSS is not a really probabilistic score. Interestingly, the FSS is highest for a large threshold of over 100 mm per 12 h and linearly decreases from 0.7 at a lead time of 12 h to 0.5 at 72 h. The skill for the smallest threshold of 0.5 mm per 12 h is almost as good and decreases from 0.5 at 12 h to 0.45 at 72 h. This indicates that both heavy and light precipitation events are well forecasted. The skill for middle thresholds of 20 mm per 12 h has with 0.1–0.2 lowest skill.

Fig. 6
figure 6

FSS with radii of influence of 15 km. Different thresholds were used: 0.5 mm per 12 h (a), 20 mm per 12 h (b), and 100 mm per 12 h (c). The different experiments are denoted by line colors: MP (black), SPPT+MP (red), SKEB+MP (green), and SKEB+SPPT+MP (blue)

Full size image

Adding stochastic perturbation to the multi-physics ensemble does not significantly change the skill in the quantitative precipitation forecasts over the verifying domain. This indicates that the stochastic schemes either do not change the precipitation forecast, or that such changes occur outside the verifying region which is relatively small compared to the domain. We stress, that the current study does not have a high-resolution nest over the Taiwanese island and that a horizontal resolution of 15 km might be too coarse to detect any impact.

4.3 Seasonal Differences

In the section 4a) we combined winter and summer cases to get an overview of the performance of the Taiwanese ensemble system and maximize sample size. In this section we report on seasonal differences. During the winter seasons, cold fronts are a typical synoptic feature in Taiwan, while typhoons are prevalent in summer.

Spread and error curves for Z500 and U850 are shown in Fig. 7 for the winter and summer cases separately. Overall, the RMSE of Z500 is with 15 m in summer and at forecast lead time of 72 h about 4 m larger than in winter. The RMSE of U850 is very similar across seasons, but the spread is over dispersive at all lead times in summer, but under-dispersive for longer lead times in winter. Similarly, the spread for Z500 is arguably over-dispersive in summer, but clearly under-dispersive in winter. Although the spread is not enough in winter, however, the stochastic parameterizations can increase the spread, especially SKEB. The SKEB is effective in both seasons in terms of spread.

Fig. 7
figure 7

RMSE of the ensemble mean (solid) and spread (dashed) of (a) Z at 500 hPa of summer cases and (b) Z at 500 hPa of winter cases (c) U at 850 hPa of summer cases and (d) U at 850 hPa of winter cases for four ensemble experiments as a function of lead time. The different experiments are denoted by line colors: MP (black), SPPT+MP (red), SKEB+MP (green), and SKEB+SPPT+MP (blue)

Full size image

To better understand the physical mechanisms responsible for these results, maps of spread and error at the lead time of a 72 h are shown in Fig. 8. The error is given as RMS difference between the ensemble mean forecast and the ECMWF analysis. For Z500, the spread and error maps agree well in winter (Fig.8a-h), but in summer, the error is smaller than the spread, especially over the ocean. In addition to, the spread of MP and SPPT+MP is almost the same in both seasons, and the spread of the experiments with SKEB increase significantly over the ocean, especially in the ocean. Meanwhile, the error of all experiments are similar. For T850 and U850 (not shown), the spread with SKEB increase most over the ocean, and the error are almost the same. This result is consistence with Z500.

Fig. 8
figure 8

The map of error and spread of winter cases of Height at 500 hPa at forecast lead time of 72 h. a to d are the spread of MP, SPPT+MP, SKEB+MP, SKEB+SPPT+MP respectively. e to h are the error of MP, SPPT+MP, SKEB+MP, SKEB+SPPT+MP respectively

Full size image

We note that one typhoons MELOR and four typhoons SOUDELOR, MOLAVE, GONI, and ATSANI passed through the West Pacific during the winter and summer verification periods, respectively. These storms likely contributed to the large ensemble spread and error of the ensemble mean.

4.4 Single-Physics Ensemble with Stochastic Perturbations and Sensitivity to Perturbation Amplitudes

To determine if a suite of stochastic parametrizations schemes can replace the multi-physics scheme over the Taiwanese domain, experiments with a single set of physical parameterization schemes were conducted. Since a single-physics ensemble is expected to have less spread, larger stochastic perturbations might be needed. In this section we first report on the sensitivity to the amplitude of the stochastic perturbations. Then we will show results for a single-physics ensemble with an optimally tuned stochastic amplitude. This was done for SPPT only. For practical reasons, the tuning and single-physics experiments described in this section were conducted for all ensemble members, but over a shorter verification period, namely for twice-daily initializations at 00 Z and 12 Z over the period August 3–7, 2016.

First, the standard deviation of the SPPT perturbation pattern at any gridpoint (gridpt_stddev_sppt) was increased from gridpt_stddev_sppt = 0.2 (SPPT) to 0.5 (LSPPT), so the standard deviation of random perturbation field would increase at each grid. This could have been done in a single-physics framework, but here we show results from making this change in the MP ensemble. Figure 9a,b shows spread and error curves of the MP ensemble together with those of MP + SPPT and MP + LSPPT. We see that for the range of amplitudes tested, SPPT impacts the spread, but not the RMSE for all verified variables. If the amplitude is increased further, the RMSE starts to increase (not shown), which is why larger SPPT amplitudes were not considered. While the spread/error ratio is best in the experiment LSPPT+MP, this combination can be computationally unstable, which is not acceptable for operational use. Hence a more conservative amplitude of gridpt_stddev_sppt = 0.2 has been chosen as optimal value for the more comprehensive verification in section 4a-c.

Fig. 9
figure 9

a to d are the verification results for tuning test. RMSE of the ensemble mean (solid) and spread (dashed) of (a) Height at 500 hPa and (b) Temperature at 850 hPa, and CRPSS of (c) Height at 500 hPa and (c) Temperature at 850 hPa. e to h are as in (a) to (d), but for single physics test. The different experiments are denoted by line colors: MP (black), SPPT+MP (red), LSPPT+MP (orange), and LSPPT (purple)

Full size image

For the single-physics experiments, we chose the larger amplitude of gridpt_stddev_sppt = 0.4 and assume that for this value, SPPT will not negatively impact the RMSE as just demonstrated for the MP system. The physical parameterizations were those used for the deterministic forecast and consist of the Kain-Fritsch cumulus scheme, the YSU PBL scheme, and Goddard microphysics scheme. Note that this particular combination is not contained in the MP configuration.

We find that the RMSE of the single-physics ensemble with LSPPT is considerably larger than the corresponding RMSE of the multi-physics scheme (Fig.9 e, f), especially for Z500. Its spread is similar to that of the MP-ensemble and markedly smaller than that of MP + SPPT. The increase in RMS error without a similar increase in spread leads to a deterioration in skill as measured by the CRPSS (Fig.9 g, h).

In summary, we conclude that for a range of amplitudes, SPPT will impact the spread but not the RMS error and can be thus used to introduce spread near the surface. Furthermore, the RMSE error of the single-physics scheme with stochastic parameterization is larger than that of the multi-physics scheme, while their spread is comparable. The magnitude of the RMS error for the range of stochastic amplitudes tested here appears to be dominated by of the choice of physics-schemes rather than the stochastic perturbations. Consequently, the multi-physics ensemble has better skill than a single-physics ensemble, even if latter uses large SPPT amplitudes.

4.5 Typhoon Case Study: GONI

Due its location in the Western North Pacific Ocean, Taiwan is frequently in the path of typhoons coming from the east and south east. Typhoons are a significant threat to human lives and result each year in substantial economic losses. Therefore, forecasting the path of typhoons, as well as their intensity, is of upmost importance to the Taiwanese Central Weather Bureau.

Only very limited work concerning the impact of stochastic parameterization on typhoon forecasts has been conducted. Judt and Chen (2016) introduced perturbations to convective, meso- and synoptic-scale features in hurricane Earl and found that perturbations on the synoptic scale lead to largest error growth.

Here, we report on the impact of the stochastic schemes investigated here on a single typhoon which occurred during our summer verification period. Typhoon GONI formed East of Philippines late on August 14, 2015, and moved west during its early stage (Fig. 10). Over the next days, its intensity increased and by August 20 it became a severe Typhoon with maximum sustained wind of 51 m/s. On August 21, Goni’s movement was nearly stationary and it lingered about 100 km North of the Northern coast of the Philippines. It then turned northward, and impacted eastern Taiwan on August 23. The CWB in Taiwan announced a typhoon warning from August 20–23 August.

Fig. 10
figure 10

Typhoon forecast track of 19 August 2015 case. a to d are the forecast track of MP, SPPT+MP, SKEB+MP, SKEB+SPPT+MP respectively. The black line is best track, red line is forecast track of ensemble mean, and gray lines are the forecast track of ensemble members

Full size image

The track forecasts of each member of the MP-ensemble are shown in Fig. 10 together with the ensemble mean forecast the and best track. According to the track forecast, it seems highly predictable, and in particularly, it’s northward turn. Indeed, the track error of the ensemble mean is with less than 200 km at a forecast lead time of 72 h small and much smaller than the ensemble spread (Fig. 11), indicating that for this typhoon forecast, and the ensemble is over-dispersive. On the other side we stress, that this is a single case and that a comprehensive analysis over a range of typhoons in different environments is needed to draw general conclusions.

Fig. 11
figure 11

Track error of the ensemble mean (solid) and spread (dashed) for four ensemble experiments as a function of lead time. The different experiments are denoted by line colors: MP (black), SPPT+MP (red), SKEB+MP (green), and SKEB+SPPT+MP (blue)

Full size image

Adding a stochastic parameterization scheme has little impact on the track error, but there is evidence that adding SKEB might reduce the RMS error for lead times between 12 h and 42 h. SKEB does increase the spread, which is detrimental since the ensemble is already over-dispersive. Looking into the individual members, we note that in the experiments with SKEB the track of five or six ensemble members reach a longitude west of 121E before turning north, while in experiments MP and MP + SPPT all but one member turn north at a longitude east of 121E. Future work will show to which degree these results are relevant for probabilistic typhoon forecasts.

5 Conclusion and Discussion

This study introduces the Taiwanese mesoscale ensemble which is centered on Taiwan and covers a large domain over East Asia. Intended for operational use, the goal is to find the optimal model configuration which will produce the best probabilistic forecasts over Taiwan. According to the previous study of WEPS, it was found that the spread with initial and boundary condition perturbations by themselves increase less with forecast lead time, making it necessary to utilize some form of model-error representation.

A central question was if a single-physics scheme augmented with a suite of stochastic parametrizations schemes can outperform the multi-physics schemes. This question was investigated by a number of studies using WRF over the domain of the contiguous United States. Jankov et al. (2017), find that a single-physics ensemble with SKEB, SPPT and stochastic parameter perturbations is able to outperform their multi-model ensemble, even for near surface variables. On the other side, Berner et al. (2011, 2015) conclude that especially for temperature at 2 m, their multi-physics ensemble consistently outperforms their single-physics ensemble which uses a number of different stochastic parameterizations as well as their combination. However, in the free atmosphere SKEB consistently outperforms the multi-physics ensemble. The studies differ in their design of the multi-physics suite as well as the WRF version and horizontal resolution and it is interesting to see which of these results carry over to the Taiwanese domain.

Over the Taiwanese domain and at a resolution of 15 km, our findings are consistent with those of Berner et al. (2011, 2015): the stochastically perturbed single-physics ensemble is unable to outperform the multi-physics ensemble. In particular, the RMS error of the ensemble mean is much larger in the single-physics ensemble and no amount of additional spread could lead to an improvement in skill over the multi-physics ensemble. This might be in part due to the unique geographic location of Taiwan, which necessitates to capture maritime convection as well as tropical/extra-tropical storms and their transition.

This leads us to the second central question of this study: Given that a multi-physics ensemble performs best, can additional stochastic perturbations further improve the probabilistic forecast skill? For this purpose, the unperturbed multi-physics ensemble was compared to three experiments, where either SKEB, SPPT or their combination was used to stochastically perturb the ensemble simulations. The qualitative impact on spread, RMS error, CPRSS for a number of dynamical variables as well as precipitation metrics are independent of lead time and shown as score card in Fig. 12. In summary, we find:

  • None of the stochastic schemes deteriorates the RMS error, but adding stochastic perturbations will improve the spread/error ratio and consequently probabilistic skill. Combining SKEB and SPPT with multiple physics packages leads to the best performance skill for Z500 and T850.

  • Currently, the Taiwanese ensemble system is over-dispersive in U850, especially in summer. Adding a stochastic parameterization, especially SKEB, makes the over-dispersion worse and results in a non-significant decrease in CRPSS for lead times up to 24 h. The underlying physical reasons and the sensitivity of the SKEB parameters shown in Table 3 will be the focus of future research.

  • Combining different model-error schemes results in the overall most skillful forecast, which is consistent with the findings of Berner et al. (2011: 2015).

  • Generally, SKEB introduces ensemble spread throughout the free troposphere and in the PBL, while SPPT is most effective near the surface, but has little impact in the free troposphere.

Fig. 12
figure 12

Score Card. Compare with MP. Green means the performance of experiments better than MP, while red means it is worse, and blue means compatible

Full size image

This study introduces the Taiwanese ensemble prediction system and discusses its optimal configuration. It exemplifies that depending on the regional characteristics and details of the ensemble setup, multi-physics approaches might still be necessary for best ensemble performance, although a less-diverse multi-physics configuration would be beneficial, for zonal wind forecasts especially in summer. The experiments conducted over this sub-tropical region confirmed the findings of previous studies that augmenting a multi-physics ensemble with a suite of stochastic parameterizations schemes results in the most skillful ensemble prediction system. However, by using the stochastic schemes, the overall computing overhead is in general 25% in addition; it must not be overlooked in operation system.