Abstract
The concept of derivative is characterised with reference to four basic mental models. These are described as theoretical constructs based on theoretical considerations. The four basic mental models—local rate of change, tangent slope, local linearity and amplification factor—are not only quantified empirically but are also validated. To this end, a test instrument for measuring students’ characteristics of basic mental models is presented and analysed regarding quality criteria.
Mathematics students (n = 266) were tested with this instrument. The test results show that the four basic mental models of the derivative can be reconstructed among the students with different characteristics. The tangent slope has the highest agreement values across all tasks. The agreement on explanations based on the basic mental model of rate of change is not as strongly established among students as one would expect due to framework settings in the school system by means of curricula and educational standards. The basic mental model of local linearity plays a rather subordinate role. The amplification factor achieves the lowest agreement values. In addition, cluster analysis was conducted to identify different subgroups of the student population. Moreover, the test results can be attributed to characteristics of the task types as well as to the students’ previous experiences from mathematics classes by means of qualitative interpretation. These and other results of students’ basic mental models of the derivative are presented and discussed in detail.
Zusammenfassung
Der Begriff der Ableitung wird anhand von vier Grundvorstellungen charakterisiert. Diese werden als theoretische Konstrukte beschrieben, die auf theoretischen Überlegungen beruhen. Die vier Grundvorstellungen – lokale Änderungsrate, Tangentensteigung, lokale Linearität und Verstärkungsfaktor – werden empirisch quantifiziert und validiert. Zu diesem Zweck wird ein Testinstrument zur Messung der Charakteristika dieser Grundvorstellungen von Lernenden erstellt, bzgl. Gütekriterien ausgewertet und an Mathematikstudierenden (n = 266) getestet. Die Ergebnisse zeigen, dass die vier Grundvorstellungen der Ableitung bei den Lernenden mit unterschiedlichen Merkmalen rekonstruiert werden können. Die Tangentensteigung weist über alle Aufgaben hinweg die höchsten Übereinstimmungswerte auf. Die Übereinstimmung bei Erklärungen, die auf der Grundvorstellung der lokalen Änderungsrate beruhen, ist bei den Studierenden nicht so stark ausgeprägt, wie man es aufgrund der Rahmenbedingungen im Schulsystem durch Lehrpläne und Bildungsstandards erwarten würde. Die Grundvorstellung der lokalen Linearität spielt eine eher untergeordnete Rolle. Der Verstärkungsfaktor erzielt die geringsten Übereinstimmungswerte. Darüber hinaus wurde eine Clusteranalyse durchgeführt, um verschiedene Untergruppen der Schülerpopulation zu identifizieren. Die Testergebnisse können mittels qualitativer Interpretation auf Merkmale der Aufgabentypen sowie auf die Vorerfahrungen der Studierenden aus dem Mathematikunterricht zurückgeführt werden. Diese und weitere Ergebnisse zu den grundlegenden mentalen Modellen der Studierenden zur Ableitung werden ausführlich dargestellt und diskutiert.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Basic Mental Models
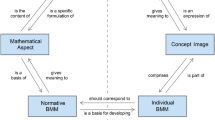
The concept of basic mental models (in German: “Grundvorstellungen”) has been well established in German-speaking didactics of mathematics for many years. It is used to describe, from a subject-didactic perspective, the content-related meaning learners should attribute to or actually give a mathematical concept (vom Hofe 1995, 1996; vom Hofe and Blum 2016). To distinguish between the prescriptive and the descriptive aspect of basic mental models (vom Hofe et al. 2005), we use the following terms according to Greefrath et al. (2021b):
-
Normative basic mental models are interpretations of a mathematical concept that learners should generally and ideally develop. “They work as educational guidelines, following a particular educational goal and describing adequate interpretations of the use of mathematical concepts.” (Hefendehl-Hebeker et al. 2019, p. 32) These basic mental models are identified by didactic analyses of the mathematical concept (see Sect. 2 for the derivative of a function). They specify learning objectives for mathematics lessons and provide orientation to teachers when designing their lessons.
-
Individual basic mental models are the specific formations of normative basic mental models in a person’s mind. They result from individual learning processes. An individual basic mental model can be described as the individual cognitive structure that a person has built up with content-related references to the respective normative basic mental model. The extent to which both are in accordance may vary with time and from person to person.
The notion of basic mental models is related to the theoretical framework of “concept image”, that has been established in the didactics of mathematics since at least the 1980s. Tall and Vinner (1981) describe the concept image of a mathematical concept as “the total cognitive structure that is associated with the concept, which includes all the mental pictures and associated properties and processes. It is built up over the years through experiences of all kinds, changing as the individual meets new stimuli and matures” (p. 152). A person’s concept image can comprise several individual basic mental models of the respective mathematical concept. These individual basic mental models are components of the concept image—parts of the entire cognitive structure related to the mathematical concept (Greefrath et al. 2021b). For example, the individual concept image of a person for the first derivative of a function might encompass the basic mental models of tangent slope and local rate of change (see Sect. 2).
The relationship between the notion of basic mental models (“Grundvorstellungen”) and the cognitive-psychological theory of “schemes” and “mental models” is thoroughly discussed by Kleine et al. (2005). They classify this mathematical didactic concept in the framework of psychological theories by identifying “Grundvorstellungen” as mental models of a mathematical content.
In the following, we use the term basic mental models in the two above-mentioned meanings: On the one hand, normative basic mental models of the concept of the first derivative of a function are presented, as they were worked out on the basis of subject-didactical analyses. A structured methodology framework for processes of identification of normative basic mental models is described by Salle and Clüver (2021). On the other hand, results of a test are presented, which measures whether and to what extent persons’ individual basic mental models of the derivative are in accordance with normative basic mental models and can be activated in corresponding mathematical situations. The results are then analysed and the concept as well as the structure of students’ self-reported basic mental models are discussed critically (based on a cluster analysis). This approach enables a more in-depth analysis of cognitive activities of learners. It also allows conclusions regarding the professional knowledge of prospective and active teachers, as noted, for example, by Castro Gordillo and Pino-Fan (2021, p. 34): “Very few studies focused on comparing didactic-mathematic knowledge of in-service and pre-service teachers aimed at identifying features of the teachers’ didactic-mathematical knowledge on specific topics that can establish a line between pre-service and in-service teachers’ knowledge for teaching.”
2 Basic Mental Models of the Derivative
Difficulties in understanding the concept of derivative are seen at various levels (Bressoud et al. 2016) and are also still found among students at university (Fuentealba et al. 2017). A valid concept definition and concept image, and especially basic mental models are required for teaching processes, otherwise difficulties in teaching the concept of derivative are predeterminated (Desfitri 2016).
The concept of basic mental models of the derivative, as presented by Greefrath et al. (2016) and Weigand et al. (2017) serves as a theoretical framework for the test construction and the empirical studies. The authors have identified four basic mental models in the normative sense of the concept of the first derivative of a function at a point—an overview is provided by Table 1.
2.1 Basic Mental Model: “Local Rate of Change”
Local changes and, in particular, the speed of processes of change in quantities can be captured quantitatively with the rate of change concept. The development of the basic mental model of the derivative as a local rate of change (RC) is based on the understanding of the mean rate of change, but then requires a qualitatively different understanding, as the local rate of change—unlike the mean—is not a quotient, but instead is the limit of quotients.
The understanding of the concept of rate or rate of change is difficult and allows many points of view (Feudel and Biehler 2021; Herbert and Pierce 2012; McDermott et al. 1987; Teuscher and Reys 2010; Zandieh 2000). For example, Teuscher and Reys (2010, p. 519) describe that students at different levels have difficulties conceptualising the idea of a rate of change and McDermott et al. (1987, p. 504) highlight typical difficulties in physical motion contexts, to establish relationships between rates of change and the slope of graphs. Herbert and Pierce (2012, p. 94) demonstrate that there are learners for whom the rate of change is a single variable, while for others it is made up of two changes (change in the x- and y-value). The lack of linking mathematical content to other contexts is also picked up by Carli et al. (2020); here particular value is cared for different forms of representation. Orton (1983) already noted that learners have difficulties in recognising the relationship between mean rates of change in intervals and local rates of change at a point. In view of this, he recommended that rates of change be calculated above all approximately numerical. In particular, the difficulty in understanding the quotient as a measure of the relative size of two quantities can hinder students’ understanding of the rate of change (Byerley et al. 2012).
Thompson and Thompson (1996; 1994) show that teaching the basic mental model of “local rate of change” places considerable demands on teachers. To teach the rate of change, physical contexts are considered beneficial (Chau et al. 2021).
With regard to the formation of this basic mental model, it can thus be seen as an objective that learners are able to give meanings to both the independent and the dependent variable as well as to the derivative as the local rate of change in functional relationships (vom Hofe and Blum 2016, p. S241).
2.2 Basic Mental Model: “Tangent Slope”
The development of the basic mental model “derivative as tangent slope” (TS) goes hand in hand with the conceptual difficulty of forming the concept of a tangent to a function graph at all. The classical approach is usually motivated geometrically with the help of secants of the function graph, whose slope can be determined easily using the coordinates of the two points of intersection with the function graph. Here one draws on experience with linear functions and slope triangles (slope as “geometric ratio” and “algebraic ratio”, see Nagle et al. 2013, p. 1493). The tangent at a point of the function graph is then defined as the straight line that passes through this point and has a slope equal to the limit of the secant slopes.
This is a substantial extension of the tangent concept, which school students have built up for tangents to circles in lower grades. In this context, the idea of a “clinging straight line” is helpful (see Blum and Törner 1983; Danckwerts and Vogel 2006). The tangent is understood as being a straight line that “clings” to the graph locally. This extends significantly the “one point of contact concept” (see Tall 2013). In the corresponding process of extending the scope of the concept (Weigand 2015, p. 264 ff.), learners can have problems understanding that the tangent and graph can have any number of common points—e.g. they can also be identical (Biza 2011).
We would like to point out a difference between the concept image for a tangent by Vinner (2002) and our concept of basic mental models according to Sect. 1. We regard the tangent as subordinate to the derivative and restrict ourselves to mathematically correct conceptions. Vinner (2002) sees the concept images more generally. With the concept of tangent visual representations or merely a collection of impressions or experiences could be connected. This also includes mathematically not (completely) correct conceptions of tangents. In contrast to this, basic mental models are valid perceptions of a concept.
Tangent slope and local rate of change are very common and also both associated with the algebraic representation of a function (Habre and Abboud 2006). There are also subject-specific preferences of students, namely that of mechanical engineering students develop towards the rate of change conception in terms of the derivative, while those of mathematics students develop towards the tangent slope conception (Bingolbali et al. 2007).
2.3 Basic Mental Model: “Local Linearity”
Kirsch (1979) described the basic mental model of local linearity (LL) with the help of the “function microscope”. Here the derivative is considered from the following perspective: If we “zoom in” on the graph of a differentiable function more and more at one point, the graph increasingly appears to be a straight line. The derivative is the slope of this straight line. Software for dynamic mathematics is very suitable for the development of this basic mental model. Zooming is easy to do, the section of the graph displayed on the screen becomes increasingly less different from a straight line. In addition to using such function plotters, for the formation of this basic mental model, Tall (2009) also proposes sketching the graph of the derivative function given the known graph of the initial function. That is, we consider an arbitrary function f at a point and look for a linear function that approximates the behaviour of the function locally as closely as possible (Teague 1996). Consideration of the derivative as the slope of the linear function which, among all linear functions, best approximates the given function f at x (vom Hofe and Blum 2016) also fits this concept. For this basic mental model, there could be connections to the tangent slope, because in a case study, descriptions of the derivative as a tangent were often found, which was not seen as a point-specific object, but also as a (linear) function defined on an interval (Park 2013).
The basic mental model of local linearity is also the basis of applications: For example, in growth models, the time dependency of the size of a population is often described locally—i.e., in a small time interval—by a linear relationship.
2.4 Basic Mental Model: “Amplification Factor”
With the basic mental model of the amplification factor (AF), the derivative is viewed as a proportionality factor of a functional relationship, which indicates how small changes to the independent variable affect the dependent variable. Lax and Terrell (2014, p. 113) describe this with the words “derivative as sensitivity to change” and “derivative as stretching”. The latter expresses that a function f maps a small interval around a value x to an interval of about m times the length where m = f ’(x) (see Greefrath et al. 2016, p. 112). The amplification factor concept cannot only be applied to the derivative, but also to the difference quotient (see Malle 2003). Mamolo and Zazkis (2012) report that university students have difficulties with tasks that require this basic mental model. It is possible that the students observed had an insufficiently developed basic mental model of the derivative as amplification factor.
3 Research Questions
In the preceding section, we presented theoretical considerations on basic mental models of the derivative concept; in particular, we described four basic mental models, which are based on our prior research central when dealing with the derivative concept. We understand these basic mental models as being a theoretical construct, which is to be empirically quantified and validated in the following. Based on this construct, the question arises to what extent these basic mental models of test persons can be empirically reconstructed.
Accordingly, our first research question is:
Q1:
Is the theoretically derived four-dimensional model valid against empirical test data?
We focus on university students and not on school students as, according to the education standards and curricula, basic mental models of the derivative are developed in the second stage of secondary education (ISCED level 3) and the test persons should already have completed the corresponding schooling up to university entrance level. Furthermore, we restrict ourselves to students of mathematics in teacher training courses or degree courses, as we expect stronger characteristics of the basic mental models in this group and the opportunity arises to examine the effects of mathematics studies on individual basic mental models. The answer to Q1 will be given by the construction and validation of a test instrument that measures to what extent self-reported students thinking corresponds to the four basic mental models.
Having this instrument available, the questions regarding which basic mental models the students have actually developed and how this knowledge can be reconciled with existing empirical findings are also of interest. This raises the second central question for us, which we want to explore in this paper:
Q2:
Which characteristics of basic mental models of the derivative can be found among students of mathematics?
We already mentioned that different basic mental models could be developed in one’s mind and that it is even the goal to develop all these basic mental models, because different problem-solving situations require different perspectives, and therefore also different basic mental models. However, these basic mental models could exist on different levels of agreement, and they could be of varying significance in persons’ minds. Q2 asks for these different levels of agreement, characteristics of basic mental models in different situations and within different groups of students.
In order to discuss the two research questions, the development and structure of a test to answer these questions and the method for checking the quality of the test, particularly its reliability and validity, are described in the following. We then present the results of a study with mathematics students.
4 Study Design
4.1 Instrument
A test was developed to assess the existence of individual basic mental models of the derivative. This test has been published and is freely available (Greefrath et al. 2021a). The test measures the degree of commonalities between one’s individual thinking and given reasonings. The methodology of the test to measure basic mental models is to present arguments to the participants in which certain basic mental models occur and ask them specific questions about whether the style of reasoning is consistent with their own thinking process. The core idea of the test is to refer to one special situation and to offer participants different argumentations that are based on certain basic mental models. The participants are asked to what extent these argumentations are close to or consistent with their own thinking. The test does not evaluate how familiar a participant is with the situation, but it determines the acceptance of argumentations with each basic mental model concerning the situation. If a participant compares a special argumentation with his/her own thinking and gives a high rank to “The explanation exactly matches my way of thinking.”, it is a very strong hint that the corresponding basic mental model is embedded in his thinking. This procedure is consistent with the procedure already described in Greefrath et al. (2021b) for measuring basic mental models of integrals.
Each task presents a mathematical situation as a stimulus and four correct argumentations within the context of this situation as possible responses (corresponding to four basic mental models). The test persons are asked to mark for each item on a five-point Likert scale to what extent the respective answer corresponds to their thinking. The Likert scales measure the self-reported congruence between the students’ thinking and the explanation based on a certain basic mental model given in the item. To simplify language, we call this measure the “extent of agreement with a particular basic mental model” or the “extent to which the basic mental model is realized within an individual”. Despite this simplifying language one should be aware that the test only is—with some measurement error—an indicator of the non-observable construct “basic mental model”. Several factors may contribute to this error. First, the item formulation may not correspond to the normative basic mental model. To minimize this error, we had experts’ feedback on the items in the pilot phase of test development. A second source may be that students simply do not understand explanations in the intended way or it may be that some students systematically over- or underestimate the similarity of their own thinking and the given explanations. However, we assume that there is no clear bias caused by this error sources so that they just add to some Gaussian noise.
The test of basic mental models of the derivative consists of 13 tasks (Table 2), an example of a task is shown in Table 3. Furthermore, general data on the test persons is acquired (age, gender, school-leaving qualification, school mathematics grade, course of study, number of semesters). This is formulated for university students of mathematics in teacher training courses or bachelor/master degree courses in scientific disciplines.
The test was piloted and developed further in several stages. It was part of a larger test that also included a section on integral calculus. A detailed description of the development process is given in Greefrath et al. (2021b).
4.2 Random Sample
With regard to the research questions, a cross-sectional survey of students—from four universities (Augsburg, Bayreuth, Münster & Würzburg)—was undertaken in an online format addressing students enrolled in university courses in Analysis 1, typically taken by students of mathematics and physics as well as mathematics teacher students. The selection of the respective courses at the named locations was made against the background that students usually take Analysis 1 at the beginning of their studies. Subject didactic courses were not included in the survey in order to obtain a result as unbiased as possible—in relation to basic mental models.
Of the 384 submissions, 266 were fully completed test sheets. All the following evaluations relate to this group. The gender distribution (109 m, 152 f, 5 other/rather not say) can be explained by the relatively high proportion of student teachers. The questionnaire was administered to students in introductory courses in the beginning of their first year at university. Yet the mean number of semesters was surprisingly high at 3.5 with a standard deviation of 2.4 and median of 2. However, students in their first year were the largest group (n = 185)—n1 = 99 in their 1st semester, n2 = 86 in the 2nd semester. The most experienced students were in their 8th semester.
4.3 Evaluation Method
For the statistical evaluation, the Likert scales were coded by natural numbers from the interval from 1 to 5 (5 means highest agreement). Incomplete cases were not taken into consideration. The reliability in the scales was estimated with Cronbach’s alpha and Guttman’s Lambda4. The dimensionality of the overall construct was determined by means of a scree plot and Vernier’s MAP test and checked by explorative and confirmatory factor analysis. All evaluations were performed with R (https://www.r-project.org).
5 Results
5.1 Structure of Students’ Self-reported Basic Mental Model Agreement
5.1.1 Descriptive-explorative Statistics
The mean values and standard deviations of the scales of the four basic mental models of differential calculus in the validation sample are shown in Table 4. Floor or ceiling effects did not occur in any of the test parts. Table 5 shows the estimates of the reliabilities of the scales. The correlations of the scales (sum scores) are included in Table 6. A more precise analysis of the scales shows that for the scale of the tangent slope, the scale homogeneity measured with Cronbach’s alpha can be improved slightly by omitting item 10b (it would then be 0.82). This item is also found to be comparatively “weak” with respect to the item-total-correlation which is used to compute its discriminatory power. In the case of the other three scales there was no single item whose exclusion would have increased Cronbach’s alpha. Table 7 shows the item-total-correlation of all items.
5.1.2 Factor Analyses
For further examination of the test, an explorative factor analysis (both orthogonal varimax rotation and non-orthogonal oblimin rotation) was carried out. The scree plot shows a clear kink after the fourth eigenvalue so that, in compliance with the theory of test construction, four factors can be assumed. The MAP test (Velicer 1976; implementation in the R package EFA.dimensions) also gives the dimension 4. If the factor analyses are performed with four factors, the items are almost completely assigned according to the theoretical postulates (see appendix).
Moreover, confirmatory factor analyses (CFA) were also carried out to check reliability of scores of the construct by another test. CFA is an adequate technique for this purpose according to Ziegler and Hagemann (2015), especially if tests are performed to detect correlations of residual errors. These tests were performed using the modification index test (T. A. Brown and Moore 2012) with the help of the modindices feature of lavaan. Only four of all possible combinations of error residual were suspicious with \(\chi ^{2}> 3.84\). However, letting these error residuals freely correlate had almost no influence on overall model fit (reported below).
According to Mardia’s test (performed with the R package QuantPsyc), there is a substantial violation of the multivariate normal distribution assumption. Therefore, and because the sample size is not sufficient for asymptotic distribution-free (ADF) methods, as in Greefrath et al. (2021b), the structural equation models were estimated by means of the WLSM estimation method in lavaan (R package).
Model 1:
Firstly, a model was estimated, which consists of four independent sub-models, each of which is a reflexive measurement model for the four scales in terms of the theoretically postulated items for the respective basic mental model. The four latent variables were assumed to be normalised. Latent correlations are allowed.
Model 2:
To further see how the four scales load upon the general understanding of the derivative by basic mental models, a model with a latent second order variable was estimated, which is also normalised and loads on the four latent basic mental model variables. The other aspects of this model are the same as in model 1. The path weights of the second order variables in model 2 are: RC: 1.4, TS: 0.35, LL: 0.88, AF: 1.28
Model fit indices for both models are reported in Table 8. The good fit of model 1 together with the adequate fit of model 2 support for the postulated four-dimensional model. The fact that the latent correlations in model 1 are of modest size further support that the conclusion the four-dimensional model reflects the data’s structure well.
5.1.3 Cluster Analyses
Cluster analyses were performed in R with the factoextra package to describe the distribution of the preferences for the basic mental models in the group of test persons.
Firstly, we examined how many clusters should be formed ideally both by using the gap statistics and the silhouette method. The gap statistic (Tibshirani et al. 2001) is an advanced method that compares the total within cluster variation for different numbers of clusters with their expected values under some null distribution. The estimate of the optimal number of clusters is the one that maximizes the gap statistic. The silhouette method (Rousseeuw 1987) evaluates for all clustered objects which cluster besides its own one would be best. A good clustering is then one for which the minimal average distance to other clusters is maximal. The analysis for both methods was carried out with the function fviz_cluster from the R package factoextra with the default Euclidean distance measure. For both methods three clusters are optimal, but for gap statistics the four or five cluster solutions score only minimally weaker, so all this seems sensible. There is no clear picture when assessing the criterion of the reduction of the sum of squares within the clusters; three or four clusters seem possible. The calculations were therefore carried out for three as well as for four clusters.
For the solution with three clusters, the following Table 9 shows the numbers of the students in the clusters and the midpoints of the clusters regarding the basic mental model scores. Unlike the above tables, the values for the basic mental models are normalised. A solution with four clusters is given in Table 10.
5.2 Characteristics of Students’ Basic Mental Models of the Derivative
Following validation, the test can be used for further studies. As shown, no items have to be removed from the test. It therefore seems possible to use the same sample for some content-related evaluations.
5.2.1 Basic Mental Models of the Derivative in Comparison
We first consider the mean values of the self-reported basic mental model agreement given by the students as explanations for their own reasoning across all 13 test tasks (see Table 11). The last row contains the mean value across all items for the respective basic mental model as well as the total standard deviation across the population for the overall scale produced by averaging. The measured variation includes the variation in the population and the different measurement characteristics of the individual items.
Across all items, explanations based on the basic mental model of tangent slope are closest to the students’ own thinking. The explanations based on the basic mental models rate of change and local linearity are less strongly agreed on, while the basic mental model amplification factor is most rarely viewed as being consistent with the students’ own reasoning. The mean values of the explanation agreements with the basic mental models tangent slope, rate of change and local linearity lie above the middle of the scale. Only the explanation with the basic mental model amplification factor lies slightly below it on average.
With one exception, within the individual tasks (see Fig. 1), explanations on basis of the basic mental model tangent slope got highest agreement. Only in task 10 does the item for explanation based on rate of change have an agreement value (M = 3.56) that lies above the value for the agreement to explanation based on tangent slope (M = 3.19).
In all tasks, the explanation based on the basic mental model amplification factor has the lowest agreement value. The distance to the agreement values for the classes of explanations on the other basic mental models is quite considerable in some cases. This distance is the smallest for task 5 (amplification factor M = 3.17; local linearity M = 3.20) and task 11 (amplification factor M = 3.58; rate of change M = 3.62). Task 5 (see Fig. 2) describes the growth behaviour of bacteria and asks about the meaning of a certain point on the x‑axis, which indicates the inflection point of the graph. Task 11 (see Fig. 3) shows the number of cars in a tunnel as a function of the speed and the change in behaviour near the maximum is addressed.
Within the respective tasks, on average, the agreement to explanation based on basic mental model of local linearity most often takes third place after the tangent slope and rate of change. In task 13, the explanation based on local linearity (M = 3.89) is selected in second place after the explanation based on tangent slope (M = 4.31). In this task (Fig. 4), a function that is not differentiable at point 0 is represented graphically and an explanation is offered for each basic mental model (see test instrument in Greefrath et al. 2021a).
The explanation based on basic mental model tangent slope was chosen as showing the highest agreement with students’ way of thinking in all tasks—with the exception of task 10. There the factor rule should be explained using an example, without the graph being shown. The task where the explanation with the tangent slope received the strongest agreement is task 2. The statement named here is that the tangent is horizontal at the maximum of the graph.
5.2.2 Tasks with High Explanation Potential Due to Basic Mental Models from the View of the Students
For the didactic discussion, it is of interest which tasks activate agreement with the explanations based on basic mental models most strongly on average from the students’ point of view. Even though the tangent slope is the preferred explanation within almost all tasks, the overall image of the explanations with basic mental models differs among the tasks. If we consider all selected basic mental models in total, the two tasks 9 and 12 are those for which the explanations based on basic mental models were chosen most clearly in total. Here the individual agreement values for three of the four explanations are above 4.0. Both tasks use a graph. One of the two tasks describes a pure mathematical problem (behaviour of \(f\left(x\right)=x^{2}\) and \(g(x)=x^{4}\) at point 1 in comparison), the other is an applied mathematical problem (flying altitude h of a glider depending on the time t at the inflection point). A distinct point on the graph is considered in each case.
Also of interest are tasks in which the agreements with basic mental models based explanations occur roughly equally strong. Task 11 (see Fig. 3) is particularly noticeable. This task has the third largest mean value after tasks 9 and 12, but by comparison, a very small standard deviation. The basic mental model agreement mean values are therefore relatively close to each other and at the same time relatively high. Such a task therefore seems suitable for activating all basic mental models in largely the same way.
5.2.3 Graphic Representations
The majority of the task contexts in the test include graphic representations of functions. Three of the contexts do not use graphic representations. For each of the four basic mental models, a scale was formed, which consists of the items that do not include any graphic representations (tasks no. 1, 4, 10) and a scale whose items include a graph (tasks no. 2, 3, 5, 6, 7, 8, 9, 11, 12, 13). Table 12 shows that, apart from the rate of change, all classes of explanations based on basic mental models could be sensitive for presentation of a function graph, and that in these cases the agreement with the explanations based on the basic mental models is increased significantly.
5.2.4 Study Experience
It can be assumed that the relevance of the basic mental models changes under the influence of experiences in university studies. To test this, the test persons were divided into students with a maximum of two semesters of study experience (129) and those with at least three semesters (133; four students did not provide any information on their semester). The agreements on explanations based on the basic mental model are understood to be the value of the total score of the respective scale for the basic mental model (see Table 13).
The results show a largely unchanged self-reported basic mental model agreement. If one differentiates according to whether the test persons have already taken the course Didactics of Analysis or a course with this content, differences can be seen: After the completion of this course the agreement on explanations based on rate of change is weighted significantly higher; the agreement on explanations based on amplification factor is also weighted higher, with p = 0.07, not significantly higher. However, the subgroup of students who had already taken a didactics course was relatively small (16).
6 Discussion
This study focussed on the two research questions which asked on the one hand for the empirical description of the structure of students’ self-reported basic mental models (Q1) and on the other hand for the actual existing characteristics of the basic mental models among students (Q2).
6.1 Structure of Students’ Self-reported Basic Mental Model Agreement (Research Question Q1)
The validity of the tests used here was ensured through expert interviews (Greefrath et al. 2021b). The reliabilities of the scales of the basic mental models are good. Their correlations are so large that, as expected, they reveal relationships, but they are still so small that the scales can be considered to be separate.
The highest correlations were found between the basic mental models of tangent slope and local linearity, tangent slope, and local rate of change as well as between amplification factor and rate of change. This is also in line with previous studies. If the tangent is not considered as a point-specific object, but within an interval (Park 2013), then the correlation of tangent slope and local linearity is obvious. In contrast, tangent slope and local rate of change can be considered related through their algebraic representation (Habre and Abboud 2006), especially through the calculation of the secant slope. This could indicate that the idea of the tangent as a “clinging straight line” (Danckwerts and Vogel 2006) is not very widespread. In addition, the relationship between amplification factor and local rate of change could be explained if the rate of change is considered as a quotient of two quantities (Byerley et al. 2012; Herbert and Pierce 2012).
The analysis of the individual items of the scales does not give any indication that an item should be eliminated as being unsuitable. Only item 10b is to be viewed as being critical in this respect.Footnote 1 However, to retain the symmetry of the test with four items each for all tasks and because the improvement in reliability that would be achieved would be marginal, this item was not excluded. The findings of the explorative factor analysis and the dimension analysis prove that the four dimensions of the theoretical model of the basic mental models of the derivative can also be separated in the empirical data. This is also supported by the confirmatory factor analysis.
We therefore obtain the following central result: The test we designed shows that the four normatively developed basic mental models of the derivative—rate of change, tangent slope, local linearity and amplification factor—can be empirically proven and separated.
6.2 Characteristics of Students’ Basic Mental Models of the Derivative (Research Question Q2)
In the following we summarize the results concerning the four basic mental models, concerning the meaning of graphical representations, the relation between students in initial and advanced studies and the possible differences of characteristics of basic mental models of different kinds of students.
Concerning the Tangent Slope
The explanations based on the tangent slope have the highest agreement values across all tasks. This not only applies to the tasks with graphic representations (where the higher agreement was to be expected), but also to the tasks, in which there was no graph (this is the case for tasks 1, 4 and 10). On the one hand, this is in line with previous empirical studies (Feudel 2015). On the other hand, the high discriminatory power for the item on the tangent slope in task 9 is surprising, since this task deals with the speed of a change process. It could have been supposed that due to the prior experience in such application tasks obtained in class, a very close link between the rate of change concept and tangent slope exists. However, Nagle et al. (2013) have already shown that the rate of change concept is hardly manifested among students. But the correlation between the tangent slope item 9d and the rate of change item 9b is only 0.23.
Concerning the Rate of Change
The dominance of the agreement on explanations based on the basic mental model tangent slope among students is particularly interesting against the background that the educational standards particularly emphasise the rate of change in the context of the derivative within the central idea of functional relationship: “interpret the derivative in particular as a local rate of change” (KMK 2012, p. 20). The concept of the rate of change, however, is less strongly manifested among the students studied than expected. This was also found by Witzke and Spies (2016) within the scope of their qualitative results. They conclude the following from their results: “the widely propagated idea to introduce terms of calculus in the context of the instantaneous rate of change … does not seem to have a sustainable effect on the views of the students” (Witzke and Spies 2016, p. S149).
This result can be explained well with the hurdles to understanding that occurred in the empirical studies of this concept (Herbert and Pierce 2012; McDermott et al. 1987; Orton 1983). They are due to more in-depth mathematical challenges with this basic mental model, such as the existence of the limit value of the difference quotient or the relationship between average and local rate of change. Our results therefore indicate the need for sustained supporting measures to develop this basic mental model (see Feudel and Biehler 2021). Concerning current mathematics teaching in school, significantly broadened measures are required to strengthen this concept. This should be possible, as the concept of rate of change is also considered to be essential by teachers and it fits also well with applications in analysis lessons (Erens and Eichler 2019).
Concerning the Local Linearity
The explanations based on the basic mental model local linearity often achieves at least the third-highest level of agreement and in task 13 even the second-highest level of agreement.Footnote 2 The concept of local linearity normally plays a rather subordinate role in analysis teaching at school.
However, the idea of the function magnifying glass—often with “zooming into the graph” with appropriate software—has a long tradition with many suggestions for analysis teaching (Elschenbroich et al. 2014). Moreover, the importance of this basic mental model should not be underestimated, particularly for mathematical education at universities, as it is a fundamental concept in many analysis courses (vom Hofe and Blum 2016).
In task 13, the high agreement value for this explanation could be due to the “kink-free” graphs. Thus, local linearity would have a particular significance in contrast examples of differentiability. Such examples, that locally are similar to the graph of the absolute value function, could have a particular significance for the understanding of the derivative and for the formation of this basic mental model (Tsamir et al. 2006).
Concerning the Amplification Factor
The explanations based on the basic mental model amplification factor achieves the lowest agreement values. This was also to be expected against the background of the usual introductions to the derivative concept and the way of dealing with derivatives in mathematics lessons. The amplification factor possibly has a particular significance, if a situation is to be described in individual distinct points (extreme points, inflection points). This is suggested by the tasks in which the amplification factor was chosen more strongly. Further in-depth research is certainly needed regarding the development of this basic mental model.
Concerning Graphical Representations
As supposed—we were able to show that a graphic representation included in the task clearly influences the response behaviour with regard to the agreement on explanations based on the basic mental model tangent slope. If this visual support is missing, as in task 10 for example, the tangent slope has only weak discriminatory power within the scale.
Concerning Students in Advances Semesters
The test results also allow a comparison of test persons in the initial semesters and advanced semesters. In general, there does not appear to be a very large change in the characteristics of basic mental models during the study period at university. There is even a trend towards a slight reduction in the basic mental model characteristics as an increase, which could possibly be expected. Here, we can only speculate about the reasons for this. For example, the strong focus on symbols in university mathematics could be decisive for this. However, if we differentiate according to whether test persons have already attended the course Didactics of Analysis, students weight expressions based on the rate of change significantly higher after completing this course. There might also be subject-specific developments of basic mental models, especially for local rate of change and tangent slope, for different study programmes that could not be further investigated in this population, but give rise to further studies (Bingolbali et al. 2007). This at least shows the possibility of specific development of basic mental models of the derivative through appropriate interventions. While there is a range of empirical studies on self-assessment, beliefs (Voss et al. 2013), on concept development (Roos 2020) and on the development of the professional knowledge of mathematics students (Baumert and Kunter 2013; Kaiser et al. 2017), a lack of research on the development of basic mental models during mathematics studies at university still exists. Available specific test instruments cover knowledge concerning derivatives (Aydın and Ubuz 2015), but not concerning basic mental models.
Different Agreement On Basic Mental Models in Different Groups of Students
It is also possible that the basic mental models differently manifest in different subgroups of the student population. A cluster analysis with three or four clusters was carried out for this reason. A possible interpretation of the clusters consists of one group each, which
In the solution with three clusters, the third group would consist of the students who only prefer the basic mental model of tangent slope (Table 9, C3). In the solution with four clusters there would on the one hand be a group that prefers few basic mental models in general (Table 10, C1) as well as a group that prefers explanations based on the geometric basic mental models (Table 10, C4).
These clusters could explain different results of various studies (Feudel and Biehler 2021; Nagle et al. 2013; Witzke and Spies 2016), as there are possibly subgroups of students with specific preferences and also those who can use all basic mental models. In particular, the preference for geometric basic mental models is also found in Vargas González et al. (2021).
6.3 Limitations of the Study
As the description of the concept of basic mental models of the derivative shows, it is a complex construct, which cannot be easily covered by a test. With the scales, it is only possible to make statements about basic mental models, which refer to the selection and rating of predefined possible answers. These items represent a certain operationalisation, which could also have an influence on agreement through the choice of certain terms. To avoid an excessively long test, predefined possible answers and selected contexts were used. This allows a reliable measurement of the ability dimensions, however it can lead to lower validity. In addition, some statements about the characteristic of basic mental models of the derivative could only be obtained due to trends in the data on a qualitative level. These require more in-depth analyses and corresponding empirical evidence. Furthermore, the test does not evaluate whether the participants are able to solve the given problems in the tasks. It is assumed that the participants are familiar with the given task situations, because the problems dealt with are largely standard problems in calculus courses at high school. However, the test does not give an answer to the question whether the ability to solve a task influenced the choice of the explanations based on the basic mental models. Moreover, further research on the development of basic mental models during university mathematics studies could help to clarify the results found between first-year students and advanced students. The present study design was not sufficient to answer this question, as this would require a longitudinal study.
7 Conclusions
From the results of these empirical studies, conclusions can be drawn in at least three respects: firstly, with regard to the theoretical and empirical further development of the concept of basic mental models, secondly with regard to the relationship between basic mental models and representations or problem contexts, and finally and thirdly with regard to mathematics teaching.
-
A further development of the test should be discussed regarding the formulation of the items related to the different basic mental models. Which characteristic formulations express a certain basic mental model adequately in a specific situation? Furthermore, the question arises which task types or problem contexts particularly emphasise certain basic mental models. The main aim here is to increase the discriminatory power between the different basic mental models.
-
Regarding the relationship between basic mental models and representations or problem contexts, the test performed here provides indications of the relationship between the activation of a certain basic mental model and the specifics of tasks. This concerns, for example, relationships between the tangent slope and graphical representations, between the amplification factor and particularly distinct points in graphical representations of functions, or between local linearity and contrast examples of differentiable functions. More in-depth studies are necessary for the local rate of change, in particular in relationship to applied situations. The results obtained on a qualitative level need to be verified on an empirical level.
-
Regarding mathematics teaching in school, learning environments are to be developed that focus on the development of certain basic mental models of the derivative. In particular with respect to the development of the basic mental model of the rate of change, more application-oriented approaches should be chosen (Hitt and Dufour 2021). However, this should be viewed as a long-term goal, as the current findings do not yet provide empirically verified results.
Complementary to our results on basic mental models of the integral (Greefrath et al. 2021b), more precise information about basic mental models of the derivative could now be obtained. In a next step, the relationships to the academic performance as well as between the constructs can also be examined.
Two important objectives are identified with regard to further studies. On the one hand, it is the development of a test to verify basic mental models among learners—both school students and university students. On the other hand, the aim is to develop adequate teaching and learning strategies for the development of basic mental models in mathematics lessons.
Notes
This is the item on the tangent slope in task 10 of the test: “On transition from f(x) to \(2\cdot f(x)\), slope triangles to tangents are stretched by a factor of 2 in the direction of the y-axis.”.
This task shows the graph of a function that is non-differentiable at a point.
References
Aydın, U., & Ubuz, B. (2015). The thinking-about-derivative test for undergraduate students: development and validation. International Journal of Science and Mathematics Education, 13(6), 1279–1303. https://doi.org/10.1007/s10763-014-9545-x.
Baumert, J., & Kunter, M. (2013). The effect of content knowledge and pedagogical content knowledge on instructional quality and student achievement. In M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krauss & M. Neubrand (Eds.), Cognitive activation in the mathematics classroom and professional competence of teachers (pp. 175–205). Springer US. https://doi.org/10.1007/978-1-4614-5149-5_9.
Bingolbali, E., Monaghan, J., & Roper, T. (2007). Engineering students’ conceptions of the derivative and some implications for their mathematical education. International Journal of Mathematical Education in Science and Technology, 38(6), 763–777. https://doi.org/10.1080/00207390701453579.
Biza, I. (2011). Students’ evolving meaning about tangent line with the mediation of a dynamic geometry environment and an instructional example space. Technology, Knowledge and Learning, 16(2), 125. https://doi.org/10.1007/s10758-011-9180-3.
Blum, W., & Törner, G. (1983). Didaktik der Analysis. Vandenhoeck & Ruprecht.
Bressoud, D., Ghedamsi, I., Martinez-Luaces, V., & Törner, G. (2016). Teaching and learning of calculus. Springer. https://doi.org/10.1007/978-3-319-32975-8.
Brown, T. A., & Moore, M. T. (2012). Confirmatory factor analysis. In R. H. Hoyle (Ed.), Handbook of structural equation modeling (pp. 361–379). Guilford.
Byerley, C., Hatfield, N., & Thompson, P. W. (2012). Calculus student understandings of division and rate. In S. Brown, S. Larson, K. Marrongelle & M. Oehrtman (Eds.), Proceedings of the 15th annual conference on research in undergraduate mathematics education. SIGMAA/RUME. (pp. 358–363).
Carli, M., Lippiello, S., Pantano, O., Perona, M., & Tormen, G. (2020). Testing students ability to use derivatives, integrals, and vectors in a purely mathematical context and in a physical context. Physical Review Physics Education Research, 16(1), 10111. https://doi.org/10.1103/PhysRevPhysEducRes.16.010111.
Castro Gordillo, W. F., & Pino-Fan, L. (2021). Comparing the didactic-mathematical knowledge of derivative of in-service and pre-service teachers. Acta Scientiae, 23(3), 34–99. https://doi.org/10.17648/acta.scientiae.5842.
Chau, L. T. H., Duc, N. M., & Tong, D. H. (2021). The teaching of the concept of derivative in high school and its relationship with physics. Universal Journal of Educational Research, 9(1), 186–201. https://doi.org/10.13189/ujer.2021.090121.
Danckwerts, R., & Vogel, D. (2006). Analysis verständlich unterrichten. Spektrum Akademischer Verlag.
Desfitri, R. (2016). In-service teachers’ understanding on the concept of limits and derivatives and the way they deliver the concepts to their high school students. Journal of Physics: Conference Series, 693, 12016. https://doi.org/10.1088/1742-6596/693/1/012016.
Elschenbroich, H.-J., Seebach, G., & Schmidt, R. (2014). Die digitale Funktionenlupe. Ein neuer Vorschlag zur visuellen Vermittlung einer Grundvorstellung vom Ableitungsbegriff. Mathematik lehren, 187, 34–37.
Erens, R., & Eichler, A. (2019). Belief changes in the transition from university studies to school practice. In M. S. Hannula, G. C. Leder, F. Morselli, M. Vollstedt & Q. Zhang (Eds.), Affect and mathematics education (pp. 345–373). Springer. https://doi.org/10.1007/978-3-030-13761-8_16.
Feudel, F. (2015). Die Ableitung als absolute Änderung? – Unterschiedliches Begriffsverständnis in Mathematik und Wirtschaftswissenschaften. In F. Caluori, H. Linneweber-Lammerskitten & C. Streit (Eds.), Beiträge zum Mathematikunterricht 2015 (pp. 1049–1052). WTM. https://doi.org/10.17877/DE290R-16820.
Feudel, F., & Biehler, R. (2021). Students’ understanding of the derivative concept in the context of mathematics for economics. Journal Für Mathematik-Didaktik, 42(1), 273–305. https://doi.org/10.1007/s13138-020-00174-z.
Fuentealba, C., Sánchez-Matamoros, G., Badillo, E., & Trigueros, M. (2017). Thematization of derivative schema in university students: nuances in constructing relations between a function’s successive derivatives. International Journal of Mathematical Education in Science and Technology, 48(3), 374–392. https://doi.org/10.1080/0020739X.2016.1248508.
Greefrath, G., Oldenburg, R., Siller, H.-S., Ulm, V., & Weigand, H.-G. (2016). Aspects and “Grundvorstellungen” of the concepts of derivative and integral: Subject matter-related didactical perspectives of concept formation. Journal Für Mathematik-Didaktik, 37(S1), 99–129. https://doi.org/10.1007/s13138-016-0100-x.
Greefrath, G., Oldenburg, R., Siller, H.-S., Ulm, V., & Weigand, H.-G. (2021a, January 8). Test zur Erfassung von Grundvorstellungen zu Ableitungen und Integralen (GV-AI), Empirische Erfassung von Grundvorstellungen zur ersten Ableitung einer Funktion an einer Stelle und zum bestimmten Integral. Archive Ouverte HAL. https://hal.archives-ouvertes.fr/hal-03103685. Accessed 04.05.2022
Greefrath, G., Oldenburg, R., Siller, H.-S., Ulm, V., & Weigand, H.-G. (2021b). Basic mental models of integrals: theoretical conception, development of a test instrument, and first results. ZDM – Mathematics Education, 53(3), 649–661. https://doi.org/10.1007/s11858-020-01207-0.
Habre, S., & Abboud, M. (2006). Students’ conceptual understanding of a function and its derivative in an experimental calculus course. The Journal of Mathematical Behavior, 25(1), 57–72. https://doi.org/10.1016/j.jmathb.2005.11.004.
Hefendehl-Hebeker, L., Hofe, R. vom, Büchter, A., Humenberger, H., Schulz, A., & Wartha, S. (2019). Subject-matter didactics. In H. N. Jahnke & L. Hefendehl-Hebeker (Eds.), Traditions in German-speaking mathematics education research (pp. 25–59). Springer. https://doi.org/10.1007/978-3-030-11069-7_2.
Herbert, S., & Pierce, R. (2012). Revealing educationally critical aspects of rate. Educational Studies in Mathematics, 81(1), 85–101. https://doi.org/10.1007/s10649-011-9368-4.
Hitt, F., & Dufour, S. (2021). Introduction to calculus through an open-ended task in the context of speed: Representations and actions by students in action. Zdm—mathematics Education. https://doi.org/10.1007/s11858-021-01258-x.
Hofe, R. vom (1995). Grundvorstellungen mathematischer Inhalte. Akad. Verl: Spektrum.
Hofe, R. vom (1996). Über die Ursprünge des Grundvorstellungskonzepts in der deutschen Mathematikdidaktik. Journal für Mathematik-Didaktik, 17(3–4), 238–264. https://doi.org/10.1007/BF03338832.
Hofe, R. vom, & Blum, W. (2016). “Grundvorstellungen” as a category of subject-matter didactics. Journal Für Mathematik-Didaktik, 37(S1), 225–254. https://doi.org/10.1007/s13138-016-0107-3.
Hofe, R. vom, Kleine, M., Blum, W., & Pekrun, R. (2005). On the role of ‘Grundvorstellungen’ for the development of mathematical literacy—First results of the longitudinal study PALMA. Mediterranean Journal for Research in Mathematics Education, 4(2), 67–84.
Kaiser, G., Blömeke, S., König, J., Busse, A., Döhrmann, M., & Hoth, J. (2017). Professional competencies of (prospective) mathematics teachers—cognitive versus situated approaches. Educational Studies in Mathematics, 94(2), 161–182. https://doi.org/10.1007/s10649-016-9713-8.
Kirsch, A. (1979). Ein Vorschlag zur visuellen Vermittlung einer Grundvorstellung vom Ableitungsbegriff. Der Mathematikunterricht, 25(3), 25–41.
Kleine, M., Jordan, A., & Harvey, E. (2005). With a focus on ‘Grundvorstellungen’ Part 1: A theoretical integration into current concepts. ZDM—Mathematics Education, 37(3), 226–233. https://doi.org/10.1007/s11858-005-0013-5.
KMK (Ed.). (2012). Bildungsstandards im Fach Mathematik für die Allgemeine Hochschulreife (Beschluss der Kultusministerkonferenz vom 18.10.2012). Wolters Kluwer.
Lax, P. D., & Terrell, M. S. (2014). Calculus with applications. Springer. https://doi.org/10.1007/978-1-4614-7946-8.
Malle, G. (2003). Vorstellungen vom Differenzenquotienten fördern. Mathematik Lehren, 118, 57–62.
Mamolo, A., & Zazkis, R. (2012). Stuck on convention: a story of derivative relationships. Educational Studies in Mathematics, 81(2), 161–177. https://doi.org/10.1007/s10649-012-9391-0.
McDermott, L. C., Rosenquist, M. L., & Zee, E. H. van (1987). Student difficulties in connecting graphs and physics: examples from kinematics. American Journal of Physics, 55(6), 503–513. https://doi.org/10.1119/1.15104.
Nagle, C., Moore-Russo, D., Viglietti, J., & Martin, K. (2013). Calculus students’ and instructors’ conceptualisations of slope: a comparison across academic levels. International Journal of Science and Mathematics Education, 11(6), 1491–1515. https://doi.org/10.1007/s10763-013-9411-2.
Orton, A. (1983). Students’ understanding of integration. Educational Studies in Mathematics, 14(1), 1–18. https://doi.org/10.1007/BF00704699.
Park, J. (2013). Is the derivative a function? If so, how do students talk about it? International Journal of Mathematical Education in Science and Technology, 44(5), 624–640. https://doi.org/10.1080/0020739X.2013.795248.
Roos, A.-K. (2020). Mathematisches Begriffsverständnis im Übergang Schule – Universität: Verständnisschwierigkeiten von Mathematik an der Hochschule am Beispiel des Extrempunktbegriffs. Springer. https://doi.org/10.1007/978-3-658-29524-0.
Rousseeuw, P. J. (1987). Silhouettes: a graphical aid to the interpretation and validation of cluster analysis. Journal of Computational and Applied Mathematics, 20, 53–65. https://doi.org/10.1016/0377-0427(87)90125-7.
Salle, A., & Clüver, T. (2021). Herleitung von Grundvorstellungen als normative Leitlinien – Beschreibung eines theoriebasierten Verfahrensrahmens. Journal für Mathematik-Didaktik. https://doi.org/10.1007/s13138-021-00184-5.
Tall, D. (2009). Dynamic mathematics and the blending of knowledge structures in the calculus. ZDM—Mathematics Education, 41(4), 481–492. https://doi.org/10.1007/s11858-009-0192-6.
Tall, D. (2013). How humans learn to think mathematically. Exploring the three worlds of mathematics. Cambridge University Press. https://doi.org/10.1017/CBO9781139565202.
Tall, D., & Vinner, S. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity. Educational Studies in Mathematics, 12(2), 151–169. https://doi.org/10.1007/BF00305619.
Teague, D. J. (1996). Utilizing precalculus experiences with graphing calculators: a local linearity approach to calculus. ICME 8, Sevilla.
Teuscher, D., & Reys, R. E. (2010). Slope, rate of change, and steepness: do students understand these concepts? The Mathematics Teacher, 103(7), 519–524. https://doi.org/10.5951/MT.103.7.0519.
Thompson, P. W. (1994). Images of rate and operational understanding of the fundamental theorem of calculus. Educational Studies in Mathematics, 26(2–3), 229–274. https://doi.org/10.1007/BF01273664.
Thompson, A. G., & Thompson, P. W. (1996). Talking about rates conceptually, part ii: mathematical knowledge for teaching. Journal for Research in Mathematics Education, 27(1), 2. https://doi.org/10.2307/749194.
Tibshirani, R., Walther, G., & Hastie, T. (2001). Estimating the number of clusters in a data set via the gap statistic. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 63(2), 411–423. https://doi.org/10.1111/1467-9868.00293.
Tsamir, P., Rasslan, S., & Dreyfus, T. (2006). Prospective teachers’ reactions to right-or-wrong tasks: the case of derivatives of absolute value functions. The Journal of Mathematical Behavior, 25(3), 240–251. https://doi.org/10.1016/j.jmathb.2006.09.001.
Vargas González, M. F., Fernández-Plaza, J. A., & Hidalgo, R. J. F. (2021). Pre-service teachers’ understanding of the derivative of a function at a point. International Journal of Mathematical Education in Science and Technology. https://doi.org/10.1080/0020739X.2021.1957504.
Velicer, W. F. (1976). Determining the number of components from the matrix of partial correlations. Psychometrika, 41(3), 321–327. https://doi.org/10.1007/BF02293557.
Vinner, S. (2002). The role of definitions in the teaching and learning of mathematics. In D. Tall (Ed.), Advanced mathematical thinking (pp. 65–81). Springer. https://doi.org/10.1007/0-306-47203-1_5.
Voss, T., Kleickmann, T., Kunter, M., & Hachfeld, A. (2013). Mathematics teachers’ beliefs. In M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krauss & M. Neubrand (Eds.), Cognitive activation in the mathematics classroom and professional competence of teachers (pp. 249–271). Springer. https://doi.org/10.1007/978-1-4614-5149-5_12.
Weigand, H.-G. (2015). Begriffsbildung. In R. Bruder, L. Hefendehl-Hebeker, B. Schmidt-Thieme & H.-G. Weigand (Eds.), Handbuch der Mathematikdidaktik (pp. 255–278). Springer. https://doi.org/10.1007/978-3-642-35119-8_9.
Weigand, H.-G., Greefrath, G., Oldenburg, R., Siller, H.-S., & Ulm, V. (2017). Aspects and basic mental models (‘Grundvorstellungen’) of basic concepts of calculus. In B. Kaur, W. K. Ho, T. L. Toh & B. H. Choy (Eds.), Proceedings of the 41st conference of the international group for the psychology of mathematics education (Vol. 4, pp. 313–320). PME. http://www.igpme.org.
Witzke, I., & Spies, S. (2016). Domain-specific beliefs of school calculus. Journal Für Mathematik-Didaktik, 37(S1), 131–161. https://doi.org/10.1007/s13138-016-0106-4.
Zandieh, M. (2000). A theoretical framework for analyzing student understanding of the concept of derivative. In E. Dubinsky, A. Schoenfeld & J. Kaput (Eds.), Research in Collegiate Mathematics Education. IV (Vol. 8, pp. 103–127). American Mathematical Society. https://doi.org/10.1090/cbmath/008.
Ziegler, M., & Hagemann, D. (2015). Testing the unidimensionality of items: pitfalls and loopholes. European Journal of Psychological Assessment, 31(4), 231–237. https://doi.org/10.1027/1015-5759/a000309.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Greefrath, G., Oldenburg, R., Siller, HS. et al. Mathematics Students’ Characteristics of Basic Mental Models of the Derivative. J Math Didakt 44, 143–169 (2023). https://doi.org/10.1007/s13138-022-00207-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13138-022-00207-9