Efficient estimation of hydraulic conductivity heterogeneity with non-redundant measurement information

Abstract

Solving the inverse problem of identifying groundwater model parameters with measurements is a computationally intensive task. Although model reduction methods provide computational relief, the performance of many inversion methods depends on the amount of often highly correlated measurements. We propose a measurement reduction method that only incorporates essential measurement information in the inversion process. The method decomposes the covariance matrix of the model output and projects both measurements and model response on the eigenvector space corresponding to the largest eigenvalues. We combine this measurement reduction technique with two inversion methods, the Iterated Extended Kalman Filter (IEKF) and the Sequential Monte Carlo (SMC) methods. The IEKF method linearizes the relationship between measurements and parameters, and the cost of the required gradient calculation increases with increase of the number of measurements. SMC is a Bayesian updating approach that samples the posterior distribution through sequentially sampling a set of intermediate measures and the number of sampling steps increases with increase of the information content. We propose modified versions of both algorithms that identify the underlying eigenspace and incorporate the reduced information content in the inversion process. The performance of the modified IEKF and SMC methods with measurement reduction is tested on a numerical example that illustrates the computational benefit of the proposed approach as compared to the standard IEKF and SMC methods with full measurement sets.

1 Introduction

Aquifer parameters governing groundwater flow, such as the hydraulic conductivity, are highly variable and heterogeneous. Knowledge of the spatial parameter distribution is essential for designing successful remediation systems and developing reliable water supply resources. However, directly measuring these parameters at local scale is practically impossible. Therefore, aquifer parameters are indirectly estimated using hydraulic head measurements under different hydraulic stress conditions, such as pumping tests. The measurements are related to the sought parameters through the numerical solution of a mathematical model. The task of determining the model parameters through comparing the model response with measurements of the underlying physical system requires the solution of an inverse problem.

Groundwater inversion involves high-dimensional parameter spaces and sparse or noisy measurement data, and hence it is typically an ill-posed problem. Conventionally, the parameter space is simplified by assuming the spatial distribution of parameters to be zoned according to an interpretation of geologic information. However, such interpretation is often subjective. Recently, Hydraulic Tomography (HT) techniques have been developed to cast the model inversion problem in a probabilistic framework that treats the model parameters as random fields. The verification of HT has been demonstrated with sandbox experiments (Illman et al. 2010) and at a highly heterogeneous field site with abundance of hydraulic head measurements and validation samples (Berg and Illman 2011). One HT approach is to formulate the model inversion in a probabilistic framework through Bayesian analysis (Ghosh et al. 2007). In this context, the information contained in the measurement data is expressed by the likelihood function, whereas any knowledge on the parameter values prior to conducting the measurements is expressed by the prior distribution. The posterior distribution of the parameter is obtained through Bayes’ rule as the normalized product of the prior distribution and likelihood function, whereby the prior distribution acts as a regularizer. The mathematical formulation for Bayesian inverse problems involving spatially variable parameters is given in Stuart (2010). Bayesian analysis is flexible with respect to the data types, it enables quantifying the uncertainty of the obtained parameter values and it facilitates spatial modeling through random fields. For these reasons its application is popular in HT problems (e.g. see Copty et al. 1993; Hachich and Vanmarcke 1983; Kitanidis and Vomvoris 1983; McLaughlin and Townley 1996).

The normalizing constant in Bayesian analysis consists of a high dimensional integral, which generally needs to be solved numerically. This leads to considerable computational cost, especially in cases where the model is computationally intensive. Analytical solutions are available for Gaussian random fields and linear inversion models (i.e., linear relationships between measurements and model parameters). Examples of Bayesian analysis with linear inversion models are given in Woodbury and Ulrych (2000) and Jiang and Woodbury (2006), where the moments of the random variables are treated as hyperparameters. Also, quasi-linear approaches are available, as given in Fienen et al. (2008). An extension of analytical solutions to nonlinear inversion models with Gaussian prior fields is given by the Successive Linear Estimator (SLE) method (Yeh and Zhang 1996). This approach iteratively linearizes the nonlinear relationship between hydraulic pressure head and the spatial distribution of hydraulic conductivity (Yeh and Liu 2000). Apart from hydraulic pressure head, other types of data can be incorporated, such as flux measurements (Zha et al. 2014), or geological data as prior information (Zhao et al. 2016). A method that is closely related to SLE is the Extended Kalman Filter (EKF) (Jazwinski 2007), which is applicable for mildly nonlinear problems. In contrast to the SLE, the measurement error, which is inherent in all field measurements, is an explicit part of the formulation. An improvement for nonlinear problems is the Iterated Extended Kalman Filter (IEKF) (Jazwinski 2007), which also explictly accounts for measurement uncertainty. Similar to SLE, the IEKF approach is based on a successive linearization of the model at a sequence of updated estimates.

The linearization assumption in SLE and IEKF, which renders the methods effective in problems where the hydraulic conductivity variance is small, leads to convergence issues in inversion problems with large variance. This can be circumvented through the application of sampling-based methods, which generate samples that follow the true posterior distribution of the sought parameters and use the actual forward simulation model without linearization. Markov Chain Monte Carlo (MCMC) methods are a popular group of algorithms for solving Bayesian inverse problems. A review of MCMC methods for subsurface problems is given in Yustres et al. (2012). One of the early applications of MCMC to hydraulic tomography is found in Oliver et al. (1997). Efendiev et al. (2005) suggested to accelerate MCMC by using intermediate, coarser-scaled models until the final model scale is evaluated. However, for MCMC methods, it is difficult to assess if the resulting distributions are accurate. Moreover, the sampling process may become computationally expensive as often large burn-in periods are required to reach the stationary distribution of the Markov chain. Alternative approaches are Importance Sampling (IS, Li and Lin 2015), blocking Markov Chain Monte Carlo (BMCMC, Fu and Gómez-Hernández 2009), Hybrid Nested Sampling (HNS, Elsheikh et al. 2014) and Sequential Monte Carlo (SMC, Neal 2001; Chopin 2002; Del Moral et al. 2006; Beskos et al. 2015). SMC generates samples from a sequence of distributions that gradually approach the posterior distribution. The method has found several applications in the subsurface inversion problem (e.g. Chang et al. 2012; Field et al. 2016; Pasetto et al. 2012; Montzka et al. 2011; Schöniger et al. 2012). Other sampling-based inversion methods include the Implicit sampling method (Chorin et al. 2010; Morzfeld et al. 2015), which is a special case of chainless sampling. In addition, the Ensemble Kalman Filter, which is a version of the Kalman Filter where the covariance is evaluated based on samples, has found wide use in different fields. It was first presented by Evensen (1994), and has found numerous applications and modifications (Kovachki and Stuart 2019; Gu et al. 2007; Iglesias et al. 2018).

The availability of measurements has been increasing, due to growing affordability of instrumentation and advancements in storage and transfer technologies. Although a large amount of data is beneficial for inversion problems, since their availability generally reduces the inversion uncertainty, many algorithms are likely to become less efficient with increasing observation data amount. This dilemma, most commonly solved by choosing a subset of data either randomly or subjectively based on selected measurements events, has also been tackled from different angles in a more systematic manner. In surface water model calibration, using a representative short calibration period instead of applying the full available measurement period has been suggested (Razavi and Tolson 2013). This is achieved by determining the period which has a similar mean squared error as the full model period. Another method of reducing the number of measurements with respect to time is limiting the measurements used for inversion by a sliding window, thus ignoring the influence of measurements that range further back in time than a certain threshold (Lamberti et al. 2017). However, the selection of this threshold seems to be arbitrary and could ignore long-term effects. In Mirhoseini et al. (2015), a method of sparsifying measurement correlation matrices has been introduced, in order to decrease computing effort for regression techniques, as well as to facilitate the data transfer between parallel computing units. Regression has been conducted with a subset of principal components of the predictor variables, obtained through a principal component analysis (PCA) (Huang and Antonelli 2001). Within this work, the optimal compression ratio with respect to reconstruction residuals was also investigated. The works of Chen et al. (2017) and Schillings et al. (2019) introduce Hessian information to improve the convergence of Monte Carlo-based method in inversion problems with large measurement sets.

This paper proposes a method for compressing measurement data in the context of groundwater inversion. For measurements with high correlation and therefore redundancy, the proposed compression approach allows decreasing the computational effort of model inversion. The proposed approach is similar to the method in Fischer et al. (2017), but instead of applying PCA to the parameter space and reducing the number of parameters, it is applied to the observation space to express the measurements with a reduced number of fixed measurement component terms, as in Rezaie et al. (2012). In meteorological forecasting, PCA has been applied for measurement reduction in data assimilation (Collard et al. 2010). Their work primarily concentrates on the removal of measurement noise by decomposition and reconstruction of measurements using PCA. The focus of this paper is the potential in computational gain of groundwater inversion algorithms through measurement reduction. The method is combined with two Bayesian inversion algorithms, the IEKF and SMC methods, and modified versions of these algorithms are proposed. The performance of the latter is investigated with a numerical example and it is demonstrated that the proposed modifications result in a substantial decrease of the computational cost without significant loss of accuracy.

The paper is organized as follows: First, the theory behind groundwater inversion based on Bayesian Analysis is presented. Then, a method of reducing the number of measurements while keeping the contained information is introduced. The application and the benefit of this measurement reduction method for two inversion algorithms, the IEKF and SMC methods, is described next. Subsequently, we use a numerical example of a theoretical aquifer to illustrate the behavior and accuracy of the modified variants of IEKF and SMC. Finally, we discuss the observations and thoughts we obtained from the numerical studies.

2 General problem

2.1 Problem setting

We consider an aquifer $\Omega$, $\Omega$ being a bounded subdomain of ${\mathbb {R}}^d, d \in {\mathbb {N}}$, with hydraulic conductivity field $K \in X$, where X is a suitable space of functions defined over the spatial domain $\Omega$. We are interested in inferring the spatial distribution of K based on measurements of the hydraulic head at certain spatial locations from a number of pumping tests. The relationship between K and hydraulic head $h^j$ for the j-th pumping test is given by the steady-state groundwater flow equation:

$$\begin{aligned} \nabla (K \nabla h^j)+Q^j \delta (x-x_{Q^j} ) = 0 \, , \end{aligned}$$

(1)

where $Q^j$ is the pumping/injection rate at location $x_{Q^j}$ and $\delta$ is the Dirac function. At the model boundary $\partial \Omega$, the hydraulic head is set to constant value $h_1$.

Equation (1) is typically solved with a numerical method, such as the finite element (FE) method. After discretization into n elements, the FE method results in a system of linear equations that takes the following form:

$$\begin{aligned} {\mathbf {A}}( {\mathbf {K}}) {\mathbf {h}}^j={\mathbf {b}}^j \, . \end{aligned}$$

(2)

Here, ${\mathbf {K}}\in {\mathbb {R}}^n$ denotes the hydraulic conductivity values at the finite elements and ${\mathbf {h}}^j \in {\mathbb {R}}^{n_h}$ is the hydraulic head values at the nodal points; ${\mathbf {A}}( {\mathbf {K}})$ is the stiffness matrix that depends on the element conductivity values ${\mathbf {K}}$, and ${\mathbf {b}}^j$ is the force vector due to the j-th pumping test. The hydraulic head values at the measurement locations can be extracted as follows:

$$\begin{aligned} {\mathbf {h}}_{{\mathrm {m}}}^j = {\mathbf {E}}_{{\mathrm {m}}}^{\mathrm {T}} {\mathbf {h}}^j \, , \end{aligned}$$

(3)

where ${\mathbf {E}}_{{\mathrm {m}}} = [{\mathbf {e}}_1,\ldots ,{\mathbf {e}}_{n_{{\mathrm {m}}}}]$, ${\mathbf {e}}_i$ is the standard basis vector corresponding to the location of the i-th measurement and $n_{{\mathrm {m}}}$ is the number of measurements. The vector ${\mathbf {h}}$ collects the hydraulic head values at all measurement locations and all pumping tests:

$$\begin{aligned} {\mathbf {h}} = [{\mathbf {h}}_{{\mathrm {m}}}^1 ;\ldots ;{\mathbf {h}}_{{\mathrm {m}}}^p] \, , \end{aligned}$$

(4)

with p denoting the number of pumping tests. Through Eqs. (2)–(4), we obtain a mapping $G:{\mathbb {R}}^n \rightarrow {\mathbb {R}}^m$ from the element hydraulic conductivities ${\mathbf {K}}$ to the hydraulic heads at the measurement locations, where $m=p n_{{\mathrm {m}}}$ denotes the total number of measurement points from all pumping tests. The goal is to determine ${\mathbf {K}}$ based on measurements ${\mathbf {d}}$ of ${\mathbf {h}}$.

2.2 Random fields and Bayesian formulation

To approach the problem introduced in Sect. 2.1, i.e. determine ${\mathbf {K}}$ by means of measurements of ${\mathbf {h}}$, we move into a Bayesian probabilistic framework. The Bayesian framework allows the construction of a stable solution of the inverse problem, through introducing prior information on ${\mathbf {K}}$. This prior information acts as a regularizer to the generally ill-posed inversion problem. Additionally, the Bayesian approach enables obtaining a probabilistic estimate of ${\mathbf {K}}$, rather than a deterministic one, which allows for quantifying the uncertainty of the estimate.

The prior information is given in terms of a prior probability distribution that expresses the observer’s belief on the distribution of ${\mathbf {K}}$ prior to collecting the measurements. In this context, ${\mathbf {K}}$ represents discrete instances of a spatially variable uncertain quantity, i.e. the hydraulic conductivity field K, which is modeled probabilistically by a random field. Here, we model the logarithm of K, $\log (K)$, by a homogeneous Gaussian random field. This implies that the marginal distribution of K, i.e. its distribution at every point in space, is lognormal and hence it cannot take negative values. The field $\log (K)$ can be completely defined by its mean and auto-covariance function, which are chosen based on past geologic investigations and information from literature. Taking $\log ({\mathbf {K}})$ to be the random variables corresponding to the midpoints of each finite element, their prior distribution will be jointly Gaussian, with mean values equal to the mean of the random field and covariance matrix evaluated based on the auto-covariance function of the random field and the coordinates of the element midpoints.

To decrease the dimensionality of the parameter space and thus further facilitate the solution of the inverse problem, the random vector $\log ({\mathbf {K}})$ can be approximated by a truncated Karhunen-Loève (KL) Expansion (Ghosal and Van der Vaart 2017), expressed as:

$$\begin{aligned} \log ({\mathbf {K}}) \approx \varvec{\mu }_{\log K}+\sum _{i=1}^{k} \sqrt{\lambda _{\text {KL},i}}{\mathbf {v}}_{\text {KL},i}\theta _i \, , \end{aligned}$$

(5)

where $\varvec{\mu }_{\log K}$ is the mean vector of $\log ({\mathbf {K}})$ and the pairs $\{ \lambda _{\text {KL},i}, {\mathbf {v}}_{\text {KL},i} \}$ are the k largest eigenvalues and corresponding eigenvectors of the covariance matrix of $\log ({\mathbf {K}})$. The truncation order k is selected such that the vector $\log ({\mathbf {K}})$ is represented without a significant loss of accuracy, in practice through requiring that the approximation captures a significant portion of the total variance of $\log ({\mathbf {K}})$. The vector $\varvec{\theta }$ follows the k-dimensional independent standard Gaussian distribution ${\mathcal {N}}({\mathbf {0}},{\mathbf {I}})$.

The parametrization of Eq. (5) implies that the identification problem is now shifted to the identification of the random variables in $\varvec{\theta }$. This is done through Bayesian updating, which applies Bayes’ rule to update the prior standard Gaussian density of $\varvec{\theta }$, denoted $f ' (\varvec{\theta })$, to a posterior density:

$$\begin{aligned} f'' (\varvec{\theta }) = c_E^{-1} L(\varvec{\theta })f ' (\varvec{\theta }) \, . \end{aligned}$$

(6)

Here, $L(\varvec{\theta })$ is the likelihood function that describes the measurement information and $c_E$ is a normalizing constant that ensures that the posterior density $f'' (\varvec{\theta })$ integrates to one:

$$\begin{aligned} c_E=\int _{\varvec{\theta }} L(\varvec{\theta }) f'(\varvec{\theta }) \text {d} \varvec{\theta } \, . \end{aligned}$$

(7)

The likelihood function $L(\varvec{\theta })$ is proportional to the probability of the measurements ${\mathbf {d}}$ given a parameter state $\varvec{\theta }$. The model outcome can be expressed as a function of the vector $\varvec{\theta }$ as ${\mathbf {h}}={\widetilde{G}}(\varvec{\theta })$, where ${\widetilde{G}}:{\mathbb {R}}^k \rightarrow {\mathbb {R}}^m$ is the composition of operator G and Eq. (5). The data vector ${\mathbf {d}}$ can then be expressed as a realization of ${\widetilde{G}}(\varvec{\theta })$ superimposed by the outcome of an error term $\varvec{\epsilon }$, i.e.

$$\begin{aligned} {\mathbf {d}}={\widetilde{G}}(\varvec{\theta })+\varvec{\epsilon }. \end{aligned}$$

(8)

The error $\varvec{\epsilon }$ models the discrepancy between measurements and model outcomes due to measurement noise and/or model uncertainty. We assume that $\varvec{\epsilon }$ follows a zero-mean Gaussian distribution with covariance matrix ${\mathbf {C}}_{\epsilon \epsilon }$. As a consequence, the likelihood function takes the following form:

$$\begin{aligned} L(\varvec{\theta })=\exp (-\Phi (\varvec{\theta })), \end{aligned}$$

(9)

where $\Phi (\varvec{\theta })$ is the so-called potential (or negative log-likelihood), defined as

$$\begin{aligned} \Phi (\varvec{\theta }) = \frac{1}{2} \Vert {\mathbf {C}}_{\epsilon \epsilon }^{-\frac{1}{2}}({\mathbf {d}}-{\widetilde{G}}(\varvec{\theta })) \Vert ^2. \end{aligned}$$

(10)

The closer the model outputs to the measurements, the higher is the likelihood that this model input $\varvec{\theta }$ is close to the true value of the parameter. The covariance matrix ${\mathbf {C}}_{\epsilon \epsilon }$ of the error is chosen to reflect the measurement and/or model uncertainty. For the case where $\varvec{\epsilon }$ models only measurement noise, it is often reasonable to assume that errors at different locations are statistically independent. In such case, the matrix ${\mathbf {C}}_{\epsilon \epsilon }$ is a diagonal matrix whose diagonal elements are the variances of the errors at the measurement locations.

The Bayesian framework serves as a basis for a number of inversion algorithms. These include approximation methods that attempt to approximate the posterior distribution and sampling-based approaches that generate samples from the posterior usually based on MCMC methods. The performance of most inversion algorithms deteriorates with increase of the dimension of the data ${\mathbf {d}}$. This is related to the fact that an increase in the data dimension usually implies a higher information content. This results in a highly peaked likelihood, which hinders exploration of the high probability mass area of the posterior distribution. Next, we discuss an approach to condense the information contained in high-dimensional data vectors ${\mathbf {d}}$. In the subsequent sections, we demonstrate how to incorporate this approach within an approximation and a sampling method, namely the IEKF and SMC methods.

3 Coping with correlated measurements

The measurements collected for an aquifer characterization effort are often numerous. This is either owed to the small temporal interval necessary for determining the specific storage of the aquifer or due to the small spatial interval, which can be necessary to identify medium-scale heterogeneity. However, in practice, it is computationally impossible to incorporate large numbers of measurements in the inversion process. We now discuss an approach for reducing the number of measurements, without neglecting potentially important information.

We aim at reducing the number of measurements for the updating process by determining linear combinations thereof with high information content. We do this through projecting the measurements on the space defined by the eigenvectors of the covariance matrix ${\mathbf {C}}_{hh}={\mathrm {Cov}}({\mathbf {h}},{\mathbf {h}})$ of the model response corresponding to the measurements ${\mathbf {h}}={\widetilde{G}}(\varvec{\theta })$. The matrix ${\mathbf {C}}_{hh}$ can be decomposed as:

$$\begin{aligned} {\mathbf {C}}_{hh}={\mathbf {V}} {\mathbf {D}} {\mathbf {V}}^{\text {T}} \, , \end{aligned}$$

(11)

where ${\mathbf {V}} = [{\mathbf {v}}_1,\ldots ,{\mathbf {v}}_m]$ is an $m {\times } m$ matrix whose columns are the eigenvectors of ${\mathbf {C}}_{hh}$ and ${\mathbf {D}}={\mathrm {diag}}(\lambda _i)$ is a diagonal matrix whose entries are the corresponding eigenvalues of ${\mathbf {C}}_{hh}$. The matrix ${\mathbf {V}}$ is orthogonal, i.e. ${\mathbf {V}}^\text {T} {\mathbf {V}}={\mathbf {I}}$ where ${\mathbf {I}}$ is the $m {\times } m$ identity matrix. Therefore, the columns of ${\mathbf {V}}$ imply orthogonal transformations in the Euclidean space ${\mathbb {R}}^m$. We define the transformation:

$$\begin{aligned} {\mathbf {a}}={\mathbf {V}}^{{\mathrm {T}}} {\mathbf {h}} \, . \end{aligned}$$

(12)

The components of ${\mathbf {a}}$ are uncorrelated, i.e. it holds

$$\begin{aligned} {\mathrm {Cov}}(a_i,a_j) = 0 \text { for } i \ne j \, . \end{aligned}$$

(13)

The vector ${\mathbf {h}}$ can be expressed in the transformed coordinate system as:

$$\begin{aligned} {\mathbf {h}}=\sum _{i=1}^m a_i {\mathbf {v}}_i = {\mathbf {V}} {\mathbf {a}} \, . \end{aligned}$$

(14)

The sum of the variances of each component of ${\mathbf {h}}$ can be expressed as the sum of the eigenvalues, i.e.

$$\begin{aligned} \sum _{i=1}^m {\mathrm {Var}}(h_i) = \sum _{i=1}^m \lambda _i\, . \end{aligned}$$

(15)

We now sort the eigenvector matrix ${\mathbf {V}}$ and eigenvalue matrix ${\mathbf {D}}$ in order of decreasing eigenvalue. ${\mathbf {h}}$ can be approximated by keeping only the first $m_{{\mathrm {r}}}$ ordered components in Eq. (14), which leads to

$$\begin{aligned} \hat{{\mathbf {h}}}=\sum _{i=1}^{m_{{\mathrm {r}}}} a_i {\mathbf {v}}_i = {\mathbf {V}}_{{{\mathrm {r}}}} {\mathbf {a}}_{{\mathrm {r}}}\, . \end{aligned}$$

(16)

The total variance of the approximation in Eq. (16) reads:

$$\begin{aligned} \sum _{i=1}^m {\mathrm {Var}}({\hat{h}}_i) = \sum _{i=1}^{m_{{\mathrm {r}}}} \lambda _i \, . \end{aligned}$$

(17)

Through Eqs. (15) and (17), we can choose the number of eigenvectors that reflect a target percentage $\alpha$ of the variability in ${\mathbf {h}}$. That is, we select $m_{{\mathrm {r}}}$ such that

$$\begin{aligned} \frac{\sum _{i=1}^{m_{{\mathrm {r}}}} \lambda _i}{\sum _{i=1}^m \lambda _i} \ge \alpha \, . \end{aligned}$$

(18)

We now formulate the Bayesian inversion problem in the transformed space defined by the truncated eigenvector matrix ${\mathbf {V}}_{{\mathrm {r}}}$ of dimensions $m \times m_{{\mathrm {r}}}$. To this end, we project the data vector ${\mathbf {d}}$ on the truncated space, which gives

$$\begin{aligned} {\mathbf {d}}_{{\mathrm {r}}} = {\mathbf {V}}^{{\mathrm {T}}}_{{\mathrm {r}}} {\mathbf {d}}\, . \end{aligned}$$

(19)

The relationship between the reduced measurement components ${\mathbf {d}}_{{\mathrm {r}}}$ and the truncated model ${\mathbf {a}}_{{\mathrm {r}}}$ reads

$$\begin{aligned} {\mathbf {d}}_{{\mathrm {r}}}= {\mathbf {V}}_{{\mathrm {r}}}^{{\mathrm {T}}} {\widetilde{G}}(\varvec{\theta })+{\mathbf {V}}_{{\mathrm {r}}}^{{\mathrm {T}}} \varvec{\epsilon }={\mathbf {a}}_{{\mathrm {r}}}+\varvec{\epsilon }_{{\mathrm {r}}}\, . \end{aligned}$$

(20)

The modified error $\varvec{\epsilon }_{{\mathrm {r}}}$ is a linear transformation of a Gaussian error and is therefore itself Gaussian with zero mean and covariance matrix ${\mathbf {C}}_{\epsilon _{{\mathrm {r}}} \epsilon _{{\mathrm {r}}}}={\mathbf {V}}_{{\mathrm {r}}}^{{\mathrm {T}}} {\mathbf {C}}_{\epsilon \epsilon } {\mathbf {V}}_{{\mathrm {r}}}$. The likelihood function expressing the reduced information is given as

$$\begin{aligned} L_{{\mathrm {r}}}(\varvec{\theta })=\exp (-\Phi _{{\mathrm {r}}}(\varvec{\theta })) \, , \end{aligned}$$

(21)

where the reduced potential $\Phi _{{\mathrm {r}}}(\varvec{\theta })$ reads

$$\begin{aligned} \Phi _{{\mathrm {r}}}(\varvec{\theta }) = \frac{1}{2} \Vert {\mathbf {C}}_{\epsilon _{{\mathrm {r}}} \epsilon _{{\mathrm {r}}}}^{-\frac{1}{2}}({\mathbf {d}}_{{\mathrm {r}}}-{\mathbf {V}}_{{\mathrm {r}}}^{{\mathrm {T}}} {\widetilde{G}}(\varvec{\theta })) \Vert ^2 \, . \end{aligned}$$

(22)

We remark that the measurement reduction approach presented in this section requires the evaluation of the covariance matrix ${\mathbf {C}}_{hh}$. Exact evaluation of ${\mathbf {C}}_{hh}$ is not possible, as ${\mathbf {h}}$ depends on the input parameters $\varvec{\theta }$ through the solution of a finite element system. Hence, ${\mathbf {C}}_{hh}$ needs to be approximated. Optimally, the approximation should be based on the posterior distributions of $\varvec{\theta }$ and therefore ${\mathbf {h}}$, in order to accurately reflect the variability of the measurements. The approach adopted to approximate ${\mathbf {C}}_{hh}$ depends on the algorithm used to solve the inversion problem and includes methods such as sampling or first-order Taylor approximations. We note that, if ${\mathbf {C}}_{hh}$ is estimated based on samples from ${\mathbf {h}}$, the projections ${\mathbf {a}}$ coincide with the principle components of these samples and, hence, the approach is equivalent to a PCA of the model output.

In the following sections, we discuss two inversion algorithms for solving the modified inversion problem of Eq. (20) that are based on extensions of the IEKF and SMC methods.

4 Iterated extended Kalman filter with reduced measurement components

4.1 Iterated extended Kalman filter (IEKF)

The IEKF method is an approximation method for solving Bayesian inverse problems that is based on an iterative linearization of the computational model and application of the Kalman filter on the respective linearized system. This results in successive estimates of the conditional mean and conditional covariance matrix of the parameters given the data. We introduce the IEKF for solving the Bayesian inverse problem of Eq (8). The conditional mean of the vector $\varvec{\theta }$, containing the random variables in the KL expansion of Eq. (5), $\varvec{\mu }_{\theta }^l$, is updated at iteration step l with the information from the vector of measurements ${\mathbf {d}}$ by the following expression:

$$\begin{aligned} \varvec{\mu }_{\theta }^{l+1}=\varvec{\mu }_{\theta }^0+ {\mathbf {C}}_{\theta h}^{l} ({\mathbf {C}}_{hh}^{l} + {\mathbf {C}}_{\epsilon \epsilon })^{-1} \left( {\mathbf {d}}-{\mathbf {h}}^{l}-{\mathbf {J}}^l(\varvec{\mu }_{\theta }^0-\varvec{\mu }_{\theta }^{l})\right) \, , \end{aligned}$$

(23)

where ${\mathbf {h}}^{l}$ is the output of the model with parameters $\varvec{\mu }_{\theta }^{l}$, i.e. ${\mathbf {h}}^{l}={\widetilde{G}}(\varvec{\mu }_{\theta }^{l})$, and ${\mathbf {J}}^l$ is the sensitivity of the measurements with respect to the model parameters. The initial value of the mean is taken as the prior mean $\varvec{\mu }_{\theta }^{0}={\varvec{0}}$. The covariance matrix of the linearized model outputs ${\mathbf {C}}_{hh}^l$ is calculated at each step l with ${\mathbf {J}}^l$ and the initial parameter covariance matrix as:

$$\begin{aligned} {\mathbf {C}}_{hh}^l={\mathbf {J}}^l {\mathbf {C}}_{\theta \theta }^0 {\mathbf {J}}^{l {\mathrm {T}}} , \end{aligned}$$

(24)

where the matrix ${\mathbf {C}}_{\theta \theta }^{0}$ is set to the unconditional parameter covariance matrix, ${\mathbf {C}}_{\theta \theta }^{0} = {\mathbf {I}}$. The cross-covariance between model response and parameters is obtained as:

$$\begin{aligned} {\mathbf {C}}_{h \theta }^l= {\mathbf {C}}_{\theta h}^{l {\mathrm {T}}}={\mathbf {J}}^l {\mathbf {C}}_{\theta \theta }^0 \, . \end{aligned}$$

(25)

The iterative updating process is continued until there is no significant change in the estimate of $\varvec{\mu }_{\theta }$. Thereafter, the conditional covariance matrix of the parameters is estimated as follows:

$$\begin{aligned} {\mathbf {C}}_{\theta \theta }^{l+1}={\mathbf {C}}_{\theta \theta }^{0}-{\mathbf {C}}_{\theta h}^{l} ({\mathbf {C}}_{h h}^{l}+{\mathbf {C}}_{\epsilon \epsilon })^{-1}{\mathbf {C}}_{h \theta }^{l} \, . \end{aligned}$$

(26)

Conventionally, the sensitivity ${\mathbf {J}}^l$ is obtained by the Adjoint State Method, e.g. Cao et al. (2003). The (i, j) component of matrix ${\mathbf {J}}^l$ can be written as

$$\begin{aligned} J_{ij}^l=\frac{\partial h_i^l}{\partial \theta _j }={\mathbf {e}}_i^{{\mathrm {T}}} {\mathbf {A}}^{-1} \left( \frac{\partial {\mathbf {b}}(\varvec{\theta })}{\partial \theta _j }- \frac{\partial {\mathbf {A}}(\varvec{\theta })}{\partial \theta _j } {\mathbf {h}}^l \right) \, . \end{aligned}$$

(27)

We define the adjoint vector $\varvec{\lambda }_i^{{\mathrm {T}}}={\mathbf {e}}_i^{{\mathrm {T}}} {\mathbf {A}}^{-1}$. $\varvec{\lambda }_i$ is obtained by solving the so-called adjoint system, which is defined by:

$$\begin{aligned} {\mathbf {A}}(\varvec{\theta })\varvec{\lambda }_i = {\mathbf {e}}_i \, . \end{aligned}$$

(28)

The adjoint system needs to be solved once for each measurement, but only one time for all parameters. This is advantageous for cases where the number of parameters is significantly larger than the number of measurements. However, at large numbers of pumping tests and corresponding measurements, a large number of adjoint systems needs be solved and hence, the sensitivity evaluation becomes computationally expensive. After solving the adjoint system, the sensitivity of model response $h_i^l$ with respect to parameter $\theta _j$ is obtained as:

$$\begin{aligned} \frac{\partial h_i^l}{\partial \theta _j }=\varvec{\lambda }_i^{{\mathrm {T}}} \left( \frac{\partial {\mathbf {b}}(\varvec{\theta })}{\partial \theta _j }- \frac{\partial {\mathbf {A}}(\varvec{\theta })}{\partial \theta _j } {\mathbf {h}}^l \right) \, . \end{aligned}$$

(29)

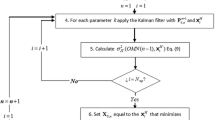
The partial derivative of the stiffness matrix $\frac{\partial {\mathbf {A}}(\varvec{\theta })}{\partial \theta _j }$ is evaluated at the element level using the expression for the element stiffness matrix and the KL expansion of Eq. (5); the element matrices are then assembled to obtain the global derivative matrix. The original IEKF algorithm is shown in Algorithm 1. We remark that the final estimate of $\varvec{\mu }_{\theta }$ obtained by the IEKF method is also a local mode of the posterior density of $\varvec{\theta }$ (Jazwinski 2007).

4.2 IEKF with reduced measurement components

The computational cost of the IEKF method scales linearly with the number of measurements m. Assuming a direct solver for the sparse matrix in the adjoint system, the cost per iteration is ${\mathcal {O}}(n_h^{2} m)$, where $n_h$ is the number of degrees of freedom in the finite element system (Davis 2006). This is because at each iteration, m adjoint systems need to be solved. To enhance its efficiency, we combine IEKF with the measurement reduction approach, introduced in Sect. 3. That is, we decompose the covariance matrix ${\mathbf {C}}_{hh}$ and project the inversion problem on the space defined by the eigenvectors ${\mathbf {V}}_{{\mathrm {r}}}$ corresponding to the $m_{{\mathrm {r}}}$ largest eigenvalues of ${\mathbf {C}}_{hh}$. As a first approximation, we compute the covariance matrix through its first-order approximation at the initial point ${\mathbf {C}}_{hh}^0$, following Eq. (24).

The sensitivity ${\mathbf {J}}_{{\mathrm {r}}}^l$ of the projected model responses ${\mathbf {a}}_{{\mathrm {r}}}^l = {\mathbf {V}}_{{\mathrm {r}}}^{{\mathrm {T}}} {\mathbf {h}}^l$ is evaluated with the adjoint method. Let us consider the case, where the data come from a single pumping test. In such case, the modified adjoint system for evaluating ${\mathbf {J}}_{{\mathrm {r}}}^l$ reads:

$$\begin{aligned} {\mathbf {A}}(\varvec{\theta })\varvec{\lambda }_{{\mathrm {r}},i} = {\mathbf {E}} {\mathbf {v}}_i \, , \end{aligned}$$

(30)

with $\varvec{\lambda }_{{\mathrm {r}},i}^{{\mathrm {T}}} = {\mathbf {v}}_i^{{\mathrm {T}}} {\mathbf {E}}^{{\mathrm {T}}}$, ${\mathbf {v}}_i$ is the eigenvector corresponding to the i-th projected response $a_{{\mathrm {r}},i}$ and ${\mathbf {E}} = [{\mathbf {e}}_1,\ldots ,{\mathbf {e}}_m]$ collects the basis vectors corresponding to each measurement location. The sensitivity is then obtained as:

$$\begin{aligned} \frac{\partial a_{{\mathrm {r}},i}^l}{\partial \theta _j }=\varvec{\lambda }_{{\mathrm {r}},i}^{{\mathrm {T}}} \left( \frac{\partial {\mathbf {b}}(\varvec{\theta })}{\partial \theta _j }- \frac{\partial {\mathbf {A}}(\varvec{\theta })}{\partial \theta _j } {\mathbf {h}}^l \right) \, . \end{aligned}$$

(31)

The cost of the Jacobian evaluation is ${\mathcal {O}}(n_h^{2} m_{{\mathrm {r}}})$, which can be significantly lower than for the case where all measurements are used, since usually $m_{{\mathrm {r}}} \ll m$.

Having evaluated the matrix ${\mathbf {J}}_{{\mathrm {r}}}^l$, the covariance of the projected model responses is calculated through:

$$\begin{aligned} {\mathbf {C}}_{aa}^{l}={\mathbf {J}}_{{\mathrm {r}}}^l {\mathbf {C}}_{\theta \theta }^0 {\mathbf {J}}_{{\mathrm {r}}}^{l {\mathrm {T}}} \, . \end{aligned}$$

(32)

The cross-covariance between projected response and parameters is obtained as follows:

$$\begin{aligned} {\mathbf {C}}_{a \theta }^{l}={\mathbf {J}}_{{\mathrm {r}}}^l {\mathbf {C}}_{\theta \theta }^0 \, . \end{aligned}$$

(33)

We are then able to perform the updating by means of the reduced measurement components ${\mathbf {d}}_{{\mathrm {r}}}$ as follows:

$$\begin{aligned} \varvec{\mu }_{\theta }^{l+1}=\varvec{\mu }_{\theta }^0+{\mathbf {C}}_{\theta a}^{l} ({\mathbf {C}}_{aa}^{l} + {\mathbf {V}}_{{\mathrm {r}}}^{{\mathrm {T}}} {\mathbf {C}}_{\epsilon \epsilon } {\mathbf {V}}_{{\mathrm {r}}})^{-1} ({\mathbf {d}}_{{\mathrm {r}}}-{\mathbf {a}}_{{\mathrm {r}}}^{l}-{\mathbf {J}}_{{\mathrm {r}}}^l(\varvec{\mu }_{\theta }^0-\varvec{\mu }_{\theta }^{l})) \, . \end{aligned}$$

(34)

The parameter covariance matrix is updated through:

$$\begin{aligned} {\mathbf {C}}_{\theta \theta }^{l+1}={\mathbf {C}}_{\theta \theta }^{0}-{\mathbf {C}}_{\theta a}^{l} ({\mathbf {C}}_{a a}^{l}+{\mathbf {V}}_{{\mathrm {r}}}^{{\mathrm {T}}} {\mathbf {C}}_{\epsilon \epsilon } {\mathbf {V}}_{{\mathrm {r}}})^{-1}{\mathbf {C}}_{a \theta }^{l} \, . \end{aligned}$$

(35)

To encode the information relevant for updating the current state of the system, we periodically update the projection based on updated estimates of the full covariance matrix. This requires evaluating the Jacobian matrix of the original response, through application of Eq. (27). To avoid a large number of Jacobian evaluations with the original response variables, we only update the projection if the available eigenvector matrix of the reduced measurement components is sufficiently non-orthogonal with respect to the current estimate of the covariance matrix ${\mathbf {C}}_{aa}^{l}$. We assess this through examining the off-diagonal terms of the following matrix:

$$\begin{aligned} \hat{{\mathbf {D}}}= {\mathbf {V}}_{a}^{{\mathrm {T}}} {\mathbf {C}}_{aa}^{l} {\mathbf {V}}_{a} \, , \end{aligned}$$

(36)

where the eigenvector matrix ${\mathbf {V}}_{a}$ is obtained by the eigendecomposition of ${\mathbf {C}}_{aa}={\mathbf {V}}_a {\mathbf {D}} {\mathbf {V}}_a^{\text {T}}$. If the ratio of the norm of the off-diagonal terms $\Vert \hat{{\mathbf {D}}} - {\mathrm {diag}}(\hat{{\mathbf {D}}}) \Vert$ divided by the norm of the diagonal terms $\Vert {\mathrm {diag}}(\hat{{\mathbf {D}}}) \Vert$ surpasses a threshold value $\eta$, we estimate the covariance of the original response and update the projection. On this occasion, an updating step is performed with the full measurement set. The algorithm is terminated, when the change between two solutions is smaller than a threshold, and a final updating step is performed with all measurements. The modified IEKF method is shown in Algorithm 2.

We remark that for the case where p pumping tests are performed, a total of p adjoint systems need to be solved per eigenvector for evaluating the Jacobian matrix at each iteration. Therefore, for large p, the computational cost for estimating the Jacobian becomes considerable, even for cases where the number of measurements are reduced significantly. This can be alleviated through decomposing the covariance matrix of the model responses separately for each pumping test and aggregating the resulting eigenvectors in ${\mathbf {V}}_{{\mathrm {r}}}$.

5 Sequential Monte Carlo with reduced measurement components

5.1 Sequential Monte Carlo (SMC)

SMC samplers is a category of methods that generate samples from a target distribution through sequentially sampling a set of intermediate distributions (Neal 2001; Chopin 2002; Del Moral et al. 2006). Consider a density sequence $\{f_l(\varvec{\theta }),l=0,\ldots ,L\}$, where $f_0$ is a density that can be easily sampled from, and $f_L$ is the target density. Each density $f_l$, $l>0$, is known up to a normalizing constant, i.e. $f_l(\varvec{\theta })=c_l^{-1} {\eta _l}(\varvec{\theta })$, and ${\mathrm {supp}}{(f_l)} \subseteq {\mathrm {supp}}{(f_{l-1})}$. Assume that at step $l-1$, a set of samples (or particles) $\{ \varvec{\theta }_j,j=1,\ldots ,N\}$ is available that provide a sample approximation of $f_{l-1}$. These samples are used to construct a weighted sample approximation of $f_l$ through importance sampling:

$$\begin{aligned} f_l (\varvec{\theta }) \approx \sum _{j=1}^N w_j \delta _{\varvec{\theta }_j}(\varvec{\theta }) \, , \end{aligned}$$

(37)

where $\delta _{\varvec{\theta }_j}$ is the Dirac mass at $\varvec{\theta }_j$ and the weights $w_j$ are evaluated as:

$$\begin{aligned} W_j = \frac{{\eta _{l}}(\varvec{\theta }_j)}{{\eta _{l-1}}(\varvec{\theta }_j)}, \; \; w_j = \frac{W_j}{\sum _{i=1}^N W_i} \, . \end{aligned}$$

(38)

To avoid degeneracy of the weights as we move towards the target distribution, the weighted samples from $f_l$ are transformed to uniformly weighted samples through a resample-move scheme. First, we resample the samples $\{ \varvec{\theta }_j,j=1,\ldots ,N\}$ with probability $w_j$ assigned to each sample. We then move the resulting samples through applying a Markov move with a Markov kernel that is reversible with respect to $f_l$.

In the context of the Bayesian inversion problem of Eq. (8), the density $f_0(\varvec{\theta })$ is the prior density $f ' (\varvec{\theta })$ and the target density $f_L(\varvec{\theta })$ is the posterior density $f '' (\varvec{\theta })$ with unnormalized form ${\eta _L}(\varvec{\theta }) = L(\varvec{\theta })f_0(\varvec{\theta })$. The choice of the intermediate densities should be such that each density $f_{l-1}$ provides a good proposal density for sampling from $f_l$. A standard choice is to introduce a set of tempering parameters $\{\beta _l,l=0,\ldots , L\}$ such that $0=\beta _0<\ldots <\beta _L=1$, and define each density $f_l$ as Neal (2001):

$$\begin{aligned} f_l (\varvec{\theta }) \propto L(\varvec{\theta })^{\beta _l} f_0(\varvec{\theta }) = \exp \left( -\beta _l \Phi (\varvec{\theta }) \right) f_0(\varvec{\theta }) \, . \end{aligned}$$

(39)

Following Eq. (39), the unnormalized weights $W_j$ take the form:

$$\begin{aligned} W_j = L(\varvec{\theta }_j)^{\beta _l-\beta _{l-1}} = \exp \left( -(\beta _l-\beta _{l-1}) \Phi (\varvec{\theta }_j) \right) \, . \end{aligned}$$

(40)

To ensure that each pair of densities $f_{l-1}$ and $f_l$ do not vary significantly from one another, each tempering parameter $\beta _l$ can be chosen adaptively such that the effective sample size ${\mathrm {ESS}}$ takes a target value (Jasra et al. 2011). ${\mathrm {ESS}}$ is defined by:

$$\begin{aligned} {\mathrm {ESS}}=\frac{\left( \sum _{j=1}^N W_j \right) ^2}{\sum _{j=1}^N W_j^2} \, . \end{aligned}$$

(41)

That is, at each iteration l, the following optimization problem is solved:

$$\begin{aligned} \beta _l = \underset{\beta \in \left( \beta _{l-1},1 \right) }{\text {argmin}}({\mathrm {ESS}}(\beta )-\tau )^2 \, , \end{aligned}$$

(42)

where $\tau >0$ is a target value. We remark that the solution of the optimization problem of Eq. (42) does not require additional model evaluations. Therefore, the contribution to the overall computational time is negligible.

For application of SMC in high-dimensional parameter spaces, it is essential to perform the move step with a Markov kernel whose acceptance probability does not degenerate with increase of the parameter dimension. Here, we apply the preconditioned Crank-Nicolson (pCN)-Metropolis-Hastings algorithm (Cotter et al. 2013). The pCN algorithm for sampling from $f_l$ generates each proposed state $\varvec{\nu }$ from a proposal that is reversible with respect to the prior $f_0$. For the present case, where the prior is independent standard normal, ${\mathcal {N}}({\mathbf {0}},{\mathbf {I}})$, the proposal is given by

$$\begin{aligned} \varvec{\nu } = \sqrt{1-b^2}\varvec{\theta }+b \varvec{\xi }, \; \; \varvec{\xi }\sim {\mathcal {N}}({\mathbf {0}},{\mathbf {I}}) \, , \end{aligned}$$

(43)

where $\varvec{\theta }$ denotes the current state. The candidate is accepted with probability $\alpha (\varvec{\theta },\varvec{\nu })$ given by:

$$\begin{aligned} \alpha (\varvec{\theta },\varvec{\nu }) = \min \left\{ 1,\frac{L(\varvec{\nu })^{\beta _l}}{L(\varvec{\theta })^{\beta _l}}\right\} =\min \left\{ 1, \exp \left[ \beta _l(\Phi (\varvec{\theta })-\Phi (\varvec{\nu }))\right] \right\} \, . \end{aligned}$$

(44)

The parameter $b \in [0,1]$ controls the variance of the proposal distribution; $(1-b^2)^{-1}$ is the correlation coefficient between candidate and current states (Papaioannou et al. 2015). We choose the parameter b adaptively to ensure a target acceptance probability close to 0.4. Details on the implementation of the adaptive version of the pCN algorithm can be found in Papaioannou et al. (2015) and Papaioannou et al. (2016).

The SMC algorithm for sampling the from the posterior distribution of the inverse problem of Eq. (8) is summarized in Algorithm 3.

5.2 SMC with reduced measurement components

In problems where the variance of the error in Eq. (8) is small or where the number of measurements is high, the computational cost of SMC is high because a large number of intermediate sampling steps is required to reach the posterior distribution. To improve the performance of SMC for such problems, we combine the method with the measurement reduction of Sect. 3. We first estimate the covariance matrix ${\mathbf {C}}_{hh}^0$ using the samples from the prior distribution at the initial step of the SMC method. The estimate of the covariance matrix is as follows:

$$\begin{aligned} {\mathbf {C}}_{hh}^0 = \frac{1}{N-1} \sum _{i=1}^N \left( {\mathbf {h}}_{i} - \varvec{\mu }_h^0 \right) \left( {\mathbf {h}}_{i}- \varvec{\mu }_h^0 \right) ^{{\mathrm {T}}} , \; \; \varvec{\mu }_h^0 = \frac{1}{N} \sum _{i=1}^N {\mathbf {h}}_{i} \, , \end{aligned}$$

(45)

where ${\mathbf {h}}_{i}$ is the output of the model with parameters $\varvec{\theta }_{i}$, i.e. ${\mathbf {h}}_{i}={\widetilde{G}}(\varvec{\theta }_{i})$, and $\varvec{\theta }_{i} \sim {\mathcal {N}}({\mathbf {0}},{\mathbf {I}})$. The matrix ${\mathbf {C}}_{hh}^0$ is decomposed to obtain the projection ${\mathbf {V}}_{{\mathrm {r}}}^0$. SMC is then applied to obtain samples from the posterior associated with the reduced measurement components:

$$\begin{aligned} f''_{{\mathrm {r}}}(\varvec{\theta }) \propto L_{{\mathrm {r}}}^0(\varvec{\theta }) f'(\varvec{\theta }) \, . \end{aligned}$$

(46)

The unnormalized weights with the reduced measurement components are evaluated as follows:

$$\begin{aligned} W_j = \exp \left( -(\beta _l-\beta _{l-1}) \Phi _{{\mathrm {r}}}^0(\varvec{\theta }_j) \right) \, , \end{aligned}$$

(47)

where $\Phi _{{\mathrm {r}}}^0(\varvec{\theta })$ is the reduced potential given in Eq. (22) with ${\mathbf {V}}_{{\mathrm {r}}}$ set to ${\mathbf {V}}_{{\mathrm {r}}}^0$. Moreover, the acceptance probability of the pCN algorithm is given by:

$$\begin{aligned} \alpha (\varvec{\theta },\varvec{\nu }) = \min \left\{ 1, \exp \left[ \beta _l(\Phi _{{\mathrm {r}}}^0(\varvec{\theta })-\Phi _{{\mathrm {r}}}^0(\varvec{\nu }))\right] \right\} \, . \end{aligned}$$

(48)

The SMC algorithm with reduced measurement components is presented in Algorithm 4.

We remark that in contrast to the IEKF approach with reduced measurement components, we do not update the estimate of the covariance matrix in the modified SMC approach. That is, we only estimate ${\mathbf {C}}_{hh}$ once with samples from the prior distribution of $\varvec{\theta }$. An alternative approach would be to update the estimate of the covariance matrix with samples from the posterior distribution based on the first projection and apply a bridging step (e.g. see Gelman and Meng 1998) to obtain samples from the next posterior distribution based on the new projection. We tested this procedure and observed that the additional bridging step may result in an increase of the total number of sampling steps and, hence, in an increased computational cost of the method, without a significant improvement of the obtained parameter estimate.

6 Numerical experiments

6.1 Model and parameters

We investigate the performance of the proposed algorithms with a numerical example. A hypothetical aquifer is simulated by a two-dimensional finite element groundwater model. The model specifications are taken from a numerical experiment presented in Huang et al. (2011), which is based on an actual field experiment. The model has a grid with 21 by 21 elements with a cell size of 1 by 1 meter (m).

The prior distribution of the log-hydraulic conductivity $\log ({\mathbf {K}})$ is modeled by a Gaussian random field with mean value of $-6.2$ and variance of 1.6. The spatial correlation structure is assumed to be exponential, hence the correlation $\rho _{ij}$ between the conductivity in element i and j is given by:

$$\begin{aligned} \rho _{ij}=\exp \left( - \frac{\Delta x_{ij}}{\lambda }\right) \, , \end{aligned}$$

(49)

where $\Delta x_{ij}$ is the Euclidean distance between the midpoints of elements i and j and $\lambda$ is the correlation length, which is set to 5 m in this example. The conductivities at the elements $\log ({\mathbf {K}})$ are modeled with a truncated KL expansion [cf. Eq. (5)], and we choose the truncation order k to ensure that 99% of the prior parameter variability is represented. This leads to $k=236$ instead of $n=441$ estimation parameters. 10 monitoring wells are placed in the model, the locations within the model are similar to the real field setup. A total of 7 hydraulic pumping tests is simulated with these wells, and, without consideration of the drawdown at the respective pumping well, a total of 70 steady state measurements are generated. The pumping rate for each test is set to 1. An overview of the mesh and the locations of pumping and monitoring wells is shown in Fig. 1. The true parameter values are generated by sampling from the prior distribution of $\log ({\mathbf {K}})$. The observations ${\mathbf {d}}$ are given by the model evaluation of the true parameter superimposed by a realization of a Gaussian measurement noise $\varvec{\epsilon } \sim {\mathcal {N}}(0, \sigma {\mathbf {I}})$, with noise level of $\sigma =0.05$. The realization of the $\log ({\mathbf {K}})$ field is shown in Fig. 2a.

To assess the quality of the results, we use two metrics. The first is the so-called relative error, related to the estimation parameters, which we define by:

$$\begin{aligned} {\mathrm {RelErr}}= \frac{|| {\mathbf {D}}_{{\mathrm {KL}}}^{1/2} (\varvec{\mu }_{\theta }-\varvec{\theta }_{{\mathrm {true}}})||_1}{|| {\mathbf {D}}_{{\mathrm {KL}}}^{1/2} \varvec{\theta }_{{\mathrm {true}}}||_1} \, , \end{aligned}$$

(50)

where ${\mathbf {D}}_{{\mathrm {KL}}}$ is the diagonal matrix of the eigenvalues in the KL expansion, $\varvec{\mu }_{\theta }$ is the estimate of the posterior mean of the random variables obtained by the respective method and $\varvec{\theta }_{{\mathrm {true}}}$ are the true variables. The second metric we introduce is the relative misfit between model output and measurements:

$$\begin{aligned} {\mathrm {RelMisfit}}= \frac{|| {\mathbf {C}}_{\epsilon \epsilon }^{-1/2} ({\mathbf {d}}-{\widetilde{G}}(\varvec{\mu }_{\theta }))||_2^2}{|| {\mathbf {C}}_{\epsilon \epsilon }^{-1/2} {\mathbf {d}}||_2^2} \, . \end{aligned}$$

(51)

For the SMC, the statistics of the errors are evaluated based on 50 independent simulation runs.

Fig. 1

Model mesh, monitoring and pumping wells

6.2 IEKF

6.2.1 IEKF with all measurements

As a base case, the complete set of 70 measurements from the numerical model are used for inversion. The convergence threshold $\delta$ is set to 0.001. The posterior of $\log ({\mathbf {K}})$ is shown in Fig. 2b and the match of the model outputs to the measurements is shown in Fig. 3a. By observation, IEKF is clearly capable of identifying the high and low K regions in-between the monitoring wells. As shown in Table 1, the minimum relative error achieved is 0.8731 and the final relative misfit is $3.6 \times 10^{-5}$. For obtaining this result, one gradient calculation per iteration and the solution of one adjoint system per measurement including the subsequent vector-matrix calculations on the element level were required. This results in $\underbrace{70}_{measurements} \times \underbrace{8}_{iterations} = 560$ adjoint system evaluations.

Fig. 2

$\log ({\mathbf {K}})$ fields. The black dots represent the measurement locations

Fig. 3

Model output versus measurements

6.2.2 IEKF with reduced measurement components

We now conduct the inversion with Algorithm 2. To obtain the projection, we separate the calculation and eigendecomposition of the observation covariance matrix for each of the 7 pumping tests. This is computationally favorable, since it decouples the calculation of the Jacobian matrix with respect to the eigenmodes and therefore avoids the solution of several adjoint systems per output sensitivity. The estimated mean of $\log ({\mathbf {K}})$, $\varvec{\mu }_{\theta }$, is shown in Fig. 2c and the match of the model outputs ${\widetilde{G}}(\varvec{\mu }_{\theta })$ to the measurements ${\mathbf {d}}$ is shown in Fig. 3b. The accuracy of the result decreases slightly compared to the solution in Fig. 2b, but the general features of the low and high K regions match well with the true solution. The input parameters defined for this algorithm and the obtained outputs are given in Table 1. It is worth pointing out the total computational effort. A total of

adjoint system evaluations was required, which is about 38 % of the effort of the case presented in Sect. 6.2.1, while losing accuracy with an increase of the relative error by about 1 %. The relative misfit increases from $3.6 \times 10^{-5}$ to $8.0 \times 10^{-4}$, which is also apparent when comparing Figs. 3a, b.

Table 1 In- and output parameters of the cases presented in Sects. 6.2.1 and 6.2.2

We remark that the IEKF approach with reduced measurement components has an additional computational cost due to the eigenmode decomposition of up to ${\mathcal {O}}(m^3)$ (Parlett 2000) per decomposition step, whereas the Jacobian calculation has complexity of ${\mathcal {O}}(n_h^{2} m_{{\mathrm {r}}})$. That is, the additional cost of the eigenmode decomposition becomes important in cases where $m \gg n_h$, (at least $> n_h^2$). This will hardly occur in problems that involve computationally intensive models (i.e. where $n_h$ is large). In the problem at hand, it is $m=70$ and $n_h = 484$ and, hence, this additional cost is negligible.

We conduct a parameter study to explore the influence of $\alpha$ through varying $\alpha$ between 0.75 and 0.99. The results, as presented in Fig. 4, show that the number of model evaluations increases with increasing $\alpha$, since the number of final eigenmodes increases from 7 to 32, but, as expected, the model error is reduced from 3% to a minimum of 0.1% compared to the base case with all measurements.

Fig. 4

IEKF with reduced measurement components: Variation of $\alpha$, $\eta =0.05$

6.3 SMC

The performance of the SMC algorithm is tested with the numerical example introduced in Sect. 6.1. Besides the relative error and the relative misfit, the number of sampling levels (tempering steps) is reported as a measure of the computational effort of the method. For all the study cases, except the study of the influence of number of samples [c.f. Sect. 6.3.3], the number of samples generated per level, N, is set to 2000 and the target effective sample size, is set to $\frac{N}{2}=1000$. The important input and output parameters are shown in Table 2.

Table 2 In- and output parameters of the cases presented in Sects. 6.3.1 to 6.3.3

6.3.1 SMC with all measurements

As a base case, the SMC was run for all 70 measurements. Figure 5a shows the average SMC result of all 50 independent simulation runs and Fig. 6a the model output using the average result. The average relative error obtained is 1.194, which is significantly larger than the corresponding IEKF result using all measurements. The relative misfit of the SMC solution is two magnitudes larger than the relative misfit of the IEKF solution. The number of levels averages to 39.6.

Fig. 5

$\log ({\mathbf {K}})$ fields, averaged from 50 independent simulation runs. The black dots represent the measurement locations

6.3.2 SMC with reduced measurement components

Figures 5b and 6b show the solution applying Algorithm 4 with $\alpha$ set to 0.95. The relative error is 1% higher, and the relative misfit is increases from $1.4 \times 10^-{3}$ to $5.8 \times 10^-{3}$. The inversion is about 10 % faster.

Fig. 6

Model output versus measurements

6.3.3 Parameter study

We conducted a parameter study to evaluate the influence of the most important parameters in Algorithm 4. It was performed with a Monte Carlo realization with smaller parameter variance (0.1 instead of 1.6) to limit the computation time for the different cases. A reference solution with IEKF was generated and is presented in Fig. 7a. The corresponding SMC solution is presented in Fig. 7b.

Fig. 7

$\log ({\mathbf {K}})$ fields with small variance. The black dots represent the measurement locations

Fig. 8

Relative error and relative misfit versus number of samples per level

Fig. 9

Influence of truncation threshold $\alpha$

In order to focus the investigation on the influence of the number of samples, instead of obtaining the observation covariance through sampling, SMC was run with constant model output eigenmodes obtained from the IEKF solution. Hence, the sampling error in the estimation of the reduced measurement components is eliminated. The model output truncation was chosen such that 99% of the model output variability was preserved (i.e., $\alpha =0.99$). As presented in Fig. 8, increasing the number of samples results in a better estimate, since the relative error decreases on average. However, one observes that the variability of the error remains constant as the samples per level increase further than 1500. The average relative misfit and its variability decrease until the number of samples per level reach 1500. Using larger sample sets, the estimate and variability of the relative misfit remain constant.

Furthermore, we vary the threshold $\alpha$ which is used to determine the number of eigenmodes in the projection. The relative error, the relative misfit and the number of levels over the different $\alpha$ are presented in Fig. 9. Using more eigenmodes decreases the relative misfit, but increases the variability of the relative error. This is related to the MCMC algorithm employed within each sampling step of the SMC approach. As the number of levels grows, the subsequent MCMC steps result in progressively correlated samples, which increases the variance of the posterior estimates based on the samples in the final level. Therefore, using less eigenmodes improves the solution, since it results in less tempering steps, and hence in a reduced uncertainty of the parameter estimates.

7 Concluding remarks

This paper presents a method that compresses measurement information from pumping tests and therefore accelerates groundwater parameter inversions. The method decomposes the model output covariance matrix and projects the measurements and model outputs on the eigenvector space corresponding to the largest eigenvalues. Therefore, it incorporates only essential information in the inversion process. The method is combined with the IEKF and SMC algorithms and modified versions of the algorithms are proposed that include reduced measurement information. The IEKF algorithm, which linearizes the relationship between measurement perturbation and parameters, relies on repeated evaluations of the sensitivity (Jacobian) matrix. The computational effort for evaluating the sensitivity matrix increases linearly with increase of the number of measurements. SMC, a sampling-based inversion method with importance sampling and move steps, yields samples from the posterior distribution of the parameters. The width of the likelihood function, describing the measurement information, decreases with increase of the measurement dimension, which leads to an increase of the number of sampling steps. Hence, a measurement reduction has potential for improvement of both inversion methods. As demonstrated by a numerical example, the inversion is generally faster than using all measurements with negligible loss of solution accuracy, provided that the parameters of the proposed algorithms are carefully chosen.

The benefit of the proposed approach increases with increase of both the size of the computational model and the number of measurements. For the IEKF method, this is because the computational cost per adjoint system evaluation is ${\mathcal {O}}(n_h^{2} m)$, where $n_h$ is the number of degrees of freedom of the computational model and m is the number of measurements. We note that the computational cost per eigenmode decomposition is up to ${\mathcal {O}}(m^3)$, so the computational benefit of the measurement reduction is more pronounced in cases where $m \ll n_h$. For large-scale inversion problems (large $n_h$) we expect that the additional computational cost of the eigendecomposition will be small compared to the computational gain. Another crucial aspect for an improved inversion process is the structure that governs the eigendecomposition. The standard approach is to collect the full model response dataset, form a covariance matrix, and then perform the decomposition. This implies that each eigenvector contains information on all pumping tests together. When the IEKF method is applied with relatively large numbers of pumping tests and small numbers of data per pumping test, the eigendecomposition should be conducted separately for each pumping test, as this decreases the cost required for evaluating the sensitivity matrix of the projected responses.

Another aspect we address in the paper is the frequency of the covariance calculations for obtaining an optimal measurement reduction. Since the prior distribution of the model parameters can differ considerably from their posterior distribution, the measurement reduction based on the prior distribution might not reflect the true behavior of the measurement correlation. Therefore, in the modified IEKF algorithm, we propose to update the response covariance matrix frequently throughout the inversion process, whenever the projection becomes too inaccurate (see Algorithm 2). Regarding the modified SMC algorithm, we observed that updating the covariance matrix leads to additional sampling steps and, hence, increased computational costs compared to the standard SMC algorithm. Hence, we recommend to form the observation covariance matrix with samples from the prior conductivity distribution and employ this first estimate in the updating process (see Algorithm 4).

Comparing the computational cost of the two inversion methods in the worked numerical example, we observe that the IEKF, although being a linearization method, performed significantly better than the SMC approach. In particular, the high variance of the estimated K field did not seem to impose a large problem for the IEKF approach, which obtained an accurate parameter estimate in a small number of iterations. In contrast, the SMC method required more sampling iterations and resulted in parameter estimates with significant associated uncertainty. The modified SMC method could be improved by changing the move step through the implementation of a more efficient MCMC algorithm, e.g. which includes gradient information (Roberts et al. 1996; Cui et al. 2016; Rudolf and Sprungk 2018). This could potentially decrease the required samples per level to obtain an accurate approximation of the posterior. Another sampling-based inversion method worth investigating in this context is the ensemble Kalman filter. This method has recently found popularity in Bayesian inverse problems and its performance can potentially profit from a reduced measurement set.