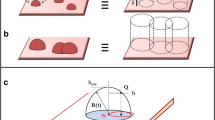
Abstract
The theory of the diffusion limited electrochemical nucleation and growth of a deposit consisting of isolated 3D hemispherical nuclei has been re-analysed. The analysis focuses on a widely discussed model which assumes formation of “diffusion zones” around the growing nuclei. It has been proposed in the literature that the deposit-free fraction of the surface area of the substrate can be directly calculated from the substrate coverage with the “diffusion zones”. The aim of this work is to analyse whether such an approach can be applied for the growth of isolated 3D hemispherical nuclei. This is accomplished by evaluation of equations which describe nuclei radii at various stages of the deposition process. The formulae allow determining the substrate surface coverage with the growing deposit. This, in turn, allows simulating and analysing faradaic currents due to other than the electrodeposition reactions which take place at the deposit-free fraction of the substrate surface. Both instantaneous and progressive modes of the nucleation are discussed and the influence of the nucleation type on the faradaic currents is outlined. A comparison with other approaches reported in the literature indicates that the deposit-free fraction of the substrate surface may not always be determined by means of recalculation of the substrate coverage with the “diffusion zones”.
Graphical abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Formation of a new phase via electrochemical deposition is a well-recognised process frequently analysed by electrochemists. It often follows nucleation and growth mechanism and there are numerous papers, which deal with its mathematical description [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15]. One of the frequently applied models assumes formation of 3D hemispherical nuclei which growth is limited by diffusion of the electroactive species from the bulk of the electrolyte [1, 2, 16, 17]. An analysis of the electric current recorded during potentiostatic electrodeposition seems to be relatively simple as long as the plating process is not accompanied by other faradaic reactions which take place at the electrode studied. Deposition of numerous metals and alloys is, however, often accompanied by other faradaic reactions, including hydrogen evolution reaction, HER [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]. The latter may take place at the surface of the growing deposit [18, 24, 26,27,28,29, 35, 36], at the surface of the substrate free from the deposit [37,38,39] or at both [31, 40, 41]. A proper analysis of the electric currents recorded for such systems requires determination of the substrate surface coverage with the deposit and/or the real surface area of the latter.
A mathematical model, describing total measured electric current in a system where electrodeposition of the metal is accompanied by HER which occurs at the surface of the deposit was introduced in [18]. This approach was subsequently used in analysis of numerous systems, including those where faradaic reactions other than HER take place parallel to the deposition [26,27,28,29, 35, 36, 42,43,44,45,46,47,48,49]. This approach focuses on determination of the real surface area of the growing deposit and is applicable when catalytic activity of the substrate towards the hydrogen evolution is insignificant as compared to the deposit. Such substrates may include carbon-based materials with high HER overpotentials [18, 26, 43, 47]. Systems with the substrate activity towards HER or other faradaic reaction significantly higher than the activity of the deposit are less common but not unlikely [37,38,39, 50, 51]. A mathematical description of the currents recorded under such conditions was discussed in [37,38,39]. This is a modification of the approach introduced in [18] and includes the problem of determination of the substrate surface area free from the deposit.
In this manuscript, we re-analyse a system where a faradaic reaction takes place on a substrate surface simultaneously to the electrodeposition process. A mathematical analysis of well-known equations describing the nucleation and growth process [2, 16, 17] is reported. It is aimed at determination of the radii of the growing nuclei, and, consequently at calculation of the substrate surface coverage with the deposit. The latter parameter allows calculating currents originating from other than the electrodeposition faradaic reactions which take place at the deposit-free surface of the substrate at the same time as the plating process.
Mathematical Analysis and Discussion
General Considerations
The model in question assumes potentiostatic formation and growth of isolated 3D hemispherical nuclei which are fed by mass fluxes driven by diffusion from the bulk of the electrolyte [1, 2, 10, 16, 17, 52, 53]. For the sake of simplicity, we do not consider adsorption, surface diffusion and aggregation of the ad-atoms formed during the electrodeposition [54,55,56,57,58,59,60,61]. We also disregard kinetic control of the deposition process at its very early stages [62,63,64]. In the following section of the text, we refer to Eqs. (1)–(9) which are already well known and which have been derived and introduced many years ago by other authors (e.g. [2, 16, 17]). Therefore, the text does not contain derivation of such equations and the reader is referred elsewhere for details (e.g. [2, 16, 17, 65,66,67] and Supplementary information file). Here, we focus on the aspects most important in discussion of the equations.
It is assumed that the early stages of the process of the growth of the nuclei are controlled by mass transport from the electrolyte which is described by spherical diffusion flux, Js, [2, 16, 17, 68]. Such an effect is observed for isolated 3D nanoparticles [69]. Under such condition, the radius of the isolated nucleus is given by a well-known Eq. (1) [2, 17, 66, 67] (Sects. S1–S3 in the Supplementary information):
where D is the diffusion coefficient of the electroactive species which concentration in the bulk of the electrolyte is equal to c. M and ρ represent molar mass and density of the newly formed phase, respectively. This equation predicts development of the radius according to t1/2 law, in agreement with diffusion limited growth of the isolated nucleus [8, 10, 14, 18, 62, 66, 70,71,72,73,74,75,76,77,78]. In order to distinguish rh values determined by various equations, this parameter is marked with a roman number, depending on the determination method.
It is further assumed [2, 4, 16, 17, 79] that Js must be equal to a respective linear diffusion flux under planar geometry conditions, Jp. The latter represents the mass flow across a flat plane parallel to the electrode surface. This plane is referred to as “diffusion zone” or “depleted zone” [2, 9, 10, 17, 61, 62, 73, 76, 79,80,81,82] and its area is equal to Ap. Jp supplies mass to the isolated nucleus with the same rate as the spherical diffusion flux, according to Eq. (2) [1, 2, 16, 17, 79, 83] (Sect. S1 in the Supplementary information):
where Ah denotes the surface area of the hemispherical nucleus exposed to the electrolyte. When Jp is given by the Cottrell Eq. (3) [84] one obtains another well-established Eq. (4) [2, 16, 17, 65] (Sects. S2–S3 in the Supplementary information) which shows variation of the “diffusion zone” radius, rp, with time:
It is important to stress that rh and rp represent two separate parameters: rp is always higher than rh [85] due to the fact that the former represents a “flat” plane which experiences the same mass transport as the hemisphere with the radius of rh and area of Ah [2, 16, 17].
The electric current due to formation and growth of N0 isolated nuclei at a constant applied potential, Idep, is given by Eq. (5). It represents the Cottrell equation corrected for the electrode surface coverage with the “diffusion zones”, θd [2, 7, 17, 86]:
where A is the electrode surface area. Determination of θd was discussed extensively in many papers [1, 2, 16, 76, 87,88,89]. It is assumed that θd cannot be considered as an algebraic sum of Ap because the “diffusion zones” are expected to overlap [2, 9, 16, 76, 79, 82, 86, 90]. This problem was addressed by application of the Avrami theorem [1, 2, 16, 17, 82, 87, 88, 91,92,93,94,95] and by introduction of the idea of the “expectation number”, E, or the “extended surface coverage” (“extended area”) [2, 5, 16,17,18, 51, 64, 71, 76, 83, 86, 88, 89, 93, 96,97,98,99]. E mirrors the probability of covering of a certain point at the electrode surface by the “diffusion zones” while the “extended area” represents the electrode surface coverage with the “diffusion zones” when they do not overlap [5, 17, 64, 71, 79, 83, 98, 100]. These two approaches may lead to substantially the same final result [5, 97, 101].
When the nucleation rate is given by Eq. (6) [1, 2, 7, 9, 16, 17, 64] one obtains Eq. (7) [1, 2, 16, 17] (Sect. S4 in the Supplementary information):
where g is the nucleation rate, N represents the density of active sites available for the nucleation while N0 stands for the maximum number density of the nucleation centres. Both N and N0 are given in respect to the substrate area. The θd is then given by Eq. (8) [71, 73, 79, 81, 96, 100]:
Instantaneous Nucleation
Instantaneous nucleation takes place when the nucleation rate in Eq. (6) is infinitely high (g → ∞) [1, 7, 16, 96, 100]. All the nuclei were “born” at the same time of t = 0 and their number, expressed as a density per surface area unit, N0, remains unchanged since then. Consequently, all the nuclei are expected to have the same average radius of rh at a given time of t [102]. It is worth to note that one of the advantages of the instantaneous nucleation approach lies in the fact that all the nuclei are of the same age and, consequently, thicknesses of their diffusion layers are the same as well [1, 76, 101].
For the instantaneous nucleation case the “expectation number” can be simplified to the following equation (Eq. (9)) [71, 73, 79, 81, 96, 100]:
A combination of Eqs. (5) and (9) gives Eq. (10) [7, 73, 76, 79] which predicts the deposition current with a well-known shape of a highly distorted peak:
The Idep and θd values calculated using Eqs. (9) and (10) are plotted in Fig. 1. The values of the parameters used in the calculations are listed in Table 1. We assume typical values of N0 [7, 17, 77, 103] and D [9, 18, 22, 77, 84, 103]. Figure 1 shows that at a sufficiently long time, all the “diffusion zones” can be considered merged (θd approaches unity). A continuous plane depleted with the electroactive species and with the area equal to A is formed [2, 69]. Since then, the current can be approximated by semi-infinite linear diffusion across this continuous plane (Eq. (3)) [1, 2, 17, 18, 52, 54, 69, 76, 89, 100] (inset in Fig. 1). It is worth to note that θd tends to unity asymptotically (Eqs. (8) and (9)) and selection of the time point for which the “diffusion zones” can be considered as completely merged is always somewhat arbitrarily.
Top panel: the substrate surface coverage with the “diffusion zones”, θd, calculated with Eqs. (9) and (26) for the instantaneous and for the progressive nucleation, respectively. Bottom panel: nucleation and growth current, Idep, calculated using Eq. (10) (instantaneous nucleation) and a combination of Eqs. (26) and (27) (progressive nucleation). The inset in the bottom panel shows a comparison of Idep with the current given by the Cottrell equation for semi-infinite diffusion across a plane with the area equal to the electrode surface area (Eq. (3)). Table 1 lists the values of the respective parameters used in the calculations
Determination of the substrate coverage with the deposit requires knowledge on the proper value of the nuclei radii. It is then interesting to evaluate whether Eq. (1) properly represents the true nucleus radius. Integration of Idep allows determining the average value of the radius of N0 completely isolated nuclei whose growth generates the flow of the current given by Eq. (10) [61, 88, 104]. For the hemispherical nuclei, this yields the following Eq. (11) (cf. [105]):
where Q(t) is the charge obtained from the integration of the current while rh denotes the average radius determined exclusively using Eq. (11). Validity of the approach represented by Eq. (10) was confirmed experimentally by numerous works (e.g. [17, 18, 21, 50, 53, 58, 72, 100, 106,107,108,109,110]).
Figure 2a plots rh values as a function of time together with r'h calculated with Eq. (1). The rate of the nucleus growth decreases with time, in agreement with other works (e.g. [13, 52, 88, 103, 111,112,113]). It follows then that r'h correctly mirrors rh values only at a very short deposition time. At longer deposition time the radius expressed by Eq. (1) becomes significantly higher than the one given by Eq. (11). This effect is attributed to the overlap of the “diffusion zones” and interaction between nuclei (“collisions”) [88]. The extent of the latter depends on the nuclei shape (hemispherical or ellipsoidal) [88]. It leads to a change in the mathematical law which governs the nucleus growth (Fig. 2b). It is important to note that such an effect is observed well before complete merging of the “diffusion zones” (θd < 1) (cf. upper abscissa axis in Fig. 2a). Experimental results [72, 111] and simulations [77, 78] show a similar evolution of the nuclei growth kinetics for electrodeposition processes. Such an effect was reported also for galvanic displacement deposition of metals on semiconductors [114].
a The average nucleus radius calculated using Eq. (11) (rh) and Eq. (1) (r'h) as a function of time (bottom abscissa axis) and θd (top abscissa axis). Note that θd tends to unity asymptotically (Eq. (9)) and selection of the point at which the coverage can be considered as equal to unity is arbitrarily. b The same as a but in the double logarithmic scale. The parameters used in the computations are listed in Table 1
The time-dependent difference between rh and r'h values is explained by the fact that Ap used in derivation of Eq. (2) is not corrected for the overlap of the “diffusion zones” and nuclei [88]. In order to maintain the mass supply predicted by Eq. (2), the mass flow across the areas where n “diffusion zones” overlap must be n times higher than for non-overlapping “diffusion zone”. Thus, the mass fluxes across the light grey and the dark grey areas in Fig. 3 should be twice and three times as large as the flux across the non-overlapping sections of the “diffusion zones”, respectively. This, however is not possible because the mass flux across Ap is limited by the semi-infinite diffusion and cannot be higher that the one resulting from the respective concentration gradient. After overlapping the “true” Ap value across which the mass is supplied to a given nucleus with the rate predicted by the Cottrell equation is smaller than the value calculated using Eq. (4). As a consequence, the “true” linear diffusion flux across the “diffusion zone” with the area equal to the “true” Ap value is too small as to maintain the r'h growth given by a combination of Eqs. (1) and (2) [52]. The overlap is insignificant only at the early stages of the deposition process, when the “diffusion zones” radii are very small. It was assumed that for θd approaching unity, the nuclei growth is no longer proportional to t1/2 [62, 73, 74] and the nucleus radius is expressed as a function of t1/6 [7, 18, 52, 75, 111, 114].
In order to better understand difference between Eqs. (1) and (11), we analyse the mass flows which feed a separate nuclei. At the beginning of the deposition process the nuclei are so small that they are completely isolated and no interaction between them needs to be considered [88]. As a result, they are considered as perfectly hemispherical and distortion from such shape due to the nuclei interaction [88, 93] is disregarded. We assume that each of the nuclei “owns” its own fraction of θd across which the mass is supplied exclusively to the given nuclei, θ'd. θ'd grows with time simultaneously to rh and is given by Eq. (12):
The mass flux which passes across θ'd represents the average mass flow which may feed single nucleus. This flux is driven by linear semi-infinite diffusion (planar geometry) which is given by the Cottrell equation (Eq. (3)). By analogy with Eq. (5), one may equalise growth of mass of the hemispherical nucleus, m, with the mass supply given by a combination of Eqs. (3) and (5). This leads to Eq. (13):
We denote the radius determined using Eq. (13) as r''h.
Separation of variables and subsequent integration of Eq. (13) yields Eq. (14) and, consequently, Eq. (15) which shows variation of the average value of r''h with time:
where erf is the error function [115]. Substantially the same type of equation can be obtained by integration of Eq. (10) but, in our opinion, the approach based on Eqs. (13)–(15) better explains why Eq. (1) cannot mirror properly the nucleus radius. The above equations indicate that at longer time the nuclei growth deviates from t1/2 law predicted by Eq. (1), in agreement with [88]. The respective r''h values are plotted in Fig. 4 together with rh. The figure clearly shows that r''h approximates rh values much more accurately than r'h calculated with Eq. (1) (cf. Fig. 2).
The average nucleus radius calculated using Eq. (11) (rh), Eq. (15) (r''h for θd < 0.998) and Eq. (19) (r'''h for θd > 0.998). Right panel: magnification for short deposition time, the parameters used in the calculations are collected in Table 1. Inset in the left panel (double logarithmic plot): a comparison of r'''h (Eq. (19)) with the “true” t1/6 law (solid blue line, calculated with Eq. (19) but for k = 0)
At a sufficiently long time, tm, the “diffusion zones” become completely merged, and form a continuous “depleted” plane with the area equal to the area of the electrode, A (θd approaches unity, Fig. 1 and Eq. (9)). Under such conditions, the areas of the “depleted zones” cannot grow further and, consequently, θ'd reaches its maximum value and becomes time independent. Equation (15) is still applicable but its use is somewhat complicated by the need of use of the error functions. Therefore, another equation which is valid at deposition time sufficiently long as to assume complete merging of the “diffusion zones” is proposed below.
It is assumed that after complete merging of the “diffusion zones” the total mass flux across the plane with the area of A must be “split” into individual mass fluxes which separately feed each of the isolated nuclei. We also assume that under such conditions each of the growing nuclei “owns” its own fraction of the area of A, AN, equal to N0−1. The latter is a time-independent value and replaces time-dependent θ'd in Eq. (13) at t > tm. This indicates a transition in the nucleus growth kinetics when the time approaches tm, in agreement with [18]. The mass gain, dm, of a single nucleus due to linear diffusion in a time window between tm and t > tm is given by Eq. (17) which comes from integration of Eq. (16):
The above equations account for the concentration profile developed between t = 0 and t and represent a difference between the two mass gains: the one between t = 0 and t > tm (B·t1/2) and another one between t = 0 and tm (Btm1/2). The first of them shows what the mass gain would be at t > tm if the process was controlled by linear diffusion from the beginning. Or, in other words, if the mass flux computed using Cottrell Eq. (3) for the area of AN was applicable starting from t = 0. The same conditions are applicable to the second term of Eq. (17) except the time window which spans from t = 0 to tm. The difference between these two terms shows the mass gain at t > tm when the process is described by linear diffusion across AN. The nucleus volume, V, at t > tm is then given by Eq. (18):
where r'''h denotes the average nucleus radius at t > tm while V0 stands for the nucleus volume developed at time window which spans from t = 0 to t = tm. Thus, the V0 mirrors the mass deposited until tm is reached, i.e. before Eq. (17) can be applied and before the “diffusion zones” can be considered as completely merged. The respective V0 value can be computed using r''h given by Eq. (15). A rearrangement of Eq. (18) yields the following relationship between r'''h and time, valid for t > tm (Eq. (19)):
where k is a parameter equal to difference between V0 and Btm1/2/ρ. The r'''h growth mirrored by Eq. (19) slightly violates from the t1/6 law predicted by other authors [7, 18, 111] but the difference vanishes with time when the first term in the brackets becomes dominating over k (inset in Fig. 4). The tm value can be determined as a time at which the current predicted by the Cottrell Eq. (3) overlaps the current profile given by Eq. (10) (Fig. 1, inset in the bottom panel). This judgement, however, is always somewhat arbitrary and k in Eq. (19) can be considered as a fitted parameter. Figure 4 shows r'''h obtained by fitting rh (Eq. (7)) with Eq. (19). It follows that the latter equation correctly approximates the average nucleus radius given by Eq. (11). An analysis of the fitted parameter k shows that the transition from the nucleus growth law given by Eq. (15) to the regime expressed by Eq. (19) takes place for θd of ca. 0.998 and a time of ca. 0.056 s (calculated for the parameters listed in Table 1).
The Electrode Surface Coverage with the Deposit Under Instantaneous Nucleation Conditions
The average radius of the nucleus obtained from the numerical integration of the current profile, rh (Eq. (11)), can be recalculated into the electrode surface coverage with the deposit, θh, using Eq. (20):
When N0 is expressed as the number of the nuclei per the surface area unit, the above equation yields a dimensionless value of θh. Derivation of Eq. (20) is based on an assumption that the electrode surface area covered with the deposit is equal to the algebraic sum of the areas of the bases of N0A isolated hemispherical nuclei. It is important to stress that this approach does not include effects of the nuclei overlap. Such an overlap, however, can be considered unimportant at early stages of the deposition process when the nuclei are relatively small and the probability of their overlap is very small as well [18, 70, 116]. Consequently, the surface coverage with the deposit containing the nuclei with the average radius of r''h (Eq. (15)), θ''h, at t < tm can be approximated by Eq. (21):
Equation (21) is valid for a short deposition time and, similarly to Eq. (20), does not include overlapping of the nuclei. Probability of the latter effect increases with the nuclei growth time [117] and randomness of the nuclei distribution [88]. When the nuclei are ordered in a lattice, the overlap effects are absent as long as distances between the islands are higher than the double of their radii. This work analyses random nuclei distribution for which the overlap is expected to take place earlier than for ordered systems although at the very beginning of the process its importance is negligible [88]. The overlapping nuclei form “merged” structures [6, 16, 71, 118, 119] which may contain distorted hemispheres. The bases of such hemispheres are smaller than those for isolated ones. Therefore, the “true” value of θh decreases when the extent of the nuclei overlapping increases.
At this point, it is worth to compare the effect of the nuclei overlapping with discussed earlier overlapping of the “diffusion zones”. The radii of the “diffusion zones” grow with time and at one point, the sum of the areas of the “zones” exceeds the electrode surface area. This leads to unrealistically high mass flux towards the electrode which is corrected by introduction of the overlapping idea. The latter approach allows determining the realistic, “true” mass flux and, consequently, leads to the equation which expresses the electrodeposition current (Eq. (10)). In contrast to the “diffusion zones”, the analysis of the nuclei overlap is conducted by an assumption that the mass flux towards the electrode is governed solely by Eq. (10) and is independent on the extent of the nuclei overlap. In other words, all mass supplied to the electrode by the flux expressed by Eq. (10) must be converted into the deposit regardless of the nuclei arrangement and overlap. As a result, the overlap of the “diffusion zones” is calculated using the “zone” radii as it would be without the overlapping (Eq. (3)) while for the nuclei itself their actual, mean radius value is used in the calculations. Such an approach allows determining nuclei overlap without changes in their volumes and masses.
The nuclei overlap leads to a change in the substrate surface coverage with the deposit and affects shape and size of the nuclei. Thus, lateral growth of the nuclei at the overlapping interfaces is terminated but the growth in direction perpendicular to the electrode surface is expected to be continued. This results in a distorted shape of the overlapping nuclei with radii departing from the mean value. The overlap is accounted for by assuming that Poisson statistics expresses probability that a point at the electrode surface is not covered by any of N0 2D circles [101, 120]. The latter are the bases of the hemispherical nuclei and their average radius grows with time according to Eq. (15) or (19). The “extended area”, θex, is given here by a ratio of sums of areas of the bases to the total electrode area [5, 101]. Thus, in contrast to the “diffusion zones” problem, the nuclei overlap approach is focused on the changes in the substrate coverage with the deposit while the overall mass flux remains unaffected. Validity of application of such approach to the overlapping nuclei generated under instantaneous nucleation conditions was confirmed in [101]. Similarly to Eqs. (S12) and (S13) in the Supplementary information, θex is calculated as an algebraic sum of the areas of the bases of the nuclei with the average radius of r'''h (Eq. (19)) [5, 97, 101] and is expressed in respect to the electrode surface area of A. This yields Eq. (22):
It is important to stress that for a given time, the θex and θh values are determined only by the respective current values of rh, r''h or r'''h. Consequently, the electrode surface coverage with the deposit containing overlapping hemispherical nuclei with the average radius of r'''h at t > tm is given by Eq. (23):
Here, we consider that the volume of the nucleus is independent on whether it overlaps with other nuclei or grows completely isolated. This is caused by the fact that the whole mass transported to the electrode by the flux given by Eqs. (16) and (17) must be transformed into the deposit and this is independent on the extent of the nuclei overlap.
The fraction of the surface area of the electrode which is free from the deposit, θf, is given by Eq. (24) [81]:
where θxh denotes θh, θ''h or θ'''h, depending on the method of the nucleus radius determination (the same nomenclature is applied also to θxf). θ''f (Eqs. (21) and (24)) is calculated for θd < 0.998 while θ'''f (Eqs. (23) and (24)) is computed for θd > 0.998. Such calculated θxf values are plotted in Fig. 5. As expected, at a short deposition time, both θ''f and θ'''f properly approximate θf values. This indicates that under such conditions, the nuclei overlap can be considered insignificant. At a longer deposition time, the θ'''f becomes greater than θf and for the deposition time of 1 h (θf of 0.70), this difference reaches ca. 16%. This effect is attributed to the fact that, in contrast to θ'''f, the θf does not include overlap of the nuclei. Without the overlap both θ'''f and θf would have the same values, as follows from Fig. 4.
Fraction of the substrate surface free from the deposit from various methods of calculation. Left panel and instantaneous nucleation: θf: a combination of Eq. (24) with Eq. (20); θ''f and θ'''f: a combination of Eq. (24) with Eq. (21) (θd < 0.998) and Eq. (23) (θd > 0.998). Inset in left panel: magnification for short deposition time. Right panel and progressive nucleation: θIVf and θVf determined according to the “Progressive Nucleation” section. Table 1 collects the parameters used in the computations
Progressive Nucleation
The progressive nucleation case (very low g values) is complicated by the fact that the mass supply to a given nucleus is changed when a new nucleus appears in the substrate surface region covered by the “diffusion zone” of the older nucleus. The newly born nucleus takes over a fraction of the mass flux of the older one and this somewhat reduces rate of the growth of the latter. In order to simplify calculations, we assume that the growth of the number of the nuclei can be approximated by a linear equation used in [7, 17, 100] (Eq. (25)):
This leads to the θd given by Eq. (26) [100, 121]:
The deposition current is then given by Eq. (27):
Term 4/3 in Eq. (27) comes from an approach proposed in [76] for the progressive nucleation case and is aimed at equalisation of thicknesses of diffusion layers for the nuclei of various age [1, 76]. As it was shown in [76], the current given by Eq. (27) exceeds the one represented by the Cottrell equation [76]. The current and the substrate surface coverage with the “diffusion zones” calculated using Eqs. (26) and (27) are included in Fig. 1.
The mass supplied to the electrode in a time window of Δt is distributed between all existing nuclei, both the oldest ones (born at t = 0) and those recently born. The number of the nuclei existing at a time of t is given by Eq. (25) and the average mass gain of single nucleus during the time interval of Δt is represented by Eq. (28):
where ΔQ'(t) is the charge obtained from numerical integration of Eq. (27) for time window which spans from t-Δt to t. In reality, the mass gain varies with the nucleus and depends on its “diffusion zone” area which, in turn, is a function of the nucleus age and the extent of the “diffusion zones” overlap. Therefore, the approach given by Eq. (28) represents the mass gain close to that typical for the nuclei of an average age. The total mass, m, supplied to a nucleus born at time of u and counted up to time of t is equal to (Eq. (29)):
Consequently, its radius is given by Eq. (30):
It can be approximated that at a given time of t the substrate surface is covered by a set of nuclei formed during each time interval equal to Δt. Average radii of these nuclei are given by Eq. (31):
where terms in the brackets represent the average radii of the nuclei, rIVh (Eq. (30)), born within time windows given by the lower limits of the summation, i.e. lasting from 0 to Δt, from Δt to 2Δt etc. ΔN denotes number of the nuclei which are born within the same Δt interval. The topmost term shows the oldest nuclei while the bottom one represents the youngest nuclei. Equation (25) shows that ΔN is the same for all time windows of the same duration. Consequently, Eq. (31) presents a range of the radii of the nuclei which are present at the substrate surface at given time equal to t. Owing to the fact that all ΔN are the same, one may calculate the average radius of the nuclei existing at given time of t, rIVhav as an arithmetic mean of the radii given in the brackets in Eq. (31). These values are calculated in respect to the number of Δt intervals. Figure 6 shows time evolution of average rIVh of the oldest nuclei, i.e. born at t = 0, over a time period covering multiple Δt intervals (Fig. 6b); distribution of rIVh of nuclei of all ages existing at an arbitrarily selected time (i.e. 1.5–620 s, Fig. 6a) and the nucleus radius averaged over all nuclei of all ages present at the electrode surface at given deposition time, rIVhav (Fig. 6b). The latter plot was constructed on the basis of the same type of data as shown in Fig. 6a for various deposition times, given in the abscissa axis. The values of the parameters used in the calculations are listed in Table 1, the assumed g value is amongst the lowest reported in the literature [18, 121].
a Distribution of rIVh of nuclei of all ages existing at various deposition times (each rIVh calculated using Eq. (30)). b Time evolution of the average radius, rIVh, of the oldest nuclei (born at t = 0) calculated using Eq. (30) and average nucleus radius, r.IVhav, calculated for each deposition time as an arithmetic mean of Eq. (31). Left panel: magnification for short time. Data calculated using parameters listed in Table 1
A comparison of Figs. 4 and 6 shows that under the progressive nucleation conditions, the rate of growth of single nucleus decreases with time faster than for the instantaneous case. This is caused by the fact that under progressive nucleation conditions, the mass transport towards a single nuclei is decelerated not only by expansion of the diffusion layers but also by the appearance of new nuclei which take over fractions of the mass flux supplying older nuclei. As a result, the radius averaged over all nuclei present at a given time at the substrate surface decreases with time after an initial increase (Fig. 6b). The rIVhav shown in Fig. 6b allows calculating the electrode coverage with the deposit as a sum of areas of bases of non-overlapping hemispheroids, θhIV (cf. Eq. (20)). The latter value may be used for calculation of θex in Eqs. (S12) and (S13) [5, 97, 101] leading to the overlap-corrected coverage θhV. Consequently, the deposit free fraction of the substrate surface, θIVf and θVf, can be determined using Eq. (24). These values are plotted in Fig. 5. Due to continuously growing number of the nuclei the deposit-free fraction of the substrate surface in the progressive nucleation decreases faster than for the instantaneous case. This is independent on whether the nuclei overlap correction is applied or not.
Faradaic Reactions Taking Place at the Deposit-free Fraction of the Surface
Knowing the electrode surface coverage with the deposit one may calculate the current originating from a faradaic reaction, which takes place at the section of the electrode surface, which is free from the deposit, Iother. This reaction occurs parallel to the electrodeposition process and the total current measured for such a system, Itot, is expressed by Eq. (32):
where jother is the current density of other than the electrodeposition reaction at a given potential value while Idep is the electrodeposition current given by Eq. (10) (instantaneous nucleation) or Eqs. (26) and (27) (progressive nucleation). θxf in Eq. (32) stands for θf, θ''f, θ'''f, θIVf or θVf and is given by a combination of Eq. (24) with Eqs. (20), (21) or (23) for the instantaneous case while for the progressive nucleation is calculated according to the description in the “Progressive Nucleation” section. Similarly to Fig. 4, the θ''f and θ'''f are calculated for θd < 0.998 and for θd > 0.998, respectively. The respective plots showing all components of the measured electric current are shown in Fig. 7a (instantaneous nucleation) and Fig. 7b (progressive case). It follows that the progressive nucleation leads to a decay in Iother which is faster than for the instantaneous case. The contribution from Idep to the total measured current depends on the nucleation type. Initially, instantaneous Idep is significantly higher than the respective current under progressive nucleation conditions. For both nucleation modes, the Idep decreases with time significantly faster than Iother and, for a sufficiently long deposition time, Iother strongly prevails over Idep.
Currents due to the electrodeposition, Idep, due to the other faradaic reaction taking place at the substrate surface free from the deposit, Iother, (Eq. (32)) and the total current, Itot, (Eq. (32)). a Instantaneous nucleation: Idep from Eq. (10), Iother calculated using θ''f (Eqs. (21) and (24), θd < 0.998) and θ'''f (Eqs. (23) and (24), θd > 0.998). b Progressive nucleation: Idep from Eqs. (26) and (27), Iother calculated using θVf determined in the same way as for Fig. 5. Inset: magnification of Iother for short time, the parameters used in the calculations are collected in Table 1. Note axis breaks for the current and the time coordinates
Comparison with Other Approaches
An approach discussed in [18] assumes that the surface area of the growing deposit constituted of isolated 3D hemispherical nuclei, S(t), can be calculated on the basis of the θd value, according to Eq. (33):
This approach was further developed by other authors with the aim to determine the fraction of the electrode surface area free from the deposit. It was assumed that the latter can be calculated using Eq. (34) [37,38,39] or Eq. (35) [40, 41]:
θVIf and θVIIf values were obtained by combining Eqs. (34) and (35) with Eq. (9) (instantaneous nucleation) or with Eq. (26) (progressive nucleation). Such calculated values are plotted in Fig. 8 together with θf calculated for the instantaneous (Eqs. (20) and (24)) and for the progressive case (“Progressive Nucleation” section). It follows that θIVf and θVf decrease much faster than θf for both the instantaneous and the progressive case. A comparison with Fig. 5 clearly shows that this difference cannot be attributed to the effect of the “diffusion zones” overlap only.
Deposit-free fraction of the substrate surface area for various methods of θxf determination. Left panel – instantaneous nucleation: θVIf: Eq. (34) combined with Eq. (9); θVIIf: Eq. (35) combined with Eq. (9). Right panel: progressive nucleation: θVIf: Eq. (34) combined with Eq. (26); θVIIf: Eq. (35) combined with Eq. (26). θ''f and θVf taken from Fig. 5. Table 1 collects parameters used in the calculations. Note axis break for the θxf coordinate
The θxf values determined on the basis of Eqs. (34) and (35) allow calculating Iother and, consequently Itot, using Eq. (32). Such calculated currents are shown in Fig. 9 together with the current calculated using Eq. (32). The latter was determined using θ''f and θ'''f computed with Eqs. (21), (23) and (24) and using θ'''f determined as described in “Progressive Nucleation” section. All reported Itot values were calculated using the set of the parameters listed in Table 1. Figure 9 clearly shows differences between the currents calculated using θ''f and θ'''f and those determined using the deposit-free fractions of the substrate surface expressed by Eqs. (34) and (35). The difference is significantly higher for the progressive case owing to the fact that θf decreases with time faster than for the instantaneous nucleation.
Total currents due to the electrodeposition and the other faradaic reaction, Itot, calculated using Eq. (32) and respective θxf values taken from Fig. 5. Left panel: instantaneous nucleation, right panel: progressive nucleation. Insets: magnification for short time. The parameters used in the calculations are collected in Table 1
The above-presented analysis was carried out for two limiting cases, i.e. for the instantaneous and the progressive nucleation, but the conclusions can be extended also to intermediate cases, i.e. for moderate values of g. It follows that Eqs. (34) and (35) predict the reduction of the deposit-free substrate area which is too fast as to be attributed to the discussed model of the growth of the 3D hemispherical nuclei. In fact, both these equations give the rate of θxf decrease the same as the rate of the θh increase. This seems to be possible when the area of the base of the nucleus grows significantly faster than its height, i.e. when the lateral growth of the nuclei becomes faster at the expense of the vertical growth. This can be considered as quasi 2D growth when the deposit free fraction of the substrate surface is reduced significantly faster than for 3D nuclei growth under conditions of the same lateral and vertical rates. It is worth to note here that the Cottrell equation, which approximates descending section of the Idep profile at a sufficiently long time (Eq. (3) and inset in Fig. 1), does not imply any constraints related to the shape of the growing nuclei. Thus, the same Eq. (3) may describe diffusion limited growth of 3D as well as 2D nuclei. This is in contrast to the short deposition time when the ascending section of the Idep curve is expressed by equations derived exclusively for the growth of 3D hemispheres (Eqs. (1), (2)). Thus, 2D growth of the nuclei and a layer-by-layer formation of the deposit, which may take place after complete merging of the “diffusion zones”, would result in a decrease in the deposit-free substrate area which is faster than that predicted for the discussed 3D growth regime. Consequently, the Iother would also decay respectively faster. It is likely that these effects may be properly mirrored by application of equations similar to Eq. (34) or (35). This, however, requires a transition of the nuclei growth kinetics from 3D mode to 2D regime at a sufficiently long time. Existence of 3D-2D and 2D-3D transitions was confirmed experimentally for the electrochemical nucleation and growth in several systems [122,123,124,125,126,127,128,129]. Experimental results also confirm that the progress in the electrodeposition leads to changes in the shape of the growing nuclei [130, 131] and may result in a deviation from 3D growth of hemispherical nuclei [83]. At this stage, however, it is difficult to evaluate if these are indeed common phenomena. It is worth to note that a model of crystal growth controlled by kinetics [51, 132] predicts a decrease in θf according to exp(-t2) or exp(-t3) laws. Such changes in the deposit-free substrate area are also significantly faster than those given by Eqs. (21) and (23). Therefore, it is extremely important to evaluate proper shape and law of the nuclei growth, e.g. determination of whether 2D or 3D species exist [25, 133]. Nevertheless, it may be suggested that an analysis of the currents due to reactions which occur at the deposit-free section of the substrate surface can be used as a tool in studies on the nuclei formation and growth.
It can be concluded that a proper analysis of currents containing contributions from electrodeposition and other faradaic reactions taking place at the deposit-free section of the substrate surface requires careful determination of the radii of the deposited nuclei. This, in turn, calls for a very careful calculation of the electrode surface coverage with the deposit. Otherwise, the applied model may not provide correct mathematical description of the deposition process and may be inconsistent with the experimental observations.
Conclusions
A well-established mathematical model of diffusion limited nucleation and growth of a deposit consisting of isolated 3D hemispherical nuclei [1, 2, 16, 17] has been re-analysed. The aim was to determine time evolution of the deposit-free fraction of the substrate surface area for both instantaneous and progressive modes of the nucleation. A classical description of this model includes idea of “diffusion zones” which surround the growing nuclei. The mathematical analysis starts with determination of mass fluxes which supply individual isolated nuclei through a linear semi-infinite diffusion and for a planar geometry. This allows calculating average radius of the growing nuclei and, consequently, surface coverage of the substrate with the growing deposit. Knowing the latter, one may determine currents due to faradaic reactions which take place at the deposit-free section of the substrate surface and which are parallel to the electrodeposition process. Such simulated total currents containing contributions from these reactions are compared with those predicted by other approaches published in the literature so far. Differences between results provided by these methods are outlined in the text. It follows that any analysis of the currents due to faradaic reactions taking place at the deposit-free section of the substrate surface requires careful determination of the radii of the growing nuclei. This, in turn, indicates a need for proper evaluation of geometry of the nuclei and, consequently, their growth mode.
Abbreviations
- a :
-
Parameter in Eq. (1) [(units of area)·(units of time)−1]
- A :
-
Surface area of the electrode (substrate) [units of area]. It is assumed that the geometrical and real surface areas are equal (surface roughness = 1).
- A h :
-
Surface area of a hemispherical nucleus exposed to the electrolyte [units of area] (Eq. (2))
- A N :
-
Area of a plane across which the diffusion flux supplies single isolated nucleus at t > tm [units of area]
- A p :
-
Average area of the “diffusion zones” [units of area] (Eq. (2))
- B :
-
Parameter in Eq. (18) [(units of mass)·(units of time)−1/2]
- b :
-
Parameter in Eq. (4) [(units of area)·(units of time)−1]
- c :
-
Molar concentration of the electroactive species in the bulk of the electrolyte [(mol)·(units of volume) −1]
- D :
-
The diffusion coefficient of the electroactive species [(units of area) ·(units of time) −1]
- E :
- F :
-
Faraday constant [96,485.33 C·(mol)−1]
- g :
-
Nucleation rate [(units of time)−1]
- I dep :
-
Deposition current [units of electric current]
- I'dep :
-
Electrodeposition current calculated using Eq. (12) [units of electric current]
- I other :
-
Electric current due to other than the electrodeposition faradaic reaction which takes place at the deposit-free section of the electrode area [units of electric current]
- I tot :
-
Total electric current calculated using Eq. (32) [units of electric current]
- j other :
-
Current density of a faradaic reaction other than the electrodeposition [(units of electric current)·(units of area)−1]
- J p :
-
Planar linear diffusion flux [(mol)·(units of time) −1·(units of area) −1] (Eq. (S5b))
- J s :
-
Spherical diffusion flux [(mol)·(units of time) −1·(units of area) −1] (Eq. (S2b))
- k :
-
Parameter in Eq. (19) [(units of length)3]
- m :
-
Mass of the nucleus [units of mass]
- M :
-
Molar mass of the deposited species [g·(mol)−1]
- N :
-
Surface density of nuclei per surface area unit at a given time [(units of area)−1]
- N 0 :
-
Maximum surface density of the nuclei per surface area unit [(units of area)−1]
- Q :
-
Electric charge from integration of Idep for the instantaneous nucleation [units of electric charge]
- Q':
-
Electric charge from integration of Idep for the progressive nucleation [units of electric charge]
- r'h :
-
Average nucleus radius calculated using Eq. (1) [units of length]
- r''h :
-
Average nucleus radius calculated using Eq. (15) [units of length]
- r'''h :
-
Average nucleus radius calculated using Eq. (19) [units of length]
- r IV h :
-
Average radius of nuclei born within a given time window (Eq. (30)) [units of length]
- r V h :
-
Average nucleus radius calculated for nuclei of all ages existing at given time (Eq. (31)) [units of length]
- r h :
-
Average radius of a nucleus calculated using Eq. (11) [units of length]
- r p :
-
Average radius of a “diffusion zone” calculated with Eq. (4) [units of length]
- S(t):
-
Surface area of the growing deposit (Eq. (33))
- t :
-
Time counted from the start of the deposition process [units of time]
- t m :
-
Deposition time required to completely merge the “diffusion zones” [units of time]
- V :
-
Volume of the hemispherical nucleus [(units of volume)]
- V 0 :
-
Volume of the hemispherical nucleus formed between t = 0 and t = tm (Eq. (18)) [(units of volume)]
- z :
-
Number of electrons exchanged in the faradaic reaction
- Δt :
-
Time window used in analysis of the progressive nucleation (Eqs. (30), (31)) [time units]
- θ d :
-
Electrode surface coverage with “diffusion zones” (Eq. (9))
- θ'd :
-
Fraction of the electrode (substrate) coverage with the “diffusion zones” across which the diffusion flux supplies single isolated nucleus (Eq. (12))
- θ f :
-
Deposit-free fraction of the electrode (substrate) surface calculated using Eqs. (20) and (24)
- θ''f :
-
Deposit-free fraction of the electrode (substrate) surface calculated using Eqs. (21) and (24)
- θ'''f :
-
Deposit-free fraction of the electrode (substrate) surface calculated using Eqs. (23) and (24)
- θ IV f :
-
Deposit-free fraction of the electrode (substrate) for progressive nucleation without correction for the nuclei overlap, calculated according to “Progressive Nucleation” section
- θ V f :
-
Deposit-free fraction of the electrode (substrate) for progressive nucleation corrected for the nuclei overlap, calculated according to “Progressive Nucleation” section
- θ VI f :
-
Deposit-free fraction of the electrode (substrate) surface calculated using Eq. (34)
- θ VII f :
-
Deposit-free fraction of the electrode (substrate) surface calculated using Eq. (35)
- θ x f :
-
General designation for the deposit-free fraction of the electrode (substrate) surface for various calculation methods
- θ h :
-
Electrode (substrate) surface coverage with the deposit calculated using Eq. (20)
- θ''h :
-
Electrode (substrate) surface coverage with the deposit calculated using Eq. (21)
- θ'''h :
-
Electrode (substrate) surface coverage with the deposit calculated using Eq. (23)
- θ x h :
-
General designation for the electrode (substrate) surface coverage with the deposit for various calculation methods
- ρ :
-
Density of the deposited species [g·(units of volume)−1].
References
M.E. Hyde, R.G. Compton, A review of the analysis of multiple nucleation with diffusion controlled growth. J. Electroanal. Chem. 549, 1–12 (2003)
B.R. Scharifker, J. Mostany, Three-dimensional nucleation with diffusion controlled growth. Part I. Number density of active sites and nucleation rates per site. J. Electroanal. Chem. 177, 13–23 (1984)
P. Altimari, F. Pagnanelli, Electrochemical nucleation and three-dimensional growth under mixed kinetic-diffusion control: analytical approximation of the current transient. Electrochim. Acta. 205, 113–117 (2016)
S. Fletcher, Electrochemical deposition of hemispherical nuclei under diffusion control some theoretical considerations. J. Chem. Soc. Faraday. Trans. I. 79, 467–479 (1983)
M.Y. Abyaneh, M. Fleischmann, The role of nucleation and of overlap in electrocrystallisation reactions. Electrochim. Acta. 27, 1513–1518 (1982)
M.Y. Abyaneh, Calculation of overlap for nucleation and three-dimensional growth of centres. Electrochim. Acta. 27, 1329–1334 (1982)
L. Guo, G. Oskam, A. Radisic, P.M. Hoffmann, P.C. Searson, Island growth in electrodeposition. J. Phys. D. Appl. Phys. 44, 443001 (2011)
A. Milchev, Nucleation and growth of clusters through multi-step electrochemical reactions. J. Electroanal. Chem. 612, 42–46 (2008)
E. Matthijs, S. Langerock, E. Michailova, L. Heerman, The potentiostatic transient for 3D nucleation with diffusion-controlled growth: theory and experiment for progressive nucleation. J. Electroanal. Chem. 570, 123–133 (2004)
G. Luo, D. Li, G. Yuan, N. Li, Potentiostatic current transient for multiple nucleation: a limited-diffusion process description. J. Electrochem. Soc. 165, D147–D151 (2018)
P.C. D’Ajello, Current–time and current–potential profiles in electrochemical film production. (I) Current–time curves. J. Electroanal. Chem. 573, 29–35 (2004)
P.C.T. D’Ajello, M.A. Fiori, A.A. Pasa, Z.G. Kipervaser, Reaction-diffusion interplay in electrochemical deposition processes. A theoretical approach. J. Electrochem. Soc. 147, 4562–4566 (2000)
M. Tomellini, Interface evolution in phase transformations ruled by nucleation and growth. Phys. A. 558, 124981 (2020)
M.J. Walters, C.M. Pettit, D. Roy, Surface kinetics of electrodeposited silver on gold probed with potential step and optical second harmonic generation techniques. Phys. Chem. Chem. Phys. 3, 570–578 (2001)
P. Altimari, F. Greco, F. Pagnanelli, Nucleation and growth of metal nanoparticles on a planar electrode: a new model based on iso-nucleation-time classes of particles. Electrochim. Acta. 296, 82–93 (2019)
M. Sluyters-Rehbach, J.H.O.J. Wijenberg, E. Bosco, J.H. Sluyters, The theory of chronoamperometry for the investigation of electrocrystallization mathematical description and analysis in the case of diffusion-controlled growth. J. Electroanal. Chem. 236, 1–20 (1987)
B.R. Scharifker, J. Mostany, in Encyclopedia of electrochemistry. ed. by A.J. Bard, M. Stratmann (Wiley, Cambridge, 2002), pp. 512–539
M. Palomar-Pardavé, B.R. Scharifker, E.M. Arce, M. Romero-Romo, Nucleation and diffusion-controlled growth of electroactive centers: reduction of protons during cobalt electrodeposition. Electrochim. Acta. 50, 4736–4745 (2005)
M. Próchniak, M. Grdeń, Electrochemical deposition of nickel from aqueous electrolytic baths prepared by dissolution of metallic powder. J. Solid. State. Electrochem. 26, 431–447 (2022)
K.I. Popov, S.S. Djokić, N.D. Nikolić, V.D. Jović, Morphology of electrochemically and chemically deposited metals (Springer, Switzerland, 2016)
J.M. Mosby, D.C. Johnson, A.L. Prieto, Evidence of induced underpotential deposition of crystalline copper antimonide via instantaneous nucleation. J. Electrochem. Soc. 157, E99–E105 (2010)
M. Schlesinger, M. Paunovic, Modern electroplating (Wiley, Hoboken, 2001)
Y. Tsuru, M. Nomura, F.R. Foulkes, Effects of boric acid on hydrogen evolution and internal stress in films deposited from a nickel sulfamate bath. J. Appl. Electrochem. 32, 629–634 (2002)
C.H. Rios-Reyes, M. Granados-Neri, L.H. Mendoza-Huizar, Kinetic study of the cobalt electrodeposition onto glassy carbon electrode from ammonium sulfate solutions. Quim. Nova. 32, 2382–2386 (2009)
A.I. Danilov, E.B. Molodkina, A.V. Rudnev, Y.M. Polukarov, J.M. Feliu, Kinetics of copper deposition on Pt(111) and Au(111) electrodes in solutions of different acidities. Electrochim. Acta. 50, 5032–5043 (2005)
M. Rezaid, S.H. Tabaian, D.F. Haghshenas, Electrochemical nucleation of palladium on graphene: a kinetic study with an emphasis on hydrogen co-reduction. Electrochim. Acta. 85, 381–387 (2013)
M.D.C. Aguirre, Nucleation and growth mechanisms of palladium, nanoflower-shaped, and its performance as electrocatalyst in the reduction of Cr(VI). J. Appl. Electrochem. 49, 795–809 (2019)
D. Kong, Z. Zheng, F. Meng, N. Li, D. Li, Electrochemical nucleation and growth of cobalt from methanesulfonic acid electrolyte. J. Electrochem. Soc. 165, D783–D789 (2018)
E.C. Muñoz, R.S. Schrebler, M.A. Orellana, R. Córdova, Rhenium electrodeposition process onto p-Si(100) and electrochemical behaviour of the hydrogen evolution reaction onto p-Si/Re/0.1 M H2SO4 interface. J. Electroanal. Chem. 611, 35–42 (2007)
P. Allongue, E. Souteyrand, Metal electrodeposition on semiconductors. Part 2. Description of the nucleation processes. J. Electroanal. Chem. 362, 79–87 (1993)
H.C. Shin, J. Dong, M. Liu, Nanoporous structures prepared by an electrochemical deposition process. Adv. Mater. 15, 1610–1614 (2003)
V.S. Nikitin, T.N. Ostanina, V.M. Rudoi, T.S. Kuloshvili, A.B. Darintseva, Features of hydrogen evolution during electrodeposition of loose deposits of copper, nickel and zinc. J. Electroanal. Chem. 870, 114230 (2020)
B. Thirumalraj, T. Teka Hagos, C.J. Huang, M. Admas Teshager, J.H. Cheng, W.N. Su, B.J. Hwang, Nucleation and growth mechanism of lithium metal electroplating. J. Am. Chem. Soc. 141, 18612–18623 (2019)
M.A. El-Jemni, H.S. Abdel-Samad, H.H. Hassan, On the deconvolution of the concurrent cathodic processes with cobalt deposition onto graphite from feebly acidic bath. J. Appl. Electrochem. 51, 1705–1719 (2021)
J. Aldana-González, M. Romero-Romo, J. Robles-Peralta, P. Morales-Gil, E. Palacios-González, M.T. Ramírez-Silva, J. Mostany, M. Palomar-Pardavé, On the electrochemical formation of nickel nanoparticles onto glassy carbon from a deep eutectic solvent. Electrochim. Acta. 276, 417–423 (2018)
E.C. Muñoz, R.S. Schrebler, P.K. Cury, C.A. Suárez, R.A. Córdova, C.H. Gómez, R.E. Marotti, E.A. Dalchiele, The influence of poly(ethylene oxide) and illumination on the copper electrodeposition process onto n-Si(100). J. Phys. Chem. B. 110, 21109–21117 (2006)
A. Prados, R. Ranchal, Electrodeposition of Bi films on H covered n-GaAs(111)B substrates. Electrochim. Acta. 305, 212–222 (2019)
A. Prados, R. Ranchal, Electrodeposition of Bi thin films on n-GaAs(111)B. I. correlation between the overpotential and the nucleation process. J. Phys. Chem. C. 122, 8874–8885 (2018)
A. Prados, R. Ranchal, Use of light for the electrochemical deposition of Bi on n-GaAs substrates. Electrochim. Acta. 316, 113–124 (2019)
X. Huang, Y. Chen, J. Zhou, Z. Zhang, J. Zhang, Electrochemical nucleation and growth of Sn onto double reduction steel substrate from a stannous fluoborate acid bath. J. Electroanal. Chem. 709, 83–92 (2013)
J. Lei, J.G. Yang, Electrochemical mechanism of tin membrane electro-deposition in chloride solutions. J. Chem. Technol. Biotechnol. 92, 861–867 (2017)
E. Garfias-García, M. Romero-Romo, M.T. Ramírez-Silva, M. Palomar-Pardavé, Overpotential nucleation and growth of copper onto polycrystalline and single crystal gold electrodes. Int. J. Electrochem. Sci. 7, 3102–3114 (2012)
D. Grujicic, B. Pesic, Electrochemical and AFM study of nickel nucleation mechanisms on vitreous carbon from ammonium sulfate solutions. Electrochim. Acta. 51, 2678–2690 (2006)
X. Zhou, Y. Wang, Z. Liang, H. Jin, Electrochemical deposition and nucleation/growth mechanism of Ni–Co–Y2O3 multiple coatings. Materials. 11, 1124 (2018)
B.M. Hryniewicz, M. Vidotti, PEDOT nanotubes electrochemically synthesized on flexible substrates: enhancement of supercapacitive and electrocatalytic properties. ACS. Appl. Nano. Mater. 1, 3913–3924 (2018)
S. Pourrahimi, M. Rezaei, S.H. Tabaian, Electrochemical investigation of Pt–Pd nanoparticles formation–reduction kinetics and nucleation mechanisms. J. Appl. Electrochem. 49, 1143–1155 (2019)
A. Gupta, C. Srivastava, Nucleation and growth mechanism of tin electrodeposition on graphene oxide: a kinetic, thermodynamic and microscopic study. J. Electroanal. Chem. 861, 113964 (2020)
Y.B. Vogel, N. Darwish, M.B. Kashi, J.J. Gooding, S. Ciampi, Hydrogen evolution during the electrodeposition of gold nanoparticles at Si(100) photoelectrodes impairs the analysis of current-time transients. Electrochim. Acta. 247, 200–206 (2017)
E. Rudnik, M. Wojnicki, G. Włoch, Effect of gluconate addition on the electrodeposition of nickel from acidic baths. Surf. Coat. Technol. 207, 375–388 (2012)
A. Sahari, A. Azizi, N. Fenineche, G. Schmerber, A. Dinia, Electrochemical study of cobalt nucleation mechanisms on different metallic substrates. Mater. Chem. Phys. 108, 345–352 (2008)
J. González-García, F. Gallud, J. Iniesta, V. Montiel, A. Aldaz, A. Lasia, Kinetics of electrocrystallization of PbO2 on glassy carbon electrodes. Partial inhibition of the progressive three-dimensional nucleation and growth. J. Electrochem. Soc. 147, 2969–2974 (2000)
F. Di Biagio, M. Tomellini, “Linear diffusion domain” approach for modeling the kinetics of electrodeposition: a two-dimensional study. J. Solid. State. Electrochem. 23, 2667–2681 (2019)
R.L. Harniman, D. Plana, G.H. Carter, K.A. Bradley, M.J. Miles, D.J. Fermín, Real-time tracking of metal nucleation via local perturbation of hydration layers. Nat. Commun. 8, 971 (2017)
M.H. Mamme, C. Köhn, J. Deconinck, J. Ustarroz, Numerical insights into the early stages of nanoscale electrodeposition: nanocluster surface diffusion and aggregative growth. Nanoscale. 10, 7194–7209 (2018)
L. Guo, A. Thompson, P.C. Searson, The kinetics of copper island growth on ruthenium oxide in perchlorate solution. Electrochim. Acta. 55, 8416–8421 (2010)
J. Ustarroz, Current atomic-level understanding of electrochemical nucleation and growth on low-energy surfaces. Curr. Opin. Electrochem. 19, 144–152 (2020)
L. Yang, A. Radisic, M. Nagar, J. Deconinck, P.M. Vereecken, A.C. West, Multi-scale modeling of direct copper plating on resistive non-copper substrates. Electrochim. Acta. 78, 524–531 (2012)
J. Ustarroz, J.A. Hammons, T. Altantzis, A. Hubin, S. Bals, H. Terryn, A generalized electrochemical aggregative growth mechanism. J. Am. Chem. Soc. 135, 11550–11561 (2013)
R.M. Stephens, R.C. Alkire, Island dynamics algorithm for kinetically limited electrochemical nucleation of copper with additives onto a foreign substrate. J. Electrochem. Soc. 156, D28–D35 (2009)
J. Ustarroz, X. Ke, A. Hubin, S. Bals, H. Terryn, New insights into the early stages of nanoparticle electrodeposition. J. Phys. Chem. C. 116, 2322–2329 (2012)
D. Šimkūunaitė, E. Ivaškevič, A. Kaliničenko, A. Steponavičius, Nucleation and growth of Cu onto polycrystalline Pt electrode from acidic CuSO4 solution in the presence of H2SeO3. J. Solid. State. Electrochem. 10, 447–457 (2006)
V.K. Laurinavichyute, S. Nizamov, V.M. Mirsky, Real time tracking of the early stage of electrochemical nucleation. Electrochim. Acta. 382, 138278 (2021)
M.H. Mamme, J. Deconinck, J. Ustarroz, Transition between kinetic and diffusion control during the initial stages of electrochemical growth using numerical modelling. Electrochim. Acta. 258, 662–668 (2017)
A. Milchev, L. Heerman, Electrochemical nucleation and growth of nano- and microparticles: some theoretical and experimental aspects. Electrochim. Acta. 48, 2903–2913 (2003)
D. Branco P, J. Mostany, C. Borrás, B.R. Scharifker, The current transient for nucleation and diffusion-controlled growth of spherical caps. J. Solid. State. Electrochem. 13, 565–571 (2009)
L. Heerman, A. Tarallo, Electrochemical nucleation on microelectrodes. Theory and experiment for diffusion-controlled growth. J. Electroanal. Chem. 451, 101–109 (1998)
G.J. Hills, D.J. Schiffrin, J. Thompson, Electrochemical nucleation from molten salts. 1. Diffusion controlled electrode position of silver from alkali molten nitrates. Electrochim. Acta. 19, 657–670 (1974)
B. Rashkova, B. Guel, R.T. Pötzschke, G. Staikov, W.J. Lorenz, Electrodeposition of Pb on n-Si(111). Electrochim. Acta. 43, 3021–3028 (1998)
S.E.F. Kleijn, S.C.S. Lai, M.T.M. Koper, P.R. Unwin, Electrochemistry of nanoparticles. Angew. Chem. Int. Ed. 53, 3558–3586 (2014)
V.A. Isaev, A.N. Barabashkin, Three-dimensional electrochemical phase formation. J. Electroanal. Chem. 377, 33–31 (1994)
E. Bosco, S.K. Rangarajan, Electrochemical phase formation (ECPF) and macrogrowth Part I. Hemispherical models. J. Electroanal. Chem. 134, 213–224 (1982)
A. Radisic, F.M. Ross, P.C. Searson, In situ study of the growth kinetics of individual island electrodeposition of copper. J. Phys. Chem. B 110, 7862–7868 (2006)
V.A. Isaev, Y.P. Zaykov, O.V. Grishenkova, A.V. Kosov, O.L. Semerikova, Analysis of potentiostatic current transients for multiple nucleation with diffusion and kinetic controlled growth. J. Electrochem. Soc. 166, D851–D856 (2019)
J.F. Lemineur, J.M. Noël, C. Combellas, F. Kanoufi, Optical monitoring of the electrochemical nucleation and growth of silver nanoparticles on electrode: from single to ensemble nanoparticles inspection. J. Electroanal. Chem. 872, 114043 (2020)
L. Wang, J. Wen, H. Sheng, D.J. Miller, Fractal growth of platinum electrodeposits revealed by in situ electron microscopy. Nanoscale. 8, 17250–17255 (2016)
L. Heerman, A. Tarallo, Theory of the chronoamperometric transient for electrochemical nucleation with diffusion-controlled growth. J. Electroanal. Chem. 470, 70–76 (1999)
J.L. Fransaer, R.M. Penner, Brownian dynamics simulation of the growth of metal nanocrystal ensembles on electrode surfaces from solution. I. Instantaneous nucleation and diffusion-controlled growth. J. Phys. Chem. B. 103, 7643–7653 (1999)
L. Guo, P.C. Searson, Simulations of island growth and island spatial distribution during electrodeposition. Electrochem. Solid. State. Lett. 10, D76–D78 (2007)
G. Gunawardena, G. Hills, I. Montenegro, B. Scharifker, Electrochemical nucleation. Part I. General considerations. J. Electroanal. Chem. 138, 225–239 (1982)
Y.D. Gamburg, G. Zangari, Theory and practice of metal electrodeposition (Springer, London, 2011)
E. Gómez, Z.G. Kipervaser, E. Vallés, Electrodeposition under a time-dependent boundary condition. Thin. Solid. Films. 440, 45–53 (2003)
L. Heerman, E. Matthijs, S. Langerock, The concept of planar diffusion zones. Theory of the potentiostatic transient for multiple nucleation on active sites with diffusion-controlled growth. Electrochim. Acta. 47, 905–911 (2001)
P. Altimari, P.G. Schiavi, A. Rubino, F. Pagnanelli, Electrodeposition of cobalt nanoparticles: an analysis of the mechanisms behind the deviation from three-dimensional diffusion-control. J. Electroanal. Chem. 851, 113413 (2019)
A.J. Bard, L.R. Faulkner, Electrochemical methods. Fundamentals and applications (Wiley, New York, 2001)
M. Tomellini, S. Politi, Kinetics of phase transformations with heterogeneous correlated-nucleation. Phys. A. 513, 175–188 (2019)
B.R. Scharifker, J. Mostany, M. Palomar-Pardavé, I. González, On the theory of the potentiostatic current transient for diffusion-controlled three-dimensional electrocrystallization processes. J. Electrochem. Soc. 146, 1005–1012 (1999)
N.V. Alekseechkin, Extension of the Kolmogorov–Johnson–Mehl–Avrami theory to growth laws of diffusion type. J. Non-Crystal. Solids 357, 3159–3167 (2011)
S. Politi, M. Tomellini, Kinetics of island growth in the framework of “planar diffusion zones” and “3D nucleation and growth” models for electrodeposition. J. Solid. State. Electrochem. 22, 3085–3098 (2018)
L. Heerman, A. Tarallo, Electrochemical nucleation with diffusion-limited growth. Properties and analysis of transients. Electrochem. Commun. 2, 85–89 (2000)
S.C.S. Lai, R.A. Lazenby, P.M. Kirkman, P.R. Unwin, Nucleation, aggregative growth and detachment of metal nanoparticles during electrodeposition at electrode surfaces. Chem. Sci. 6, 1126–1138 (2015)
F.C. Pérez-Cárdenas, The irrelevance of phantom nuclei in crystallization kinetics: an integral equation approach. J. Non-Crystal. Solids. X. 1, 100002 (2019)
E. Bosco, Some new insights into the old Avrami’s equation. J. Chem. Phys. 97, 1542–1547 (1992)
E. Bosco, S.K. Rangarajan, Electrochemical phase formation (ECPF) and macrogrowth Part II. Two-rate models. J. Electroanal. Chem. 134, 225–241 (1982)
P. Bruna, D. Crespo, R. González-Cinca, E. Pineda, On the validity of Avrami formalism in primary crystallization. J. Appl. Phys. 100, 054907 (2006)
M. Avrami, Kinetics of phase change. II. Transformation-time relations for random distribution of nuclei. J. Chem. Phys. 8, 212–224 (1940)
E. Bosco, S. Rangarajan, Electrochemical phase formation time-dependent nucleation and growth rates. J. Chem. Soc. Faraday. Trans. I. 77, 483–495 (1981)
U.R. Evans, The laws of expanding circles and spheres in relation to the lateral growth of surface films and the grain-size of metals. Trans. Faraday. Soc. 41, 365–374 (1945)
M.V. Mirkin, A.P. Nilov, Three-dimensional nucleation and growth under controlled potential. J. Eletroanal. Chem. 283, 35–51 (1990)
M.Y. Abyaneh, Generalization of transient equations due to the growth of hemispheroids. J. Electroanal. Chem. 387, 29–34 (1995)
B. Scharifker, G. Hills, Theoretical and experimental studies of multiple nucleation. Electrochim. Acta. 28, 879–889 (1983)
W.H. Mulder, J.H.O.J. Wijenberg, M. Sluyters-Rehbach, J.H. Sluyters, On the validity of the Avrami theorem in the case of decelerating growth. J. Electronnal. Chem. 270, 7–19 (1989)
Y. Cao, A.C. West, Nucleation and three-dimensional growth: deviation from diffusion control. J. Electrochem. Soc. 149, C223–C228 (2002)
Y. Cao, P.C. Searson, A.C. West, Direct numerical simulation of nucleation and three-dimensional, diffusion-controlled growth. J. Electrochem. Soc. 148, C376–C382 (2001)
W.S. Kruijt, M. Sluyters-Rehbach, J.H. Sluyters, The diffusion-controlled growth of an assembly of mercury spheres on a conducting substrate. A combined study by electrochemical and light scattering methods. J. Electroanal. Chem. 351, 115–135 (1993)
G. Gunawardena, G. Hills, I. Montenegro, B. Scharifker, Electrochemical nucleation: Part III. The electrodeposition of mercury on vitreous carbon. J. Electroanal. Chem. 138, 255–271 (1982)
H. Zargarnezhad, A. Dolati, A 3D continuum-kinetic Monte Carlo simulation study of early stages of nucleation and growth in Ni electrodeposition. Electrochim. Acta. 236, 1–9 (2017)
J. Mostany, J. Mozota, B.R. Scharifker, Three-dimensional nucleation with growth diffusion controlled. Part II. The nucleation of lead on vitreous carbon. J. Electroanal. Chem. 177, 25–31 (1984)
S.P. Arkhipov, A.P. Apisarov, O.V. Grishenkova, A.V. Isakov, A.A. Chernyshev, Y.P. Zaikov, Electrochemical nucleation and growth of rhenium on glassy carbon in the KF-KBF4-B2O3-KReO4 melt. J. Electrochem. Soc. 166, D935–D939 (2019)
Y. Surendranath, D.A. Lutterman, Y. Liu, D.G. Nocera, Nucleation, growth, and repair of a cobalt-based oxygen evolving catalyst. J. Am. Chem. Soc. 134, 6326–6336 (2012)
F. Mechehoud, A. Khelil, N.E. Hakiki, J.L. Bubendorff, Potentiostatic controlled nucleation and growth modes of electrodeposited cobalt thin films on n-Si(1 1 1). Eur. Phys. J. Appl. Phys. 75, 30301 (2016)
A. Radisic, P.M. Vereecken, J.B. Hannon, P.C. Searson, F.M. Ross, Quantifying electrochemical nucleation and growth of nanoscale clusters using real-time kinetic data. Nano. Lett. 6, 238–242 (2006)
V.A. Isaev, O.V. Grishenkova, A.V. Kosov, O.L. Semerikova, Y. Zaikov, Simulation of 3D electrochemical phase formation: mixed growth control. Materials. 14, 6330 (2021)
Y. Gimeno, A. Hernández Creus, P. Carro, S. González, R.C. Salvarezza, A.J. Arvia, Electrochemical formation of palladium islands on HOPG: kinetics, morphology, and growth mechanisms. J. Phys. Chem. B. 106, 4232–4244 (2002)
R.G. Milazzo, S.M.S. Privitera, S. Scalese, S. Mirabella, C. Bongiorno, S.A. Lombardo, E. Rimini, New insight into Pt nucleation mechanism on Si surface during galvanic displacement deposition. J. Phys. Chem. Solids. 148, 109722 (2021)
B.R. Frieden, Probability, statistical optics, and data testing. A problem solving approach (Springer, Heidelberg, 2001)
M. Saitou, Probability analysis of island distribution at the early stage in electrodeposition based on a fixed length segment model. Int. J. Electrochem. Sci. 11, 7830–7842 (2016)
A. Bewick, M. Fleischmann, H.R. Thirsk, Kinetics of the electrocrystallization of thin films of calomel. Trans. Faraday. Soc. 58, 2200–2216 (1962)
M.Y. Abyaneh, Formulation of current-time transients due to nucleation and coalescence of spherical-cap growth forms. J. Electroanal. Chem. 209, 1–10 (1986)
D. Grujicic, B. Pesic, Electrodeposition of copper: the nucleation mechanisms. Electrochim. Acta. 47, 2901–2912 (2002)
W. Schmickler, E. Santos, Interfacial electrochemistry (Springer, Heidelberg, 2010)
D. Mazaira, C. Borrás, J. Mostany, B.R. Scharifker, in Theoretical and experimental advances in electrodeposition. ed. by L.H. Mendoza-Huizar (Research Signpost, Trivandrum, 2008), pp. 1–23
E.N. Schulz, A. Ruderman, G.J. Soldano, S.G. García, E. Santos, Key role of anions in the 2D–3D electrochemical deposition of Rh on Ag Electrodes. Electrochim. Acta. 178, 813–822 (2015)
O.M. Magnussen, K. Krug, A.H. Ayyad, J. Stettner, In situ diffraction studies of electrode surface structure during gold electrodeposition. Electrochim. Acta. 53, 3449–3458 (2008)
S. Bijani, R. Schrebler, E.A. Dalchiele, M. Gabás, L. Martínez, J.R. Ramos-Barrado, Study of the nucleation and growth mechanisms in the electrodeposition of micro- and nanostructured Cu2O thin films. J. Phys. Chem. C 115, 21373–21382 (2011)
K. Chat-Wilk, E. Rudnik, G. Włoch, P. Osuch, Importance of anions in electrodeposition of nickel from gluconate solutions. Ionics. 27, 4393–4408 (2021)
M. Palomar-Pardavé, M. Miranda-Hernández, I. González, N. Batina, Detailed characterization of potentiostatic current transients with 2D–2D and 2D–3D nucleation transitions. Surf. Sci. 399, 80–95 (1998)
M. Jafarian, M.G. Mahjani, F. Gobal, I. Danaee, Effect of potential on the early stage of nucleation and growth during aluminum electrocrystallization from molten salt (AlCl3–NaCl–KCl). J. Electroanal. Chem. 588, 190–196 (2006)
E.N. Schulz, D.R. Salinas, S.G. García, Electrodeposition of rhodium onto a pre-treated glassy carbon surface. Electrochem. Commun. 12, 583–586 (2010)
B.J. Hwang, R. Santhanam, Y.L. Lin, Nucleation and growth mechanism of electroformation of polypyrrole on a heat-treated gold/highly oriented pyrolytic graphite. Electrochim. Acta. 46, 2843–2853 (2001)
A. Lachenwitzer, S. Morin, O.M. Magnussen, R.J. Behm, In situ STM study of electrodeposition and anodic dissolution of Ni on Ag(111). Phys. Chem. Chem. Phys. 3, 3351–3363 (2001)
P.C. Hsu, Y. Chu, J.M. Yi, C.L. Wang, S.R. Wu, Y. Hwu, G. Margaritondo, Dynamical growth behavior of copper clusters during electrodeposition. Appl. Phys. Lett. 97, 033101 (2010)
Y.G. Li, W. Chrzanowski, A. Lasia, Nucleation and crystal growth in gold electrodeposition from acid solution. Part I: Soft gold. J. Appl. Electrochem. 26, 843–852 (1996)
D. Grujicic, B. Pesic, Electrochemical and AFM study of cobalt nucleation mechanisms on glassy carbon from ammonium sulfate solutions. Electrochim. Acta. 49, 4719–4732 (2004)
Funding
Financial support from the Faculty of Chemistry, University of Warsaw (grant nos. 501-D112-01–1120000 (501100299) and 501-D112-64–0185200-80) is acknowledged. The contribution of Martyna Próchniak, M.Sc., was realized within Project No POWR.03.02.00–00-I009/17–00 (Operational Project Knowledge Education Development 2014–2020 co-financed by European Social Fund).
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of Interest
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Grdeń, M., Próchniak, M. Electrode Surface Coverage with Deposit Generated Under Conditions of Electrochemical Nucleation and Growth. A Mathematical Analysis. Electrocatalysis 14, 39–54 (2023). https://doi.org/10.1007/s12678-022-00771-1
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s12678-022-00771-1