1 Introduction

Short-term hydropower scheduling seeks to find an optimal dispatch of stored water through a cascade of plants and gates that maximizes the profit. Besides producing power, hydropower also plays an important role with respect to flood management [1, 2]. Accurate descriptions of the water flow is therefore important both for economical and societal reasons.

A hydropower reservoir typically has three different water routes: power plant discharge, bypass, and overflow. Whereas the first two alternatives are explicit decisions taken by the operator, the overflow is an implicit decision. It occurs when the reservoir is unable to store more water. In long-term hydropower scheduling, where the optimization horizon can be several years, the overflow is typically modelled as an additional large gate, sometimes with a relative high operating cost that penalizes operation of the overflow gate such that it is not used unless it is highly necessary [3, 4]. However, the only mathematical relation between reservoir level and overflow is that overflow is the last possible way to get rid of water when a reservoir is full. This approach does neither consider the physical characteristic nor the time delay associated with overflow since computationally efficient linear formulations are more important than high physical accuracy of this phenomenon.

For short-term hydropower scheduling, with a typical optimization horizon in the range 1–14 days, it is necessary to consider the coupling between overflow and water levels of the reservoirs, especially for small reservoirs. A common approach is to assume a functional relation between the overflow and reservoir head [5], for example a polynomial relation [6, 7], that is approximated by a piecewise linear relaxation. Although these formulations are more physically accurate, they also permit so-called nonphysical overflow, that will be further explained in Sect. 2. However, previous research does not discuss challenges arising when using a relaxation of the overflow function.

To overcome the challenges with nonphysical behaviour of the optimization model, we present a mixed-integer linear programming (MILP) formulation of the reservoir overflow. The proposed formulation also serves as a tight relaxation when the binary variables are replaced by their continuous counterparts. We also propose a heuristic for estimating coefficients that reduces the computation time of the MILP problem when solving the hydropower scheduling problem with successive linear programming (SLP). We test the effectiveness of the proposed heuristic with respect to reducing the computation time of the combined SLP/MILP problem for the Fossdal watercourse in Norway.

2 A hydropower scheduling model

This paper considers the hydropower producer perspective in a competitive market where the objective is to maximize the revenue for an exogenous market price. The presented formulation summarizes the key properties of the hydropower scheduling problem and we refer to [8] for a comprehensive description.

2.1 Hydropower formulation

Consider a planning horizon divided into a set T of time periods of possibly unequal lengths, and let \(\Delta _t\) denote the length of period \(t\in T\). A watercourse consists of a set R of possibly connected reservoirs. Each reservoir may have a downstream plant, bypass gate and overflow route. Let \(U_r\subseteq R\setminus \{r\}\) denote the set of hydraulic upstream objects discharging into reservoir \(r\in R\). We assume, to ease the notation, that each plant consists of one producing unit, but the plant description can be further generalized to include multiple sets of generators and turbines as shown in [8, 9].

In the objective function

$$ \max \sum\limits_{{t \in T}} {\left( {M_{t}^{{SALE}} \cdot \Delta _{t} \cdot p_{t}^{{SALE}} } \right)} + \sum\limits_{{r \in R}} {W_{{r,\bar{t}}}^{{END}} } \cdot E_{r} \cdot v_{{r,\bar{t}}}, $$
(1)

\(M_t^{\textit{SALE}}\) and \(p_t^{\textit{SALE}}\) denote, respectively, the market price and the produced power at time t. The value of storing water beyond the optimization horizon is given by the outgoing reservoir volume \(v_{r,{\bar{t}}}\) multiplied with their respective water values \( W_{{r,\bar{t}}}^{{END}} [\EUR {\text{/MWh}}] \) and an energy conversion factor \(E_r [MWh/Mm^3]\). The water value represents the opportunity value of storing the water for later use rather than using it now. The energy conversion factor is in reality a function of the head, but is often approximated with a constant value. The water value, that also can be a function of the reservoir levels in cascaded systems, typically comes from a medium- or long-term model [9].

Hydrological balance in the reservoirs is expressed as

$$\begin{aligned} v_{r,t}= & {} v_{r,t-1} + \Delta _t \cdot \Bigg ( Q_{r,t}^{\textit{INFLOW}} \nonumber \\{} & {} + \sum _{u \in U_r} \left( q_{u,t-\tau _{u,t}}^P + q_{u,t-\tau _{u,t}}^B + q_{u,t-\tau _{u,t}}^S \right) - q_{r,t}^P - q_{r,t}^B - q_{r,t}^S \Bigg ), \end{aligned}$$
(2)

where the variable \(v_{r,t}\) denotes the hydro storage in reservoir r at time t, \(Q_{r,t}^{\textit{INFLOW}}\) the reservoir inflow, and \(q_{r,t}^P\), \(q_{r,t}^B\), and \(q_{r,t}^S\) the reservoir discharge from the plant production, bypass, and overflow, respectively. The delay from water is released at upstream object u until it arrives the reservoir is enforced by the time delay \(\tau _{u,t}\), and the initial storage \(V_r^{\textit{INIT}}\) is enforced by

$$\begin{aligned} v_{r,0} = V_{r}^{\textit{INIT}}. \end{aligned}$$
(3)

Let \(\ell _r(v)\) denote the water level of reservoir r as a function of its volume. The power \(p_{r,t}\) produced by plant r in period t is proportional to the turbine efficiency \(\eta _r^{\textit{TURB}}\), which, in its turn, is a function of the net head \(h_{r,t}^{\textit{NET}}\) of the unit and the discharge \(q_{r,t}^P\). The gross head at r in period t is simply the difference \(\ell _{r}\left( v_{r,t}\right) -L_r\) between the water level \(\ell _{r}\left( v_{r,t}\right) \) at the intake reservoir r and the level \(L_r\) of the plant outlet or the downstream head if the plant is hydraulically connected to the reservoir below. Accounting for the friction \(\alpha _r \cdot {q_{r,t}^P}^2\), where \(\alpha _r\) is a constant friction factor, the net head becomes

$$\begin{aligned} h_{r,t}^{\textit{NET}}=\ell _{r}\left( v_{r,t}\right) -L_r-\alpha _r \cdot {q_{r,t}^P}^2. \end{aligned}$$
(4)

Scaled by the turbine efficiency \(\eta _{r}^{\textit{TURB}}\left( h_{r,t}^{\textit{NET}}, q_{r,t}^P\right) \) and the generator efficiency \(\eta _{r}^{\textit{GEN}}\left( p_{r,t}\right) \), the power production \(p_{r,t}\) is given by

$$\begin{aligned} p_{r,t} = \rho \cdot g \cdot \eta _{r}^{\textit{GEN}}\left( p_{r,t}\right) \cdot \eta _{r}^{\textit{TURB}}\left( h_{r,t}^{\textit{NET}}, q_{r,t}^P\right) \cdot h_{r,t}^{\textit{NET}} \cdot q_{r,t}^P, \end{aligned}$$
(5)

where the constant water density and gravity are denoted \(\rho \) and g, respectively.

When a unit is turned off, the corresponding production and discharge variables equal zero. Otherwise, their values are constrained within some interval between lower and upper bounds. For the production and discharge at plant r, the bounds, denoted \(P_{r}^{\min }\), \(P_{r}^{\max }\), \(Q_{r}^{\min }\), and \(Q_{r}^{\max }\) respectively, are assumed to be constant. Defining \(\omega _{r,t}\) as a binary variable indicating whether or not the unit is operating in period t, we hence arrive at the inequalities

$$\begin{aligned} P_{r}^{\min }\cdot \omega _{r, \, t}\le & {} p_{i,s,t} \le P_{r}^{\max }, \end{aligned}$$
(6)
$$\begin{aligned} Q_{r}^{\min }\cdot \omega _{r, \, t}\le & {} q_{r,t} \le Q_{r}^{\max }\cdot \omega _{r,t}. \end{aligned}$$
(7)

constraining power and discharge, respectively.

Finally, the power balance constraint says that the total production sums up to the total sale:

$$\begin{aligned} \sum _{r \in R} p_{r,t} = p_t^{\textit{SALE}} \end{aligned}$$
(8)

2.2 Overflow model

Whereas the discharge from production and bypass represents explicit decisions, the overflow is a consequence of a full reservoir and can only be controlled implicitly by adjusting the production and bypass into and out of a reservoir. The overflow typically represents a water flow over a crest, where the relation between the flow q and the water level above the crest h is

$$\begin{aligned} q = C \cdot L \cdot h^\frac{3}{2}, \nonumber \end{aligned}$$

where C is a friction coefficient and L the crest width [10]. In its turn, the water level is a function of the volume of the reservoir, and a typical correspondence between volume and overflow is illustrated by the curve in Fig. 1.

Fig. 1
figure 1

Overflow as a function of volume

Full size image

Denote by \(V_r^{\max }\) the maximum volume of reservoir r before overflow occurs, and assume that the overflow is a function of the excess volume. Let \(VS_{r,i}, QS_{r,i}\) denote points of a piecewise linear approximation of the flow curve with I segments. The minimum overflow can then be expressed as

$$\begin{aligned} QS_{r,0}&= 0 \end{aligned}$$
(9)
$$\begin{aligned} VS_{r,0}&= V_r^{\max } \end{aligned}$$
(10)
$$\begin{aligned} q_{r,t}^S&\ge QS_{r,i} + \frac{QS_{r,i+1} - QS_{r,i}}{VS_{r,i+1} - VS_{r,i}} \cdot (v_{r,t}-VS_{r,i}), i \in \{1, \ldots ,I\} \end{aligned}$$
(11)
$$\begin{aligned} q_{r,t}^S&\le Q_r^{S,\max }. \end{aligned}$$
(12)

A weakness of the formulation is that \(q_{r,t}^S\) may be positive even when \(v_{r,t} < V_r^{\max }\), and this phenomenon is referred to as nonphysical overflow, reflecting that it does not make physical sense. To reduce this effect, \(q_{r,t}^S\) is often penalized in the objective. Nevertheless, nonphysical overflow may still occur in some situations which will be further explained in the experimental results in Sect. 4.

A possible approach to avoid nonphysical overflow is introducing a binary variable \(\delta _{r,t}\), which takes the value 1 if \(q_{r,t}^S\) is nonzero. To that end, the constraints

$$\begin{aligned} q_{r, \, t}^S\le & {} Q_{r,t}^{S,\max }\cdot \delta _{r,t}, \qquad \qquad \text {and} \end{aligned}$$
(13)
$$\begin{aligned} q_{r, \, t}^S\le & {} \frac{Q_r^{S,\max }}{VS_r^{\max } - V_r^{\max }} \cdot (v_{r,t} - V_r^{\max } \cdot \delta _{r,t}), \end{aligned}$$
(14)

where \(VS_r^{\max }=VS_{r,I}\), are imposed. Constraint (13) forces the overflow variable \(q_{r,t}^S\) to zero if \(\delta _{r,t}=0\). Constraint (11) and (14) further ensure that if \(\delta _{r,t}=1\), then \(q_{r,t}^S\) stays within the light gray area in Fig. 1.

Owing to the computational burden introduced by the new binary variables, common practice in the industry is to relax the integrality constraint, and allow fractional values of all variables \(\delta _{r,t}\) yielding the feasible region illustrated by the light and dark gray area in Fig. 1. Without prior knowledge to any lower bound on the reservoir volume beyond \(V_r^{\max }\), the figure illustrates the tightest possible convex relaxation of this problem. Access to any stronger bound, however, enables a closer linear approximation of the non-linear curve, and thereby a stronger relaxation. The benefit of an approach involving relaxation of the integrality restrictions is a considerably easier problem to solve than the mixed-integer formulation, but comes with a risk of nonphysical overflow.

2.3 Linearization

To arrive at a computationally tractable model, all nonlinear functions that appear in any of the constraints discussed in Sect. 2.1 are linearized. Linearization techniques adopted from [9] are applied:

  • The discharge bound functions \(Q_{r}^{\min }\) and \(Q_{r}^{\max }\) appearing in (7) are approximated by piecewise linear functions. That is, the set of feasible values \(q_{r,t}^P\) can attain is partitioned into a finite set of intervals. A binary variable is associated with each interval, and corresponds to the decision whether or not to assign \(q_{r,t}^P\) a value in the interval. The sum of these variables is, for each nonlinear function, bounded above by one. Within each interval [l, u], \(Q_{r}^{\min }\) is replaced by a linear function interpolating \(\left( l,Q_{r}^{\min }(l)\right) \) and \(\left( u,Q_{r}^{\min }(u)\right) \), and \(Q_{r}^{\max }\) is handled analogously.

  • The relation between production \(p_{r,t}\) and discharge \(q_{r,t}^P\) becomes a concave and monotonously increasing curve when the efficiencies \(\eta _r^{\textit{GEN}}\) and \(\eta _r^{\textit{TURB}}\) are taken into account. The efficiencies are given as a set of points based on measurements of the specific generator and turbine. The said shape of the curves is exploited in a piecewise linear approximation, written

    $$\begin{aligned} p_{r,t}&= \sum _{s \in S} a_{s,r, \, t} \cdot q_{s,r, \, t}^P, \end{aligned}$$
    (15)
    $$\begin{aligned} q_{r,t}^P&= \sum _{s \in S} q_{s,r, \, t}^P, \end{aligned}$$
    (16)

    where S is a set of integer segment indices, \(q_{s,r,t}^P\) is the discharge contribution from segment \(s\in S\), and \(a_{s,r,t}\) is the slope of the curve in segment s. Because \(a_{s,r,t}\) is decreasing with increasing segment index, it is also optimal to assign positive values uniquely to \(q_{s,r,t}^P\) for a set of consecutive segments, starting with the smallest index value.

  • All other nonlinear functions are processed by means of a SLP technique. In short, this implies that a sequence of linear approximations to the model are solved. In the first iteration, an initial guess of the values of all variables occurring in the functions is made. The functions are next replaced by a first order Taylor approximation in the guessed point. An optimal solution to the resulting linear model yields the next linearization point, and the procedure is continued until convergence (two consecutive solutions are sufficiently close).

More involved hydro production functions than those considered in the current work fail to satisfy the concavity condition exploited in (15)–(16). As a consequence, piecewise linear approximations require the introduction of a binary variable for each segment in question. Because the extension applies to all time periods and all reservoirs, it implies a significant increase in the computational burden. Readers are referred to Borghetti et al. [11] and Diniz and Maceira [12] for examples of MILP models incorporating piecewise linear approximations to non-concave production curves.

3 Tight formulations of overflow constraints

It is well known that the computational performance of integer programming models may depend heavily on the formulation of the constraints. Nevertheless, Belotti et al. [13] argue that aggressive bound tightening is often overlooked in works on such models. With a problem in supervised classification as an example, it is demonstrated in [13] how significantly the constraint formulation may impact the running time. Their approach is pursued and further developed in [14].

In this section, we focus on how the constraints involving the binary variables controlling the overflow can be formulated in a way that favors fast solution. Particular attention is given to inequality (13), to which \(q_{r,t}^S\le M_{r,t}\cdot \delta _{r,t}\) is an equivalent formulation, given that \(M_{r,t}\) is a sufficiently large number. For a tight formulation, a small value should be assigned to \(M_{r,t}\), but it is essential that \(M_{r,t}\) (in popular terms, referred to as the ‘big-M’ coefficient) is not so small that the constraint cuts off feasible solutions.

3.1 Computing an upper bound on the overflow

As long as \(M_{r,t}\) is no larger than the maximum possible overflow at reservoir r in period t, the inequality \(q_{r,t}^S\le M_{r,t}\cdot \delta _{r,t}\) is valid. An estimate of the maximum is therefore helpful in cutting the running time of the model, and a heuristic estimation method is given next.

Recall from Sect. 2.3 that the SLP procedure involves solving a sequence of linear problem instances. For SLP iteration j, the idea is to use the solution from the previous SLP iteration \(V_{r,t}^{j-1}\) plus a tolerance to approximate \(M_{r,t}\). However, there exists no previous solution in the first iteration, and hence it must be approximated. By assuming maximum discharge into and minimum discharge out of the reservoir for each timestep, we obtain Eq. (17) and (18):

$$\begin{aligned} V_{r,0}^0&= V_r^{INIT}, \end{aligned}$$
(17)
$$\begin{aligned} V_{r,t+1}^0&= V_{r,t}^0 + Q_{r,t}^{INFLOW} - f_r(V_{r,t}^0)+ \sum _{i \in D_r^{UP}} Q_{i,t}^{MAX} - \sum _{i \in D_r^{DOWN}} Q_{i,t}^{MIN}, \end{aligned}$$
(18)

where \(D_r^{UP}\) denotes the set of plants and gates discharging into reservoir r, \(D_r^{DOWN}\) an analogous set for discharge out of reservoir r, and \(Q_i^{MAX}, Q_i^{MIN}\) the maximum and minimum possible discharge from element i, respectively. Given the inflow, the overflow function and the minimum and maximum discharge for gates and plants are known, \(V_{r,t}^0\) can be computed sequentially for increasing values of t.

The difference between the current reservoir volume and the volume \(V_r^{\max }\) at which overflow occurs constitutes an upper bound on the overflow. Consequently, the heuristic approach is to let \(M_{r,t}=(1+g^0)\cdot V_{r,t}-V_r^{\max }\) for some (small) positive number \(g^0\). Multiplying \(V_{r,t}\) by \(1+g^0\) accounts for the risk of inaccuracy in \(V_{r,t}\) as an estimate of the actual reservoir volume, and helps to avoid feasible solutions being cut off.

In other iterations but the first of the SLP procedure, the volume estimate is rather given as the optimal value \(v_{r,t}^{*}\) of the volume variable \(v_{r,t}\) obtained in the preceding iteration. Then, the bound is set to \(M_{r,t}=(1+g^1)\cdot v_{r,t}^{*}\), where \(g^1\) is a small positive number, possibly different from \(g^0\).

4 Experimental results

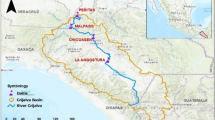
The proposed method has been implemented in the short-term optimization model SHOP [15] that is developed by SINTEF Energy Research, and has been tested on the Fossdal watercourse in Norway, illustrated in Fig. 2, which is operated by Eviny Fornybar AS. The upper reservoir, Gråsidevatn, discharges water into Fossdalsvatn through a gate, and the released water is delayed by up to three hours. Overflow from Gråsidevatn also goes to Fossdalsvatn, but the overflow has a delay up to 48 h. The overflow from Fossdalsvatn goes to the sea. The reservoir sizes are \(0.6 Mm^3\) and \(1.25 Mm^3\) for Gråsidevatn and Fossdalsvatn, respectively, and the plant maximum production capacity is 8.85MW. The water value in this experiment is 9.76 €\(/MWh\), which is below the electricity price for the whole optimization period.

Fig. 2
figure 2

Fossdal watercourse topology

Full size image

This system occasionally experiences nonphysical overflow, as illustrated in Fig. 3. We observe a spike in the overflow around day 12 when using the convex relaxation, which does not make physical sense. At the same time, Fig. 4 shows abrupt changes to the head at both reservoirs. In contrast, the MILP formulation effectively avoids nonphysical overflow yielding a smooth overflow curve consistent with the reservoir inflow. Gråsidevatn has a high initial level and a high inflow, and the bypass capacity is too low to avoid overflow. When using the linear relaxation, the overflow variable appears as an additional gate that can increase the discharge capacity. In many situations, nonphysical overflow is avoided due to the overflow penalty. However, in situations where overflow is unavoidable, shifting the overflow in time can improve the objective function. The end level of Gråsidevatn is equal for both cases, hence the total overflow and overflow penalty are equal. However, with the nonphysical overflow, the overflow reaches Fossdalsvatn by the end of the optimization period enabling Fossmark to produce more than what is the case of the more physically correct model. In all experiments, the first three iterations are spent finding a stable unit commitment using integer variables for the power production, followed by three iterations adjusting the production given the unit commitment is known. This solution methodology is described more in detail in [8]. The instances solved in the first three iterations have 13.364 variables and 6.254 constraints, where 314 variables are binary. Using overflow MIP gives additional 672 binary variables. In the final three iterations, the MIP-instances have 8.750 variables and 4.533 constraints, where there are no binary variables except from the 314 overflow MIP variables.

Fig. 3
figure 3

Market price, and inflow and overflow at Gråsidevatn

Full size image
Fig. 4
figure 4

Reservoir head compared to higher- and lower regulated levels

Full size image

The use of integer variables to avoid nonphysical overflow has a significant disadvantage with respect to solving time of the MILP problem. Whereas the linear model using 6 SLP iterations is solved within a few seconds, the corresponding MILP model takes up to around 300 s to solve for the same number of iterations, and the solving times grows even more than the problem size as shown in Fig. 5. When applying the proposed heuristic to dynamically update the value of \(M_{r,t}\), the solving time is reduced to less than 40 s.

Fig. 5
figure 5

Solving time with static big M value compared to proposed dynamic big M

Full size image

Since the solving time is sensitive to the numerical input, the experiment has also been repeated with low and high inflow, where the original inflow has been scaled with factors 0.5 and 1.5, respectively. Moreover, since the initial reservoir level is high in the base case, two additional combinations with medium and low initial reservoir storage have been added, where the volume has been scaled with factors 0.5 and 0.2, respectively. The total number of experiments will therefore sum up to nine and the resulting solving times are summarized in Table 1.

Table 1 Solving time for linear relaxation, MIP and dynamic big M for different combinations of inflow and initial reservoir volumes
Full size table

The results show that the MIP solving time increases more with high inflow and high initial reservoir level. In all situations, the dynamic assessment of the big-M coefficient reduces the solving time. In the low-low scenario (low inflow, low initial storage), overflow does not occur at all and the overflow MIP has no effect.

The value \(g^i\) in the experiments adds a tolerance to the approximated value of big-M to prevent too tight bounds resulting in an infeasible model formulation or penalties in the solution. The sensitivity of this value with respect to computation time has therefore been assessed. Figure  6 shows how the solving time changes for increasing value of \(g^i\).

Fig. 6
figure 6

Change in solving time (y-axis) for different values of \(g^i\) (x-axis). Left figure shows for the first MIP iteration of the optimization where a distinct heuristic is used, while the right figure shows the average solving time for remaining MIP iterations

Full size image

For the first iteration in the left part of Fig. 6, where a different heuristic has been used, the change in solving time is rather irregular. For the remaining iterations, there is a clear connection between the tightness of the big-M coefficient and the solving time. Further reductions in the tolerance would incur a reservoir penalty, which means that the model formulation is too strict such that the water has no way to escape in case of overflow.

5 Discussion

The solving time in the demonstrated case can be reduced significantly by lowering the values of the big-M coefficients. However, the proposed heuristic is not guaranteed to work for other numerical inputs of the given system, nor for more complex watercourses. A main challenge is therefore to obtain both tight and robust coefficients, especially in the first iteration where there exists no good initial solution. The hydropower scheduling problem is typically solved multiple times every day as new information becomes available, and hence, solutions from previous runs may provide a good starting point for such a heuristic approach.

Methods in the domain of artificial intelligence have recently gained increased interest as supplementary methods to formal optimization, and [16] demonstrates that they can be used to improve the inputs to the formal optimization in a systematic way.

6 Conclusion

Risk of overflow influences the short-term operation of hydropower systems, and accurate physical descriptions of the watercourses are necessary to provide optimal operation plans that respect the limitations of the system. In this paper, we address a common problem associated with the use of a relaxation to describe overflow in real-life operation planning. We present an alternative MILP formulation that prevents model errors like overflow from reservoirs that are not full. The proposed formulation is implemented in the short-term hydro scheduling model SHOP from SINTEF Energy Research, which applies SLP to manage non-linearities. We also present a heuristic for updating the coefficient of the new integer variable. The results show that the MILP formulation effectively prevents nonphysical overflow, but that introducing integer variables increases the solving time of the MILP problems from a few seconds to around 30 min for a relatively small case. However, by using the proposed heuristic to update the so-called big-M coefficient of the integer variable reduces the solving time by more than 90%.

Solving time of the proposed MILP formulation is sensitive to how the big-M coefficients are assessed, and hence, the coefficients need to be chosen carefully. The presented results consider a relatively small system, and deriving tight but still feasible upper bounds on the overflow variables will be more difficult in more complex systems. Moreover, it is also important to emphasize that there is no guarantee that larger systems will achieve a similar reduction in solving time. Therefore, to arrive to more solid conclusions, applications to larger systems need to be addressed in future work.