Introduction

Landslides are one of the most common natural events in Türkiye, especially after earthquakes. Given Türkiye's active tectonic characteristics, earthquakes are expected to be an important triggering factor for landslide occurrence. However, it is well known that precipitation is also a significant factor contributing to landslides in Türkiye. The Black Sea Region of Türkiye is particularly susceptible to landslides due to the triggering effect of precipitation, as well as its geological, topographical, and environmental factors. As a result, both the western and eastern parts of the region have become attractive areas for landslide researchers in Türkiye (Baltacı et al. 2010; Akçalı 2011; Akçalı and Arman 2013; Dağ et al. 2020; Akinci et al. 2021; Keles and Nefeslioglu 2021; Kavzoglu and Teke 2022; Sahin 2022).

A review of the landslide susceptibility literature shows that a significant number of studies have been conducted in the last two decades (Chen et al. 2019; Chang et al. 2023; Liu et al. 2022; Pourghasemi et al. 2012; Pradhan 2010; Regmi et al. 2014; Sun et al. 2021; Wu et al. 2020; Yilmaz 2009; Yi et al. 2022; Zhang et al. 2023; Zhu et al. 2020). In these studies, researchers have concentrated their efforts in different parts of the world, especially in areas with steep geomorphology dominated by hydro-meteorological conditions and favorable predisposing geological and environmental factors. When an overview of these studies is provided, it is seen that they have carried out landslide susceptibility mapping for the relevant areas by using different modeling methods considering the mentioned conditions. Among these modeling tools, logistic regression (Bhardwaj and Singh 2023; Boussouf et al. 2023; Can et al. 2005; Chen and Yang 2023; Chen et al. 2016, 2017, 2019; Liu et al. 2022; Rai et al. 2022; Sun et al. 2021; Yilmaz 2009), artificial neural networks (Adnan Ikram et al. 2023; Can et al. 2019; Choi et al. 2010; Conforti et al. 2014; Ermini et al. 2005; Kalantar et al. 2018; Moayedi et al. 2023; Nefeslioglu et al. 2008; Selamat et al. 2022; Yi et al. 2022), fuzzy set membership rating (Kumar and Anbalagan 2015; Okoli et al. 2023; Pradhan 2010; Shahabi et al. 2015; Zhang et al. 2023; Zhu et al. 2020), decision tree (Miao et al. 2023; Nefeslioglu et al. 2010; Saygin et al. 2023; Tsangaratos and Ilia 2016; Wu et al. 2020), analytical hierarchy process (Bahrami et al. 2021; Cengiz and Ercanoglu 2022; El Jazouli et al. 2019; Hsekioğulları and Ercanoglu 2012; Okoli et al. 2023; Pourghasemi et al. 2012; Saygin et al. 2023), multivariate and bivariate statistics such as frequency ratio, expert opinion-based and heuristic methods have come to the fore to a considerable extent. However, when we look at the studies in the last decade, it is also seen that there has been a significant increase in the widespread use of machine learning methods (Al-Shabeeb et al. 2022; Chang et al.2023; Chen et al. 2018; Ganesh et al. 2023; Goetz et al. 2015; Kavzoglu et al. 2019; Liu et al. 2023; Merghadi et al. 2020; Nanehkaran et al. 2023; Pham et al. 2016). Of course, the main purpose of this methodological richness can be considered as the determination of the advantages or weaknesses of the methods, as well as the highest accuracy of the landslide susceptibility maps to be produced for the studied areas.

It should be emphasized that methods based on physical models such as Shalstab, Sinmap, TRIGRS (Akgun and Erkan 2016; Cabral and Reis 2021; Ciurleo et al. 2019, 2021; do Pinho and Augusto Filho 2022; Ji and Cui 2023; Michel et al. 2014; Nery and Vieira 2015; Pradhan and Kim 2015; Rana and Babu 2022; Vieira et al. 2018; Wei et al. 2023), which are not among the methods mentioned above, are used much less frequently compared to other methods. The main reason for this is that it takes relatively more time and effort to obtain the material parameters needed as a requirement of the method. However, it should be emphasized that these methods should also be taken into consideration since the results obtained fill an important gap such as the lack of material properties and hydrological-hydrometeorological parameters in the results obtained by probabilistic methods.

In this study, we focus on the eastern part of the Black Sea Region, specifically the Beşikdüzü district of Trabzon province. This region is highly susceptible to shallow slip and flow type mass failure and flood events, as evidenced by a large number of incidents that occurred on September 21, 2016. Due to the sensitivity of the region to similar processes and the frequency of such incidents, numerous susceptibility, hazard, and risk assessment studies have been carried out by researchers in the region (Akgun and Bulut 2007; Akgun et al. 2008; Nefeslioglu et al. 2011; Dağ and Bulut 2012; Kavzoglu et al. 2014).

Despite the previous studies (Akgun and Erkan 2016; Keles and Nefeslioglu 2021), however, most of these assessments were based on probabilistic models rather than physical data. This study seeks to address this gap by conducting a landslide susceptibility assessment based on physical data for the Besikduzu district. We compare our findings with previous studies to provide a more comprehensive understanding of the processes and better solutions for managing potential disasters in the future.

Study area

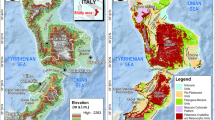
The study area, situated in the Eastern Black Sea part of the Black Sea Region, encompasses approximately 121 km2 (Fig. 1). This district exhibits the highest level of precipitation, with a long-term average (1927–2021) of 828.9 mm (URL 2020). The region's steep topographical characteristics, weathering conditions of lithological units, heavy precipitation, and misuse of land cover contribute to the frequent occurrence of shallow-seated landslides.

Fig. 1
figure 1

Location map of the study area by a digital elevation model

Full size image

Analysis of lithological units in the study area (Fig. 2) reveals the presence of units with ages ranging from Middle-Upper Eocene to Quaternary. The oldest units are composed of Middle-Upper Eocene-aged basalt-andesites, their pyroclastics, and alternation of sedimentary rock units (Tek). The youngest units consist of Quaternary-aged alluviums (Qal) (Güven 1993; Akbaş et al. 2011).

Fig. 2
figure 2

Lithological map of the study area (modified from Güven 1993; Akbaş et al. 2011)

Full size image

Data and methods

The focus of this study was on spatial data, with an emphasis on two important facets: the mapping of shallow landslide inventory and the production of conditioning factors. These two facets together comprise the dataset for analyses and will be further discussed in the following sections.

Shallow landslide inventory mapping

The previous occurrences of landslides in a region play an important role in further landslide susceptibility analyses (Varnes 1984). Therefore, landslide inventory mapping is an essential step in landslide susceptibility assessments. However, carrying out field surveys to ascertain exact locations and the damage caused is challenging due to inaccessibility and time constraints. With advancements in remote sensing (RS) and geographic information system (GIS), mapping landslides has become relatively quick and easy (Sachdeva et al. 2020).

To produce the landslide inventory for the study area, temporal satellite images from the Google Earth application were utilized (Google Earth Pro 2020). The inventory includes shallow landslide locations that occurred between 2000 and 2018, and a total of 117 such locations were identified by inspecting the temporal satellite images of the study area using Google Earth Pro. 8 landslides locations taken from General Directorate of Mineral Research and Exploration landslide inventory (Duman et al. 2007). The visual interpretation focused mainly on changes in vegetation cover, which changes quickly in the region. To verify these landslide locations, newspaper articles, technical reports, and interviews with local people were also used.

The landslide inventory was randomly split into a training dataset comprising 88 landslide locations and a testing dataset with 37 shallow landslide locations. A sample of the training and testing landslide and non-landslide locations used in the study is shown in Fig. 3.

Fig. 3
figure 3

Landslide inventory map of the area

Full size image

As a result of the inventory mapping study, a total of 125 shallow landslide locations were identified, with 8 occurring before 2005 and 117 mapped between 2000 and 2018 (Tezel 2021). The areal extent of these shallow seated landslides ranged from 53.28 to 902,809 m2. Given the absence of definitive records regarding the main triggering factors for these shallow landslides, precipitation is accepted as the unique triggering factor, given the high annual average precipitation rate of 828 mm in the area. This result is also consistent with field observations made in the area after heavy precipitation cases. These mapped shallow landslides were also checked on-site during field studies carried out in August 2017 and September 2018 (Fig. 3), and the approximate depths of the earthflows were determined to be between 3 and 10 m, with an average of 5 m, based on direct field measurements. Almost all of these shallow landslides were found to be located in hazelnut plantation areas, which are the most important agricultural product for the region (Fig. 4).

Fig. 4
figure 4

Some field views for the shallow landslides mapped in the study area

Full size image

During the digitization of the shallow landslides on the satellite images obtained from Google Earth, both the depletion and accumulation zones were drawn as polygons. Although there is no consensus on the best landslide sampling strategy, a few studies have been carried out for this purpose (Suzen and Doyuran 2004; Gorum et al. 2008; Yilmaz 2010; Nefeslioglu et al. 2011; Dagdelenler et al. 2016). Dagdelenler et al. (2016) provided detailed explanations on this issue. Considering the suggestions made in this study, buffer zones of 50 m were drawn around the earthflow polygons. Then, only the main scarp portions of these buffered polygons, which are recognized as the landslide occurrence area, were distinguished for use in the modeling and validation stages of the predicted results.

Multicollinearity analysis of conditioning factors

According to Yange et al. (2020), the presence of multicollinearity, particularly among multiple variables in regression analysis, can lead to various issues such as instability in parameter estimates, counterintuitive parameter signs, elevated coefficient of determination (R2) diagnostics despite few or no significant parameters, and other challenges (Fotheringham and Oshan 2016). Given the intricate nature of landslide data and the complex interplay between geological and topographical factors, a careful consideration of multicollinearity is crucial in landslide susceptibility assessment (Yange et al. 2020).

To address this concern, a thorough multicollinearity analysis was conducted to examine the correlation among the landslide conditioning parameters. Multicollinearity, defined as a statistical scenario characterized by a high correlation between two or more predictor variables in a multiple regression model (O'brien 2007; Wang et al. 2019), was assessed in this study. Specifically, tolerance (TOL) and variance inflation factor (VIF) were employed to gauge the extent of multicollinearity among the conditioning parameters, focusing exclusively on DEM derivative parameters.

Let X = {X1, X2,…,XN} represent the given independent variable set, and Rj2 denote the coefficient of determination when the jth independent variable Xj is regressed on all other predictor variables in the model. The VIF value was computed using the formula:

$${\text{VIF }} = { 1}/\left( {{1} - {\text{R}}_{{\text{j}}}^{{2}} } \right)$$
(1)

The TOL value is the reciprocal of the VIF value and represents the degree of linear correlation between independent variables (Wang et al. 2019). If the VIF value is higher than 10 or the TOL value is lower than 0.1, the corresponding factors are multicollinearity and should be eliminated from the landslide susceptibility models.

The reciprocal of the VIF value is the TOL value, representing the degree of linear correlation between independent variables (Wang et al. 2019). If the VIF value exceeds 10 or the TOL value falls below 0.1, it indicates the presence of multicollinearity, prompting the need to eliminate the corresponding factors from the landslide susceptibility models.

The multicollinearity analysis yielded TOL and VIF values, which are presented in Table 1. Based on these values, it was determined that there was no evidence of multicollinearity among the DEM derivative parameters used in the models. This suggests that the selected parameters maintained sufficient independence in the regression analysis, ensuring the reliability of the landslide susceptibility assessment.

Table 1 Multicollinearity analysis results for the DEM derivative landslide conditioning factors
Full size table

Conditioning factors

In this study, the main conditioning factors for shallow landslides were parameters such as lithology, slope gradient, slope aspect, stream power index (SPI), topographical wetness index (TWI), as well as plan and profile curvature (Fig. 5) (ArcGIS 2018; SAGA 2019).

Fig. 5
figure 5

Landslide conditioning factors considering for the study area

Full size image

Lithology

The lithology map of the study area at a scale of 1:25.000, prepared by Güven (1993; Akbaş et al. 2011), was used in this study (Fig. 5a). The analysis of the spatial distribution of shallow landslides shows that all of the movements occurred in the study area are confined to Eocene-aged andesite-basalt and pyroclastics units, which are highly weathered.

Slope gradient

The study utilized a slope gradient map, produced using a 10 m resolution digital elevation model (DEM) (Fig. 5b), and categorized into different classes to determine gradient intervals.

The spatial distribution of these classes, including those with earthflow and slide occurrences, were determined and presented in Table 2. Low and moderate gradient values, ranging from 20 to 30°, were found to be the most abundant in the study area, making up approximately half of them with 47%. Analysis of past landslide occurrences revealed that 91% of landslides occurred on slopes with moderate gradient, ranging from 10° to 40°.

Table 2 Frequency ratio values of landslide conditioning factors
Full size table

Slope aspect

The slope aspect map, an important parameter for an area prone to heavy rainfall, was generated using a numerical elevation model (Fig. 5c) and classified into nine different classes. Table 2 presents these classes and their corresponding spatial distribution of landslide studies.

Analysis of landslide distribution showed a proportionally similar distribution regarding general gradient aspect class.

Stream power index (SPI)

The stream power index (SPI) parameter, a secondary derivative of topographic data, was used to describe potential flow erosion and related landscape processes (Moore et al. 1991). The SPI was calculated using the equation given below (Eq. 2), taking into consideration the relationship between slope gradient and drainage area (Lee and Min 2001; Gokçeoglu et al. 2005).

$$SPI \, = \, A_{S} \times \, \tan \beta$$
(2)

whereas gives the specific basin area (m2/m) and β is the gradient value in degrees.

The SPI map in Fig. 5d, indicated that areas with a low SPI index comprised over half of the study area, while areas with high SPI index values had a spatial distribution of approximately 16%.

Analysis of landslide spatial distribution revealed that around 70% of landslides occurred in areas with SPI index values less than 222 (Table 2).

Topographical wetness index (TWI)

The topographic wetness index (TWI) is an important parameter for evaluating the probability of water content increase on slopes and determining lithological units susceptible to landslides. It is calculated using the specific basin area (As) and gradient value (β) in degrees according to the equation given by Beven and Kirkby (1979):

$$TWI \, = \, \ln \, \left( {A_{S} /\tan \beta } \right)$$
(3)

Using the numerical elevation model for the upper section of the study area, the TWI map was generated and divided into 5 classes as shown in Table 2 and Fig. 5g. The data indicate that the study area has landslide spatial distribution close to each other in all TWI classes.

Slope curvature

The slope curvature maps for the study area were generated based on the numerical land model and is presented in Fig. 5e, f. While negative values represent concave slopes, positive values represent convex slopes for profile curvature, the same representation is opposite for the plan profile. 0 represents flat surfaces both profile and plan curvatures. The data in Table 2 indicates that almost equal motion development was observed on concave and convex slopes on both maps in the study area.

Modeling methods

Logistic regression

Logistic regression is a statistical method that establishes a multivariate regression relationship between a dependent variable and several independent variables (Lee 2005). In landslide susceptibility mapping studies, the purpose of logistic regression is to find the most appropriate model to describe the relationship between the dependent variable (presence or absence of a landslide) and independent parameters such as slope and lithology (Ayalew and Yamagishi 2005). The relationship between occurrence and its dependence on multiple variables can be expressed numerically as follows (Hosmer and Lemeshow 1989):

$$p = 1/\left( {1 + e^{( - z)} } \right)$$
(4)

Here, "p" represents the probability of landslide occurrence, and "z" is the linear combination of the independent variables. Logistic regression includes an equation shown in the form below, which corresponds to the "z" value given above:

$$z \, = \, b_{0} + \, b_{1} X_{1} + \, b_{2} X_{2} + \cdots + \, b_{n} X_{n}$$
(5)

Here, "b0" is the constant of the model, "bi" values (i = 0,1,2,…, n) are the slope coefficients of the logistic regression model, and "xi" values (i = 1,2, …, n) are the independent variables. This linear model shows the occurrence (yes/no) of the landslide based on the pre-occurrence conditions of the independent variables. The probability of landslide occurrence ranges from 0 to 1 and is expressed as an S-shaped curve.

Random forest

Random Forest is a popular ensemble method that combines multiple decision trees trained with different subsets of data to improve accuracy and reduce overfitting (Breiman 2001). Unlike traditional decision trees, which select the best split for each node based on all available features, Random Forest selects the best split based on a random subset of features. The trees are grown without pruning, and predictions are made by averaging the results of all trees in the forest (Archer 2008; Breiman 2001) (Fig. 6).

Fig. 6
figure 6

The basic working principle of the Random Forest algorithm (Şahin 2018)

Full size image

The algorithm uses the Gini index method to measure the homogeneity of classes at each split. The Gini index measures the probability of misclassification, and a lower Gini index value indicates a more homogeneous split. The algorithm stops splitting a node when the Gini index reaches zero, or when a specified depth or minimum number of samples per leaf is reached.

The Random Forest algorithm requires two parameters to be specified: the number of variables used for each split (m) and the number of trees in the forest (N). The algorithm is flexible and can handle both continuous and categorical variables (Watts et al. 2011).

Shalstab mathematical model

The Shalstab model is a mathematical model that combines the infinite slope and stable hydrological models to predict the potential for slope failure (Dietrich and Montgomery 1998). The model is an add-on to ArcView 3.x Geographic Information Systems software and determines stability classes based on height, slope, and drainage network data from the Digital Elevation Model (see Table 3).

Table 3 The relative importance of parameters
Full size table

Equation 6 of the model is used to calculate the h/z value (saturated soil layer) required for mass failure development. The equation considers soil parameters, slope angle, and water table height. If h/z equals 0, then the slope is absolutely unstable, and if h/z is equal to 1, the slope is absolutely stable. Partial ground saturation leads to slope failure when the slope is neither absolutely unstable nor stable (see Table 4).

$$h/z \, = \, \delta_{s} /\delta_{w} (1 - \tan q/\tan ) \, + \, c/\cos^{2} q\tan \delta_{w} g \, z$$
(6)
Table 4 Representation of the stability classes obtained in the Shalstab model (Michel et al. 2014)
Full size table

The Shalstab model combines the infinite slope and stable hydrological models to predict slope failure. The final formula of the model is produced by modifying Eq. 6 according to the q and T parameters. The model requires cohesion (c), internal friction angle (f), dry density (gs), and total soil thickness (z) as input parameters. Other variables such as slope drainage area, contour length, and slope gradient are determined through the digital elevation model.

$$q \, a/T \, b \, \sin q = \, \delta_{s} / \, \delta_{w} (1 - \tan q/\tan ) \, + \, c/\cos^{2} q\tan \delta_{w} g \, z$$
(7)

The model classifies the area into seven classes of instability based on the hydrological ratio (q/T) required to ensure instability. The two extreme classes are absolutely unstable and absolutely stable, and the other five classes emerge as a function of q/T among them. Refer to Table 6 for more information on the classes of instability.

$$q/T = b/a \, \sin q[\delta_{s} /\delta_{w} (1 - \tan q/\tan ) \, + \, c/\cos^{2} q\tan \delta_{w} g \, z]$$
(8)

To fulfill the input requirements of the Shalstab mathematical model, it is necessary to ascertain certain physical properties of landslides. In identifying suitable locations for sampling, susceptibility maps were overlaid, focusing on areas categorized as "high" and "very high" sensitivity across all maps within slope units. Subsequently, following the removal of the overlying vegetable soil layer (approximately 0.10–0.20 m), samples were collected both in a disturbed manner using shovels and undisturbed using sampler tubes driven into the ground and then extracted. All tests were conducted at the Applied Geology Laboratory of the Department of Geological Engineering at KTU.

In the laboratory, the initial step involved determining the natural and dry densities of the samples, adhering to the ASTM (D7263-09 2018) test standard. Wet sieve analyses and hydrometer tests were then performed following the (ASTM D422-63 1998) standard. For disturbed samples, liquid limit values were assessed using the falling cone method (penetration) as per the BS (1377-2:4.3 1990) standard, while plastic limit values were determined in accordance with the ASTM (D4318-17e1 2017) standard.

To ascertain shear strength parameters, direct shear tests without consolidation and drainage (UU) were executed, aligning with ASTM D3080/D3080M–11 (2011) test standards. The choice of the UU test was motivated by the absence of soil consolidation and impractical groundwater drainage conditions in the field.

The Unified Soil Classification System (USCS) (ASTM D2487-11 2011) was used to classify the soil types, and the permeability coefficients were calculated. Transmissibility (T) values were then computed using the permeability coefficient (K) (m/s) and the average floor profile thickness (z) as shown in Eq. 8, where K is given in m/day:

$$T \, = \, K \, * \, z$$
(9)

The susceptibility classes obtained from the Shalstab model were reclassified into sensitivity classes (very low, low, medium, high, and very high) similar to those obtained by LR and RF methods. Akgün and Erkan (2016) approach was used to achieve this reclassification.

Results

To assess susceptibility, landslides were prepared using the "seed cell sampling strategy" method (Suzen and Doyuran 2004). This method aims to obtain the best undisturbed morphological conditions from the periphery of the landslide polygon by adding a buffer zone to the top and sides of the landslides. According to Suzen and Doyuran (2004), the buffer distance should be selected based on the distance between the slip boundary and the micro-catchment separation line, as well as the spatial resolution. Dagdelenler et al. (2016) used different buffer distances and spatial resolutions with this method in a landslide susceptibility study, and found that the optimal buffer distance was 50 m. Therefore, susceptibility assessments were carried out by drawing 50 m buffers on the top and sides of the landslides.

To prepare the landslide susceptibility map with the LR method, the GIS-based ArcGIS program and “ArcGIS tools created with the help of R programming language”, which were produced as a result of a “Tubitak Project” conducted and concluded by Sahin et al. (2021). The LR method was performed using 70% of the data for training and 30% for verification, randomly selected. According to the map produced by the LR method, the study area was classified as follows: 19.42% very low, 20.28% low, 20.98% medium, 19.22% high, and 20.11% very high susceptibility class (Fig. 7a).

Fig. 7
figure 7

Landslide susceptibility maps prepared by: a logistic regression, b random forest and c Shalstab mathematical models

Full size image

The landslide susceptibility map obtained from the LR method showed that 19.77% of the mapped landslides were in very low, 20.46% in low, 19.65% in moderate, 20.50% in high, and 19.62% in very high susceptible areas. The statistical results of the model indicated that the beta coefficient for "lithology" was the highest, while the coefficient for "topographic wetness index" was the lowest (Table 5).

Table 5 Statistical results of the logistic regression method used
Full size table

The regression equation of the LR model used in this study is presented below, where the dependent variable is the logarithm of the odds of landsliding, and the independent variables are various topographic and geological factors:

$$\begin{gathered} {\text{Logit }}\left( {\text{p}} \right) \, = \, - {26}.{933 } + { 1}.{1}0{483}*{\text{slope aspect }} + { 4}.{624}0{4}*{\text{plan curvature }} + { 5}.{19821}*{\text{profile curvature }} + { 5}.{21897}*{\text{slope gradient}} \hfill \\ \, + { 2}.0{27}0{6}*{\text{stream power index }} + \, 0.0{5779}*{\text{topographic wetness index }} + { 7}.{3}0{645}*{\text{lithology}} \hfill \\ \end{gathered}$$
(10)

The RF method was also used to prepare a landslide susceptibility map in the same GIS environment and with the same data split ratio as the LR method (Sahin et al. 2021). According to the resulting map, 19.91% of the study area is very low, 19.61% is low, 20.1% is medium, 18.43% is high, and 21.95% is in the very high susceptibility class. Figure 7b shows the susceptibility map obtained with the RF method.

The Shalstab model was employed to assess landslide susceptibility based on the physical properties of the slope material and various terrain attributes derived from the digital elevation model (DEM). To this end, cohesion and dry density values of the slope material were determined through field sampling and laboratory experiments, while the DEM-based parameters (e.g., slope angle, contour length, drainage area) were extracted from the DEM data. The resulting map shows that 20.61% of the study area is very low, 24.56% is low, 11.58% is medium, 23.44% is high, and 19.81% is in the very high susceptibility class.

Validation of the results

In this study, various performance evaluation metrics, including Accuracy, AUC, RMSE, Kappa value, and F1 score, were employed to assess the models (Table 6). Accuracy measures were computed based on the Confusion Matrix, an N x N matrix where N represents the number of classes or predicted categories. It is important to note that the confusion matrix presupposes pre-labeled test data with 1 denoting landslide-prone areas and 0 indicating non-landslide-prone areas. True positive (TP) represents the number of positive values correctly predicted as actual positives, false positive (FP) is the count of negative values incorrectly predicted as positive, false negative (FN) signifies positive predictions incorrectly classified as negative, and true negative (TN) denotes the number of negative values correctly predicted as actual negatives. The accuracy assessment metrics obtained in this study are given in Table 6.

Table 6 Confusion matrix and values of performance metrics of the landslide susceptibility models obtained
Full size table

The validation evaluation was conducted using ArcGIS tools created with the "R" statistical software language, which was conducted and concluded by Sahin et al. (2020, 2021). The results indicate that all three methods exhibit a very high performance, with the random forest method having the highest value of 0.99 and the Shalstab model having the lowest value of 0.93, while the logistic regression model has a 0.97 value of AUC (Fig. 8).

Fig. 8
figure 8

Comparison of performance of the susceptibility maps with ROC curves

Full size image

Conclusions

In this research, Geographic Information Systems (GIS) and remote sensing techniques were harnessed to generate medium-scale shallow landslide susceptibility maps for the central district of Besikduzu province in Türkiye. The following key findings and conclusions emerge:

  1. 1.

    Utilizing high-resolution satellite images from Google Earth Pro, a multi-temporal inventory of earthflow-type shallow landslides was meticulously created for the study area.

  2. 2.

    Earthflow susceptibility maps were developed using logistic regression, random forest, and the Shalstab mathematical model. These maps, classified into five categories (very low, low, moderate, high, and very high), revealed that approximately 60% of the study area exhibits a susceptibility ranging from moderate to very high. This underscores the high susceptibility of the Besikduzu province's central district to earthflow-type shallow landslides.

  3. 3.

    Evaluation of model prediction performance through the Receiver Operating Characteristic (ROC) approach yielded AUC values of 0.99, 0.97, and 0.93 for random forest, logistic regression, and the Shalstab mathematical model, respectively. These high AUC values indicate a commendable level of predictive capability for the models.

  4. 4.

    The study underscores the significance of creating earthflow inventories and susceptibility maps as crucial tools in minimizing the impact of mass movements on lives and property. The resulting database establishes a solid foundation for hazard and risk mapping, essential for planning new settlement areas and roads.

  5. 5.

    Emphasizing the need for careful evaluation at an appropriate scale, the generated susceptibility maps should guide regional and local planning, discouraging construction in high or very high landslide susceptibility areas. Adequate precautions should also be implemented for existing settlements.

  6. 6.

    In summary, the research advocates for nationwide landslide susceptibility mapping and inventory creation in Türkiye as essential components in mitigating the damages associated with mass movements. Such comprehensive maps can play a pivotal role in disaster risk reduction and management strategies across the country.