1 Introduction

Susceptibility to landslides is defined as the probability that a risk phenomenon will occur in a specific area and an undetermined future based on the correlation of conditioning factors with the distribution of past events (Brabb 1984; Fell et al. 2008). Thus, in studies of landslides susceptibilty, only the spatial variable of the probability of occurrence of landslides is taken into account without the involvement of the temporal variable. Both variables, together with the magnitude of the landslide phenomena, constitute the hazard (Guzzetti et al. 2005) and should be the starting point for the risk assessment analyses (Brabb 1991; Fell et al. 2008; Remondo et al. 2008; van Westen et al. 2008). The evaluation and mapping of susceptibility through the spatial zoning of areas prone to movements, that is, areas where landslides are likely, even without their temporal variable, are very useful for the prevention and forecast of risks (Einstein 1988).

Since the first attempts to assess and determine susceptibility in the 1960s (Macau 1963; Milliès-Lacroix 1968) through to the present, a multitude of methods have been used depending on the extension of the study areas and the approaches adopted (Boussouf 1995; Aleotti & Chowdhury 1999; Van Westen 2000; Chacón et al. 2006; Reichenbach et al. 2018) with the later providing a detailed overview and review of approaches frequently adopted. These methods can be grouped into two large groups: (1) qualitative methods and (2) quantitative methods.

The qualitative methods (Carrara & Merenda 1974; Stevenson 1977) are the direct result of analysing the landslide inventory or the geomorphological and geoenvironmental conditions of the study region. The susceptibility zoning depends on experience and the direct appreciation by the author of the analysis, which can hinder the reproducibility of the results from one author to another, and even the comparisons of these results. In short, while these methods are based on understanding the geological and geomorphological ground conditions of a project area and how they relate to landslide activity, and perhaps less on the use of sophisticated statistical methods, the landslide susceptibility results can sometimes be highly subjective.

Quantitative methods make it possible to determine areas of landslide susceptibility using statistical/probabilistic models or deterministic methods (Aleotti & Chowdhury 1999; Van Westen 2000), which increases the objectivity of the methods compared to qualitative methods, limiting, although not completely eliminating the degree of freedom left to the author of the study. This can allow for the identification, through statistical analysis, of relationships between different factors and processes (or combinations of factors and processes) that might be influencing landslide behaviour. However, the results should always be checked and challenged to ensure that any statistical relationships being identified in the data fit with an understanding of the ground conditions and slope processes acting across a chosen study area. This also includes checking the quality of the data being used in the analysis––both the factor mapping and the landslide inventory data––as well as how it is being used.

Statistical models of landslide susceptibility are based on cross-correlation analysis and zonal statistics between the dependent variable (landslides) and the independent variables represented by the conditioning factors of instability (geoenvironmental variables) to determine the areas prone to landslides instability. There is a wealth of statistical methods for assessing and mapping susceptibility to landslides. According to Reichenbach et al. 2018, statistical methods can be grouped into classic statistical methods such as linear regression, logistic regression or discriminant analysis (Carrara 1988; Chung et al. 1995; Baeza & Corominas 2001; Guzzetti et al. 1999, 2005); methods based on indices such as the weight of evidence or matrices (DeGraff & Romesburg 1980; Bonham-Carter et al. 1990; Irigaray et al. 1999, 2007; Fernández et al. 2003); multi-criteria evaluation (Irigaray et al. 1996; Castellanos Abella & Van Westen 2008; Gorsevski & Jankowski 2010); machine learning methods such as decision trees, random forest or support vector machines (Ballabio & Sterlacchini 2012; Goetz et al. 2015; Hong et al. 2015); deep learning methods such as neural networks (Lee et al. 2004; Melchiorre et al. 2008; Pradhan & Lee 2010; Yilmaz 2010; Zare et al. 2013) and other methods.

In relation to these methods, there is an evolution in the use of classification methods from simpler classical linear models towards models that reduce their limitations, such as generalized linear models (GLM) and generalized additive models (GAM). This leads to advanced models that use machine learning (ML) spatial statistics, such as geostatistics or global spatial regression models and geographically weighted regression models (GWR) (Florez García & Pérez Castillo 2019). The search to capture nonlinear relationships and local variations between the dependent variable and the independent variables with the availability of statistical data analysis software and geographic information systems (GIS) have contributed to this evolution (Van Westen et al. 2000).

In southern Spain (Andalusia), the areas of greatest landslide susceptibility are located in the whole of the Betic Cordilleras (Pita et al. 1999; Chacón et al. 2006; Irigaray et al. 2007). This is due to a landscape dominated by many of conditioning factors widely attributed to landslide activity: steep slopes, a geology prone to landslide activity, a regime dominated by very dry periods punctuated by extremely high-intensity rainstorms and a scarce to very scarce vegetation cover as a consequence of regional climate and also deforestation. More specifically, in southeastern Spain, several research studies on landslides have been carried out (Fernández et al. 1994, 2003; Alcantara-Ayala & Thornes 1996; El Hamdouni et al. 2008; Jiménez-Perálvarez et al. 2011). In the province of Almería, however, although many studies have looked at the causes and distribution of landslide in the area (e.g. Ferre 1997; Griffiths et al. 2002; Hart 2004; Geach et al. 2017), there are currently no published examples of landslide susceptibility mapping using statistical methods despite Almería being one of the provinces most affected by landslide activity in the Andalusia region (Pita et al. 1999).

As an objective of the research presented here, the results of a statistically based approach to landslide susceptibility mapping of the Río Aguas catchment within the province of Almería are presented. This includes using statistical models based on maximum entropy (MaxEnt) and geographically weighted logistic regression (GWLR). This last model is based on logistic regression (LR) but also allows the authors to capture the local spatial variations between the variables. Previous studies showed the good performance of the MaxEnt and LR models in comparison with other models to perform landslide susceptibility mapping (Felicísimo et al. 2013; Hong et al. 2016). Likewise, a comparison of the results of both models is established and landslide susceptibility mapping of the hydrographic basin is proposed, thus contributing to the knowledge of the processes of slope instability in the area.

2 Materials and methods

2.1 The study area

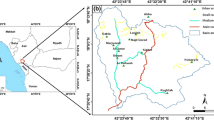
The study area is located in the southeast of Spain and belongs to the province of Almería (Fig. 1), it covers the Río Aguas catchment with a surface area of 541.32 km2. The climate is arid with a mean annual precipitation of less than 210 mm (Esteban‐Parra et al. 1998), torrential and highly irregular; the average temperature is 17° according data from the Environmental Information Network of Andalusia of the Andalusian Regional Government (REDIAM 2022).

Fig. 1
figure 1

Geographic location

Full size image

The hydrographic basin of the Río Aguas drains the Neogene intramountain depressions of Sorbas and a small part of Vera. It has an average altitude and slope of 454 m and 14°, respectively, and is bounded by the Sierra de Los Filabres to the north, where it reaches its maximum altitude (1353 m), the Sierras Alhamilla and Cabrera to the south, the dividing line with the Tabernas basin to the west and the Mediterranean Sea to the east, where the Río Aguas flows into.

The Sorbas Neogene Basin is a sector of the Tabernas–Sorbas Basin (Ott d’Estevou and Montenat 1990) that is arranged on a metamorphic basement of the Alpujárride and Nevado–Filábride complexes of the Internal Zones of the Eastern Betic Cordillera (Fig. 2). It is an elongated depression about 40 km whose morphology is conditioned by folding with kilometric axes of ENE-WSW orientation (Weijermars et al. 1985); from north to south the antiform of Sierra de Los Filabres, the synclines of Tabernas-Sorbas and the antiform of Sierra Alhamilla and Sierra Cabrera can be distinguished.

Fig. 2
figure 2

Geological context a Part of Eastern Betic; b Almeria province; c Details of the study area (modified from the geological map 1:400,000 of Andalusia, Consejería de Política Industrial y Energía, 2011; with data from Sanz de Galdeano et al. 2010)

Full size image

The post-orogenic filling of the Sorbas Basin is made up of sedimentary formations from the Middle Miocene to the Quaternary, which rest in unconformity on the metamorphic Paleozoic and carbonate Mesozoic rocks of the Betic substratum that make up the mountains (Sierras) that delimit the basin in its southern and northern part. These basin deposits show great variability both in surface extension and in thickness, giving rise to several stratigraphic units separated by unconformities (Dabrio & Polo 1995; Martín & Braga 1994). It is worth highlighting the presence of levels of Messinian gypsum that reach up to 40 m thick and are intensely karstified in the Sorbas outcrop -The Karst of Sorbas- (Pulido-Bosch 1986; Calaforra & Pulido-Bosch 1997).

With continued tectonic uplift and sea level fluctuations linked to Quaternary climate changes, sedimentation across the area moved from marine to terrestrial conditions, leading to the formation of a proto-drainage system. Mapping of river terraces across the region has shown that the Sorbas Basin initially drained southwards through a low between the Sierras Cabrera and Alhamilla, before being beheaded by a rapidly headward eroding, eastward-flowing Vera Basin drainage approximately 70 ka (Harvey & Wells 1987; Candy et al. 2005). The landscape response to this river capture event, which increased the catchment area by 50% and resulted in a 90 m base-level difference at the capture site (Harvey & Wells 1987), was the propagation of a wave of fluvial incision-erosion upstream into the captured network (Mather 2000; Mather et al. 2002; Stokes et al. 2002). At present, the upstream limit of this capture-related wave of incision decays approximately 20 km from the capture site (Mather et al. 2002; Stokes et al. 2002) with the rate and style of landscape response being controlled by the bedrock geology into which the fluvial erosion and incision are occurring (Griffiths & Stokes 2008). A key part of the landscape response and rapid incision of the drainage network within this part of the Rio Aguas catchment area (predominantly upstream but also downstream of the capture site) has been the formation of oversteepened and unstable slopes, resulting in landslides (Griffiths, et al. 2002; Hart 2004). Landslides are also seen within the steep mountainous terrain of the area, again, a response to the relatively rapid tectonic uplift of the region and incision of the drainage network.

2.2 Landslide inventory

To Hart’s inventory of 2004, which reached 315 movements, another 254 have been added, which amounts to 569 movements (Fig. 3). The area affected by the landslides is 13.96 km2, which represents 2.58% of the surface of the Río Aguas catchment/basin. For the inventory, photointerpretation with the stereoscopic vision of multitemporal and multiscale orthophotos from Google Earth and with support from the Iberpix 4 stereo web of the National Geographic Institute (IGN) was applied. The use of this approach with images available on web map servers for the elaboration of landslide inventories has already been addressed in various studies (Costanzo et al. 2012; Eeckhaut et al. 2012; Zhang et al. 2015; Lombardo et al. 2016a). Based on this procedure and on the table of coordinates of the movements by Hart (2004), the corresponding polygons have been digitized.

Fig. 3
figure 3

Landslide inventory map

Full size image

61.86% of movements are classified as rock fall type (representing 44.22% of the area), 29.70% slides (29.44% of the area), 6.50% complex movements (24.91% of the area) and 1.93% debris flow (1.43% of the area). Apart from the recorded debris flows, there is a great shortage of flows in the study area, which has already been verified in previous studies in areas with similar characteristics (Jiménez-Perálvarez et al. 2011). This fact could be related to the ephemeral nature and reduced size of these movements, which is consistent with semi-arid environments in which the movements originate after torrential rains with a return period of several years. After a certain period of time, the traces of the ephemeral flows, especially the smaller ones, disappear from the landscape.

The mean surface of the movement is 2.45 ha, the minimum is 0.03 ha and the maximum is 49.56 ha. 74.34% of these movements (423) have a surface less than or equal to the average, with 44.64% of the total being less than one ha. The distribution of movements and affected areas, as well as the average surface according to the landslide type, is shown in Table 1.

Table 1 Landslide distribution by type
Full size table

In addition to the four main sectors in which the movements described by Griffiths et al. (2005) are located, near the towns of Sorbas, Cariatiz (Los Alías), Góchar and along a section of the Jauto River, the new inventory shows a fifth zone of landsliding to the south of Sorbas (between Sorbas and Los Risas) (Fig. 4) and a sixth zone in the Sierra Cabrera to the southwest of La Alcantarilla, perhaps reflecting the higher resolution of the imagery being used in the landslide mapping. In other locations, landslides concentrate along with normal contacts between competent and underlying incompetent weaker materials (e.g. gypsum overlying calcareous mudstones).

Fig. 4
figure 4

Río Aguas catchment landslide heat map

Full size image

The movements in the vicinity of Sorbas and Góchar are the smallest (an average of 0.88 ha), those of the Jauto River and Sierra Cabrera reach an average of 2.8 ha and those with the largest surface are of the complex type, with an average of 4.6 ha, which are located mainly in the contacts between competent and incompetent materials.

The distribution of movements by lithologies is shown in Fig. 5. Approximately 37% of the total surface affected by movements is located in the metamorphic materials of the Alpujárride and Nevado-Filábride complexes of the Betic Internal Zones and the remaining 63% is located in the post-orogenic deposits of the Sorbas Basin. Among the former, carbonate rocks and phyllites stand out, which in absolute terms reach 18.65 and 7.77% of the landslides area, respectively, and in relative terms 7.55 and 6.25% of the area of each lithological unit. Within the post-orogenic materials, the conglomerates, sands and marl, limestone, marl and gypsum stand out in absolute terms (between 11 and 13%) and in relative terms the conglomerates, sands and marl, and gypsum (percentages close to 10%).

Fig. 5
figure 5

Landslide distribution as a function of lithology

Full size image

2.3 Methods

Two statistical methods have been used for the evaluation of susceptibility, the maximum entropy (MaxEnt) and the geographically weighted logistic regression (GWLR). Both methods are used for the study of binomial dependent variables (presence/pseudo-absence and presence/absence, respectively) and allow the management of continuous and categorical independent variables or predictors. The modelling has been carried out with software applications, MaxEnt 3.4.4 (Phillips et al. [internet]) and SAGA 7.8.2 for the GWLR (Conrad et al. 2015), also using QGIS 3.10.12, ArcGIS 10.5 and SPSS2.3.1.

2.3.1 Maximum entropy model (MaxEnt)

The first method used is a statistical-probabilistic modelling approach of machine learning based on maximum entropy. For this, the MaxEnt software has been used (Phillips et al. 2006), developed by Steven J. Phillips of AT&T Labs together with Miroslav Dudik and Robert E. Schapire of Princeton University, for the Center for Biodiversity and Conservation of the American Museum of Natural History (AMNH). This approach has been widely used in ecology (distribution of species and modelling of ecological niches); in fact, in just seven years, its use exceeded 1000 publications to predict species distribution (Merow et al. 2013). However, its application for landslide susceptibility models had never been used before 2012, but since then, it has been applied with great success for susceptibility mapping by several authors (Vorpahl et al. 2012; Felicísimo et al. 2013; Pourghasemi et al. 2012a, b; Convertino et al. 2013; O’Banion & Olsen 2014; Kim et al. 2015; Park 2015; Davis & Blesius 2015; Lombardo et al. 2016b; Kornejady et al. 2017; Chen et al. 2017; Kerekes et al. 2018; Jiao et al. 2019; Pandey et al. 2020). MaxEnt is based on a presence-only methodology and can generate correlations between the points of occurrence or presence and the environmental predictor variables. Therefore, it is ideal for analysing the variety of geospatial and geological variables that contribute to landslide risks (O’Banion & Olsen 2014).

Entropy is an indicator that has its origin in information theory (Shannon 1948) and allows us to measure the degree of disorder in a data set. It can be interpreted as the expected value of the information contained in the data (Jaynes 1982; Kleidon et al. 2010) that is needed to describe a pattern or a process. MaxEnt estimates the probability of occurrence of landslides by finding the probability distribution of the maximum entropy, that is, the closest to a uniform distribution throughout the study area and therefore converts it into a less arbitrary distribution to represent a incomplete information, from points of presence and a set of associated geoenvironmental data. Maximizing entropy (Jaynes 1957), MaxEnt detects the variables with the highest information value to predict the patterns, in our case, the landslide distribution pattern. This method has also been reinterpreted as a type of logistic regression based on presence/pseudo-absence (Renner & Warton 2013).

To achieve the adjustment of a distribution function, MaxEnt uses an algorithm iteratively; the adjustment process involves a random-walk in the parameter space (the coefficients for each predictor) with the assignment of a parameter value. Per iteration, the software proposes new parameter values trying to increase the gain up to its asymptote, or up to the number of iterations defined by the user in the advanced parameters tab of MaxEnt. The software seeks to maximize the profit to obtain the best model. The higher the gain, the more discriminant the distribution. The random-walk starts from a uniform probability of occurrence in a geographic space and moves away from this distribution due to data restrictions and continues in successive iterations until the increase in gain falls below a convergence threshold, set by default in MaxEnt but which can be defined by the user (Phillips et al. [Internet]).

2.3.2 Geographically weighted logistic regression model (GWLR)

In addition, a spatial statistical model, the geographically weighted logistic regression (GWLR), has been applied. Local models GWR were first developed in the late twentieth century by Brunsdon et al. (1996) and Fotheringham et al. (1996, 1997, 2002). Unlike global models such as neural networks or logistic regression (LR), GWRs do take into account spatial variations between variables for susceptibility assessments, since some spatial variables show certain trends and not spatial stationarity. The theoretical basis for the GWR is Tobler’s observation that “everything is related to everything else, but near things are more related than distant things” (Tobler 1970).

The GWLR, instead of establishing a single global model for the prediction, is based on moving windows in which the coefficients of each of the predictors vary from one spatial unit to another, using the surrounding samples, giving greater weight when the sample is closer. Its principle, quite simple, consists of estimating local models by least squares, weighting each observation by a decreasing function according to its distance from the estimation point. The distance from which the weight of the observations is considered zero is known as bandwidth. The choice of the bandwidth value has a great influence on the results. The higher the bandwidth value, the greater the number of observations that the kernel will give a nonzero weight. The combination of local models allows the construction of a global model with specific properties (Ardilly et al. 2018).

2.4 Models application

MaxEnt uses as input a list of specific locations with only the presence of species, in our case the set of points corresponding to the centroid of each of the surfaces of the rupture zone or equivalent (Boussouf et al. 1994) of the inventoried landslides. The environmental predictors or conditioning factors used for modelling in raster format have been selected from a broad set of geoenvironmental factors.

Unlike MaxEnt, the GWLR model requires presence and absence data for the dependent variable; in this case, the same number of absence and presence data has been added. The input data, as with MaxEnt, are made up of a point data file of locations (landslide centroids) and a set of predictor layers. Table 2 summarizes the formats of the input and output variables of the two models.

Table 2 Input and output of models
Full size table

For the GWLR, a bandwidth must also be established. From the model input data, the SAGA software suggests a bandwidth based on the size and resolution of the grid system, but these data can be changed. To set the bandwidth, the Akaike Information Criterion (AICc) (Fotheringham et al. 2002) was also applied in ArcGIS and the highest bandwidth value was chosen, this being the one proposed by default by SAGA.

2.4.1 Predictor factors selection

For the susceptibility mapping of the study area, in addition to the dependent variable, 12 conditioning or predictive factors have been taken into account, which act as independent variables (Fig. 6). These are (1) Altitude; (2) Aspect; (3) Curvature;(4) Distance to faults; (5) The density of first-order streams; (6) Land cover; (7) Lithology; (8) Slope; (9) Distance to the streams; (10) Distance to geological boundaries between competent and incompetent materials; (11) Topographic Position Index (TPI); (12) Terrain Ruggedness Index (TRI).

Fig. 6
figure 6

The conditioning factors of landslides

Full size image

The morphometric parameters were obtained from the Digital Terrain Model 1st Coverage, with 5 m grid spacing available at the download centre of the National Geographic Institute (IGN), as well as the drainage network. For the other factors, the Geological Map at 1/50,000 scale has been used, MAGNA, acquired from the Portal of the Geological and Mining Institute of Spain (IGME) and the land use was obtained from The CORINE LandCover (CLC) 2018 of European Environment Agency. Once the data are downloaded, the corresponding geoprocesses are applied in ArcGIS to obtain derived raster maps with the same resolution (5 m) as the morphometric parameters and their classifications. In the case of the drainage network, contacts and fractures distance operators are applied around the linear elements; meanwhile for lithology, rasterization is applied.

In reference to the conditioning factors, from a traditional statistical model point of view (Renner & Warton 2013), the use of the whole highly correlated predictors is not recommended for MaxEnt and they should be preselected. Meanwhile, based on machine learning, it is suggested to include all reasonable predictors in the model and let the algorithm decide which ones are important, through regularization.

Nevertheless, a statistical approach was adopted instead of varying the regularization as occurs in machine learning. Thus, to use only one variable from each pair of highly correlated predictors, the multicollinearity test between the independent variables allows selecting the variables to be taken into account for modelling with MaxEnt. This same multicollinearity analysis should also be applied to choose the predictors to use with GWLR since the existence of multicollinearity between predictors reduces the degree of efficiency of the GWLR model.

To determine the degree of correlation between predictors, the Pearson coefficient has been used. For this reason, categorical data (lithology and landcover) have been hierarchized to convert them into scalar data; an approximate classification based on the work of Nicholson & Hencher (1997) was applied to lithology and a ranking based on the relationship between land use as a function of the slope has been used for landcover. Table 3 shows the correlations between the independent variables that are all below the critical level of 0.7 (Clark & Hosking 1986) except for the Slope and TRI variables that present a bivariate correlation (Pearson’s r) of 0.98. Thus, 11 of the 12 predictors have been selected for modelling, excluding the TRI variable.

Table 3 Bivariate correlations (Pearson r) between predictors (D-stream1: density of first-order streams; d-stream: distance to streams; d-faults: distance to faults; dgeob: distance to geological boundarie)
Full size table

Regarding the conditions in which landslides occur, lithology has already been described, the more susceptible materials being the carbonate rocks and phyllites of Alpujarride Complex, as well as the post-orogenic conglomerates, sands and marl, limestone, marl and gypsum. This ocurrs particularly where stronger lithologies are ovelrying weaker ones. Among the other factors, landslides show an exponential trend that increases with the slope. Moreover, the movements are distributed in a wide range of height and aspect, although they present a higher concentration at heights close to 400 m and N orientation. In terms of the hydrographic network, the distances to channels of between 50 and 150 m are the most prone for the terrain instability. Meanwhile, the maximum concentration of movements occurs at distances of up to 200–500 m from mapped geological faulting and up to 10 m for geological contacts between competent and underlying incompetent weaker materials. Areas of open space with little or no vegetation were seen as those mostly affected by the mapped landslide distribution, possibly reflecting the nature of land use in the area, as well as the semi-arid to arid climate.

2.4.2 Susceptibility modelling

From the selected conditioning factors and the inventory data, three models were carried out with each method, a first model using Hart’s inventory, 2004 (315 movements, approx. 55%) as training data and our inventory as test or validation data (254 movements, approx. 45%). A second model was developed with the same data, exchanging the training data for the test data and vice versa. Both models have been developed in order to study the influence of the inventory on the modelling. A third model was elaborated as the result of the average of ten models obtained by bootstrapping, joining the two inventories and using randomly 60% of movements as training and the remaining 40% as tests in each of the ten executions. The same parameters were applied for both MaxEnt and GWLR. In the case of MaxEnt, it should be noted that its application allows producing three types of results in its predictions: without format (raw), cumulative and logistic. The susceptibility maps generated in this study by MaxEnt are of the cumulative type.

3 Results

3.1 Susceptibility maps

The cumulative map obtained with the MaxEnt method has been classified to delimit five classes of susceptibility from very low (green) to very high (dark red); the same classification was applied to the GWLR result. The spatial distribution of the differentiated susceptibility classes is shown in the maps in Figs. 7, 8 and 9, for the three models (samples) described in the previous section. In them, it is found that the exchange of the training and test data between models 1 and 2 (Figs. 7 and 8) produces different results of susceptibility zoning. At the same time, the results of modelling 3 (Fig. 9) are closer to those of modelling 2 (Fig. 8).

Fig. 7
figure 7

Susceptibility modelling 1

Full size image
Fig. 8
figure 8

Susceptibility modelling 2

Full size image
Fig. 9
figure 9

Susceptibility modelling 3

Full size image

In general, there is a good fit between the isopleth map in Fig. 4 and the areas most affected by landslides, described in Sect. 2.2, and the established models.

3.2 Results verification

There are several metrics that can be used to evaluate and validate a susceptibility model. In this work, we refer to evaluation as the quantification of the fit between the susceptibility classification model and the distribution of landslides used to calibrate or train the model. However, validation is the estimation of the fit of the model’s predictive capacity, using landslides not used for the model’s calibration or training.

A useful statistical tool for measuring the discriminant ability of the model and for comparing the relative validity between models is the Area Under the Curve (AUC) of the Receiver Operating Characteristic (ROC) that is provided between the different MaxEnt output plots. The ROC curve is a statistical tool used to determine the discrimination capacity of a binomial test or model; it is a graph resulting from representing, for each threshold value, the measures of sensitivity and specificity and in which the sensitivity evaluates the “commission” while the complementary of the specificity (1- specificity) evaluates the “omission”.

The goodness of the models is estimated using the AUC, whose values can be between 0.5 and 1; the higher the AUC, the better the prediction. Ideally, the AUC values should be above 0.5; an AUC equal to or less than this threshold indicates a random prediction or model without discriminant ability, and a value of 1 indicates that the model has a perfect fit.

There are several conventional scales of interpretation of the AUC that allow classifying the results according to their degree of accuracy or goodness. The Swets (1988) criterion establishes that an area below 0.7 has a low discriminant capacity and that one below 0.9 can be useful for some purposes, cataloguing those greater than 0.9 with high accuracy. The AUC-ROC values > 0.90 are considered excellent, according to Metz (1978), between 0.80 and 0.89 good; 0.70 and 0.79 regular and < 0.70 bad.

For both MaxEnt and GWLR, we have applied two evaluation and validation techniques with the ROC tool, the cross-validation for models 1 and 2, and bootstrapping for model 3, using the proportions indicated in Sect. 2.4.2. The AUC values are shown in Figs. 10 and 11, and in Table 4, where it is observed that both algorithms offer good discriminating capacity. According to the Metz criterion, the AUCs obtained allow the models to be rated as excellent both in classification (training sample) and in prediction (testing or validation sample), except for the 1-MaxEnt model, which presents an excellent classification but only good prediction.

Fig. 10
figure 10

Receiver operating characteristic (ROC) curves of training and validation datasets (a: MaxEnt, b: GWLR)

Full size image
Fig. 11
figure 11

Receiver operating characteristic (ROC) curves of training (Model 3, a: MaxEnt, b: GWLR)

Full size image
Table 4 AUC values for training and testing datasets of model 3 of the ten executions
Full size table

However, for the evaluation of the performance of the models, apart from the AUC-ROC, we have used the index of the degree of fit (Goodchild 1986; Baeza 1994) that allows us to calculate the percentage of the mobilized surface in each degree or class of susceptibility and thus determine the fit of the movements to the established susceptibility, using the following formula:

$$ {\text{DF}}_{i} = \left[ {\frac{{{{m_{i} } \mathord{\left/ {\vphantom {{m_{i} } {t_{i} }}} \right. \kern-0pt} {t_{i} }}}}{{\sum {{{m_{i} } \mathord{\left/ {\vphantom {{m_{i} } {t_{i} }}} \right. \kern-0pt} {t_{i} }}} }}} \right] \times 100 $$

where (mi) is the mobilized surface in class (i) of susceptibility and (ti) total surface of class (i) of susceptibility.

In this way, the spatial extension of both landslides and susceptibility zoning is taken into account, which is not done when using performance metrics such as the AUC-ROC approach. Since the final objective of the research is to establish the spatial distribution of the susceptibility projected on a map and that the landslides themselves correspond more to polygons––not points-, it seems important to carry out the evaluation with data of the degree of fit (DF), which is based on the zonal nature of the phenomena and factors.

The distribution by classes of the susceptibility of the study area, as well as the degree of fit of the movements (considering all of them, that is, the sum of the test sample and the validation sample), for each model, is collected at Fig. 12. The results obtained suggest that there is a good degree of fit for all the models, with the MaxEnt results being better than those of the GWLR, as the first ones present lower DF values in the low susceptibility classes and higher in levels of high susceptibility.

Fig. 12
figure 12

Distribution of susceptibility and degree of fit of the three models

Full size image

4 Discussion

First, regarding the inventory, the Río Aguas catchment has an incidence of landslides of 2.58% of its total area in the same order of magnitude than those found in other areas of similar characteristics in the Betic Cordilleras (Fernández et al. 2003; Irigaray et al. 2007; Jiménez-Perálvarez et al. 2011). By landslide type, rock fall is abundant, followed by slides and complex movements, with debris flows being the scarcest group. The scarcity of flows that have already been observed in other semi-arid zones of similar characteristics stands out (Jiménez-Perálvarez et al. 2011) and could be related to the ephemeral nature and the small size of these movements, generated in torrential rainstorms across the area.

Factor analysis reveals that approximately 37% of the total surface of the drainage basin affected by movements is located in metamorphic materials of the Alpujárride and Nevado–Filábride complexes, and the remaining 63% is located in the post-orogenic fills of the Sorbas Basin. Among the former, the most susceptible lithologies are carbonate rocks related to rock falls and slides, and phyllites related mainly to slides, the complex movements being related to the geological boundaries between competent and underlying incompetent weaker materials, which all agree with previous works (Fernández et al. 1994; 2003). Among the latter, conglomerates, sands and marls; gypsum; limestone and gravels, sands and silts are the more prone materials to instability. Meanwhile, landslides show a increasing distribution with the slope-angle is typically expected (Brabb et al. 1972; DeGraff & Romesburg 1980), but a concentration at around 400 m elevation and on mainly north-facing slopes possibly indicates some form of structural, as well as micro-climatic, control. Moreover, the landslides are predominantly located within close proximity of the drainage network (consistent with observations made by Hart (2004) and Geach et al. (2017)), faulting and geological boundaries between incompetent and competent underlying materials due to the weakening that these features produce in rocks.

This observation fits with the geological and geomorphological evolution of the Rio Aguas catchment area, and in particular, the ongoing impact of the Río Feos-Río Aguas river capture event described above, as well as the effects of tectonic uplift and incision of the drainage network across the wider region. As noted by Geach et al (2017), many of these drainage lines are still actively responding to a combination of the river capture, tectonic uplift and base-level change, with this being reflected in the landslide distribution mapped by Griffiths et al. (2002) and Hart (2004), as well the landslide susceptibility mapping presented here (Fig. 9).

The results obtained when using AUC values to evaluate the performance of the methods and models allow qualifying these as excellent (AUC > 0.9). No great differences are observed between these statistical adjustment values, although model 2 presents higher values than model 1, as well as the GWLR method values higher than the MaxEnt, especially if we consider the validation samples. However, the greatest differences are observed in the susceptibility distribution and the degree of adjustment (Fig. 12). In general, the maps obtained with the MaxEnt method are less conservative (without a tendency to overpredicting), that is, they present a smaller extension of the areas of high-very high susceptibility regarding to low-very low and present a better degree of adjustment than those obtained with GWLR. At the same time, in the MaxEnt method, the zones of medium susceptibility predominate over the extreme ones, unlike in the GWLR method, where extreme susceptibilities predominate. Furthermore, in the MaxEnt method, the distribution of classes is quite similar in the three models used, while in the GWLR, there is a certain shift towards classes with higher susceptibility in model 3 (it is more conservative/tendency to overpredicting).

Regarding the predictive capacity of the models, for which the validation samples have been considered, model 2 allows to obtain better AUC values compared to model 1 (Fig. 10). These results are also reflected in the distribution of the degree of adjustment by susceptibility classes (DF), with the adjustment results at the very high susceptibility class being higher in the case of model 2 than in model 1 (Fig. 13). It must be taken into account that the models are trained from data obtained by different authors, the first data set of 315 movements is from Hart (2004) and the second of 254 movements has been obtained for this work, which could be significant for the study of the influence of the inventory on the modelling. By repeating the same effect of improvement of model 2 in the AUC and the DF, both in the prediction with MaxEnt as with the GWLR, we believe that there is a clear influence from used inventory data. Modelling 2 (254 movements for training) improves the prediction over modelling 1 (315 movements for training). This could be explained by a certain bias in the 2004 inventory, due to the space–time scale used, since that the 2004 inventory was based on aerial photographs at a scale of 1:30,000 of flights between September 1984 and April 1985 that covered the majority of the área, in addition to 1:13,333 photographs taken in 1996 that only covered a small part of the área, and field verification mapping (Griffiths et al. 2002; Hart 2004). Meanwhile, the new inventory has been compiled using multiscale and multitemporal photointerpretation as indicated above.

Fig. 13
figure 13

Degrees of fit of training and test for models 1 and 2

Full size image

For model 3, the mean AUC values for the training and test data set, obtained with the GWLR (0.994 and 0.972), are better than those of MaxEnt (0.93 and 0.927); however, the MaxEnt models are somewhat less conservative and present a better degree of fit (DF) than the GWLR (Fig. 12), as happened in models 1 and 2. Furthermore, if we compare the DF values with their respective distributions of susceptibility, MaxEnt modelling has a clear advantage, since in this case, the surfaces classified as high to very high susceptibility represent only 17.24% of the study area, but they concentrate more than 92% of the areas affected by landslides. However, for GWLR, those same susceptibility levels, whose value is more than double that in MaxEnt (approximately 41% of the total area), are affected by approximately 86% of the landslides in the area, which implies a better capacity to susceptibility discrimination of the MaxEnt model. Therefore, it can be concluded that both methods allow obtaining models with excellent AUC values, even with differences in the AUC themselves and in the DFs.

In this way, to obtain the susceptibility distribution of the area, we have resorted to a consensus model of both methods, used in other disciplines (Araújo & New 2007) and also proposed for mapping susceptibility to landslides (Felicísimo et al. 2013). This model is the arithmetic mean of the obtained models and is established by simple GIS geoprocessing with map algebra. The new resulting susceptibility distribution has been subjected to a new evaluation and validation using the same data sets used for the GWRL bootstrapping (used to obtain model 3) obtaining average AUC values of 0.990 for performance and 0.991 for validation. We have also calculated the susceptibility distribution (Table 5) and the degrees of fit (Fig. 14).

Table 5 Consensus model susceptibility distribution
Full size table
Fig. 14
figure 14

Distribution of landslides by susceptibility levels

Full size image

This model proposed as the final susceptibility map of the study area (Fig. 15) allows to obtain an average training AUC equivalent to the best AUC of the two performed (GWLR) and even improves the one corresponding to the validation. Likewise, an improvement is observed in the DF of the GWLR, which were below the DF of MaxEnt. Compared to the GWLR, the adopted model improves performance by lowering the DF values of the susceptibility levels, very low, low and moderate, maintaining the high grade and increasing the DF of the very high level.

Fig.15
figure 15

Proposed landslide susceptibility map

Full size image

5 Conclusions

The Río Aguas catchment has an incidence of landslides of 2.58% of its total area. By type and area affected, rock fall is abundant, followed by slides and complex movements, with debris flow being the scarcest group. Approximately 37% of the total surface of the drainage basin affected by landslides is located in metamorphic materials of the Alpujárride and Nevado–Filábride complexes, and the remaining 63% is located in the post-orogenic fills of the Sorbas Basin. Of the former, the most susceptible lithologies are carbonate rocks and phyllites and of the latter, conglomerates, sands and marls; gypsum; limestone and gravels, sands and silts.

Two statistical models have been used for the landslide susceptibility modelling, MaxEnt (maximum entropy) and GWLR (geographically weighted logistic regression) where each landslide is represented as a point location corresponding to the centroid of the rupture zone and the factor layers being converted into a raster format. This study has used 11 predictors related to morphometry, hydrography, geology and land cover, with 5 m grid spacing. This resolution and the representation of landslides as point location make it necessary to have inventories that capture the full range of landslide activity as a gridded format. This study has been able to verify that the inventory obtained from Google Earth images can be recommended for this type of modelling by offering multiscale and multitemporal data, in addition to its advantage of free access to data, as have already used in previous works (Costanzo et al. 2012; Eeckhaut et al. 2012; Zhang et al. 2015; Lombardo et al. 2016a).

For the proposal of a susceptibility model of the Río Aguas catchment, the performance and predictive capacities of both methods were determined (MaxEnt and GWLR) by using the evaluation and validation statistics of the ROC curves, considering different configurations of the training and validation samples. Thus, excellent values of the area index parameter under the ROC curve (AUC), higher than 0.9, have been obtained. However, it was considered important to combine the statistical metrics used here with the fit of the polygonal data to the models, since the final object of the research is to establish the spatial distribution of susceptibility projected on a map and the mapped polygonal landslides data, not with the point locations used in the analysis. This study therefore also evaluated the degree of fit (DF) of the results, thus measuring the fit of the landslides polygons to the susceptibility areas. This also showed good results with the two models.

The evaluation and validation of the results of the MaxEnt and GWLR models have not allowed us to rule out one model or another for the mapping of susceptibility by producing comparable yields, so a consensus model (the arithmetic mean of both) (Araújo & New 2007; Felicísimo et al. 2013) was used. This simple model combination technique has been shown to further improve the fit data for both performance and prediction of the final proposed model (AUC = 0.99). In this way, around 36% of the surface of the Río Aguas basin has been classified as having high to very high susceptibility, both zones presenting a DF of 90%, which reports the excellent fit of the model.

The authors are very aware that similar studies are frequently published, seeking to demonstrate how different statistical methods and techniques have been used and tested to map landslide susceptibility across different project study areas. As noted by Hearn & Hart (2019), many of these papers aspire to develop methodologies that could be used by engineering or planning practitioners, but often appear to ignore the geological and geomorphological evolution of those study areas (and therefore, the context of why those landslides are occurring) and thus ignoring those factors that are of relevance to those same practitioners. As well as focussing on assessing different statistical models and how they might predict the mapped landslide datasets used in this study, this study has also sought to use a landslide dataset that was based on both detailed mapping of the Rio Aguas catchment area and an understanding of those overarching factors that were potentially driving that landslide activity (e.g. tectonic uplift, base-level change and drainage evolution through river capture).