Introduction

Forms and process in bedrock rivers reflect the interactions between erosive dynamic and the resistance of the substrate through flow. Under a theoretical framework, bedrock rivers are characterized by erosion and transport taxes more important than production (i.e., capacity to generate sediments) and storage (Wohl 2015). Conversely, in alluvial rivers, production and storage are more present than erosion and transport. On these theoretical conceptions, there are a multitude of intermediate situations derived from the energy and granulometric variety of bedrock rivers (Ortega 2010). The geomorphological and the topographical singularities of the bedrock rivers make them high ecological, scenic, landscape, and recreational values (García et al. 2021; Ollero 2017). Unlike alluvial rivers, bedrock rivers have been the great forgotten of fluvial geomorphology globally (Garzón-Heydt 2010).

Longitudinal profiles have been one of the most used tools for the characterization of bedrock rivers due to their ability to describe their geomorphological evolution through, basically, detecting changes in slope. Following the proposal launched by Hayakawa and Oguchi (2009), for this work, I define these geomorphological attention points as knickzones: “locally steep riverbed segment”. This definition also encompasses the term knickpoint, generally defined as referred to the exact location where there is a sharp change in channel slope (downstream increases) (Bierman and Montgomery 2013; Tinkler 2004). In geometric terms, a knickpoint is a single record represented by a point while a knickzone refers to a linear entity. In the first case, the topographic change location is recorded; in the second a change transition.

Bedrock rivers from Courel Mountains Geopark (onwards, CMG) (Galicia, NW of Iberian Peninsula) are one of the geo-assets that favored its designation as UNESCO Global Geoprak in 2019. However, for this region from Spain, there are still few works on both fluvial geomorphological dynamics and bedrock rivers although some of the descriptive types stand out (Pérez-Alberti 1982, 1985, 2000), others on granitic forms (Álvarez-Vázquez and De Uña-Álvarez 2021; De Uña-Álvarez et al. 2014, 2009), or others that include bedrock rivers as part of classification processes (García, 2014). The reference work on bedrock rivers of the Iberian Peninsula (Ortega and Durán, 2010) does not include Galicia, possibly due to this lack of studies on bedrock rivers (despite having a rich and varied representation). This gap, not remedied in the last decade, must be a challenge and a need to which this article tries to contribute.

The main objective of this paper is to identify knickzones from CMG bedrock rivers following the GIS procedure proposed by Hayakawa and Oguchi (2006) for Japanese mountain rivers. To achieve this aim, it is necessary to set the rivers of the study area a topographical criterion to define the knickzones in terms of stream gradient threshold and reach length. Subsequently, the distribution control factors and the geomorphological characteristics of the knickzones are analyzed. By geomorphological characterization, I mean both topographical, tectonic, and lithological aspects.

Study area

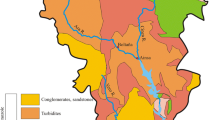
CMG is in the Northwest of the Iberian Peninsula (Fig. 1), inside of the limits of Galicia region (Spain). The total area of the study zone is ~ 600 km2. 73% belongs to the CMG, which one is not included at whole (southern zone—more or less south of Quiroga village—was removed because the predominance of Cenozoic rocks and lower slopes). In order not to divide the basins that partially form part of the CMG, they were fully incorporated as part of the study area. These zones represent the remaining 27% and correspond to the “surrounding area” (north and west flank of the Lor-Lóuzara river basin). From here, I will only use the acronym CMG to refer to the study area, which one is made up of the river watersheds: Lor, Parteme, Quiroga, Castelo das Eiras, Soldón, Casas, and Selmo (only river head) (Fig. 1).

Fig. 1
figure 1

Location of the study area and main physical characteristics. Geological map shows slate and quartzite as the lithology dominant, but there is also the presence of another metamorphic (e.g., schist) or sedimentary rocks (e.g., sandstone). Fracture is representing only the main

Full size image

Horacio et al. (2018) developed a classification for Galicia based on areas with similar topography and lithology and, in consequence, analogous geomorphological processes, named lithotopo units (see also Montgomery 1996). According to these authors, CMG belongs to the lithotopo unit named A3–A2, characterized by an area with compact materials (metamorphic rocks, mainly slate and quartzite bands), marked orientation and a relief with high slope and roughness. The average elevation of CMG is close to 900 m (~ 225 min, ~ 1650 max, ~ 1400 range), with an average slope of ~ 25 degrees (°). Table 1 contains detailed elevation and slope information by basin and on the fluvial network, which is dominated by a dendritic pattern, but with some subdendritic connotation or even areas with rectangular patterns. The average length of the main river by basin is 19.2 km, oscillating on a length range from ~ 4 to 56 km.

Table 1 Main hydrographic and topographical characteristics by basin of the study area
Full size table

The hydrological regime is a mix between the oceanic pluvial regime and the Mediterranean regime, except for the most mountainous areas that have some snowfall. The average precipitation ranges between 1100 and 1400 l m−2 per year, and an annual average temperature of ~ 10–12 ºC. The curve prototype of the hydrological regime is characterized by an intense period of high waters in winter (mainly from November to February), followed by a slight second regrowth at the end of April–May, which serves to slow down the languid drop little bit in flow experienced during spring. The flow reaches its most critical point in summer (from July to September). The average flow of the main river of the CMG (Lor) (Fig. 1) is ~ 14 m3 s−1, with a monthly maximum and minimum in the series of 64 m3 s−1 and 1.7 m3 s−1, respectively.

CMG is a rural area in clear demographic decline, with scarce urban centers (such as small villages) distributed throughout its territory. This decline caused many cultivated meadows to be abandoned and a process of plant succession began. Currently, CMG has a wide expanse of native forests (oak, chestnut, holm oak) dotted with shrubby undergrowth and meadows.

Methodological framework

Previous considerations

Methodological workflow is structured in two stages. The first one focuses on defining the relative steepness index. Here, I employed several rivers from the lithotopo unit to which CMG belongs. The second stage looks toward calculating the stream gradient on the CMG rivers to identify the knickzones and analyzing their control factors and geomorphic characteristics. A geodatabase for the whole NW Iberian Peninsula was generated, so the study area and other zones used in this paper were clipped from the geodatabase.

Data

Digital elevation model

A 5 × 5 m digital elevation model (DEM) was done by creating a mosaic with 81 DEMs-sheets at 1:50,000 scale (50 K) from the Spanish National Geographic Institute (IGN). Then, DEM-5 × 5 m was resized by means of a bilinear procedure to new raster with pixel size 25 × 25 m and 50 × 50 m. The different spatial resolutions were used to determine the most appropriate DEM according to draw the drainage network and detect knickzones.

Lithology

The lithological data used correspond to the named MAGNA series of the Geological and Mining Institute of Spain (IGME) at 50 K. The original cartography contains 13 lithological units for the study area classified according to different variables (e.g., rock type, age, degree of permeability, and alterability). The data was supplied in a GIS vector layer.

Fluvial network

Fluvial network was developed through GIS hydrological tools (ArcGIS PRO) following the common steps to get the drainage network and basins from a DEM. Initially, I used a DEM with cell size 25 × 25 m. The reason for this resolution choice is because it fits well to the drawing of the river from national topographic map 25 K. Besides, DEM-5 × 5 m generates a fluvial network with excessive detail, while DEM-50 × 50 m is too rough. Briefly, those steps were: (1) filling of holes or small depressions to eliminate possible imperfections in the data. (2) Create a flow direction raster from each cell to its neighbor(s) with the steepest downward slope (method Deterministic 8, D8). (3) Creation of an accumulated flow raster in each cell following the previously calculated flow directions. (4) Using map algebra, a threshold value of 20,000 accumulated pixels was set as the start of the drainage network delineation, that is, the channel drawing will be made from those cells that have more than 20,000 cells flowing toward them. The designation of the threshold value does not follow any analytical method (e.g., Tarboton et al. 1991), but a visual comparison in which the density and traced of the drainage network calculated was like the drainage network of the 25 K national topographic map. (5) Determine the contributing area over a set of cells from a raster (i.e., catchment). (6) Conversion of the accumulated flow to a linear vector layer and the basins to polygonal vector layer. The reaches artificialized by reservoirs were eliminated (source: IGN). Also stream reaches over Cenozoic sediments (source: IGME). This drainage network was used to identify the relative steepness index.

Selection of rivers to define the relative steepness index

Rivers selected to define the relative steepness index (first stage of the methodological process; see Sub-section. “Previous considerations”) had to meet two conditions: (i) belonging to the same lithotopo unit where is the CMG rivers, and (ii) have a “high probability” to be a bedrock river. First point was explained in the study area section. Regarding the second one, I followed a previous work in which the probability of bedrock rivers in the drainage network of the NW Iberian Peninsula was identified (García and Pérez-Alberti 2021). These authors applied a method supported by GIS to discriminate (at 102–103 m scale analysis) between potentially bedrock rivers, and those that are potentially not, through the topo-geomorphological descriptors: type of lithology, surrounding slope, and fractures density. The results offer three levels of bedrock reach probability (high, medium, and low) for the whole Galician fluvial network.

Finally, a total of 25 rivers with both conditions were selected to define the relative steepness index (Fig. 2). The results achieved were used later to apply on the CMG rivers and identify the knickzones and analyze their geomorphic characteristics and control factors. The rivers selected sum 585 km and combine whole rivers (i.e., from the head to the mouth) and continuous parts of rivers (i.e., from the head to reaches excluded according to criteria explained above), moving on a length range from ~ 8 to 72 km and mean and standard deviation values of 23.3 km and 15.2 km, respectively.

Fig. 2
figure 2

Rivers/reaches selected to define the relative steepness index. See Fig. 1 for more information about the location. Note in this figure Courel Mountains Geopark does not include the surrounding area (see about this in Section: “Study area”)

Full size image

Identification of knickzones

I followed the method of Hayakawa and Oguchi (2006) to detected knickzones thought the KET (Knickzone Extraction Tool) GIS toolset for automatic extraction of knickzones from a DEM based on multi-scale stream gradients (Zahra et al. 2017) (second stage of the methodological process; see Sub-section “Previous considerations”). The tool was run with python language from PyCharm. The procedure is quickly explained here because its details are described in the cited article. The calculation procedure can be summed up in three steps: (1) calculation of stream gradients with several measurement lengths to set a relative steepness index; (2) determine knickzones using a threshold value previously defined; and (3) extraction of the knickzones the general properties. Stream gradient (Gd; m m−1) at each reach is defined as (Eq. 1):

$${G}_{d}=\frac{\left({e}_{2}-{e}_{1}\right)}{d},$$
(1)

where e1 and e2 are the elevations (m) upstream and downstream from the midpoint (d/2) of a stream reach, respectively; d refers at the stream reach length (m).

Using a regression line is possible to analyze the Gd–d relation (Eq. 2):

$${G}_{d}=a\cdot d+b,$$
(2)

where a and b are coefficients of the linear regression. Because Gd decreases with increasing d, the negative slope of the regression line (Rd = –a; m−1) marks how the local gradient of the measurement point is steeper than its trend gradient (Hayakawa and Oguchi 2009). The Rd value applied along the riverbed draws the relative steepness. The Rd standard deviation was used to set an extraction threshold and locate those river segments as knickzones.

For this study, I calculated the stream gradients along the streamline previously extracted of the DEM. The minimum distance between measurement point was 150 m to ensure an interval longer than the diagonal length of the DEM resolution (for example, for the lowest resolution DEM, 50 × 50 m = 70.7 m diagonal length of the cell size) and reduce the presence of negative values between two consecutive measurement points. Gd values were estimated for divers d from 150 to 10,000 m. A first set of values was divided at intervals of 150 m (from 150 to 1500), which yields 10 types of segments with different length. The second one, it was divided at intervals of 300 m from 1500 to 3000, i.e., 5 types of segments with different length. The last set of values moves from 3000 to 10,000 at intervals of 1,000 m, i.e., 7 types of segments with different length.

Results

Calculation and analysis of stream gradients to identify knickzones

DEM cell size adjusts

The calculation of Gd was performed by extracting values from the DEM with cell size of 5 × 5 m, 25 × 25 m and 50 × 50 m for measurement points with d = 150, d = 300, d = 450, d = 600 (Fig. 3). The presence of negative values was checked as quality measurement to verify the most appropriate DEM resolution. Gd < 0 is because of adjacent valley-side slopes and/or the fact that all cells were forced to flow outward to avoid sinks in the DEM. This explains why some of the downstream measurement points could get a higher elevation value than the upstream one, which is unrealistic in terms of flow movement.

Fig. 3
figure 3

Stream gradients from measurement points (m) obtained each 300 m from three different DEM resolutions along Lóuzara River, where: streams gradients calculated directly from cell values extracted from the DEM, therefore negative values could be present (A); streams gradients calculated directly from cell values extracted of the DEM but as absolute values (i.e., without negative values) (B); errors detected after crossing streams gradient calculated with and without negative values (C)

Full size image

According to the data in Table 2, the sum of negative values of Gd increases considerably with DEM cell size but decreases with increasing d. Considering the total of Gd values obtained for the 25 rivers analyzed to define the relative steepness index and for DEM-5 × 5 m, ~ 12% of the Gd values are negative for d = 150, ~ 5% for d = 300, and < 0.6% since d = 900. Based on these observations, d can be equal or larger than 150 m, assuming some values (the negatives) must be removed (or averaged) for calculations of the relative steepness index. Using d = 300 the number of negative values decreases ostensibly.

Table 2 Sum of negative values of Gd for different DEM cell size and value of d (Navia River data)
Full size table

Figure 3 shows an example of Gd calculated for the Lóuzara River (main Lor tributary; see Fig. 1) with different DEM cell sizes and d = 300. Gd obtained from 50 × 50 m DEM reveals a much broader threshold value than for the other two resolutions, with numerous negative cases (Fig. 3A). The same pattern is repeated considering only the absolute values, but it is not a valid procedure because numerous unrealistic values are generated as potential knickzones (Fig. 3B). In the case of the Lóuzara River (~ 32 km), only five errors were detected due to Gd < 0, three with an elevation difference between measurement points low or very low, and two slightly higher (Fig. 3C).

Analysis of stream gradient

The relation between Gd and d displays a tendency from short d to mark the local slope to longer d to draw the trend gradient (Table 3). Gd values calculated along each river show a large fluctuation with d ≤ 900 and smoothing with d > 900 (Fig. 4). The first type reflects the local riverbed form and the second one the trend gradient. In other words, the local gradient is defined by a much stronger rate of change than the gradient trend. The slope of linear regression from d = 300 to d = 3000 considering the Gd mean and standard deviation is − 1.36·10–6 and 2.61·10–6, respectively. For local gradient, the slope is − 3.68·10–6 (mean) and 4.87·10–6 (standard deviation), while for trend gradient, the slope is − 1.03·10–6 (mean) and − 2.24·10–6 (standard deviation). Internally, transition zones between gradients can also be differentiated. In the local gradient, with d ≤ 600, the rate of change is very steep, and it decreases until d = 900. In the trend gradient, since d = 1500, the rate of change is softer.

Table 3 Summary statistics of stream gradients
Full size table
Fig. 4
figure 4

Example of workflow for the definition of knickzones (Lóuzara River). A represents the stream gradients for all values of d along the Lóuzara River. B, C shows the longitudinal profile and knickzone segments above a threshold of 5.05 × 10–6

Full size image

Identification of knickzones through the relative steepness index

Following Hayakawa and Oguchi (2006) method, the standard deviation of Rd for each river was calculated. Its average for all rivers was 5.05 10–6, so river segments with values of Rd larger than this value were classified as knickzones (Fig. 4). Height less than 10 m should be removed to ensure an interval longer than the diagonal length of the DEM resolution (5 × 5 m = 7.1 m diagonal length of the cell size). Note that the second package of the KET GIS toolset (“Extraction of knickzones”), was applied using 300 m like knickzone length threshold (d) and DEM-5 × 5 m to minimize the number of negative values (see Table 2). Knickzones were drawn under a flow accumulation threshold of 20,000, following the same criteria as the fluvial network done to define the relative steepness index. The use of a DEM with more detail (5 × 5 m) than the one used to calculate the relative steepness index is also due to (i) CMG area and rivers are smaller; and (ii) presence of waterfalls, gorges and canyons everywhere, which requires a higher degree of finesse to detect them.

Description of knickzones from Courel Mountains Geopark

The number of the extracted knickzones rises to 325. The total length of the knickzones is 285 km, which represents about half of the drainage network as knickzone (47%), and a frequency of knickzones of 0.467 km−1. The mean height, the length, and the gradient of all the knickzones are ~ 110 m (min.: 10 m; max.: 507 m), ~ 880 m (min.: 305 m; max.: 3,463 m), and 0.178 m·m−1 (min.: 0.007 m·m−1; max.: 1.083 m·m−1), respectively. Largest knickzones (from 3rd quartile of length and height) correspond to the ~ 5% of total knickzones. Smallest knickzones (until 1st quartile of length and height) correspond to the ~ 6%. Considering only one of the two conditions, the largest occupy 45% and the smallest 44%.

In the next two subsections, I address in more detail the knickzones abundance and its forms. In the third, the correlation between the knickzones and different parameters is analyzed.

Knickzones abundance

Knickzone abundance was analyzed crossing for each central point of the knickzones its value knickzone frequency with four watershed relevant variables organized by classes (elevation, distance from riverhead, gradient of knickzone, and drainage area) (see Fig. 5). Knickzone frequency was obtained from GIS through a line density operation. The search radius to estimate the knickzone per square kilometer was 1000 m (raster output cell size of 25 × 25 m), equivalent to a circumference of ~ 0.3 km2 (circumference area = (0.3/Π)1/2 × 1000). The minimum value of knickzone frequency detected for the study area is 0.102 km−1, and maximum of 2.152 km−1. Mean value is 0.725 km−1 (median 0.708 km−1). Note that this frequency was calculated from the average of the raster pixels from the algebraic operation performed with GIS, and it is different from the frequency calculated directly by dividing knickzone length (km) by watershed area (km2) (0.467 km−1). The GIS procedure was necessary to obtain a particular value for each knickzone (i.e., x, y coordinate of midpoint of the line).

Fig. 5
figure 5

Knickzone frequency for different classes of altitude (A), distance from riverhead (B), gradient of knickzone (C), and drainage area (D)

Full size image

Except for the elevation variable, the other three variables shown in Fig. 5 reflect a decreasing trend from low values to the highest. This trend is not very intensive, but it is clear. Happened the same with the elevation, there is a soft growing trend. In general terms, apparently there is no distribution pattern and the knickzones are everywhere. However, knickzones are more abundant along steep river reaches. In fact, close to 70% of knickzones are located on the reaches of order 1 (Strahler method), and 95% if orders 1 and 2 are considered.

Form of knickzones

Knickzones form was defined through the height, length, and relative steepness of each knickzone. Table 4 shows a first attempt to understand the form of knickzones according to the stream order. A priori, it seems logical to think that the knickzones located in streams of order 1 will be the ones with the highest values of three analyzed variables. Based on the data, in general, that is true, nevertheless, some of these principles could be broken. Clearly, the statistical descriptive values sign out that in order 1 reaches are located the knickzones with the highest height, length, and relative steepness, although a more detailed analysis uncovers other relevant aspects. Focus on the height, median, and mean is higher in order 2 than order 1 knickzones. The maximum values show a decrease with increasing order, while the minimum value reflects an inverse behavior, that is, higher order implies a greater minimum height. Regarding length, there is a decrease in the median, mean, and maximum values with increasing stream order. Once again, the minimum value shows a different behavior, increasing the knickzone length from order 1 to 3, to decrease with stream order 4, although not with values below stream order 1. Finally, the relative steepness shows a decrease in the median, mean, and minimum with increasing stream order, but not with the maximum, which increases slightly with higher stream order. Anew, a strong pattern of behavior is not observed, being able to affirm that any form of knickzone can appear anywhere, especially small knickzones, although large knickzones seem to be reserved mainly for stream order 1. This statement can be verified by looking at the XY graphs in Fig. 6, where the relationships between form parameters of knickzones and drainage area reflect how the dispersion of height and length is large, although with greater concentration in small drainage areas. Relative steepness shows a higher concentration of the data.

Table 4 Characteristics of the form of knickzones by Strahler stream order, considering a descriptive statistic for the value of height, length, and relative steepness
Full size table
Fig. 6
figure 6

Relationships between form parameters of knickzones (height, length, and relative steepness, Rd) and drainage area. Note knickzones with drainage area > 25 km2 are not included to avoid a big data scatter. These represent less than 1% of the total knickzones

Full size image

Correlation for knickzone parameters

All knickzones were correlated according to various parameters (Fig. 7) to establish some kind of explanation not discussed yet. In total, 11 variables were used, eight already ran to analyze the abundance and form of knickzones (i.e., length, height, relative steepness, drainage area, distance upstream, gradient, elevation, and knickzone frequency), and three are newly incorporated (fracture density, circularity index, and knickzone direction). Fracture density was obtained from García and Pérez-Alberti (2021), who established a density map of Galicia using ~ 19,600 km of fracture lines. Circularity index (Miller 1953) defines how the redounded the watershed is. The direction variable corresponds to the compass angle of the linear directional mean to each knickzone. Some variables were converted into natural logarithm to help to reduce the impact of outliers and decrease the skewness in the dataset. Spearman’s non-parametric method was used to determine the linear relationship between variables.

Fig. 7
figure 7

Correlation matrix for several knickzone parameters

Full size image

The correlation matrix does not reveal a strong relationship between variables, except those that would be expected but are not relevant to deepen the geomorphic knowledge of the knickzones. On average, the correlation values hover between − 0.1 and 0.1. Apart from certain logical relationships, as mentioned, there is a positive correlation between elevation and fracture density (0.57), as well as a negative correlation between gradient and length (− 0.56). Outside of these cases, the correlations are very low.

Discussion

Investigations based on DEMs have, at least, two critical points. On the one hand, they are highly conditioned by the available spatial resolution and, on the other, by decision-making prior to the calculations. There are numerous studies focusing on the effect of DEM pixel size as a key factor in hydrological and geomorphological research (e.g., Muthusamy et al. 2021; Cantreul et al. 2018; Sharma et al. 2011). The spatial resolution maintains a close relationship with the analysis scale, but a more detailed scale does not necessarily offer better results. In fact, excessive detail can “contaminate” the objective of the study. The most appropriate resolution was addressed using different spatial resolutions (Fig. 3), both to determine the density of the drainage network, and to know the number of negative values of Gd for different DEM cell size and value of d (Table 2).

The second critical venue (i.e., decision-making prior) refers to the minimum distance between the measurement points (ensured an interval longer than the diagonal length of the DEM resolution) to calculate the Gd. Of course, can be seen as an arbitrary decision, and strictly it is, nevertheless, I tried to follow an analytical procedure like previous studies, with special mention to Hayakawa and Oguchi (2006). As the study area is a place with numerous knickzones, the use of one value of d or another will identify different amounts and forms (e.g., height, length) of knickzones. For example, the use of d = 300 in Lor Basin generates 213 knickzones, with an average length of 866.5 m and height of 105.3 m. If a value of d = 200 is applied, the number of knickzones increases by ~ 10%, and the average length and the height become 802.8 m and 106.3 m, respectively. In general, a smaller d value means more knickzones than a larger d value. The height of the knickzones is more stable, staying at similar values, but not the length, which is usually shortened by the increase in d due to the greater fragmentation of the knickzones. The value that is given to d allows, then, “scanning” the drainage network with different detail. In turn, it will be the cell size that determines from what interval the number of negative values is acceptable. In short, our decision-making prior have consequences on the results and on the statistical validations and interpretations that we carry out later. To minimize the subjective impact that can occur in this kind of research, (i) a complete analysis of d was performed (see Tables 2 and 3, and Fig. 3); and (ii) it was verified in several rivers what knickzone segments manually detected above a threshold of 5.05 × 10–6 (Rd) are also generated by running the tool with same Rd but moving d value.

In the next subsections, I discuss the knickzone identification by means of rates of gradient decrease, what role geological structure plays as an environmental factor, and how the results of this study can have an impact on geopark managers.

Knickzones based on rates of gradient decrease

Many studies have shown how the decrease in Gd with increasing d when d is shorter than certain distance (Byun and Paik 2021; Hayakawa and Oguchi 2006, 2009). The results of this research suggest that this trend between the gradient change with increasing d is very changeable according to the analyzed river. The cases shown in Fig. 8 are an example of the diversity of situations. Saa River represents the more common situation in the scientific literature reviewed, showing a fast decrease in Gd with increasing d. Narón River is a similar case, however, the point of decrease occurs with much larger values of d. Lóuzara and Suarna Rivers are two examples how this trend is not clear. The behavior of Gd does not show signs of confluence for the Lóuzara River, or it is more anarchic if we look at the Suarna River.

Fig. 8
figure 8

Several cases of gradient change with increasing d at a measurement point. Data are from Saa River (A), Narón River (B), Lóuzara River (C), Suarna River (D)

Full size image

This seems to point out that a unitary behavior pattern valid for all rivers cannot be applied, even if these all belong to the same lithotopo unit. Data from the correlation matrix for several knickzone parameters (Fig. 7) could suggest a deeper understanding of the structural characteristics (i.e., tectonic and lithology) at meso-scale in which each river is framed. Since the lithology is almost the same, mainly slate and quartzite, it seems that the tectonic component (represented by fractures, that is, any parting that allows open space or discontinuity, which includes joints, faults, and fractures; Selby 1993) can play a relevant role to understand more about the location of knickzones (Comas et al. 2019; Lima and Binda 2013). However, lithological conditions such as anisotropy are also very decisive in the rate and style of erosion (DiBiase et al. 2018).

The role of the geological structure as environmental factor

Bedrock rivers are a response to the erosion process of rock materials and tectonic characteristics over time. In turn, knickzones can be caused by a variety of processes and environmental and local conditions. The marked structural control of the CMG landscape means that tectonics and lithology play a determining role in the configuration of its drainage network (Scott and Wohl 2019; Pérez-Alberti 1993). Consequently, also in the knickzones as an example of associated form. At landscape scale (103–106 m), the fracture system of the NW Iberian Peninsula is related to the presence of large strike-slip faults that moved in a general NNE–SSW direction (de Vicente and Vegas 2009). This direction is the one followed by the Lor, Soldón, Selmo, or Quiroga rivers. The upper half of the Lóuzara River also follows this direction (then changes to N–S and NW–SE). At a more detailed level, there is a wide network of fractures with different directions, the aforementioned NNE–SSW, plus others, such as NW–SE and E–W, which break the CMG.

To analyze the impact of the tectonics, linear directional was calculated for the set of lines that make up the fractures and the knickzones (Fig. 9). The use of mean values—commonly used in most GIS tools—was scrapped owing to can hide information. First, because a direction NE–SW averaged with another NW–SE can give an E–W direction; and second, because the calculations are done considering the length of lines so, for example, a single fracture can be longer than many small fractures in the opposite direction. In that case, the direction of the largest fracture will have more weight in the mean value than the sum of all small fractures. In fact, employing the linear directional mean for the set of fractures and knickzones these follow an E-W direction. For everything explained, it is more reliable to analyze the direction frequency (Fig. 9).

Fig. 9
figure 9

Linear directional mean of fractures and knickzones (A) and knickzones frequency and fractures frequency from four main rivers and the total rivers of CMG (B). The numbers refer to the watersheds (see also Fig. 1): Lor River without Lóuzara watershed (1), Parteme River (2), Quiroga River (3), Castelo das Eiras River (4), Soldón River (5), Casas River (6), Selmo (river head) (7), and Lóuzara River (8). Each linear segment was framed in ones of the next directional options: < 22.5 (North), ≥ 22.5 and < 67.5 (Northeast),  ≥ 67.5 and < 112.5 (East),  ≥ 112.5 and < 157.5 (Southeast),  ≥ 157.5 and < 202.5 (South),  ≥ 202.5 and < 247.5 (Southwest),  ≥ 247.5 and < 292.5 (West),  ≥ 292.5 and < 337.5 (Northwest),  ≥ 337.5 (North). Note the knickzones are drawn as straight lines

Full size image

The frequency of NE–SW fractures exceeds one-third of the total for CMG. This pattern is repeated for the Lor, Lóuzara, and Quiroga Rivers. The same does not happen for Soldón, where NE–SW represents 20%, NW–SE 39%, and E–W 34%. The least dominant direction is N–S, with values not higher than 15%, except in the Quiroga River where the N–S direction accounts for 21% and E–W for 11%. Regarding the dominant direction of the knickzones, in the analyzed rivers and the total, the NW–SE direction dominates, always being greater than 30%. Directions less frequently vary more by basin. In short, although each basin keeps its particularities, knickzone frequencies are dominated by NW–SE direction, followed by NE–SW. In fractures frequency, NE–SW is the dominant direction, followed by NW–SE. Both types of direction represent in all cases more than 50% of the frequencies. This suggests that the knickzones are more present in what we could call a “secondary fracture network”, considering the main one to be in the NE–SW direction (de Vicente and Vegas 2009; Pérez-Alberti 1993). Secondary direction seems to move more to hillslope or valley scale (102–104 m).

Note not all knickzones are related to (i) a fracture or (ii) its direction. It must be considered that, first, fluvial network from CMG generally follows fractures, however, not all fractures are exploited by the streams; and second, the scale at which the fractures were mapped (i.e., drain density threshold) and the knickzones calculated are not the same, so the level of detail is different, being higher in the knickzones. For this last reason, areas with knickzones but fractures free can be observed (Fig. 9). In the areas where both sets of lines are mapped, the fit between the direction of the fracture and the knickzone is very high. In this line, Scott and Wohl (2019) sign out that fractures control the shape, orientation, and location of landforms by two mechanisms: (i) higher fracture density tends to increase the erodibility of the landscape by focusing on incision erosion, and (ii) due to fractures bound eroded blocks. These mechanisms run together on multiple and overlapping temporal and spatial scales. The positive correlation between elevation and fracture density (Fig. 7), as well as the one that can be established between stream order, elevation and knickzone frequency, agrees with the first of the mechanisms.

If the great lines of landscape architecture are marked by tectonics (i.e., fractures), the relationship between knickzones and lithology, expressed at a more detailed level (~ from reach scale, 102 m, to hillslope-valley scale, 104 m), “oversees” the singularity forms. The lithological control explains why the CMG knickzones are often due to an abrupt succession of knickpoints. These landforms have their origin in the CMG because of how metamorphic rocks, such as slate, schist, or quartzite, influence over the erosive geomorphic process (Wohl 2015), reproducing the typically stepped morphologies of the CMG (Fig. 10A). The presence of stratified (with or without rake) or jointed rocks, and/or differential erosion explain this extensive network of waterfalls and gradient changes. On the one hand, in rocks with weakness planes, quarrying processes dominate, being one of the most effective forms of incision (Hankock et al. 1998). Large blocks are cracked following discontinuity planes and the dominant direction that governs the landscape. This fluvial evolution mechanism over rock generates abrupt morphologies, with forms characterized by very vertical walls that follow one another along the longitudinal profile of the river (Fig. 10B).

Fig. 10
figure 10

Diverse images about the bedrock rivers characteristics from CMG. Canyoning map to downfall the Ferreiriño Stream (Quiroga River tributary) and Seco Stream (Ferreiriño Stream tributary); courtesy from Alemparte and Vila (2018) (A). Quarrying erosion processes with different detail scale, showing how form and processes are the same, only change the zoom (B). Two examples of waterfalls (© Ramón Vila) (C): O Pombar waterfall (20 m height) in Quiroga River (left), where a quartzite band offer major resistance to the erosion than slate or schist, and waterfall in Seco Stream with ~ 35 m height (right), where the erosive action triggered a setback in this reach embedded in quartzite and slate (see image A to locate the waterfall)

Full size image

On the other hand, numerous knickpoints are due to the existence of rocks with different resistance to erosion. These knickpoints usually coincide with inclined quartzite layers (which are more resistant than slates or schists) that form positive reliefs (Fig. 10C).

From identification to utility: can knickzones help Geopark management?

Three pillars support the creation and operation of a geopark: geological heritage, geo-conservation, and local development. This means that a sustainable territorial development strategy based on education and tourism is fundamental. Courel Mountains UNESCO Global Geoprak was the first geopark from Galicia (2019), hence currently, and because of its young age, it is immersed yet in an intense process of divulgation of its geo-assets.

In view of the foregoing, the first question that emerges is what bedrock rivers contribute as geo-assets. Second, what the knickzones provide. And third, how managers can use scientific knowledge to launch measures and plans based on educational tourism. Regarding the first point, bedrock rivers typically have steep gradients and are often characterized by rapids, waterfalls, and other erosional features. This kind of river is commonly found in mountainous regions like CMG and is responsible for dramatic landscape features, such as waterfalls, gorges, and canyons. As a matter of fact, gorges and canyons from CMG have a length of between 200 and 7 km, a depth of up to 200 m and a drop of between 70 and 600 m (Alemparte and Vila 2018). Therefore, it seems coherent to say that the geodiversity associated to bedrock rivers, with a singular environmental condition (Wohl 2015), is a value in itself that must be protected and valued as elements of geological heritage (Boothroyd and McHenry 2019; Ortega-Becerril et al. 2017, 2019; Ollero 2017; Gray 2008). Besides, geomorphological processes and their associated forms determine the structure of a fluvial system (Brierley et al. 2013), both being critical components for the sustainable rehabilitation of aquatic ecosystems (Brierley et al. 2002). In alluvial rivers, the dynamics and geomorphological characteristics of the channel reflect the biophysical conditions of the basin and the processes that take place there (Simon et al. 2016; Ibisate et al. 2011). However, the “hard” conditions of the rivers (reaches) worked over rock act as control elements of the longitudinal dynamics of the river (Garzón et al. 2008; Wohl 1998). And although riverbeds are adjustable in dimension and shape according to changes in the volume of water and sediments (Church and Ferguson 2015), these processes follow very different rhythms in bedrock rivers (Ortega 2007). According to all this, the singularities of bedrock rivers should be valued for two reasons: (i) because the dramatic landscape of the CMG is the result of intense work of the fluvial network over millions of years, and (ii) because its geomorphological characteristics grant to the bedrock rivers a high ecological, scenic, landscape and recreational value.

Looking at the second question, knickzones play an essential role in the form and processes of the bedrock river. In addition to their geomorphic significance previously discussed, knickzones can also have ecological implications, as they can create barriers to fish migration and affect the distribution of aquatic species (Wright 2020; May et al. 2017).

From a point of view of managers and how to transfer scientific knowledge over bedrock rivers and knickzones through educational and sustainable tourism, it would be about looking for new productive rationalities based on the potential of nature (Ashmore 2015). These would be aligned with the principles that have to govern a geopark, offering alternative approaches to production and consumption that prioritize environmental sustainability, social equity, and economic viability (Henriques et al. 2011; Hose et al. 2011). Take as a precedent that the increase in geosites experienced in the last two decades seems to mark a change in the trend toward a more “geo-aware” society (Ortega-Becerril et al. 2019; Ruban 2016; Crofts 2014; Gray 2008).

Supported by conservation principles, two types of tourism could be proposed to take advantage of the scientific work carried out on bedrock rivers and knickzones: (i) exploration or adventure tourism with a scientific dimension, and (ii) only scientific tourism. Each of them is framed in a modality, but all should have in common the participation of visitors in the acquisition and/or generation and dissemination of scientific knowledge that strengthens the values of the geopark in line with sustainable local development. Scientific tourism can appeal to a wide range of travelers, including families, students, scientists, and enthusiasts of science, however, knickzones have the particularity of being in places with difficult access, so the best way to explore them is through canyoning and rappelling down its walls. This makes it a type of adventure tourism not suitable for everyone and with a marked seasonality since it cannot be practiced with high flows. The placement of information panels in optimal viewpoints may help to learn about the importance of bedrock rivers and knickzones and their impact on the landscape, and also would further democratize the exchange of scientific information by making it accessible to everyone.

It would be worth questioning whether the prosperity that geotourism has experienced as a new tourism model comes more from the academic and local environment, as promoters of its geological heritage, than from society, whose knowledge about geotourism is still scarce (Horacio et al. 2019). In fact, various studies show that, in general terms, tourists who visit places with an important geological heritage do so more for the scenic value of their landscapes than for the geological value of the element visited (Chen et al. 2015; Mikhailenko et al. 2017). In order for the visitor to add scientific-geological value to the scenic value of the landscape, it is necessary (i) more scientific studies that delve into, on the one hand, GIS as a geospatial dissemination tool (Zgłobicki and Baran-Zgłobicka 2013), and on the other, on the geo-aspects that are the reason to be of the geopark, doing it both at the level of detail and in an integrated way with the dynamics of the landscape; (ii) educate in local schools and high schools about the value of geodiversity, since those generations will be the defenders of their territory; and (iii) re-educate the adult population so that they rethink what they are visiting because only what is known is valued. Regarding this, it should be noted that many tourists visit sites with geological heritage of great importance, but they do not do so for their intrinsic value, but for their esthetic manifestation (Horacio et al. 2019). The enhancement of the knickzones as singular elements could help to slowly reverse this situation for the CMG case.

Conclusions

Four main conclusions can be drawn from the findings of this research. First, CMG can be considered as the “knickzone land” (i.e., “waterfall land”) from Galicia. Close half of the drainage network was identified as knickzone (47%), which translates into a mean knickzone frequency of 0.467 km−1. In this study, a distribution pattern was not identified and the knickzones are everywhere. Second, the longitudinal profile forms that the river adopts in the form of waterfalls and rapids to overcome the heavy steepness is a direct consequence of its lithological characteristics and tectonic structures. Tectonic controls river trajectory, while lithological control plays a fundamental role as an influential factor in the appearance of characteristic forms and gives “personality” to CMG rivers.

Third, knickzones form, analyzed from the height, length, and relative steepness variables, are not governed by a specific spatial distribution. For example, streams order 1 host 70% of the knickzones, and greater length and relative steepness. However, if the height is looked at, the mean value is higher in order 2 than in order 1 knickzones.

Fourth, the visual expression in CMG is resolved with a landscape with marked scenic impact. Findings from this study can be used by managers to develop and/or improve strategies for conservation, valorisation, and how to approach the tourist who visits the CMG. Scientific tourism is able to offer a unique and educational travel experience, allowing participants to learn about bedrock rivers and knickzones in the biophysical and cultural context of CMG. This can also contribute to the local economy by supporting science-related businesses and research institutions.

Future research on bedrock rivers planned by CMG Scientific Committee looks forward (i) to focus on more detailed morphologies from LiDAR data and topographical fieldwork (e.g., hydraulic geometric); (ii) to analyze the interaction of flow and sediment transport in the self-formed waterfalls (e.g., Scheingross et al. 2019); and (iii) measure the flow characteristics (such as water depth, discharge, specific stream power) to relationship them with forms and processes of the bedrock rivers). With all this, is hoped to know more about the effects of rock properties and environmental factors on the frequency and shape of knickzones.