Introduction

Saturated hydraulic conductivity (K) reflects a rock or soil’s ability to transmit water through pore spaces and/or fractures under a hydraulic gradient (Fetter 2013). When the pore space of the soil is not fully saturated with water, this property is referred to as unsaturated hydraulic conductivity. As such K plays a crucial role influencing groundwater flow and contaminant migration and can vary up by more than 10 orders of magnitude from coarse to very fine grained solids. Moreover, hydraulic conductivity typically varies within natural geological units (Mitchell and Soga 2005), with this spatial heterogeneity giving rise to considerable scale-dependent uncertainties in determining an appropriate value (Mallants et al. 1997; Boschan and Nœtinger 2012; Piña et al. 2019; Águila et al. 2022a). Consequently, determining realistic values of K can prove essential in fields including civil engineering (Liu and Rowe 2016; Tan et al. 2017; Chen et al. 2021), mining (McCoy et al. 2006; Meiers et al. 2011), chemical engineering (Francisca and Glatstein 2010; Wu et al. 2020), agronomy (Peña-Haro et al. 2011; Picciafuoco et al. 2019) and environmental geology (Akcanca and Aytekin 2014; Gao et al. 2018). It is important to note that, in some disciplines such as geotechnical engineering, hydraulic conductivity is often referred to as permeability coefficient, more commonly abbreviated as permeability. Nevertheless, the way that a fluid passes through a soil or rock mass depends not only on the properties of the soil/rock but also on the properties of the permeating fluid. When using the term hydraulic conductivity, it is specified that it refers to water flow.

Several different approaches can be taken to estimate K which, according to the classification proposed by Ritzema (1994), can be grouped into two general categories: empirical and hydraulic methods. Empirical or correlation approaches employ empirical relationships between readily evaluated soil properties (texture, pore-size distribution, grain-size distribution or soil mapping unit) and K values. The advantage of correlation methods is that their estimates of K are usually simpler, faster and cheaper than those obtained using hydraulic methods. However, empirical relationships can be inaccurate and subject to random errors (Stibinger 2014), especially related to the small size of the samples analyzed, which do not reach the “representative elementary volume” (REV) required to determine characteristic K values of geological formations (Zhang 2013). For instance, the application of different empirical equations to estimate K from grain‐size distribution could lead to errors ranging over 500% according to Rosas et al. (2013). Despite this, many scientists use and continue to investigate indirect methods for estimating K from commonly available soil information. This is the case of pedotransfer functions that are becoming increasingly popular for estimating hydraulic properties from soil physical properties such as soil texture, bulk density, organic matter content, and water retention (Zhang and Schaap 2019; Abdelbaki 2021; Singh et al. 2022). On the other hand, hydraulic or experimental methods are based on Darcy’s Law and usually estimate K from head variations caused by water injection or extraction. These approaches can be classified into laboratory (ex-situ) methods such as constant head (Amoozegar 2020) and falling head (Pedescoll et al. 2011) tests; and field (in-situ) methods such as pumping tests (Kruseman et al. 1994), slug tests (Butler 2019), auger-hole method (Van Beers 1958), well dilution tests (Piccinini et al. 2016), borehole flowmeter method (Zlotnik and Zurbuchen 2003) and Direct-Push Injection Logger (DPIL) methods (Liu et al. 2012). K estimates from field tests are generally representative of larger geological/rock bodies than those estimated using laboratory methods, so they tend to show less variability (Ritzema 1994).

The scale effect on K has been the subject of many studies in the last decades (e.g., Smith et al. 2016; Yang et al. 2017; Godoy et al. 2018), although some authors suggested that the differences found when estimating K using diverse measurement scales may be caused by interpretation errors and inadequate procedures when performing the tests (Butler and Healey 1998; Lee and Lee 1999). Most investigations reported an increase in K when increasing the measurement scale (Schulze-Makuch and Cherkauer 1999; Martínez-Landa and Carrera 2005; Hunt 2006; Fallico et al. 2010; Piña et al. 2019; Yu et al. 2020). The spatial heterogeneity of the medium increases with volume when measuring K, causing the scale dependency of hydraulic conductivity (Schulze-Makuch et al. 1999). However, Ghanbarian (2022) notes that current knowledge remains far from fully understanding how hydraulic properties of soils and rocks, such as permeability, porosity and dispersivity, may vary with scale. The scale effect of K may vary according to the geological characteristics of the site under study and the measurements conditions. Zlotnik et al. (2000), after comparing various field studies, concluded that the scale dependence of K is not readily apparent due to the limitations of the experimental techniques, and highlighted the need for additional investigations measuring K at different scales and depths in a wide variety of geological formations.

Selecting suitable methods to obtain reliable hydraulic conductivity values proves essential as no one method is appropriate for all geological media, while inappropriate choices can lead to large estimation errors. In practice, however, the economic cost or the application time of the methods often prove as important as accuracy in method selection. Comparison of methods in diverse environments provides an essential source of information to help establish a suitable technique for specific circumstances. In the absence of a standard benchmark for measuring K, some studies have focused on comparing estimated K using various methods (Mohanty et al. 1994; Verbist et al. 2013; Batlle-Aguilar et al. 2016; Smith et al. 2016; Hwang et al. 2017; Hangen and Vieten 2018). Cheong et al. (2008) compared K values using particle-size analysis, pumping and slug tests, and numerical modeling in a riverside alluvial system and reported values determined by particle-size analyses were more than three times greater than those obtained from pumping tests, while K estimated from slug tests were one to two orders of magnitude lower than that from pumping tests and grain-size analyses. Similarly, Pucko and Verbovšek (2015) found poor correlations between K values determined by grain-size analysis and pumping tests in Quaternary gravels. The use of grain size data for initial assessment of K was endorsed by Vienken and Dietrich (2011), but they discouraged the use of this method to characterize aquifers accurately, since it is not sufficiently reliable. Elhakim (2016), after estimating K using widely used techniques, notably pumping tests, falling head tests, grain-size analysis and Cone Penetrometer Tests (CPT), highlighted the importance of calibrating empirical methods using actual field measurements to obtain reliable values of K.

On the other hand, some methods for determining K are only applicable in specific locations. This includes Tide-Aquifer interaction techniques (Ferris 1951), which are only applicable in coastal areas. Millham and Howes (1995) compared five techniques to determine K (tidal, tracer, slug, permeameters and grain-size analysis methods) in both upland and shoreline regions of a shallow coastal aquifer. Their results illustrated greater K values (between 1.3 and 2.4 times) in the upland as compared with shoreline settings and differences of up to a factor of 5 between the K values estimated using the five methods. Moreover, the tidal K measurements were similar to the tracer results, but were highly variable due to the large aquifer storativity, small tidal amplitude, and irregular tides. Tber and Talibi (2007) presented a numerical method to automatically determine K in coastal aquifers, modeled with sharp freshwater/saltwater interfaces. Nevertheless, given the importance of accurately estimating K values in coastal areas (Strack et al. 2016; Moghaddam et al. 2017; Mahmoodzadeh and Karamouz 2019; Etsias et al. 2021a,b,c) and the lack of knowledge about differences found between methods (Jačka et al. 2014) and scale dependence, further comparisons of techniques to estimate K in coastal areas are essential for the choice of suitable measurement methods in coastal environments (Merli et al. 2016). Despite the numerous studies published in recent decades on the variability of soil parameters, there is still a need for further research on in situ K values and estimation methods in natural deposits, since the conclusions obtained from previous are influenced by the different levels of heterogeneity of the sites, usually poorly characterized. Few studies have investigated K values in relatively homogeneous natural deposits and always using a limited number of estimation methods and scales of investigation (Chapuis et al. 2005). Therefore, further investigations on K at different scales using different measurement techniques in homogeneous and well-characterized natural deposits would provide more detailed knowledge of its variability independent of the effects of heterogeneity.

This paper presents a comparison of the saturated hydraulic conductivity values, determined through empirical, hydraulic and numerical modeling approaches in the well-characterized, relatively uniform and highly homogeneous coastal sand aquifer underlying Benone Strand at Magilligan (Northern Ireland). K has been estimated using eight different methods (Cone Penetration Test [CPT], Hydraulic Profiling Tool [HPT] system, Tide-Aquifer interaction techniques [by using the tidal efficiency and time lag models, and analytical solutions on sloping beaches], grain-size analysis, pumping tests, slug tests, single-borehole dilution tests and numerical modeling). This approach achieves two fundamental objectives. Firstly, comparison of different methodologies to estimate K in a coastal environment in order to assess the capacities and limitations of each method, especially for the identification of spatial variations in K. The second objective is to evaluate scale effects when estimating K using various techniques with different measurement scales (from 0.01 to 100 m) in a well-characterized homogeneous aquifer (Águila et al. 2022b). The lack of geological heterogeneities that cause significant variations in K has made it possible to investigate the scale dependence of K related exclusively to the measurement method. Conversely, the absence of significant heterogeneity in the findings helps highlight the role-played geological variability in explaining the scale dependence of hydraulic conductivity in more complex deposits.

Site description and instrumentation

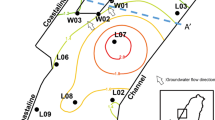
The study area is located at Magilligan, in the northwest of Northern Ireland (United Kingdom). Magilligan is one of the largest coastal dune systems in Britain and Ireland, measuring 7.5 × 1.5 km, and which grades into beach sands. The Benone Strand Study Site (Benone) lies in the central part of Magilligan (Fig. 1). It has a mildly sloping (~ 2%) sandy beach with an intertidal zone of up to 150 m wide at spring tide. Tides at Benone are semidiurnal, with a mean range of 1.72 and 0.65 m for spring and neap tides, respectively. Previous geotechnical and geophysical tests carried out in the study area suggested that the ~ 20 m thick coastal sand aquifer underlying the site was relatively homogeneous, and directly overlies Lr. Jurassic mudstones (Águila et al. 2022b). Geochemically the sand is dominated by quartz (> 90%), although there are local concentrations of calcium carbonate (shell debris) and heavy minerals such as magnetite, epidote and biotite (Carter 1975). Groundwater levels are not influenced by anthropogenic activities such as external pumping, as no significant abstractions (> 100 m3/day) are recorded in the area. Groundwater within the sand has a Ca-HCO3 signature, reflecting the influence of shell debris. Robins and Wilson (2017) estimate annual average groundwater recharge at around 400 mm.

Fig. 1
figure 1

Location of the study area with the position of the CPT and HPT soundings (yellow squares), monitoring wells (red circles) and pumping wells (blue circles)

Full size image

With the objective of better characterizing the coastal aquifer underlying Benone, 12 monitoring wells and two pumping wells were drilled in the upper part of the site at distances ranging between 12 and 23 m south of the mean high water mark (Fig. 1). The monitoring wells have a diameter of 100 mm and were grouped into three clusters of four piezometers each (clusters A, B and C). Monitoring piezometers have 0.5 mm slot 1 m long well screens at 1–2 m, 3–4 m, 5–6 m and 7–8 m deep in each cluster. The nomenclature assigned to each piezometer in Fig. 1 consists of a letter corresponding to the cluster and a number that refers to the maximum depth of the well. Solinst LTC Leveloggers were installed in each monitoring well to monitor groundwater levels, temperature and specific conductivity. On the other hand, the two pumping wells have a diameter of 150 mm and 5 m long well screens surrounded by 300 μm geotextile wrap. Pumping well depths range between 10.5 m (PW1) and 8 m (PW2). Both monitoring and pumping wells were installed 0.5 m below ground surface (BGS) outside investigation periods to prevent any impact to the public amenity function of the site. Águila et al. (2022b) and McDonnell et al. (2023) present a more detailed description of the aquifer.

Materials and methods

Empirical or correlation methods

Four empirical/correlation methods were used in this study to obtain K estimates from the coastal sand aquifer at Magilligan: (1) Grain-size analysis (GSA); (2) Cone penetrometer test (CPT); (3) Hydraulic profiling tool (HPT) system; and (4) Tide-Aquifer interaction techniques.

Shell and auger drilling permitted collection of representative soil samples at Benone for GSA up to a depth of 10 m (Uma et al. 1989; Vienken and Dietrich 2011; Rosas et al. 2013; Wang et al. 2017). Ten sieves between 0.063 and 5 mm were utilized to determine the equivalent particle diameters by sieving, while no hydrometer analysis was performed due to the lack of fines on the samples. K was determined using seven different empirical relationships proposed by Hazen (1892), Kozeny (1927), Slichter (1898), Terzaghi (1925), Breyer (1964), USBR (Vukovic and Soro 1992), and Alyamani and Sen (1993) following the general equation:

$$K\left[m/s\right]=C\cdot f\left(n\right)\cdot {d}_{e}^{2},$$
(1)

where C is an empirical coefficient which in most methods generally includes gravity (g) and kinematic viscosity of water (υ), f(n) is a function that depends on porosity (n), and de is the effective grain size. Table 1 presents a more detailed description of the formulations used in this study. After drying the samples in an oven at 110 ± 5 °C, known volumes of sand were submerged in a previously measured volumes of water for one day. Porosity of each sample was calculated following methods described by Cheong et al. (2008) and Fetter (2013). The average of the calculated porosities was equal to 0.35 ± 0.02.

Table 1 Empirical formulas used to estimate hydraulic conductivity from grain-size analysis
Full size table

CPT and HPT are direct-push in-situ method widely used in geotechnical engineering to determine the subsurface stratigraphy and to assess soil properties in unconsolidated formations (Lunne et al. 1997). Both methods are also commonly used to estimate spatial variations of K (Butler 2005; McCall et al. 2014). Seven CPT soundings were performed down to refusal (maximum depth of 22.64 m BGS) on Benone Strand using a 14-ton track mounted CPT rig. Figure 1 presents test locations (T1-T7). Each test measured cone resistance (qc), sleeve friction (fs), porewater pressure (u2) and inclination (I) every 10 mm of penetration. K can be estimated from CPT data based on the soil type though soil behavior type (SBT) charts or by correlating with the SBT Index (Ic). SBT charts proposed by Robertson et al. (1986) consisting of twelve zones distinguished by the measured qc and fs providing reasonable predictions of soil type and K ranges. Ic, on the other hand, is determined iteratively from the normalized cone resistance and friction ratio (Robertson 2010), increasing in value as the soil becomes finer (Cetin and Ozan 2009). Hence, K generally decreases as Ic increases and can be estimated from Ic by the following relationships (Robertson 2010):

$$\mathrm{When }\,1.0<{I}_{c}\le 3.27, K=\frac{{10}^{\left(0.952-3.04{I}_{c}\right)}\mathrm{m}}{\mathrm{s}},$$
(2)
$$\mathrm{When }\,3.27<{I}_{c}\le 4.0, K=\frac{{10}^{\left(-4.52-1.37{I}_{c}\right)}\mathrm{m}}{\mathrm{s}}.$$
(3)

On the other hand, the HPT system employs a down-hole transducer to measure the pressure required to inject a constant flow of water into the soil, thus providing an indication of formation permeability. Seven HPT profiles were conducted at Magilligan to a depth of 13 m BGS within 0.5 m of the CPT soundings locations (T1-T7, Fig. 1). Probe advancement and water flow stopped approximately every meter of drilling to perform dissipation tests and determine the local piezometric pressure. However, McCall and Christy (2020) note that HPT dissipation tests are not recommended for directly estimating K as the trunk-line above the water level interferes with the early time dissipation of the observed pressure down hole. To address this issue, hydraulic conductivity logs were estimated at Magilligan by using an empirical model developed by Geoprobe Systems® (McCall and Christy 2010) implemented into the software DI Viewer®, which determines K as follows:

$$K=21.14\mathrm{ ln}\left(\frac{Q}{{P}_{c}}\right)-41.71,$$
(4)

where Q is the HPT flow rate and Pc is the corrected HPT pressure at each depth increment.

More recently, Borden et al. (2020) presented the following revised approach, based on numerical simulations of the physical flow processes, which take place during probe advance and water injection and can prove important in less permeable settings (K < 0.305 m/d):

$$K=\mathrm{E}\left(0.1235V{D}^{2}+0.119Q\right){P}_{c}^{-1.017},$$
(5)

where E is an empirically derived hydraulic efficiency factor, V is the probe advance rate and D is the probe diameter. Borden et al. (2020) proposed 2.02 as value for E, but cautioned of the need for further research to better understand the impact of this parameter.

Tide-Aquifer interaction techniques permit analysis of fluctuations in wells during tidal cycles to determinate aquifer hydraulic properties in coastal settings (Mao et al. 2006). Direct calculations using time lag and tidal efficiency models are commonly used to estimate hydraulic diffusivities in coastal aquifers (Jha et al. 2008).

The time lag (tlag) method estimates aquifer parameters by analyzing the time difference between peaks or troughs of tidal and groundwater hydrographs. The tlag of groundwater fluctuations in a well with respect to tidal oscillations is defined as (Ferris 1951; Todd 1980):

$${t}_{\mathrm{lag}}=\frac{x}{2}\sqrt{\frac{{t}_{0}S}{\pi T}},$$
(6)

where x is the distance from the observation wells to the seashore, t0 is the tidal period, S is the aquifer storage coefficient and T is the transmissivity (T = KD, where D is the saturated thickness of the aquifer).

Tidal efficiency (TE) is the ratio of the amplitude of groundwater fluctuations recorded in wells close to the shoreline to the amplitude of tidal fluctuations. Hydraulic diffusivity can be estimated by using the TE method according to (Ferris 1951; Todd 1980):

$$\mathrm{TE}={e}^{-\left(\sqrt{\frac{\pi {x}^{2}S}{{t}_{0}T}}\right)}.$$
(7)

The main advantage of the above direct methods is simplicity of application. However, these models do not take into account various factors, such as the effects of beach slopes, aquifer leakage and density differences, that are considered in more sophisticated analytical solutions or semi-numerical models (Li et al. 2000; Teo et al. 2003; Jeng et al. 2005). Nielsen (1990) derived an analytical solution from the Boussinesq equations to examine tidal dynamics of the water table on sloping beaches:

$$h\left(x,t\right)=\mathrm{D}+\mathrm{Acos}\left(wt-kx\right){e}^{-kx}+\varepsilon A\left[\frac{1}{2}+\frac{\sqrt{2}}{2}\mathrm{cos}\left(2wt+\pi /4-\sqrt{2}kx\right){e}^{-\sqrt{2}kx}\right]+{\varepsilon }^{2}A\left(\frac{1}{4}-\frac{\sqrt{2}}{2}\right)\left[\mathrm{sin}\left(wt-kx\right){e}^{-kx}+\mathrm{sin}\left(3wt-\sqrt{3}kx\right){e}^{-\sqrt{3}kx}\right],$$
(8)

where h is the (fluctuating) water table elevation, A is the tidal amplitude, w is the angular frequency, t is time, k is the wave number given by \(k = \left( {n_{e} w/2KD} \right)^{0.5}\) with ne being the effective porosity and K the hydraulic conductivity, and \(\varepsilon =kA\mathrm{cot}\beta\) with β being the beach slope.

Both direct methods and the analytical solution proposed by Nielsen (1990) on sloping beaches were used to estimate K in the coastal aquifer at Benone by analyzing groundwater level responses in monitoring wells to changes in sea level during three three-day periods in November 2019 and in January and May 2020. Data on tidal variations were measured at the Portrush tide gauge site located 15 km from the study area. As an example, tidal oscillation and groundwater level fluctuations recorded in 2 m and 8 m deep monitoring wells in November 2019 are shown in Fig. S1 of the electronic supplementary material (ESM). For K estimates, a tidal amplitude of 1.14 m and a period of 12.5 h were considered, while the distances from the monitoring wells to the sea varied between 34 and 42 m. The average slope of the Benone beach is about 2%, but in the vicinity of the monitoring wells it is slightly higher (3.5%). Effective porosity (ne = 0.28) was determined in laboratory from sand samples collected from the beach (Rosas et al. 2013). Solver application in Excel was used to minimize the differences between the measured and calculated water level fluctuations (Kargas et al. 2022).

Hydraulic methods

Three hydraulic techniques based on the Darcy’s law were applied at Benone Strand to estimate K of the sand deposit: (1) pumping test; (2) slug tests; and (3) single-borehole dilution tests.

A constant-rate pumping test and two multiple stage step-drawdown tests were conducted to determine aquifer parameters and well efficiency. The constant-rate pumping test was carried out pumping 1.25 L/s over 328 min from PW1 well, while multiple stage step-drawdown tests were conducted in PW1 and PW2 wells pumping during 370 and 280 min, respectively. The initial pumping rate in the step test performed in PW1 well was equal to 0.52 L/s, increasing approximately every hour until reaching a maximum pumping rate of 1.25 L/s in the sixth and last step. By contrast, the pumping rate in the step-drawdown test carried out in PW2 well was increased four times from 0.83 to 1.25 L/s. Water level variations were automatically registered every minute using the CTD loggers installed in the twelve monitoring wells.

Slug testing at Benone consisted of measuring the recovery of water level in a well after a near-instantaneous change in water level. A solid cylindrical slug with a diameter of 50 mm and a length of 1 m was introduced (falling-head tests) and extracted (rising-head tests) in the twelve monitoring wells installed at Magilligan, causing initial water level variations of approximately 0.25 m. The recovery of the water levels was measured automatically every two seconds until reaching equilibrium using Solinst Leveloggers. Data analysis employed the four most commonly used solutions for unconfined aquifers proposed by Hvorslev (1951), Bouwer and Rice (1975), Dagan (1978), and the Kansas Geological Survey (KGS; Hyder et al. 1994).

Pumping and slug test data were analyzed with the software AQTESOLV Pro (ver. 4.50) (Duffield 2007). Hydraulic properties of the coastal aquifer were determined using pumping test data by applying the Neuman (1975), solution as it was the best one reproducing the measured drawdowns among the options available in the software. On the other hand, K of the aquifer was estimated from data collected during the slug tests by automatically matching the type curves of the four solutions to water-level displacement data collected during the slug tests.

Single-borehole dilution tests were conducted at Magilligan in six wells (A2, A4, A6, A8, B4 and B6) by injecting a full miscible NaCl solution into the screened interval of the wells increasing between three and eight times the initial groundwater specific electrical conductance. Groundwater horizontal Darcy velocity (vd) in the aquifer surrounding the well can be estimated from the dilution ratio of the tracer within the well according to (Drost et al. 1968):

$${v}_{d}=\frac{\pi r}{2\alpha t}ln\left[\frac{{C}_{t}}{{C}_{0}}\right],$$
(9)

where r is the radius of the well, t is time, C0 is the initial concentration of the tracer in the well, Ct is the tracer concentration in the well at time t, and α is a correction factor to account for the distortion of groundwater flow by the well. α ranges from 0.5 to 4 in sand aquifers (Drost et al. 1968), although a value of 2 is widely accepted (Shafer et al. 2010).

Electrical conductivity of water was measured at various depths using a calibrated YSI Professional Plus Multiparameter quality meter to ensure uniformity of tracer concentration across the well screen. The decrease in specific electrical conductivity was monitored at the center of the well screen every minute for four days using CTD Solinst loggers placed. Darcy velocities were calculated using the linear least-squares regression method (classical method) and the CXTFIT code (Parker and van Genuchten 1984; Toride et al. 1999) implemented in the STANMOD software (van Genuchten et al. 2012) by inverting the one-dimensional equilibrium advection–dispersion equation (Piccinini et al. 2016). K estimates were performed by applying Darcy’s Law accounting for the hydraulic gradient in the study area is equal to 0.006 (see Sect. “K values derived from numerical modeling”)

Numerical modeling

Groundwater models are commonly used to estimate aquifer properties by calibration processes or inverse modeling (Zhou and Li 2011; Moharir et al. 2017; Águila et al. 2019). One of the most widely used groundwater flow codes is MODFLOW, which solves the three-dimensional groundwater flow equation for porous media by using the finite-difference method (Harbaugh et al. 2000). This code, together the pre- and post-processor GMS v.10.2 (Groundwater Modeling System), was utilized to generate a 3D groundwater model to simulate flow. The model domain was discretized with a finite difference scheme through a non-uniform grid of 1200 × 1000 × 40 m, while the grid was further refined in the study area with cells of 1 × 1 m2 taking into account the topography of the beach. The sand aquifer was discretized in 15 layers with thickness between 0.5 m and 1.75 m to take into account variations in the aquifer parameters with depth, while the mudstone substrate acted as a no flow boundary. Since hydraulic head data revealed groundwater to flow from the dunes to the sea, no flow boundaries were defined to the east and west of the model. The numerical model was used to reproduce the drawdowns measured in the monitoring wells during the pumping test performed in well PW1. Since tides did not have a significant effect during the pumping test, tidal variations were neglected in the model, with the sea simulated as a constant hydraulic head boundary (H = 0 m). The model assumed a constant groundwater recharge of 400 mm/y (Robins and Wilson 2017).

Data analysis methodology

In the present study, estimates of K in the coastal sand aquifer at Magilligan were obtained using 22 different methods and formulations. In order to compare the estimates obtained with each method and to facilitate the discussion and interpretation of the results, several statistical parameters have been analyzed: number of estimates (N), maximum and minimum, range, geometric mean, median, standard deviation (StD), coefficient of variation (COV), mean squared error (MSE), root mean squared error (RMSE), and coefficient of determination (R2). The definition, formulas and use of these statistical parameters are included in Table S1 of the ESM. In addition, to facilitate the comparison of results, specific graphs such as spider charts and box plots have been applied. Radar or spider plots are two-dimensional plots designed to plot one or more series of values over multiple quantitative variables and were used in this research work to compare K estimates obtained with different formulations and at various locations (monitoring wells). The box plot, on the other hand, is a standardized way of displaying the dataset based on the five-number summary: the minimum, the maximum, the sample median, and the first (Q1) and third quartiles (Q3). This last graph was used in this study to show a joint comparison of the K estimates obtained with the different methods and formulations taking into account their scales of interpretation. As for quartiles, they are a set of descriptive statistics that divide the number of data points into four parts. The first quartile (Q1) is known as the 25th empirical quartile where 25% of the data are below this point. In contrast, in the case of the third quartile (Q3) or 75th empirical quartile, 75% of the data are below this point. In this study, histograms and the normal distribution of the data were also used to analyze the frequency distributions of the K estimates obtained from the different methods. Moreover, the skewness was calculated to study the degree of asymmetry observed in the probability distribution. Distributions can have positive skewness when the right tail is longer or negative skewness when the left tail is longer.

Results

K values derived from grain-size analysis

The grain-size distribution curves of the soil samples collected at Magilligan correspond to medium- to fine-grained sands in which the mean of d10 (grain diameter for which 10% of the sample is finer) was determined as 0.162 (Fig. 2a). A consistently low uniformity coefficient (Cu) of less than 1.7, revealed the sand to be well sorted (Fetter 2013). However, when classifying the samples by depth (grouped in categories of approximately 0.5 ± 0.5, 2 ± 0.5, 4 ± 0.5, 6 ± 0.5, and 8.5 ± 0.5 m deep), a greater amount of shell debris and medium-sized particles were detected between 2 and 4 m deep, causing slightly greater variations in the grain-size distribution curves at these depths (Fig. 2a).

Fig. 2
figure 2

Grain-size distribution curves of the soil samples collected at Magillgian (a), and hydraulic conductivity estimated using seven empirical relationships (b). Soil samples and estimates were classified by depths

Full size image

K estimated from 20 sand samples using the seven empirical relationships (Table 1) ranged between 3.1 and 39.5 m/d. The highest geometric means were calculated using the Breyer and Alyamani & Sen methods, reaching values of 26.8 and 28.3 m/d, respectively. By contrast, the lowest K values were calculated using the Slichter and USBR methods, with geometric means of K less than 6.4 m/d. The geometric mean of K calculated with the Hazen, Kozeny and Terzaghi equations were 20.1, 14.9 and 9.6 m/d, respectively. Figure 2b shows the K estimates classified by depths. Except for estimates made from soil samples collected near the surface (less than 1 m deep), K gradually decreases with depth when applying any of the methods. The soil samples collected at around 2 m depth provided the highest K values, while the lowest ones were calculated from the deepest samples (9 m depth). K estimated from 2 and 9 m deep samples decreases by a factor of between 1.75 and 2, depending on the method used.

K values derived from CPT data

Figure 3 shows the hydraulic conductivity estimated from the seven CPT soundings by using the soil behavior type index. To analyze K variations in depth, K has been calculated using a moving average for every meter of depth in each CPT sounding (T1–T7). Results in each depth interval display remarkable uniformity. K of the sands ranges from between 1.5 and 87.6 m/d, while it is around four orders of magnitude lower in the mudstones (20 m deep). CPT data shows a slight decrease in K values with depth in the uppermost 12 m of the aquifer, with the exception of the first meter of the aquifer, where incompletely saturation of the sands generated lower estimates of K. Beyond 13 m BGS, K values estimated from CPT data increase slightly and remain stable to the base of the aquifer. Thus, the highest K values in the sand aquifer were calculated at a depth of 2 m. There are no significant variations between profile-averaged K estimates, further highlighting the homogeneity of the sand (Águila et al. 2022b).

Fig. 3
figure 3

Hydraulic conductivity estimated from the data obtained in the seven CPT soundings (T1–T7) by using the soil behavior type index. The dashed line and symbols show geometric means of K at different depths without distinguishing between CPT soundings

Full size image

K values derived from HPT data

The application of the HPT method in a deposit consisting mainly of fine-grained sands caused the partial blockage of the HPT port in several sections of soundings T2, T4 and T7, leading to the measurement of anomalous pressure injections (much higher than expected). To address this issue, estimates of K have been made from the data collected in HPT soundings T1, T3, T5 and T6 using a moving average for every meter of depth (Fig. 4). K estimated from HPT data using the approach proposed by McCall and Christy (2010) ranges from between 2.4 and 21 m/d, while using the equation proposed by Borden et al. (2020), K ranges from between 0.85 and 15.4 m/d. Thus, K estimates using the Borden approach are approximately three times lower than those obtained with the McCall & Christy solution. However, both approaches indicated that K decreases slightly with depth, in line with CPT observations. Similarly, the geometric mean of K in the shallowest 2 m of the aquifer reaches 12 and 4 m/d, using the equations proposed by McCall & Christy and Borden et al., respectively. From 2 to 12 m depth, K decreases by a factor of approximately 2.5 in both cases.

Fig. 4
figure 4

Hydraulic conductivity estimated from data obtained from HPT soundings T1, T3, T5 and T6 using the equations proposed by McCall and Christy (2010) and Borden et al. (2020). Dashed lines show the geometric means of K at different depths calculated using both methods

Full size image

K values derived from tide-aquifer interaction techniques

K was estimated from data measured in eleven monitoring wells using the direct methods (time lag and tidal efficiency models) and the analytical solution proposed by Nielsen (1990) on sloping beaches (Table 2), since K could not be estimated from data measured in well C6 due to data logger malfunction. Aquifer storage coefficient (S) was assumed equal to 0.1 (derived from preliminary pumping tests) to calculate K from Eqs. (6) and (7). Regarding the direct methods, K estimated using the time lag model ranges between 27.6 and 103.6 m/d, while K derived from the tidal efficiency method ranges between 3.2 and 17.4 m/d. Consequently, K values based on the time lag model are larger (by ten times when comparing the geometric means) than those based on tidal efficiency model. Standard deviation of K estimated using the time lag method ranges between 7.9 and 15.6 m/d, while that estimated using the tidal efficiency model rages between 0.65 and 3.6 m/d. Significant differences were also found between K estimates made from the direct methods using data collected at different dates. For instance, the geometric mean of K estimated using the tidal efficiency method in November 2019 was almost twice that estimated in May 2020.

Table 2 Hydraulic conductivity values and main statistical parameters estimated with the time lag and tidal efficiency methods in each monitoring well during three one-week periods
Full size table

K estimated from the analytical solution on sloping beaches ranges between 5.7 and 15.7 m/d, with a geometric mean of K equal to 7.8 m/d. Standard deviation of K estimated ranges between 0.8 and 2.4 m/d. These values are more similar to the estimates of K achieved using the tidal efficiency model than the time lag method. Figure S2 of ESM shows several examples (wells B2, A8 and C4) of the fit achieved between measured and calculated water level elevations. The average water levels calculated from the analytical solution are similar to those measured on the field in all cases. However, there are slight differences between measured and calculated values when comparing the magnitude of water level fluctuations caused by tidal variations.

K values derived from pumping tests

The agreement achieved between observed monitoring well drawdown data, carried out at constant and variable flow rate in PW1 and PW2 wells, with type curve responses derived from the Neuman solution proved highly satisfactory (see Fig. 5a, b, c, and from Figs. S3–S5 of the ESM). Figure 5d presents a comparison of the K values estimated from data collected in the three pumping tests. K estimated from the constant discharge pumping test ranges from between 4.9 and 7 m/d, while K estimated from data collected during the two step-drawdown tests ranges from between 5.1 and 10.4 m/d.

Fig. 5
figure 5

Neuman solution (blue lines) matched to drawdown data collected in monitoring well C8 (symbols) during the constant-rate pumping test (a) and the variable-rate pumping tests performed on PW1 (b) and PW2 (c) wells; and comparison of the hydraulic conductivity values estimated from data collected in the three pumping tests (d)

Full size image

Data collected in the monitoring wells during the constant-discharge pumping test was also used to estimate transmissivity (T), specific yield (Sy), specific storage (Ss) and anisotropy (Table 3). The geometric means of Sy and Ss estimated using the Neuman solution were 0.11 and 3.05·10–4 m−1, respectively; while the geometric mean of the anisotropy (Kv/Kh) was equal to 1.09, which suggests that the sand aquifer may be considered isotropic over the uppermost 10 m of the sands. The geometric mean of T was 119 m2/d with a standard deviation of 13.7 m2/d. No clear links could be established between the values of the parameters estimated from the pumping test and the depth of the monitoring wells.

Table 3 Hydraulic parameters determined from the constant-discharge pumping test performed in PW1 well
Full size table

K values derived from slug tests

Figure 6 shows the K values estimated from the falling-head and rising-head slug tests conducted in the twelve monitoring wells. The agreements reached between the Hvorslev, Bouwer & Rice, Dagan and KGS solutions and the measured water level variations during the slug tests in all the wells are shown from Figure S5 to Figure S13 of the ESM. The geometric mean of K obtained from the falling-head tests, determined by applying the four different solutions ranges from 7.3 and 9.9 m/d, while that obtained from rising-head slug tests ranges from 6.6 and 9 m/d. Consequently, the estimates of K made from the falling-head slug tests are slightly larger than those made from the rising-head tests. In addition, K values estimated from the rising-head tests show greater variation between the monitoring wells than that observed in K values estimated from the falling-head tests. When comparing the radar graphs in Fig. 6, the distribution of K estimates from the rising-head tests in the 12 monitoring wells is more uniformly concentrated in the area between 3 and 12 m/d, while the shape of the radar graph representing the estimates from the falling-head tests is sharper, reaching values of 18 m/d. The standard deviation of K values estimated from falling-head slug tests ranges from 2.4 to 3.3 m/d, while that determined from rising-head tests ranges from 1.3 to 2 m/d.

Fig. 6
figure 6

Hydraulic conductivities estimated from data collected during slug tests performed in the twelve monitoring wells by applying four different solutions (a); and radar charts of K estimates made from the rising-head (b) and falling-head (c) slug tests

Full size image

In both rising-head and falling-head slug tests, the highest K values were estimated when applying the Hvorslev method, while the lowest ones were obtained using the Bouwer & Rice solution. The geometric mean of K estimated using the Hvorslev method was equal to 9.4 m/d, while it was 6.9 m/d when applying the Bouwer & Rice solution. The geometric means of K estimated using the Dagan and KGS methods were 7.4 and 9.2 m/d, respectively. The data collected during the slug tests did not show a clear relationship between the depth of the wells and the K estimates made with any of the four methods.

K values derived from single-borehole dilution tests

The geometric means of the Darcy’s velocities calculated using the classical method and the CXTFIT model are equal to 1.32·10–1 and 2.06·10–1 m/d, respectively (Table 4). A good agreement was reached between the experimental data and the theoretical solutions in both approaches; the coefficients of determination (R2) of the regression lines ranges from 0.999 to 0.983 for the classical method, while the mean squared errors (MSE) ranged between 2.11·10–6 and 3.63·10–4 for the CXTFIT model. The geometric means of K determined from the classical method and the CXTFIT model are equal to 11.05 and 17.12 m/d, respectively. Therefore, K estimates made from the equilibrium advection–dispersion equation are 1.55 times greater than those estimated using the classical method. In addition, the application of the CXTFIT model also allowed the longitudinal dispersion (D) and dispersivity (λ) of the aquifer to be estimated. D ranged from 8.90·10–3 to 4.01·10–2 m2/d, while λ ranges from 0.06 to 0.19 m (Table 4).

Table 4 Results of the single-borehole dilution tests analyzed with the classical method and the CXTFIT model
Full size table

K values derived from numerical modeling

Hydraulic conductivities determined from the 3D groundwater flow model were calibrated by trial and error to reproduce the observed hydraulic gradient and the drawdowns measured in the twelve monitoring wells during the constant-rate pumping test. The best fit between measured and computed drawdowns was achieved where the K of the sands slightly decreases with depth and the model considers an anisotropy (Kh/Kv) of 1.75. Calibrated horizontal hydraulic conductivity (Kh) decreases from 20 to 5 m/d in the first 10 m of the sand aquifer and remains constant (5 m/d) to the base of the aquifer (see Fig. 7). K of the mudstone was assumed equal to 10–3 m/d, while other parameters such as the specific yield and specific storage were also calibrated with the numerical model (Sy = 0.1 and Ss = 3.5·10–4 m−1).

Fig. 7.
figure 7

3D groundwater flow model with the spatial distribution of horizontal hydraulic conductivity and the hydraulic heads computed under steady-state conditions. The computed hydraulic gradient in the study area is equal to 0.006

Full size image

Following calibration, the computed hydraulic gradient under steady-state conditions in the study area was observed as 0.006, which is within the range of hydraulic gradients estimated on the beach from the water levels recorded in the monitoring wells (between 0.005 and 0.0085). Under transient conditions, the calibrated numerical model successfully reproduced the drawdowns measured in the twelve monitoring wells during the constant discharge pumping test performed on PW1 well. The root-mean-square error (RMSE) between measured and computed drawdowns is equal to 0.02 m (Fig. 8a). Additional sensitivity runs were performed with the model to know the impact of hydraulic parameter variations on groundwater levels. When considering the sand aquifer as isotropic, with a constant hydraulic conductivity equal to the geometric mean of K determined from the pumping test data by applying analytical solutions (5.95 m/d), the RMSE between measured and computed drawdowns increases to 0.031 m (Fig. 8b). Figure 8c presents a comparison between the measured drawdown in the monitoring wells C4 and A8 and those computed with the numerical model in the base run (calibrated model), considering hydraulic parameter values determined from the constant-discharge pumping test, and assuming an anisotropy (Kh/Kv) equal to 5. The best agreement between the measured and computed drawdowns is achieved after calibrating the numerical model, although an acceptable agreement is also obtained with the numerical model assuming a K of the sands is constant and equal to 5.95 m/d. The measured and calculated drawdown are markedly different with increasing Kh relative to Kv, suggesting that the sand aquifer does not exhibit strong anisotropy.

Fig. 8
figure 8

Comparison of the drawdowns measured during the constant-rate pumping test and those computed with the numerical model after calibration (a) and considering values of hydraulic parameter determined from analytical solutions (b); and comparison between the measured drawdown in the monitoring wells C4 and A8 and those computed in the base run (calibrated model) and two sensitivity runs assuming that K = 6 m/d and Kh/Kv = 5 (c)

Full size image

Discussion

Previous studies (Rovey 1998; Schulze-Makuch and Cherkauer 1998; Martínez-Landa and Carrera 2005; Cheong et al. 2008; Smith et al. 2016) pointed out that hydraulic conductivity depends on the measurement scale and highlighted that estimated values of K used to increase with increasing the measurement scale. Nevertheless, no clear consensus exists on whether scale dependency of K reflects aquifer heterogeneity or, instead, depends on additional factors such as the measurement methods (Godoy et al. 2018). Schulze-Makuch et al. (1999) note that if the intrinsic heterogeneity in a medium is what causes the scale effect in K, then no scale effect should be observed in a perfectly homogeneous medium. However, experimental investigations conducted by Fallico et al. (2010) for relatively homogeneous sands in the laboratory showed a trend of K increasing with the scale. Testing this in real-word settings proves challenging, since natural perfectly homogeneous media do not exist. However, some media approach this ideal state; this includes the coastal sand deposits at Magilligan. This aquifer was exhaustively characterized through geophysical, geotechnical and hydrogeological tests, confirming the great uniformity and high levels of homogeneity (Águila et al. 2022b; McDonnell et al. 2023). Consequently, the high homogeneity of this site makes it an excellent study area to investigate and increase the current state of knowledge on the scale effect of K when estimating this parameter using different measurement methods. Differences found between K values determined using various techniques can be attributed with greater confidence to uncertainties arising from analytical methodologies and their associated scale effects than those caused by geological heterogeneities.

Figure 9 summarizes and compares the ranges of K values determined in the shallowest 10 m of the well-characterized homogeneous coastal sand aquifer of Magilligan using eight methodologies and various formulations for quantifying hydraulic conductivity, representing them according to the approximate integration scale of each method. K values lie within the typical ranges for sands in all cases (Earle 2015), although there exist discrepancies of greater than an order of magnitude between K values estimated using different solutions. The range of values estimated from CPT data proved wider than that calculated using the other methods. In fact, for a better comparison between the K estimates using all techniques, the maximum K values in Fig. 9, calculated from CPT data, have been limited to the 90th percentile, since K values greater than 250 m/d were calculated in a limited locations and proved anomalous (see Table 5 and Figure S14 for the maximum K values). On the contrary, K estimates obtained from pumping tests, especially the one performed at constant flow rate, show the least variability. According to the classification proposed by Wilding and Drees (1983) on the variability of soil properties, K estimates from pumping tests fall into the category with the lowest variability (COV < 15%), while estimates from slug tests and GSA belong to the moderate variability category (COV ranging from 15 to 35%). The other techniques used in this study showed a higher spatial variability of K (COV > 35%). As for the geometric means of the K estimates, the time lag method of the tide-aquifer iteration techniques and the formulation proposed by Alyamani & Sen within the GSA methodology revealed the highest ones exceeding by a factor of nine and four times the geometric mean estimated from pumping tests, respectively. The highest standard deviations among the methods correspond to the estimates from the CPT technique (see Table 5 and Fig. S14).

Fig. 9
figure 9

Comparison of the hydraulic conductivity determined by eight different methodologies with the approximate integration scale of each method. Q1 is the first quartile (25% of the data is below this point) and Q3 is the third quartile (75% of the data lies below this point). For CPT data, the 90th percentile is displayed instead of the maximum for better visualization. BR: Breyer; AS: Alyamani & Sen; HZ: Hazen; TZ: Terzaghi; SL: Slitcher; US: USBR; KZ: Kozeny; MC: McCall and Christy; BD: Borden; CL: Classical method (dilution tests); CX: CXTFIT model; BO: Bouwer and Rice; HV: Hvorslev; DG: Dagan; ST: Step-drawdown test; CD: Constant discharge; SB: Analytical solution on sloping beaches; TE: tidal efficiency. Results obtained from the time lag model of the Tide-Aquifer iteration techniques are not included on the figure

Full size image
Table 5 Main statistical parameters of K estimated using different methodologies and evaluation of variations in K with depth in the shallowest 10 m of the aquifer (see Fig. S14)
Full size table

The use of empirical or indirect methods, such as GSA or pedotransfer functions, makes it possible to estimate soil hydraulic properties from more easily measured parameters and, consequently, the number of K estimates that can be obtained at a specific site is usually greater than that obtained by applying hydraulic methods, generally much more costly and time-consuming. This is the case at Benone Strand where after the application of indirect methods to determine K such as HPT more than 2900 estimates were obtained, while other techniques such as the single-borehole dilution tests only yielded six K estimates. After a comparative analysis between the values of K and the number of estimates, it was found that the COV tends to increase as the number of estimates obtained from the indirect methods, such as CPT and HPT from formulations proposed by Barden et al., increases. However, this increase is not such when comparing the geometric means and, especially, the medians of K, where no dependence was found with respect to the number of estimates (see Fig. S15). Figure S16 of the ESM show the histograms of K estimates and normal distributions obtained by applying different methodologies in the coastal aquifer at Magilligan. Most histograms show a unimodal distribution of the data (e.g., HPT or Terzaghi and Slitcher models from GSA), although some of them exhibit a bimodal dataset (e.g., USBR from GSA or the time lag method). Estimates from single-well dilution tests are not sufficient to define an appropriate distribution of data. K estimates from the GSA and step pumping tests show a slight negative skewness, while the skewness of K values obtained from the other methods is positive (see Fig. S17). The largest skewness occurs in the estimates of K from CPT, HPT (Borden et al. method), and Tide-Aquifer iteration techniques (the tidal efficiency model and the analytical solution proposed by Nielsen (1990)) since these techniques yielded above-average K estimates (see Fig. S16), as evidenced by their elevated COV values (Table 5).

As stated by Robertson (2010), normalized CPT parameters respond to the mechanical behavior of the soil, so the estimates of K from Ic should be only used as a guide. Nevertheless, the CPT method has been, among those used in this research work, the most suitable to obtain information on the aquifer characteristics at greater depths. Incorporating a high-resolution hydraulic profiling tool system (HPT) into CPT equipment helped reduce uncertainties when estimating K (Butler 2005). K estimated from HPT data varies from 0.01 to 27 m/d, which is a much narrower range than that estimated from CPT data. Consequently, K values calculated with the HPT method may be more accurate than those calculated with the CPT method. Nevertheless, K estimates using the HPT method in fine- and medium-grained deposits should be compared with those calculated with other methods, since the HPT injection port can easily be blocked with the unconsolidated material and underestimate K. In addition, significant differences were found when estimating K using the formulas proposed by McCall and Christy (2010) and Borden et al. (2020). The first (Q1) and third (Q3) quartiles of the K data estimated using McCall & Christy equation are equal to 5.6 and 12.5 m/d, respectively, while those estimated from the Borden et al. method are 1.3 and 3.9 m/d. Furthermore, the COV and skewness calculated from the K estimates using the model proposed by Borden et al. are larger than those obtained from the method of McCall & Christy (Fig. S17 and Table 5). Such differences may be due to the fact that the Borden et al. (2020) equation was proposed to be preferably applicable in less permeable environments (< 0.3 m/d).

The grain-size distribution method and the Tide-Aquifer interaction techniques provided order of magnitude estimates of K. However, different equations commonly used to estimate K from both approaches showed considerable variations, which is in agreement with Jha et al. (2008) and Vienken and Dietrich (2011) (see Fig. 2 and Table 2). K estimated using the formulas proposed by Breyer and Alyamani & Sen are larger than that calculated using other formulae from GSA. Both methods do not take into account porosity when estimating K (see Table 1) and some authors, such as Sahu and Saha (2016), had already reported that these formulas are significantly sensitive to the shape of the size grading curve, which makes them more suitable for estimating K from more heterogeneous soil samples. By contrast, the equations proposed by Slitcher and USBR underestimated K of the sands in comparison to the other grain-size distribution method, which is consistent with Odong (2007). Nevertheless, the findings in the present study are in disagreement with Pucko and Verbovšek (2015) who reported that the USBR method overestimates K values with respect to those estimated from hydraulic tests. Estimates of K using the three remaining methods from GSA (Hanzen, Kozeny and Terzaghi) resulted in intermediate values ranging between 5 and 27 m/d. By contrast, K estimates obtained from the GSA of the soil samples collected at a depth greater than 2 m showed that K decreases with depth when applying any of the methods. Sample disturbance contributes to the differences found in the estimation of K with the GSA method, highlighting the advantages of applying in situ techniques over laboratory methods. For instance, single-borehole dilutions tests provide a good alternative to make preliminary estimates of groundwater velocity and K in coastal aquifers, although prior knowledge of hydraulic gradients proves necessary (Carr and van der Kamp 1969; Butler 2005).

The effectiveness of Tide-Aquifer interaction techniques for determining hydraulic properties in coastal aquifers has received much attention in recent decades due to their simplicity and low cost (Zhang et al. 2020). The application of two direct methods in the coastal sand aquifer at Magilligan yielded significant differences in determining K and assuming the storage coefficient of the aquifer is known (one of the disadvantages of these methods). Hydraulic conductivity values estimating from the time lag model were approximately ten times larger than those based on the tidal efficiency model and significantly greater than those estimated from the other method such as pumping test, slug test or numerical models. These results are in agreement with research conducted by Jha et al. (2008), who reported that the time lag method consistently yielded very large hydraulic diffusivity values for both unconfined and confined sites compared to the tidal efficiency method. The present research supports the recommendations of these authors that the time lag method should be avoided or used to obtain rough estimation of the aquifer parameters. On the other hand, K estimates made from the analytical solution proposed by Nielsen (1990) on sloping beaches were similar to those obtained with the tidal efficiency method, although the application of the former is more complex than the latter than the other methods used. In both cases, the K estimates from the two methods showed significant variability (COV > 50%) and strong positive skewness (see Fig. S17 and Table 5). However, as pointed out by Zang et al. (2020), cautions should be taken when applying any of the Tide-Aquifer iteration techniques since variations in other parameters such as changes in local atmospheric pressure could induce tidal fluctuations in the hydraulic head within observations wells.

The constant-rate pumping test is one of the most commonly used methods in groundwater-resource investigations to estimate aquifer parameters, providing average values of K representative of a relatively large volume of the aquifer (Butler 2005; Lu et al. 2021). This was apparent at Magilligan where, due to the homogeneity of the aquifer, the range of variation in K estimates made from the constant-rate pumping test proved the lowest among all the methods (Table 5). The coefficient of variation (COV) of K was equal to 12%, while Q1 and Q3 were equal to 5.4 and 6.8 m/d, respectively. Nevertheless, K estimated from drawdown data measured in wells of different depths failed to detect a decrease in K with depth in the uppermost 8 m of the sands, as suggested from the GSA, CPT and HPT methods. K estimated from step-drawdown tests proved 1.3 times larger than that estimated from the constant rate pumping test. Moreover, the range of variation in K estimates made from drawdown data collected during the step-drawdown tests was also greater (COV = 15%).

Some authors such as Butler and Healey (1998) and Cheong et al. (2008) reported that K estimates from pumping tests are, on average, larger than the estimates obtained from slug tests. This response was not observed at Benone with the geometric mean of K estimated from the slug tests was between 1.2 and 1.6 times (depending on the method used) larger than that estimated from the constant-rate pumping test. However, this study agrees with Ismael (2016) in the finding that estimates of K obtained from falling-head slug tests are slightly larger than those made from the rising-head tests (Fig. 6), which may be due to the fact that falling-head tests are less affected by soil compressibility (Choi and Daniel 2006). In addition, K values estimated from slug tests using the Hvorslev method were slightly larger than those estimated using the KGS, Bouwer and Rice and Dagan methods. For instance, the geometric mean of K calculated from the Hvorslev method was 36 percent higher than that calculated from the Bouwer and Rice method, which is in line with what was reported by Alfaifi (2015).

The application of eight methodologies for estimation of K at different scales varying from 0.01 to 100 m in the homogeneous real aquifer at Magilligan fail to display an increase in K when increasing the measurement scale, suggesting that there is no scale effect when significant heterogeneities are not present within the aquifer. Given the large potential variation of K in natural deposits, the K values estimated with the eight methods prove broadly consistent, with differences observed suspected to arise largely from assumptions associated with each technique. The lack of evidence of scale effects when estimating K in the aquifer at Magilligan is in agreement with the results reported by Chapuis et al. (2005) who estimated K from grain-size analysis, slug tests and pumping test in another quasi-homogeneous coastal sand aquifer, and with the research work carried out by Schulze-Makuch et al. (1999) and Zlotnik et al. (2000) analyzing the scale effect of K in aquifers with different degrees of heterogeneity reported in previous investigations.

Some authors such as Sobieraj et al. (2004) and Yang et al. (2017) pointed out that K estimated from laboratory methods tend to show smaller means and larger variances than K estimated on a larger scale with field methods. After analyzing the main statistical parameters of K estimated using the different methodologies in the aquifer at Magilligan (Table 5 and Fig. S14), there is no clear evidence when comparing the means or variances calculated from the GSA (the only laboratory method in this study) with respect to other field techniques with larger measurement scales. The geometric means of K estimated from the different formulations proposed for the GSA range from 5.6 to 28.3 m/d, while the standard deviations of K range from 1.5 to 7.1 m/d. These geometric means are not lower or the StDs larger than those estimated from the field tests. Therefore, the differences found seem to be caused by the particularities and limitations of the methods and formulations, rather than by variations in the measurement scale. However, the ability of methods to predict variations of K with depth is influenced by the measurement scale (Table 5 and Fig. S18). At Benone, techniques that determine K from smaller aquifer volumes (GSA, CPT and HPT) have shown a decrease in K with depth in the shallowest 10 m of the aquifer. More efficient grain packing with increasing depth could explain the observed decrease in K at depth. The decrease in K with depth has been identified at other sites in previous research (e.g., Kuang and Jiao 2014) and, is also in agreement with the results of the numerical model simulating the aquifer at Magilligan. The simulations showed a better fit between measured and calculated groundwater levels when considering a decrease in K values with depth. This is in agreement with the skewness identified after analyzing the estimates of K through the different methods, suggesting the existence of some variability of K (Figs. S16 and S17). The rate of decrease of K with depth depends significantly on the empirical relationship used to estimate K and range from 0.1 to 3.8 m/d per meter depth (see Table 5). Methods that used larger volumes of the aquifer to estimate K failed to display clear evidence of a decrease in K with depth (Fig. S18).

Conclusions

Estimating accurate values of hydraulic conductivity proves crucial in coastal environments due to the key role that K plays in processes such as seawater intrusion, migration of contaminants, and stability of coastal engineering structures. Eight different approaches to estimate K, encompassing empirical, hydraulic and numerical modeling methods, were applied to a quasi-homogeneous coastal sand aquifer with the aim of comparing the capacities and limitations of each method and evaluating the scale dependence of K. The absence of significant geological heterogeneities with large influence on K made it possible to investigate the scale effect when estimating K using different measurement methods in real coastal aquifers. A total of 22 estimates of K were made from the eight methods and considering, in turn, several formulations in each of them. Comparison of the results yielded the following main conclusions:

  • The geometric means of K estimates from the different methodologies ranged between 3.6 and 58.3 m/d. Such discrepancies are significant, but taking into account the different approaches used to estimate K with measurement scales varying from 0.01 m to 100 m and the high potential variability of this parameter within the same deposit, the results broadly consistent across a range of investigation scales.

  • Increases in K when increasing the measurement scale were not evidenced, proving that K estimates do not depend on the scale of measurement when significant heterogeneities are not present within the aquifer.

  • Techniques that determined K from smaller aquifer volumes (GSA, CPT and HPT) showed a decrease in K with depth, while such decrease was not detected in larger-scale K estimates.

  • The range of variation of K values estimated from CPT data was much greater than that obtained using the other methods, with the mean overestimating K calculated from HPT data and pumping tests.

  • Empirical equations commonly used to estimate K from GSA showed variations of one order of magnitude, highlighting the advantages of applying in situ methods over laboratory methods. The Breyer and Alyamani & Sen methods provided the highest K estimates, while the lowest ones were obtained using the formulas proposed by Slichter and USBR.

  • K estimated from Tide-Aquifer interaction techniques depend greatly on the model selected, with hydraulic conductivities estimated using the time lag model are ten times larger than those estimated using the tidal efficiency model and the analytical solution proposed by Nielsen (1990) on sloping beaches. The time lag method should be avoided or limited to obtain rough estimation of aquifer parameters.

  • Single-well tracer dilution tests provide an alternative for making preliminary estimates of K in coastal aquifers when hydraulic gradients are known.

  • The range of variation of K estimates made from constant-rate pumping test data was one of the lowest among all the methods, providing a representative average K of the aquifer.

  • Estimates of K from the slug tests were between 1.2 and 1.6 times larger than K estimated from the constant-rate pumping test, with the falling-head tests showing slightly greater estimates of K than those obtained from the rising-head tests. K values estimated from slug tests using the Hvorslev model were slightly larger than those estimated using the KGS, Bouwer & Rice and Dagan methods.

  • The formula proposed by McCall & Christy to estimate K from HPT data proved more suitable than the one proposed by Borden et al. in aquifers of relatively high permeability.

  • The numerical model proved useful to test the differences found when estimating K using different methods, in particular regarding the spatial distribution of K.

  • The combination of several techniques at the same site helps to increase the confidence in the estimation of K in real aquifers. However, from the present research work it is concluded that pumping tests are the preferred method to obtain an average of the aquifer hydraulic conductivity, while the HPT technique is the most suitable for determining spatial variations of K.