Benchmarking a new TH²M implementation in OGS-6 with regard to processes relevant for nuclear waste disposal

Abstract

In this paper, thermo-hydro-mechanically (THM) coupled processes triggered during the construction, operation and closure of a deep geological repository for heat generating, high level radioactive waste are discussed based on a generic disposal concept. For this purpose, we are using the numerical non-isothermal two-phase–two-component flow in deformable porous media (TH²M) implementation (Grunwald et al. in Geomech Geophys Geo-energy Geo-resour, 2022) in the open-source software OpenGeoSys (Bilke et al. in Transport Porous Media 130(1):337–361, 2019, https://doi.org/10.1007/s11242-019-01310-1). THM coupled effects covered in this work focus on single and two-phase-flow phenomena, gas and heat generation as well as poro-elastic medium deformation. A suitable set of benchmarks covering aforementioned THM-effects, devised in the scope of the BenVaSim benchmarking project (Lux et al. in Synthesis report. BenVaSim—International Benchmarking for Verification and Validation of TH2M Simulators with Special Consideration of Fluid Dynamical Processes in Radioactive Waste Repository Systems. Tech. rep., 2021, https://doi.org/10.13140/RG.2.2.28998.34887) is chosen and one additional benchmark is presented, allowing for the demonstration and comparison of the OGS-6 TH²M implementation against results obtained by other well-established codes used in the field. Apart from the code comparison, the benchmarks also serve as means to analyze THM coupled processes in a repository based on very simplified geometries. Therefore, they can help to improve the process understanding, but any quantitative results should not be interpreted as predictions of the behaviour of a real repository. The results obtained in this work agree well with the results presented by the project partners in BenVaSim—both in single phasic, fully liquid saturated cases and in partially saturated two phase regions. Hence, the suitability of the OGS-6 TH²M implementation for the application in the field of radioactive waste management, supporting the safety case and analyzing the integrity of the geological and geotechnical barrier systems is demonstrated. Finally, a detailed discussion of observed phenomena in the benchmarks increases our understanding and confidence in the prediction of the behaviour of TH²M coupled systems in the context of deep geological radioactive waste disposal.

Introduction

The concept of deep geological storage for the final disposal of heat-generating, high level radioactive nuclear waste (HLW) presents various challenges to radioactive waste management organisations (WMO) around the world (IAEA 2010). A suitable host rock formation has to be identified satisfying an extensive set of geoscientific criteria. Subsequently, the ability of the geotechnical and geological barriers to safely and predictably seal the waste container in order to prevent transport of radionuclides into the biosphere above certain thresholds—in short, the safety of the geological and geotechnical barriers and their integrity over geological time scales—has to be proven for the reference period of the repository, typically a duration of hundreds of thousands up to one million years. The predictability of the short-term behaviour of the geological and geotechnical materials under certain boundary conditions can be improved by laboratory and in-situ experiments on small and medium scales; however, our general understanding of the relevant processes occurring during the life-time of the site (i.e. geological time scales) and on large spatial scales can not only be tackled by such experiments. And while natural analogues are a powerful way to increase process understanding on geological scales, numerical tools remain the only way for quantitative predictions of the system behaviour. Modelling capabilities are not only important for implementers but also for regulators. Both need a deep understanding of the relevant processes, suitable simulating tools and the capabilities to apply them on the relevant problems. Based on this a deeper understanding of the future evolution of a geological repository can be achieved.

The THM coupled processes triggered by the construction and operation of a deep geological repository and the complex interplay between the processes can be described by a set of partial differential equations (PDE) based on conservation of mass, momentum and energy. These PDEs are mathematical expressions of conceptual process models describing the coupled flow of mass and energy as well as deformation processes—an idealized representation of the real-world-processes. Testing and validating these conceptual models against experiments and real-world-findings has a long scientific tradition (Darcy 1856; Terzaghi 1923; Biot 1941; Richards 1931) and continues to be an ever-important topic (Birkholzer et al 2019; Lux et al. 2021; Lux and Rutenberg 2018; Bourgeat et al. 2013; Rutqvist et al. 2008). The solution of these PDEs through analytical methods, while accurate, is mostly mathematically challenging, if not impossible, and would often bring forth a number of constraining assumptions considering the system behavior and characterization. Therefore, the application of numerical tools to solve PDEs has been a common practice in geo-engineering.

Quality assurance (QA) by code verification against analytical studies or observations and measurements as well as the comparison of numerical results obtained by different code implementations (code benchmarking) are important for the application of numerical tools in general. In radioactive waste disposal, QA needs to be especially emphasised, because confidence in a given code’s capability to capture the relevant processes accurately needs to be built and deepened for acceptance among both the scientific and civil communities. In this work, the TH²M formulation (Grunwald et al. 2022) implemented in the open-source software OpenGeoSys (Bilke et al. 2019; Naumov et al. 2022; Kolditz et al. 2012), is used as a numerical tool, since its accuracy was already partially demonstrated in a series of benchmarks, mostly against analytical solutions (Grunwald et al. 2022; Grunwald et al 2020). In Grunwald et al. (2022), benchmark cases using OGS-6 TH²M including the Liakopoulos test (Liakopoulos 1964), the heat pipe test (Udell 1985), and the Ogata-Banks transport test (Ogata and Banks 1961) are presented, all of which feature homogeneous materials. However, analytical solutions become scarce or cease to exist as soon as the benchmark complexity is increased with regard to geometry (e.g. heterogeneous materials) or the level of process coupling induces strong non-linearities. For applications in radioactive waste disposal, a high level of complexity is commonly encountered and therefore, code testing by comparison of results obtained by independent codes and modelling teams is the strategy pursued in this work for the TH²M implementation in OGS-6, thus building on the verification work already carried out for this implementation (Grunwald et al. 2022).

In this work, we discuss THM-coupled processes triggered by the construction and operation of a repository as well as during the post-closure period. We then move on to express the THM process mathematically through the PDEs. Finally, we present a series of benchmark tests and corresponding results obtained by the OGS-6 TH²M implementation and present a comparison against results obtained by other codes. The benchmarks chosen for this work comprise of a series of test cases devised in the scope of the BenVaSim¹ benchmarking project (Lux et al. 2021; Rutenberg et al. 2022; Czaikowski and Friedenberg 2020; ENSI 2018), in which a number of teams using different codes participated by modelling test cases motivated by THM-coupled processes in deep geological nuclear waste repositories. The numerical codes used in the BenVaSim project (taken as reference for the OGS-6 TH²M model results in this work) comprise CODE_BRIGHT (Olivella et al. 1996; Czaikowski and Friedenberg 2020), three different versions of TOUGH-FLAC (Rutqvist 2011; Rinaldi et al. 2022; Seher et al. 2019), Comsol^® Multiphysics (Diaz-Viera 2008), FTK (Lux et al. 2015; Lux and Rutenberg 2018), OGS-5 (Kolditz et al. 2012) and Jife (Faust 2022). The BenVaSim tests are especially suited for this work, because material parameters, geometries and boundary conditions are specifically tailored to represent a wide scope of processes in nuclear waste disposal. Finally, we present an additional benchmark which is similar to the heat pipe test (Grunwald et al. 2022), featuring water vaporization and water vapour diffusion as a transport mechanism for mass, momentum and energy. The boundary conditions of the original heat pipe test were modified to better represent the situation in the late stages of the repository evolution.

With this outline, this paper has three aims: Firstly, it aims to illustrate the safety-relevant THM-coupled processes which take place during the construction, operation and post-closure phase of a repository in argillaceous host rock formations. Secondly, it aims to show that the TH²M implementation mathematically represents each of the previously identified coupled processes. Thus, we demonstrate that the TH²M implementation is suitable to represent the chosen simplified and generalized behaviour of the repository system under a wide range of conditions, whereas other conceptual models such as implementations utilizing the Richards equation (Richards 1931) are suitable to consider specific processes under certain simplifying assumptions (Pitz et al. 2022a). Thirdly and finally, a series of benchmark tests devised specifically with nuclear waste disposal in mind allows for the verification and confidence-building of similar process model implementations in other codes.

Safety-relevant THM processes in nuclear waste repositories considered in this work

Relevant THM-coupled processes in HLW repositories

The benchmarks discussed in this work and in the reference material (Lux et al. 2021) are motivated by deep geological disposal of heat producing nuclear waste in argillaceous host rock formations. Numerous thermo-hydro-mechanically coupled mechanisms occur during and after the disruption of the geological system. They are due to the construction and operation of the repository as well as due to the materials brought into the repository. In addition to the heat generating radioactive waste itself, materials for the technical and geotechnical barrier or structural supports (e.g. steel, concrete, bentonite, asphalt, sand) are present. In the following chapter, we identify THM processes relevant for the integrity of the barrier system and their couplings in the context of deep geological HLW disposal.

Fig. 1

Sketch of a generic repository and processes therein, which are considered in the benchmarks in this work. The location of motivation of each benchmark (BM) is marked and color coded. The sketch does not take into account that the different processes may occur at different points in time

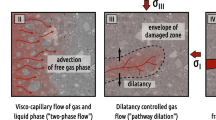
The THM-coupled processes considered in the scope of this work, illustrated in Fig. 1, are briefly discussed in the following section. A comprehensive discussion of TH²M coupled effects can be found in Hudson et al. (2001). In the following as well as in the benchmarks discussed in this work, we assume a deep geological repository situated in an argillaceous host rock formation. However, our discussion will mainly focus on near-field processes (Fig. 1). We furthermore assume that the repository is backfilled mostly with initially partially saturated bentonite, whereas the host rock remains fully saturated outside of the excavation damaged zone (EDZ). The EDZ is a zone adjacent to the excavated drifts, boreholes or shafts, where stress redistribution can cause dilatant deformation. In the EDZ, hydraulic and mechanic properties of the medium can be significantly altered (and impacts from thermal-mechanical effects may extend well beyond the EDZ in the post-closure phase). The main processes occurring in this repository system include:

• Heat generation: The undisturbed temperature field present in the generic repository is given by the local geothermal gradient as well as the depth at which the repository is located. While ventilation during operation and hydration of concrete components (Glasser and Atkins 1994) will likely have minor cooling and heating effects, respectively, the heat generation by the radioactive decay will have a significant impact on the temperature field, which will continue thousands of years post-closure (Finsterle et al. 2019). Apart from thermal pressurization in the host rock, this heat production will drive hydraulic processes such as vapour diffusion in the near field (Philip and De vries 1957; Wang 2010). Furthermore, multiple fluid properties of the gaseous and liquid phases such as viscosity and density as well as chemical properties such as solubility of components and connected phase equilibrium conditions are strongly temperature-dependent. As discussed above, thermal stresses caused by thermal expansion of the solid, can translate mechanically fast and far into the overlying rock formations (Min et al. 2005; Pluá et al. 2021) and at interfaces to adjacent rock formations, e.g. the cap rock.

• Liquid pressurization and flow: Apart from natural aquitards embedded by upper and lower aquifers ground water flow systems which might exist at the location of a future repository, there are liquid transport mechanisms triggered by the repository itself (Chang et al. 2022): Liquid pressure gradients between the fully saturated, undisturbed argillaceous host rock and the initially partially saturated geotechnical materials of the repository will drive a water influx into the repository. Additionally, liquid pressure build up or loss as a consequence of medium deformation or temperature changes can create pore pressure gradients in the host rock, which take a long time to equilibrate due to the low permeability of the host rock. During the operation of the repository, liquid will be removed from the system, due to ventilation and pumping of infiltrating formation waters. Post closure, however, this liquid influx will re-saturate the back-filled repository (Kröhn 2005). At the same time, water vapour transport in the gaseous phase driven by vapour mass fraction and temperature gradients created by the heat generation of the high-level-waste takes place, leading to a dry-out of the bentonite in the vicinity of the waste-containing canisters (Schäfers et al. 2019; Gens and Olivella 2001). In the fully saturated host rock, temperature increase might lead to a pore liquid pressurization (due to the volumetric expansion of water with increasing temperature) which in turn could trigger liquid flow or, in the worst case could cause the loss of integrity of the host rock. Any deformations induced by the repository (expansion or compaction) will impact pore liquid pressures as well (Jacquey et al. 2018) and visa versa, according to Biot’s consolidation theory (Biot 1941).

• Deformation: Possibly the strongest disturbance in the geological formation is caused by the repository excavation, which can lead to dilatant deformation in the host rock as well as to the formation of an excavation damaged zone around the excavated regions (Ziefle 2022; Kelsall et al. 1984). Heat-induced thermal stresses and strains will cause further deformation. The complex hydro-mechanical coupling, e.g. caused by bentonite swelling, pore water pressurization (according to Biot’s theory of consolidation (Biot 1941), gas pressure build-up or saturation-suction effects constitute some of the most significant post-excavation and post-closure effects (Chin-Fu 2012). In comparison to the temperature and hydraulic processes which take place over longer time spans, the momentum transfer due to solid deformation propagates almost instantaneously and can translate into MH-coupled effects even in the far distance (Jacquey et al. 2018).

• Gas transport: due to the partial liquid saturation in the back-filled and sealed sections of the deposition tunnels and access sections, air (mostly $\text {N}_2$ and $\text {O}_2$)is initially present in the repository. Additionally, the metallic components of the repository such as the waste canisters and structural components will likely undergo anaerobic corrosion after a short time of aerobic corrosion, thus releasing large amounts of $\text {H}_2$ gas. This will change the gas phase composition (and consequently gas phase properties) and drive diffusive transport in the gaseous phase. Gas pressure build-up due to $\text {H}_2$ release might lead to gas migration in the geotechnical and geological barrier (Levasseur 2022). In the initially partially liquid saturated repository where a distinct gaseous phase is present, gas migration will likely occur via advection whereas in the fully liquid saturated host rock (and after the re-saturation of the backfilled repository, in the saturated bentonite), dissolved gas will be transported diffusively, driven by dissolved gas concentration gradients (Jacops et al. 2021; Marschall et al. 2005). The transport of gas, be it by diffusion or advection in the liquid or gaseous phase, can imply the transport of radio nuclides (Mathieu et al. 2008). Therefore, one of the primary safety functions of the deep geological repository can be directly affected by gas migration. When gas pressure build-up occurs, hydro-mechanically induced deformation of the host rock and geotechnical materials can lead to the formation of fissures and, subsequently, preferential pathways for radio nuclides (Marschall et al. 2005; Levasseur 2022). This effect represents a potential diminishing of the integrity of the geological and geotechnical barrier system. Finally, gas generation leads to the appearance or persistence of a distinct, free gaseous phase which might impair the swelling process of bentonites, because it delays the re-saturation of the bentonite (Liu et al. 2014).

As discussed, while some of the mentioned processes take place at different points in time (such as during operation or post-closure), others take place simultaneously or trigger each other. Biological and chemical processes also take place and could be incorporated in PDEs (Wang and Nackenhorst 2020, 2022) but so far, they are not considered by the TH²M implementation or the benchmarks in this work. In order to simulate and quantify the impact of aforementioned processes on the system consisting of the repository and geosphere, they must be considered as a whole, coupled system and not separately. In the following section, the mathematical representation and implementation of above mentioned processes in the open-source finite element code OGS-6 (Bilke et al. 2019) by the TH²M model (Grunwald et al. 2022) is shown and discussed.

Mathematical representation of processes by the TH²M model in OGS-6

Fig. 2

Sketch of driving forces of the system, in which four thermo-hydro-mechanically coupled processes are present. They interact through numerous coupling mechanisms

The TH²M implementation in OGS-6 describes the coupled processes taking place in a deformable porous medium by assuming the presence of a solid phase representing the solid skeleton and two fluid phases (gaseous and liquid $\alpha \in \{\text {G, L}\}$) with their constituents water and a second component²$\zeta \in \{\text {W, C}\}$, which can be exchanged between the phases by the process of phase transition. The two-phase–two-component hydraulic process is described by considering two mass balances for the two components using the capillary pressure $p_\textrm{cap}$ and the gas pressure $p_\textrm{GR}$ as primary variables. The liquid pressure $p_\textrm{LR}$ is defined through the hydraulic primary variables using

$$\begin{aligned} p_\textrm{LR}= p_\textrm{GR}- p_\textrm{cap}. \end{aligned}$$

(1)

The primary variable for the medium deformation process is the solid displacement vector ${{\varvec{u}}}=[u_\text {x} \, u_\text {y} \, u_\text {z}]^T$ used to solve the momentum balance. Lastly, the heat transport process is described by the energy balance with temperature itself as the primary variable. Numerous coupling mechanisms are taken into account when considering the different balance equations as illustrated in Fig. 2. The component mass balances are identical for both components and can be obtained by inserting $\zeta \in \{\text {W, C}\}$ for the water and gas component:

$$\begin{aligned} \begin{aligned} 0&= \rho ^{\zeta }_\textrm{FR}(\alpha _\textrm{B}- \phi ) \beta _{p,\textrm{SR}}\frac{\text {d}p_\textrm{GR}}{\text {d}t} - \rho ^{\zeta }_\textrm{FR}(\alpha _\textrm{B}- \phi ) \beta _{p,\textrm{SR}}S_\textrm{L}\frac{\text {d}p_\textrm{cap}}{\text {d}t}\\&\quad - \rho ^{\zeta }_\textrm{FR}(\alpha _\textrm{B}- \phi ) \, \text {tr}\left( \varvec{\alpha }_{T,\textrm{S}}\right) \frac{\text {d}T}{\text {d}t} \\&\quad + \phi \left[ (1 - S_\textrm{L}) \frac{\text {d}\rho ^{\zeta }_\textrm{GR}}{\text {d}t} + S_\textrm{L}\frac{\text {d}\rho ^{\zeta }_\textrm{LR}}{\text {d}t} \right] \\&\quad + \left[ \phi (\rho ^{\zeta }_\textrm{LR}- \rho ^{\zeta }_\textrm{GR}) - \rho ^{\zeta }_\textrm{FR}p_\textrm{cap}(\alpha _\textrm{B}- \phi ) \beta _{p,\textrm{SR}}\right] \frac{\text {d}S_\textrm{L}}{\text {d}t} \\&\quad + \rho ^{\zeta }_\textrm{FR}\alpha _\textrm{B}\,\textrm{div}\,\left( \frac{\text {d}{{\varvec{u}}}_\textrm{S}}{\text {d}t} \right) + \,\textrm{div}\,\left( \varvec{A}^{\zeta }+ \varvec{J}^{\zeta }\right) , \\ \end{aligned} \end{aligned}$$

(2)

where $\rho ^{\zeta }_\textrm{FR}$ represents the effective density of component $\zeta$ present in both phases with

$$\begin{aligned} \rho ^{\zeta }_\textrm{FR}= (1-S_\textrm{L}) \rho ^{\zeta }_\textrm{GR}+ S_\textrm{L}\rho ^{\zeta }_\textrm{LR}, \end{aligned}$$

(3)

with $S_\textrm{L}$ as the liquid saturation and $\rho ^{\zeta }_\textrm{GR}$ and $\rho ^{\zeta }_\textrm{LR}$ representing the partial density of component $\zeta \in \{\text {W, C}\}$ in the gaseous and liquid phases, respectively. $\alpha _\textrm{B}$ represents the Biot coefficient and $\phi$ is the medium porosity; the solid grain compressibility and thermal expansivity are represented by $\beta _{p,\textrm{SR}}$ and $\varvec{\alpha }_{T,\textrm{S}}$, respectively. The advective and diffusive flux of each component in each phase are given by $\varvec{A}^{\zeta }= \varvec{A}^{\zeta }_\textrm{G}+ \varvec{A}^{\zeta }_\textrm{L}$ and $\varvec{J}^{\zeta }= \varvec{J}^{\zeta }_\textrm{G}+ \varvec{J}^{\zeta }_\textrm{L}$, which are defined in the following. The phase transition models and the resulting partial densities of each component in each phase are discussed in greater detail in Grunwald et al. (2022); Pitz et al. (2022a, 2022b). Phase transitions are neglected in the BenVaSim benchmarks for reasons of simplicity and for facilitating the derivation of analytical solutions. Therefore, we briefly discuss the simplification of the component mass balance equations without phase transitions: We firstly note that $\rho ^\textrm{W}_\textrm{GR}= \rho ^\textrm{C}_\textrm{LR}= 0$ as well as $\frac{\text {d}\rho ^\textrm{W}_\textrm{GR}}{\text {d}t} = \frac{\text {d}\rho ^\textrm{C}_\textrm{LR}}{\text {d}t} = 0$ without phase transition. At the same time, we can drop the component designators and note $\rho ^\textrm{C}_\textrm{GR}= \rho _\textrm{GR}$ as well as $\rho ^\textrm{W}_\textrm{LR}= \rho _\textrm{LR}$. Additionally, there are no diffusive fluxes without phase transitions (Pitz et al. 2022a) $\varvec{J}^{\zeta }= 0$ and advective transport of each component takes place only in its respective corresponding phase. We can therefore denote advection in the liquid and gaseous phase by ${{\varvec{A}}}_\textrm{L}$ and ${{\varvec{A}}}_\textrm{G}$. Inserted into the component mass balance (2), this yields the simplified equations

$$\begin{aligned} \begin{aligned} 0&= S_\textrm{L}\rho _\textrm{LR}\left[ (\alpha _\textrm{B}- \phi ) \beta _{p,\textrm{SR}}\frac{\text {d}p_\textrm{GR}}{\text {d}t} - (\alpha _\textrm{B}- \phi ) \beta _{p,\textrm{SR}}S_\textrm{L}\frac{\text {d}p_\textrm{cap}}{\text {d}t}\right. \\&\quad \left. - (\alpha _\textrm{B}- \phi ) \, \text {tr}\left( \varvec{\alpha }_{T,\textrm{S}}\right) \frac{\text {d}T}{\text {d}t} \right] \\&\quad + \phi S_\textrm{L}\frac{\text {d}\rho _\textrm{LR}}{\text {d}t} + \left[ \phi \rho _\textrm{LR}- S_\textrm{L}\rho _\textrm{LR}p_\textrm{cap}(\alpha _\textrm{B}- \phi ) \beta _{p,\textrm{SR}}\right] \frac{\text {d}S_\textrm{L}}{\text {d}t}\\&\quad + S_\textrm{L}\rho _\textrm{LR}\alpha _\textrm{B}\,\textrm{div}\,\left( \frac{\text {d}{{\varvec{u}}}_\textrm{S}}{\text {d}t} \right) + \,\textrm{div}\,{{\varvec{A}}}_\textrm{L}\\ \end{aligned} \end{aligned}$$

(4)

for the liquid mass balance and

$$\begin{aligned} \begin{aligned} 0&= (1-S_\textrm{L}) \rho _\textrm{GR}\left[ (\alpha _\textrm{B}- \phi ) \beta _{p,\textrm{SR}}\frac{\text {d}p_\textrm{GR}}{\text {d}t}\right. \\&\quad \left. - (\alpha _\textrm{B}- \phi ) \beta _{p,\textrm{SR}}S_\textrm{L}\frac{\text {d}p_\textrm{cap}}{\text {d}t} - (\alpha _\textrm{B}- \phi ) \, \text {tr}\left( \varvec{\alpha }_{T,\textrm{S}}\right) \frac{\text {d}T}{\text {d}t} \right] \\&\quad + \,\textrm{div}\,{{\varvec{A}}}_\textrm{G}+ \phi (1 - S_\textrm{L}) \frac{\text {d}\rho ^{\zeta }_\textrm{GR}}{\text {d}t} - \left[ \phi \rho ^{\zeta }_\textrm{GR}+ (1-S_\textrm{L}) \rho _\textrm{GR}p_\textrm{cap}\right. \\&\quad \left. \times (\alpha _\textrm{B}- \phi ) \beta _{p,\textrm{SR}}\right] \frac{\text {d}S_\textrm{L}}{\text {d}t} + (1-S_\textrm{L}) \rho _\textrm{GR}\alpha _\textrm{B}\,\textrm{div}\,\left( \frac{\text {d}{{\varvec{u}}}_\textrm{S}}{\text {d}t} \right) \\ \end{aligned} \end{aligned}$$

(5)

for the gas mass balance. $S_\textrm{L}$ is the liquid saturation, given in this work by $S_\textrm{L}= S_\text {e}\left( S_\text {L,max}-S_\text {L,res} \right) + S_\text {L,res}$, where the effective saturation $S_\text {e}$ is a function of capillary pressure according to van Genuchten (Van Genuchten 1980)

$$\begin{aligned} S_\text {e} = \left( 1+\left( \frac{p_\textrm{cap}}{p_\text {e}} \right) ^n\right) ^{\frac{1}{n}-1}, \end{aligned}$$

(6)

with $p_\text {e}$ as the entry pressure and n as empirically determined material property. $\phi$ denotes the medium porosity and $\alpha _\textrm{B}$ represents the Biot-Willis coefficient, while $\varvec{\alpha }_{T,\textrm{S}}$ and $\beta _{p,\textrm{SR}}$ represent the solid/grain thermal expansivity and its compressibility. Advection occurs in both phases and is driven by the phase pressures $p_{\alpha {\textrm{R}}}$ according to Darcy’s law:

$$\begin{aligned} {{\varvec{A}}}_{\alpha }= \rho _{\alpha {\textrm{R}}}\tilde{{{\varvec{w}}}}_{\alpha {\textrm{S}}}= - \rho _{\alpha {\textrm{R}}}\frac{{k^\textrm{rel}_{\alpha }}{{{\varvec{k}}}_\textrm{S}}}{\mu _{\alpha {\textrm{R}}}} \,\textrm{grad}\,p_{\alpha {\textrm{R}}}, \end{aligned}$$

(7)

where ${{{\varvec{k}}}_\textrm{S}}$ denotes the intrinsic medium permeability, $\mu _{\alpha {\textrm{R}}}$ is the viscosity of phase $\alpha$ which is assumed to be constant in this work and $\tilde{{{\varvec{w}}}}_{\alpha {\textrm{S}}}$ is the Darcy velocity w.r.t. the solid. Gravity-induced flow is disregarded in this work for simplicity. The relative phase permeability of the gaseous and liquid phases are defined according to the Mualem/van Genuchten models (Mualem 1976):

$$\begin{aligned} k^\text {rel}_\text {L}=\sqrt{S_\text {e}}\left( 1-\left( 1-S_\text {e}^{n/(n-1)}\right) \right) ^{(2n-2)/n} \end{aligned}$$

(8)

for the liquid phase as well as

$$\begin{aligned} k^\text {rel}_\text {G}=\sqrt{1-S_\text {e}}\left( 1-S_\text {e}^{n/(n-1)}\right) ^{2-\frac{2}{n}} \end{aligned}$$

(9)

for the gas phase, where $S_\text {e}$ and n are defined in accordance with (6). A potential hysteresis in multiphase flow properties is neglected in this work. The gas phase density is described by the ideal gas law

$$\begin{aligned} \rho _\textrm{GR}= \frac{p_\textrm{GR}M_\text {G}}{RT}, \end{aligned}$$

(10)

where R is the universal gas constant and $M_\text {G}$ is the average molar mass of the gaseous phase, which in this work is assumed to be constant and equal to the molar mass of the gas constituent because of the neglection of water vaporization. The liquid phase density is modeled using a linear, liquid pressure dependent model for the isothermal test cases and a linear, liquid pressure and temperature dependent model for the non-isothermal test cases:

$$\begin{aligned} \rho _\textrm{LR}= \rho _\text {LR,ref} \left( 1+\beta _{p,\textrm{LR}}\left( p_\textrm{LR}-p_\text {LR,ref}\right) -\beta _{T,\textrm{LR}}\left( T-T_\text {ref}\right) \right) , \end{aligned}$$

(11)

with $\beta _{p,\textrm{LR}}$ and $\beta _{T,\textrm{LR}}$ representing the liquid compressibility and thermal expansion and some reference values $\rho _\text {LR,ref}$, $p_\text {LR,ref}$ and $T_\text {ref}$. Momentum balance given by Grunwald et al. (2022) takes into account gravity-induced stresses, which we will neglect for simplicity, thus yielding:

$$\begin{aligned} 0 = \,\textrm{div}\,\left( \varvec{\sigma }' - \alpha _\textrm{B}\left[ \chi p_\textrm{LR}+ \left( 1- \chi \right) p_\textrm{GR}\right] {{\varvec{\textrm{I}}}}\right) , \end{aligned}$$

(12)

where $\varvec{\sigma }' = \mathcal {\textbf{C}} :\left( \varvec{\epsilon }- \varvec{\epsilon }_{\text {thermal}} \right)$ represents the effective stress tensor with the thermal strain $\frac{\text {d}}{\text {d}t}\varvec{\epsilon }_{\text {thermal}}= \varvec{\alpha }_{T,\textrm{S}}\frac{\text {d}T}{\text {d}t}$ and ${{\varvec{\textrm{I}}}}$ representing the second-order identity tensor. $\chi$ is the Bishop coefficient, for which different models are typically chosen, e.g. a power law or, as in this work, a linear saturation-dependent relation with $\chi = S_\textrm{L}$. The energy balance equation derived by Grunwald et al. (2022) takes into account heat transport by diffusion as well as energy stored in the pressure work of the system. Since both phase transitions and consequently diffusion as well as the gravitational force are neglected here, the equation therein simplifies to:

$$\begin{aligned} \begin{aligned} 0&=\underbrace{\frac{\text {d}}{\text {d}t}({\Sigma _\alpha \rho _{\alpha }u_\alpha })}_{\text {storage}} \underbrace{+\,\textrm{div}\,\left( \Sigma _\alpha h_\alpha {{\varvec{A}}}_\alpha \right) }_{\text {transport by advection}} \underbrace{+\left( \Sigma _\alpha \rho _{\alpha }h_\alpha \right) \,\textrm{div}\,\left( \frac{\text {d}{{\varvec{u}}}_\textrm{S}}{\text {d}t} \right) }_{\text {medium volume change}} \\&\quad \underbrace{-\,\textrm{div}\,(\varvec{\lambda }_\textrm{eff}\,\textrm{grad}\,T)}_{\text {heat conduction}}. \end{aligned} \end{aligned}$$

(13)

Therein, $\rho _{\alpha }$ represents the apparent density of each phase, $u_\alpha$ is the specific internal energy of each phase and $h_\alpha = \frac{p_{\alpha }}{\rho _{\alpha }} + u_\alpha$ is the phase specific enthalpy. Considering that $\frac{\text {d}h_\alpha }{\text {d}t}=c_{p\alpha }\frac{\text {d}T}{\text {d}t}$ (Grunwald et al. 2022), one can see that the presence of $u_\alpha$ in above equation reflects the specific heat capacities. The advective mass flux ${{\varvec{A}}}_\alpha$ is defined in Eq. 7. The effective medium thermal conductivity is linearly dependent on the liquid saturation for the test cases in this work, with

$$\begin{aligned} \varvec{\lambda }_\text {eff} = \varvec{\lambda _\text {dry}} + S_\textrm{L}\left( \varvec{\lambda _\text {sat}}-\varvec{\lambda }_\text {dry}\right) \end{aligned}$$

(14)

A more detailed description of the TH²M model as well as the constitutive setting can be found in Grunwald et al. (2022) and Pitz et al. (2022a).

Verification benchmarks

Overview of selected benchmarks

Table 1 Material properties for benchmarks in this work (properties for Benchmarks 1–4 adapted from the BenVaSim project (Lux et al. 2021))

The benchmarks in the following sections are used to test and illustrate the suitability of the OGS-6 TH²M implementation to simulate and predict system behaviour as it is expected in nuclear waste disposal systems. Benchmarks 1 through 4 are chosen using the set of benchmarks devised in the BenVaSim project (Lux et al. 2021). They all feature simple, 1D geometries and are introduced and schematically located in Fig. 1 as follows:

• Benchmark 1: A poro-elastic consolidation problem. This isothermal benchmark represents a homogeneous and fully liquid saturated bar, which gets compressed and in which water build-up occurs at one side. As a result of these boundary conditions, the pore water pressure increases in accordance with Biot’s consolidation theory and a liquid flow takes place driven by the water pressure gradient. The liquid pressure pulse propagates through the bar at a rate determined by the liquid compression and poro-elastic medium expansion. These effects occur in the host rock in the near field of the repository as marked by the yellow dot in Fig. 1. This benchmark was taken from the BenVaSim project (Lux et al. 2021) and the analytical solution therein as well as results obtained by different teams (and different numerical codes) participating in the project serve as reference for this work.

• Benchmark 2: Gas pressure build-up in a homogeneous material. This isothermal benchmark considers a homogeneous, one-dimensional bar as well. In this case, however, the medium is initially unsaturated and a gaseous phase is present. External total stress boundary conditions (BC) and the suction due to partial saturation are initially in an equilibrium so that no initial deformation takes place. Liquid and gas are injected from the opposing boundaries of the bar, imposing two phase flow on the model. Effects like these could occur in the drift seal between a deposition drift and access gallery of the repository as marked by the red dot in Fig. 1. This benchmark was taken from the BenVaSim project (Lux et al. 2021) and the results obtained by different teams (and different numerical codes) participating in the project serve as reference for this work.

• Benchmark 3: Gas pressure build-up in a heterogeneous material. This isothermal benchmark comprises a more complex albeit still one-dimensional geometry featuring two different materials and non-homogeneous initial conditions. As in benchmark 2, the given situation reflects the drift seal with two adjacent back-filled drifts. The HM-coupled process is driven both by gradients imposed by the initial conditions as well as imposed boundary conditions. This benchmark was taken from the BenVaSim project (Lux et al. 2021) and the results obtained by different teams (and different numerical codes) participating in the project serve as reference for this work.

• Benchmark 4: A transient heat and gas production problem in complex geometry. This non-isothermal benchmark comprises all geometrical features illustrated in Fig. 1 in a 1D layout. Transient heat and gas mass source terms are applied to the two canister sections and the entire repository is slowly filled by liquid seeping into the repository from the host rock. The characteristics of the transient source terms were chosen in order to reflect the general expected behaviour while remaining simple (linear dependence on time). In this work it is chosen to compare OGS-6 results only to results obtained by the authors using its predecessor OGS-5, featuring a sequentially coupled TH²M implementation. This allows for a discussion of the numerical effects of process couplings and differences in the results obtained. This benchmark was devised within the scope of the BenVaSim project (Lux et al. 2021), but a comparison of the results has not been finalized. Thus, the analysis in this paper contributes and extends the discussion in the project report.

• Benchmark 5: Thermally driven vapour diffusion problem. The last non-isothermal benchmark featured in this work focuses on vapour diffusion driven foremost by temperature gradients. This process can lead to a dry-out of the bentonite in adjacent to the HLW containing canisters. This process is counteracted by liquid seepage into the deposition drift, so that in this particular benchmark, a steady state condition is found. In reality, the heat generation decays, thus allowing the complete flooding of the deposition drift over long time scales. This benchmark relies on code comparison as well and here, we compare results obtained by various codes in use by the authors.

Fig. 3

Overview of benchmark geometries: Benchmarks 1, 2 and 5 use a homogeneous geometry depicted in (a), whereas benchmarks 3 and 4 use the geometries (b) and (c), respectively. The length of the bar (a) for benchmarks 1 and 2 is 10.0m and for benchmark 5, it is 1.0m and the width of all bars is 1.0m

Numerical settings

All model geometries are discretized in a quasi-one dimensional mesh composed of quadrilateral Taylor-Hood elements (approximation functions bi-quadratic for the solid displacement and bi-linear for the pressures and temperature). The element size is refined towards the left and right model boundaries in all benchmarks as well as around material interfaces in the heterogeneous benchmarks 3 and 4. The temporal discretization is realized with the implicit Euler method with adaptive time stepping. In all cases, the initial time step size is 1.0 s. The resulting linear equation system is solved using the stabilized bi-conjugate gradient method with a relative error tolerance of $1.0 \times 10^{-6}$. The non-linear equation system is solved using the Newton–Raphson method with a tolerance of $1.0 \times 10^{-7}$ (relative error) per component. In benchmark 4, an absolute tolerance of $1.0 \times 10^{-3}$, $1.0 \times 10^{-5}$ and $1.0 \times 10^{-6}$ was used as convergence criterion for the hydraulic, thermal and mechanical process, respectively. Depending on the number of non-linear iterations required for meeting the convergence criteria, the time step size for the next step is multiplied by a factor $f \in \left[ 1.025, 1.2\right]$. In the case of a diverging numerical solving procedure, the respective time step is repeated with a multiplier of $f = 0.625$. This temporal discretization results in a total number of time steps between about 500 and 1500 in the different benchmarks, depending on their respective complexity. Further information on numerical solution strategies in OGS-6 can be found in Bilke et al. (2019); Grunwald et al. (2022); Naumov et al. (2022) and more details on domain discretization approaches for each BenVaSim benchmark can be found in Lux et al. (2021)).

Benchmark 1: poro-elastic consolidation problem

The first numerical benchmark case represents a hydro-mechanical coupled problem in a homogeneous material. A fully saturated 10 m $\times$ 1 m bar is first mechanically compressed leading to an instantaneous, homogeneously distributed increase of liquid pressure and mechanical stresses in the entire bar according to Biot’s consolidation theory. A liquid pressure differential subsequently imposed by boundary conditions at the left and right sides of the bar then leads to liquid flow with a poro-elastic deformation response. The top and bottom boundaries are impermeable and mechanically fixed in the y direction; the Poisson number of the considered material is assumed to be equal to zero and stress boundary conditions are imposed only with respect to the x direction, leading to a quasi-1D problem.

General benchmark description: geometry, BCs, ICs

The initial boundary conditions are defined as follows: Initially, the domain is fully saturated with a liquid pressure of ${0.1013}\,\text {MPa}$ and an effective stress of ${0.0}\,\text {Pa}$. Since OGS-6 uses gas pressure $p_\textrm{GR}$ and capillary pressure $p_\textrm{cap}$ as primary variables for the two-component–two-phase hydraulic process, we choose to set the initial gas pressure to ${0.1013}\,\text {MPa}$ and the initial capillary pressure to ${0.0}\,\text {Pa}$, thus yielding the correct initial liquid pressure according to (1). We note in passing, that one could also have chosen $p_\textrm{GR}= {0.0}\,\text {Pa}$ and $p_\textrm{cap}= {-0.1013}\,\text {MPa}$ in order to satisfy the initial condition. The boundary conditions are defined as follows: The right side of the model is mechanically fixed to zero displacement, whereas the left hand side boundary can move freely in the x direction. There is a compressive stress applied at the left side boundary and perpendicular to the boundary with $\sigma _\text {tot, xx} ={1.0}\,\text {MPa}$. At the left hand boundary, the liquid pressure is increased ${1}\,\text {MPa}$ and at the right hand side, the liquid pressure boundary condition is kept constant and equal to value of the initial condition. The material parameters can be found in Table 1.

Benchmark variations discussed in this work

Scenario a is the base case described above. In the first variation (scenario b), the Biot coefficient of the material is set to 0.75, and in the second variation (scenario c), Young’s modulus of the material is decreased to 150 MPa.

Results and benchmark discussion

Fig. 4

Results obtained by OGS-6 TH²M compared to results obtained by the BenVaSim project partners for Benchmark 1, scenarios a, b and c

As already described by Lux et al. (2021), this single phase HM-coupled benchmark shows an effect as it might occur in principle in the host rock in the mid to far field from a high level waste repository. A host rock might be subject to some compression and pore water pressures might be increased before drainage leads to a decrease in pore pressure. The compressive stress boundary condition leads to both a strain and increased effective stresses (both spatially constant across the bar) as well as to a liquid pressure increase. The distribution of forces on the porous medium and pore liquid is a function of porosity, Young’s modulus and water bulk modulus, governed by Biot’s consolidation theory and it can be checked for plausibility as follows: In the 1D-case it follows from (12) with neglection of body forces, assuming full liquid saturation and $\alpha _\textrm{B}= 1.0$ as well as $\nu = 0$³ that

$$\begin{aligned} \Delta \sigma _{\text {tot, }xx} = \Delta \sigma _{\text {eff, }xx} - \Delta p_\textrm{LR}\end{aligned}$$

(15)

Therein, the effective stress increase can be expressed for 1D-case by applying linear elasticity together with a vanishing Poisson’s ratio $\Delta \sigma _{\text {eff, }xx} = E \cdot \Delta \epsilon _{xx}$. Furthermore, the pore liquid pressure increase can be expressed by evaluating the water component mass balance Eq. 4: With $\alpha _\textrm{B}= 0$, it is implied that the solid grains are incompressible ($\beta _{p,\textrm{SR}}= 0$) and corresponding terms vanish. When considering the initial poro-elastic response of the saturated medium, one can also neglect liquid advection because this process is much slower than the instantaneous medium deformation. Thus, one can see that the pore pressure increase depends only on the water bulk modulus, medium porosity as well as the medium deformation. The former properties are constants and the medium deformation can be expressed in terms of strains with $\Delta p_\textrm{LR}= - \,\textrm{div}\,\Delta u_{x} \cdot \left( \phi \beta _{p, \text {LR}} \right) ^{-1} = - \Delta \epsilon _{xx} \cdot \left( \phi \beta _{p, \text {LR}} \right) ^{-1}$. Like this, both the effective stress and liquid pressure increase can be substituted in Eq. 15, hence linking the strain induced by the initial compression of the bar to the total stress boundary condition:

$$\begin{aligned} \Delta \epsilon _{xx} = \frac{\Delta \sigma _\text {tot}}{E+\frac{1}{\phi \beta _{p, \text {LR}}}} \end{aligned}$$

(16)

With this equation, the poro-elastic response of the bar calculated by the numerical simulators can be quickly analytically checked for plausibility: The total stress increase due to the boundary condition is $\Delta \sigma _\text {tot, xx} = {0.8987}\,\text {MPa}$. Equation 16 yields a resulting strain increase of $\Delta \epsilon _{xx} = {0.41} \times 10^{-4}$. For a bar with a length of ${10}\,\text {m}$, this strain means an x displacement of ${0.41} \times 10^{-3}\,\text {m}$ at the left hand side and a liquid pressure increase to ${0.6732}\,\text {MPa}$ in the entire beam—both values can be visually recognized in Fig. 4a.

After the initial compression of the bar, the subsequent HM-coupled process is dominated by the liquid flow. The boundary conditions on the bar’s left and right sides lead to water ingress and drainage, respectively, thus causing an expansion and compression of its respective halves in the course of the simulation. Since the bar is fully saturated, the liquid relative permeability is constant and the steady state corresponds to a linear liquid pressure gradient across the bar. The two scenarios (b) and (c) are briefly discussed, both with regard to the reference scenario (a): Scenario (b) features a lower Biot coefficient of $\alpha _\textrm{B}= 0.7$. This implies that solid grains are compressible and the hydro-mechanical poro-elastic response coupling is attenuated with regard to the reference scenario (a). As a consequence, the liquid pressure increase is lower in response to the initial bar compression. The momentum transfer from the solid to the liquid phase is weakened as well due to $\alpha _\textrm{B}< 1$, and therefore, more momentum is transferred to the solid, thus yielding larger x-displacements. In the later stages of the simulation, the bar does not deform as much in response to pore pressure changes and this is also a direct consequence of the weakened HM-coupling. Scenario (c) features a lower Young’s modulus. When considering the initial compression of the bar, this has the opposite effect compared to scenario (b). The softer medium leads to a momentum transfer to the liquid phase and therefore, liquid pressures rise to almost ${1.0}\,\text {MPa}$—the value of the compressive mechanical boundary condition. This effect becomes clear as well from Eq. 16: Therein, the denominator of the fraction on the right side of the equation is dominated by the liquid bulk modulus, which is several orders of magnitude larger than Young’s modulus for this specific scenario. In the later stages, the deformation of the bar is large compared to the scenario (a). This is due to the strong HM-coupling ($\alpha _\textrm{B}= 1$) in combination with the soft medium. In general, it can be seen in Fig. 4 that the OGS-6 results match the BenVaSim partner’s results very well and that the HM-coupling according to Biot’s consolidation theory is captured well by the TH²M implementation, even in a single-phasic environment.

Benchmark 2: gas pressure build-up (homogeneous material)

This benchmark is similar to the one discussed above, because it comprises a homogeneous material and the same model geometry. However, the motivation and possible location of the featured effects in Fig. 1 are different. As indicated by the red circle in Fig. 1, this benchmark reflects processes as they might take place in the drift seal. At one boundary, boundary conditions impose a gas pressure build-up driving a gas flow through the model. At the other boundary, a liquid pressure boundary condition (Dirichlet) reflects the flooding of the repository by formation water entering the galleries and drifts.

General benchmark description: geometry, BCs, ICs

Benchmark 2 uses the same geometry as the previous benchmark (Fig. 3) but in this case, a partially saturated medium is considered and a gas injection takes place in addition to a water injection. Similarly to the previous benchmark, the top and bottom boundaries are restricted from movement in the y direction and the right hand side boundary is fixed in the x direction. The left hand side is free to move in the x direction but in contrast to benchmark 1, there is no compressive stress boundary at the left hand side. Instead, the stress boundary condition at the left side is chosen such that the systems remains in an equilibrium and no deformation takes place initially. Hydraulically, the initial state of the system is defined by a gas phase pressure of $p_\textrm{GR}= {0.2}\,\text {MPa}$ and a capillary pressure of ${13.8}\,\text {MPa}$, leading to a saturation of 0.63. The boundary conditions for the gas pressure consist of constant pressures of ${3.0}\,\text {MPa}$ at the left boundary and ${0.5}\,\text {MPa}$ at the right boundary. The capillary pressure boundary conditions comprise a constant pressure of ${19.6}\,\text {MPa}$ at the left boundary and ${5.4}\,\text {MPa}$ at the right boundary, leading to a liquid saturation of 0.5 and 0.9, respectively. Material parameters for this model can be found in Table 1.

Results and benchmark discussion

Fig. 5

Results obtained by OGS-6 TH²M compared to results obtained by the BenVaSim project partners for benchmark 2

The boundary conditions imposed on the model lead to a liquid flow from the right side to the left side, whereas gas is injected from both sides into the domain initially before a gas flow from the left side to the right side dominates the process. At the right boundary, both gas and liquid pressures increase with respect to the initial conditions as a consequence of the boundary conditions, leading to an expansion of the bar at this side. At the left hand side, the liquid pressure drops by ${2.8}\,\text {MPa}$ due to the boundary conditions, but at the same time, this liquid pressure drop gets compensated by the increase of gas pressure by the same amount. Hence, the resulting pore fluid pressure in the entire domain increases during the simulation, leading to an expansion of the entire bar. The steady states show that there is a non-linear distribution of pore gas pressure and liquid pressure which is mostly caused by the non-linear relation of the relative permeability and liquid saturation. The pressure dependence of gas and, to a much smaller extent, liquid density also contributes to the non-linear gas and liquid pressure distributions in the steady state of the system. Over all, the OGS-6 TH²M results plot in very good agreement with those of the BenVaSim project partners (Fig. 5).

Benchmark 3: gas pressure build-up (heterogeneous material)

General benchmark description: geometry, BCs, ICs

This benchmark test represents an increase in geometric complexity with regard to the previous models which featured homogeneous materials. As opposed to the previous benchmark, there are two different types of material groups present (Fig. 3: The first material is in the center of the model (henceforth called drift seal) and the second material is present at the left and right sides of the model (henceforth called left and right backfill, respectively). Similarly to the previous models, the top and bottom boundaries are mechanically fixed in the y direction. The right boundary is fixed in the x direction whereas the left hand side is free to move. The initial liquid and gas pressures are not spatially constant throughout the domain, because the drift seal is assigned an initial liquid saturation of 0.7, corresponding to a capillary pressure of ${50.49}\,\text {MPa}$, whereas the backfills are assigned an initial liquid saturation of 0.25, corresponding to a capillary pressure of ${72.19}\,\text {MPa}$. The initial gaseous phase pressure is ${0.25}\,\text {MPa}$ in the backfills and ${0.2}\,\text {MPa}$ in the drift seal. The hydraulic boundary conditions of this benchmark consist of constant gas pressures with ${4.0}\,\text {MPa}$ at the left boundary and ${0.25}\,\text {MPa}$ (equal to the initial condition in the backfill) on the right side. The liquid saturation at the left boundary is held constant at 0.2, corresponding to a capillary pressure of ${94.96}\,\text {MPa}$, and at the right boundary it is held at its initial value of 0.25 and capillary pressure of ${72.19}\,\text {MPa}$.

Benchmark variations discussed in this work

In addition to the base case (scenario a), there is a variation (scenario b), in which the Dirichlet BC fixing the gas pressure at the left boundary is replaced by a Neumann BC, whereby the gas mass influx from the left side is prescribed rather than the pressure. The value of the gas source is $6.0 \times 10^{-9}\,\text {kg}\,\text {s}^{-1}\,\text {m}^{-2}$. Additionally, the liquid pressure is not fixed by a Dirichlet BC at the left side. Instead, a Neumann zero flux boundary condition is applied. Such a boundary condition might be applied if symmetries of a system are to be exploited (cf. benchmark 4) and this variation thus offers the opportunity to investigate effects caused by the boundary condition type chosen.

Results and benchmark discussion

Fig. 6

Results obtained by OGS-6 TH²M compared to results obtained by the BenVaSim project partners for benchmark 3

Due to the non-constant pore fluid pressure in the domain, the divergence $\,\textrm{div}\,\left( \chi p_\textrm{LR}+ (1-\chi ) p_\textrm{GR}\right) {{\varvec{\textrm{I}}}}$ becomes non-zero and the momentum balance given by (12) is not satisfied unless an instantaneous medium deformation takes place. The benchmark however requires that no such instantaneous initial deformation takes place and this can be realised by compensating the non-equilibrium in the balance equation, such that:

$$\begin{aligned} 0= & {} \,\textrm{div}\,\left( \varvec{\sigma }' - \alpha _\textrm{B}\left[ \chi \left( p_\textrm{LR}-p_\text {LR, initial}\right) \right. \right. \nonumber \\{} & {} \left. \left. + \left( 1- \chi \right) \left( p_\textrm{GR}-p_\text {GR, initial}\right) \right] {{\varvec{\textrm{I}}}}\right) , \end{aligned}$$

(17)

The hydro-mechanically coupled process in this benchmark is driven both by strong pressure gradients in the initial pore gas and pore liquid pressure fields as well as by pressure gradients created by the boundary conditions. In case of the gas phase, the gradients imposed by the left hand boundary condition (pressure increase from 0.25 to ${4.0}\,\text {MPa}$) are much greater than the gradients in the initial gas pressure field (${0.05}\,\text {MPa}$ difference at the backfill/drift seal interfaces). As a consequence, a gas flow from the left to the right takes place throughout the simulation and the gradients in the initial field are equilibrated rather early on in the simulation. In case of the liquid phase, gradients imposed by the initial liquid pressure field and boundary conditions are in the same order of magnitude and they both impact the hydraulic process equally. In the central drift seal, liquid pressures are initially much higher than in the adjacent backfills due to its higher initial saturation. This gradient causes a drainage of the pore water from the drift seal both towards the left and right backfill. At the same time, the drainage caused by the boundary condition at the left boundary causes a liquid flow from the right side towards the left side of the domain. While the liquid pressure in the steady state shows a continuous distribution across all materials, the liquid saturation shows discontinuities at the material interfaces between the backfills and the drift seal. These discontinuities are caused by different water retention properties of the materials (see Table 1 for material properties).

In the steady state, both the gaseous and liquid phase pressure profiles show abrupt changes of the slope at the material interfaces and more continuous change of the slope within the material. The latter is caused by the Mualem relation of relative permeability and liquid saturation causing a non-linearity in the Darcy flow terms, similar to the previously discussed model 2, whereas the former is a result of the contrast of intrinsic permeabilities between the two material groups. The displacement of the bar is governed by the poro-elastic response of the porous medium to the hydraulic process. In Fig. 6, a positive slope of the x displacement profiles corresponds to medium expansion whereas a negative slope corresponds to medium compression. It can be seen that the drift seal mainly undergoes a compression or consolidation process, which is due to the pore liquid drainage from the drift seal. Although there is liquid drainage mainly in the left part of the backfill as well, these parts of the domain do not consolidate, but they expand. This is a result of the Bishop model applied in Eq. (12): because the contribution of changes of liquid pressures to the momentum balance is scaled by the liquid saturation, which is rather low in the backfill, the impact of water drainage on the created momentum is diminished. It is rather the gas pressure playing the decisive role in the backfill and gas pressures are increased due to the gas injection imposed by the left side boundary condition, leading to an expansion of the porous medium.

In scenario (b), the gas source at the left boundary is represented by a Neumann flux across the boundary instead of a Dirichlet BC fixing the gas pressure. Additionally, the Dirichlet BC fixing the liquid pressure is replaced by a Neumann zero flux BC. This scenario therefore has more degrees of freedom compared to scenario (a), because both the liquid and gas pressure can evolve freely. It can be seen in Fig. 6 that the agreement between results obtained by different codes is not as good as in the previous scenario. One possible reason for this could be that in the original project, the gas molar mass was never specified for this scenario (cf. Lux et al. 2021). Therefore, the teams might have assumed different molar masses to represent air (e.g. they might have used Nitrogen or air mixture molar masses). The boundary condition prescribe a gas mass production with units $\text {kg}\,\text {m}^{-3}\,\text {s}^{-1}$. Therefore, a lighter gas such as Hydrogen would require a much higher number of molecules than for example Nitrogen in order to constitute the same mass. Because the ideal gas law is applied (where gas pressure is proportional to the amount of molecules in a given Volume), this can lead to differing calculated gas pressures.

Benchmark 4: transient heat and gas production

In addition to the hydro-mechanically coupled process, this benchmark takes heat production and temperature-induced processes into account. With regard to Fig. 1, it reflects a 1D section across the entire deposition drift, taking into account canister sections, backfills, the drift seal, access gallery and host rock. Hence, it represents the geometrically most complex benchmark featured in this work.

Fig. 7

Time dependent source terms for benchmark 4, scenario (a)

General benchmark description: geometry, BCs, ICs

This model distinguishes itself from the previous cases with regard to its size, processes considered and number of material groups. While the geometry remains a quasi-one-dimensional bar, there are 8 materials present in the model which can be grouped into four material groups: Backfill, canister sections, drift seal and host rock. The materials are arranged as shown in Fig. 3. In this model, all edges are mechanically fixed, i.e. the left and right boundaries are restricted from movement in the x direction whereas the top and bottom boundaries are fixed in the y direction. In the canister sections (Fig. 3), both heat and gas production takes place, represented by time-dependent volumetric source terms (Fig. 7). Between the data points in Fig. 7, the production rates increase or decrease linearly. The linear behaviour is chosen for reasons of simplicity. The respective peak heat power and gas production rate is chosen in order to achieve reasonable peak gas pressures and temperatures in the domain. Due to the one-dimensional layout of this benchmark, the source term values are not realistic. The values of the initial conditions per material group as well as material parameters can be found in Table 1.

Benchmark variations discussed in this work

For this benchmark, one variation is discussed (scenario b). It represents the same model geometry, but is reduced to a homogeneous case as all material groups are assigned identical properties (Table 2). The considered process is also reduced to a TM-coupled test case and mechanical and thermal medium parameters are averaged. Thus, the heat conduction as well as thermal strain calculation of the codes can be verified as there exists an analytical solution (Lux et al. 2021). There is no gas production in this variation and the heating power is assumed to be constant throughout the simulation, so that a steady-state temperature profile is created. The constant heating power is equal to ${0.75}\,\text {W}\,\text {m}^{-3}$, thus leading to a accumulative heating power of 3W in both canister sections, assuming a width (and depth) of ${1.0}\,\text {m}$ of the bar.⁴

Results and benchmark discussion

Firstly, the simplified scenario (b) is analysed. It features a medium porosity of 0.0 so that only the solid phase properties determine the heat conduction and deformation process (Table 2). In the two canister sections, there are heat sources with a constant power of ${1.5}\,\text {W}$ each. The heating power is applied evenly to each canister section surface. The initial temperature in the entire bar is ${298.15}\,\text {K}$ and at the right boundary, there is a Dirichlet boundary condition fixing the temperature at this initial value throughout the simulation. All other temperature boundary conditions are Neumann zero flux conditions. Figure 8 shows the resulting temperature and x displacement profiles obtained by different teams and codes as well as the analytical solution for this benchmark. As energy can only exit the model at the right boundary the temperatures in the domain rise until a steady state is reached. In the steady state, all heat must flow from the left to the right, thus resulting in three different temperature gradients left of the heaters, between the heaters and right of the heaters, respectively. Using the formula

$$\begin{aligned} \,\textrm{grad}\,T = \frac{\hat{Q}}{\lambda _\text {S}}, \end{aligned}$$

(18)

we can insert the heat powers of ${0.0}\,\text {W}$, ${1.5}\,\text {W}$ and ${3.0}\,\text {W}$ corresponding to the steady state condition, yielding the respective temperature gradients of ${0.0}\,\text {K}\,\text {m}^{-1}$, ${1.04}\,\text {K}\,\text {m}^{-1}$ and ${2.10}\,\text {K}\,\text {m}^{-1}$ for the bar intervals left of the leftmost canister, between the two canisters and right of the rightmost canister, respectively. These three gradients can be visually recognised in Fig. 8, allowing for a fast plausibility check.

Table 2 Material properties for the TM variation (scenario b) of benchmark 4 (modified after Lux et al. 2021)

We now proceed to analyse scenario (a) of this benchmark featuring a fully coupled TH²M process in a heterogeneous bar. The left boundary is assumed to be an axis of symmetry, which could, in reality, be the case in a large repository with a high number of deposition tunnels. Consequently, there are Neumann zero flux boundary conditions in place at the left boundary both for temperature and the two hydraulic processes. At the right boundary, Dirichlet boundary conditions fix the temperature, the gas and capillary pressures at the initial value at this location, i.e. at the initial temperature and pressures defined for the host rock. x-displacements are held at zero at both the left and right side boundaries.

Fig. 8

Results obtained by OGS-6 TH²M compared to results obtained by the BenVaSim project partners for the TM variation (scenario b) of benchmark 4

Fig. 9

Results obtained by OGS-6 TH²M compared to results obtained by OGS-5 for benchmark 4 (scenario a)

This benchmark was discussed in the BenVaSim synthesis report (Lux et al. 2021), but we choose here to compare only results obtained by the authors of this paper using OGS-5 and OGS-6. Since the process coupling is realised sequentially and monolithically in OGS-5 and OGS-6, respectively, this allows for a brief discussion of the effects of different numerical coupling schemes. Figure 9 shows the results obtained by the two codes for model 4, scenario b. Initially, the system is in an equilibrium with regard to the momentum and energy balance, but the hydraulic initial state features some gradients driving the subsequent system behaviour: On one hand there are gas and liquid pressure gradients between the host rock and geotechnical materials of the repository. On the other hand, differences between the drift seal and backfills with regard to the retention behaviour also create liquid pressure gradients at the respective material interfaces. In the time interval from $t={0}\,\text {s}$ to $t={1.5} \times 10^{11}\text {s}$, these gradients cause a liquid and gas flow from the host rock into the repository as well as a suction-driven liquid flow into the drift seal from the adjacent backfills. In the backfills, whose intrinsic permeability is relatively high compared to the drift seal and host rock, these two liquid flows have opposing effects: Firstly, the suction in the drift seal leads to a de-saturation in the backfills while the liquid saturation in the drift seal increases; the corresponding liquid-flow-driving liquid pressure gradient between backfill and drift seal is equilibrated in the process. Later on in the simulation, the liquid flow from the host rock into the repository, which is a much slower process, leads to re-saturation in the entire repository. The entire system gravitates towards a state, where the gas and capillary pressure are uniformly equal to the Dirichlet type boundary conditions applied to the right model boundary, featuring a capillary pressure of about ${0.1}\,\text {MPa}$ corresponding to almost full liquid saturation as well as a gas pressure of ${4.0}\,\text {MPa}$. Regarding the gas transport, the process is initially driven by gradients prescribed by the initial conditions: Gas flow starts from the host rock with initial gas pressures of ${4.0}\,\text {MPa}$ into the repository where gas pressures are atmospheric at the beginning of the simulation. As a consequence, gas pressures approximate each other as gas pressures in the repository rise whereas they fall in the host rock.

The profile marked by the green crosses in the central plot in Fig. 9 shows the gas pressures in the system at the onset of gas production in the two canister sections. Therein, it can be seen that the gas pressure dropped considerably in the host rock, whereas is has not risen as significantly in the repository. This is due to the initial liquid saturation, which is very high (at an initial value of 0.995) in the host rock, but much lower in the repository (at an initial value of 0.75). Therefore, the gas volume or mass available in the the host rock is much lower when compared to the repository and subsequently, if a certain gas mass flows from the host rock into the repository, changes in gas pressures in the former are higher than in the latter. The gas pressure profiles during and after the gas injection are shown by the red and purple lines. In the repository, there are only small gas pressure gradients over the course of the simulation due to the relatively high effective gas permeability. The effective permeability is high in the repository both due to the higher intrinsic permeability of the geotechnical materials and due to the lower liquid saturation, leading to higher relative gas permeabilities.

The deformation process in this benchmark is driven by the solid thermal expansion on one hand as well as the hydro-mechanical coupling on the other hand. In the x displacement plots in Fig. 9, the largest differences between results obtained by OGS-6 and reference results can be seen in this process variable. The reason for the differences is likely the coupling scheme, which is sequential T-H-M coupling in case of the OGS-5 results and monolithic coupling in case of OGS-6. Therefore, in the presented OGS-5 results, changes in pore pressure cause a deformation (expansion of the drift seal), but the resulting increase in pore space is not taken into account in the calculation of pore pressures. If it was, the expansion would cause a decrease in pore pressure thus leading to smaller deformations, which is what one can see in the OGS-6 results with full THM-coupling.

Benchmark 5: vapour diffusion test

The very last test presented in this work aims at testing thermally and hydraulically driven dry-out and subsequent re-saturation taking place in the bentonite buffer around a nuclear waste canister. The latter generates heat and the resulting temperature gradient creates a vapour density (or vapour mass fraction in air) gradient, driving a diffusive flux (Philip and De vries 1957) of water away from the heat source. At the same time, water is flowing into the domain from the ”cold ”side, representing water influx into the repository from the host rock. These two driving forces work against each other. Depending on the amount of heat generated and water flowing in, a fully or partially saturated steady state condition can be found. Because water vaporization and vapour diffusion are considered in this benchmark, Eq. (2) should be used without simplifications to describe the gas and water transport in this case. A description of the constitutive laws for the vaporization and diffusion is given and discussed in Pitz et al. (2022a).

General benchmark description: geometry, BCs, ICs

The domain consists of a quasi-1D bar with a length of ${1.0}\,\text {m}$. As in the previous benchmarks, the right boundary is mechanically fixed in the x direction, the top and bottom boundaries are fixed with regard to the y direction, whereas the left boundary is free to move in the x direction. Initially, the domain has a uniform temperature of ${291.15}\,\text {K}$ and is partially saturated with an initial capillary pressure $p_\textrm{cap}$ of ${60.0}\,\text {MPa}$ and a gas pressure $p_\textrm{GR}$ of one atmosphere ${0.1013}\,\text {MPa}$. It is assumed that the initial conditions cause no deformation in the domain. The temperature at the right hand boundary is kept at its initial value throughout the simulation and at the left side, a temperature source is realised by imposing a Neumann boundary condition with a heating power of ${75.0}\,\text {W}\,\text {m}^{-2}$.

Reference results

Since this benchmark was not part of the BenVaSim project, we use here a number of results obtained by different codes as reference:

• A non-isothermal Richards flow in deformable porous media model, implemented as well in OGS-6 (Wang 2010; Pitz et al. 2022a).

• A non-isothermal Richards flow implementation in the FEM code Jife (Faust 2022).

• An implementation of the same set of balance equations as used by OGS-6 TH²M (Grunwald et al. 2022), implemented in Python as 1-dimensional TH²M finite volume scheme.

Hence, results obtained by the two Richards and two two-phase formulations can be compared here. The Richards equation is derived based on the assumption that no significant gas pressure built-up occurs and any gas can escape the system faster than the other considered processes take place. The circumstances, under which Richards and two-phase implementations are comparable, are discussed in detail in Pitz et al. (2022a). Because of the implicit Richards assumption, the values for the initial and boundary conditions of the liquid flow are offset by one atmosphere (i.e. ${0.1013}\,\text {MPa}$) for the Richards models. Thus, the restriction given in Eq. 1 is fulfilled. In order to obtain comparable results using the Richards flow and multi phase flow models, a high relative gas permeability has to be assumed, because gas pressure build-up will take place otherwise. This is achieved by setting the relative gas permeability to constant $1.0 \times 10^{3}$ instead of using the van Genuchten model (Eq. 9) for the two phase models.

Results and benchmark discussion

Figure 10 shows the evolution of primary variables calculated by the OGS-6 TH²M model as well as the TRM model at four points across the domain plotted over time. It can be seen that the heating power at the left hand boundary quickly increases the temperature (in the entire domain) and reaches a nearly linear gradient across the domain. This happens because the effective thermal conductivity of the medium is assumed to be constant for simplicity and thus independent of liquid saturation. This disables one of the most significant hydraulic-thermal coupling mechanisms. Advective heat transport plays a minor role due to the low permeability of the porous medium rendering the corresponding terms in the energy balance negligible in comparison to the heat source. Thus, the temperature gradient is dominated by the effective medium thermal conductivity, which results in the quasi-linear temperature gradient. The liquid pressure at the left boundary decreases rapidly as a result of the thermal vapour diffusion. This dry-out effect becomes weaker with increasing distance from the heat source because water inflow occurs from the opposite right hand side. It can be seen that liquid pressures at the rightmost points increase fast and this ”signal” propagates through the entire domain, overpowering the thermal diffusion and re-saturating the domain. The displacements occur as a result of the solid thermal expansion as well as in poro-elastic response to the pore pressure change in the medium. The contribution of the former is however much smaller than the latter, due to the large increase of pore pressure during the re-saturation phase. The liquid pressure distribution both at the beginning and the end of the simulation is almost equal in the entire domain. Hence, the momentum generated from the re-saturation is also almost equal. This leads to equal strains across the bar and thus to a linear x displacement gradient in the steady state. The gas pressures in the domain show two peaks each. Firstly, in the beginning of the simulation, gas pressures increase due to thermal pressurization. Subsequently, they equilibrate due to gas drainage towards the right side where the boundary condition at ${0.1013}\,\text {MPa}$ is imposed. The second peak is due to the reduction of volume available to the gas, when the saturation front propagates through the domain. It can be seen that the time of second gas pressure peak at each observation point coincides with the time at which the saturation front passes through. Afterwards, the gas is again drained and eventually, a steady state condition is found.

Fig. 10

Results obtained by OGS-6 TH²M compared to results obtained by OGS-6 TRM (Pitz et al. 2022a), a TR implementation in the FEM code Jife (Faust 2022) and a finite volume TH²M implementation in Python for benchmark 5

Discussion

The results obtained by the OGS-6 TH²M implementation show in general very good agreement with results obtained by other numerical codes. Minor differences in results may originate from different temporal and spatial discretizations (Lux and Rutenberg 2018; Schmidt et al. 2009) as well as different numerical coupling schemes and the exact formulations of the considered processes or PDEs in each reference code. The benchmarks considered in this work provide a framework to analyze reasons for different results.

• In a fully liquid saturated medium, such as in benchmark 1 (consolidation problem), the simplified gas mass balance equation (5) collapses because every term is multiplied by the gas saturation $S_\text {G} = (1-S_\textrm{L})$, thus rendering the equation undefined. This situation is evaded by considering the general gas mass balance equation Eq. (2) and allowing the dissolution and diffusion of gas in the liquid phase so that $\rho ^\textrm{C}_\textrm{LR}> 0$. Thus, the gas mass balance remains defined. In case of benchmark 1, the effects of dissolved gas on the results obtained by the models are negligible as it can be seen in the results of this benchmark, where nearly perfect agreement with the reference results is achieved.

• In benchmarks 2 and 3 (homogeneous and heterogeneous gas pressure build-up problems), two-phase regions are considered so that Eq. (5) can be used again to describe the gas mass transport accurately. Both the gaseous and liquid phase are present throughout the entire simulation so that the PDE does not collapse. The interaction of the two phases (such as liquid phase pressurization as a consequence of gas pressure build-up) was observed. It should be noted that OGS-6 assembles and solves the full mass balance equation Eq. (5) in both single and two phase regions (even if parts of the PDE collapse due to single phase conditions).

• In benchmark 4 (hydro-mechanically coupled processes with heat production and temperature-induced effects), minor differences in results obtained by codes can be attributed to differing numerical coupling schemes. The coupling mechanism according to Biot’s poro-elastic consolidation theory is sensitive to the coupling scheme especially in stiff systems, such as in fully saturated systems, where mass storage can only happen due to solid/liquid compression or expansion of the porous medium itself. The same holds for thermal pressurization processes (Pitz et al. 2022a). The monolithic coupling scheme implemented in OGS-6 performs well in these situations whereas a sequentially coupled system can struggle with stiff HM-coupled problems, if a high strain rate occurs (Rutqvist et al. 2002).

• Some minor differences are visible in the results obtained by the different codes for benchmark 5 (vapour diffusion test). The reference results for this test case were obtained using the Richards approximation. This approximation assumes that there is no pressure build-up in the gas phase. In contrast to this, the gas mass balance is considered explicitly in the TH²M formulation, leading to variable gas pressures over time and slightly different calculated water vapour fluxes (a detailed comparison of Richards and two phase formulations is conducted in Pitz et al. (2022a)). Therefore, the calculated temporal evolution of the liquid pressure differs slightly, but the deformation and temperature values agree very well between TH²M and the reference results.

The observed THM phenomena and process driving forces are discussed directly in each benchmark featured in “Verification benchmarks”. Over all, the results obtained by OGS-6 TH²M show good agreement with reference results in all benchmarks and minor deviations could be analyzed and explained.

Conclusion

In this paper, we firstly discussed TH²M coupled processes as they are expected to take place during the lifetime of a deep geological nuclear waste repository. Next, the mathematical representation of said THM processes in the open source code OGS-6 was presented and we can conclude that all significant processes are represented within the limits of the continuum porous media approach. Finally, we have compared results obtained by the OGS-6 TH²M implementation against results obtained by different other numerical codes in a series of benchmarks, mostly derived in the scope of the BenVaSim benchmarking initiative (Lux et al. 2021). It was shown that the code works well both in single and multi-phasic problems. The main TH²M coupled effects covered by this work comprise the poro-elastic response in single phase and two phase regions according to the Biot theory, temperature-induced effects and gas pressure build-up. Phase transitions are covered with regard to water evaporation. The dissolution of gas in the liquid phase was neglected in this work and will be the matter of future work (Pitz et al. 2022b).

Appendix A: Overview of symbols

See Table 3.

Table 3 Explanation of symbols