Extended analysis of benchmarks for gas phase appearance in low-permeable rocks

Abstract

This manuscript presents a comprehensive study on the numerical simulation of gas transport in clay rock using the finite-element method, with a specific focus on the transition of the transport regime from single-phase to two-phase conditions. Our code demonstrates the capability to cover this transition seamlessly, without relying on common approaches such as the use of persistent primary variables or the switching of primary variables. In our simulations, the primary variables are gas pressure, capillary pressure, temperature, and displacement of the solid phase. To validate our approach, two benchmark tests were conducted. The first benchmark replicates a well-known scenario in the field of radioactive waste disposal, where gas injection induces a transition from single-phase to two-phase flow. The second benchmark simulates a core drilling experiment, where the mechanical unloading of a fully saturated domain results in the appearance of a gas phase. In addition to analyzing primary quantities, a comprehensive set of secondary variables was introduced to gain deeper insights into the model’s operation and enhance understanding of the underlying processes. By plotting these secondary variables alongside the primary quantities, a comprehensive understanding of the system’s behavior during the transition of flow regimes was obtained. The primary objective of this work is to improve our understanding and confidence in the model used for simulating large repository systems, particularly in the context of nuclear waste disposal and CO$_2$ storage. By successfully capturing the transition from single-phase to two-phase gas transport, our study provides valuable insights into the behavior of gas in clay rock. This enhanced understanding lays the groundwork for utilizing the model effectively in large-scale repository simulations, contributing to the advancement of the field of gas transport in clay rock.

Article Highlights

• The presented numerical simulation code demonstrates the capability to smoothly model the transition of gas transport in clay rock from single-phase to two-phase conditions, without the need for common approaches such as persistent primary variables or variable switching.

• The proposed approach is validated through two benchmark tests—one replicating a well-known scenario in radioactive waste disposal involving gas injection-induced flow regime transition, and the other simulating a core drilling experiment where mechanical unloading leads to the appearance of a gas phase.

• The study includes a comprehensive investigation of secondary variables alongside primary quantities, offering valuable insights into the model’s behavior during the transition of flow regimes. This deeper understanding enhances confidence in the simulation for large repository systems and advances the field of gas transport in clay rock.

1 Introduction

The disposal of high-level radioactive waste (HLW) is a major challenge for society. One approach to this problem is the storage of waste in deep geological repositories, where clay rock formations are considered favorable host rocks due to their low permeability and high sorption capacity. However, the presence of hydrogen gas resulting from corrosion of waste containers may pose a potential risk to the integrity of the clay barriers designed to isolate the waste from the biosphere for extended periods on the order of a million years.

Understanding these processes is critical, yet direct empirical measurements over the necessary timescales are impractical, and laboratory tests cannot fully replicate the scale and complexity of geological systems. Therefore, to bridge the gap between short-term experiments and the long-term performance predictions, numerical simulations have become a fundamental tool in the field of thermo-hydro-mechanical gas transport in clay rock. Such simulations can help to understand the complex interactions between the gas phase, the water phase, and the host rock over large time scales, and can provide insight into the fate of the hydrogen formed in the repository, including its dissolution in the water phase, and the impact of gas pressure on the integrity of geotechnical and geological barriers.

One of the key challenges in modeling the transport of hydrogen gas in clay rock is the multiphase nature of the system. Hydrogen gas can exist as a separate phase or can dissolve in the water phase, and its transport can be controlled by both advective and diffusive processes. Moreover, the presence of hydrogen gas can have thermo-mechanical effects, such as the generation of gas pressure, which can impact the mechanical and hydraulic integrity of the clay barriers.

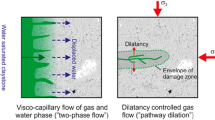
In Marschall et al. (2005), different gas transport regimes in clay rocks were classified, cf. Fig. 1. At low gas pressures or production rates, the gases dissolve in a liquid water phase and are transported both by advection with the water flow and move along the concentration gradient by diffusion (case I).

Fig. 1

Classification of gas transport regimes in clay rock, adapted and modified from Marschall et al. (2005, Figure 2) and Cuss et al. (2014, Figure 1)

If the gas pressure or production rate is increased, the dissolution rate exceeds the gas transport rate until a distinct gas phase is formed, which partially displaces the water phase. In addition to the advective-diffusive transport of dissolved gas, this newly formed gas phase now flows against its own pressure gradient (case II). At even higher gas pressures, the transport properties of the host rock itself can be altered, leading to the formation of a dilatancy zone which could preferentially transport gas in a network of microfissures (case III). In extreme cases, the gas pressure can increase to the point where the strength of the medium is exceeded and the solid rock is damaged, creating microcrystalline cracks which provide new pathways for the flowing gas phase (case IV).

To determine which of these transport regimes will prevail under which conditions, extensive investigations and experiments are being conducted. This research encompasses activities in diverse environments, from specialized underground laboratories for in-situ experiments to traditional surface-based laboratories for standard tests, and includes numerical simulations utilizing computational models. Numerical simulations can not only support physical experiments but also enhance our understanding of the gas transport processes in clay rock and in multi-barrier systems. This knowledge can be utilized to optimize the design and operation of geological repositories and to evaluate the long-term safety of such facilities. Additionally, given the enormous time scales on which diffusion processes occur at the level of a repository, numerical analyses are key for gaining insight at this scale.

Benchmark tests are an essential part of numerical modeling, providing a means to validate or verify models through comparison with established standards, such as empirical, analytical, or other numerical benchmarks. A prominent example of the latter type was proposed by the French National Radioactive Waste Management Agency (ANDRA) as part of the MoMaS project. The model is based on a geometrically very simple set up that uses realistic material parameters and considers a highly simplified injection scenario that is intended to simulate the introduction of hydrogen formed by corrosion processes into a clay host rock. The benchmark test was then computed by several groups and different codes, after which the results were compared (Bourgeat et al. 2013). The published results illustrate general agreement but are limited to a few select quantities, making wider interpretation of the physical mechanisms as well as broader code verification difficult when based on the published data alone.

In the pursuit of enhancing our understanding of the fate of hydrogen in barriers and improving the numerical simulation of two-phase flow in porous media, this paper is driven by two interconnected objectives.

Our first objective is to provide a comprehensive reproduction of the MoMaS benchmark, extending the available data with additional insights. We offer a deeper dive into internal variables such as concentration, partial density, diffusion velocity, boundary fluxes, etc., which illuminate the behavior of hydrogen over time and contribute to a more robust comparison and identification of key parameters in the system.

Simultaneously, our second objective builds upon the foundation laid by the first, by applying the insights gained to a new scenario that tests the robustness of our approach. We investigate the dynamic interplay of process coupling in phase appearance and disappearance, with a particular emphasis on mechanical deformation as the driving force. This allows us to not only validate our model in a controlled benchmark scenario but also to extend its applicability to more complex, realistic systems.

This dual focus enables us to deliver a set of benchmarks that are instrumental for cross-verification of TH$^2$M simulators and advance the current state of numerical modeling in two-phase two-component fluids in deformable porous media under non-isothermal conditions.

In repositories for highly radioactive waste, the expected gas production rates are low and it is assumed that in many areas transport classes I and II are dominant. This is the setting addressed by the MoMaS benchmark. The switch between both transport modes involves phase appearance and disappearance. When a phase disappears in a non-isothermal two-phase flow simulation, the primary variables associated with that phase, such as the phase saturation and phase pressure, may become undefined or void of physical meaning. As a result, the simulation usually must be modified to account for the disappearance of the phase.

Recent advances in numerical simulations of two-phase flow in porous media have led to the development of several approaches to handle the appearance or disappearance of phases. One approach is to use a pseudo-phase or pseudo-variables to represent the disappeared phase. This pseudo-phase does not correspond to any physical fluid phase, but it allows the simulation to continue without explicitly accounting for the disappeared phase and ensures well-posedness of the governing equations. Such approaches have been used by several authors in water-gas as well as water-oil systems, e.g. by Kirkland et al. (1992) and Binning et al. (1999). However, these methods seem unwieldy and not generally applicable to multiphase, multi-component problems (Martinez and Stone 2008).

Another approach is to switch the primary variables when phases appear or disappear. In the variable-switching method or primary variable substitution, the primary variables that correspond to the disappeared phase (e.g., phase pressure and phase saturation) are replaced by primary variables that correspond to the remaining phase. The switching of the primary variables takes place in the Newton loop, depending on the local phase condition (Class et al. 2002). This condition is evaluated at each node by considering another persistent variable in addition to classical variables such as saturation and pressure.

The variable-switching method can be implemented using a variety of techniques, such as the “upwinding” approach or the “characteristic” approach. These techniques differ in how they handle the convective terms in the governing equations, which can become singular when the phase disappears. This method has been used in a number of studies to model disappeared phases in non-isothermal two-phase flow simulations in porous media, e.g. Diersch and Perrochet (1999), Class et al. (2002) and Class and Helmig (2002).

Instead of changing the primary variables in case of disappearing phases, it is also possible to choose persistent quantities that maintain their validity in all phase states. The main idea behind this persistent primary variables (PPV) method is that these variables can be maintained in the numerical solution, even when a phase disappears or appears. By retaining the primary variables of the disappeared phase, the PPV method ensures that the numerical solution remains consistent even when a phase reappears later on. This is important for simulating complex multiphase flow phenomena in porous media, such as hysteresis, where the flow behavior depends on the history of the system. The PPV method was first proposed by Corapcioglu and Panday (1991) and has since been used in a variety of applications, including oil and gas reservoir simulation, geothermal energy systems, and environmental remediation (Marchand and Knabner 2014; Huang et al. 2015; Rebecca 2015; Huang et al. 2017).

Yet another approach proposed by Amaziane et al. (2010, 2014), employs a global pressure to streamline the equations governing two-phase flow in porous media. This single scalar variable integrates the pressures of both fluid phases, weighted by their saturation and interfacial tension, to represent their collective pressure state in the porous medium. This approach acknowledges that the pressure drop across a porous medium correlates with the saturation levels and interfacial areas of the phases. Consequently, the two-phase flow equations are formulated in terms of global pressure and saturation of each phase, rather than the separate pressures of the individual phases, enabling a simplified and more computationally efficient numerical solution. Furthermore, the global pressure framework accommodates the simulation of phase appearance or disappearance, which is pertinent when one phase saturation reaches a threshold that affects the occupation of the pore space by the other phase.

In this work, we use a variation of persistent primary variables without abandoning the use of classical approaches. As described in Grunwald et al. (2022), gas pressure and the capillary pressure are used as primary variables.

If there is no gas phase (e.g., because all gas components are dissolved in the liquid phase) then the gas pressure no longer describes a physical quantity, but instead represents the quantity of dissolved gas in the liquid phase as a virtual equilibrium pressure.

In summary, our work unfolds in a dual approach: initially, we expand upon the MoMaS benchmark, offering an in-depth analysis to yield greater clarity on hydrogen transport dynamics. Subsequently, we scrutinize the use of persistent primary variables to proficiently manage phase transitions amidst non-isothermal states affected by mechanical deformations. Together, these focused objectives fortify our comprehensive benchmark suite, aimed at advancing the cross-verification of TH$^2$M simulators.

2 Theory

In the field of continuum mechanics, a phase is a self-contained region of material that has approximately homogeneous properties. Examples of phases include the aqueous or non-aqueous fluid phase, or the solid phase of a porous medium. Phases can themselves be composed of either pure substances, such as water, or mixtures of substances, such as air, which primarily consists of nitrogen and oxygen. In this work, pure substances are referred to as components and represent the constituents of a phase.

Classical multiphase models typically consider at least two immiscible phases, such as water and oil. On the other hand, multi-component models describe mixtures of different components within a single phase.

It is imperative to carefully distinguish between the traditional terminologies in fluid mechanics. Terms such as single-phase or two-phase flow typically focus solely on the fluid phases, excluding stationary entities such as solids. However, in our context, when we refer to the system as a whole, we consider a three-phase system, encompassing gas, liquid, and solid phases.

The approach used in this work is a multi-phase, multi-component model, which is an established method for describing multi-phase systems whose constituents can cross the boundaries between phases (phase change). The numerical model gives emphasis to this three-phase system consisting of gas, liquid, and solid phases. Phase transitions are taken into account between the fluid phases, such as the evaporation of liquid phase components and the dissolution of gas phase components. The primary variables are the pressure of the gas phase $p_{\textrm{GR}}$, capillary pressure $p_\textrm{cap}$, temperature T, and displacement ${\varvec{u}}_\textrm{S}$. All three phases are compressible, but can be considered incompressible when simpler equations of state are used.

The model equations are developed from mass, linear momentum, and energy balance equations, together with constitutive relations, and are implemented as a monolithic system of partial differential equations. A detailed description of the derivation of the model equations and their implementation is given in Grunwald et al. (2022). As both fluid phases are considered compressible, and the phase transition takes both fluid components into account, the mass balance equations for both components $\zeta =\textrm{W,H}$ (water, hydrogen in the present case) are symmetrical and can be expressed by

$$\begin{aligned} 0=\sum _{\alpha =\textrm{L,G}} \left\{ {\left( \rho ^\mathrm {\zeta }_{\alpha }\right) '_{\textrm{S}}} +\,\textrm{div}\,{\varvec{A}}^\mathrm {\zeta }_{\alpha }+\,\textrm{div}\,{\varvec{J}}^\mathrm {\zeta }_{\alpha }+\rho ^\mathrm {\zeta }_{\alpha }\,\textrm{div}\,{\left( {\varvec{u}}_\textrm{S}\right) '_{\textrm{S}}} \right\} \end{aligned}$$

(1)

where ${\left( \bullet \right) '_{\textrm{S}}}$ denotes the material time derivative of a quantity $\bullet$ with respect to the velocity of the solid phase $\textrm{S}$, defined by

$$\begin{aligned} {\left( \bullet \right) '_{\textrm{S}}}=\frac{\partial (\bullet )}{\partial t}+{\varvec{v}}_\textrm{S}\cdot \,\textrm{div}\,(\bullet ) \end{aligned}$$

(2)

where $\frac{\partial (\bullet )}{\partial t}$ represents the local temporal rate of change, and ${\varvec{v}}_\textrm{S}\cdot \,\textrm{div}\,(\bullet )$ accounts for the advective change due to the movement of the solid phase S.

${\varvec{A}}^{\zeta }_{\alpha }$ and ${\varvec{J}}^ {\zeta }_ {\alpha }$ represent advective and diffusive mass fluxes, respectively, while $\rho ^ {\zeta }_ {\alpha }$ denotes the apparent (partial) density of component $\zeta$ in phase $\alpha$. This apparent density accounts for the presence of pores and phase occupancy and is related to the real intrinsic density of the component through the equation $\rho ^ {\zeta }_ {\alpha }=\phi _ {\alpha }\rho _ {\alpha R}^ {\zeta }$, where $\phi _ {\alpha }$ represents the volume fraction of phase $\alpha$ and $\rho _ {\alpha R}^ {\zeta }$ is the real (intrinsic) density. The volume fraction is defined as the product of the porosity $\phi$ and the phase saturation $s_\alpha$, which is the ratio of the volume of phase $\alpha$ to the volume of all fluid phases. A saturation condition demands $s_{\textrm{L}}+s_{\textrm{G}}=1$.

The phase velocity $\tilde{{\varvec{w}}}_ {\alpha S}$ is derived from the balance equation of linear momentum and Darcy-type linear momentum exchange and given by

$$\begin{aligned} \phi _ {\alpha }{\varvec{w}}_ {\alpha S} = \tilde{{\varvec{w}}}_ {\alpha S}= -\frac{{k^\textrm{rel}_ {\alpha }}{{\varvec{k}}_\textrm{S}}}{\mu _ {\alpha R}^\mathrm {\nu }} \left( \,\textrm{grad}\,p_ {\alpha R}+\rho _ {\alpha R}{\varvec{a}}_\alpha -\rho _ {\alpha R}{\varvec{b}}_\alpha \right) \end{aligned}$$

(3)

while the diffusion velocity ${\varvec{{\tilde{d}}}}^ {\zeta }_ {\alpha }$ follows Fick’s law and reads

$$\begin{aligned} \phi _ {\alpha }{\varvec{d}}^ {\zeta }_ {\alpha }= {\varvec{{\tilde{d}}}}^ {\zeta }_ {\alpha }= -\phi _{\alpha }x_{m,\alpha }^{\zeta \,\;-1}\tau {\varvec{D}}_{\alpha }\,\textrm{grad}\,x_{m, {\alpha }}^ {\zeta } \end{aligned}$$

(4)

where $x_{m, {\alpha }}^ {\zeta }$ is the mass fraction of the component $\zeta$ in the phase $\alpha$, which defines the composition of the phase.

Phase transitions are subject to a local equilibrium condition and occur instantaneously. These transitions include dissolution of gas components in the liquid phase and the evaporation of liquid-phase components in the gas phase. The composition of the gas phase is calculated using Dalton’s law, such that

$$\begin{aligned} p_{\textrm{GR}}= \sum _\zeta p_{\textrm{GR}}^ {\zeta }\end{aligned}$$

(5)

where the total gas phase pressure is the sum of the partial pressures $p_{\textrm{GR}}^ {\zeta }$ of all gas components.

In this work, a multi-linear equation of state for water (pressure, temperature, concentration-dependent)

$$\begin{aligned} \rho _{\textrm{LR}}=\rho ^\textrm{0}_{\textrm{LR}}\left[ \beta _{p,{\textrm{LR}}}\left( p_{\textrm{LR}}-p^\textrm{0}_{\textrm{LR}}\right) +\beta _{T,{\textrm{LR}}}\left( T-T^\textrm{0}\right) +{\beta _{c,{\textrm{LR}}}}c^{\textrm{H}}_\textrm{L}\right] \end{aligned}$$

(6)

and the ideal gas law for gas mixtures are used,

$$\begin{aligned} \rho ^ {\zeta }_{\textrm{GR}}=\frac{p_{\textrm{GR}}^ {\zeta }M^\zeta }{RT} \end{aligned}$$

(7)

The amount of water evaporation is determined by the water vapour pressure, which is coupled to the energy balance through a temperature dependency. The amount of dissolved hydrogen in the liquid phase is proportional to the hydrogen partial pressure, which is described by Henry’s law. Most of the constitutive relations can be chosen freely, thanks to the built-in material property interface in OpenGeoSys (Bilke et al. 2022). For most applications, the use of the ideal gas law for binary mixtures, as well as a simple multi-linear equation of state for the liquid phase, is sufficient. However, more complex equations of state such as the fundamental equation can be used, or own expressions can be utilized, either in the form of an expression or implemented directly into the source code of the simulator. The governing equations of the fluids are written in terms of components and incorporate the change of component mass by advection, diffusion, and other processes.

The approach chosen in this work is motivated by the approximation underlying the Richards equation; In this approach, positive capillary pressures are interpreted as suction and correspond to negative water pressures. Since Richards’ approximation usually assumes $p_{\textrm{GR}}=0$, the capillary pressure simply corresponds to the negative water pressure $p_\textrm{cap}=-p_{\textrm{LR}}$. This allows the consideration of unsaturated groundwater or soil water systems without an additional gas mass balance (Fig. 2). If larger changes in the gas phase are relevant (gas injection, gas production through corrosion, etc.), then a separate equation must be considered (Pitz et al. 2023).

Fig. 2

Exemplary curves for water pressure ($p_{\textrm{LR}}$, left) and saturation ($s_\textrm{L}$, right) profiles in the unsaturated zone ($z\ge {-4\,\mathrm{\text {m}}}$) and in the groundwater zone ($z<{-4\,\mathrm{\text {m}}}$)

In this case, we refer to classical two-phase flow, which has already been extensively used in numerical flow simulation, for example to describe the processes occurring in oil reservoirs or water gas systems.

The same approach is chosen in this work. Partially saturated conditions can only form if the gas pressure can overcome the water pressure, respectively exceed the gas entry pressure value. In the case of negative capillary pressures $p_\textrm{cap}=p_{\textrm{GR}}-p_{\textrm{LR}}$, fully saturated conditions prevail since the pressure of the aqueous phase exceeds that of the gas phase. This means, however, that for $p_{\textrm{GR}}<p_{\textrm{LR}}$, no gas phase exists, and that the physical interpretation of $p_{\textrm{GR}}$ has to be re-evaluated. A re-interpretation becomes possible in the context of the phase equilibrium relations. Gas dissolution is governed by Henry’s law, where the partial pressure of the gas-component (in case of the MoMas benchmark this refers to hydrogen) in the gas phase determines the concentration of the dissolved gas component in the water phase. Once all gas present goes into solution, the gas phase disappears entirely leaving a certain amount of dissolved hydrogen in the water phase. One can still calculate the pressure of a hypothetical hydrogen atmosphere in equilibrium with this amount of dissolved hydrogen. Thus, when no gas phase is present, the gas pressure in the present model can be seen as a virtual pressure that corresponds to the partial pressure of a hydrogen gas that would establish equilibrium with the amount of dissolved hydrogen. In other words, this virtual pressure is simply a measure of the hydrogen concentration in the liquid phase, the link being Henry’s law.

The disadvantage of this method is that when interpreting the simulation results, one must pay attention to whether a gas phase exists and whether the gas pressure represents the phase pressure or the hypothetical equilibrium pressure corresponding to and indicating the dissolved amount of gas. The advantage is that neither do variables have to be switched nor less convenient variables (such as the mole fraction) have to be used to describe the system.

3 MoMas benchmark: phase appearance test

The MoMaS benchmark was defined as one of several test cases to investigate the capabilities of various simulation tools for their application to the design and assessment of deep geological repositories of high-level radioactive waste. Despite its seemingly simple structure, this test exhibits a range of interesting phenomena and merits a thorough study of its results.

Fig. 3

Domain and model concept of the 1d test

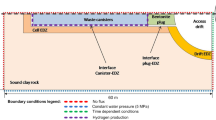
The test is described by a two-dimensional model domain with a height of $H={20\,{\text {m}}}$ and a length of $L={200\,{\text {m}}}$. With impermeable upper and lower boundaries, only horizontal flows are considered, so the test is considered as a one-dimensional problem (c.f. Fig. 3). Initially, the entire model domain is fully saturated with water, and a continuous and constant mass flux of hydrogen is set at the left model boundary $\Gamma _\textrm{in}$. This mass injection rate is kept constant for 500,000 years. During this time period, a gas phase temporarily appears in the domain due to the continued gas injection, transforming the gas transport regime from single-phase to two-phase conditions. The test is carried on for a duration of one million years.

At the right model boundary $\Gamma _\textrm{out}$, both water pressure and gas pressure are set to be constant, allowing both water and hydrogen to leave the domain via this boundary. Properties of the porous medium, the fluid phases and the components are shown in Tables 1 and 2, initial and boundary conditions are shown in Table 3.

Due to its simple description on the one hand and its high process complexity on the other hand, the MoMaS test is an excellent tool to describe and simulate the effects of corrosion gas intrusion in the disposal area of highly radioactive waste, but also to compare different mathematical model concepts. The test case has already been studied by many authors in the past to test their tools and verify their results (cf. Bourgeat et al. 2010, 2013; Amaziane et al. 2014; Gharbia and Jaffré 2014; Marchand and Knabner 2014; Huang et al. 2015; Huang et al. 2017).

Table 1 Properties of the porous medium used in the MoMas test

Table 2 Fluid properties used in the MoMas test

Table 3 Initial- and boundary conditions used in the MoMas test

In this section, this test case is computed using the TH $^{2}$ M process class (Grunwald et al. 2022) of OpenGeoSys (Bilke et al. 2022) for code verification and a more detailed evaluation of state and process variables of interest from a physics point of view.

In Bourgeat et al. (2013), the authors compare the results of six different modeller groups and provide insight into the problem by plotting the primary variables of the simulation (liquid and gas phase pressure) together with gas saturation.

Fig. 4

Comparative plot of results of different codes (Bourgeat et al. 2013) of gas pressure (a), pressure of liquid phase (b) as well as gas saturation (c) at the point of injection $\Gamma _\textrm{in}: x={0\,\textrm{m}}$

Figure 4 shows those variables compared to the output of OGS-TH $^{2}$ M. The OGS results agree well with most of the curves of phase pressures and gas saturation presented in Bourgeat et al. (2013).¹ All the models presented capture the phenomena described below.

Initially, only the gas pressure increases slowly, while the liquid phase pressure and gas saturation remain constant for about $t=12{,}700$ years. Eventually, the gas pressure exceeds the liquid pressure, leading to the appearance of a separate gas phase and increasing gas saturation and liquid phase pressure. While gas saturation continues to rise steadily until the end of gas injection,the pressures of gas and liquid phases reach their respective maxima at about $t={150{,}000\,\textrm{a}}$ and $t={100{,}000\,\textrm{a}}$. Thereafter, the gas pressure decreases only slightly until the end of the gas injection, while the liquid pressure drops back almost to its initial level. Gas saturation is reaching its maximum value of $s_{\textrm{G}}=0.0162$ at $t={500{,}000\,\textrm{a}}$ when the hydrogen injection is stopped abruptly.

Since no further hydrogen is injected into the domain, both pressures and gas saturation begin to decrease. The liquid pressure drops below its initial level, reaching a minimum and then gradually recovers. Meanwhile, the gas pressure steadily decreases until the point where full liquid saturation is restored, which occurs at about $t=680{,}000$ years. At this moment, the liquid pressure is also restored, but the gas pressure gradually decreases over the following million years towards its initial level.

The behaviour of gas and liquid pressures as well as saturation is not immediately intuitive and straightforward, especially in view of the simplicity of the given boundary conditions. In order to better explain the phenomena shown, it is certainly helpful to also consider the secondary variables that depend on the primary quantities.

In the period $t\le {12{,}700\,\textrm{a}}$, single-phase conditions prevail in the system; the capillary pressure is negative and thus no gas phase is present. The reason for this is that the injection rate is so low that all the hydrogen can be dissolved in the water phase.²

The gas pressure shown and discussed is not physically measurable as such, it is instead a virtual gas pressure in the sense explained in the previous section, i.e. representative of the concentration of dissolved hydrogen via Henry’s law. The absence of a gas phase is also the reason for the different gas pressure curves of two of the models compared in Fig. 4a (gas pressure is either zero or equal to liquid pressure in these cases). These models use a different method to describe the transition from single-phase to two-phase behavior and therefore do not provide gas pressure when no gas phase is present.

Fig. 5

Hydrogen concentration at injection point over time

To better understand the increase of this virtual pressure, Fig. 5 shows the concentration of dissolved hydrogen in the liquid phase at $x={0\,{\text {m}}}$ over time. As expected, it increases slowly due to the continuous injection at the Neumann boundary $\Gamma _\textrm{in}$. It is worth noting again that the hydrogen concentration is always in equilibrium governed by Henry’s law, that means that for every concentration, there is an associated gas pressure (virtual or physical) given by

$$\begin{aligned} p_{\textrm{GR}}=\frac{c^{\textrm{H}}_\textrm{L}}{H_{\textrm{H}}x_{n,{\textrm{G}}}^{\textrm{H}}} \end{aligned}$$

(8)

with Henry-constant $H_{\textrm{H}}$ and molar fraction of hydrogen in the gas phase $x_{n,{\textrm{G}}}^{\textrm{H}}$.

Because both the Henry coefficient and the hydrogen molar fraction in the gas phase³ are constant and the gas pressure is always proportional to the hydrogen concentration, the gas pressure rises accordingly.

The total hydrogen mass flux in the domain is the sum of advective and diffusive fluxes in both phases.

$$\begin{aligned} {\varvec{F}}^{\textrm{H}}=\sum _{\alpha =\textrm{L,G}}\left( {\varvec{A}}^{\textrm{H}}_ {\alpha }+{\varvec{J}}^{\textrm{H}}_ {\alpha }\right) \end{aligned}$$

(9)

Advective and diffusive mass fluxes are given by

$$\begin{aligned} {\varvec{A}}^{\textrm{H}}_ {\alpha }=\rho ^{\textrm{H}}_ {\alpha R}\tilde{{\varvec{w}}}_ {\alpha S},\;\text {and}\,{\varvec{J}}^{\textrm{H}}_ {\alpha }=\rho ^{\textrm{H}}_ {\alpha R}{\varvec{d}}^{\textrm{H}}_ {\alpha }\end{aligned}$$

(10)

for liquid and gas phases $\alpha =\textrm{L,G}$, with the partial density of hydrogen $\rho ^{\textrm{H}}_ {\alpha R}$, Darcy velocities $\tilde{{\varvec{w}}}_ {\alpha S}$ and with the diffusion velocity of hydrogen ${\varvec{d}}^{\textrm{H}}_ {\alpha }$. Since the gas phase consists of hydrogen only, it yields $\rho ^{\textrm{H}}_{\textrm{GR}}=\rho _{\textrm{GR}}$, while the partial hydrogen density in the liquid phase is given by the simple linear equation of state

$$\begin{aligned} \rho ^{\textrm{H}}_{\textrm{LR}}=\rho ^\textrm{0}_{\textrm{LR}}\beta ^{{\textrm{H}}}_{c,{\textrm{LR}}}c^{\textrm{H}}_\textrm{L}\end{aligned}$$

(11)

with $\beta ^{{\textrm{H}}}_{c,{\textrm{LR}}}$= $2 \times10^{-6}$ m $^{3}$ mol $^{-1}$

Since no physical gas pressure exists in this first stage and the injected hydrogen is only in a dissolved form, the pressure of the water phase hardly increases in this phase,⁴ as shown in Fig. 4c. Due to the absence of the gas phase, the only transport mechanisms of hydrogen is due to diffusion ${\varvec{J}}^{\textrm{H}}_\textrm{L}$ and advection ${\varvec{A}}^{\textrm{H}}_\textrm{L}$ in the liquid phase. However, the advective portion of the total mass flux is very small, in fact, with ${\varvec{A}}^{\textrm{H}}_\textrm{L}\approx {10^{18}\,{\text {kg}\square \text {m}^{-1}\text {s}^{-1}}}$ it is about five orders of magnitude below the level of diffusive flux.

At time $t={12{,}700}$ a the capillary pressure finally becomes positive and thus a gas phase is formed. The diffusive hydrogen mass flux in the liquid phase now decreases strongly because from now on, increasing proportion of of the hydrogen is transported advectively in the gas phase (${\varvec{A}}^{\textrm{H}}_{\textrm{G}}$), as can be seen in Fig. 6.

Fig. 6

Hydrogen mass fluxes ${\varvec{A}}^{\textrm{H}}_{\textrm{G}}$ (solid) and ${\varvec{J}}^{\textrm{H}}_\textrm{L}$ (dashed) at the injection point in the period between $t=10{,}000$ years and $t=1{,}000{,}000$ years. With the appearance of the gas phase at $t_1={12{,}700\,\textrm{years}}$, the hydrogen is transported advectively in the gas phase to an increasing extent

Fig. 7

Time-domain plot of gas saturation for $t\le {1 \times 10^{6}\,\textrm{a}}$

In the phase that follows until the end of the injection period at $t={500,000\,\textrm{a}}$, the saturation of the gas phase increases steadily. Figure 7 shows the shape of the gas phase over domain and time. Here the horizontal axis shows a cross-section through the model domain from $x={0\,{\text {m}}}$ to $x={200\,{\text {m}}}$ at $y={0\,{\text {m}}}$, and the horizontal axis denotes the simulation time from $t={0\,\textrm{a}}$ to $x={1 \times 10^{6}\,\textrm{a}}$. The colour at each coordinate point indicates the gas saturation according to the legend on the right side of the figure. It can be seen that at the beginning of the simulation, no gas phase was present (lower area of the diagram near the right axis), but after its appearance it spreads rapidly to a distance of about $x={160\,{\text {m}}}$ from the injection point. From about $t={270{,}000}$ a, the position of the boundary of the gas phase no longer changes. With the end of the injection phase, the gas phase decreases rapidly until it disappears completely at $t={680{,}000}$ a.

In contrast to gas saturation, both gas and liquid phase pressure reach a maximum long before the hydrogen injection ends. This behaviour can only be explained by boundary effects that occur on the right side of the model. The original size of the model domain was set to a width of 200 m. The resulting gas phase spreads to the right, but then stops at a distance of approx. 40 m from the right boundary and then does not progress any further until the end of the injection period.

Since the pressures of the liquid and gaseous phases are kept constant at the right model boundary, an artificially sustained pressure gradient (and thus also hydrogen concentration gradient) is created towards the right side, which would not occur if the model domain were larger.

These gradients strongly influence the mass transport in the domain by forming higher diffusion and advection velocities, which lead to increased removal of water and hydrogen. In addition, the proximity to the right model boundary prevents further spreading of the gas phase between $t={270{,}000}$a and $t={500{,}000}$ a as shown in Fig. 7.

In a comparative example with an enlarged model domain ($L={1000\,{\text {m}}}$), and an extended simulation time of 100 million years, it can be observed that the pressure maxima are indeed shifted in time and no steady state occurs until the gas injection is switched off. In this case, the right model boundary with its constant pressure Dirichlet boundary conditions is sufficiently far away from the injection, so that the naturally developing pressure gradients prevent the increased discharge of water and hydrogen from the area, and that the gas and liquid phase pressure curves do not experience maxima before the injection is ended, cf. Fig. 8. Therefore, it takes much longer for the gas phase to disappear (about 4 million years instead of only 270,000 years) compared to the original MoMas test.

The recovery of the initial level of the pressures of liquid phase and gas phase also takes considerably longer in this case (4.2 million years for $p_{\textrm{LR}}$ and even 50 million years for $p_{\textrm{GR}}$) than in the MoMas test. Since 200 m is a plausible width for clay layers, this means that such boundary effects will also occur in real repositories and that they must therefore be considered in the numerical modelling. This comparative test with increased model domain is not presented in detail in the paper in order not to make the paper too extensive.

Fig. 8

Comparison of the pressures in the gas and liquid phases of the original MoMas test (solid lines) and the version with a significantly enlarged model domain and simulation time (dashed lines)

We thus return to the discussion of the original model. After the end of the injection phase, the hydrogen present in the area dissolves completely into the water phase again and leaves the area over the course of many years via the right model boundary. For the purpose of detailed comparability, further dependent variables are shown below in their temporal development or in the profile at different points in time. Note, for example, the significant liquid phase permeability drop due to the formation of a free gas phase in Fig. 11, despite the low gas saturation.

In Figs. 9 and 10 a distribution of the total hydrogen mass in two different phases is shown. These figures illustrate that at time t = 500,000 years almost half of the total hydrogen mass originating from the feed point is in the gas phase. Although the saturation of the gas phase is only 1.6 %, its influence on the hydraulic properties of the system is remarkably large. The presence of this seemingly inconspicuous gas phase has a profound influence on the behaviour of the system. One notable phenomenon is the change in the relative permeability of the liquid phase, which undergoes a significant reduction of about 60 % as shown in Fig. 11. This means that the mobility of the liquid phase is more than halved by the inclusion of this tiny volume fraction of gas in the pore space. To better illustrate this effect, we’ve included a direct plot of relative permeabilities against liquid saturation in Fig. 12, showcasing the sharp decline of liquid relative permeability as saturation nears its endpoint.

Fig. 9

Total hydrogen mass in the domain ($\rho ^{\textrm{H}}_\textrm{tot}$) and proportion of hydrogen dissolved in the liquid phase ($\rho ^{\textrm{H}}_\textrm{L})$ during the injection period. The difference between both lines is the gaseous hydrogen mass

Fig. 10

Total hydrogen mass in the domain ($\rho ^{\textrm{H}}_\textrm{tot}$) and proportion of hydrogen dissolved in the liquid phase ($\rho ^{\textrm{H}}_\textrm{L})$ after the injection period. The difference between both lines is the gaseous hydrogen mass

Fig. 11

Relative permeabilities of gas and liquid phases over time at $x={0\,{\text {m}}}$

Fig. 12

Relationships between liquid saturation ($s_\textrm{L}$), capillary pressure ($p_\textrm{cap}$), and the relative permeabilities of gas (${k^\textrm{rel}_{\textrm{G}}}$) and liquid (${k^\textrm{rel}_\textrm{L}}$) phases. The plot elucidates the steep behavior of liquid relative permeability as $s_\textrm{L}$ nears full saturation

These results highlight the complicated nature of multiphase flow in porous media and shed light on the interplay between different phases and their effects on the overall behaviour of the system. The observed distribution of hydrogen mass between the gas and liquid phases highlights the complex dynamics that unfold in porous media and emphasises the importance of considering even slight variations in phase composition when analysing hydraulic properties.

4 Desaturation through mechanical unloading

The disappearance or appearance of the gas phase described in the above sections can, of course, be initiated by other processes. Conceivable scenarios are those in which the temperature of the water-saturated zone rises so much that the resulting vapour pressure exceeds the water pressure and a gas phase of evaporated water forms.

In addition, by applying or relieving stress on the domain, the pore space fraction can be changed in such a way that the water pressure drops until it falls below the level of the gas pressure. This can initiate the appearance of a gas phase if the permeability of the medium is so low that the newly created pore space cannot be filled with water quickly enough.

Both of these conceivable phenomena can occur in the context of highly radioactive repositories. This is where the major advantage of the presented coupled TH $^{2}$ M numerical model comes into play, as it is capable of describing mechanical, thermodynamic, and pressure- or injection-driven desaturation.

The following test case describes this scenario and was motivated by the example presented in Khaledi et al. (2021). It focuses on a core drilling experiment in Opalinus clay. The core is drilled to a diameter of $d={0.17\,{\text {m}}}$ and the drilling process takes $t={1000\,{\text {s}}}$. The region around the core is flooded, the liquid phase in this case consists of pure water with dissolved air. The liquid phase pressure is held constant at $p_{\textrm{LR}}={2 \times 10^{5}\,{\text {Pa}}}$, while the air dissolved in the water corresponds to a gas pressure of $p_{\textrm{GR}}={2 \times 10^{4}\,{\text {Pa}}}$.⁵ It is noteworthy that this gas pressure is below the water pressure, resulting in a negative capillary pressure and consequently the absence of a gas phase. A sketch of the model design assumptions is shown in Fig. 13 and the properties of the materials are summerized in Table 4.

Fig. 13

Overview, initial and boundary conditions of the drill core test

Table 4 Properties of the deformation-induced desaturation test

During the drilling process, the core material undergoes stress relaxation. This excavation is modeled by reducing the radial stress at the outer edge of the region. The initial effective stress of the material is assumed to be isotropic at ${\varvec{\sigma }}^\text {eff}={2.0\,{\text {M}\text {Pa}}}{\varvec{\textrm{I}}}$, while the initial pore fluid pressure is $p_\textrm{FR}= {0.2\,{\text {MPa}}}$. The initial total radial traction at the right boundary of the domain is $\sigma _{rr}|_{r=d/2}={-2.2\,{\text{MPa}}}$, considering the hydrostatic water pressure.

The drilling phase is simplified in the model. Over a duration of $t={1000\,{\text {s}}}$, the radial traction decreases linearly from its initial value to $\sigma _{rr}|_{r=d/2}={-0.2\,{\text{MPa}}}$, simulating the excavation process.

In Fig. 14, the evolution of the effective radial stress is shown for nine observation points located within the core. These points are positioned at radial distances from the core center as follows: $r_0$ at $r={0.\,{\text {m}}}$, $r_1$ at $r={0.05\,{\text {m}}}$, $r_2$ at $r={0.10\,{\text {m}}}$, $r_3$ at $r={0.12\,{\text {m}}}$, $r_4$ at $r={0.13\,{\text {m}}}$, $r_5$ at $r={0.14\,{\text {m}}}$, $r_6$ at $r={0.15\,{\text {m}}}$, $r_7$ at $r={0.16\,{\text {m}}}$, and $r_8$ at the outer boundary at $r={0.17\,{\text {m}}}$. The effective stress evolution at these points is captured through the plot, highlighting the changes in effective stress over time. Since curve $r_8$ corresponds to an observation point at the outer boundary, it inherently reflects the prescribed boundary conditions.

Curves $r_0$ to $r_7$ represent observation points located at various distances within the domain. During the drilling phase, all of these curves exhibit identical behavior. This phase is characterized by linear elastic response, leading to a simultaneous relaxation of the entire inner domain. The effective stress in this stage increases from $\sigma ^\textrm{eff}_{rr}={-2\,{\text {MPa}}}$ to $\sigma ^\textrm{eff}_{rr}={-1\,{\text{MPa}}}$.

Fig. 14

Evolution of radial stress at different locations of the probe ($r_0={0\,{\text {m}}}$, $r_8={0.17\,{\text {m}}}$)

As a result of this relaxation, the material experiences a small expansion towards the outer boundary. The increase in the size of the domain leads to a change of pore volume. Consequently, the fluid pressure decreases from $p_{\textrm{LR}}={0.2\,{\text {MPa}}}$ to $p_{\textrm{LR}}={-0.8\,{\text{MPa}}}$ due to the increase in pore volume, resulting in a difference of 1 MPa at all internal observation points, as shown in Fig. 15, which also corresponds exactly to the increase in effective stress.

The pressure drop in the liquid phase is significant enough to initiate the formation of a gas phase. This gas phase isn’t highly pronounced; the gas saturation rises to a value of only about $s_{\textrm{G}}=0.25\%$ (c.f. Fig. 16), representing a mix of out-gassed air and water vapor, as the water pressure falls below the virtual gas pressure (and thus capillary pressure becomes positive).

Fig. 15

Evolution of pore fluid pressure $p_\textrm{FR}$ at different locations of the probe

Fig. 16

Evolution of gas phase saturation at different locations of the probe

After the drilling phase at $t>{1000\,{\text {s}}}$, the drained unloading phase commences as the total traction boundary condition has reached zero. In this phase, the stress curves in Fig. 14 start to rise from $\sigma ^\textrm{eff}_{rr}={-1\,{\text{MPa}}}$ to $\sigma ^\textrm{eff}_{rr}={0\,{\text{MPa}}}$. However, the rate of stress increase near the boundary is faster compared to locations closer to the center. This disparity in stress evolution within the core can be attributed to the gradual re-saturation process that originates from the outer boundary. As the sample expands, additional pore space is created, which eventually gets re-saturated with water, starting from the outer edge. Due to the low permeability of the clay rock, this re-saturation process occurs over several months and progresses from the outside towards the center of the sample. The gas phase, which has a significantly higher mobility than the liquid phase penetrating from the outside, is displaced towards the centre by the advancing water phase. Consequently, the gas pressure increases in the center, while the water phase still exhibits strongly negative pressures at that location. The gas pressure increase in the center of the specimen resembles a Mandel–Cryer effect. As the gas pressure increases, resulting in a reduction of the total stress within the solid matrix, the pressure of the liquid phase is further lowered until the gas phase completely disappears.

Furthermore, the increasing gas pressure reverses the gas pressure gradient, causing gas components to flow towards the periphery and exit the domain. This gradual outflow reduces the gas pressure. Since full saturation is maintained on the core mantle by means of boundary conditions, the outbound gas transport has to proceed via diffusion. Eventually, the incoming water reaches the center, leading to the disappearance of the gas phase. As a result, the initial liquid phase pressure of $p_{\textrm{LR}}={0.2\,{\text{MPa}}}$ is re-established.

Fig. 17

Evolution of the gas phase: Uniformly distributed formation of the gas phase during the relaxation of the domain ($t\le {1000\,{\text {s}}}$, left), compression of the gas phase towards the centre during ${1000\,{\text {s}}}<t\le {200{,}000\,{\text {s}}}$ (middle), disappearance of the gas phase by diffusion, advection and re-dissolution from $t>{200{,}000\,{\text {s}}}$ (right)

Fig. 18

Evolution of gas phase pressure at different locations of the probe. Coloured pressures indicate real gas pressures, gray lines show pseudo gas pressures where no gas phase exists

Additional insights into the evolution of the gas phase can be obtained from Fig. 17. This figure provides a visual representation of the gas phase progression, illustrating three distinct stages. In the first stage (drilling stage at $t\le {1000\,{\text {s}}}$), which corresponds to the unloading phase or drilling phase of the core sample, the gas phase appears and grows simultaneously over the entire domain, resulting in a final gas saturation of approximately $s_{\textrm{G}}={0.24\,{\%}}$ at this stage (as depicted in the left part of the figure). Transitioning into the second stage at ${1000\,{\text {s}}}<t\le {200{,}000})$ s, as shown in the center part of the figure and referred to as the compression phase, the gas saturation is further increased towards the centre. Subsequently, for $t\ge {2 \times 10^{5}\,{\text {s}}}$, the gas phase gradually dissipates due to outbound gas diffusion, leading to the eventual disappearance of the gas phase (as illustrated in the right part of the figure).

As explained earlier, the term $p_{\textrm{GR}}$ corresponds to a measurable physical pressure only in the presence of a gas phase. When $p_{\textrm{GR}}$ is lower than the pressure of the liquid phase (when the capillary pressure is negative), the value of $p_{\textrm{GR}}$ describes the concentration of dissolved gases in the liquid phase.⁶ Figure 18 illustrates the variation of $p_{\textrm{GR}}$ over time at different locations. The gray lines represent the virtual effective gas pressure, while the colored lines represent the real, measurable gas pressure. The graph also shows that the gas pressure significantly increases above its initial value during the compression phase, particularly towards the center of the sample. This behavior closely resembles the effects described by Mandel and Cryer (cf. Mandel 1953; Cryer 1963).

5 Summary and discussion

In this paper, the purpose of our study was to investigate the ability of our numerical tool to handle the appearance of a gas phase in fully saturated media and transition from single-phase flow to two-phase flow regimes, which are two of the main transport processes of gas in clay rock as classified by Paul Marschall. We used a numerical approach to consider multiphase systems without additional methods such as variable switching or persistent primary variables to study the transition between these flow regimes.

To assess the performance of our tool, we conducted two tests that showcased the capabilities of our model.

The first test involved a widely recognized benchmark, which has been used to compare different tools in the field. In our case, we compared our own tool against this benchmark and provided a more detailed view of the results by analyzing not only primary variables but also several secondary variables. This comprehensive analysis led to a better understanding of the underlying processes and provided valuable insights.

The second test was developed by us to establish a gas phase by mechanically unloading a compressed material. This showed that desaturation can also have mechanical causes and that these can be computed numerically. This opens up possibilities for further investigations into the behaviour of gas in clay rock and its effects on various technical applications.

Although both tests had simple setups, they revealed a surprisingly complex behavior of the processes involved. The significance of the results is particularly notable when considering the large time scales required for simulating high-level waste repositories. With long simulation times, boundary effects become important even with distant boundaries, which underlines the need to take such factors into account when modelling real-world scenarios.

The findings from our study have several implications. Firstly, we have successfully demonstrated that our numerical tool is capable of effectively handling the transition from single-phase flow to two-phase flow without the need for additional methods. This showcases the robustness and reliability of our tool in accurately capturing the intricate gas transport phenomena occurring in clay rock. Secondly, through a meticulous examination of all process variables, we have gained a deeper understanding of the underlying mechanisms driving the transport processes. This is of potential value to other modellers that wish to have a more complete benchmark case at their disposal. Such enhanced understanding paves the way for more informed decision-making and optimization of these processes in various applications.

While the simplified model setups used in this study have provided valuable insights, it is crucial to validate the applicability of our findings to more complex and realistic scenarios. Additionally, it is important to acknowledge the limitations of our numerical tool. Although it has demonstrated promising capabilities in capturing complex process behaviors, further evaluation of its performance and robustness across a wider range of scenarios and parameter settings is necessary. This can be achieved through sensitivity analyses, validation against experimental data, and potential model refinements.

In conclusion, our study highlights the importance of employing simplified process models, conducting benchmark tests, and continuously improving numerical tools for process modeling. By successfully handling the transition from single-phase flow to two-phase flow in gas transport simulations, we have increased confidence in the capabilities of our tool and its potential for accurate predictions and efficient designs of repositories for nuclear waste. Through ongoing research and iterative improvements, we can further enhance our understanding of complex processes and facilitate advancements in gas transport modeling in clay rock environments.