Introduction

Low-temperature geothermal energy sources represent renewables that could contribute to the achievement of the environmental goals (EU Directive 2018/2001/EC 2018; EGEC 2021). Their use for heating and cooling of buildings should therefore be important in future energy management plans (Bayer et al. 2019), as it could help to reduce greenhouse gas emissions. This is especially important in densely populated areas, which are often developed on alluvial plains. Alluvial plains mainly consist of unconsolidated sediments, which are naturally occurring material composed of minerals and organic particles displaced by a variety of earth processes (Megahan 1999). Sediments have different thermal properties, so their accurate determination is important for planning subsurface heat utilisation. Among them, bulk thermal conductivity (\({\lambda }_{b}\)) is the key parameter as it controls the ability of sediments to transfer heat (Somerton 1992). It can be influenced by many factors such as water content, density, mineral composition, particle size and anisotropy (Woodside and Messmer 1961; Fuchs et al. 2013; Luo et al. 2016; Albert et al. 2017a,b; Yan et al. 2021). The thermal response test is the most reliable method for determining thermal properties in the field (Gehlin 2002), but its performance requires specialized equipment and evaluations. Therefore, this method can be expensive and time-consuming. To evaluate the thermal properties of sediments more quickly and easily, thermal conductivity estimation models (TCEM), based on the physical parameters, are often used (Somerton 1992; Dong et al. 2015; Ren et al. 2019).

Various TCEM have been presented and discussed previously (Fuchs and Förster 2010; Fuchs et al. 2013; Dong et al. 2015; Barry-Macaulay et al. 2015; Zhang and Wang 2017; Kämmlein and Stollhofen 2019; Hajto et al. 2020; Yan et al. 2021). Dong et al. (2015) classified them into three main groups: mixing, empirical, and mathematical models. Mixing models define \({\lambda }_{b}\) as a function of matrix thermal conductivity (\({\lambda }_{m}\)), fluid thermal conductivity (\({\lambda }_{f}\)), and the porosity (\(n\)), representing a multiphase system. The phase distribution could be arranged parallel or perpendicular to the direction of the heat flow, or the intermediate value is used. Depending on that, the models are further divided into geometric, arithmetic, and harmonic mean models (Fuchs et al. 2013; Kämmlein and Stollhofen 2019). Empirical models define \({\lambda }_{b}\) as a function of measured physical parameters of sediment, e.g., water content, bulk density, porosity (Kersten 1949; Johansen 1975; Cote and Konrad 2005; Lu et al. 2007; Zhang and Wang 2017). On the other hand, mathematical models are based on heat transfer theory in simplified geometry of the two-phase system (Somerton 1992). They approximate \({\lambda }_{b}\) based on a mathematical algorithm that gives thermal conductivity of each system component and their volume fractions.

In this paper, a relation of laboratory-measured \({\lambda }_{b}\) with density, porosity and water content was analysed, to evaluate the relationship between different physical properties of sediments and their thermal conductivity. Secondly, the universally applicable TCEM for cohesive and non-cohesive sediment samples with different water contents was trying to be determined among geometric, arithmetic and harmonic mean model and Kersten, Johansen and Côté&Konrad model. For evaluation of TCEMs modelled and measured \({\lambda }_{b}\) were analysed with the coefficient of determination and the root mean square error.

Methods

Samples preparation

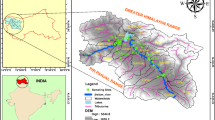
The sediments were collected from the sedimentary basin of the Polish lowlands. They represent the 30 samples of unconsolidated sediments, taken at a depth of 0.9–4.2 m. They were separated based on their shear strength into cohesive (silt, clay, glacial till) and non-cohesive groups (gravel, sand), according to EN 1997-2:2007 (2007) (Tables 3, 4). Eighteen cohesive samples were collected near the Baltic Sea in the engineering-geological unit of Pomorian phase of North Polish Glaciation (sampling location A on Fig. 1). Six non-cohesive and six cohesive samples were collected near Warsaw in the engineering-geological unit of Wartanian phase of North Polish Glaciation (sampling location B on Fig. 1).

Fig. 1
figure 1

Locations of analysed unconsolidated samples according to the engineering-geological subdivision of Poland (Kaczyński 2017)

Full size image

Samples were prepared in a 10 cm high cylinder or mould with a diameter of 7 cm. The 6 non-cohesive sediments were prepared in three water content conditions, as saturated, partially saturated and dried to a constant mass, while the 24 cohesive sediments were saturated or dried to a constant mass. The latter is defined as the point at which there is less than 0.1% further change in mass of the dry sediment sample in at least one hour (ISO 17892-1:2014 2014). To ensure a dry condition, samples were dried on 105 °C for 72 h for cohesive and 12 h for non-cohesive samples. Tap water was used for their saturation. Measurements were carried out under ambient room temperature and performed three times on the same sample to provide a representative result. Bulk density measurements on 3 non-cohesive sediment samples were measured under three different compaction levels, named loose (\({I}_{D}\le 0.33\)), medium compacted (\(0.33\le {I}_{D}\le 0.67\)) and fully compacted (\({I}_{D}\ge 0.67\)). This was performed using the tapping fork test method, which is based on the principle of putting vibrations into the sediment sample (Łukawska et al. 2020). For 6 cohesive sediments, samples were prepared so that small lumps of sediment were placed into a mould and manually recompacted. 19 samples from this group were measured as undisturbed sediment structure. A more detailed description of the used tools, measurement procedure and standards have been described in Łukawska et al. (2020).

Laboratory measurements

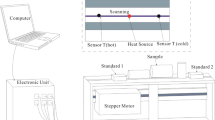
The bulk thermal conductivity of sediment samples was measured using the handheld KD-2 device (Fig. 2) (Decagon Devices Inc. 2016). A TR-1 single needle probe was used, which measures the \({\lambda }_{b}\) with an accuracy of ± 10%. The single needle algorithm is based on the line heat source analysis of Carslaw and Jaeger (1959) and Kluitenberg et al. (1993). Bulk thermal conductivity is derived from:

Fig. 2
figure 2

Equipment used in the laboratory for measuring the thermal conductivity of a non-cohesive samples and b cohesive samples

Full size image
$${\lambda }_{b}=\frac{q}{4\times \pi \times {m}_{3}}$$
(1)

Measurements of the early-time stage (1/3) were omitted, due to possible errors caused by contact resistance (Carslaw and Jaeger 1959). The bulk density and porosity of each sediment sample were determined for further analysis. The bulk density was calculated with the linear measurement method described in standard ISO 17892-2:2014 (2014) and defined as:

$${\rho }_{b}=\frac{{m}_{d}}{{V}_{total}}$$
(2)

Porosity was determined from the bulk density (Carter and Gregorich 2007) as:

$$n=1-\frac{{\rho }_{b}}{{\rho }_{s}}$$
(3)

Water content was determined as:

$$w=\frac{{m}_{1}-{m}_{2}}{{m}_{2}-{m}_{c}}$$
(4)

Thermal conductivity estimation models (TCEM)

Six TCEM were evaluated, three mixing and three empirical models. The mixing models (geometric, arithmetic, harmonic mean) were chosen because they are based on the conceptualized multiphase sediment system that includes only the sediment matrix, pore fluid, and porosity for \({\lambda }_{b}\) determination (Lichtenecker 1924; Voigt 1928). Therefore, they are easy to apply and are often used for a first approximation of \({\lambda }_{b}\). They have been successfully used for estimating the \({\lambda }_{b}\) of rocks (Fuchs et al. 2013; Tatar et al. 2021), so in this study, they were applied to sediments as well. Used empirical models (Kersten, Johansen, Côté&Konrad) were chosen because they are based on mathematical equations with logarithmic and potential functions established on similar sediment types that were studied. The parameters of the model can be modified to better fit the model to the experimental data. The Kersten model (1949) was developed for similar sediment types that were analysed and are based on water content and bulk density. The Johansen model (1975) was used because \({\lambda }_{m}\) is determined from quartz content and also because the equations use a normalized thermal conductivity, called a Kersten number, which reflects the effects of sediment type, porosity, and mineralogy in relation to water content. As an extension of the Johansen model, Cote and Konrad (2005) proposed new equations with empirical parameters defining sediment type, grain size and shape distribution.

Modelled results were evaluated using the coefficient of determination (\({R}^{2})\), which is a relative measure of the fit between the measured and predicted values and the root mean square error (\(\mathrm{RMSE}\)), which is the square root of the residual variance and indicates the absolute fit of the model to the data. It is expressed in the same units as the observed variable, with lower values indicating better model fit.

Mixing models

The geometric mean model (Woodside and Messmer 1961) provides a mathematical expression for calculating the \({\lambda }_{b}\) of sediments using standard values of \({\lambda }_{f}\), like air [0.025 W/(m × K)] or water [0.6 W/(m × K)], defined as:

$${\lambda }_{b}={\lambda }_{m}^{1-n}\times {\lambda }_{f}^{n}$$
(5)

The arithmetic mean model (Voigt 1928) represents the heat flow that passes parallel to the geological boundaries. Blocks have the same temperature gradient but different heat flows. The \({\lambda }_{b}\) of each block can be defined as:

$${\lambda }_{b}=\left(1-n\right){\lambda }_{m}+n\times \lambda _{f}$$
(6)

The harmonic mean model (Voigt 1928) represents the heat flow perpendicular to the geological boundaries. Blocks have a different temperature gradient but a constant heat flow. The \({\lambda }_{b}\) of blocks can be defined as:

$${\lambda }_{b}=\frac{1}{\left(\frac{\left(1-n\right)}{{\lambda }_{m}}\right)+(\frac{n}{{\lambda }_{f}})}$$
(7)

First \({\lambda }_{m}\) for mixing models was calculated from the measured dry and saturated \({\lambda }_{b}\) values of the corresponding sample, using Eqs. (5–7). Later the calculated \({\lambda }_{m}\) of the dry sample from the previous step was used for the calculation of \({\lambda }_{b}\) of saturated sample and similarly the calculated \({\lambda }_{m}\) of the saturated sample was used for the calculation of \({\lambda }_{b}\) of dry sample.

Empirical models

Kersten (1949) analysed thermal conductivities of various sands, silts and clays measured with the single needle probe method, considering the effects of temperature, density, water content, sediment texture and mineralogy on the \({\lambda }_{b}\). Depending on water content and bulk density, the equations were defined for unfrozen silt or clay sediments as:

$${\lambda }_{b}=\left[0.130\mathit{log}w-0.0288\right]\times {10}^{0.000624{\rho }_{b}}$$
(8)

and for unfrozen sandy sediments as:

$${\lambda }_{b}=\left[0.101\mathit{log}w+0.0577\right]\times {10}^{0.000624{\rho }_{b}}$$
(9)

Johansen (1975) proposed to calculate \({\lambda }_{m}\) based on the \({\lambda }_{b}\) of quartz (\({\lambda }_{q}\)) and other sediment minerals (\({\lambda }_{o}\)) in proportion to the quartz content (\(q\)) as a fraction of the total solids. Since this analysis did not include measurements of these properties, the estimation of \(q\) based on grain size distribution were performed as proposed by Johansen (1975) (Table 1). It was defined as:

Table 1 Recommended values for quartz content based on grain size distribution (Johansen 1975)
Full size table
$${\lambda }_{m}={\lambda }_{o}^{1-q}\times {\lambda }_{q}^{q}$$
(10)

For non-cohesive sediments, \(q\) of 0.45 and \({\lambda }_{o}\) of 3.5 \(W/(m\times K)\) were used. For cohesive sediments, \(q\) of 0.15 and \({\lambda }_{o}\) of 2.3 \(W/(m\times K)\) for silty sediments or \(q\) of 0 and \({\lambda }_{o}\) of 2.0 \(W/(m\times K)\) for clayey sediments were used. Based on the fit of the experimental data, Johansen (1975) defined empirical equations for the so-called Kersten number \({\lambda }_{K}\), reflecting the influence of soil type, porosity, water content and mineralogy. With the adjustment of the experimental data, the \({\lambda }_{K}\) for non-cohesive (Eq. 11) and cohesive sediments (Eq. 12) was defined as:

$${\lambda }_{K}=0.7\mathrm{log}\left({S}_{r }\right)+1$$
(11)
$${\lambda }_{K}=\mathrm{log}\left({S}_{r}\right)+1$$
(12)

The \({\lambda }_{b}\) was then defined as:

$${\lambda }_{b}=\left({\lambda }_{f}^{n}{\lambda }_{m}^{1-n}-\frac{0.137{\rho }_{b}+64.7}{2650-0.947{\rho }_{b}}\right){\lambda }_{K}+\frac{0.137{\rho }_{b}+64.7}{2650-0.947{\rho }_{b}}$$
(13)

Following the Johansen method (1975), Cote and Konrad (2005) proposed new parameters χ, η and κ depending on soil type and grain shape effect (Table 2). They rewrote Eq. 13 as:

Table 2 Recommended values for the parameter \(\kappa\), \(\chi\) and \(\eta\) (Cote and Konrad 2005)
Full size table
$${\lambda }_{b}=\left({\lambda }_{f}^{n}{\lambda }_{m}^{1-n}-\chi {10}^{-\eta n}\right)\left[\frac{\kappa {S}_{r}}{1+\left(\kappa -1\right){S}_{r}}\right]+\chi {10}^{-\eta n}$$
(14)

Results

Laboratory measured properties

Laboratory measurements are shown in Table 3 for non-cohesive samples and in Table 4 for cohesive samples. Beside \({\lambda }_{b}\) values sediment type, water content, compaction, bulk density and porosity are presented. The values represent the average of three measurements taken on the same sample, all the measured values, that were used for model estimations, are in Supplementary material.

Table 3 Results for non-cohesive sediment samples, measured in the laboratory
Full size table
Table 4 Results for cohesive sediment samples, measured in the laboratory
Full size table

Influence of water content, porosity and bulk density on measured \({{\varvec{\lambda}}}_{{\varvec{b}}}\)

Evaluation of the relationship between water content and measured \({\lambda }_{b}\) (Fig. 3) for non-cohesive and cohesive sediments were performed. For non-cohesive sediments, a high positive correlation between \({\lambda }_{b}\) and water content (R2 = 0.81) was observed. For cohesive sediments, the evaluation was separated because there are two characteristic trends. Up to 20% water content, a positive correlation is observed (\({R}^{2}\) = 0.86). For water content above 20% the correlation reverses to negative (\({R}^{2}\) = 0.85).

Fig. 3
figure 3

Relation between water content and measured \({\lambda }_{b}\) of sediment samples

Full size image

To analyse the influence of porosity on the measured \({\lambda }_{b}\), separate analyses of dried and saturated samples were performed (Fig. 4). In all four groups, a negative correlation between \({\lambda }_{b}\) and porosity is present. For non-cohesive samples R2 = 0.42 and for cohesive samples R2 = 0.88, both values represent dry conditions. For saturated conditions, the correlation between the observed variables is R2 = 0.48 in the case of non-cohesive samples and for cohesive R2 = 0.85.

Fig. 4
figure 4

Relationship between porosity and measured \({\lambda }_{\mathrm{dry}}\) (left) and \({\lambda }_{\mathrm{sat}}\) (right) for non-cohesive and cohesive sediments

Full size image

Bulk density measurements were made for each sample and different compaction levels. On average, these values do not deviate more than ± 300 kg/m3 from the average bulk density. The values of \({\lambda }_{b}\) (Fig. 5) for non-cohesive sediments increase more steeply than for cohesive sediments. The correlation between \({\lambda }_{b}\) and density is positive, for non-cohesive R2 = 0.58 and cohesive sediments R2 = 0.82.

Fig. 5
figure 5

Relation between bulk density and measured \({\lambda }_{b}\) of sediment samples

Full size image

Modelled bulk thermal conductivity

In Figs. 6 and 7, the results of TCEM compared to measured \({\lambda }_{b}\) are presented. The results for mixing models (geometric, arithmetic mean) and the empirical models (Kersten, Johansen, Côté&Konrad) are divided into cohesive and non-cohesive samples and based on water content. The results of the harmonic mean model were not presented and discussed further as they gave unreasonable results, but are presented in the Supplementary material. Sixty percent of the calculated \({\lambda }_{m}\) values were negative, which can be attributed to the equation used to calculate \({\lambda }_{m}\), which allows the negative denominator. In our case, negative values occurred for non-cohesive and cohesive samples when the porosity was higher than 21% and the bulk density was lower than 1700 kg/m3.

Fig. 6
figure 6

Evaluation of measured \({\lambda }_{b}\) and modelled \({\lambda }_{b}\), obtained with the geometric and arithmetic mean model

Full size image
Fig. 7
figure 7

Evaluation of measured and modelled \({\lambda }_{b}\), obtained with the Kersten, Johansen and Côté&Konrad model

Full size image

The geometric and arithmetic mean model equations for \({\lambda }_{b}\) consist of \({\lambda }_{m}\), \({\lambda }_{f}\) and \(n\), where the calculated \({\lambda }_{m}\) should be independent due to water saturation. For all three mixing models, λm was calculated from Eqs. (5–7). In our study for non-cohesive samples, values of \({\lambda }_{m}\) showed high dependence on water content, which is reflected in high deviations of modelled \({\lambda }_{b}\) (Fig. 6). Values of \({\lambda }_{m}\) calculated from dry samples were always lower than \({\lambda }_{m}\) calculated from saturated samples. For cohesive samples, the results were the same, except for the arithmetic mean model in some cases. Nevertheless, the model fit obtained with the \(RMSE\) was better with the geometric mean model than with the arithmetic mean model. The \({R}^{2}\) shows slightly better fit for the arithmetic mean model.

The empirical models provided a better fit than mixing models. Modelling of \({\lambda }_{b}\) with the Kersten model (Fig. 7) was based on water content and bulk density. The results show high \(RMSE\) for non-cohesive and cohesive sediments [\(\mathrm{RMSE}=0.726-0.966\,W/\left(m\times K\right)]\) (Table 5), except for partially saturated non-cohesive samples, where the model fit reaches \(RMSE=0.208\,W/\left(m\times K\right)\). The Johnson and Côté&Konrad models require values of \({\lambda }_{m}\), calculated with Eqs. 10. For both models, a \({\lambda }_{m}\) of \(4.991\,W/\left(m\times K\right)\) was calculated for non-cohesive sediments. Two values were used for cohesive sediments, \(2.757\,W/\left(m\times K\right)\) for silts and \(2.000\,W/\left(m\times K\right)\) for clays. Modelling \({\lambda }_{b}\) with the Johansen model shows slightly better fit of the \(\mathrm{RMSE}\) [\(\mathrm{RMSE}=0.374-0.820\,W/\left(m\times K\right)\)], and is especially low for dry non-cohesive samples [\(\mathrm{RMSE}=0.207\,W/\left(m\times K\right)\)] (Table 5), which could be related to the Kersten number used, reflecting the soil type and mineralogy. The Côté&Konrad model shows the lowest \(\mathrm{RMSE}\) values among the models considered and therefore provides the best fit to the experimental data [\(\mathrm{RMSE}=0.111-0.347\,W/\left(m\times K\right)]\). The exceptions are dry non-cohesive samples, which showed the highest deviation among the empirical models \(\mathrm{RMSE}=0.9\,W/\left(m\times K\right)\) (Fig. 7). \({R}^{2}\) for all empirical models varies between 0.34 and 0.90, with values higher than 0.6 already predicting good estimation values. The ranges of \({R}^{2}\) are also in agreement with the lowest \(\mathrm{RMSE}\) values of the empirical models.

Table 5 Evaluation between TCEM and measured \({\lambda }_{b}\), divided into non-cohesive and cohesive groups. The lowest RMSE are marked in bold, representing the best fit between modelled and measured \({\lambda }_{b}\)
Full size table

The evaluation of modelled results is presented in Table 5. The lowest \(\mathrm{RMSE}\) are marked in bold, representing the best fit between modelled and measured \({\lambda }_{b}\). The results are separated by water content.

Modifying empirical parameters

Empirical models are developed on sediment samples, where obtained mathematical equations include their properties, e.g., mineralogy. Despite being of the same sediment type, they may not be appropriate for the samples that were not included in the model layout. Therefore, modifications are often made to the empirical parameters (Barry-Macaulay et al. 2015). In this study, manual fitting of the empirical parameters in the Kersten and Côté&Konrad model was made (Eqs. 8, 9 and 14) (Fig. 8), to improve RMSE between modelled and measured \({\lambda }_{b}\). The Kersten model for non-cohesive sediments was defined as:

Fig. 8
figure 8

Evaluation of measured and modelled \({\lambda }_{b}\), obtained with the modified parameters of Kersten and Côté&Konrad model

Full size image
$${\lambda }_{b}=\left[0.101\,\mathit{log}\,w+0.0277\right]\times {10}^{0.000624{\rho }_{b}}$$
(15)

For cohesive sediments, the equations were separated for dry and saturated conditions, which resulted in a better agreement for some sediment sample conditions. For dry conditions, the equation parameters were modified as:

$${\lambda }_{b}=\left[0.25\,\mathit{log}\,w-0.0088\right]\times {10}^{0.000624{\rho }_{b}}$$
(16)

And for saturated conditions as:

$${\lambda }_{b}=\left[0.1\,\mathit{log}\,w-0.0088\right]\times {10}^{0.000624{\rho }_{b}}$$
(17)

For the Côté&Konrad model, modification of the parameter \(\kappa\) describing the sediment type was made (Table 6).

Table 6 Modified values of parameter \(\kappa\), used in Côté&Konrad model
Full size table

Discussion

Using the laboratory measurements (Tables 3, 4), the influence of water content, porosity and bulk density on \({\lambda }_{b}\) of selected samples was evaluated. A high positive correlation was observed between water content and \({\lambda }_{b}\) for non-cohesive sediments (\({R}^{2}=0.8\)) (Fig. 3). For cohesive sediments, a positive correlation is observed up to 20% water content (\({R}^{2}=0.86\)) and a negative correlation after additional saturation (\({R}^{2}=0.84\)). This is probably caused due to the loos of mineral particle connectivity with an increase of water content in the sample, as also observed in Dong et al. (2015) and Łukawska et al. (2020). The variation of thermal conductivity with increasing water content also agrees with the consistency indices \({I}_{c}\) that can be used to define cohesive sediments—very stiff, stiff, firm, soft, very soft (EN 1997-2:2007 2007). Therefore, the results fit into the proposed nomograms for thermal conductivity coefficient estimation, proposed by Łukawska et al. (2020). The relationship between porosity and laboratory-measured \({\lambda }_{b}\), divided into dry and saturated (Fig. 4), showed a negative correlation between \({\lambda }_{b}\) and \(n\) (\({R}^{2}=0.42-0.88\)), which is consistent with the physical principles and findings of Albert et al. (2017a) and Kämmlein and Stollhofen (2019). The lower \({R}^{2}\) for non-cohesive sediments could be caused due to the wider range of grain fractions in the non-cohesive group (from fine, medium, coarse sand to gravel), which increases the possibility of variations in the measurements. It confirms that multiphase mixing models based mainly on \(n\) are not accurate enough in contrast to empirical models for non-cohesive sediments. On the other hand, the correlation between bulk density and \({\lambda }_{b}\) is positive (\({R}^{2}=0.53-0.82\)) (Fig. 5), which is consistent with the fact that a larger number of contact points between minerals increases the thermal conductivity of sediments, as discussed by Abu-Hamdeh and Reeder (2000) and Barry-Macaulay et al. (2013). Higher variability is observed between 1700 and 1900 \(\mathrm{kg}/{\mathrm{m}}^{3}\) for the non-cohesive samples, which is related to different grain sizes and consequently a highly variable porosity of these sediments. It is assumed that this is the reason why the correlation between \({\lambda }_{b}\) and density is lower for non-cohesive sediments, than for cohesive ones.

Estimation of \({\lambda }_{b}\) of cohesive and non-cohesive sediments was performed using mixing and empirical models to obtain the best agreement with laboratory-measured \({\lambda }_{b}\). The results were statistically analysed using the \({R}^{2}\) and \(\mathrm{RMSE}\) (Tables 5, 7), focusing on the latter as it indicates absolute deviation between measured and modelled \({\lambda }_{b}\). Samples prepared in the laboratory were manually compacted at three compaction levels.

Table 7 Evaluation of Kersten and Côté&Konrad model based on parameter modification. The lowest RMSE are marked in bold, representing the best fit between modelled and measured \({\lambda }_{b}\)
Full size table

The selected mixing models were chosen because they are based on the conceptualized multiphase sediment systems (\({\lambda }_{b}\), \({\lambda }_{m}\), \(n\)). Their results showed that the modelled \({\lambda }_{m}\) are always higher than the measured \({\lambda }_{b}\), which is consistent with the fact that the \({\lambda }_{m}\) increases with decreasing porosity, as previously discussed by Fuchs and Förster (2010) and Albert et al. (2017a). The latter authors make such conclusions for sedimentary rocks (e.g., sandstones), but results of this study confirm this fact also for unconsolidated sediments (cohesive, non-cohesive). For mixing models, high variability of the modelled dry and saturated \({\lambda }_{m}\) occurred for the same sample (Horai and Baldridge 1972; Kämmlein and Stollhofen 2019), resulting in a high deviation of the obtained \({\lambda }_{b}\) values. Theoretically, modelled \({\lambda }_{m}\) should remain the same, but studies such as that of Albert et al. (2017a, b, c), showed that changing water content could affect modelled \({\lambda }_{m}\), and hence the hygroscopic properties of minerals composing sedimentary rocks. The minerals composing our sediment samples seem to be even more sensitive to water content, as the deviations between dry and saturated \({\lambda }_{m}\) are high. This is probably related to the degree of compaction of our sediment samples compared to the rock samples. The water content in the rock samples does not have such a high influence (Albert et al., 2017a, b, c). Nevertheless, we have no information about the mineral structure and composition of our samples, so we cannot make any further assumptions.

However, the effect of water content on the thermal properties of minerals has not yet been analysed. In some cases, researchers also recommended the use of average \({\lambda }_{m}\) from dry and saturated samples (Fuchs et al. 2013). In this analysis, even averaging of the \({\lambda }_{m}\) lead to a high deviation of the modelled \({\lambda }_{b}\). There is also an assumption that, despite water content, the large deviation is caused due to the influence of sediment properties that are not included in the equations of the mixing models (grain geometry, grain connectivity). Nevertheless, the geometric mean model showed a better fit of \({\lambda }_{b}\) compared to the arithmetic mean model for all groups of sediments (Table 5, Fig. 6). But still, TCEM values of non-cohesive sediments are overestimated for the dry condition and underestimated for the saturated condition. For cohesive sediments, the TCEM values are slightly overestimated (Fig. 6). The harmonic mean model was not included in the discussion because it showed unreasonable values. This was also previously observed in Fuchs et al. (2013) for sedimentary rocks.

The empirical models were chosen because they are based on mathematical equations that represent similar sediment types that were studied, while allowing parameters to be changed to better fit experimental data. The \({\lambda }_{m}\) used was estimated from the quartz content for all sediments to provide a constant value regardless of water content. The Kersten empirical equations were developed on 19 samples, having the best fit for non-cohesive sediments (Eqs. 9) at water content of 1% or more, and for cohesive sediments (Eqs. 8) at water content of 7% or more. Considering this criterion in the analysis, only dry cohesive samples could have higher deviations (Table 5) but were observed in all sediment sample conditions. Only the \(RMSE\) of partially saturated non-cohesive sediments show the best fit between all models with \(RMSE=0.208\,W/\left(m\times K\right)\). The best fit for dry non-cohesive samples (Fig. 7) was obtained with the Johansen model, with \(RMSE=0.207\,W/\left(m\times K\right)\) and for saturated with Côté&Konrad model and \(RMSE=0.274\,W/\left(m\times K\right)\). The Johansen model uses porosity, bulk density and Kersten number in addition to the matrix and fluid thermal conductivity. The Kersten model, on the other hand, considers only the water content, bulk density, and predetermined empirical numbers. For dry cohesive samples, the best fit was obtained with the Côté&Konrad model with an \(RMSE=0.111\,W/\left(m\times K\right)\) and for the saturated conditions with an \(RMSE=0.347\,W/\left(m\times K\right)\). The fit of measured and modelled \({\lambda }_{b}\) was improved by modifying the empirical parameters (Fig. 8) in the Kersten and Côté&Konrad equations (Tables 6, 7). The modification of the parameters improved the deviations of the Kersten model for dry and saturated cohesive and non-cohesive samples. For the Côté&Konrad model, the modification had a positive effect only for dry and partially saturated non-cohesive samples, while dry non-cohesive samples still showed a high deviation from the measured values.

The evaluation has shown that no universally applicable TCEM can be recommended. Different TCEM needs to be used depending on the sediment type and water content. The better fit of the empirical models with the mixing models is related to the experimentally defined equations established on samples with similar geological properties.

Conclusions

This study describes the analytical determination of thermal conductivities for cohesive and non-cohesive sediment samples used in engineering geology and solid earth studies. In the future, such an approach could contribute to the faster creation of a database that determines \({\lambda }_{b}\) based on known physical parameters of an area. Laboratory measurements obtained with the specific methodology of preparing samples were used to predict \({\lambda }_{b}\) with three mixing and three empirical models: the geometric, arithmetic, and harmonic mean models, as well as the Johansen, Kersten, and Côté&Konrad models. First, the correlation between measured thermal conductivities and water content, porosity and density was evaluated. Secondly, the correlation between measured \({\lambda }_{b}\) and the selected TCEM was analysed. The main findings from this study are:

  1. 1.

    The correlation of measured \({\lambda }_{b}\) with density, porosity and water content showed a high \({R}^{2}\) for cohesive samples (\({R}^{2}\approx 0.8\)) and a slightly lower \({R}^{2}\) for non-cohesive samples (\({R}^{2}\approx 0.4\)). The lower correlation is influenced by different grain sizes causing higher data variation.

  2. 2.

    The mixing models are not suitable to predict the \({\lambda }_{b}\) of studied cohesive and non-cohesive sediments. The main reason is that the modelled \({\lambda }_{m}\) obtained under dry and saturated conditions for the same sample, were not the same, resulting in a high deviation of the modelled \({\lambda }_{b}\) compared to the measured \({\lambda }_{b}\). It is assumed that the reason for this could be the changing thermal properties of the minerals, which are affected by the varying water content.

  3. 3.

    The empirical models gave better agreement as they represent mathematical functions developed on an experimental set of similar sediment types where the influence of the changing properties is taken into account. Additional modifications to the parameters for the Kersten model improved the prediction for dry and saturated non-cohesive and dry cohesive sediments. Also in the Côté&Konrad model, the parameter describing the sediment type was modified, which showed an improvement of the fit for dry and partially saturated non-cohesive sediments.

  4. 4.

    It was not possible to determine a universally applicable model, as the best fit varies according to sediment type and water content. For dry non-cohesive sediments, the best fit was obtained with the Johansen model (\(RMSE=0.207\,W/\left(m\times K\right)\)), for partially saturated with the Kersten model (\(RMSE=0.208\,W/\left(m\times K\right)\)), and for saturated the best fit was obtained with the modified Kersten model (\(RMSE=0.264\,W/\left(m\times K\right)\)). For cohesive sediments, the best fit was obtained with the Côté&Konrad model for all water conditions (\(RMSE=0.141 \mathrm{and} \, 0.293\,W/\left(m\times K\right)\)).