Abstract
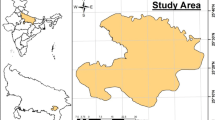
The investigation region is found in the central part of Iraq within the of Karbala Governorate, where it is located in the western part of the Governorate and Lake Razaza in the north of the region, while in the western and southern part of the region is Anbar Governorate and geographically (43° 10′ 25.7″, 43° 39″ 0.3″) longitude and (32° 10′ 25.7″, 32° 36′ 25.7″) latitude. The area of study is about 2400 Km2. The groundwater modeling system (GMS) v10.3 program was used for the modeling of ground water in the area containing about 22 wells distributed throughout the study area and the discharge of these wells ranges from 7 to 100 l/s and the rate of discharge of these wells up to 36 l/s. The model was initially operated within a steady state and after obtaining a match between the models results with the initial values of groundwater levels, the results of this case were adopted as inputs to run the model within the unsteady state. The model was worked within the sight of the above wells for 3 years and the results of the operation indicate a decrease in groundwater levels ranging from 2 to 21 m distributed uniformly throughout the study area.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The interaction between groundwater and surface water is a basic piece of the water cycle, and the management and utilization of one of these resources regularly impacts the availability of the other. Inappropriate administration and over-misuse of these water assets affects the entire water resource of a region and the environments that depend on water availability. Excessive groundwater use can cause the elevation of the water table to decline, and can therefore influence surface water bodies associated with springs (Abbas et al. 2018). For waterways in which a significant part of the stream is base flow, this can affect the general stream cause the collapse of stream-dependent environments (Pardo and Garcia 2016).
In excess of 33% of all water utilized worldwide by people originates from groundwater. In many countries, the proportion of groundwater use is much higher and most drinking water throughout the world is provided from groundwater (Harter 2015). Water use from surface water bodies in many parts of the world has been poorly managed due to a lack of resources. The consequent decline in surface water quality has been a significant driver for increased groundwater use which in turn is threatening groundwater availability (Al-Sudani 2018). Excessive groundwater use coupled with a lack of understanding of the underlying hydrogeological setting is a significant threat to sustaining groundwater resources in many regions (Ramesh and Fritz 2016).
Groundwater modeling is a useful tool for assessing the effects that groundwater abstraction will have on the elevation of the water table and on groundwater availability. This is usually carried out by creating a finite-element or finite-difference grid in a region through the process of discretization. The number of cells that are created in such a discretized grid is a balance between developing accurate numerical solutions for groundwater flow and the cost and resources required to construct, calibrate and run the model (Klaas et al. 2016).
These models need a range of data including topographic, hydrogeological, hydrological and climatic data to simulate groundwater flow in a region (Rapantova et al. 2017). In developing countries, these data may have a limited availability which can greatly increase the difficulty of undertaking groundwater modeling investigations (Hogeboom et al. 2015). The nature of the informationutilized in groundwater models can significantly affect the model outcomes and, wherever possible, exact information should be provided as model inputs (Baalousha 2009). The GMS: MODFLOW model (groundwater modeling system) is a software package that is widely used for simulating groundwater flow under a range of hydrogeological conditions (Panagopoulos 2012). In this study, a groundwater flow model was developed for a region in Iraq.
Description of the study area
The study area is located in the central part of Iraq within the Karbala Governorate, It is located in the western part of the Governorate between (43o 10′ 25.7″, 43o 39″ 0.3″) longitude and (32o 10′ 25.7″, 32o 36′ 25.7″) latitude covering an area of about 2400 km2 Fig. 1.The main geological layer of the study area is called “Dammam”. Dammam Formation is one of the most important aquifers in south west of Iraq. It is composed of variable carbonate rocks mainly limestone, dolomitic limestone and dolomite with marl deposits. It is characterized by the presence of cavities and certified canals in addition to fractures fissures and joints which cause the formation to have highest transmissivity and permeability in most area (Jassim and Gaff 2006).
Materials and methods
Data for the investigated area were providing by the General Administration of groundwater in the Karbala Governorate, data obtained from this source included climate data, topographic maps, hydrological data for 22 existing wells and general information about the area.
Second: state the suitable software for building up the study model such as groundwater modeling system (GMS) software. The GMS is used to simulate the steady and unsteady states of flow based on two-dimensional finite-difference techniques.
A finite-difference grid for the modeled domain was developed using 56 rows and 92 columns. The modeled domain consisted of 5112 cells, of which 34,102 were active cells and17050 were inert cells. The model covered an area of 1288 km2. The model consisted of one layer that had a thickness of 155 m. Each cell had an area of 0.25 km2 as indicated in Fig. 1.
Several factors were considered in this design: the nature of the change in hydraulic properties, the hydraulic gradient, and the distribution of wells in the area and the availability of information on groundwater levels at specific points.
The calibration is an important part of any groundwater modeling process. Moreover, to successfully implement the groundwater model for any management system, simulation of the aquifer behavior must be established (Anderson and Woessner 1992).
Calibration is a process where certain parameters of the model such as recharge and hydraulic conductivity are changed in a systematic fashion and the model is repeatedly run until the computed solution matches field-observed values within an acceptable level of accuracy.
Steps of actualize GMS model
The GMS numerical model was initially developed natural groundwater flow conditions without groundwater abstraction. A steady state model was then run to help calibrate the model using existing water level data from the area. The results of steady state simulation were then used as the initial conditions for an unsteady state simulation in which the existing 22 wells were considered as shown in Table 1.The models were operated for 5 years to determine the amount of drawdown in groundwater during that period.
Initial and boundary conditions
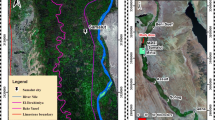
Constant-head boundary conditions were used to constrain groundwater flow conditions in the modeled domain. These boundaries were established in a fringe zone that was located sufficiently far from the well-field to limit effects on simulated heads within the model domain (Al-Basrawi 1996), Constant-head boundaries of 14.0 m were set on the right (East direction) of the model domain and 54.0 m at the left side (West direction) of the area in Fig. 2a.
a Initial groundwater levels in the study area (m.a.s.l). b Hydraulic conductivity contour map. c Storage coefficients contour map. d Initial and calculated head in the area of study for steady state simulation. e Pumping wells locations in steady area. f Drawdown of groundwater level after 3 years of pumping
Input parameters
Hydraulic properties for the aquifers in the study area were estimated using pumping tests analysis and on from their lithology as follows:
Hydraulic conductivity
The Dibdibba aquifer represents the uppermost principal unconfined aquifer in the study area and covers an area of 1100 km2from the Karbala–Najaf plateau. The aquifer is fed by seasonal flow stream from direct rainfall within the Plateau. The seasonal flow stream-oriented 40°N towards the Mesopotamian Basin, (GCGW 2018). The Dibdibba alluvial fan delta formed in the early Miocene as a result of a drainage system which remains visible upstream on the Western Desert’s carbonate platform (Jassim and Goff 2006). The Dibdibba fan delta appears disconnected today from this drainage system, most likely because of recent tectonic movement along the active Abu Jir fault. The delta of Dibdibba.
Initial values of aquifer hydraulic conductivity for the unconfined aquifer were evaluated from pumping test results of wells within the studied area. These qualities were used as initial parameter estimates in the model. These values were modified later during through experimentation during the calibration of the model. In the final distribution of hydraulic conductivity values in the model domain are shown in Fig. 2b.
Storage coefficients
The unsteady simulation requires initial evaluation for the storage coefficients in the unconfined aquifer. Contour map of the storage coefficient values, Fig. 2c, was drawn in surfer software and used as input data for GMS. The storage coefficient values were evaluated from pumping test results of wells within the studied area.
Results
Steady state flow simulation
A steady state flow is the first step in identifying the behavior of the system under normal conditions. This helps to understand this behavior first and then use the results of this condition as preliminary inputs to the unsteady state flow which is the basis for the long-term aquifer behavior with various pumping operations.
After the installation of all data and inputs of the numerical model, the model was run under stable flow conditions up to the field levels registered in the study area and the levels derived from the model to the highest level of conformance. This process often requires modifications in the values of the hydraulic conductivity or connectivity, the amount of water entering the model boundary is the ideal feeding of the layers of the aquifer and up to the levels to the match Fig. 2d shows a map of the similarity of the field aquifers with the derived numerical model for steady state. It is noted that there is a good general consensus for these levels reflecting the general trend of flow. It is important to note that it is difficult to obtain a perfect match between the field and calculated values because the model is based on many theoretical assumptions. It is also difficult to have a porous media with the same characteristics on which the model is based and the same assumptions apply.
Unsteady state simulation (with pumping wells)
This is the most important step in expressing the behavior of the aquifer as a result of its impact on pumping operations as it gives a long-term perception of this behavior.
The values of the resulting heads of the standard model for the steady flow state were used as primary inputs to represent the unsteady flow, and the wells in the modeled area Fig. 2e were operated. As for the boundary conditions, the outer boundaries of the model were chosen as constant head. The use of these boundaries to represent the unsteady flow state is only if the studied system is part of a larger aquifer, provided that the boundaries are chosen away from the effect in the drainage areas, when the surface of the aquifer matches any water body, such as a sea or lake and the rest of the cells were considered variable (Fetter 1988).
Due to no periodic readings data of the field aquifers during the operation of dug wells in the area and for long periods of time, we were unable to calibrate the model under this case but the model was operated with the (22) pumping wells for 3 years. The wells' discharge values ranged from 7.5 to 100 l/s and the average of well discharge was around 36 l/s The operating results of the model showed that the value of the drawdown in groundwater levels during the period of operation ranged between 2.0 and 22.0 m where it was obtained in areas where the presence of wells is concentrated while the other areas of study area showed very low drop in ground water levels as shown in the Fig. 2f.
Conclusion
The main conclusions of the modeling study can be summarized as follows:
-
1.
The operational results of the model showed that the value of drawdown in groundwater levels during the 3 year period ranged between 2.0 and 22.0 m with 22 wells obtained in areas where wells are concentrated contrasted with different zones of the examination region.
-
2.
Due to the fact that the pumping rates of the wells are distributed throughout the center of study area, the extent of groundwater drawdown was uniformly distributed near wells in the study area except some areas where the wells were very convergent where the rate of decrease in groundwater levels reached the limits of 7 m.
References
Abbas S, Xuan Y, Bailey R (2018) Improving river flow simulation using a coupled surface‐groundwater model for integrated water resources management. EPiC series in engineering, vol 3. In: (HIC 2018) 13th International Conference on Hydroinformatics, 1–6 July 2018, Palermo, Italy, pp 1–9
Al-Basrawi NH (1996) Hydrogeology of Razzaza Lake Iraq's Western Desert, PhD Thesis. College of Science, University of Baghdad, Baghdad, Iraq.
Al-Ghanimy MA (2013) The hydrogeology of Dammam aquifer in the west and south-west of the Kerbala City, PhD Thesis, College of Science, University of Baghdad, Baghdad, Iraq.
Al-Sudani HZ (2018) Hydrogeological properties of groundwater in Karbala’a Governorate-Iraq. J Univ Babylon EngSci 26(4):70–84
Anderson MP, Woessner WW (1992) Applied groundwater modelling, simulation of flow and vertical transport. Academic Press Inc, San Diego, p 246
Baalousha H (2009) Fundamentals of groundwater modeling. In: Konig LF, Weiss JL (eds) Groundwater: modeling, management and contamination. Nova Science Publishers Inc, New York, pp 149–166
Fetter CW (1988) Applied Hydrogeology, 2nd edn. Macmillan Inc, New York
GCGW (General Commission of Groundwater) (2018) Advanced Survey of Hydrogeologic Resources in Iraq, Phase II (ASHRI-2) Ministry of Water Resources of Iraq, Bagdad, Iraq.
Harter T (2015) Basic Concepts Of Groundwater Hydrology. ANR Publication 8083, FWQP Reference Sheet 11.1, University of California
Hogeboom RHJ, van Oel PR, Krol MS, Booij MJ (2015) Modeling the influence of groundwater abstractions on the water level of Lake Naivasha, Kenya under data-scarce conditions. Water ResourManag 29:4447–4463
Jassim S, Goff GC (2006) Groundwater assessment development and management. Tata McGraw-Hill Offices, NewDelhi, p 720
Klaas DKSY, Imteaz MA, Arulrajah A (2016) Evaluating the impact of grid cell properties in spatial discretization of groundwater model for a tropical Karst catchment in rote island, Indonesia. Hydrol Res. https://doi.org/10.2166/nh.2016.250
Panagopoulos G (2012) Application of MODFLOW for simulating groundwater flow in the Trifilia Karst aquifer. Greece Environ Earth Sci 67:1877–1889
Pardo I, Garcia L (2016) Water abstraction in small lowland streams: unforeseen hypoxia and anoxia effects. Sci Total Environ 568:226–235. https://doi.org/10.1016/j.scitotenv.2016.05.218
Ramesh D, Fritz F (2016) Water balance to recharge calculation implications for watershed management using systems dynamics approach. J Hydro 3(13):19p
Rapantova N, Tylcer J, Vojtek D (2017) Numerical modeling as a tool for optimization of groundwater exploitation in urban and industrial areas. ProcedEng 209:92–99
Funding
Open access funding provided by Lulea University of Technology.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hussain, T.A., Ismail, M.M. & Al-Ansari, N. Simulation of the ground water flow in Karbala Governorate, Iraq. Environ Earth Sci 80, 182 (2021). https://doi.org/10.1007/s12665-021-09452-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s12665-021-09452-6