Analysis of a priority queueing system with the enhanced fairness of servers scheduling

Abstract

A multi-server queueing system with two types of customers is analyzed. Both types of customers have own reserved servers and also there is a pool of servers that can be used by both types of customers. Type 1 customers have almost preemptive priority with flexible use of a priority depending on the current number of customers of this type in an infinite buffer. Type 2 customers do not have an input buffer and are lost in cases of absence of available servers upon arrival or expelling (forced termination) from service by Type 1 customers. A multi-dimensional Markov chain, which defines the dynamics of the considered system under the fixed total number of servers, numbers of reserved servers, a pattern of the correlated arriving processes, service rates, and the thresholds defining the mechanism of expelling Type 2 customers from service, is analyzed. A numerical example of solving an optimization problem based on the obtained results is considered. Results can be used for the elaboration of enhanced protocols of servers scheduling in many real-world systems including cognitive radio networks with channels leasing.

1 Introduction

Queueing theory is a well-recognized mathematical tool for the optimization of restricted resource scheduling in many real-world systems. One of the important branches of queueing theory is the theory of priority systems. In such systems, customers are classified into different categories, depending on the urgency of their service and importance, and service is provided according to a certain fixed priority scheme. E.g., various priority schemes are used in hospital emergency departments during the triage, i.e., sorting incoming patients according to the severity of the injury or disease, see, e.g. He et al. (2012), Alipour-Vaezi et al. (2022), Elalouf and Wachtel (2022).

They are used for medical packet transmission scheduling system in e-health networks, see Raj and Chinnadurai (2021), for ambulances scheduling, etc.

It is well-known that priority queueing models are effectively used in various applications in telecommunication networks, where traffic prioritization is usually required. E.g., they are required when using the IEEE 1588 synchronization protocol in cellular networks, DVB-T2 video transmission for synchronizing TV transmitters, unmanned vehicle systems, telemedicine applications, etc, for references see, e.g., Klimenok et al. (2020b). In communication systems, the users can sign agreements with different service levels (and different fees) and need a distinct treatment. The ultra-reliable low-latency communication (URLLC) applications in 5G networks have higher priority than the enhanced mobile broadband (eMBB) applications, etc. A proper choice of the priorities can significantly increase the economic profit gained from the operation of a corresponding system and revenue-generating businesses.

In particular, a popular subject of applications of the theory of priority queueing systems are the systems of cognitive radio in which the licensed (primary) users (PU) have a priority over the cognitive (or secondary) users (SU). Note that there is a great variety of the analyzed schemes for providing a priority to PUs. The most frequent scenario assumes that PUs have the preemptive priority. There is no queue for storing PUs and they are lost at an arrival moment when all servers are busy by providing service to PUs. If all servers are busy but a part of users obtaining service at the PU arrival epoch are SUs, the service of one of SUs is terminated. This phenomenon may lead to very frequent interruption of service of SUs and their dissatisfaction and permanent departure from the system. To mitigate this effect, the mechanism of reservation of channels is sometimes suggested which assumes temporal termination of admission of new SUs when the number of free channels is still not equal to zero but is less than some preassigned threshold value. Also, different other mechanisms for providing more fairness to SUs are used. One of these new mechanisms suggests the so-called subleasing of channels, see, e.g., Huang et al. (2019) and Zhao et al. (2022). The system can obtain profit from allowing SUs to temporarily use the free channels without (or almost without) the harsh interruption of the ongoing service of SU. Therefore, to earn more profit, PUs should be ready to partially sacrifice their strict priority over SUs.

In this paper, we propose and analyze a scheme that may be suitable for providing a more tolerant attitude to SUs than the majority of existing schemes assumes. To this end, we exclude mandatory immediate forced termination of service of a SU in case of the lack of channels at the moment of a PU arrival. Instead, we suppose that there is a buffer for storing PUs (while such a buffer is not suggested in the majority of existing papers) and the service of SUs is sequentially terminated according to a threshold strategy when the number of PUs in the system increases. Situations when not all available servers are busy by PUs but some PUs wait in the queue are possible. To the best of our knowledge, this reasonable scheme is novel in the literature.

The literature devoted to the application of queueing theory for modeling cognitive radio systems is really huge. The search in Google Scholar implemented at the end of January 2022, by keywords “queueing theory, cognitive radio” resulted in more than 2370 links to works published only during the years 2021 and 2022. So, we do not aim to give any more or less comprehensive survey of the state of the art in this field. The reader can look, e.g., at the recent book (Maharaj and Awoyemi 2021) and papers (Palunčić et al. 2018; Okegbile et al. 2021; Kumar and Kumar 2020; Piran et al. 2020; Hu et al. 2018; Arikatla et al. 2022; Dasari and Venkatram 2021). To essentially reduce the number of relevant references, it is worth mentioning that in the vast majority of the papers authors assume that arrival flows of PUs and SUs are defined by the stationary Poisson processes. This assumption drastically simplifies the analysis of the queueing system (due to smaller dimension of the stochastic process under study and much easier operation with scalars than with vectors and matrices) but is rarely true in modern telecommunication networks providing service to the versatile and highly bursty traffic. The set of papers devoted to priority queues where the arrival flows are assumed to be more realistic MAP (Markov arrival process), see Lucantoni (1991), Chakravarthy et al. (2001), Dudin et al. (2020a), Vishnevskii and Dudin (2017), or MMAP (Marked Markov arrival process), see He (1996), is essentially narrower. For references see, e.g., (He et al. 2012; Klimenok et al. 2020a, b; Bocharov et al. 2004; Choi and Hwang 1997; Machihara 1995; Takine and Sengupta 1997; Choi et al. 1998; Krishnamoorthy and Divya 2018; Sun et al. 2014a, b; Dudin et al. 2016, 2015, 2020b; Horváth 2012; Krishnamoorthy et al. 2008; Brandwajn and Begin 2017; Raj and Jain 2021; Vishnevsky et al. 2021). Some of these works, namely (Klimenok et al. 2020a; Bocharov et al. 2004; Choi and Hwang 1997; Machihara 1995; Takine and Sengupta 1997; Choi et al. 1998; Krishnamoorthy and Divya 2018; Dudin et al. 2020b; Horváth 2012) are devoted to single server queues which are simpler for analysis and hardly may be good models of cognitive radio.

A short overview of the relevant papers devoted to multi-server queues is as follows. In He et al. (2012), the model with an arbitrary number of types of customers, MMAP and PH (phase-type) distribution of service times and the preemptive priority is considered. Priorities can increase during the customer waiting in a queue. The ergodicity condition is obtained in terms of parameters that characterize the arrivals and service of the customers of the highest priority. Due to the high generality of the model, the distribution of the system states is not derived, but some bounds are given. In Klimenok et al. (2020b), a partial case where the number of types of customers is equal to two of the model considered in He et al. (2012) is under study. This allows obtaining not only bounds but the distribution of the number of customers in the system. In Sun et al. (2014a), it is assumed that the arrival process of PUs and SUs is defined by the MMAP,  there is an infinite buffer for arriving SUs and a finite buffer for SUs, service of which is forcedly terminated. In Sun et al. (2014b), it is assumed that the arrival process of PUs and SUs is defined by two independent MAPs. There is no buffer and arriving or forcedly terminated SUs go to the so-called orbit of an infinite capacity and repeat attempts to enter the service after the exponentially distributed intervals of time. In both papers Sun et al. (2014a) and (b), the preemptive priority of PUs over SUs is assumed and R of all N servers are reserved for service of only PUs. The goal of the reservation is to reduce the probability of the forced termination of service of SUs via their rejection at the entrance to the system when the number of free servers is small and termination occurrence, due to a new PU arrival, is anticipated. Stability conditions of the models are derived, stationary probabilities of the system states are computed. Examples of solutions to the problem of computing the optimal value of R are given. The high importance of account of correlation in the arrival process for the correct choice of value R is demonstrated. In Dudin et al. (2016), essential generalization of the model from Sun et al. (2014b) is considered. It is supposed that there are several types of PUs having the same priority, but their services times have a phase-type (PH) distribution with distinct parameters. Additionally, the realistic feature of many real systems of cognitive radio is taken into account. This feature consists of a possibility of division of the server (channel, frequency band) to a finite number of sub-servers for providing service to SUs while the service of a PU requires a whole server. Again, as in Sun et al. (2014a) and (b), the problem of optimal choice of the number of reserved servers is numerically solved via analysis of a multi-dimensional Markov chain describing the dynamics of the system. In Dudin et al. (2015), the extension of the model from Sun et al. (2014b) to the case when the priority queueing system operates under the influence of the external random environment is analyzed. The change of the state of the random environment implies an immediate change in the numbers of available servers and reserved servers. In Krishnamoorthy et al. (2008), the considered model assumes self-generation of non-preemptive priority during the stay of non-priority customers in the system. Service times have distinct PH distribution for priority and non-priority customers. The problem of optimal choice of the number of necessary servers is numerically solved. The paper Brandwajn and Begin (2017) is devoted to the analysis of the M/PH/N system with many types of customers and preemptive priorities. One of the sections of this paper considers a more general PH/PH/N type queueing system (PH arrival flow is the particular case of the MAP). An approximate solution to the problem of computation of stationary probabilities of the system states is given. In recent paper Raj and Jain (2021), the MMAP/PH/N type queue with two kinds of customers, retrials and both, non-preemptive and preemptive, priorities is analyzed. One type customers are handoff customers having high priority. The another type customers are new customers having a low priority. Retrials of non-priority customers from the orbit are assumed. Inter-retrial times have a PH distribution. Under the formulated conditions, the considered model looks to be extremely difficult to study. The authors avoid the existing difficulties by the rough truncation of the system of equilibrium equations and solution of the corresponding finite system of linear algebraic equations by a known in the literature method. In Vishnevsky et al. (2021), the priority multi-server system MMAP/PH/M/N is analyzed using machine learning methods.

Concluding the short overview of the papers devoted to priority queues, it is possible to formulate the main contributions of our paper that are as follows:

• Invention of a novel flexible priority scheme. This scheme is the significant generalization of known in the literature effective schemes and is more friendly to the low priority customers. Such friendliness (fairness) is achieved via (1) reservation of the sets of servers not only for service of high priority customers but for service of low priority customers as well; (2) maintenance of a buffer for temporary storing the high priority customers what makes them more tolerant with respect to the low priority customers; (3) permission of the sequential forced termination of service of low priority customers only after reaching the fixed thresholds by the queue length of high priority customers.

• Algorithmic analysis of a multi-server queueing system applying such a scheme including description of operation of the system by the continuous-time multi-dimensional Markov chain with complex boundary behavior, derivation and explanation of the infinitesimal generator of the chain, derivation of a simple ergodicity condition for this chain.

• Effective algorithm for computation of the stationary distribution of the states of the queueing system. This algorithm requires much less computer memory and runtime than the known in the existing literature.

• Analysis of the proposed priority scheme under the assumption that the flows of customers are defined by two MAP arrival processes. This makes the considered model much more adequate to real systems, telecommunication systems in particular, where the flows of PUs and SUs have a correlated bursty nature compared to the models with the stationary Poisson arrival process common in the existing literature.

• Numerical illustration of the impact of parameters of control strategy on the key performance measures of the system and possible economical effect of application of the proposed and analyzed priority scheme.

The section-wise breakup of this paper is as follows. A mathematical model is described in Sect. 2. The multi-dimensional process describing the behavior of the system is analyzed in Sect. 3. The generator of the process is derived. The ergodicity condition is presented. A numerically stable algorithm for the computation of the stationary distribution of the system states is outlined. Expressions for the computation of some performance measures are given in Sect. 4. Section 5 contains brief description of two sets of numerical examples. Section 6 concludes the paper.

2 Mathematical model

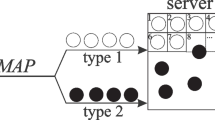
We consider the complex of two interacting multi-server queueing systems that partially share the servers. Each system provides service to its own arrival process using currently available for this system servers. The structure of this complex is presented in Fig. 1.

Fig. 1

Structure of the systems

The total number of servers in both systems is equal to N. The systems share the existing servers in the following way. The number of servers reserved exclusively for using by System 1 (for service of Type-1 customers) is equal to R. The number of servers reserved exclusively for using by System 2 (for service of Type-2 customers) is equal to $M,\,1\le M\le N-R-1.$ The rest pool consisting of common $N-R-M$ servers can be used by both systems only when all their own reserved servers are busy. A certain priority in access to the common pool is given to Type-1 customers. Namely, if the number of customers requiring service in System 1 is not large, then all $N-R$ servers, which are not reserved exclusively for using by System 1, are available for the use by System-2. However, when the number of customers in System 1 increases, this system may sequentially withdraw servers (one-by-one) from the common pool. This can lead to termination of service of Type 2 customer receiving service by the server from the pool if all servers of this pool are busy.

The exact rule of servers withdrawal by System 1 from the common pool is defined by the set of thresholds $(B_1,B_2,\ldots ,B_{N-R-M})$ arranged as

$$\begin{aligned} R<B_1<B_2<\cdots <B_{N-R-M}. \end{aligned}$$

When the number of customers presenting in System 1 is less than the threshold $B_1,$ then only R servers operate (provide service or stay idle) in System 1. When the number of customers in System 1 belongs to the interval $[B_1,B_2),$ then $R+1$ servers provide service in System 1,..., when the number of customers in System 1 belongs to the interval $[B_k,B_{k+1}),\,k=\overline{2,N-R-M-1},$ then $R+k$ servers provide service in System 1. When the number of customers in System 1 exceeds the threshold $B_{N-R-M},$ then the number of servers providing service in System 1 is $N-M.$ We assume that if during the epoch when System 1 needs to withdraw a server from the common pool there are free servers in the pool, one of the free servers will start operation as part of System 1. If all servers from the common pool are busy and at least one of them provides service to a Type 2 customer, one of these servers immediately terminates the current service and starts service of the first Type 1 customer from the buffer. A customer, the service of which was terminated, is lost. When all servers from the common pool provide service to Type 1 customers, further withdrawal of servers becomes impossible. When the queue of Type 1 customers decreases, the corresponding servers from the common pool become available for Type 2 customers again depending on the relation of the current number of Type 1 customers in the system and the thresholds $B_k,\;k=\overline{1,N-R-M}.$

Note that in the particular case of thresholds choice such as $B_k=R+k,\;k=\overline{1,N-R-M},$ the considered priority scheme turns to the usual discipline with a preemptive priority of Type 1 customers and servers reservation for both types of customers. Note also that usually in the literature reservation of servers for service of SUs (Type 2 customers) is not implemented. Formally, we obtain this usual case by setting in our more general model the threshold M equal to zero.

System 1 has an infinite buffer. The arrival process at System 1 is the MAP, coded as $MAP_1.$ It is defined by the underlying process $\nu _t$ with finite state space $\{1,2,\ldots , W\}$ and two square matrices $D_0$ and $D_1$ of size W. For more information about MAP,  its properties and usefulness for modeling telecommunication networks see, e.g, Lucantoni (1991), Chakravarthy et al. (2001), Dudin et al. (2020a), Vishnevskii and Dudin (2017). The average arrival rate of the $MAP_1$ is denoted as $\lambda _1.$ It can be found as $\lambda _1={\varvec{\theta }}D_1\mathbf{e},$ where ${\varvec{\theta }}$ is an invariant vector of the $MAP_1$ satisfying equations ${\varvec{\theta }}(D_0+D_1)=\mathbf{0},\; {\varvec{\theta }}\mathbf{e}=1,$ and $\mathbf{e}=(1,1,\ldots ,1)^T,$ $\mathbf{0}=(0,0,\ldots ,0).$

System 2 has no buffer. The arrival process at System 2 is also MAP. It is coded as $MAP_2$ and defined by the underlying process $v_t$ with finite state space $\{1,2,\ldots , V\}$ and two square matrices $H_0$ and $H_1$ of size V. The average arrival rate of the $MAP_2$ is denoted as $\lambda _2$. If at an arrival moment of a customer there are no available servers, this customer is lost.

The service time in System $r,\,r=1,2,$ is exponentially distributed with the parameter $\mu _r,\,\mu _r> 0.$

Now, let us analyze the described queueing model.

3 Process of the system states

The behavior of the system under study can be described by the regular irreducible continuous-time Markov chain

$$\begin{aligned} \xi _{t} =\{i_t, r_t, \nu _t,\,v_t\},\, t\ge 0, \end{aligned}$$

where during the epoch t, 

• $i_t$ is the number of customers in System 1, $i_{t}\ge 0;$

• $r_t$ is the number of busy servers in System 2, $r_t=\overline{0,N-R}$ if $i_t<B_1$;  $r_t=\overline{0,N-R-k}$ if $B_k\le i_t<B_{k+1}$and $r_t=\overline{0,M}$ if $i_t\ge B_{N-R-M};$

• $\nu _{t}$ is the state of the underlying process of the $MAP_1$, $\nu _{t}=\overline{1,W};$

• $v_{t}$ is the state of the underlying process of the $MAP_2$, $v_{t}=\overline{1,V}.$

Here and further, the notation like $x=\overline{0,X}$ means that the parameter x admits values from the set $\{0,\ldots ,X\}.$

Let us enumerate the states of the Markov chain $\xi _{t},\,t\ge 0,$ in the direct lexicographic order of the components $\{i_t,\,r_t,\,\nu _t,\,v_t\}$ and assume that the set of the states having the value i of the component $i_t$ is a level i. Let the intensities of transition of the process $\xi _t$ be defined by the entries of its infinitesimal generator Q.

Theorem 1

The generator Q of the Markov chain $\xi _{t} ,\; t\ge 0,$ has the block three-diagonal structure. The non-zero blocks of the generator are defined as follows:

$$\begin{aligned} Q_{0,0}= & {} I_{N-R+1}\otimes D_0\otimes I_V+\mu _2C_{N-R}E^{-}_{N-R}\otimes I_{WV} \\&-\mu _2C_{N-R}\otimes I_{WV}+E^+_{N-R}\otimes I_{W}\otimes H_1+I_{(N-R+1)W}\otimes H_0, \\&Q_{i,i}=Q_{0,0}-i\mu _1I_{(N-R+1)WV},\,i=\overline{1,R}, \\&Q_{i,i}=Q_{0,0}-R\mu _1 I_{(N-R+1)WV},\,i=\overline{R+1,B_1-1}, \\ Q_{i,i}= & {} I_{N-R-k+1}\otimes D_0\otimes I_V+\mu _2C_{N-R-k}E^{-}_{N-R-k}\otimes I_{WV} \\&-\mu _2C_{N-R-k}\otimes I_{WV}+E^+_{N-R-k}\otimes I_{W}\otimes H_1 \\&+I_{(N-R-k+1)W}\otimes H_0- \mu _1(R+k)I_{(N-R-k+1)WV}, \\&\,i=\overline{B_k,B_{k+1}-1},\,k=\overline{1,N-R-M-1}, \\ Q_{i,i}= & {} Q^0=I_{M+1}\otimes (D_0+D_1)\otimes I_V+\mu _2C_{M}E^{-}_{M}\otimes I_{WV} \\&-\mu _2C_{M}\otimes I_{WV}+E^+_{M}\otimes I_{W}\otimes H_1 \\&+I_{(M+1)W}\otimes H_0- \mu _1(N-M)I_{(M+1)WV},\,i\ge B_{N-R-M}, \\ Q_{i,i-1}= & {} \mathrm{min}\{i,R\}\mu _1 I_{(N-R+1)WV},\,0<i< B_1, \\ Q_{i,i-1}= & {} (R+k)\mu _1 {{\tilde{E}}}^+_{N-R-k}\otimes I_{WV},\,i=B_k, \\ k= & {} \overline{1,N-R-M}, \\ Q_{i,i-1}= & {} (R+k)\mu _1 I_{(N-R-k+1)WV},\,i=\overline{B_k+1,B_{k+1}-1}, \\ k= & {} \overline{1,N-R-M-1}, \\ Q_{i,i-1}= & {} Q^-=(N-M)\mu _1 I_{(M+1)WV},\,i>B_{N-R-M}, \\ Q_{i,i+1}= & {} I_{N-R+1}\otimes D_1\otimes I_V,\,i=\overline{0,B_1-2}, \\ Q_{i,i+1}= & {} {{\tilde{E}}}^-_{N-R-k+1}\otimes D_1\otimes I_V,\,i=B_k-1, \\ k= & {} \overline{1,N-R-M}, \\ Q_{i,i+1}= & {} I_{N-R-k+1}\otimes D_1\otimes I_V,\,i=\overline{B_k,B_{k+1}-2}, \\ k= & {} \overline{1,N-R-M-1}, \\ Q_{i,i+1}= & {} Q^+=I_{M+1}\otimes D_1\otimes I_V,\,i\ge B_{N-R-M}, \end{aligned}$$

where

• $\otimes$ and $\oplus$ indicate the symbols of the Kronecker product and sum of matrices, see Graham (2018);

• $C_i=\mathrm{diag}\{0,1,\ldots ,i-1,i\}$ where $\mathrm{diag}\{\dots \}$ denotes the diagonal matrix having the diagonal entries listed in the brackets;

• $E^-_k$ is the square matrix of size $k+1$ with all zero entries except the entries $(E^-_k)_{l,l-1}=1,\,l=\overline{1,k};$

• $E^+_k$ is the square matrix of size $k+1$ with all zero entries except the entries $(E^+_k)_{l,l+1}=1,\,l=\overline{0,k-1}$ and $(E^+_k)_{k,k}=1;$

• ${{\tilde{E}}}^-_k$ is the matrix of size $(k+1)\times k$ with all zero entries except the entries $\left( {{\tilde{E}}}^-_k \right) _{l,l}=1,\,l=\overline{0,k-1}$ and $({{\tilde{E}}}^-_k)_{k,k-1}=1;$

• ${{\tilde{E}}}^+_k$ is the matrix of size $(k+1) \times (k+2)$ with all zero entries except the entries $({{\tilde{E}}}^+_k)_{l,l}=1,\,l=\overline{0,k}.$

Let us briefly prove this theorem. The proof is implemented via the analysis of all variants of the Markov chain $\xi _{t},\,t\ge 0,$ transitions during an interval of the infinitesimal length.

The diagonal entries of the matrix $Q_{i,i}$ are negative and the modulus of the diagonal entry defines the rate of the exit from the corresponding state of the Markov chain $\xi _{t},\,t\ge 0.$ The non-diagonal entries of the matrix $Q_{i,i}$ define the rates of transition of the Markov chain between the states within the level i. Let us explain the expression for the matrix $Q_{i,i}$ for $i=\overline{B_k,B_{k+1}-1},\,k=\overline{1,N-R-M-1}.$ In this case, the number of servers currently providing service to Type 1 customers is equal to $R+k$ and the number of servers providing service to Type 2 customers can take values from the set $\{0,\dots ,N-R-k\}.$ The exits from the states that belong to the level i can happen due to: (a) the exit of the underlying process of the $MAP_1$ from its states; (b) the exit of the underlying process of the $MAP_2$ from its states; (c) service completion of a Type 1 customer in one of $R+k$ servers or (d) service completion of a Type 2 customer in one of currently busy by providing service to this type of customers servers. Therefore, the rates of the exits are given (with the opposite sign) by the diagonal entries of the matrix $I_{N-R-k+1}\otimes D_0\otimes I_V-\mu _2C_{N-R-k}\otimes I_{WV}+I_{(N-R-k+1)W}\otimes H_0-\mu _1(R+k)I_{(N-R-k+1)WV}.$

Here, the symbol of the Kronecker product of matrices is used to describe simultaneous transitions of several components of the multi-dimensional Markov chain. The non-diagonal entries of the just written matrix define the sum of the rates of transition of the Markov chain between the states within the level i due to the reasons (a)–(d) listed above. But the transitions within the level i can occur also due to two other reasons: (e) service completion of a Type 2 customer and (f) arrival of a Type 2 customer. The rates of transition due to the reason (e) are given by the matrix $\mu _2C_{N-R-k}E^{-}_{N-R-k}\otimes I_{WV}.$ Here, the multiplier $\mu _2C_{N-R-k}$ reflects the rates of service completion while the multiplier $E^{-}_{N-R-k}$ reflects the decrease by one of the number of servers providing service to Type 2 customers. The rates of transition due to the reason (f) evidently are given by the matrix $E^+_{N-R-k}\otimes I_{W}\otimes H_1.$ Here, the matrix $H_1$ defines the rates of transitions of the underlying process of the $MAP_2$ at a Type 2 customer arrival moment, while the multiplier $E^{+}_{N-R-k}$ reflects the increase by one of the number of servers providing service to Type 2 customers. As the result of consideration of reasons (a)-(f) of the Markov chain transitions within the level i,  we obtain the formula for the matrix $Q_{i,i}$ which we prove. The proof of the formulas for the matrix $Q_{i,i}$ with other values of i is made analogously.

Now, let us explain the expressions for the matrix $Q_{i,i-1}.$ We consider the most difficult case when $i=B_k,\,k=\overline{1,N-R-M}$. Transitions from level i to level $i-1$ occur only due to service completion of a Type 1 customer. In the considered case, $R+k$ servers were providing service to Type 1 customers. Therefore the total rate of service completion in these servers is equal to $(R+k)\mu _1.$ The matrix ${{\tilde{E}}}^+_{N-R-k}$ reflects the fact that, according to the suggested threshold strategy, after this service completion moment the number of servers from the common pool that can provide service to Type 1 customers decreases by one. Correspondingly, the number of servers from the common pool that can provide service to Type 2 customers increases by one. As the result of these considerations, we obtain the formula for the matrix $Q_{i,i-1}$ which we prove. For other values of i,  the proof is similar and a bit easier because for that values the number of servers from the common pool that can provide service to Type 2 customers does not change. Correspondingly, instead of the matrix ${{\tilde{E}}}^+_{N-R-k}$ we have the identity matrix of the suitable size.

Now, let us explain the expressions for the matrix $Q_{i,i+1}.$ We consider the most difficult here case $i=B_k-1,\,k=\overline{1,N-R-M}.$ Transitions from level i to level $i+1$ occur only due to the arrival of a Type 1 customer. Intensities of the corresponding transitions are given by the entries of the matrix $D_1.$ In the considered case, the arrival of a Type 1 customer leads to reaching the threshold $B_k.$ This implies that, in addition to $k-1$ servers from the common pool, which provide service to Type 1 customers, one more server starts service of a Type 1 customer. Respectively, the number of servers from the common pool that are available for Type 2 decreases by one. If all servers from the pool were busy, one of Type 2 customers is expelled from the service. Probabilities of the corresponding transitions of the number of Type 2 customers are given by the entries of the matrix ${{\tilde{E}}}^-_{N-R-k+1}.$ The proof of the formula for the matrix $Q_{i,i+1}$ in the considered case is finished. Other cases are simpler and are proven analogously. Theorem 1 is proven.

Theorem 2

The considered queueing model is stable (i.e., the Markov chain describing its behavior is ergodic) if and only if the inequality

$$\begin{aligned} \lambda _1<(N-M)\mu _1 \end{aligned}$$

holds true.

The intuitive proof is the following. One can see that System 2 is stable for any values of parameters because it has a finite state space. Let us consider System 1. The stability of a queueing system means its ability to reduce the number of customers faster, on average, than customers arrive in the case when the system is overloaded. It is easy to see that, if System 1 is overloaded, it behaves as a classical $MAP/M/N-M$ queueing system with $N-M$ servers, the ergodicity condition of which is defined by inequality (1). More formal proof can be easily done with the use of the corresponding results from the theory of Quasi-Birth-and-Death processes or M/G/1 type Markov chains, see, e.g., Dudin et al. (2020a), Neuts (1994, 2021).

Remark

Having the average arrival rate $\lambda _1$ and the service rate $\mu _1$ of Type 1 customers fixed, it is obvious that the total number N of servers has to be larger than $\frac{\lambda _1}{ \mu _1}$ while the number M of servers reserved for service of Type 2 customers must be less than $N- \frac{\lambda _1}{ \mu _1}.$ To make a more exact evaluation of the required number N of servers and admissible values of the numbers of reserved servers R and M for providing the desired level of service to both types of customers, it is necessary to compute the stationary distribution of the system states.

It is easy to see that the Markov chain $\xi _t$ belongs to the class of Quasi-Birth-and-Death processes with many boundary levels and level-independent transitions between the levels having the numbers larger than $N-R-M.$ Let us assume that ergodicity condition (1) is fulfilled. Then the stationary probabilities $\pi (i,r,\nu ,v)=\lim \limits _{t\rightarrow \infty } P\{i_t=i,r_t=r,\nu _t=\nu ,v_t=v\}$ exist. Let us enumerate these probabilities in accordance with the introduced lexicographical order of the states of the Markov chain $\xi _t$ and form the row vectors

$$\begin{aligned} \varvec{\pi }(i,r)=(\pi (i,r,0,0),\,\pi (i,r,0,1),\dots , \end{aligned}$$

$$\begin{aligned}&\pi (i,r,0,V),\pi (i,r,1,0),\pi (i,r,1,1),\dots ,\pi (i,r,W,V)), \\&\varvec{\pi }_i=\varvec{\pi }(i)=(\varvec{\pi }(i,0),\varvec{\pi }(i,1),\dots ,\varvec{\pi }(i,R_i)), \end{aligned}$$

where

$$\begin{aligned} R_i=\left\{ \begin{array}{ll} N-R,&{} \mathrm{if }\,\, i<B_1,\\ N-R-k,&{} \mathrm{if }\,\, B_k\le i<B_{k+1},\\ M,&{} \mathrm{if }\,\, i \ge B_{N-R-M}.\\ \end{array}\right. \end{aligned}$$

It is well-known fact that the stationary probabilities of Markov chain $\xi _t$ can be found as the unique solution to the system

$$\begin{aligned} \varvec{\pi }Q=\mathbf{0},\,\varvec{\pi }\mathbf{e}=1, \end{aligned}$$

where $\varvec{\pi }=(\varvec{\pi }_0,\varvec{\pi }_1,\varvec{\pi }_2,\dots ).$

To solve the infinite system of equations (2), the following numerically stable algorithm can be used.

Theorem 3

The vectors ${\varvec{\pi }}_i,\,i\ge 0,$ are calculated as

$$\begin{aligned} {\varvec{\pi }}_{i} =\varvec{\phi }_{i}\biggl (\sum \limits _{l=0}^{\infty } \varvec{\phi }_{l}\mathbf{e}\biggr )^{-1},i\ge 0, \end{aligned}$$

where the vectors $\varvec{\phi }_{i},\; i \ge 0,$ are defined by the recursive formulas

$$\begin{aligned}&{\varvec{\phi }}_{0} (Q_{0,0}+Q_{0,1}G_0)=\mathbf{0}, {\varvec{\phi }}_{0}{} \mathbf{e}=1, \\&\varvec{\phi }_{i} =-\varvec{\phi }_{i-1}Q_{i-1,i} {(Q_{i,i}+Q_{i,i+1}G_i)}^{-1}, i=\overline{1,B_{N-R-M}-1},\; \\&\varvec{\phi }_{B_{N-R-M}} = \\&-\varvec{\phi }_{B_{N-R-M}-1}Q_{B_{N-R-M}-1,B_{N-R-M}} {(Q^0+Q^+G)}^{-1}, \\&\varvec{\phi }_{i} =-\varvec{\phi }_{i-1}Q^+ {(Q^0+Q^+G)}^{-1},\,i>B_{N-R-M}. \end{aligned}$$

Here, matrices $G_{i}$ are calculated using the following backward recursion

$$\begin{aligned}&G_{B_{N-R-M}} =G, \\&G_{B_{N-R-M}-1} =-(Q^0+ \\&Q^+G_{B_{N-R-M}})^{-1} Q_{B_{N-R-M},B_{N-R-M}-1}, \\&G_{i} =-(Q_{i+1,i+1}+ Q_{i+1,i+2}G_{i+1})^{-1} Q_{i+1,i}, \\&i=B_{N-R-M}-2,B_{N-R-M}-3,\ldots ,0, \end{aligned}$$

where the matrix G is the minimal nonnegative solution to the equation

$$\begin{aligned} Q^+G^2+Q^0G+Q^-=O. \end{aligned}$$

This algorithm is the improved version of the algorithm presented in Dudin et al. (2013). The improvement consists of using the recursion for vectors $\varvec{\phi }_{i},\; i \ge 0,$ instead of the recursion for matrices $\Phi _{i},\; i \ge 0,$ of the corresponding dimension in Dudin et al. (2013). This improvement is very essential from the point of view of the reduction of the required for numerical realization computer memory and runtime.

4 Performance measures

Having calculated stationary probabilities, for the qualitative study of the model, we look at the following key system performance measures.

The average number L of customers in both systems can be found as

$$\begin{aligned} L=\sum \limits _{i=0}^\infty \sum \limits _{r=0}^{R_i}(i+r)\varvec{\pi }(i,r)\mathbf{e}. \end{aligned}$$

The average number $L_1$ of customers in System 1 can be found as

$$\begin{aligned} L_1=\sum \limits _{i=1}^\infty i\varvec{\pi }_i\mathbf{e}. \end{aligned}$$

The average number $L_2$ of customers in System 2 can be found as

$$\begin{aligned} L_2=\sum \limits _{i=0}^\infty \sum \limits _{r=1}^{R_i}r\varvec{\pi }(i,r)\mathbf{e}. \end{aligned}$$

The average number $N_{serv-1}$ of servers in System 1 can be found as

$$\begin{aligned} N_{serv-1}=\sum \limits _{i=0}^\infty (N-R_i)\varvec{\pi }_i\mathbf{e}. \end{aligned}$$

The average number $N_{serv-2}$ of servers in System 2 can be found as

$$\begin{aligned} N_{serv-2}=\sum \limits _{i=0}^\infty R_i\varvec{\pi }_i\mathbf{e}=N-N_{serv-1}. \end{aligned}$$

The average number $N_{serv-1}$ of busy servers in System 1 can be found as

$$\begin{aligned} N_{busy-1}=\sum \limits _{i=0}^\infty \mathrm{min}\{i,N-R_i\}\varvec{\pi }_i\mathbf{e}. \end{aligned}$$

The average number $N_{buffer-1}$ of customers in the buffer of System 1 can be found as

$$\begin{aligned} N_{buffer-1}=\sum \limits _{i=R}^\infty \mathrm{max}\{i-(N-R_i),0\}\varvec{\pi }_i\mathbf{e}=L_1-N_{busy-1}. \end{aligned}$$

The average intensity $\lambda _{out-1}$ of the output flow of successfully serviced customers from System 1 is defined as

$$\begin{aligned} \lambda _{out-1}=\mu _1N_{busy-1}=\lambda _1. \end{aligned}$$

The average intensity $\lambda _{out-2}$ of the output flow of successfully serviced customers from System 2 is defined as

$$\begin{aligned} \lambda _{out-2}=\mu _2L_2. \end{aligned}$$

The probability $P_{ent}$ of a customer loss in System 2 upon arrival is computed as

$$\begin{aligned} P_{ent}=\frac{1}{\lambda _2}\sum \limits _{i=0}^\infty \varvec{\pi }(i,R_i)(I_{W}\otimes H_1)\mathbf{e}. \end{aligned}$$

The loss probability $P_{force}$ of a customer in System 2 due to the forced termination of the service is computed as

$$\begin{aligned} P_{force}=\frac{1}{\lambda _2}\sum \limits _{k=1}^{N-R-M}\varvec{\pi }(B_k-1,N-R-k+1)( D_1\otimes I_V)\mathbf{e}. \end{aligned}$$

The probability $P_{loss}$ of an arbitrary customer loss in System 2 is computed as

$$\begin{aligned} P_{loss}=P_{ent}+P_{force}=1-\frac{\lambda _{out-2}}{\lambda _2}. \end{aligned}$$

5 Numerical example

Let the arrival flow of Type 1 customers be defined by the matrices $D_0$ and $D_1$ of the form

$$\begin{aligned} D_0=\left( \begin{array}{cc} -21000 &{} 60 \\ 3&{}-600 \\ \end{array} \right) ,\, D_1=\left( \begin{array}{cc} 20880 &{} 60 \\ 3&{}594 \\ \end{array} \right) . \end{aligned}$$

The average arrival rate is $\lambda _1=1565.71$ customers per second. The coefficient of correlation of successive inter-arrival times is equal to $c_{cor}^{(1)}=0.368483,$ and the coefficient of variation is equal to $c_{var}^{(1)}=3.98.$

Let the arrival flow of Type 2 customers be defined by the matrices $H_0$ and $H_1$ of the form

$$\begin{aligned} H_0=\left( \begin{array}{cc} -60000&{}60 \\ 3&{}-600 \\ \end{array} \right) ,\, H_1=\left( \begin{array}{cc} 59880 &{} 60 \\ 3&{}594 \\ \end{array} \right) . \end{aligned}$$

The average arrival rate is $\lambda _2=3422.86$ customers per second. The coefficient of correlation is equal to $c_{cor}^{(2)}=0.4439,$ and the coefficient of variation is equal to $c_{var}^{(2)}=9.87.$

Customers correspond to requests for the transmission of information. The average size of Type 1 customers is 6.4 kilobytes (KB). We assume that each server corresponds to a channel having a throughput of 10 megabits per second (Mbps). Thus, the average service intensity $\mu _1$ of Type 1 customers is $\mu _1=\frac{10000000 \mathrm{bps}}{6400*8 \mathrm{bits}}=195.313$ customers per second. The average size of Type 2 customers is 0.8 KB. Thus, the average service intensity $\mu _2$ of type 2 customers is $\mu _2=\frac{10000000 \mathrm{bps}}{800*8 \mathrm{bits}}=1562.5$ customers per second.

Since the considered model has a lot of control parameters ($N,\,R,\,M,\, B_k,$ $\,k=\overline{1,N-R-M})$ and it is impossible to graphically illustrate the dependence of the main performance measures on all these parameters, we have to somehow fix all control parameters, except two of them, that we will vary. To this end, first of all let us assume that the thresholds $B_1,B_2,\dots ,B_{N-R-M}$ are defined as $B_k=kB,\,k=\overline{1,N-R-M},$ where B is a fixed integer parameter.

We present below two sets of the numerical results. In the first set, we assume that the total number N of servers in the queueing system is equal to 50. The parameter R defining the number of servers reserved for service of only Type 1 customers is fixed by $R=1.$ Therefore, we can vary only the values of the parameters M and B and show their impact on the key performance measures of the system and dependence of the introduced cost criterion on these parameters. The corresponding dependencies are given by Figs. 2, 3, 4, 5, 6 and 7.

After that, we fix the optimal value $B=6$ of the parameter B and present the results from the second set. In this set, we illustrate the dependencies of the same performance measures on the parameters N and M. They are given by Figs. 9, 10, 11, 12 and 13 below.

Let us describe the first set of the results. We vary the parameter B defining the step of increasing of the thresholds $B_k$ over the interval [2, 20]. The parameter M defining reservation of servers for Type 2 customers in the model can take values from the interval $[0,N-R).$ However, based on the inequality $M< N- \frac{\lambda _1}{ \mu _1},$ which was derived from the ergodicity condition (1), it is easy to calculate that in the considered example the parameter M cannot be larger than 41. Thus, we vary the parameter M over the interval [0, 41] with step 1.

Figure 2 illustrates the dependence of the average number L of customers in both systems on the threshold M and the parameter B defining the values of the thresholds $B_k,\,k=\overline{1,N-R-M}$.

Fig. 2

Dependence of the average number L of customers in both systems on the parameters M and B

As it is seen from Fig. 2, the average number of customers in both systems significantly increases with the increase of the parameters M and B. This increase is mainly caused by the increase of the number $N_{buffer-1}$ of Type 1 customers in the buffer. Note, that in the considered example the value $N_{busy-1}$ does not depend on the parameters M and B and is equal to 8.016457. This can be explained by the fact that there are no losses of Type 1 customers and all they obtain service. Thus, the mean value of the number $N_{busy-1}$ of busy servers is always equal to $\lambda /\mu _1.$ But, the distribution of this number depends on the parameters M and B.

Figure 3 illustrates the dependence of the loss probability $P_{loss}$ of a Type 2 customer on the parameters M and B.

Fig. 3

Dependence of the loss probability $P_{loss}$ of a Type 2 customer on the parameters M and B

One can see that the loss probability $P_{loss}$ sharply increases with the decrease of the parameters M and B. This is clear because the decrease of these parameters leads to worse conditions for Type 2 customers. When B decreases, servers from the common pool are more frequently occupied by Type 1 customers. When M (the number of servers reserved exclusively for service of Type 2 customers) decreases, more Type 2 customers are rejected upon arrival. Also, more Type 2 customers are forced to terminate service due to the capture of servers from a common pool by Type 1 servers.

Figure 4 illustrates the dependence of the loss probability $P_{force}$ of a Type 2 customer due to the forced service termination on the parameters M and B. The dependence of the probability $P_{ent}$ of a customer loss upon arrival to System 2 on the parameters B and M is presented in Fig. 5. Because $P_{loss}=P_{ent}+P_{force},$ the sharp increase of these probabilities with the decrease of M and B was obviously anticipated.

Fig. 4

Dependence of the loss probability $P_{force}$ on the parameters M and B

Fig. 5

Dependence of the probability $P_{ent}$ of a Type 2 customer loss upon arrival on the parameters M and B

Let the quality of the system operation be evaluated by the following economical criterion:

$$\begin{aligned} E(B,M)=a\lambda _{out-1}+b \lambda _{out-2}-c\lambda _2 P_{force}-d\lambda _2 P_{ent}. \end{aligned}$$

We aim to find the set of parameters (B, M) providing the optimum (maximum) value of the criterion under fulfillment of the constraint

$$\begin{aligned} V_{wait}<V \end{aligned}$$

where $V_{wait}$ is the mean waiting time of Type 1 customers and V is an arbitrarily fixed in advance number. The mean waiting time can be found according to Little’s formula as

$$\begin{aligned} V_{wait}=\frac{N_{buffer-1}}{\lambda _1}. \end{aligned}$$

Here, the parameter a defines the average profit earned by successful service of one Type 1 customer; the parameter b defines the average profit earned by successful service of one Type 2 customer; the parameter c defines the charge paid by the system due to the interruption of the service of a Type 2 customer; the parameter d defines the charge paid by the system due to the loss of a Type 2 customer at the entrance to the system.

In this example, we fix the cost parameters as follows: $a= 0.05,\,b = 0.03,\, c = 50,\, d = 0.2.$ The parameter V is fixed as $V=0.05.$

The criterion E(B, M) defines the average profit obtained by the system per unit of time. We aim to find the values of M and B that maximize the profit of the system under the constraint that the average waiting time of an arbitrary Type 1 customer will not exceed 0.05 seconds.

Figure 6 illustrates the dependence of the average waiting time of a Type 1 customer on the parameters M and B.

Fig. 6

Dependence of the average waiting time of Type 1 customer on the parameters M and B

The dependence of the criterion E(B, M) on the parameters B and M is presented in Fig. 7.

Fig. 7

Dependence of the criterion E(B, M) on the parameters M and B

The optimal value of the cost criterion E(B, M) is equal to 108.657 and is achieved for $B=6$ and $M=31.$ Computations were implemented using Wolfram Mathematica on notebook Lenovo with CPU Intel(R) Core(TM) i7-1165G7 2.80GHz and 16 GB RAM. Running time for computation of the value E(B, M) of the cost criterion for one point (B, M) was equal in average to 15 seconds. It is worth noting that, because computation time was acceptable for preparation of the examples, no optimization of the code was made. Computation time can be essentially reduced via such an optimization and the use of more powerful notebook or PC.

Now, let us describe the second set of the numerical results. Let us fix $B=6$ and vary the total number of servers N. All other parameters are assumed to be the same as in the previous set of examples. Based on the ergodicity condition (1), we conclude that the minimal number of servers N should be greater than $\frac{\lambda _1}{\mu _1}$. Thus, in the considered example the minimal admissible number of servers is 9 and we vary the parameter N over the interval [9, 70] with step 1. The parameter M varies over the interval $[0, N-8).$

Figure 8 illustrates the dependence of the average number L of customers in both systems on the total number of servers N and the number M of the servers reserved for Type 2 customers.

Fig. 8

Dependence of the number L of customers in both systems on the parameters N and M

Figures 9, 10 and 11 illustrate the dependence of the loss probabilities $P_{loss},$ $P_{force}$ and $P_{ent}$ on the parameters N and M. These figures show that in this example the main reason for Type 2 customers’ loss is their rejection at the entrance to the system. It is worth noting the non-monotonic behavior of the loss probability $P_{force}$ for a small number M of reserved servers. Firstly, with the increase of N,  $P_{force}$ increases because a larger number N of servers gives higher chances to enter the service for Type 2 customers and, correspondingly, the higher rate of expelling these customers from service due to Type 1 customers arrival. After reaching the maximum, the probability $P_{force}$ decreases with a further increase of N because under large N Type 1 customers succeed to obtain service practically without interruption of Type 2 customers service. With the increase of M,  the probability $P_{force}$ quickly decreases because the majority of Type 2 customers succeed to obtain service in the reserved servers where service cannot be forcedly terminated.

Fig. 9

Dependence of the loss probability $P_{loss}$ of a Type 2 customer on the parameters N and M

Fig. 10

Dependence of the loss probability $P_{force}$ on the parameters N and M

Fig. 11

Dependence of the probability $P_{ent}$ of loss a customer upon arrival to System 2 on the parameters N and M

Figure 12 illustrates the dependence of the average waiting time of Type 1 customers on the parameters N and M. The obvious observation follows from this figure. $V_{wait}$ sharply increases with the decrease of the total number N of servers and the increase of the number M of servers reserved for service only Type 2 customers.

Fig. 12

Dependence of the average waiting time of a customer in System 1 on the parameters N and M

Let us slightly change the economical criterion. We assume now that the quality of the model operation is evaluated by the cost criterion

$$\begin{aligned} E(N,M)=a\lambda _{out-1}+b \lambda _{out-2}-c\lambda _2 P_{force}-d\lambda _2 P_{ent}-fN. \end{aligned}$$

The meaning of the coefficients $a,\,b,\,c,$ and d is the same as in the previous example. The coefficient f is the cost of maintenance of one server per unit of time.

We aim to find the maximum value of the criterion E(N, M) under constraint (3).

Let in this numerical example the cost coefficients are chosen as follows: $a= 0.02,\,b = 0.01,\, c = 1,\, d = 0.01,\,f=0.5.$ The parameter V is fixed as $V=0.05.$

The dependence of the criterion E(N, M) on the parameters N and M is presented in Fig. 13.

Fig. 13

Dependence of the criterion E(N, M) on the parameters N and M

The optimal value of the cost criterion E(N, M) is equal to 35.7289 and achieved for $N=52$ and $M=33.$

6 Conclusions

A novel priority scheme suitable, in particular, for scheduling PUs and SUs in cognitive radio systems under realistic assumptions about the arrival process is investigated. This scheme is more friendly to SUs than the majority of other schemes considered in the literature, in particular, a preemptive priority of PUs. Possibility of PUs waiting in a queue and non-instantaneous termination of service of SUs when a PU arrives, reservation of servers for exclusive service of PUs and SUs are allowed. Under any fixed values of the parameters defining the arrival and service processes and any fixed number of servers and thresholds defining admission control, the stationary distribution of the system states is computed. Dependencies of performance measures of the system on parameters of admission control strategy are numerically shown. The possibility of using the obtained results for solving optimization problems is demonstrated.

As the possible directions for future research, the following ones deserve to be mentioned: (1) analysis of systems with several types of SU. This direction is important because in many real systems (see, e.g., Kalil et al. (2017), El-Toukhy and Arslan (2019), Goel and Kulshrestha (2021)) SUs are divided into several subclasses, e.g., real-time and non-real-time SUs, new SUs and SUs, service of which is interrupted, etc.; (2) analysis of systems with PU or (and) SU retrials (see, e.g., Sun et al. (2014b), Jain et al. (2022), Phung-Duc et al. (2022)); (3) analysis of systems operating in a random environment; (4) analysis of systems with priorities upgrades; (5) analysis of systems with the phase-type distribution of service times; (6) analysis of systems with group service of SUs, (see, e.g., Brugno et al. (2018), D’Arienzo et al. (2020)), etc.

It is also planned to discuss the possibilities of application of the obtained results in the context of the problems considered in Zhang et al. (2019), Li et al. (2018).