Stability in distribution for uncertain delay differential equations based on new Lipschitz condition

Abstract

Stability in distribution for uncertain delay differential equations based on the strong Lipschitz condition only involving the current state has been successfully investigated. In reality, the uncertain delay differential equation is not only relate to the current state, but also relate to the past state, so it is very hard to obtain the strong Lipschitz condition. In this paper, the new Lipschitz condition concerning the current state and the past state is provided, if the uncertain delay differential equation satisfies the strong Lipschitz condition, it must satisfy the new Lipschitz condition, conversely, it may not be established. By means of the new Lipschitz condition, a sufficient theorem for the uncertain delay differential equation being stable in distribution is proved. Meanwhile, a class of uncertain delay differential equation is certified to be stable in distribution without any limited condition. Besides, the effectiveness of the above sufficient theorem is verified by two numerical examples.

1 Introduction

Delay differential equations have been successfully applied in the feedback mechanism systems, such as the SIS epidemic system (Liu 2015a), the competitive diffusive system (Lin 2018), and the hepatitis B virus infection system (Guo and Cai 2012). The feedback mechanism systems are affected by the “noise”, such as the biologically motivated signal transmission system (Xu et al. 2009), the optimal control system (Ma and Liu 2017), and the financial system (Shen et al. 2014). If the “noise” are modelled by Wiener processes, stochastic delay differential equations (Hereinafter called SDDEs for short) involving the Wiener processes are employed to model the feedback mechanism systems, where the Wiener processes stand for a series of random variables under the framework of probability theory. A prerequisite of probability theory is that the distribution is close enough to the real frequency. In some cases, this prerequisite can not be satisfied, for example, Liu (2015b) pointed out evolutions of some undetermined phenomena do not behave like randomness, Tang and Yang (2021) presented that stochastic chemical reaction involving the Wiener process is unsuitable, Lio and Liu (2021) introduced that stochastic COVID-19 spread model involving the Wiener process is unreasonable.

In addition to probability theory, Liu processes under the framework of uncertainty theory (Liu 2015b) were applied to describe the “noise”. Liu processes indexed by a series of uncertain variables were designed by Liu (2008). By means of the Liu process, uncertain differential equations (Hereinafter called UDEs for short) were suggested by Liu (2008). After that, Liu (2009), Sheng and Gao (2016), and Sheng and Wang (2014) investigated the stability of UDEs, Yao and Chen (2013), Yang and Shen (2015), and Yang and Ralescu (2015) used different numerical methods to obtain the numerical solutions of UDEs. Moreover, the UDEs have been extensively used in the spread of COVID-19 (Lio and Liu 2021), the pharmacokinetics (Liu and Yang 2021), the finance (Zhu 2014), and the insurance (Liu and Yang 2020). Besides, the different styles of UDEs were explored, including the UDEs with jump (Yao 2012), the multi-dimensional UDEs (Yao 2014), the high-order UDEs (Yao 2016), the UDEs with a delay time (Hereinafter called UDDEs for short) (Barbacioru 2010), the UDEs with partial information (Liu and Zhang 2020), and the UDEs with multifactor (Li et al. 2015).

The stability of systems plays a significant role in modelling the real world. In other words, if the system is not stable, even though the difference between the given initial value and the precise initial value is small, the difference between the results becomes larger. At present, many styles of stability for UDDEs were investigated containing the stability in measure (Wang and Ning 2017), the almost sure stability (Wang and Ning 2019), and the stability in distribution (Jia and Sheng 2019). The above stability in distribution for UDDEs was studied based on the strong Lipschitz condition only concerning the current state, which was difficult to be obtained due to the fact that the UDDEs include both the current and the past states. Therefore, the new Lipscitz conditions involving the current and the past states are proposed to solve this issue in this paper. In fact, the new Lipschitz condition is weaker than the strong Lipschitz condition. In other words, if the UDDEs satisfy the strong Lipschitz condition, it must satisfy the new Lipschitz condition, conversely, it may not be established. Based on the new Lipschitz condition, a sufficient theorem for UDDEs being stable in distribution is verified. Meanwhile, a class of UDDEs is proved to be stable in distribution without any limited condition. Moreover, two numerical examples are provided to verify the effectiveness of the above sufficient theorem. If we can not obtain the new Lipschitz condition, we can not judge the stability in distribution for UDDEs. In the future, we can consider the stability in p-th moment based on the new Lipschitz condition and the p-th moment exponential stability for UDDEs.

The rest of this paper is structured as follows. Section 2 introduces the related work. Section 3 gives an overview of UDDEs. Section 4 presents a sufficient theroem of stability in distribution based on new Lipschitz condition for UDDEs. Section 5 proves a class of UDDEs being stable in distribution without any limited condition. Section 6 provides two numerical examples to verify the effectiveness of the above sufficient theorem. Section 7 discusses some results of this article.

2 Related work

Uncertainty theory was founded by Liu (2015b), which has been investigated by many scholars. Uncertain process in uncertainty theory stands for a sequence of uncertain variables indexed by time. Liu process as a class of uncertain process satisfies the conditions that almost all sample paths are Lipschitz continuous, and has stationary and independent increments, every increment is a normal uncertain variable with expected value 0 and variance $t^2$.

Differential equations involving the Liu process were called uncertain differential equations(UDEs) (2008), the existence and uniqueness theorem of solution for UDEs was proved by Chen and Liu (2010) and Gao (2012). Later, the concept of stability in measure was provided by Liu (2009), and the corresponding theorems of stability in measure was verified by Yao et al. (2013). Moreover, the stability in mean (Yao et al. 2015), the stability in p-th moment (Sheng and Wang 2014), the stability in inverse distribution (Yang et al. 2017a), the almost sure stability (Liu et al. 2014), and the exponential stability (Sheng and Gao 2016) of UDEs were successfully explored. In order to obtain the numerical solution of UDEs, many numerical methods are proposed including the 99-method (Yao and Chen 2013), the Runge–Kutta method (Yang and Shen 2015; Yang and D 2015), the Milne method (Gao 2016), and the Hamming method (Zhang et al. 2017).

As a special UDEs, the UDEs with jumps have been investigated by many scholars, for example, the existence and uniqueness theorem of solutions was considered by Yao (2015), the stability in measure (Yao 2015), the almost sure stability (Ji and Ke 2016), the stability in mean (Gao 2019), the stability in p-th moment (Ma et al. 2017b), and the p-th moment exponential stability (Liu et al. 2020) were presented. Except for the above UDEs with jumps, the existence and uniqueness theorem (Ji and Zhou 2015), the stability in measure (Su et al. 2016), the stability in p-th moment (Shi et al. 2020), the stability in mean (Sheng and Shi 2019) for multi-dimensional UDEs were successfully explored. Besides, the stability analysis of nonlinear uncertain fractional differential equations with Caputo derivative was presented by Lu et al. (2021), and the stability in mean for uncertain delay differential equations based on new Lipschitz conditions was investigated by Gao and Jia (2021).

In some special cases, the systems were affected by many factors, multifactor uncertain differential equations were proposed by Li et al. (2015), the almost sure stability (Sheng et al. 2017), the stability in mean (Zhang et al. 2016), the stability in measure (Zhang et al. 2016), and the stability in distribution (Ma et al. 2017a) for multifactor uncertain differential equations were investigated. Additionally, many scholars studied the stability analysis for uncertain spring vibration equations (Jia et al. 2021), uncertain wave equations (Gao et al. 2019), and uncertain heat equations (Liu and Zhang 2020).

3 Preliminaries

For the purpose of modelling the dynamics of uncertain phenomena, Liu (2009) designed a Liu process to cope with the environmental noise perturbations.

Definition 1

Liu (2015b) An uncertain process $C_{t}$ is said to be a Liu process if:

• $C_{0}=0$ and almost all sample paths are Lipschitz continuous.

• $C_{t}$ has stationary and independent increments.

• Every increment $C_{s+t}-C_{s}$ is a normal uncertain variable with expected value 0 and variance $t^2$, whose uncertain distribution is

  $$\begin{aligned} \Lambda (x)=\left( 1+\exp \left( \frac{-\pi x}{\sqrt{3}t}\right) \right) , x\in \textit{R}. \end{aligned}$$

Based on the Liu process, Barbacioru (2010) defined the following UDDEs.

Definition 2

Barbacioru (2010) Assume that $f_{1}$ and $f_{2}$ are two real-valued functions, $C_{t}$ stands for the Liu process, then the following equation

$$\begin{aligned} \mathrm{d}U_{t}=f_{1}(t,U_{t},U_{t-\tau })\mathrm{d}t +f_{2}(t,U_{t},U_{t-\tau })\mathrm{d}C_{t} \end{aligned}$$

(1)

is termed as an UDDE, where $C_{t}$ and the positive number $\tau$ stand for the Liu process and a time delay, respectively.

Moreover, Yao and Chen (2013) proved the following existence and uniqueness theorem.

Theorem 1

Yao and Chen (2013) The UDDE (1) with initial states has a unique solution if the coefficients

$$\begin{aligned} |f_{1}(t,u,v)|+|f_{2}(t,u,v)|\le L(1+|u|+|v|), \quad \forall u,v\in \Re , t\ge 0 \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&|f_{1}(t,u_{1},v)-f_{1}(t,u_{2},v)|+|f_{2}(t,u_{1},v)-f_{2}(t,u_{2},v)|\\&\quad \le L|u_{1}-u_{2}|, \quad \forall u_{1}, u_{2}, v\in \Re , t\ge 0 \end{aligned} \end{aligned}$$

for some positive constant L.

Theorem 2

Yao and Chen (2013) Let $\mathcal{M}$ denotes the uncertain measure defined in Liu’s book Liu (2015b), $U_{t}$ be the solution of the uncertain differential equation

$$\begin{aligned} \mathrm{d}U_{t}=f_{1}(t,U_{t})\mathrm{d}t+f_{2}(t,U_{t})\mathrm{d}C_{t}, \end{aligned}$$

(2)

and $U_{t}^{\alpha }$ stands for the $\alpha$-path of $U_{t}$, $0<\alpha <1$, it is obtained by solving the following equation

$$\begin{aligned} \mathrm{d}U_{t}^{\alpha }=f_{1}(t,U_{t}^{\alpha })\mathrm{d}t+|f_{2}(t,U_{t}^{\alpha })|\Lambda ^{-1}(\alpha )\mathrm{d}t, \end{aligned}$$

(3)

where $\Lambda ^{-1}(\alpha )$ be the inverse distribution function of normal uncertain variables, i.e.,

$$\begin{aligned} \Lambda ^{-1}(\alpha )=\frac{\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }, \end{aligned}$$

then

$$\begin{aligned} \mathcal{M}\{U_{t}\le U_{t}^{\alpha },\forall t\}=\alpha , \mathcal{M}\{U_{t}>U_{t}^{\alpha }, \forall t\}=1-\alpha . \end{aligned}$$

(4)

Besides, Wang and Ning (2017) defined the stability in measure, the stability in mean, and the stability in p-th moment, and gave the corresponding sufficient theorem based on the strong Lipschitz condition, Jia and Sheng (2019) introduced the definition of the stability in distribution, and provided a sufficient theorem based on the strong Lipschitz condition.

Definition 3

Wang and Ning (2017) The UDDE (1) is said to be stable in measure if for any two solutions $U_{t}$ and $V_{t}$ with different initial states, we have

$$\begin{aligned} \lim \limits _{\sup \limits _{s\in [-\tau ,0]}|U_{s}-V_{s}|\rightarrow 0}\mathcal{M}\{|U_{t}-V_{t}|>\epsilon \}=0,\quad \forall t>0 \end{aligned}$$

(5)

for any given number $\epsilon >0$.

Theorem 3

Wang and Ning (2017) Assume the UDDE (1) has a unique solution for each given initial state. Then it is stable in measure if the coefficients $f_{1}(t,u,v)$ and $f_{2}(t,u,v)$ satisfy the strong Lipschitz condition

$$\begin{aligned} \begin{aligned}&|f_{1}(t,u_{1},v)-f_{1}(t,u_{2},v)|\vee |f_{2}(t,u_{1},v)-f_{2}(t,u_{2},v)|\\&\quad \le L_{t}|u_{1}-u_{2}|, \quad \forall u_{1}, u_{2}, v\in \Re , t>0 \end{aligned} \end{aligned}$$

where $L_{t}$ is a bounded function satisfying

$$\begin{aligned} \int _{0}^{+\infty }L_{t}\mathrm{d}t<+\infty . \end{aligned}$$

Definition 4

Wang and Ning (2017) The UDDE (1) is said to be stable in mean if for any two solutions $U_{t}$ and $V_{t}$ with different initial states, we have

$$\begin{aligned} \lim \limits _{\sup \limits _{s\in [-\tau ,0]}|U_{s}-V_{s}|\rightarrow 0}\mathrm{E}[|U_{t}-V_{t}|]=0, \quad \forall t>0. \end{aligned}$$

(6)

Theorem 4

Wang and Ning (2017) Assume the UDDE (1) has a unique solution for each given initial state. Then it is stable in mean if the coefficients $f_{1}(t,u,v)$ and $f_{2}(t,u,v)$ satisfy the strong Lipschitz condition

$$\begin{aligned} \begin{aligned}&|f_{1}(t,u_{1},v)-f_{1}(t,u_{2},v)|\le F_{t}|u_{1}-u_{2}|,\\&|f_{2}(t,u_{1},v)-f_{2}(t,u_{2},v)|\le G_{t}|u_{1}-u_{2}|,\\&\quad \forall u_{1}, u_{2}, v\in \Re , t>0, \end{aligned} \end{aligned}$$

where $F_{t}$ and $G_{t}$ are two bounded functions satisfying

$$\begin{aligned} \int _{0}^{+\infty }F_{t}\mathrm{d}t<+\infty , \int _{0}^{+\infty }G_{t}\mathrm{d}t<\frac{\pi }{\sqrt{3}}. \end{aligned}$$

Definition 5

Wang and Ning (2017) The UDDE (1) is said to be stable in p-th moment ($0<p<+\infty$) if for any two solutions $U_{t}$ and $V_{t}$ with different initial states, we have

$$\begin{aligned} \lim \limits _{\sup \limits _{s\in [-\tau ,0]}|U_{s}-V_{s}|\rightarrow 0}\mathrm{E}[(|U_{t}-V_{t}|)^{p}]=0, \quad \forall t>0. \end{aligned}$$

(7)

Theorem 5

Wang and Ning (2017) Assume the UDDE (1) has a unique solution for each given initial state. Then it is stable in p-th moments ($0<p<+\infty$) if the coefficients $f_{1}(t,u,v)$ and $f_{2}(t,u,v)$ satisfy the strong Lipschitz condition

$$\begin{aligned} \begin{aligned}&|f_{1}(t,u_{1},v)-f_{1}(t,u_{2},v)|\le F_{t}|u_{1}-u_{2}|,\\&|f_{2}(t,u_{1},v)-f_{2}(t,u_{2},v)|\le G_{t}|u_{1}-u_{2}|,\\&\quad \forall u_{1}, u_{2}, v\in \Re , t>0 \end{aligned} \end{aligned}$$

where $F_{t}$ and $G_{t}$ are two bounded functions satisfying

$$\begin{aligned} \int _{0}^{+\infty }F_{t}\mathrm{d}t<+\infty , \int _{0}^{+\infty }G_{t}\mathrm{d}t<\frac{\pi }{\sqrt{3}p}. \end{aligned}$$

Theorem 6

Wang and Ning (2017) For any two real numbers $p_{1}$ and $p_{2}$ ($0<p_{1}<p_{2}<+\infty$), if the UDDE (1) is stable in $p_{2}$-th moment, then it is stable in $p_{1}$-th moment.

Theorem 7

Wang and Ning (2017) If the UDDE (1) is stable in mean, then it is stable in measure.

Theorem 8

Wang and Ning (2017) If the UDDE (1) is stable in p-th moment ($0<p<+\infty$), then it is stable in measure.

Definition 6

Wang and Ning (2019) Suppose that $U_{t}$ and $V_{t}$ are two solutions of the UDDE (1) with different initial states $u_{j}$ and $v_{j}$ for any $j\in [-\tau ,0]$, respectively. Uncertain delay differential equation is said to be stable almost surely if

$$\begin{aligned} \mathcal{M}\left\{ \gamma \in \Gamma \left| \right. \lim \limits _{\sup \limits _{j\in [-\tau ,0]}|u_{j}-v_{j}|\rightarrow 0}|U_{t}(\gamma )-V_{t}(\gamma )|=0\right\} =1. \end{aligned}$$

Theorem 9

Wang and Ning (2019) Suppose that the UDDE (1) has a unique solution for each given initial state, then the UDDE (1) is stable almost surely if the coefficients $f_{1}(t,u,v)$ and $f_{2}(t,u,v)$ satisfy

$$\begin{aligned} \begin{aligned}&|f_{1}(t,u_{1},v)-f_{1}(t,u_{2},v)|+|f_{2}(t,u_{1},v)-f_{2}(t,u_{2},v)|\\&\quad \le L_{t}|u_{1}-u_{2}|, \quad \forall u_{1}, u_{2}, v\in \Re , t\ge 0, \end{aligned} \end{aligned}$$

where $L_{t}\ge 0$ and

$$\begin{aligned} \int _{0}^{+\infty }L_{t}\mathrm{d}t<+\infty . \end{aligned}$$

Definition 7

Jia and Sheng (2019) Assume that $U_{t}$ and $V_{t}$ are the solutions of the UDDE (1) for different prescribed initial states $U_{s}$ and $V_{s}$ ($s\in [-\tau , 0]$), respectively. If the following condition holds,

$$\begin{aligned} \lim \limits _{\sup \limits _{s\in [-\tau ,0]}|U_{s}-V_{s}|\rightarrow 0}|\Theta _{t}(x)-\Psi _{t}(x)|=0, \quad \forall t>0, \end{aligned}$$

(8)

where $\Theta _{t}(\cdot )$ and $\Psi _{t}(\cdot )$ stand for the distribution functions of $U_{t}$ and $V_{t}$, respectively, $\forall x\in \Re$, then the UDDE (1) is stable in distribution.

Theorem 10

Jia and Sheng (2019) Assume the coefficients of the UDDE (1) with a unique solution for each prescribed initial state satisfy the strong Lipschitz condition

$$\begin{aligned} \begin{aligned}&|f_{1}(t,u_{1},v)-f_{1}(t,u_{2},v)|+|f_{2}(t,u_{1},v)-f_{2}(t,u_{2},v)|\\&\quad \le H_{t}|u_{1}-u_{2}|, \quad \forall u_{1}, u_{2}, v\in \Re , t>0 \end{aligned} \end{aligned}$$

where $H_{t}$ is a positive function satisfying

$$\begin{aligned} \int _{0}^{+\infty }H_{t}\mathrm{d}t<+\infty , \end{aligned}$$

then the UDDE (1) is stable in distribution.

4 A sufficient theorem

In this section, a sufficient theorem of stability in distribution for UDDEs based on new Lipschitz condition is explored. Firstly, we introduce two important theorems as below, which play a significant role in proving the sufficient theorem.

Theorem 11

Yang et al. (2017b) Let $\eta , \eta _{1}, \eta _{2}, \dots$ be a series of uncertain variables, their corresponding regular uncertainty distributions be $\Phi , \Phi _{1}, \Phi _{2}, \dots ,$ respectively. Then $\{\eta _{n}\}$ converges in inverse distribution to $\eta$ if and only if it converges in distribution to $\eta$.

Theorem 12

Gronwall (1919) Set I denotes $[c_{1},+\infty )$, $[c_{1},c_{2}]$ or $[c_{1},c_{2})$ with $c_{1}<c_{2}$. Let $\varrho$ and $\sigma$ defined on I are two real-valued non-negative continuous functions, $\rho$ is integrable on every closed and bounded subinterval of I. If the following inequality

$$\begin{aligned} \sigma (s)\le \rho (s)+\int _{c}^{s}\varrho (u)\sigma (u)\mathrm{d}u, \quad \forall s\in I \end{aligned}$$

holds and $\rho$ is non-decreasing, then we have

$$\begin{aligned} \sigma (s)\le \rho (s)\exp \left( \int _{c}^{s}\varrho (u)\mathrm{d}u\right) , \quad \forall s\in I. \end{aligned}$$

Theorem 13

If the coefficients of the UDDE (1) with a unique solution for each prescribed initial state satisfy the new Lipschitz condition

$$\begin{aligned} \begin{array}{c} |f_{1}(t,u_{1},v_{1})-f_{1}(t,u_{2},v_{2})|\le B_{1t}|u_{1}-u_{2}|+B_{2t}|v_{1}-v_{2}|\\ |f_{2}(t,u_{1},v_{1})-f_{2}(t,u_{2},v_{2})|\le B_{3t}|u_{1}-u_{2}|+B_{4t}|v_{1}-v_{2}| \end{array} \end{aligned}$$

(9)

$\forall u_{i}, v_{i}\in \Re , i=1, 2, t>0$, where the functions $B_{jt}$ satisfies the conditions

$$\begin{aligned} \int _{0}^{+\infty }B_{jt}\mathrm{d}t<+\infty , j=1,2,3,4, \end{aligned}$$

then the UDDE (1) is stable in distribution.

Proof

For the different prescribed initial states $u_{s}$ ($s\in [-\tau ,0]$) and $v_{s}$ ($s\in [-\tau ,0]$), we assume that $U_{t}$ and $V_{t}$ are the corresponding solutions of the UDDE (1). According to the Theorem 2, the corresponding inverse uncertainty distributions $\Theta _{t}^{-1}(\alpha )$ and $\Psi _{t}^{-1}(\alpha )$ of $U_{t}$ and $V_{t}$ satisfy the following equations

$$\begin{aligned} \begin{aligned} \mathrm{d}\Theta _{t}^{-1}(\alpha )& = f_{1}(t,\Theta _{t}^{-1}(\alpha ),\Theta _{t-\tau }^{-1}(\alpha ))\mathrm{d}t\\&\quad +|f_{2}(t,\Theta _{t}^{-1}(\alpha ),\Theta _{t-\tau }^{-1}(\alpha ))|\Lambda ^{-1}(\alpha )\mathrm{d}t,\\ \mathrm{d}\Psi _{t}^{-1}(\alpha )& = f_{1}(t,\Psi _{t}^{-1}(\alpha ),\Psi _{t-\tau }^{-1}(\alpha ))\mathrm{d}t\\&\quad +|f_{2}(t,\Psi _{t}^{-1}(\alpha ),\Psi _{t-\tau }^{-1}(\alpha ))|\Lambda ^{-1}(\alpha )\mathrm{d}t, \end{aligned} \end{aligned}$$

respectively, where

$$\begin{aligned} \Lambda ^{-1}(\alpha )=\frac{\sqrt{3}}{\pi }\ln \frac{\alpha }{1-\alpha }. \end{aligned}$$

For all $\alpha \in \text {(0,1)}$, we obtain

$$\begin{aligned} \begin{aligned} \Theta _{t}^{-1}(\alpha )& = U_{0}+\int _{0}^{t}f_{1}(s,\Theta _{s}^{-1}(\alpha ),\Theta _{s-\tau }^{-1}(\alpha ))\mathrm{d}s\\&\quad +\int _{0}^{t}|f_{2}(s,\Theta _{s}^{-1}(\alpha ),\Theta _{s-\tau }^{-1}(\alpha ))|\Lambda ^{-1}(\alpha )\mathrm{d}s,\\ \Psi _{t}^{-1}(\alpha )& = V_{0}+\int _{0}^{t}f_{1}(s,\Psi _{s}^{-1}(\alpha ),\Psi _{s-\tau }^{-1}(\alpha ))\mathrm{d}s\\&\quad +\int _{0}^{t}|f_{2}(s,\Psi _{s}^{-1}(\alpha ),\Psi _{s-\tau }^{-1}(\alpha ))|\Lambda ^{-1}(\alpha )\mathrm{d}s. \end{aligned} \end{aligned}$$

Apply the new Lipschitz condition (9), we have

$$\begin{aligned} \begin{aligned} |\Theta _{t}^{-1}&(\alpha )-\Psi _{t}^{-1}(\alpha )|\\ & = \left| \left\{ U_{0}+\int _{0}^{t}f_{1}(s,\Theta _{s}^{-1}(\alpha ),\Theta _{s-\tau }^{-1}(\alpha ))\mathrm{d}s\right. \right. \\&\qquad +\left. \int _{0}^{t}|f_{2}(s,\Theta _{s}^{-1}(\alpha ),\Theta _{s-\tau }^{-1}(\alpha ))|\Lambda ^{-1}(\alpha )\mathrm{d}s\right\} \\&\qquad -\left. \left\{ V_{0}+\int _{0}^{t}f_{1}(s,\Psi _{s}^{-1}(\alpha ),\Psi _{s-\tau }^{-1}(\alpha ))\mathrm{d}s\right. \right. \\&\qquad +\left. \left. \int _{0}^{t}|f_{2}(s,\Psi _{s}^{-1}(\alpha ),\Psi _{s-\tau }^{-1}(\alpha ))|\Lambda ^{-1}(\alpha )\mathrm{d}s\right\} \right| \\ \quad \le&|U_{0}-V_{0}|+\left| \int _{0}^{t}f_{1}(s,\Theta _{s}^{-1}(\alpha ),\Theta _{s-\tau }^{-1}(\alpha ))\right. \\&\qquad -f_{1}(s,\Psi _{s}^{-1}(\alpha ),\Psi _{s-\tau }^{-1}(\alpha ))\mathrm{d}s\biggl |\\&\qquad +\left| \Lambda ^{-1}(\alpha )\right| \left| \int _{0}^{t}f_{2}(s,\Theta _{s}^{-1}(\alpha ),\Theta _{s-\tau }^{-1}(\alpha ))\right. \\&\qquad -f_{2}(s,\Psi _{s}^{-1}(\alpha ),\Psi _{s-\tau }^{-1}(\alpha ))\mathrm{d}s\biggl |\\ \le&|U_{0}-V_{0}|+\int _{0}^{t}\left| f_{1}(s,\Theta _{s}^{-1}(\alpha ),\Theta _{s-\tau }^{-1}(\alpha ))\right. \\&\qquad \left. -f_{1}(s,\Psi _{s}^{-1}(\alpha ),\Psi _{s-\tau }^{-1}(\alpha ))\right| \mathrm{d}s\\&\qquad +\left| \Lambda ^{-1}(\alpha )\right| \int _{0}^{t}\left| f_{2}(s,\Theta _{s}^{-1}(\alpha ),\Theta _{s-\tau }^{-1}(\alpha ))\right. \\&\qquad \left. -f_{2}(s,\Psi _{s}^{-1}(\alpha ),\Psi _{s-\tau }^{-1}(\alpha ))\right| \mathrm{d}s\\ \quad \le&|U_{0}-V_{0}|+\int _{0}^{t}\left\{ B_{1s}|\Theta _{s}^{-1}(\alpha )-\Psi _{s}^{-1}(\alpha )|\right. \\&\qquad \left. +B_{2s}|\Theta _{s-\tau }^{-1}(\alpha )-\Psi _{s-\tau }^{-1}(\alpha )|\right\} \mathrm{d}s\\&\qquad +\left| \Lambda ^{-1}(\alpha )\right| \int _{0}^{t}\left\{ B_{3s}|\Theta _{s}^{-1}(\alpha )-\Psi _{s}^{-1}(\alpha )|\right. \\&\qquad \left. +B_{4s}|\Theta _{s-\tau }^{-1}(\alpha )-\Psi _{s-\tau }^{-1}(\alpha )|\right\} \mathrm{d}s. \end{aligned} \end{aligned}$$

Meanwhile, we set $u=s-\tau$, and obtain

$$\begin{aligned} \begin{aligned}&\int _{0}^{t}B_{2s}|\Theta _{s-\tau }^{-1}(\alpha )-\Psi _{s-\tau }^{-1}(\alpha )|\mathrm{d}s\\&\quad \quad =\int _{-\tau }^{t-\tau }B_{2(u+\tau )}|\Theta _{u}^{-1}(\alpha )-\Psi _{u}^{-1}(\alpha )|\mathrm{d}u\\&\quad \quad =\int _{-\tau }^{0}B_{2(u+\tau )}|\Theta _{u}^{-1}(\alpha )-\Psi _{u}^{-1}(\alpha )|\mathrm{d}u\\&\quad \quad \quad \quad +\int _{0}^{t-\tau }B_{2(u+\tau )}|\Theta _{u}^{-1}(\alpha )-\Psi _{u}^{-1}(\alpha )|\mathrm{d}u\\&\quad \quad =\int _{-\tau }^{0}B_{2(u+\tau )}|U_{u}-V_{u}|\mathrm{d}u\\&\quad \quad \quad \quad +\int _{0}^{t-\tau }B_{2(u+\tau )}|\Theta _{u}^{-1}(\alpha )-\Psi _{u}^{-1}(\alpha )|\mathrm{d}u\\ \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned}&\quad \quad \le \sup \limits _{s\in [-\tau ,0]}\{|U_{s}-V_{s}|\}\int _{-\tau }^{0}B_{2(u+\tau )}\mathrm{d}u\\&\quad \quad \quad \quad +\int _{0}^{t-\tau }B_{2(u+\tau )}|\Theta _{u}^{-1}(\alpha )-\Psi _{u}^{-1}(\alpha )|\mathrm{d}u\\&\quad \quad \le \sup \limits _{s\in [-\tau ,0]}\{|U_{s}-V_{s}|\}\int _{0}^{\tau }B_{2u}\mathrm{d}u\\&\quad \quad \quad \quad +\int _{0}^{t}B_{2(u+\tau )}|\Theta _{u}^{-1}(\alpha )-\Psi _{u}^{-1}(\alpha )|\mathrm{d}u. \end{aligned} \end{aligned}$$

Similarly, we have

$$\begin{aligned} &\int _{0}^{t}B_{4s}|\Theta _{s-\tau }^{-1}(\alpha )-\Psi _{s-\tau }^{-1}(\alpha )|\mathrm{d}s \\ &\quad \le \sup \limits _{s\in [-\tau ,0]}\{|U_{s}-V_{s}|\}\int _{0}^{\tau }B_{4u}\mathrm{d}u\\&\quad \quad +\int _{0}^{t}B_{4(u+\tau )}|\Theta _{u}^{-1}(\alpha )-\Psi _{u}^{-1}(\alpha )|\mathrm{d}u. \end{aligned}$$

Set $N_{1}=\int _{0}^{\tau }B_{2u}\mathrm{d}u$ and $N_{2}=\int _{0}^{\tau }B_{4u}\mathrm{d}u$, we have

$$\begin{aligned} \begin{aligned} |&\Theta _{t}^{-1}(\alpha )-\Psi _{t}^{-1}(\alpha )|\le |U_{0}-V_{0}|\\&\qquad +(N_{1}+N_{2}|\Lambda ^{-1}(\alpha )|)\sup \limits _{u\in [-\tau ,0]}\{|\Theta _{u}^{-1}(\alpha )-\Psi _{u}^{-1}(\alpha )|\}\\&\qquad +\int _{0}^{t}(B_{1s}+B_{2(s+\tau )})|\Theta _{s}^{-1}(\alpha )-\Psi _{s}^{-1}(\alpha )|\mathrm{d}s\\&\qquad +|\Lambda ^{-1}(\alpha )|\int _{0}^{t}(B_{3s}+B_{4(s+\tau )})|\Theta _{s}^{-1}(\alpha )-\Psi _{s}^{-1}(\alpha )|\mathrm{d}s\\&\quad \le \left\{ 1+(N_{1}+N_{2}|\Lambda ^{-1}(\alpha )|)\right\} \sup \limits _{s\in [-\tau ,0]}\{|U_{s}-V_{s}|\}\\&\qquad +\int _{0}^{t}\left\{ (B_{1s}+B_{2(s+\tau )})\right. \\&\qquad +\left. |\Lambda ^{-1}(\alpha )|(B_{3s}+B_{4(s+\tau )})\right\} |\Theta _{s}^{-1}(\alpha )-\Psi _{s}^{-1}(\alpha )|\mathrm{d}s. \end{aligned} \end{aligned}$$

(10)

The above Eq. (10) satisfies the Theorem 12, then we have

$$\begin{aligned} \begin{aligned}&|\Theta _{t}^{-1}(\alpha )-\Psi _{t}^{-1}(\alpha )|\\&\quad \le \left\{ 1+(N_{1}+N_{2}|\Lambda ^{-1}(\alpha )|)\right\} \sup \limits _{s\in [-\tau ,0]}\{|U_{s}-V_{s}|\}\cdot \\&\qquad {\exp \left\{ \int _{0}^{t}B_{1s}+B_{2(s+\tau )}+|\Lambda ^{-1}(\alpha )|(B_{3s}+B_{4(s+\tau )})\mathrm{d}s\right\} }\\&\quad \le \exp \left\{ (N_{1}+N_{2}|\Lambda ^{-1}(\alpha )|)\right\} \sup \limits _{s\in [-\tau ,0]}\{|U_{s}-V_{s}|\}\\&\qquad \cdot \exp \left\{ \int _{0}^{+\infty }(B_{1s}+B_{2(s+\tau )})\mathrm{d}s\right. \\&\qquad \left. +|\Lambda ^{-1}(\alpha )|\int _{0}^{+\infty }(B_{3s}+B_{4(s+\tau )})\mathrm{d}s\right\} \\&\quad \le \sup \limits _{s\in [-\tau ,0]}\{|U_{s}-V_{s}|\}\exp \left\{ (N_{1}+N_{2}|\Lambda ^{-1}(\alpha )|)\right. \\&\qquad +\int _{0}^{+\infty }(B_{1s}+B_{2s})\mathrm{d}s\left. +|\Lambda ^{-1}(\alpha )|\int _{0}^{+\infty }(B_{3s}+B_{4s})\mathrm{d}s\right\} \\ \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned}&\le \sup \limits _{s\in [-\tau ,0]}\{|U_{s}-V_{s}|\}\exp \left\{ \int _{0}^{+\infty }(B_{1s}+2B_{2s})\mathrm{d}s\right. \\&\quad \quad \quad \quad \quad \quad \left. +|\Lambda ^{-1}(\alpha )|\int _{0}^{+\infty }(B_{3s}+2B_{4s})\mathrm{d}s\right\} .\\ \end{aligned} \end{aligned}$$

Since

$$\begin{aligned} \int _{0}^{+\infty }B_{1t}\mathrm{d}t<+\infty , \int _{0}^{+\infty }B_{2t}\mathrm{d}t<+\infty , \\ \int _{0}^{+\infty }B_{3t}\mathrm{d}t<+\infty , \int _{0}^{+\infty }B_{4t}\mathrm{d}t<+\infty , \end{aligned}$$

there exists a real number $M>0$ such that

$$\begin{aligned} \begin{aligned}&\exp \left\{ \int _{0}^{+\infty }(B_{1s}+2B_{2s})\mathrm{d}s\right. \\&\quad \quad \quad +\left. |\Lambda ^{-1}(\alpha )|\int _{0}^{+\infty }(B_{3s}+2B_{4s})\mathrm{d}s\right\} <M. \end{aligned} \end{aligned}$$

Assume that $\delta =\epsilon /M$, then we have

$$\begin{aligned} \begin{aligned} |&\Theta _{t}^{-1}(\alpha )-\Psi _{t}^{-1}(\alpha )|\le \sup \limits _{s\in [-\tau ,0]}\{|U_{s}-U_{s}|\}\\&\cdot \exp \left\{ \int _{0}^{+\infty }(B_{1s}+2B_{2s})\mathrm{d}s\right. \\&\quad \quad \quad \quad \left. +|\Lambda ^{-1}(\alpha )|\int _{0}^{+\infty }(B_{3s}+2B_{4s})\mathrm{d}s\right\} \\&<\delta M=\epsilon \end{aligned} \end{aligned}$$

for any $t\ge 0$ and $\epsilon >0$ provided

$$\begin{aligned} \sup \limits _{s\in [-\tau ,0]}\{|U_{s}-V_{s}|\}<\delta . \end{aligned}$$

Thus, we have

$$\begin{aligned} \lim \limits _{\sup \limits _{s\in [-\tau ,0]}\{|U_{s}-V_{s}|\}\rightarrow 0}|\Theta _{t}^{-1}(\alpha )-\Psi _{t}^{-1}(\alpha )|=0, \quad \forall \alpha \in (0,1). \end{aligned}$$

According to the Theorem 11, we have

$$\begin{aligned} \lim \limits _{\sup \limits _{s\in [-\tau ,0]}\{|U_{s}-V_{s}|\}\rightarrow 0}|\Theta _{t}(y)-\Psi _{t}(y)|=0, \quad \forall t>0, y\in \Re . \end{aligned}$$

Therefore, the UDDE (1) is stable in distribution based on the new Lipschitz condition (9).

Remark 41

If the UDDEs satisfy the strong Lipschitz condition of Theorem 10, we set $B_{2t}=0$ and $B_{4t}=0$, it must satisfy the new Lipschitz condition in Theorem 13. In contrast, it is obvious that it may not be established, the Example 1 can be employed to illustrate this point.

Example 1

Consider the UDDE

$$\begin{aligned} \begin{aligned} \mathrm{d}U_{t}& = \left( \frac{2t}{1+t^4}U_{t}+\exp (-t^2)U_{t-0.4}\right) \mathrm{d}t\\&+\left( \frac{t}{1+t^4}U_{t}+2\exp (-t^2)U_{t-0.4}\right) \mathrm{d}C_{t}. \end{aligned} \end{aligned}$$

(11)

Firstly, we set

$$\begin{aligned} \begin{aligned}&f_{1}(t,u,v)=\frac{2t}{1+t^4}u+\exp (-t^2)v,\\&f_{2}(t,u,v)=\frac{t}{1+t^4}u+2\exp (-t^2)v. \end{aligned} \end{aligned}$$

If we want to use the Theorem 10, we can easily find that it does not follow the strong Lipschitz condition, and if we use the Theorem 13, we obtain that the following equations hold,

$$\begin{aligned} \begin{aligned}&\int _{0}^{+\infty }B_{1t}\mathrm{d}t=\int _{0}^{+\infty }\frac{2t}{1+t^4}\mathrm{d}t=\frac{\pi }{2}<+\infty ,\\&\int _{0}^{+\infty }B_{2t}\mathrm{d}t=\int _{0}^{+\infty }\exp (-t^2)\mathrm{d}t=\frac{\sqrt{\pi }}{2}<+\infty ,\\&\int _{0}^{+\infty }B_{3t}\mathrm{d}t=\int _{0}^{+\infty }\frac{t}{1+t^4}\mathrm{d}t=\frac{\pi }{4}<+\infty ,\\&\int _{0}^{+\infty }B_{4t}\mathrm{d}t=\int _{0}^{+\infty }\exp (-t^2)\mathrm{d}t=\frac{\sqrt{\pi }}{4}<+\infty . \end{aligned} \end{aligned}$$

According to the Theorem 13, the UDDE (11) is stable in distribution.

Corollary 41

If the coefficients of the UDDE (1) with a unique solution for each prescribed initial state satisfy the new Lipschitz condition

$$\begin{aligned} \begin{aligned}&|f_{1}(t,u_{1},v_{1})-f_{1}(t,u_{2},v_{2})|+|f_{2}(t,u_{1},v_{1})-f_{2}(t,u_{2},v_{2})|\\&\quad \quad \le D_{1t}|u_{1}-u_{2}|+D_{2t}|v_{1}-v_{2}| \end{aligned} \end{aligned}$$

(12)

$\forall u_{i}, v_{i}\in \Re , i=1, 2, t>0$, where the functions $D_{jt}$ satisfy the conditions

$$\begin{aligned} \int _{0}^{+\infty }D_{jt}\mathrm{d}t<+\infty ,\quad j=1,2, \end{aligned}$$

then the UDDE (1) is stable in distribution.

Proof

By using the condition (12), we obtain

$$\begin{aligned} \begin{array}{c} |f_{1}(t,u_{1},v_{1})-f_{1}(t,u_{2},v_{2})|\le D_{1t}|u_{1}-u_{2}|+D_{2t}|v_{1}-v_{2}|,\\ |f_{2}(t,u_{1},v_{1})-f_{2}(t,u_{2},v_{2})|\le D_{1t}|u_{1}-u_{2}|+D_{2t}|v_{1}-v_{2}|. \end{array} \end{aligned}$$

According to the Theorem 13, we set

$$\begin{aligned} B_{1t}=D_{1t}, B_{2t}=D_{2t}, B_{3t}=D_{1t}, B_{4t}=D_{2t}, \end{aligned}$$

then the UDDE (1) based on the new Lipschitz condition (12) is stable in distribution.

Remark 42

In fact, Theorem 13 and Corollary 41 have a equivalence relation. If the new Lipschitz condition of Theorem 13 holds, we set $B_{1t}=D_{1t}, B_{2t}=D_{2t}, B_{3t}=D_{1t}, B_{4t}=D_{2t}$, then the Lipschitz condition of Corollary 41 holds. Conversely, if the new Lipschitz condition of Corollary 41 holds, we set $D_{1t}=B_{1t}+B_{3t}, D_{2t}=B_{2t}+B_{4t}$, then the new Lipschitz condition of Theorem 13 holds.

Corollary 42

Assume the UDDE

$$\begin{aligned} \mathrm{d}U_{t}=(b_{1t}U_{t}+b_{2t}U_{t-\tau }+b_{3t})\mathrm{d}t+(b_{4t}U_{t}+b_{5t}U_{t-\tau }+b_{6t})\mathrm{d}C_{t}\ \end{aligned}$$

(13)

satisfying

$$\begin{aligned} \begin{aligned} \int _{0}^{+\infty }b_{1t}\mathrm{d}t<+\infty , \int _{0}^{+\infty }b_{2t}\mathrm{d}t<+\infty ,\\ \int _{0}^{+\infty }b_{4t}\mathrm{d}t<+\infty , \int _{0}^{+\infty }b_{5t}\mathrm{d}t<+\infty , \end{aligned} \end{aligned}$$

(14)

then the UDDE (13) is stable in distribution.

Proof

We set $f_{1}(t,u,v)= b_{1t}u+b_{2t}v+b_{3t}$ and $f_{2}(t,u,v)= b_{4t}u+b_{5t}v+b_{6t}$, then we have

$$\begin{aligned} B_{1t}=b_{1t}, B_{2t}=b_{2t}, B_{3t}= b_{4t}, B_{4t}=b_{5t}. \end{aligned}$$

By use of the condition (14) and Theorem 13, we obtain that the UDDE (13) is stable in distribution.

Example 2

Consider the UDDE

$$\begin{aligned} \begin{aligned} \mathrm{d}U_{t}& = \left( \exp (-t)U_{t}+\frac{1}{1+t^2}U_{t-1}\right) \mathrm{d}t\\&+\left( \frac{1}{2}t\exp (-t)U_{t}+\frac{\pi }{2\sqrt{3}}t\exp (-t^2)U_{t-1}\right) \mathrm{d}C_{t}. \end{aligned} \end{aligned}$$

(15)

Then, we have

$$\begin{aligned} \int _{0}^{+\infty }b_{1t}\mathrm{d}t=\int _{0}^{+\infty }\exp (-t)\mathrm{d}t=1<+\infty , \end{aligned}$$

$$\begin{aligned} \int _{0}^{+\infty }b_{2t}\mathrm{d}t& =\int _{0}^{+\infty }\frac{1}{1+t^2}\mathrm{d}t=\frac{\pi }{2}<+\infty , \\ \int _{0}^{+\infty }b_{4t}\mathrm{d}t & =\int _{0}^{+\infty }\frac{1}{2}t\exp (-t)\mathrm{d}t=\frac{1}{2}<\frac{\pi }{\sqrt{3}}, \\ \int _{0}^{+\infty }b_{5t}\mathrm{d}t & =\int _{0}^{+\infty }\frac{\pi }{2\sqrt{3}}t\exp (-t^2)\mathrm{d}t=\frac{\pi }{4\sqrt{3}}<+\infty . \end{aligned}$$

By using the Corollary 42, the UDDE (15) is stable in distribution.

5 Stability in distribution for a special UDDEs

In this section, a class of UDDEs being stable in distribution are investigated.

Theorem 14

Consider the UDDEs

$$\begin{aligned} \mathrm{d}U_{t}=K_{t}U_{t-\tau }\mathrm{d}t+a \mathrm{d}C_{t}, \end{aligned}$$

(16)

where $K_{t}$ and a are the real-valued function and the constant number, respectively, $t\in [0,T]$, then the UDDE (16) is stable in distribution.

Proof

For the different prescribed initial states $n_{\theta }$ and $m_{\theta }$, $\theta \in [-\tau ,0]$, the corresponding solutions are $U_{t}$ and $V_{t}$. According to the Theorem 2, we have

$$\begin{aligned} \begin{aligned}&\mathrm{d}\Theta _{t}^{-1}(\alpha )=K_{t}\Theta _{t-\tau }^{-1}(\alpha )\mathrm{d}t+a \Lambda ^{-1}(\alpha )\mathrm{d}t,\\&\mathrm{d}\Psi _{t}^{-1}(\alpha )=K_{t}\Psi _{t-\tau }^{-1}(\alpha )\mathrm{d}t+a \Lambda ^{-1}(\alpha )\mathrm{d}t, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&\Theta _{t}^{-1}(\alpha )=U_{0}+\int _{0}^{t}K_{s}\Theta _{s-\tau }^{-1}(\alpha )\mathrm{d}s+a \Lambda ^{-1}(\alpha )t,\\&\Psi _{t}^{-1}(\alpha )=Y_{0}+\int _{0}^{t}K_{s}\Psi _{s-\tau }^{-1}(\alpha )\mathrm{d}t+a \Lambda ^{-1}(\alpha )t. \end{aligned} \end{aligned}$$

Thus,

$$\begin{aligned} \begin{aligned}&|\Theta _{t}^{-1}(\alpha )-\Psi _{t}^{-1}(\alpha )|\\&\le \left\{ \begin{array}{l} |n_{t}-m_{t}|, t\in [-\tau ,0]\\ |n_{0}-m_{0}|+\int _{0}^{t}|K_{s}||n_{s-\tau }-m_{s-\tau }|\mathrm{d}s, t\in (0,\tau ]\\ |\Theta _{\tau }^{-1}(\alpha )-\Psi _{\tau }^{-1}(\alpha )|+\int _{\tau }^{t}|K_{s}||\Phi _{s-\tau }^{-1}(\alpha )-\Psi _{s-\tau }^{-1}(\alpha )|\mathrm{d}s, \\ t\in (\tau ,2\tau ]\\ \dots \end{array} \right. \end{aligned} \end{aligned}$$

Then,

$$\begin{aligned} \lim \limits _{\sup \limits _{s\in [-\tau ,0]}\{|U_{s}-V_{s}|\}\rightarrow 0}|\Theta _{t}^{-1}(\alpha )-\Psi _{t}^{-1}(\alpha )|=0, \quad \forall \alpha \in (0,1). \end{aligned}$$

According to the Theorem 11, we have

$$\begin{aligned} \lim \limits _{\sup \limits _{s\in [-\tau ,0]}\{|U_{s}-V_{s}|\}\rightarrow 0}|\Theta _{t}(y)-\Psi _{t}(y)|=0, \quad \forall t>0, y\in \Re . \end{aligned}$$

Remark 51

The Theorem 14 is different from the Theorems 7 and 13. Example 3 shows that it is stable in distribution, but it becomes invalid by using the Theorems 7 and 13.

Example 3

Consider the UDDE

$$\begin{aligned} \mathrm{d}U_{t}=t^2 U_{t-1}\mathrm{d}t+\mathrm{d}C_{t}, t\in[0,1000]. \end{aligned}$$

(17)

According to the Theorem 14, the UDDE (17) is stable in distribution. Due to the fact that

$$\begin{aligned} \int _{0}^{+\infty }t^2\mathrm{d}t= +\infty , \end{aligned}$$

so the Theorems 7 and 13 are invalid for this example.

6 Numerical experiments

The stability is a significant issue for systems to model the real world. In other words, if the system is not stable, even though the difference between the given initial value and the precise initial value is small, the difference between the results becomes larger. This section devotes to illustrating the effectiveness of the Theorem 13.

Example 4

The UDDE (15) has been proved that it is stable in distribution, and has a following $\alpha$-path obtained by the Theorem 2,

$$\begin{aligned} \begin{aligned}&\mathrm{d}U_{t}^{\alpha }=\left( \exp (-t)U_{t}^{\alpha }+\frac{1}{1+t^2}U_{t-1}^{\alpha }\right) \mathrm{d}t\\&\quad +\left| \left( \frac{1}{2}t\exp (-t)U_{t}^{\alpha }+\frac{\pi }{2\sqrt{3}}t\exp (-t^2)U_{t-1}^{\alpha }\right) \right| \Lambda ^{-1}(\alpha )\mathrm{d}t. \end{aligned} \end{aligned}$$

(18)

According to the Eq. (18), the algorithm to calculate $U_{t}$ is design as below.

• Step 0: Set $t_{i}=iT/M, i=1,2,\dots ,M,$ where M are two large numbers.

• Step 1: Set $i=0$.

• Step 2: Set $i=\leftarrow i+1$.

• Step 3: Set $U_{t_{i+1}}^{\alpha }=U_{t_{i}}^{\alpha }+\left\{ \left( \exp (-t_{i})U_{t_{i}}^{\alpha }+\frac{1}{1+t_{i}^2}U_{t_{i}-1}^{\alpha }\right) +\right. \left| \frac{1}{2}t_{i}\exp (-t_{i})U_{t_{i}}^{\alpha }+\frac{\pi }{2\sqrt{3}}t_{i}\exp (-t_{i}^2)U_{t_{i}-1}^{\alpha }\right| \Lambda ^{-1}(\alpha )\Big \}(t_{i+1}-t_{i})$.

Table 1 Data of Fig. 1

Table 2 Data of Fig. 2

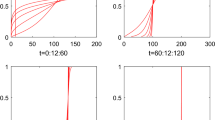
In the Figs. 1 and 2, Tables 1 and 2, we found that, when the difference between two initial values is enough small, the difference between the corresponding values $U_{t}$ is sufficiently close together after a period of time. Therefore, it is verified that the UDDE (15) is stable in distribution.

Fig. 1

Relations of $U_{t}$ and h in the UDDE (15)

Fig. 2

Relations of $U_{t}$ and h in the UDDE (15)

Example 5

The well-known delay Logistic model

$$\begin{aligned} \mathrm{d}P_{t}=r P_{t}\left( 1-\frac{P_{t-\tau }}{N}\right) \mathrm{d}t, \end{aligned}$$

(19)

was introduced to model population by Hutchinson 1948, where $P_{t}$ is the number of population at time t, r is a constant of proportionality, and N is the carrying capacity, which means $P_{s}<N, \forall s>0$. Assume that this ecological system suffers from infectious diseases, then we set that r is exponential decrease with t, and have

$$\begin{aligned} \mathrm{d}P_{t}=r\exp (-rt) P_{t}\left( 1-\frac{P_{t-\tau }}{N}\right) \mathrm{d}t. \end{aligned}$$

(20)

In real world, there must be many uncertain factors for population growth, such as man-made and natural disasters, so we add an uncertain term in the above Logistic model to write as

$$\begin{aligned} \mathrm{d}P_{t}=\exp (-rt)r P_{t}\left( 1-\frac{P_{t-\tau }}{N}\right) \mathrm{d}t+\exp (-at)P_{t}\mathrm{d}C_{t} \end{aligned}$$

(21)

with constant $a>0$. Next, we analyze the stability in distribution of system (21).

Let

$$\begin{aligned} \begin{aligned} f_{1}(t,u,v)=r\exp (-rt) u\left( 1-\frac{v}{N}\right) , \quad f_{2}(t,u,v)=\exp (-at)u, \end{aligned} \end{aligned}$$

then, we obtain

$$\begin{aligned} \begin{aligned}&|f_{1}(t,u_{1},v_{1})-f_{1}(t,u_{2},v_{2})|\\&=r\exp (-rt)\left| u_{1}\left( 1-\frac{v_{1}}{N}\right) -u_{2}\left( 1-\frac{v_{2}}{N}\right) \right| \\&\le r\exp (-rt)\left\{ |u_{1}-u_{2}|+\frac{1}{N}|u_{1}(v_{1}-v_{2})+(u_{1}-u_{2})v_{2}|\right\} \\&\le 2r\exp (-rt)|u_{1}-u_{2}|+r\exp (-rt)|v_{1}-v_{2}|, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} |f_{2}(t,u_{1},v_{1})-f_{2}(t,u_{2},v_{2})|=\exp (-at)\cdot |u_{1}-u_{2}|. \end{aligned} \end{aligned}$$

Due to the fact that

$$\begin{aligned} \int _{0}^{+\infty }r\exp (-rt)\mathrm{d}t=1, \int _{0}^{+\infty }\exp (-at)\mathrm{d}t=\frac{1}{a}. \end{aligned}$$

According to the Theorem 13, the system (21) is stable in distribution. Next, we verify the above conclusion by numerical experiments. The following $\alpha$-path of the system (21) can be obtained by the Theorem 2,

$$\begin{aligned} \begin{aligned} \mathrm{d}P_{t}^{\alpha }&=\exp (-rt)r P_{t}^{\alpha }\left( 1-\frac{P_{t-\tau }^{\alpha }}{N}\right) \mathrm{d}t\\&\quad \quad \quad \quad \quad \quad +\left| \exp (-at)P_{t}^{\alpha }\right| \Lambda ^{-1}(\alpha )\mathrm{d}t. \end{aligned} \end{aligned}$$

(22)

According to the Eq. (22), the algorithm to calculate $U_{t}$ is design as below.

• Step 0: Set $t_{i}=iT/N, i=1,2,\dots ,N,$ where N are two large numbers.

• Step 1: Set $i=0$.

• Step 2: Set $i=\leftarrow i+1$.

• Step 3: Set $P_{t_{i+1}}^{\alpha }=P_{t_{i}}^{\alpha }+\left\{ \exp (-rt_{i})r P_{t_{i}}^{\alpha }\left( 1-\frac{P_{t_{i}-\tau }^{\alpha }}{N}\right) \right. +\left| \exp (-at_{i})P_{t_{i}}^{\alpha }\right| \Lambda ^{-1}(\alpha )\Big \}(t_{i+1}-t_{i})$.

Fig. 3

Relations of $P_{t}$ and h in the system (21)

Fig. 4

Relations of $P_{t}$ and h in the system (21)

Table 3 Data of Fig. 3

Table 4 Data of Fig. 4

In the Fig. 3 and Table 3, we assume that $N=100, r=0.1, a=0.4, \tau =0.1, \alpha =0.3,$ then, we found that, when the difference among the initial values is enough small, the number of population $P_{t}$ is also sufficiently close together after a period of time. In the Fig. 4and Tab.4, we assume that $N=1000, r=0.7, a=0.2, \tau =0.7, \alpha =0.65,$ then the conclusion is the same as the Fig. 3. Therefore, the system (21) is confirmed that it is stable in distribution obtained from the Figs. 3 and 4.

7 Conclusions

The stability in distribution for UDDEs has been investigated by means of the strong Lipschitz condition, but it was difficult to obtain the strong Lipschitz condition. In this paper, the new Lipschitz condition concerning the current and the past states was proposed. Based on the new Lipschitz condition, a sufficient theorem of stability in distribution for the UDDEs was proved. Without any limited condition, a class of UDDEs being stable in distribution was successfully proved. Through the Figs. 1,  2,  3 and 4, Tables 1, 2, 3 and 4, the difference between the given initial value and the precise initial value is small enough, the difference between the results becomes smaller. In other words, the effectiveness of the above sufficient theorem was verified. If the new Lipschitz condition can not be obtained, we can not judge the stability in distribution for the UDDEs. In the future, we can consider the stability in p-th moment based on the new Lipschitz condition and the p-th moment exponential stability for the UDDEs.