1 Introduction

Yemen is a country located in the southwest of Asia on 2000 km coastline, and it is considered one of the tropical countries. Therefore, infectious and seasonal diseases are highly prevalent there, such as Aedes aegypti, Aedes albopictus, dengue, Chikungunya, malaria, cholera, and other infectious diseases. Recently, the Chikungunya virus (CHIKV) has spread in some areas, especially in Al-Hadidah, Lahj and Aden. Spread of the Chikungunya virus coincided with the COVID-19 pandemic, causing many deaths. It is well known in epidemiology that Chikungunya is an infectious disease caused by a virus of the Togaviridae family and transmitted to humans by either the genus Aedes aegypti or Aedes albopictus mosquitoes. COVID-19 is an infectious disease caused by the virus SARS-CoV-2 of the Coronaviridae family and transmitted to humans by infectious droplets of another human. Hence, most of the studies that addressed epidemiological optimal control models focused on break of the vector-borne using some intervention strategies.

Lately, several studies have been proposed to explore optimal control models for infectious diseases including Chikungunya diseases. Ruiz-Moreno et al. (2012) combined stochastic model, which is related to season-based mosquito vector dynamics with an epidemiological model, to investigate the potential risk of Chikungunya entering the US. Moulay et al. (2012) formulated an optimal control problem for the Chikungunya model, which is controlled by three time-dynamic variables: prevention and treatment and vector breeding sites destruction. Yakob and Clements (2013) addressed the Chikungunya outbreak in Réunion 2006, and Monte Carlo simulation is used in the sensitivity analysis study. Liu and Stechlinski (2015) discussed the spread of CHIKV outbreak in Réunion with respect to some time-varying parameters that are related to the rate of breeding of mosquitoes in the rainy and dry climate and the rate of dynamic contact between the mosquitoes and the human. Agusto et al. (2016) developed a transmission model with focusing on the influence of age on Chikungunya transmission. The population is classified into three age-structured: Juveniles, adults and senior subcategories. Zhu et al. (2018) employed the input–output polynomials with QR decomposition to estimate the parameters of a CHIKV transmission model. Liu et al. (2020) investigated the impact of temperature and rainfall on the CHIKV model. Dodero-Rojas et al. (2020) formulated a compartmental mathematical model, which was implemented in the city of Rio de Janeiro in the period 2017–2019 on the Chikungunya epidemic. The basic reproduction number was estimated, and a potential outbreak of Mayaro virus was predicted. Moreover, a number of different intervention strategies were simulated with the aim of reducing the number of infected individuals. The optimal control model was proposed for the Chikungunya epidemic model in Gonzalez-Parra et al. (2020) when Pontryagin’s maximum principle was utilized to solve the optimal controls and to find the optimal final time. This study was also carried out on real data in Colombia 2015. The optimal control policies of the Chikungunya epidemic model were presented through three time-varying variables to control the spread of the CHIKV between humans and vectors. The first time-varying variable related to educational awareness and personal protection through bed nets, wearing full body clothing, and avoiding water stagnation. The second time-varying variable relied on the impact of the treatment of infected individuals. The third time-varying variable related to spraying insecticides in order to reduce mosquito population to reduce the proportion of the infected individuals. (Ali et al. 2020) presented a clinical study on the Chikungunya outbreak in Yemen (March 2020–May 2020).

On the other hand, this year, coinciding with the outbreak of the COVID-19, many studies have emerged that addressed the epidemiological model of COVID-19. (Abbasi et al. 2020) proposed a dynamic of SQEIAR Susceptible, Quarantined, Exposed, Infected, Asymptomatic, and Recovered individuals model considering two time-varying variables to control the outbreak: quarantine and treatment. Besides, they used Pontryagin’s maximum principle to solve the optimal controls model. Kouidere et al. (2020) considered three actions to control the COVID-19 outbreak, i.e. prevention, quarantine, and treatment. Also, Pontryagin’s maximum principle utilized and analyzed the model. The Susceptible-Exposed-Asymptomatic-Infected-Removed (SEAIR) model was expanded to include the perished class due to infection with COVID-19 in Tsay et al. (2020). Social distancing, quarantining, and availability of testing kits were used as time-dynamic variables for dynamic optimal control. The aim of the optimization problem was to minimize social and economic costs provided that the size of the epidemic remains under a given epidemic peak value. The optimal control model was solved directly by Python by considering the discretization of time domain into one finite element per day. Morato et al. (2020a, b) proposed epidemic models of COVID-19 with respect to the real data from Brazil. Social distancing was investigated as the time-varying parameter for controlling the optimization model. Ullah and Altaf (2020) formulated a mathematical model to explore COVID-19 in Pakistan, presenting a mathematical analytic study. The parameters were estimated using a least square fitting method. Moreover, two actions were investigated for controlling the epidemic, namely, quarantine, and hospitalization. Also, some articles addressed the optimal distribution of vaccines, such as Narayanamoorthy et al. (2021), Hezam et al. (2021b) or discussed the humanitarian response plan for high-priority countries as an optimal distribution model (Hezam 2021a).

There are a number of epidemiological models in the literature that try to describe the co-infection models. Samat and Ma’Arof (2014) presented a stochastic susceptible–infective–recovered (human); susceptible–infective (vector) SIR-SI model to estimate the relative risk of Chikungunya and dengue infection in Malaysia. They determined the high-risk and low-risk area of Dengue and Chikungunya, which can be employed for the prevention and control of both outbreaks. Kumar et al. (2019) studied the Chikungunya, dengue and zika outbreaks in Mexico 2015–2016. They estimated the parameters for each virus. Besides, they presented some strategies based on isolation and self-protection factors to control the outbreaks. Aldila and Agustin (2018) proposed a transmission model of dengue-Chikungunya coinfection and presented the mathematical analysis and numerical simulation. In Isea and Lonngren (2016), transmission dynamics models were developed of Dengue, Chikungunya and Zika, including the possibility of a dual-infection of any two infectious diseases in the same population. Musa et al. (2020) proposed a co-infection transmission dynamics model for Chikungunya and dengue. The model was implemented on real data from India and a study of sensitivity analysis for model parameters was presented. An interesting study was presented in Jindal (2020), in which the authors investigated the effect of the lockdowns due to COVID-19 on outbreaks of mosquito-borne diseases, including dengue, Chikungunya and malaria. They found that the risk and severity of the outbreak increased with lockdowns. Hezam et al. (2021a) addressed the COVID-19 and Cholera coinfection in Yemen 2020. Four time-dynamic variables were investigated to show its impact on epidemics curbing: social distancing, quarantine, test kits availability, rate of the population able to access to pure water. Also, some studies discussed the interactive COVID-19 with other outbreaks like dengue (Lam et al. 2020), HIV (Doungmo Goufo et al. 2020), Ebola (Zhang and Jain 2020), or the impact of COVID-19 pandemic on TP patients (Marimuthu et al. 2020), or on unemployment problem (Hezam 2021b).

Limited studies have been carried out with respect to solving the epidemiological models using metaheuristic algorithms. Yan and Zou (2008) used genetic algorithm to find sub-optimal solution of the optimal control in SARS epidemics. Florentino et al. (2014) employed genetic algorithm to solve multi-objective optimal control models derived from a dynamical model of dengue virus epidemic. Florentino et al. (2018) also used genetic algorithm to solve the optimal control model that aims to reduce Aedes mosquitoes through preventing breeding or spreading insecticides. Chaikham and Sawangtong (2018) used differential evolution to solve the optimal control model applied to curb the Zika virus outbreak. Rahmalia and Herlambang (2018) applied artificial bee colony algorithm to find the optimal weights of objective function in optimal control derived from Influenza epidemic models. In Akman et al. (2018), particle swarm optimization was employed to solve the parameter estimation problem in ordinary differential equations. Putra and Mu (2019) used particle swarm optimization to estimate the parameters, then Euler method was used to solve Susceptible, Infected and Resistant (SIR) models. Kmet and Kmetova (2019) introduced two approaches for solving the optimal control model, i.e. the direct method and the indirect method. The direct methods were based on collaborating Bernstein–Bézier parametrization for control variables, in addition to invasive weed optimization algorithm and particle swarm optimization for solving the optimal control model, while Pontryagin’s maximum principle and the necessary conditions of optimal control model are the indirect methods. Windarto et al. (2020) employed particle swarm optimization to estimate the parameters of dengue transmission model. Lobato et al. (2020) applied stochastic fractal search algorithm to solve both parameters estimation problem and multi-objective optimal control model of COVID-19 outbreak in China. Mahmoodabadi (2020) used PSO to find the unknown variables in the epidemic model, comparing it to other classical methods. Yousefpour et al. (2020) used a genetic algorithm to solve the multi-objective optimal control model of COVID-19 outbreak. Besides, some control strategies were discussed and analyzed, which can contribute to curbing the COVID-19 epidemic. Similarly, in Okuonghae and Omame (2020), social distancing, use of face mask and case detection of COVID-19 outbreak in Nigeria were the investigated actions. Salgotra et al. (2020) used Genetic Evolutionary Programming (GEP) to predict confirmed cases and death cases of COVID-19 in 15 worst affected countries in the world for the period (February 1st, 2020, to last of May 2020. He et al. (2020) employed PSO to estimate the parameters of the SEIR model based on real data from Hubei province. A similar study, Abdallah and Nafea (2021), used PSO to estimate the parameters of the SEIQRD model and predict the COVID-19 outbreak in Italy.

However, up to the time of writing this paper, no study has formulated a mathematical model of the coinfection COVID-19 and Chikungunya. The contributions of this work are as follows. Firstly, the present study formulates a new dynamic transmission model of the coinfection COVID-19 and Chikungunya. Secondly, PSO will be used to estimate the parameters based on historical data for both infections in Yemen from March 1, 2020, to May 30, 2020, and also to predict the trajectories of both outbreaks for one year. Thirdly, we present an optimal control model that includes two objective functions: minimizing the expected cumulative number of infected people for COVID-19 and Chikungunya, and minimizing the total cost associated with the intervention strategies. The optimal solutions of the optimal control model will be found also by PSO. Fourthly, we investigate the sensitivity of the time-dynamic inputs of the optimal control by evaluating a novel set of control strategies. The focus is on time-dynamic inputs related to lockdown, social distancing, test kits numbers, personal protection and insecticides and larvicides to fight mosquitoes. These five actions are used to identify the optimal strategies that contribute to infection mitigation. Lastly, all the strategies are carried out for COVID-19 and Chikungunya outbreaks in Yemen to determine the suitable optimal strategy in Yemen under the conditions and available resources.

The remainder of this work is organized as follows. In Sect. 2, we discuss the co-infection model formulation. PSO is presented in Sect. 3, while the estimated parameters are discussed in Sect. 4. In Sect. 5, we provide the optimal control model and its analysis. In Sect. 6, we discuss several strategies. Finally, in Sect. 7, we summarize and conclude the work.

2 Model formulation

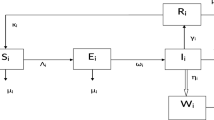
To describe the co-infection dynamics of COVID-19 and Chikungunya, the dynamical compartment model includes both human and mosquito population. The human population will be divided into sixteen different epidemiological classes, while mosquito vector will include three classes. Descriptions of the present classes with associate parameters are defined in Tables 1 and 2, respectively.

Table 1 Description and initial values of model variables
Full size table
Table 2 Parameters description and their values
Full size table

The classes of human population are \(S\left(t\right),{E}_{1}\left(t\right),{A}_{1}\left(t\right),{I}_{1}\left(t\right),{R}_{1}\left(t\right),{P}_{1}\left(t\right),\) \({I}_{R2}\left(t\right),{E}_{2}\left(t\right),{A}_{2}\left(t\right),\) \({I}_{2}\left(t\right),{R}_{2}\left(t\right),{P}_{2}\left(t\right),{I}_{1R}\left(t\right),\) \({I}_{12}\left(t\right),{R}_{12}\left(t\right)\) and \({P}_{12}\left(t\right)\) correspond to the number of individuals in the sixteen epidemiological classes at time \(t\). The total human population at time t, denoted by \({N}_{H}\left(t\right)\), is given by:

$$\begin{aligned} N_{H} \left( t \right) = & S\left( t \right) + E_{1} \left( t \right) + A_{1} \left( t \right) + I_{1} \left( t \right) \\ & + R_{1} \left( t \right) + P_{1} \left( t \right) + I_{R2} \left( t \right) + E_{2} \left( t \right) \\ & + A_{2} \left( t \right) + I_{2} \left( t \right) + R_{2} \left( t \right) + P_{2} \left( t \right) \\ & + I_{1R} \left( t \right) + I_{12} \left( t \right) + R_{12} \left( t \right) + P_{12} \left( t \right) \\ \end{aligned}$$

Moreover, the classes of mosquito vector population are \(X\left(t\right),Y\left(t\right),\) and \(Z\left(t\right)\) where the total mosquitoes’ population at time \(t\) is given by:

$$N_{m} \left( t \right) = X\left( t \right) + Y\left( t \right) + Z\left( t \right)$$

The structure schematic diagram of the compartmental COVID-19- Chikungunya co-infection model is illustrated in Fig. 1.

Fig. 1
figure 1

Schematic diagram of the compartmental Chikungunya and COVID-19 co-infection model

Full size image

The proposed co-infection model is described by the following dynamic differential equations system.

$$\begin{aligned} \frac{dS\left( t \right)}{{dt}} = & - \left( \begin{gathered} \frac{{\left( {1 - u_{1} \left( t \right)} \right)}}{{N_{H} }}E_{1} \left( t \right) + \frac{{\left( {1 - u_{2} \left( t \right)} \right)}}{{N_{H} }}I_{1} \left( t \right) \hfill \\ + \alpha_{c} \frac{{\left( {1 - u_{4} \left( t \right)} \right)}}{{N_{H} }}E_{2} \left( t \right)\left( {1 - u_{5} \left( t \right)} \right)Z\left( t \right) + \alpha_{12} \hfill \\ \end{gathered} \right)S\left( t \right) \\ & + \mu_{1} R_{1} \left( t \right) + \mu_{2} R_{2} \left( t \right) + \mu_{12} R_{12} \left( t \right) + \mu N_{H} \\ \end{aligned}$$
(1)
$$\begin{aligned} \frac{{dE_{1} \left( t \right)}}{dt} = & \left( {\frac{{\left( {1 - u_{1} \left( t \right)} \right)}}{{N_{H} }}E_{1} \left( t \right) + \frac{{\left( {1 - u_{2} \left( t \right)} \right)}}{{N_{H} }}I_{1} \left( t \right)} \right)S\left( t \right) \\ & - \left( {1 - \varphi_{1} } \right)\alpha_{1} E_{1} \left( t \right) - \varphi_{1} \alpha_{1} E_{1} \left( t \right) \\ \end{aligned}$$
(2)
$$\frac{{dA_{1} \left( t \right)}}{dt} = \left( {1 - \varphi_{1} } \right)\alpha_{1} E_{1} \left( t \right) - \left( {\delta_{1} + u_{3} \left( t \right) + \beta_{1} + \omega_{1} } \right)A_{1} \left( t \right)$$
(3)
$$\frac{{dI_{1} \left( t \right)}}{dt} = u_{3} \left( t \right)A_{1} \left( t \right) + \varphi_{1} \alpha_{1} E_{1} \left( t \right) - \left( {\delta_{1} + \beta_{1} + \omega_{1} } \right)I_{1} \left( t \right)$$
(4)
$$\frac{{dR_{1} \left( t \right)}}{dt} = \beta_{1} \left( {A_{1} \left( t \right) + I_{1} \left( t \right)} \right) - \left( {\mu_{1} + \lambda_{1} } \right)R_{1} \left( t \right)$$
(5)
$$\frac{{dP_{1} \left( t \right)}}{dt} = \omega_{1} \left( {A_{1} \left( t \right) + I_{1} \left( t \right)} \right)$$
(6)
$$\frac{{dI_{R2} \left( t \right)}}{dt} = \lambda_{1} R_{1} \left( t \right) - \upsilon_{1} I_{R2} \left( t \right)$$
(7)
$$\begin{aligned} \frac{{dI_{12} \left( t \right)}}{dt} = & \alpha_{12} S\left( t \right) + \delta_{1} \left( {A_{1} \left( t \right) + I_{1} \left( t \right)} \right) \\ & + \delta_{2} \left( {A_{2} \left( t \right) + I_{2} \left( t \right)} \right) - \left( {\upsilon_{12} + \omega_{12} } \right)I_{12} \left( t \right) \\ \end{aligned}$$
(8)
$$\frac{{dR_{12} \left( t \right)}}{dt} = \upsilon_{1} I_{R2} \left( t \right) + \upsilon_{2} I_{1R} \left( t \right) + \upsilon_{12} I_{12} \left( t \right) - \mu_{12} R_{12} \left( t \right)$$
(9)
$$\frac{{dP_{12} \left( t \right)}}{dt} = \omega_{12} I_{12} \left( t \right)$$
(10)
$$\begin{aligned} \frac{{dE_{2} \left( t \right)}}{dt} = & \alpha_{c} \frac{{\left( {1 - u_{4} \left( t \right)} \right)}}{{N_{H} }}E_{2} \left( t \right)\left( {1 - u_{5} \left( t \right)} \right)Z\left( t \right)S\left( t \right) \\ & - \left( {1 - \varphi_{2} } \right)\alpha_{2} E_{2} \left( t \right) - \varphi_{2} \alpha_{2} E_{2} \left( t \right) \\ \end{aligned}$$
(11)
$$\frac{{dA_{2} \left( t \right)}}{dt} = \left( {1 - \varphi_{2} } \right)\alpha_{2} E_{2} \left( t \right) - \left( {\delta_{2} + \beta_{2} + \omega_{2} } \right)A_{2} \left( t \right)$$
(12)
$$\frac{{dI_{2} \left( t \right)}}{dt} = \varphi_{2} \alpha_{2} E_{2} \left( t \right) - \left( {\delta_{2} + \beta_{2} + \omega_{2} } \right)I_{2} \left( t \right)$$
(13)
$$\frac{{dR_{2} \left( t \right)}}{dt} = \beta_{2} \left( {A_{2} \left( t \right) + I_{2} \left( t \right)} \right) - \left( {\mu_{2} + \lambda_{2} } \right)R_{2} \left( t \right)$$
(14)
$$\frac{{dP_{2} \left( t \right)}}{dt} = \omega_{2} \left( {A_{2} \left( t \right) + I_{2} \left( t \right)} \right)$$
(15)
$$\frac{{dI_{1R} \left( t \right)}}{dt} = \lambda_{2} R_{2} \left( t \right) - \upsilon_{2} I_{1R} \left( t \right)$$
(16)
$$\frac{dX\left( t \right)}{{dt}} = \mu_{3} - X\left( t \right)\left( {\alpha_{3} \left( {1 - u_{4} \left( t \right)} \right)\left( {A_{2} \left( t \right) + I_{2} \left( t \right)} \right) + \mu_{3} + u_{5} \left( t \right)} \right)$$
(17)
$$\begin{aligned} \frac{dY\left( t \right)}{{dt}} = & X\left( t \right)\left( {\alpha_{3} \left( {1 - u_{4} \left( t \right)} \right)\left( {A_{2} \left( t \right) + I_{2} \left( t \right)} \right)} \right) \\ & - Y\left( t \right)\left( {\mu_{3} + \lambda_{3} + u_{5} \left( t \right)} \right) \\ \end{aligned}$$
(18)
$$\frac{dZ\left( t \right)}{{dt}} = \lambda_{3} Y\left( t \right) - \left( {\mu_{3} + u_{5} \left( t \right)} \right)Z\left( t \right)$$
(19)

Equation (1) defines all susceptible humans’ populations for both COVID-19 and Chikungunya infections. We will consider that the total population in Yemen, including those individuals recovered from any infectious, are susceptible to infection with COVID-19 or Chikungunya infections, or both, in varying proportions. Four times-variant variables are suggested to reduce the susceptible individuals: social distancing, quarantining, personal protection and rate of pesticides that are used to kill mosquitoes. \({u}_{1}\left(t\right)\) and \({u}_{2}\left(t\right)\) which correspond to the social measures taken during the course of the COVID-19 pandemic. \({u}_{1}\left(t\right)\) refers to the control rate of social distancing of the exposed individuals. \({u}_{2}\left(t\right)\) refers to the control rate of the quarantine of the infected individuals. On the other hand, \({u}_{4}\left(t\right),\) and \({u}_{5}\left(t\right)\) correspond to the measures taken during the course of the Chikungunya pandemic. The time-dependent input \({u}_{4}\left(t\right)\) measures the personal protection from CHIKV through education and awareness from the risk of CHIKV and how to protect yourself and your family using mosquitoes’ nets, wearing long clothes and not exposing the body to mosquitoes’ bites. \({u}_{5}\left(t\right)\) refers to the control rate of using the insecticides and larvicides to fight mosquitoes. Equation (2) describes the individuals exposed to COVID-19. This epidemiological class includes a fraction of susceptible individuals minus infected individuals with COVID-19, irrespective of the fact that they have symptoms or not. Equation (3) describes the individuals infected with COVID-19 that are asymptomatic or unconfirmed. The individuals for this epidemiological class come from the exposed class at a rate of \(\left(1-{\varphi }_{1}\right){\alpha }_{1}\). This class will be left, either by confirmation of COVID-19 infection through a screening test, by direct recovery, by direct perished due to COVID-19 infection, or by co-infection at a rate of \({\delta }_{1}\). This epidemiological class contributes to spreading infection in a latent way, so our aim in this work is to reduce the number of the individuals of this class by increasing the level of test kits for the largest possible rate of the exposed individuals. The screening level is measured by a time-dependent parameter \({u}_{3}\left(t\right)\). Equation (4) describes the confirmed infected individuals who have been tested. The individuals of this class come directly from the exposed class at a rate of \({\varphi }_{1}{\alpha }_{1}\) or by confirming the asymptomatic individuals at a rate of \({u}_{3}\left(t\right)\). This epidemiological class will be left either for recovery at a rate of \({\beta }_{1}\), for death at a rate of \({\omega }_{1}\), or for co-infection at a rate of \({\delta }_{1}\). Equation (5) describes the individuals who have recovered from COVID-19 with or without symptoms. This class is increased by the recovery of the individuals affected with COVID-19 of both classes at a rate of \({\beta }_{1}\). Also, this class is decreased by infection with Chikungunya at a rate \({\lambda }_{1}\) or again infection by COVID-19 at a rate \({\mu }_{1}\). Equation (6) describes the individuals perished due to COVID-19 at a rate of \({\omega }_{1}\). Equation (7) represents the individuals who have recovered from COVID-19 but are still susceptible to Chikungunya. This class is increased by recovering the individuals infected with COVID-19 and still susceptible to CHIKV at a rate of \({\lambda }_{1}\). It is decreased by recovery from both diseases at a rate of \({\upsilon }_{1}\). Equation (8) characterizes the individuals infected with both COVID-19 and Chikungunya diseases, either consecutively or simultaneously. The inputs of this class come from either the infection of susceptible individuals or if a patient with one infection becomes infected of the other infection at rates \({\alpha }_{12},{\delta }_{1}, \mathrm{and }\quad{\delta }_{2},\) respectively. It is decreased by the individuals’ recovered at a rate of \({\upsilon }_{12}\) or individuals’ death at a rate of \({\omega }_{12}.\) Equation (9) describes the individuals recovered from both COVID-19 and Chikungunya diseases, either consecutively or simultaneously. It is increased when infected individuals recover from Chikungunya, COVID-19, or both at rates of \({\upsilon }_{1}, { \upsilon }_{2}, \mathrm{and }\quad {\upsilon }_{12}\), respectively. It is decreased by natural death or by being susceptible to both infections at a rate of \({\mu }_{12}.\) Equation (10) describes the individuals perished due to both COVID-19 and Chikungunya diseases at a rate of \({\omega }_{12}\).

Equation (11) defines the individuals exposed to Chikungunya. This epidemiological class includes a fraction of susceptible individuals minus infected individuals with Chikungunya, with or without symptoms. The time-dynamic variables \({u}_{4}\left(t\right)\) and \({u}_{5}\left(t\right)\) are being entered to control the number of the exposed individuals to Chikungunya. Equation (12) describes the individuals infected with Chikungunya who are asymptomatic or unconfirmed. The individuals for this epidemiological class come from the exposed class at a rate of \(\left(1-{\varphi }_{2}\right){\alpha }_{2}\). Leaving this class is carried out with four possibilities, either by confirming the individuals infected with CHIKV by testing, by direct recovery, by direct death due to Chikungunya, or by co-infection. Equation (13) describes the individuals infected with Chikungunya. The individuals of this class come directly from the exposed class at a rate of \({\varphi }_{2}{\alpha }_{2}\). Leaving this class also carried out three possibilities, either by recovery at a rate of \({\beta }_{2}\), or death at a rate of \({\omega }_{2}\), or for co-infection at a rate of \({\delta }_{2}\). Equation (14) defines the individuals recovered from Chikungunya at a rate of \({\beta }_{2}\). This epidemiological class is decreased by returning to being susceptible to coinfection or COVID-19 at rates of \({\mu }_{2}\quad \mathrm{and }\quad {\lambda }_{2}\), respectively. Equation (15) describes individuals’ deaths due to Chikungunya at a rate of \({\omega }_{2}\). Equation (16) describes the individuals recovered from Chikungunya but are still susceptible to COVID-19 at a rate of \({\lambda }_{2}\).

On the other hand, the last three equations describe mosquito vectors. Equation (17) determines all the susceptible mosquito populations. Equation (18) describes the exposed mosquito. This epidemiological class increases when the mosquito bites a person infected with Chikungunya at a rate of \({\alpha }_{3}\). Equation (19) describes all the infected mosquito populations. This class is the most dangerous class in the spread of the virus among humans. However, time-dynamic variables \({u}_{4}\left(t\right)\) and \({u}_{5}\left(t\right)\) are used to control of the number of the mosquitoes in these classes. \({u}_{4}\left(t\right)\) controls the number of the individuals infected with Chikungunya and thus reduces the number of the infected mosquitoes. \({u}_{5}\left(t\right)\) is used to eliminate mosquito colonies or larvae and eggs as a whole by using pesticides as well as not to create a fertile environment for mosquitoes to breed. Overall, the parameters in this work are divided into three categories. The first category of parameters includes time-varying inputs that reflect levels of measures taken during the course of the COVID-19 and Chikungunya pandemics. Social distancing, quarantining, COVID-19 test kits, personal protection from Chikungunya using mosquito nets, and wearing long-sleeved shirts and pants as well as insecticides and larvicides to fight mosquitoes are the five parameters in this category. The second category of parameters includes values that need to be estimated from real data collected from Yemen such as transmission rate, recovered rate, and death rate. The third category of parameters includes values taken from the literature.

3 Particle swarm optimization

Particle swarm optimization is a metaheuristic algorithm based on the principles of behavior of flocks of birds, fish schooling, or insect swarms for finding food positions. This algorithm was developed by Kennedy and Eberhart (1995). The optimal solution of the given function is the swarm position that can be calculated using the following equation:

$$x_{k + 1}^{i} = x_{k}^{i} + v_{k + 1}^{i}$$
(20)

where \(x\) is the particle position, and \(v\) is the velocity of the particle that are given in the following equation:

$$\begin{aligned} v_{k + 1}^{i} = & \omega v_{k}^{i} + c_{1} \cdot \gamma_{1} \left( {x_{{\left( {Pbest} \right)k}}^{i} - x_{k}^{i} } \right) \\ &+ c_{2} \cdot \gamma_{2} \left( {x_{{\left( {Gbest} \right)}}^{i} - x_{k}^{i} } \right) \\ \end{aligned}$$
(21)

where \(\omega\) is the inertia weight, \({c}_{1}, {c}_{2}\) are coefficients that indicate the swarm’s ability level to the cognitive of personal and social successes,\({\gamma }_{1},{\gamma }_{2}\in rand \left(\mathrm{0,1}\right)\), \({x}_{(Pbest)k}^{i}\) is the personal best solution of swarm position, and \({x}_{(Gbest)}^{i}\) is the global best solution for all swarms and for all iterations as well. Table 3 report the parameters of PSO that are used in this work. Besides, the PSO pseudo-code is expressed in detail by the following algorithm:

Table 3 PSO configuration parameters
Full size table
figure a

4 Parameter estimation

In this section, the parameters estimation problem is solved by using PSO. The real data on COVID-19 and Chikungunya outbreaks in Yemen during the period March 1, 2020 to May 30, 2020 are used to solve the parameters estimation problem. The COVID-19 data were taken from the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University (https://github.com/CSSEGISandData/COVID-19). The Chikungunya data were obtained from health officials in Yemen. Since the Chikungunya data in Yemen were recorded weekly, we considered the data for both diseases weekly, not daily.

The mean squared error (MSE) between the historical data and the predicted data is minimized using the PSO, where the Eq. (22) is used as the fitness function in PSO.

$$\min E_{0} = \mathop \sum \limits_{l = 0}^{N} w_{l} x_{l} - \widehat{{x_{l} }}\left( t \right)^{2}$$
(22)

where \({w}_{l}\) represents normalization weights and \({x}_{l} \mathrm{and }\widehat{{x}_{l}}\) represent the number of each epidemiological class and its predictions, respectively. Table 1 reports the mean and standard deviation (Std.) of the estimated parameters for Yemen during the period (March 2020–May 2020).

For brevity, only one of the experiments, which were carried out during solving the parameters estimation problem, is discussed and shown in Fig. 2. The first panel displays simulations for all human classes of historical data and the data calculated using the system of Eqs. (1)–(19). The second panel shows the estimated trajectories of time-dynamic functions, and the rest of the panels illustrate the infected, death, and recovered for both the COVID-19 and CHIKV, while the last panel shows the trajectory of the mosquito vector obtained from simulating the system (1)–(19). It’s clear from the panel of infected with COVID-19 that the end of the epidemic is not coming soon, while the CHIKV epidemic curve will come back down faster as shown in the panel of infected with CHIKV. Also, from the same panel, the curve fitting does not exactly match the historical data, but the predicted data are still logical. We can see from the panels of the death and recovered individuals for both infections the cumulative numbers continue to increase over time. Besides, the panel of the mosquito populations continues to decrease by the passage of time, which explains the effectiveness of pesticides and the different seasons as well. On the other hand, we can clearly see in panels 3 to 9 that the curves obtained using PSO are more fitness than those obtained using Pyomo optimization modelling. This confirms that the proposed algorithm is effective.

Fig. 2
figure 2

The result of simulation for all human classes, the estimated trajectories of the time-dynamic functions, and analysis and week-wise prediction using the proposed system. The real data represented by the black dotted, the red dotted lines represent the fitting line from the proposed system, the predicted data using PSO represented by the red solid lines, and the predicted data using Pyomo optimization modelling represented by the blue solid lines (color figure online)

Full size image

5 Optimal control problem

The basic principle of the proposed optimal control model is to curb epidemic outbreaks by breaking the link between the epidemic vector with individuals through time-dynamic interventions, so that the number of infected individuals is reduced as well as the detection of infected individuals without symptoms by increasing test kits and then isolating and treating affected individuals. Moreover, minimizing the cost associated with optimal control is another goal for decision makers. Five control functions, i.e. \({u}_{1}\left(t\right),{u}_{2}\left(t\right),{u}_{3}\left(t\right)\), \({u}_{4}\left(t\right)\) and \({u}_{5}\left(t\right)\), are considered in this work. The first control function \({u}_{1}\left(t\right)\) represents the control rate of the social distancing. This variable can be applied to the whole society by raising awareness and obliging individuals to wear masks, personal protection, hygiene and spacing between individuals at least a meter distance, and this, in turn, contributes greatly to breaking the chain of transmission between humans for COVID-19 directly and also indirectly contributes to limiting the transmission of the Chikungunya. By increasing the control rate of this variable, the number of people who are at risk of infection decreases. The second control function \({u}_{2}\left(t\right)\) indicates quarantine and insolation rates. It is easy to apply isolation of individuals who are confirmed to be infected, but it is difficult to implement quarantine on a large scale, especially in Yemen, where most of the population live on daily wages. Hence, comes the importance of the third variable \({u}_{3}\left(t\right)\), which is to increase the number of tests. It is possible to discover infected individuals without symptoms and work to isolate and treat them, which contributes to curbing the spread of COVID-19. The fourth variable \({u}_{4}\left(t\right)\) refers to the rate of personal protection through protective clothing and the rate of awareness and education of the risks of infectious diseases by mosquitoes including CHIKV. Increasing the rate contributes to reducing the infected individuals with CHIKV. The fifth variable \({u}_{5}\left(t\right)\) indicates the importance of purity of the surrounding environment, the seriousness of the swamps, and the fertile places for mosquito breeding. Increasing the use of pesticides contributes to killing mosquitoes and reduces the transmission rate of CHIKV to humans.

Two objectives are proposed in this work. The first one is to minimize the infected individuals with each infection or both. The second one is to minimize the cost associated with optimal control strategies.

$$f_{1} = \mathop {\min }\limits_{{I_{1} \left( t \right),I_{2} \left( t \right),I_{12} \left( t \right)}} \mathop \smallint \limits_{{t_{0} }}^{{t_{f} }} z_{1} I_{1} \left( t \right) + z_{2} I_{2} \left( t \right) + z_{3} I_{12} \left( t \right)$$
(23)
$$\begin{aligned} f_{2} = & \mathop {\min }\limits_{{u_{1} \left( t \right),u_{2} \left( t \right),u_{3} \left( t \right),u_{4} \left( t \right),u_{5} \left( t \right)}} \mathop \smallint \limits_{{t_{0} }}^{{t_{f} }} A\left( {u_{1} \left( t \right)} \right)^{2} + B\left( {u_{2} \left( t \right)} \right)^{2} \\ & + C\left( {u_{3} \left( t \right)} \right)^{2} + D\left( {u_{4} \left( t \right)} \right)^{2} + E\left( {u_{5} \left( t \right)} \right)^{2} \\ \end{aligned}$$
(24)

(1–19)

$$\mathop {\max }\limits_{t} L{(t)} \leq \mathop {L^{peak}}, \quad L = I_{1}, I_{2}, Z$$
(25)
$$u_{1} \left( t \right) \in \left[ {0.05, 0.5} \right]$$
(26)
$$u_{2} \left( t \right) \in \left[ {0.01, 0.3} \right]$$
(27)
$$u_{3} \left( t \right) \in \left[ {0.1, 0.3} \right]$$
(28)
$$u_{4} \left( t \right) \in \left[ {0, 1} \right]$$
(29)
$$u_{5} \left( t \right) \in \left[ {0, 1} \right]$$
(30)

The objective function in Eq. (23) minimizes the number of the individuals infected with COVID-19, CHIKV, and both. The objective function in Eq. (24) represents the cost associated with the optimal control strategies. The dynamic differential Eqs. (1)–(19) are also included as constraints of the optimal control model. Constraint (25) defines the maximum limit of the infected individuals for each infection and the peak value of the infected mosquitoes as well. The constraint bounds (26)–(30) define the ranges of the time-dynamic parameters, where \({z}_{1}, {z}_{2},{z}_{3}, A, B, C,D,\) and \(E\) are weight coefficients. The optimal control model is assumed during the full-time horizon \(\left[{t}_{0}, {t}_{f}\right]\), where \({t}_{f}\) is 52 weeks.

The summarized steps of the present work are given as the following:

figure b

There are two approaches to solve the above optimal control model, namely, indirect methods such as mathematical analysis and direct methods such as PSO. In this work, we use the PSO to solve the optimal control model. Before we solve it using PSO, we briefly illustrate the mathematical analysis to prove the theorem of the solution.

In mathematical (indirect) methods, Pontryagin’s maximum principle is used to solve the optimal control model, through driving the Hamiltonian function and defining the necessary conditions for the optimal control. The optimal solution of the control model is \(\left({u}_{1}^{*}\left(t\right),{u}_{2}^{*}\left(t\right),{u}_{3}^{*}\left(t\right),{u}_{4}^{*}\left(t\right),{u}_{5}^{*}\left(t\right)\right)\) in which

$$\begin{gathered} J\left( {u_{1}^{*} \left( t \right),u_{2}^{*} \left( t \right),u_{3}^{*} \left( t \right),u_{4}^{*} \left( t \right),u_{5}^{*} \left( t \right)} \right) \hfill \\ \quad = \min \left\{ \begin{gathered} J\left( {u_{1} \left( t \right),u_{2} \left( t \right),u_{3} \left( t \right),u_{4} \left( t \right),u_{5} \left( t \right)} \right) \hfill \\ \left| {u_{1} \left( t \right),u_{2} \left( t \right),u_{3} \left( t \right),u_{4} \left( t \right),u_{5} \left( t \right) \in {\Psi }} \right. \hfill \\ \end{gathered} \right\}, \hfill \\ \end{gathered}$$
(31)

where \(\Psi =\left({u}_{1}\left(t\right),{u}_{2}\left(t\right),{u}_{3}\left(t\right),{u}_{4}\left(t\right),{u}_{5}\left(t\right)\right)\) and \(0\le {u}_{1}\left(t\right)\le 0.5\), \(0\le {u}_{2}\left(t\right)\le 0.3\), \(0\le {u}_{3}\left(t\right)\le 0.3\), \(0\le {u}_{4}\left(t\right)\le 1\), and \(0\le {u}_{5}\left(t\right)\le 1\)

The Hamiltonian H is defined as:

$$\begin{aligned} H = & z_{1} I_{1} \left( t \right) + z_{2} I_{2} \left( t \right) + z_{3} I_{12} \left( t \right) \\ & + A\left( {u_{1} \left( t \right)} \right)^{2} + B\left( {u_{2} \left( t \right)} \right)^{2} \\ & + C\left( {u_{3} \left( t \right)} \right)^{2} + D\left( {u_{4} \left( t \right)} \right)^{2} \\ & + E\left( {u_{5} \left( t \right)} \right)^{2} + \mathop \sum \limits_{l = 1}^{19} M_{l} g_{l} \\ \end{aligned}$$

where \({M}_{l}\) is an adjoint variables, which corresponds to each \({g}_{l}\) that represents the right-hand side of the system Eqs. (1)–(19).

$$\begin{aligned} H = & z_{1} I_{1} \left( t \right) + z_{2} I_{2} \left( t \right) + z_{3} I_{12} \left( t \right) + A\left( {u_{1} \left( t \right)} \right)^{2} \\ \, + B\left( {u_{2} \left( t \right)} \right)^{2} + C\left( {u_{3} \left( t \right)} \right)^{2} + D\left( {u_{4} \left( t \right)} \right)^{2} + E\left( {u_{5} \left( t \right)} \right)^{2} \\ \, + M_{S} \left( \begin{gathered} \mu_{1} R_{1} \left( t \right) + \mu_{2} R_{2} \left( t \right) + \mu_{12} R_{12} \left( t \right) + \mu N_{H} \hfill \\ - \left( \begin{gathered} \frac{{\left( {1 - u_{1} \left( t \right)} \right)}}{{N_{H} }}E_{1} \left( t \right) + \frac{{\left( {1 - u_{2} \left( t \right)} \right)}}{{N_{H} }}I_{1} \left( t \right) \hfill \\ + \alpha_{c} \frac{{\left( {1 - u_{4} \left( t \right)} \right)}}{{N_{H} }}E_{2} \left( t \right)\left( {1 - u_{5} \left( t \right)} \right)Z\left( t \right) + \alpha_{12} \hfill \\ \end{gathered} \right)S\left( t \right) \hfill \\ \end{gathered} \right) \\ & + M_{{E_{1} }} \left( \begin{gathered} \left( {\frac{{\left( {1 - u_{1} \left( t \right)} \right)}}{{N_{H} }}E_{1} \left( t \right) + \frac{{\left( {1 - u_{2} \left( t \right)} \right)}}{{N_{H} }}I_{1} \left( t \right)} \right)S\left( t \right) \hfill \\ - \left( {1 - \varphi_{1} } \right)\alpha_{1} E_{1} \left( t \right) - \varphi_{1} \alpha_{1} E_{1} \left( t \right) \hfill \\ \end{gathered} \right) \\ & + M_{{A_{1} }} \left( {\left( {1 - \varphi_{1} } \right)\alpha_{1} E_{1} \left( t \right) - \left( {\delta_{1} + u_{3} \left( t \right) + \beta_{1} + \omega_{1} } \right)A_{1} \left( t \right)} \right) \\ & + M_{{I_{1} }} \left( {u_{3} \left( t \right)A_{1} \left( t \right) + \varphi_{1} \alpha_{1} E_{1} \left( t \right) - \left( {\delta_{1} + \beta_{1} + \omega_{1} } \right)I_{1} \left( t \right)} \right) \\ & + M_{{R_{1} }} \left( {\beta_{1} \left( {A_{1} \left( t \right) + I_{1} \left( t \right)} \right) - \left( {\mu_{1} + \lambda_{1} } \right)R_{1} \left( t \right)} \right) \\ & + M_{{P_{1} }} \left( {\omega_{1} \left( {A_{1} \left( t \right) + I_{1} \left( t \right)} \right)} \right) + M_{{I_{R2} }} \left( {\lambda_{1} R_{1} \left( t \right) - \upsilon_{1} I_{R2} \left( t \right)} \right) \\ & + M_{{I_{12} }} \left( \begin{gathered} \alpha_{12} S\left( t \right) + \delta_{1} \left( {A_{1} \left( t \right) + I_{1} \left( t \right)} \right) \hfill \\ + \delta_{2} \left( {A_{2} \left( t \right) + I_{2} \left( t \right)} \right) - \left( {\upsilon_{12} + \omega_{12} } \right)I_{12} \left( t \right) \hfill \\ \end{gathered} \right) \\ & + M_{{R_{12} }} \left( {\upsilon_{1} I_{R2} \left( t \right) + \upsilon_{2} I_{1R} \left( t \right) + \upsilon_{12} I_{12} \left( t \right) - \mu_{12} R_{12} \left( t \right)} \right) \\ & + M_{{P_{12} }} \left( {\omega_{12} I_{12} \left( t \right)} \right) + M_{{E_{2} }} \left( \begin{gathered} \alpha_{c} \frac{{\left( {1 - u_{4} \left( t \right)} \right)}}{{N_{H} }}E_{2} \left( t \right)\left( {1 - u_{5} \left( t \right)} \right)Z\left( t \right)S\left( t \right) \hfill \\ - \left( {1 - \varphi_{2} } \right)\alpha_{2} E_{2} \left( t \right) - \varphi_{2} \alpha_{2} E_{2} \left( t \right) \hfill \\ \end{gathered} \right) \\ & + M_{{A_{2} }} \left( {\left( {1 - \varphi_{2} } \right)\alpha_{2} E_{2} \left( t \right) - \left( {\delta_{2} + \beta_{2} + \omega_{2} } \right)A_{2} \left( t \right)} \right) \\ & + M_{{I_{2} }} \left( {\varphi_{2} \alpha_{2} E_{2} \left( t \right) - \left( {\delta_{2} + \beta_{2} + \omega_{2} } \right)I_{2} \left( t \right)} \right) \\ & + M_{{R_{2} }} \left( {\beta_{2} \left( {A_{2} \left( t \right) + I_{2} \left( t \right)} \right) - \left( {\mu_{2} + \lambda_{2} } \right)R_{2} \left( t \right)} \right) \\ & + M_{{P_{2} }} \left( {\omega_{2} \left( {A_{2} \left( t \right) + I_{2} \left( t \right)} \right)} \right) + M_{{I_{1R} }} \left( {\lambda_{2} R_{2} \left( t \right) - \upsilon_{2} I_{1R} \left( t \right)} \right) \\ & + M_{X} \left( {\mu_{3} - X\left( t \right)\left( {\alpha_{3} \left( {1 - u_{4} \left( t \right)} \right)\left( {A_{2} \left( t \right) + I_{2} \left( t \right)} \right) + \mu_{3} + u_{5} \left( t \right)} \right)} \right) \\ & + M_{Y} \left( {X\left( t \right)\left( {\alpha_{3} \left( {1 - u_{4} \left( t \right)} \right)\left( {A_{2} \left( t \right) + I_{2} \left( t \right)} \right)} \right) - Y\left( t \right)\left( {\mu_{3} + \lambda_{3} + u_{5} \left( t \right)} \right)} \right) \\ & + M_{Z} \left( {\lambda_{3} Y\left( t \right) - \left( {\mu_{3} + u_{5} \left( t \right)} \right)Z\left( t \right)} \right) \\ \end{aligned}$$
(32)

where \({M}_{S}, {M}_{{E}_{1}}, {M}_{{A}_{1}}, {M}_{{I}_{1}}, {M}_{{R}_{1}}, {M}_{{P}_{1}},{M}_{{I}_{R2}}, {M}_{{I}_{12}}, {M}_{{R}_{12}},{M}_{{P}_{12}},{M}_{{E}_{2}}, {M}_{{A}_{2}},{M}_{{I}_{2}}, {M}_{{R}_{2}}, {M}_{{P}_{2}}\),\({M}_{{I}_{1R}},\) \({M}_{X}\) \({M}_{Y},\) and \({M}_{Z}\) are adjoint variables or co-state variables.

Theorem

Given the optimal control \({u}_{1}^{*}\left(t\right),{u}_{2}^{*}\left(t\right),{u}_{3}^{*}\left(t\right),{u}_{4}^{*}\left(t\right), {u}_{5}^{*}\left(t\right)\) and solutions \(S, {E}_{1}, {A}_{1}, {I}_{1}, {R}_{1}, {P}_{1},{I}_{R2},{I}_{12}, {R}_{12},{P}_{12},{E}_{2}, {A}_{2},{I}_{2}, {R}_{2}, {P}_{2}\),\({I}_{1R}, X,Y\) and \(Z\) of the corresponding state system (1)–(19) that minimize \(J\left({u}_{1}\left(t\right),{u}_{2}\left(t\right),{u}_{3}\left(t\right),{u}_{4}\left(t\right),{u}_{5}\left(t\right)\right)\) over \(\Psi .\) There exist adjoint variables \({M}_{S}, {M}_{{E}_{1}}, {M}_{{A}_{1}}, {M}_{{I}_{1}}, {M}_{{R}_{1}}, {M}_{{P}_{1}},{M}_{{I}_{R2}}, {M}_{{I}_{12}}, {M}_{{R}_{12}},{M}_{{P}_{12}},{M}_{{E}_{2}}, {M}_{{A}_{2}},{M}_{{I}_{2}}, {M}_{{R}_{2}}, {M}_{{P}_{2}}\),\({M}_{{I}_{1R}},\) \({M}_{X}\) \({M}_{Y},\) and \({M}_{Z}\) such that

$$\frac{{ - dM_{l} }}{dt} = \frac{\partial H}{{\partial l}}$$
(33)

where \(l=S, {E}_{1}, {A}_{1}, {I}_{1}, {R}_{1}, {P}_{1},{I}_{R2},{I}_{12}, {R}_{12},{P}_{12},{E}_{2}, {A}_{2},{I}_{2}, {R}_{2}, {P}_{2}\),\({I}_{1R}, X,Y\) and \(Z\) with transversality conditions

$$\begin{gathered} M_{S} \left( {t_{f} } \right) = M_{{E_{1} }} \left( {t_{f} } \right) = M_{{A_{1} }} \left( {t_{f} } \right) = M_{{I_{1} }} \left( {t_{f} } \right) \hfill \\ \quad = M_{{R_{1} }} \left( {t_{f} } \right) = M_{{P_{1} }} \left( {t_{f} } \right) = M_{{I_{R2} }} \left( {t_{f} } \right) = M_{{I_{12} }} \left( {t_{f} } \right) \hfill \\ \quad = M_{{R_{12} }} \left( {t_{f} } \right) = M_{{P_{12} }} \left( {t_{f} } \right) = M_{{E_{2} }} \left( {t_{f} } \right) = M_{{A_{2} }} \left( {t_{f} } \right) \hfill \\ \quad = M_{{I_{2} }} \left( {t_{f} } \right) = M_{{R_{2} }} \left( {t_{f} } \right) = M_{{P_{2} }} \left( {t_{f} } \right) = M_{{I_{1R} }} \left( {t_{f} } \right) \hfill \\ \quad = M_{X} \left( {t_{f} } \right) = M_{Y} \left( {t_{f} } \right) = M_{Z} \left( {t_{f} } \right) = 0 \hfill \\ \end{gathered}$$

and

$$\begin{gathered} u_{1}^{*} \left( t \right) = \min \left\{ {1,\max \left( {0,{\Omega }_{1} } \right)} \right\} \hfill \\ u_{2}^{*} \left( t \right) = \min \left\{ {1,\max \left( {0,{\Omega }_{2} } \right)} \right\} \hfill \\ u_{3}^{*} \left( t \right) = \min \left\{ {1,\max \left( {0,{\Omega }_{3} } \right)} \right\} \hfill \\ u_{4}^{*} \left( t \right) = \min \left\{ {1,\max \left( {0,{\Omega }_{4} } \right)} \right\} \hfill \\ u_{5}^{*} \left( t \right) = \min \left\{ {1,\max \left( {0,{\Omega }_{5} } \right)} \right\} \hfill \\ \end{gathered}$$

where

$${\Omega }_{1} = \frac{{\left( {M_{{E_{1} }} - M_{S} } \right)E_{1} \left( t \right)S\left( t \right)}}{{2AN_{H} }}$$
$${\Omega }_{2} = \frac{{\left( {M_{{E_{1} }} - M_{S} } \right)I_{1} \left( t \right)S\left( t \right)}}{{2BN_{H} }}$$
$${\Omega }_{3} = \frac{{\left( {M_{{A_{1} }} - M_{{I_{1} }} } \right)A_{1} \left( t \right)}}{2C}$$
$${\Omega }_{4} = \frac{1}{2D}\left[ \begin{gathered} \left( {M_{{E_{2} }} - M_{S} } \right)\left( {\frac{{\alpha_{c} E_{2} \left( t \right)\left( {1 - u_{5} \left( t \right)} \right)Z\left( t \right)S\left( t \right)}}{{N_{H} }}} \right) \hfill \\ + \left( {M_{Y} - M_{X} } \right)\left( {\alpha_{3} X\left( t \right)\left( {A_{2} \left( t \right) + I_{2} \left( t \right)} \right)} \right) \hfill \\ \end{gathered} \right]$$
$${\Omega }_{5} = \frac{1}{2E}\left[ \begin{gathered} \left( {M_{{E_{2} }} - M_{S} } \right)\left( {\frac{{\alpha_{c} E_{2} \left( t \right)\left( {1 - u_{4} \left( t \right)} \right)Z\left( t \right)S\left( t \right)}}{{N_{H} }}} \right) \hfill \\ + M_{X} X\left( t \right) + M_{Y} Y\left( t \right) + M_{Z} Z\left( t \right) \hfill \\ \end{gathered} \right]$$
(34)

Proof.

See Appendix A.

6 Numerical simulations

In this section, we investigated and analyzed the impact of the five dynamic control measures, the peak limits, and the coefficient weights of control measures in the objective function, which will determine the best strategy to curb the rapid spread of both Chikungunya and COVID-19 in Yemen in 2020. The initial conditions that are used in all the strategies of the present model are mentioned in Table 1. Besides, the parameters that are needed for estimation are reported in Table 4, and the other parameters are reported in Table 2. We assume the weights A, B, C, D, and E are equal one all simulations except when discussing the impact of their changes. We also used the same limit peaks for all simulations except when discussing the impact of limit peaks constraints. The weighted method was employed to convert the bi-objective optimization model into a single-objective optimization model. In addition, the dynamic differential equations system (1–19) was discretized using the orthogonal collocation method with considering the time domain which consists of weekly finite elements. Also, we used the penalty function to deal with the constraints. Then, the new optimization model was be solved using PSO. It is worth mentioning here that the proposed algorithm was implemented in Python 3.7. Plus, the figures were omitted for each case, and only the figures that are related to the comparisons were shown, for the sake of brevity. The strategies are discussed in this work as the following.

Table 4 The estimated parameter values using PSO
Full size table

Strategy 1: In this strategy, we discussed three levels of controls, which are max control, partial control and no control (baseline). In the max control level, the range of time-dynamic variables were \({0.4\le u}_{1}\left(t\right)\le 0.5\), \({0.2\le u}_{2}\left(t\right)\le 0.3\), \(0.2\le {u}_{3}\left(t\right)\le 0.3\), \(0.4\le {u}_{4}\left(t\right)\le 0.6\), \(0.3\le {u}_{5}\left(t\right)\le 0.5\), while were \({0.2\le u}_{1}\left(t\right)\le 0.4\), \({0.1\le u}_{2}\left(t\right)\le 0.2\), \(0.1\le {u}_{3}\left(t\right)\le 0.2\), \(0.3\le {u}_{4}\left(t\right)\le 0.4\), \(0.2\le {u}_{5}\left(t\right)\le 0.3\) in the partial control level. Here, the range of the inequalities for the \({u}_{1}\left(t\right), {u}_{2}\left(t\right)\) and \({u}_{4}\left(t\right)\) means that a fraction of the population who implement these rules lies between the values of the left and right sides of the inequalities. For \({u}_{3}\left(t\right)\), the rate of the availability of screening tests for the individuals exposed with COVID-19 is located between the boundaries of \({u}_{3}\left(t\right)\) inequality. Also, the rate of using the insecticide lies between the values of the left and right sides of the \({u}_{5}\left(t\right)\) inequality. We also set the coefficients of the time-dynamic variables equals zeros in the objective function in the baseline (without control) level. Figure 3 illustrates the compression of the max control, partial control, and baseline levels for both infected, death, the individuals recovered from COVID-19, infected, death, individuals recovered from CHIKV and infected mosques vector throughout the simulated time. We can see that max control comes in the first rank. It is more effective to reduce the number of infected individuals and to decrease the time-span of both epidemics, then partial control comes in the second rank, and no-control (without control) level comes in the last rank. It is normal to expect this ranking due to the impacts of interventions through applying social distancing, quarantine, detection of latent cases by providing test kits, personal protection and use of insecticides, which in turn reduces the number of individuals with both diseases. On the other hand, the cost associated with max optimal control was higher than the cost associated with other optimal controls.

Fig. 3
figure 3

Comparison of the simulation results of the control levels of strategy 1

Full size image

Strategy 2: we concentrated on the effect of the limit of the peaks in the constraint (25). Two cases were investigated, i.e. small and large limit peaks. For infected humans, the small limit of peaks was \({10}^{5}\) while the large limit of the peaks equals the total of population in Yemen \(29\times {10}^{6}\). The small and large limit peaks for the infected mosquitos were \({10}^{4}\) and \({10}^{5}\) respectively. We also used the same range of time-dynamic variables in all cases. As it is shown in Fig. 4, the right-hand side values of limit constraints affect all epidemiological classes. The number of individuals was less when the limit constraints were small. We conclude that the number of individuals can be reduced by decreasing the right-hand side values of limit constraints and vice versa, i.e., we can increase the number of individuals for all classes by neglecting limit constraints. However, the cost associated with small limit peaks was higher than the cost associated with large limit peaks.

Fig. 4
figure 4

Comparison of the simulation results of two cases of strategy 2

Full size image

Strategy 3: In this strategy, we focused on the effect of the combination of the coefficients of intervention variables in the second objective function, and whether or not they will be reflected in the number of individuals in the epidemiological classes. We investigated that in two cases. In the first case, all the coefficients were equal one \(A=B=C=D=E=1\), and in the another case, \(A=0.3\), \(B=0.1\), \(C=0.4\), \(D=0.6\), and \(E=0.5.\) Figure 5 shows the simulation of the two cases throughout the time horizon. It is clear that the first case is superior to the other case in all epidemiological classes. It is also known that the coefficients of the intervention variables are the relative cost associated with these interventions. Therefore, the more coefficient values are, the higher the cost value is. Thus, as expected, the cost of the first case (with coefficients are one) is higher than the cost of the other case (with coefficients are less than one).

Fig. 5
figure 5

Comparison of the simulation results of two cases of strategy 3

Full size image

Figure 6 shows the trade-off curve of both functions that can be obtained when using different weights, \({w}_{1}{f}_{1}+{w}_{2}{f}_{2}.\)

Fig. 6
figure 6

Trade-off curve of both functions for all cases

Full size image

It can be concluded that we need some interventions to curb the spread of the epidemics. These interventions depend on the awareness of the community as well as its economic capacity and response to implement them. It should be borne in mind that some interventions cannot be applied such as imposing quarantine and total closure, especially in poor societies that depend on daily income. Hence, we recommend that partial control is the closest and most appropriate solution that can be applicable in the Yemen case, as it will be more harmonious and compatible with other economic, social, cultural factors outside the framework of this study.

7 Conclusions

In this study, an optimal control model with strategies of COVID-19 and CHIKV co-infection was investigated. First, the state-space model was formulated, and then the parameters were estimated for the outbreaks in Yemen for the period (March 2020–May 2020). Critical epidemiological interventions were identified, and their impact on the optimal control model was investigated. The bi-objective optimal control model aims to minimize the infected individuals and the cost associated with the corresponding control. PSO algorithm was used to solve the parameter estimation problem and the optimal control model as well. Numerical simulations clearly show the importance of the present optimal control model for controlling epidemics, which may give the government highlights to select the suitable strategies that curb epidemics while simultaneously preventing economic collapse. As a future suggestion, the introduction of uncertainty to some parameters of the model can be considered.