Fermatean fuzzy soft aggregation operators and their application in symptomatic treatment of COVID-19 (case study of patients identification)

Abstract

The main focus of this paper is the application of aggregation operators (AOs) in the environment of Fermatean fuzzy soft sets (FFSS). The unique feature of the work is its application in the symptomatic treatment of the COVID-19 disease. For this purpose, the idea of FFSS is introduced which is based on the Senapati and Yagar’s Fermatean fuzzy set. Next we have defined Fermatean fuzzy soft aggregation operators (FFSAOs) like, Fermatean fuzzy soft weighted averaging (FFSWA) operator, Fermatean fuzzy soft ordered weighted averaging (FFSOWA) operator, Fermatean fuzzy soft weighted geometric (FFSWG) operator and Fermatean fuzzy soft ordered weighted geometric (FFSOWG). The prominent properties of these operators are given in details. We have also developed some approaches to solve multi-criteria decision making (MCDM) problems in Fermatean fuzzy soft (FFS) information. An introduction to the novel pandemic, safety measures, and then its possible symptomatic treatment is also provided. The developed operators are utilized in the symptomatic treatment of COVID-19 disease in order to show the practical applications and importance of these AOs as well as Fermatean fuzzy soft information. The stability of the proposed work is also proved by the comparative analysis.

Graphical abstract

1 Introduction

Decision making (DM) assumes an imperative part in real life experiences of people, it alludes to a cycle that spreads out all the choices according to the appraisal information of the makers and then chooses the brilliant one, generally occurring in regular day to day existences of ours. In the early time of social advancement, leaders utilized the genuine numbers if all else fails to offer their evaluation information. As the multi attribute decision-making (MADM) issues are getting intricate, the specialists can’t give genuine numbers to evaluate the other options. The imprecision and ambiguities of man kind decisions featured the insufficiency of the fresh set theory. Consequently, Zadeh (1965) established the set up of the fuzzy set theory for uncertain information. A fuzzy set is characterized by a membership function only and so, the concept of fuzzy set was extended to intuitionistic fuzzy sets (IFS) by Atanassov (1986). IFS consists of two functions known as the membership $\left( \mu \right)$ and non-membership $\left( \nu \right)$ functions satisfying the condition that $0\le \mu +\nu \le 1$. Since the IFS was proposed, it has received a lot of attention in many fields, such as pattern recognition, medical diagnosis, and so on (see e.g. Dengfeng and Chuntian 2002; Liu et al. 2017; Xu and Yager 2006). Since there may occur situations when decision-makers independently evaluate the degree of membership and non-membership and the sum may be greater than 1. To handle this problem in Yager (2013), the notion of Pythagorean fuzzy set (PFS) was proposed in which the quadratic sum of membership and non-membership degree is less then 1 i.e., $0\le \left( \mu \right) ^{2}+\left( \nu \right) ^{2}\le 1$, allowing decision makers to easily infer that the PFS is more useful than IFS in depicting fuzzy information. Although the PFS generalizes the IFS, it cannot describe the following decision information. A panel of experts were invited to give their opinions about the feasibility of an investment plan, and they were divided into two independent groups to make a decision. One group considered the degree of the feasibility of the investment plan as 0.8, while the other group considered the non-membership degree as 0.78. It was clearly seen that $0.8+0.78>1$, $\left( 0.8\right) ^{2}+\left( 0.78\right) ^{2}>$ 1 and thus the situation could not be described by IFS and PFS. To describe such evaluation information, Senapati and Yager (2020) proposed the Fermatean fuzzy set (FFS). FFS gives more freedom to decision makers in situation when IFS and PFS fails to support data containing uncertainty. Compared to IFS and PFS, the FFS gains a stronger ability to describe uncertain information by expanding the spatial scope of membership and non-membership. Based on FFS, Wang et al. (2019) developed a hesitant Fermatean fuzzy multicriteria decision-making method using Archimedean Bonferroni mean operators. Senapati and Yager (2019a) proposed Fermatean fuzzy information weighted aggregation operators, and Liu et al. (2019b) developed a distance measure method for Fermatean fuzzy linguistic term sets. Furthermore, Liu et al. (2019a) defined a new concept of Fermatean fuzzy linguistic set and some new operations between Fermatean fuzzy numbers (FFNs) were developed in Senapati and Yager (2019b).

Just like IFS and PFS, almost all fuzzy set extensions have some sorts of limitations. As an effective mathematical tool, Molodtsov (1999) initiated the concept of soft set theory which is free of limitations and has been demonstrated as super smart tool to deal with problems encompassing uncertainties or inexact data. Old-fashioned tools such as fuzzy set, rough set (Pawlak 1982), vague set (Chen and Tan 1994) etc., cannot be cast-off effectively because one of the root problems with these models is the absence of a sufficient number of expressive parameters to deal with uncertainty. In order to add a reasonable number of expressive parameters, Molodtsov has shown that soft set theory has a rich potential to exercise in various fields of Mathematics. Works on soft set theory are growing very rapidly with all its potentiality and are being cast-off in different areas of Mathematics (see e.g. Herawan and Deris 2011; Xiao et al. 2009). In case of the soft set, the parametrization is done with the assistance of words, sentences, functions etc. Due to the parametrization property of soft set, researchers have used soft set with different extensions of fuzzy sets like, intuitionistic fuzzy soft set (Maji et al. 2001b) and Pythagorean fuzzy soft set (Kirişci 2019). Fuzzy soft sets (Maji et al. 2001a), rough soft sets ( Feng et al. (2011)), vague soft sets (Xu et al. 2010), neutrosophic soft sets (Maji 2013), Fuzzy bi-polar soft sets (Zeb et al. 2021) etc, have been introduced with the passage of time and still research is in progress in the field of soft set theory. Considering, (i) the property of parametrization of soft set, and (ii) the stronger ability of Fermatean fuzzy set to describe uncertain information by expanding the spatial scope of membership and non-membership that allows more freedom in DM problems, we are going to define the Fermatean fuzzy soft set (FFSS). We also define some aggregation operators in the environment of FFSS. These AOs are utilized in a decision making process of investigating most serious patient among some patients with common symptoms of COVID-19. The rest of the paper is arranged as follows: In Sect. 2, basic concept related to FFSS are reviewed. The novel aggregation operators and their properties are studied in Sect. 3 and its subsections. A decision-making approach has been elaborated in Sect. 4 and its practical illustration has been provided in Sect. 5. In order to show the stability of the proposed work, a comparative analysis has been made in Sect. 6. Finally, conclusion of the presented work is given in Sect. 7.

2 Preliminaries

Some basic definitions are given here that will help in the subsequent discussion.

Definition 1

(Atanassov 1986) Let U be a universal set. An intuitionistic fuzzy set (IFS) A of U is defined as $A=\left\{ x_{i},\mu _{A}\left( x_{i}\right) ,\upsilon _{A}\left( x_{i}\right) \text { }|\text { }x_{i}\in U\right\}$ where $\mu _{A}\left( x_{i}\right)$ and $\upsilon _{A}\left( x_{i}\right)$ are respectively denoting the membership and non-membership grades of $x_{i}$ to the set A such that $0\le \mu _{A}\left( x_{i}\right) ,\upsilon _{A}\left( x_{i}\right) \le 1$ and $0\le \mu _{A}\left( x_{i}\right) +\upsilon _{A}\left( x_{i}\right) \le 1.$ The degree of indeterminacy of $x_{i}$ in the IFS A is calculated by

$$\begin{aligned} \pi _{A}\left( x_{i}\right) =1-\mu _{A}\left( x_{i}\right) -\upsilon _{A}\left( x_{i}\right) . \end{aligned}$$

Definition 2

(Yager 2013) Let U be a universal set. A Pythagorean fuzzy set (PFS) P of U is defined as P $=\left\{ x_{i},\mu _{P}\left( x_{i}\right) ,\upsilon _{P}\left( x_{i}\right) \text { }|\text { }x_{i}\in U\right\}$ where $\mu _{P}\left( x_{i}\right)$ and $\upsilon _{P}\left( x_{i}\right)$ are respectively denoting the membership and non-membership grades of $x_{i}$ to the set P such that $0\le \mu _{P}\left( x_{i}\right) ,\upsilon _{P}\left( x_{i}\right) \le 1$ and $0\le \left( \mu _{P}\left( x_{i}\right) \right) ^{2}+\left( \upsilon _{P}\left( x_{i}\right) \right) ^{2}\le 1.$ The degree of indeterminacy of $x_{i}$ in the PFS P is calculated by

$$\begin{aligned} \pi _{P}\left( x_{i}\right) =\sqrt{1-\left( \mu _{P}\left( x_{i}\right) \right) ^{2}-\left( \upsilon _{P}\left( x_{i}\right) \right) ^{2}.} \end{aligned}$$

Definition 3

(Senapati and Yager 2020) Let U be a universal set. A Fermatean fuzzy set (FFS) F of U is defined as F $=\left\{ x_{i},\mu _{F}\left( x_{i}\right) ,\upsilon _{F}\left( x_{i}\right) \text { }|\text { }x_{i}\in U\right\}$ where $\mu _{F}\left( x_{i}\right)$ and $\upsilon _{F}\left( x_{i}\right)$ are respectively denoting the membership and non-membership grades of $x_{i}$ to the set F such that $0\le \mu _{F}\left( x_{i}\right) ,\upsilon _{F}\left( x_{i}\right) \le 1$ and $0\le \left( \mu _{F}\left( x_{i}\right) \right) ^{3}+\left( \upsilon _{F}\left( x_{i}\right) \right) ^{3}\le 1$ for all $x_{i}$ in U. Also, the degree of indeterminacy of $x_{i}$ in the FFS F is calculated by,

$$\begin{aligned} \pi _{F}\left( x_{i}\right) =\root 3 \of {1-\left( \mu _{F}\left( x_{i}\right) \right) ^{3}-\left( \upsilon _{F}\left( x_{i}\right) \right) ^{3}} \end{aligned}$$

The stronger ability of Fermatean fuzzy set to describe uncertain information by expanding the spatial scope of membership and nonmembership that allows more freedom in DM problems is illustrated in Fig. 1 below.

Fig. 1

Spatial scope of IFS, PFS and FFS

Let $P\left( U\right)$ be the power set of universal set U and E be the set of parameters. Let $A\subseteq E$ then,

Definition 4

(Molodtsov 1999) A pair (F, A) is called soft set over U where F is a mapping from A into the set $P\left( U\right) ,$ i.e., $F:A\rightarrow P(U).$ Soft set is a parameterized family of subsets of the set U. Every set $F(\varepsilon )$ where $\varepsilon \in$ A,  from this family may be considered as the set of $\varepsilon$ elements of the soft set $(F,A)=\left\{ F_{e}\text { }|\text { }e\in A\right\}$ where each $F_{e}$ is some subset of U.

Definition 5

(Maji et al. 2001a) Suppose FP(U) be the collection of all fuzzy subsets of universal set U. A pair $\left( F,A\right)$ is called fuzzy soft set over U where F is mapping from A into the set FP(U) i.e., $F:A\rightarrow FP(U)$ and is given by,

$$\begin{aligned} \left( F,A\right)&=\left\{ F_{e_{j}}\text { }|\text { }e_{j}\in A\right\} \text { where} \end{aligned}$$

(1)

$$\begin{aligned} F_{e_{j}}&=\left\{ \left\langle x,\mu _{j}\left( x\right) \right\rangle \text { }|\text { }x\in U\right\} \text { with }0\le \mu _{j}\left( x\right) \le 1. \end{aligned}$$

(2)

Definition 6

(Arora and Garg 2018) Suppose IFP(U) be the collection of all intuitionistic fuzzy subsets of universal set U. A pair $\left( F,A\right)$ is called intuitionistic fuzzy soft set over U where F is mapping from A into the set IFP(U) i.e., $F:A\rightarrow IFP(U)$ and is given by, $\left( F,A\right) =\left\{ F_{e_{j}}\text { }|\text { }e_{j}\in A\right\} ~$where

$$\begin{aligned} F_{e_{j}}=\left\{ \left\langle x,\mu _{j}\left( x\right) ,\nu _{j}\left( x\right) \right\rangle \text { }|\text { }x\in U\right\} \,\,\text { with } \,\,0\le \mu _{j}\left( x\right) +\nu _{j}\left( x\right) \le 1 \end{aligned}$$

(3)

Definition 7

(Kirişci 2019) Suppose PFP(U) be the collection of all Pythagorean fuzzy subsets of universal set U. A pair (F, A) is called Pythagorean fuzzy soft set where F is a mapping from A into the set PFP(U) i.e., $F:A\rightarrow PFP(U)$ and is given by, $\left( F,A\right) =\left\{ F_{e_{j}}\text { }|\text { }e_{j}\in A\right\} ~$where

$$\begin{aligned} F_{e_{j}}&=\left\{ \left\langle x,\mu _{j}\left( x\right) ,\nu _{j}\left( x\right) \right\rangle \text { }|\text { }x\in U\right\} \text { with} \nonumber \\ 0&\le \left( \mu _{j}\left( x\right) \right) ^{2}+\left( \nu _{j}\left( x\right) \right) ^{2}\le 1 \end{aligned}$$

(4)

Definition 8

Suppose FFP(U) be the collection of all Fermatean fuzzy subsets of universal set U. A pair (F, A) is called.Fermatean fuzzy soft set where F is a mapping from A into the set FFP(U) i.e., $F:A\rightarrow FFP(U)$ and is given by, $\left( F,A\right) =\left\{ F_{e_{j}}\text { }|\text { }e_{j}\in A\right\} ~$where

$$\begin{aligned} F_{e_{j}}&=\left\{ \left\langle x,\mu _{j}\left( x\right) ,\nu _{j}\left( x\right) \right\rangle \text { }|\text { }x\in U\right\} \text { with} \nonumber \\ 0&\le \left( \mu _{j}\left( x\right) \right) ^{3}+\left( \nu _{j}\left( x\right) \right) ^{3}\le 1 \end{aligned}$$

(5)

Example 1

Let $U=\left\{ q_{1},q_{2},q_{3},q_{4}\right\}$ be the set of four medicines that are used for the treatment of a single disease and $E=\left\{ e_{1},e_{2},e_{3},e_{4}\right\}$ where $e_{1}\equiv$ cheap, $e_{2}\equiv$ no side effects, $e_{3}\equiv$ availability in market $e_{4}\equiv$ expiration period. Then,

• (i) A soft set $\left( F,A\right)$ where $A=\left\{ e_{1},e_{3}\right\}$ can be,

  $$\begin{aligned} F\left( x\right) =\left\{ \begin{array} [c]{c} \left\{ q_{1},q_{3}\right\} \text { if }x=e_{1}\\ \left\{ q_{1},q_{2}\right\} \text { if }x=e_{3} \end{array} \right. \end{aligned}$$

• (ii) A FSS $\left( F,A\right)$ where $A=\left\{ e_{1},e_{2},e_{3}\right\}$ describing the characteristics of a medicine can be,

  $$\begin{aligned} F\left( x\right) =\left\{ \begin{array} [c]{c} \left\{ \left( q_{2},0.4\right) ,\left( q_{4},0.9\right) \right\} \text { if }x=e_{1}\\ \left\{ \left( q_{1},0.6\right) ,\left( q_{3},0.3\right) \right\} \, \text { if }x=e_{2}\\ \left\{ \left( q_{1},0.1\right) ,\left( q_{2},0.3\right) ,\left( q_{4},0.8\right) \right\} \text { if }x=e_{3} \end{array} \right. \end{aligned}$$

• (iii) An IFSS $\left( F,A\right)$ where $A=\left\{ e_{2},e_{4}\right\} ,$ describing the characteristics of a medicine can be,

  $$\begin{aligned} F\left( x\right) =\left\{ \begin{array} [c]{c} \left\{ \left\langle \left( q_{1},0.6,0.5\right) ,(q_{2} ,0.3,4.1)\right\rangle \right\} \, \text { if }x=e_{2}\\ \{ \left\langle \left( q_{3},0.7,0.3\right) ,\left( q_{4},0.5,0.1\right) \right\rangle \} \text { if }x=e_{4} \end{array} \right. \end{aligned}$$

• (iv) A PFSS $\left( F,A\right)$ where $A=\left\{ e_{3},e_{4}\right\} ,$ describing the characteristics of a medicine can be,

  $$\begin{aligned} F\left( x\right) =\left\{ \begin{array} [c]{c} \left\{ \left( q_{1},0.1,0.9\right) ,\left( q_{2},0.3,0.8\right) \right\} \, \text { if }x=e_{3}\\ \{ \left\langle \left( q_{3},0.7,0.5\right) ,\left( q_{4},0.5,0.6\right) \right\rangle \} \text { if }x=e_{4} \end{array} \right. \end{aligned}$$

• (v) A FFSS $\left( F,A\right)$ where $A=\left\{ e_{1},e_{2},e_{3},e_{4}\right\} ,$ describing the characteristics of a medicine can be,

  $$\begin{aligned} F\left( x\right) =\left\{ \begin{array} [c]{c} \left\{ \left( q_{2},0.7,0.8\right) ,\left( q_{4},0.5,0.9\right) \right\} \text { if }x=e_{1}\\ \left\{ \left( q_{1},0.6,0.8\right) ,\left( q_{3},0.9,0.3\right) \right\} \, \text { if }x=e_{2}\\ \left\{ \left( q_{2},0.4,0.8\right) ,\left( q_{3},0.6,0.7\right) ,\left( q_{4},0.9,0.8\right) \right\} \, \text { if }x=e_{3}\\ \left\{ \left( q_{1},0.4,0.6\right) ,\left( q_{2},0.3,0.7\right) ,\left( q_{4},0.9,0.5\right) \right\} \, \text { if }x=e_{3} \end{array} \right. \end{aligned}$$

It is important to note that, throughout this work, we will denote any Fermatean fuzzy soft number (FFSN) $F_{e_{ij}}=\left\{ \left\langle x_{i} ,\mu _{j}\left( x_{i}\right) ,\nu _{j}\left( x_{i}\right) \right\rangle \text { }|\text { }x_{i}\in U,\text { }e_{j}\in A\right\}$ of an element $x_{i}$ corresponding to a parameter $e_{j}$ by $F_{e_{ij}}=\left\langle \mu _{ij},\nu _{ij}\right\rangle .$ For practical application the ranking of alternatives is done on the basis of their score values, thus we define the score and accuracy functions for FFSNs.

Definition 9

Let $F_{e_{ij}}$ be a FFSN, the score of $F_{e_{ij}}$ is $S\left( F_{e_{ij} }\right) =\left( \mu _{ij}\right) ^{3}-\left( \nu _{ij}\right) ^{3}.$ Clearly, $S\left( F_{e_{ij}}\right) \in \left[ -1,1\right]$ and if two FFSNs have same scores then, we calculate the accuracy of the FFSNs by $H(F_{e_{ij}})=\mu _{ij}^{3}+\eta _{ij}^{3}$ which implies that $H(F_{e_{ij}})\in [0,1].$ We use the score function and accuracy function for ranking of two FFSNs,  $F_{e_{ij}}$and $F_{e_{pq}}$ according to the following.

• (i) if $S(F_{e_{ij}})>S(F_{e_{pq}}),$ then $F_{e_{ij}}>F_{e_{pq}},$

• (ii) if $S(F_{e_{ij}})=S(F_{e_{pq}}),$ then

• (a) if $H(F_{e_{ij}})>H(F_{e_{pq}}),$ then $F_{e_{ij}}>F_{e_{pq}},$

• (b) if $H(F_{e_{ij}})=H(F_{e_{pq}}),$ then $F_{e_{ij}}=F_{e_{pq}}.$

Definition 10

Let $F_{e_{ij}}=\left\langle \mu _{ij},\upsilon _{ij}\right\rangle ,$ $F_{e_{pq}}=\left\langle \mu _{pq},\upsilon _{pq}\right\rangle$ be two FFSNs and $\lambda \left( >0\right) \in {\mathbb {R}} ,$ we have :

• (i) $F_{e_{ij}}\oplus F_{e_{pq}}=\left\langle \root 3 \of {\mu _{ij}^{3}+\mu _{pq}^{3}-\mu _{ij}^{3}\mu _{pq}^{3}},~\upsilon _{ij}\upsilon _{pq}\right\rangle$

• (ii) $F_{e_{ij}}\otimes F_{e_{pq} }=\left\langle \mu _{ij}\mu _{pq},\root 3 \of {\upsilon _{ij}^{3}+\upsilon _{pq} ^{3}-\upsilon _{ij}^{3}\upsilon _{pq}^{3}}\right\rangle$

• (iii) $\lambda F_{e_{ij}}=\, \left\langle \root 3 \of {1-(1-\mu _{ij}^{3})^{\lambda } },\upsilon _{ij}^{\lambda } \right\rangle$

• (iv) $F_{e_{ij} }^{\lambda }=\left\langle \mu _{ij}^{\lambda },\root 3 \of {1-(1-\upsilon _{ij} ^{3})^{\lambda }}\right\rangle$

• (v) $F_{e_{ij}}^{c}=\left( \upsilon _{ij},\mu _{ij}\right) .$

3 Aggregation operators for Fermatean fuzzy soft numbers (FFSNs)

Here we introduce aggregation operators in the environment of FFSS such as, Fermatean fuzzy soft weighted averaging (FFSWA) operator, Fermatean fuzzy soft ordered weighted averaging (FFSOWA) operator, Fermatean fuzzy soft weighted geometric (FFSWG) operator and Fermatean fuzzy soft ordered weighted geometric (FFSOWG) operator.

3.1 Fermatean fuzzy soft weighted averaging (FFSWA) operator

Definition 11

Let $\Upsilon ^{n\times m}$ be matrix of order $n\times m$ in which entries are from the collection $\left\{ F_{e_{ij}}=\left\langle \mu _{ij},\nu _{ij}\right\rangle ,\left( i=1,2,\ldots ,n\ \, \text { and }j=1,2,\ldots ,m\right) \right\}$ of FFSNs and $\tau =\left( \tau _{1},\tau _{2},\ldots ,\tau _{m}\right) ^{T},$ $\xi =\left( \xi _{1},\xi _{2},\ldots ,\xi _{n}\right) ^{T}$ be the weighted vectors expressing importance of each parameter $e_{j}$ and importance of opinion of experts $x_{i\text { }}$respectively such that $\tau _{j}>0,~\xi _{{\dot{i}}}>0$ and $\underset{j=1}{\overset{m}{\sum }}\tau _{j}=1,$ $\overset{n}{\underset{i=1}{\sum }}\xi _{i}=1$ then FFSWA operator is a mapping $FFSWA:\Upsilon ^{n\times m}\rightarrow \Upsilon$ defined as

$$\begin{aligned}&FFSWA\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}},F_{e_{21}},\ldots ,F_{e_{2m}},\ldots ,F_{e_{n1}},F_{e_{n2}},\right. \\&\quad \left. F_{e_{22} },\ldots , F_{e_{nm}}\right) =\bigoplus \limits _{j=1}^{m}\tau _{j}\left( \bigoplus \limits _{i=1}^{n}\xi _{i}F_{e_{ij}}\right) \end{aligned}$$

Theorem 1

Let $F_{e_{ij}}=\left\langle \mu _{ij},\nu _{ij}\right\rangle$ $(i=1,2,\ldots ,n;~j=1,2,\ldots ,m)$ be any collection of FFSNs, then the aggregated value by the FFSWA operator is also a FFSN and

$$\begin{aligned}&FFSWA\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}},F_{e_{21}},F_{e_{22} },\ldots ,\right. \nonumber \\&\qquad \left. F_{e_{2m}},\ldots ,F_{e_{n1}},F_{e_{n2}},\ldots ,F_{e_{nm}}\right) \nonumber \\&\quad =\left\langle \root 3 \of {1-\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1} ^{n}\left( 1-\mu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}} ,\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{n}\left( \nu _{ij}\right) ^{\xi _{i}}\right) ^{\tau _{j}}~\right\rangle . \end{aligned}$$

(6)

Proof

By mathematical induction, for $n=1$, we have $\sum \nolimits _{i=1}^{n}\xi _{i}=1$ so by operations laws in Definition 10,

$$\begin{aligned}&FFSWA\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}}\right) \\&\quad =\bigoplus \limits _{j=1}^{m}\tau _{j}\left( F_{e_{1j}}\right) =\left\langle \root 3 \of {1-\prod \limits _{j=1}^{m}\left( 1-\mu _{1j}^{3}\right) ^{\tau _{j}} },\prod \limits _{j=1}^{m}\left( \nu _{1j}\right) ^{\tau _{j}}\right\rangle \\&\quad =\left\langle \root 3 \of {1-\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1} ^{1}\left( 1-\mu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}} ,~\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{1}\left( \nu _{ij}\right) ^{\xi _{i}}\right) ^{\tau _{j}}\right\rangle \end{aligned}$$

Similarly, for $m=1,~$we have $\sum \nolimits _{i=1}^{n}\tau _{j}=1.$ So,

$$\begin{aligned}&FFSWA(F_{e_{11}},F_{e_{21}},\ldots ,F_{e_{n1}})\\&\quad =\bigoplus \limits _{i=1}^{n}\xi _{i}(F_{e_{i1}})=\left\langle \root 3 \of {1-\prod \limits _{i=1}^{n}\left( 1-\mu _{i1}^{3}\right) ^{\xi _{i}}},\prod \limits _{i=1}^{n}\left( \nu _{i1}\right) ^{\xi _{i}}\right\rangle \\&\quad =\left\langle \root 3 \of {1-\prod \limits _{j=1}^{1}\left( \prod \limits _{i=1} ^{n}\left( 1-\mu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}} ,\prod \limits _{j=1}^{1}\left( \prod \limits _{i=1}^{n}\left( \nu _{ij}\right) ^{\xi _{i}}\right) ^{\tau _{j}}\right\rangle \end{aligned}$$

Thus, the result is true for $n=m=1$. Suppose, the result holds for $m=k_{1}+1,$ $n=k_{2}~$and $m=k_{1},$ $n=k_{2}+1$

$$\begin{aligned}&\bigoplus \limits _{j=1}^{k_{1}+1}\tau _{j}\left( \bigoplus \limits _{i=1}^{k_{2} }\xi _{i}F_{e_{ij}}\right) \\&\quad =\left\langle \root 3 \of {1-\prod \limits _{j=1} ^{k_{1}+1}\left( \prod \limits _{i=1}^{k_{2}}\left( 1-\mu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}},~\prod \limits _{j=1}^{k_{1}+1}\left( \prod \limits _{i=1}^{k_{2}}(\nu _{ij})^{\xi _{i}}\right) ^{\tau _{j} }\right\rangle \end{aligned}$$

and

$$\begin{aligned}&\bigoplus \limits _{j=1}^{k_{1}}\tau _{j}\left( \bigoplus \limits _{i=1} ^{k_{2}+1}\xi _{i}F_{e_{ij}}\right) \\&\quad =\left\langle \root 3 \of {1-\prod \limits _{j=1}^{k_{1}}\left( \prod \limits _{i=1}^{k_{2}+1}\left( 1-\mu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}},~\prod \limits _{j=1}^{k_{1} }\left( \prod \limits _{i=1}^{k_{2}+1}(\nu _{ij})^{\xi _{i}}\right) ^{\tau _{j} }\right\rangle \end{aligned}$$

Now for $m=k_{1}+1,$ $n=k_{2}+1~$we get,

$$\begin{aligned}&\bigoplus \limits _{j=1}^{k_{1}+1}\tau _{j}\left( \bigoplus \limits _{i=1} ^{k_{2}+1}\xi _{i}F_{e_{ij}}\right) \\&\quad = \bigoplus \limits _{j=1}^{k_{1}+1} \tau _{j}\left( \bigoplus \limits _{i=1}^{k_{2}}\xi _{i}F_{e_{ij}}\oplus \xi _{k_{2}+1}F_{e_{\left( k_{2}+1\right) j}}\right) \\&\quad = \bigoplus \limits _{j=1}^{k_{1}+1}\bigoplus \limits _{i=1}^{k_{2}}\tau _{j} \xi _{i}F_{e_{ij}}\oplus \bigoplus \limits _{j=1}^{k_{1}+1}\tau _{j}\xi _{e_{k_{2}+1}}F_{e_{\left( k_{2}+1\right) j}}\\&\quad =\left\langle \begin{array}[c]{c} \root 3 \of {1-\prod \limits _{j=1}^{k_{1}+1}\left( \prod \limits _{i=1}^{k_{2} }\left( 1-\mu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}\oplus 1-\prod \limits _{j=1}^{k_{1}+1}\left( \left( 1-\mu _{(k_{2}+1)j}^{3}\right) ^{\xi _{k_{2}+1}}\right) ^{\tau _{j}}},\\ ~\prod \limits _{j=1}^{k_{1}+1}\left( \prod \limits _{i=1}^{k_{2}}\left( \nu _{ij}\right) ^{\xi _{i}}\right) ^{\tau _{j}}\oplus \prod \limits _{j=1} ^{k_{1}+1}\left( \nu _{(k_{2}+1)j}^{\xi _{k_{2}+1}}\right) ^{\tau _{j}}\\ \end{array} \right\rangle \\&\quad =\left\langle \root 3 \of {1-\prod \limits _{j=1}^{k_{1}+1}\left( \prod \limits _{i=1}^{k_{2}+1}\left( 1-\mu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}},~\prod \limits _{j=1}^{k_{1}+1}\left( \prod \limits _{i=1}^{k_{2} +1}(\nu _{ij})^{\xi _{i}}\right) ^{\tau _{j}}\right\rangle \end{aligned}$$

Thus it is true for $m=k_{1}+1$ and $n=k_{2}+1$ and hence, by induction, the result holds for all $m,n\ge 1$ Since

$$\begin{aligned}&0\le \mu _{ij}\le 1\iff 0\le \root 3 \of {\prod \limits _{i=1}^{n}\left( 1-\mu _{ij}^{3}\right) ^{\xi _{i}}}\le 1\\&\quad \iff 0\le \root 3 \of {\prod \limits _{j=1} ^{m}\left( \prod \limits _{i=1}^{n}\left( 1-\mu _{ij}^{3}\right) ^{\xi _{i} }\right) ^{\tau _{j}}}\le 1 \end{aligned}$$

And so, $\ \ 0\le \root 3 \of {1-\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{n}\left( 1-\mu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}}\le 1$ Also, $0\le \nu _{ij}\le 1\iff 0\le \prod \limits _{i=1}^{n}\left( \nu _{ij}\right) ^{\xi _{i}}\le 1\iff 0\le \prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{n}\left( \nu _{ij}\right) ^{\xi _{i}}\right) ^{\tau _{j}}\le 1$ Finally,

$$\begin{aligned}&\root 3 \of {1-\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{n}\left( 1-\mu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}}+\prod \limits _{j=1} ^{m}\left( \prod \limits _{i=1}^{n}\left( \nu _{ij}\right) ^{\xi _{i}}\right) ^{\tau _{j}} \\&\quad \le \root 3 \of {1-\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{n}\left( 1-\mu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j} }}\\&\qquad +\root 3 \of {1-\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{n}\left( 1-\mu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}} \le 1. \end{aligned}$$

This completes the proof. $\square$

Example 2

Consider the situation of Example 1. Suppose the rating values of experts about five medicines in terms FFSNs are,

$$\begin{aligned}&\, \text { By~d}_{1}\\&\begin{array} [c]{c} F\left( e_{1}\right) =\left\{ q_{1}/\left( 0.7,0.8\right) ,q_{2}/\left( 0.6,0.8\right) ,q_{3}/\left( 0.9,0.4\right) ,q_{4}/\left( 0.9,0.6\right) \right\} \\ F\left( e_{2}\right) =\left\{ q_{1}/\left( 0.9,0.5\right) ,q_{2}/\left( 0.7,0.8\right) ,q_{3}/\left( 0.5,0.4\right) ,q_{4}/\left( 0.8,0.7\right) \right\} \\ F\left( e_{3}\right) =\left\{ q_{1}/\left( 0.7,0.4\right) ,q_{2}/\left( 0.6,0.5\right) ,q_{3}/\left( 0.7,0.4\right) ,q_{4}/\left( 0.7,0.3\right) \right\} \\ F\left( e_{4}\right) =\left\{ q_{1}/\left( 0.8,0.5\right) ,q_{2}/\left( 0.6,0.3\right) ,q_{3}/\left( 0.4,0.3\right) ,q_{4}/\left( 0.9,0.7\right) \right\} \end{array}\\&\, \text { By~d}_{2}\\&\begin{array} [c]{c} F\left( e_{1}\right) =\left\{ q_{1}/\left( 0.5,0.4\right) ,q_{2}/\left( 0.7,0.8\right) ,q_{3}/\left( 0.9,0.3\right) ,q_{4}/\left( 0.7,0.6\right) \right\} \\ F\left( e_{2}\right) =\left\{ q_{1}/\left( 0.9,0.5\right) ,q_{2}/\left( 0.8,0.3\right) ,q_{3}/\left( 0.5,0.4\right) ,q_{4}/\left( 0.6,0.2\right) \right\} \\ F\left( e_{3}\right) =\left\{ q_{1}/\left( 0.6,0.4\right) ,q_{2}/\left( 0.8,0.5\right) ,q_{3}/\left( 0.5,0.4\right) ,q_{4}/\left( 0.7,0.3\right) \right\} \\ F\left( e_{4}\right) =\left\{ q_{1}/\left( 0.7,0.5\right) ,q_{2}/\left( 0.8,0.3\right) ,q_{3}/\left( 0.7,0.3\right) ,q_{4}/\left( 0.5,0.7\right) \right\} \end{array} \end{aligned}$$

$$\begin{aligned}&\text {By d}_{3}\\&\begin{array} [c]{c} F\left( e_{1}\right) =\left\{ q_{1}/\left( 0.4,0.6\right) ,q_{2}/\left( 0.7,0.5\right) ,q_{3}/\left( 0.8,0.4\right) ,q_{4}/\left( 0.8,0.7\right) \right\} \\ F\left( e_{2}\right) =\left\{ q_{1}/\left( 0.6,0.5\right) ,q_{2}/\left( 0.7,0.4\right) ,q_{3}/\left( 0.5,0.4\right) ,q_{4}/\left( 0.6,0.2\right) \right\} \\ F\left( e_{3}\right) =\left\{ q_{1}/\left( 0.8,0.4\right) ,q_{2}/\left( 0.6,0.5\right) ,q_{3}/\left( 0.6,0.4\right) ,q_{4}/\left( 0.7,0.1\right) \right\} \\ F\left( e_{4}\right) =\left\{ q_{1}/\left( 0.7,0.5\right) ,q_{2}/\left( 0.6,0.3\right) ,q_{3}/\left( 0.4,0.3\right) ,q_{4}/\left( 0.5,0.3\right) \right\} \end{array} \end{aligned}$$

In matrix from these information are summarized as,

$$\begin{aligned}&\text {Fermatean Fuzzy soft matrix for }q_{1}\\&\begin{bmatrix} &{} e_{1} &{} e_{2} &{} e_{3} &{} e_{4}\\ d_{1} &{} \left\langle 0.7,0.8\right\rangle &{} \left\langle 0.9,0.5\right\rangle &{} \left\langle 0.7,0.4\right\rangle &{} \left\langle 0.8,0.5\right\rangle \\ d_{2} &{} \left\langle 0.5,0.4\right\rangle &{} \left\langle 0.9,0.5\right\rangle &{} \left\langle 0.6,0.4\right\rangle &{} \left\langle 0.7,0.5\right\rangle \\ d_{3} &{} \left\langle 0.4,0.6\right\rangle &{} \left\langle 0.6,0.5\right\rangle &{} \left\langle 0.8,0.4\right\rangle &{} \left\langle 0.7,0.5\right\rangle \end{bmatrix}\\&\text {Fermatean Fuzzy soft matrix for }q_{2}\\&\begin{bmatrix} &{} e_{1} &{} e_{2} &{} e_{3} &{} e_{4}\\ d_{1} &{} \left\langle 0.6,0.8\right\rangle &{} \left\langle 0.7,0.8\right\rangle &{} \left\langle 0.6,0.5\right\rangle &{} \left\langle 0.6,0.3\right\rangle \\ d_{2} &{} \left\langle 0.7,0.8\right\rangle &{} \left\langle 0.8,0.3\right\rangle &{} \left\langle 0.8,0.5\right\rangle &{} \left\langle 0.8,0.3\right\rangle \\ d_{3} &{} \left\langle 0.7,0.5\right\rangle &{} \left\langle 0.7,0.4\right\rangle &{} \left\langle 0.6,0.5\right\rangle &{} \left\langle 0.6,0.3\right\rangle \end{bmatrix} \end{aligned}$$

$$\begin{aligned}&\text {Fermatean Fuzzy soft matrix for }q_{3}\\&\ \begin{bmatrix} &{} e_{1} &{} e_{2} &{} e_{3} &{} e_{4}\\ d_{1} &{} \left\langle 0.9,0.4\right\rangle &{} \left( 0.5,0.4\right) &{} \left( 0.7,0.4\right) &{} \left\langle 0.4,0.3\right\rangle \\ d_{2} &{} \left\langle 0.9,0.3\right\rangle &{} \left( 0.5,0.4\right) &{} \left( 0.5,0.4\right) &{} \left\langle 0.7,0.3\right\rangle \\ d_{3} &{} \left\langle 0.8,0.4\right\rangle &{} \left( 0.5,0.4\right) &{} \left( 0.6,0.4\right) &{} \left\langle 0.4,0.3\right\rangle \end{bmatrix}\\&\text {Fermatean Fuzzy soft matrix for }q_{4}\\&\begin{bmatrix} &{} e_{1} &{} e_{2} &{} e_{3} &{} e_{4}\\ d_{1} &{} \left\langle 0.9,0.6\right\rangle &{} \left\langle 0.8,0.7\right\rangle &{} \left\langle 0.7,0.3\right\rangle &{} \left\langle 0.9,0.7\right\rangle \\ d_{2} &{} \left\langle 0.7,0.6\right\rangle &{} \left\langle 0.6,0.2\right\rangle &{} \left\langle 0.7,0.3\right\rangle &{} \left\langle 0.5,0,7\right\rangle \\ d_{3} &{} \left\langle 0.8,0.7\right\rangle &{} \left\langle 0.6,0.2\right\rangle &{} \left\langle 0.7,0.1\right\rangle &{} \left\langle 0.5,0.3\right\rangle \end{bmatrix} \end{aligned}$$

Let $\tau =\left( 0.3,0.2,0.4,0.1\right) ^{T}$ and $\xi =(0.5,0.2,0.3)^{T}$ be the weight vectors of the parameters and experts respectively. Here we are considering only the Fermatean fuzzy soft matrix for $q_{1}.~$By FFSWA operator,

$$\begin{aligned}&FFSWA\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}},F_{e_{21}},F_{e_{22} },\ldots ,F_{e_{2m}},\ldots ,F_{e_{n1}},F_{e_{n2}},\ldots ,F_{e_{nm}}\right) \\&\quad =\left\langle \root 3 \of {1-\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1} ^{n}\left( 1-\mu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}} ,\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{n}\left( \upsilon _{ij}\right) ^{\xi _{i}}\right) ^{\tau _{j}}~\right\rangle \\&\quad =\left\langle \begin{array} [c]{c} \root 3 \of { \begin{array} [c]{c} 1-\left( \left( 1-\left( 0.7\right) ^{3}\right) ^{0.5}\left( 1-\left( 0.5\right) ^{3}\right) ^{0.2}\left( 1-\left( 0.4\right) ^{3}\right) ^{0.3}\right) ^{0.3}\\ \left( \left( 1-\left( 0.9\right) ^{3}\right) ^{0.5}\left( 1-\left( 0.9\right) ^{3}\right) ^{0.2}\left( 1-\left( 0.6\right) ^{3}\right) ^{0.3}\right) ^{0.2}\\ \left( \left( 1-\left( 0.7\right) ^{3}\right) ^{0.5}\left( 1-\left( 0.6\right) ^{3}\right) ^{0.2}\left( 1-\left( 0.8\right) ^{3}\right) ^{0.3}\right) ^{0.4}\\ \left( \left( 1-\left( 0.8\right) ^{3}\right) ^{0.5}\left( 1-\left( 0.7\right) ^{3}\right) ^{0.2}\left( 1-\left( 0.7\right) ^{3}\right) ^{0.3}\right) ^{0.1} \end{array} },\\ \left( \left( 0.8\right) ^{0.5}\left( 0.4\right) ^{0.2}\left( 0.6\right) ^{0.3}\right) ^{0.3}\left( \left( 0.5\right) ^{0.5}\left( 0.5\right) ^{0.2}\left( 0.5\right) ^{0.3}\right) ^{0.2}\\ \left( \left( 0.4\right) ^{0.5}\left( 0.4\right) ^{0.2}\left( 0.4\right) ^{0.3}\right) ^{0.4}\left( \left( 0.5\right) ^{0.5}\left( 0.5\right) ^{0.2}\left( 0.5\right) ^{0.3}\right) ^{0.1} \end{array} \right\rangle \\&=\left\langle 0.740\,,0.492\, \right\rangle \end{aligned}$$

Lemma 1

If $e_{1}$ is the only parameter then, FFSWA operator reduces to Fermatean fuzzy weighted FFWA operator (Senapati and Yager 2019a).

Proof

If $e_{1}$ is the only parameter then, $m=1$ thus Eq. 6 becomes,

$$\begin{aligned}&FFSWA\left( F_{e_{11}},F_{e_{21}},F_{e_{31}},\ldots ,F_{e_{n1}}\right) \\&\quad =\left\langle \root 3 \of {1-\prod \limits _{i=1}^{n}\left( 1-\mu _{i}^{3}\right) ^{\xi _{i}}},\prod \limits _{i=1}^{n}\left( \nu _{i}\right) ^{\xi _{i} }~\right\rangle , \end{aligned}$$

which is weighted averaging aggregation operator in the environment of Fermatean fuzzy information. $\square$

3.2 Properties of FFSWA operator

The FFSWA operator has the following properties which are stated without proof.

Property 3.2.1

(Idempotency) If $F_{e_{ij}} =F_{e}=(\mu ,\nu )$ $\forall \ i,j$ then

$$\begin{aligned}&FFSWA\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}},F_{e_{21}},F_{e_{22} },\ldots ,\right. \\&\quad \left. F_{e_{2m}},\ldots ,F_{e_{n1}},F_{e_{n2}},\ldots ,F_{e_{nm}}\right) =F_{e}. \end{aligned}$$

Property 3.2.2

(Shift-Invariance) If $F_{e}=(\mu ,\nu )$, is any other FFSN, then

$$\begin{aligned}&FFSWA\left( \begin{array} [c]{c} F_{e_{11}}\oplus F_{e},F_{e_{12}}\oplus F_{e},\ldots ,F_{e_{1m}}\oplus F_{e},F_{e_{21}}\oplus F_{e},F_{e_{22}}\oplus F_{e},\\ \ldots ,F_{e_{2m}}\oplus F_{e},\ldots ,F_{e_{n1}}\oplus F_{e},F_{e_{n2}}\oplus F_{e}\ldots ,F_{e_{nm}}\oplus F_{e} \end{array} \right) \\&\quad =FFSWA\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}},F_{e_{21}},F_{e_{22} },\ldots ,\right. \\&\left. F_{e_{2m}},\ldots ,F_{e_{n1}},F_{e_{n2}},\ldots ,F_{e_{nm}}\right) \oplus F_{e}. \end{aligned}$$

Property 3.2.3

(Homogeneity) For any real number$~\lambda$ $>0$ we have

$$\begin{aligned}&FFSWA\left( \lambda F_{e_{11}},\lambda F_{e_{12}},\ldots ,\lambda F_{e_{1m} },\lambda F_{e_{21}},\right. \\&\qquad \left. \lambda F_{e_{22}},\ldots ,\lambda F_{e_{2m}},\ldots ,\lambda F_{e_{n1}},\lambda F_{e_{n2}},\ldots ,\lambda F_{e_{nm}}\right) \\&\quad =\lambda \left\{ FFSWA\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}} ,F_{e_{21}},F_{e_{22}},\ldots ,\right. \right. \\&\qquad \left. \left. F_{e_{2m}},\ldots ,F_{e_{n1}},F_{e_{n2}},\ldots ,F_{e_{nm} }\right) \right\} . \end{aligned}$$

Property 3.2.4

(Boundedness) Let $F_{e_{ij}}^{-}=\left\langle \underset{j}{\min }\underset{i}{\min }\{ \mu _{ij}\},\underset{j}{~\max } \underset{i}{\max }\{ \nu _{ij}\} \right\rangle$

and $F_{e_{ij}}^{+}=\left\langle \underset{j}{\max }\underset{i}{\max }\text { }\{ \mu _{ij}\},\underset{j}{\min }\underset{i}{\min }\{ \nu _{ij}\} \right\rangle$ then,

$$\begin{aligned} F_{e_{ij}}^{-}\le & {} FFSWA(F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}},F_{e_{21} },F_{e_{22}},\ldots ,\\&F_{e_{2m}},\ldots ,F_{e_{n1}},F_{e_{n2}},\ldots ,F_{e_{nm}} )\le \ F_{e_{ij}}^{+}. \end{aligned}$$

3.3 Fermatean fuzzy soft ordered weighted averaging (FFSOWA) operator

Definition 12

Let $\Upsilon ^{n\times m}$ be matrix of order $n\times m$ in which entries are from the collection $\left\{ F_{e_{ij}}=\left\langle \mu _{ij},\nu _{ij}\right\rangle ,\left( i=1,2,\ldots ,n\ \, \text { and }j=1,2,\ldots ,m\right) \right\}$ of FFSNs and$\ \tau =\left( \tau _{1},\tau _{2},\ldots ,\tau _{m}\right) ^{T}$, $\xi =\left( \xi _{1},\xi _{2},\ldots ,\xi _{n}\right) ^{T}$ be the weighted vectors expressing importance of each parameter $e_{j}$ and importance of opinion of experts $x_{i\text { }}$respectively such that $\tau _{j}>0,~\xi _{{\dot{i}}}>0$ and ${\sum \nolimits _{j=1}^m}\tau _{j}=1,$ ${\sum \nolimits _{i=1}^n}\xi _{i}=1$ then FFSOWA operator is a mapping $FFSOWA:\Upsilon ^{n\times m}\rightarrow \Upsilon$ defined as

$$\begin{aligned}&FFSOWA\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}},F_{e_{21}},F_{e_{22} },\ldots ,F_{e_{2m}},\ldots ,F_{e_{n1}},\right. \\&\quad \left. F_{e_{n2}},\ldots ,F_{e_{nm}}\right) = {\displaystyle \bigoplus \limits _{j=1}^{m}} \tau _{j}\left( {\displaystyle \bigoplus \limits _{i=1}^{n}} \xi _{i}F_{e_{\sigma \left( _{ij}\right) }}\right) \end{aligned}$$

where $\left( \sigma _{12},\sigma _{13},\ldots ,\sigma _{nm}\right)$ is a permutation of $\left( 1,2,\ldots ,n:~j=1,2,\ldots ,m\right)$, such that $F_{e_{\sigma (i-1)(j-1)}}\ge$ $F_{e_{\sigma (ij)}}$ for all $i=2,3,\ldots ,n$ and $j=2,3,\ldots ,m$.

Theorem 2

Let $F_{e_{ij}}=\left\langle \mu _{ij},\upsilon _{ij}\right\rangle ,$ $\left( i=1,2,\ldots ,n:j=1,2,\ldots ,m\right)$ be any FFSNs, then the aggregated value by the FFSOWA operator is a FFSN and is given by,

$$\begin{aligned}&FFSOWA\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}},F_{e_{21}},F_{e_{22} },\ldots ,\right. \nonumber \\&\qquad \left. F_{e_{2m}},\ldots ,F_{e_{n1}},F_{e_{n2}},\ldots ,F_{e_{nm}}\right) \nonumber \\&\quad =\left\langle \root 3 \of {1-\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1} ^{n}\left( 1-\mu _{\sigma _{\left( ij\right) }}^{3}\right) ^{\xi _{i} }\right) ^{\tau _{j}}},\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1} ^{n}\left( \nu _{\sigma _{\left( ij\right) }}\right) ^{\xi _{i}}\right) ^{\tau _{j}}\right\rangle \end{aligned}$$

(7)

Proof

Follows from Theorem 1$\square$

3.4 Properties of FFSOWA operator

We state some properties of the FFSOWA operator without proof.

Property 3.4.1

(Idempotancey) If $F_{e_{ij} }=F_{e}=(\mu ,\nu )$ $\forall \ i,j$ then

$$\begin{aligned}&FFSOWA\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}},F_{e_{21}},F_{e_{22} },\ldots ,\right. \\&\quad \left. F_{e_{2m}},\ldots ,F_{e_{n1}},F_{e_{n2}},\ldots ,F_{e_{nm}}\right) =F_{e}. \end{aligned}$$

Property 3.4.2

(Shift-Invariance) If $F_{e}=(\mu ,\nu )$, is any other FFSN, then

$$\begin{aligned}&FFSOWA\left( \begin{array} [c]{c} F_{e_{11}}\oplus F_{e},F_{e_{12}}\oplus F_{e},\ldots ,F_{e_{1m}}\oplus F_{e},F_{e_{21}}\oplus F_{e},F_{e_{22}}\oplus F_{e},\\ \ldots ,F_{e_{2m}}\oplus F_{e},\ldots ,F_{e_{n1}}\oplus F_{e},F_{e_{n2}}\oplus F_{e},\ldots ,F_{e_{nm}}\oplus F_{e} \end{array} \right) \\&=FFSOWA\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}},F_{e_{21}},F_{e_{22} },\ldots ,\right. \\&\quad \left. F_{e_{2m}},\ldots ,F_{e_{n1}},F_{e_{n2}},\ldots ,F_{e_{nm}}\right) \oplus F_{e}. \end{aligned}$$

Property 3.4.3

(Homogeneity) For any real number$~\lambda$ $>0$ we have,

$$\begin{aligned}&FFSOWA\left( \lambda F_{e_{11}},\lambda F_{e_{12}},\ldots ,\lambda F_{e_{1m} },\lambda F_{e_{21}},\right. \\&\qquad \left. \lambda F_{e_{22}},\ldots ,\lambda F_{e_{2m}},\ldots ,\lambda F_{e_{n1}},\lambda F_{e_{n2}}\ldots ,\lambda F_{e_{nm}}\right) \\&\quad =\lambda \left\{ FFSOWA\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m} },F_{e_{21}},\right. \right. \\&\qquad \left. \left. F_{e_{22}},\ldots ,F_{e_{2m}},\ldots ,F_{e_{n1}},F_{e_{n2}} ,\ldots ,F_{e_{nm}}\right) \right\} . \end{aligned}$$

Property 3.4.4

(Boundedness) Let $F_{e_{ij}} ^{-}=\left\langle \underset{j}{\min }\underset{i}{\min }\{ \mu _{ij} \},\underset{j}{~\max }\underset{i}{\max }\{ \nu _{ij}\} \right\rangle$ and $F_{e_{ij}}^{+}=\left\langle \underset{j}{\max }\underset{i}{\max }\text { } \{ \mu _{ij}\},\underset{j}{\min }\underset{i}{\min }\{ \nu _{ij}\} \right\rangle$ then,

$$\begin{aligned} F_{e_{ij}}^{-}\le & {} FFSOWA(F_{e_{11}},F_{e_{12}},F_{e_{13}},\ldots ,F_{e_{1m} },F_{e_{21}},\\&F_{e_{22}},\ldots ,F_{e_{2m}},\ldots ,F_{e_{n1}},F_{e_{n2}} ,\ldots ,F_{e_{nm}})\le \ F_{e_{ij}}^{+}. \end{aligned}$$

3.5 Fermatean fuzzy soft weighted geometric (FFSWG) operator

Definition 13

Let $\Upsilon ^{n\times m}$ be matrix of order $n\times m$ in which entries are from the collection $\left\{ F_{e_{ij}}=\left\langle \mu _{ij},\nu _{ij}\right\rangle ,\left( i=1,2,\ldots ,n\ \, \text { and }j=1,2,\ldots ,m\right) \right\}$ of FFSNs and $\tau =\left( \tau _{1},\tau _{2},\ldots ,\tau _{m}\right) ^{T}$, $\xi =\left( \xi _{1},\xi _{2},\ldots ,\xi _{n}\right) ^{T}$ be the weighted vectors expressing importance of each parameter $e_{j}$ and importance of opinion of experts $x_{i\text { }}$respectively such that $\tau _{j}>0,~\xi _{{\dot{i}}}>0$ and $\underset{j=1}{\overset{m}{\sum }}\tau _{j}=1,$ $\overset{n}{\underset{i=1}{\sum }}\xi _{i}=1$ then FFSWG operator is a mapping $FFSWG:\Upsilon ^{n\times m}\rightarrow \Upsilon$ defined as

$$\begin{aligned}&FFSWG\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}},F_{e_{21}},F_{e_{22} },\ldots ,\right. \\&\left. \qquad F_{e_{2m}},\ldots ,F_{e_{n1}},F_{e_{n2}},\ldots ,F_{e_{nm}}\right) \\&\quad =\bigotimes \limits _{j=1}^{m}\left( \bigotimes \limits _{i=1}^{n}\xi _{i}F_{e_{ij}}\right) ^{\tau _{j}} \end{aligned}$$

Theorem 3

Let $F_{e_{ij}}=\left\langle \mu _{ij},\nu _{ij}\right\rangle$ $(i=1,2,\ldots ,n;~j=1,2,\ldots ,m)$ be any collection of FFSNs, then the aggregated value by the FFSWG operator is also a FFSN and is given by

$$\begin{aligned}&FFSWG\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}},F_{e_{21}},F_{e_{22} },\ldots ,\right. \nonumber \\&\qquad \left. F_{e_{2m}},\ldots ,F_{e_{n1}},F_{e_{n2}},\ldots ,F_{e_{nm}}\right) \nonumber \\&\quad =\left\langle \prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{n}\left( \mu _{ij}\right) ^{\xi _{i}}\right) ^{\tau _{j}},\root 3 \of {1-\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{n}\left( 1-\nu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}}~\right\rangle \end{aligned}$$

(8)

Proof

We use mathematical induction to prove the required result. For $n=1$ $\sum \nolimits _{i=1}^{n}\xi _{i}=1,$

$$\begin{aligned}&FFSWG\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}}\right) \\&\quad =\bigotimes \limits _{j=1}^{m}\left( F_{e_{1j}}\right) ^{_{\tau _{j}}}=\left\langle \prod \limits _{j=1}^{m}\left( \mu _{ij}\right) ^{\tau _{j}},\root 3 \of {1-\prod \limits _{j=1}^{m}\left( 1-\nu _{ij}^{3}\right) ^{\tau _{j}} }\right\rangle \\&\quad =\left\langle \prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{1}\left( \mu _{ij}\right) ^{\xi _{i}}\right) ^{\tau _{j}},\root 3 \of {1-\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{1}\left( 1-\nu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}}\right\rangle \end{aligned}$$

Similarly, for $m=1,~$we have $\sum \nolimits _{i=1}^{m}\tau _{j}=1.$ So,

$$\begin{aligned}&FFSWG\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{n1}}\right) \\&\quad =\bigotimes \limits _{i=1}^{n}\left( F_{e_{i1}}\right) ^{\xi _{i}}=\left\langle \prod \limits _{i=1}^{n}\left( \mu _{ij}\right) ^{\xi _{i}},\root 3 \of {1-\prod \limits _{i=1}^{n}\left( 1-\nu _{ij}^{3}\right) ^{\xi _{i}} }\right\rangle \\&\quad =\left\langle \prod \limits _{j=1}^{1}\left( \prod \limits _{i=1}^{n}\left( \mu _{ij}\right) ^{\xi _{i}}\right) ^{\tau _{j}},\root 3 \of {1-\prod \limits _{j=1}^{1}\left( \prod \limits _{i=1}^{n}\left( 1-\nu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}}\right\rangle \end{aligned}$$

Thus, the result is true for $n=m=1$Suppose, the result holds for $m=k_{1}+1$, $n=k_{2}$ and $m=k_{1}$, $n=k_{2}+1$

$$\begin{aligned}&\bigotimes \limits _{j=1}^{k_{1}+1}\tau _{j}\left( \bigotimes \limits _{i=1} ^{k_{2}}\xi _{i}F_{e_{ij}}\right) \\&\quad =\left\langle \prod \limits _{j=1}^{k_{1} +1}\left( \prod \limits _{i=1}^{k_{2}}\left( \mu _{ij}\right) ^{\xi _{i} }\right) ^{\tau _{j}},\root 3 \of {1-\prod \limits _{j=1}^{k_{1}+1}\left( \prod \limits _{i=1}^{k_{2}}\left( 1-\nu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}}\right\rangle \end{aligned}$$

and

$$\begin{aligned}&\bigotimes \limits _{j=1}^{k_{1}}\tau _{j}\left( \bigotimes \limits _{i=1} ^{k_{2}+1}\xi _{i}F_{e_{ij}}\right) \\&\quad =\left\langle \prod \limits _{j=1}^{k_{1} }\left( \prod \limits _{i=1}^{k_{2}+1}\left( \mu _{ij}\right) ^{\xi _{i} }\right) ^{\tau _{j}},\right. \\&\qquad \left. \root 3 \of {1-\prod \limits _{j=1}^{k_{1}}\left( \prod \limits _{i=1}^{k_{2}+1}\left( 1-\nu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}}\right\rangle \end{aligned}$$

Now for $m=k_{1}+1,$ $n=k_{2}+1,$ we get,

$$\begin{aligned}&\bigotimes \limits _{j=1}^{k_{1}+1}\left( \bigotimes \limits _{i=1}^{k_{2} +1}F_{e_{ij}}^{\xi _{i}}\right) ^{\tau _{j}}\\&\quad =\bigotimes \limits _{j=1}^{k_{1} +1}\left( \bigotimes \limits _{i=1}^{k_{2}}F_{e_{ij}}^{\xi _{i}}\otimes F_{e_{\left( k_{2}+1\right) j}}^{\xi _{k_{2}+1}}\right) ^{\tau _{j}}\\&\quad =\bigotimes \limits _{j=1}^{k_{1}+1}\left( \bigotimes \limits _{i=1} ^{k_{2}}F_{e_{ij}}^{\xi _{i}}\right) ^{\tau _{j}}\otimes \left( \bigotimes \limits _{j=1}^{k_{1}+1}\left( F_{e_{\left( k_{2}+1\right) j}}^{\xi _{k_{2}+1}}\right) ^{^{\tau _{j}}}\right) \\&\quad =\left\langle \begin{array}[c]{c} \prod \limits _{j=1}^{k_{1}+1}\left( \prod \limits _{i=1}^{k_{2}}\left( \mu _{ij}\right) ^{\xi _{i}}\right) ^{\tau _{j}}\otimes \prod \limits _{j=1} ^{k_{1}+1}\left( \mu _{\left( k_{2}+1\right) j}^{\xi k_{2}+1}\right) ^{^{\tau _{j}}},\\ \qquad \root 3 \of {1-\prod \limits _{j=1}^{k_{1}+1}\left( \prod \limits _{i=1}^{k_{2} }\left( 1-\nu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}\otimes 1-\prod \limits _{j=1}^{k_{1}+1}\left( \left( 1-\nu _{\left( k_{2}+1\right) j}\right) ^{\xi _{k_{2}+1}}\right) ^{\tau _{j}}} \end{array} \right\rangle \\&\quad =\left\langle \prod \limits _{j=1}^{k_{1}+1}\left( \prod \limits _{i=1}^{k_{2} +1}\left( \mu _{ij}\right) ^{\xi _{i}}\right) ^{\tau _{j}},\root 3 \of {1-\prod \limits _{j=1}^{k_{1}+1}\left( \prod \limits _{i=1}^{k_{2}+1}\left( 1-\nu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}}\right\rangle \end{aligned}$$

Thus it is true for $m=k_{1}+1$ and $n=k_{2}+1$ and by induction, the result holds for all $m,n\ge 1$Since,

$$\begin{aligned}&0\le \nu _{ij}^{3}\le 1\iff 0\le \root 3 \of {\prod \limits _{i=1}^{n}\left( 1-\nu _{ij}^{3}\right) ^{\xi _{i}}}\le 1\\&\quad \iff 0\le \root 3 \of {\prod \limits _{j=1} ^{m}\left( \prod \limits _{i=1}^{n}\left( 1-\nu _{ij}^{3}\right) ^{\xi _{i} }\right) ^{\tau _{j}}}\le 1 \end{aligned}$$

And so, $\ 0\le \root 3 \of {1-\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1} ^{n}\left( 1-\nu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}}\le 1.$ Furthermore,

$$\begin{aligned}&0\le \mu _{ij}\le 1\iff 0\le \prod \limits _{i=1}^{n}(\mu _{ij})^{\xi _{i}}\le 1\\&\quad \iff 0\le \prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{n}(\mu _{ij} )^{\xi _{i}}\right) ^{\tau _{j}}\le 1 \end{aligned}$$

Finally,

$$\begin{aligned}&\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{n}(\eta _{ij})^{\xi _{i} }\right) ^{\tau _{j}}+\root 3 \of {1-\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{n}\left( 1-\mu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j} }} \\&\quad \le \root 3 \of {1-\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{n}\left( 1-\mu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}}\\&\qquad +\root 3 \of {1-\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{n}\left( 1-\mu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}} \le 1. \end{aligned}$$

Thus the aggregated value obtained by FFSWG operator is again a FFSN. $\square$

Example 3

Take Fermatean fuzzy soft matrix for $q_{2}$ from Example 2,

$$\begin{aligned} \begin{bmatrix} &{} e_{1} &{} e_{2} &{} e_{3} &{} e_{4}\\ d_{1} &{} \left\langle 0.6,0.8\right\rangle &{} \left\langle 0.7,0.8\right\rangle &{} \left\langle 0.6,0.5\right\rangle &{} \left\langle 0.6,0.3\right\rangle \\ d_{2} &{} \left\langle 0.7,0.8\right\rangle &{} \left\langle 0.8,0.3\right\rangle &{} \left\langle 0.8,0.5\right\rangle &{} \left\langle 0.8,0.3\right\rangle \\ d_{3} &{} \left\langle 0.7,0.5\right\rangle &{} \left\langle 0.7,0.4\right\rangle &{} \left\langle 0.6,0.5\right\rangle &{} \left\langle 0.6,0.3\right\rangle \end{bmatrix} \end{aligned}$$

Using FFSWG operator,

$$\begin{aligned}&FFSWG\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}},F_{e_{21}},F_{e_{22} },\ldots ,\right. \\&\qquad \left. F_{e_{2m}},\ldots ,F_{e_{n1}},F_{e_{n2}},\ldots ,F_{e_{nm}}\right) \\&\quad =\left\langle \prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{n}\left( \mu _{ij}\right) ^{\xi _{i}}\right) ^{\tau _{j}},\root 3 \of {1-\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{n}\left( 1-\nu _{ij}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}}~\right\rangle \\&\quad =\left\langle \begin{array} [c]{c} \left( \left( 0.6\right) ^{0.5}\left( 0.7\right) ^{0.2}\left( 0.7\right) ^{0.3}\right) ^{0.3}\left( \left( 0.7\right) ^{0.5}\left( 0.8\right) ^{0.2}\left( 0.7\right) ^{0.3}\right) ^{0.2}\\ \left( \left( 0.6\right) ^{0.5}\left( 0.8\right) ^{0.2}\left( 0.6\right) ^{0.3}\right) ^{0.4}\left( \left( 0.6\right) ^{0.5}\left( 0.8\right) ^{0.2}\left( 0.6\right) ^{0.3}\right) ^{0.1},\\ \root 3 \of { \begin{array} [c]{c} 1-\left( \left( 1-\left( 0.8\right) ^{3}\right) ^{0.5}\left( 1-\left( 0.8\right) ^{3}\right) ^{0.2}\left( 1-\left( 0.5\right) ^{3}\right) ^{0.3}\right) ^{0.3}\\ \left( \left( 1-\left( 0.8\right) ^{3}\right) ^{0.5}\left( 1-\left( 0.3\right) ^{3}\right) ^{0.2}\left( 1-\left( 0.4\right) ^{3}\right) ^{0.3}\right) ^{0.2}\\ \left( \left( 1-\left( 0.5\right) ^{3}\right) ^{0.5}\left( 1-\left( 0.5\right) ^{3}\right) ^{0.2}\left( 1-\left( 0.5\right) ^{3}\right) ^{0.3}\right) ^{0.4}\\ \left( \left( 1-\left( 0.3\right) ^{3}\right) ^{0.5}\left( 1-\left( 0.3\right) ^{3}\right) ^{0.2}\left( 1-\left( 0.3\right) ^{3}\right) ^{0.3}\right) ^{0.1} \end{array} }\\ =\left\langle 0.635,0.655\right\rangle \end{array} \right\rangle \end{aligned}$$

Lemma 2

If $e_{1}$ is the only parameter then, FFSWG operator reduces to Fermatean fuzzy weighted FFWG operator (Senapati and Yager 2019a).

Proof

If $e_{1}$ is the only parameter then, $m=1$ thus Eq. 8 becomes,

$$\begin{aligned}&FFSWA\left( F_{e_{11}},F_{e_{21}},F_{e_{31}},\ldots ,F_{e_{n1}}\right) \\&\quad =\left\langle \prod \limits _{i=1}^{n}\left( \mu _{i}\right) ^{\xi _{i} },\root 3 \of {1-\prod \limits _{i=1}^{n}\left( 1-\nu _{i}^{3}\right) ^{\xi _{i}} }~\right\rangle , \end{aligned}$$

which is weighted geometric aggregation operator in the environment of Fermatean fuzzy information. $\square$

3.6 Properties of the FFSWG operator

Property 3.6.1

(Idempotancey) If $F_{e_{ij} }=F_{e}=(\mu ,\nu )$ $\forall \ i,j$ then

$$\begin{aligned}&FFSWG\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}},F_{e_{21}},F_{e_{22} },\ldots ,\right. \\&\quad \left. F_{e_{2m}},\ldots ,F_{e_{n1}},F_{e_{n2}},\ldots ,F_{e_{nm}}\right) =F_{e}. \end{aligned}$$

Property 3.6.2

(Shift-Invariance) If $F_{e} =(\mu ,\nu )$, is any other FFSN, then

$$\begin{aligned}&FFSWG\left( \begin{array} [c]{c} F_{e_{11}}\oplus F_{e},F_{e_{12}}\oplus F_{e},\ldots ,F_{e_{1m}}\oplus F_{e},F_{e_{21}}\oplus F_{e},F_{e_{22}}\oplus F_{e},\\ \ldots ,F_{e_{2m}}\oplus F_{e},\ldots ,F_{e_{n1}}\oplus F_{e},F_{e_{n2}}\oplus F_{e},\ldots ,F_{e_{nm}}\oplus F_{e} \end{array} \right) \\&\quad =FFSWG \left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}},F_{e_{21}},F_{e_{22} },\ldots ,\right. \\&\qquad \left. F_{e_{2m}},\ldots ,F_{e_{n1}},F_{e_{n2}},\ldots ,F_{e_{nm}}\right) \oplus F_{e}. \end{aligned}$$

Property 3.6.3

(Homogeneity) For any real number$~\lambda$ $>0$ we have,

$$\begin{aligned}&FFSWG \left( \lambda F_{e_{11}},\lambda F_{e_{12}},\ldots ,\lambda F_{e_{1m} },\lambda F_{e_{21}},\lambda F_{e_{22}},\ldots ,\lambda \right. \\&\quad \left. F_{e_{2m}},\ldots ,\lambda F_{e_{n1}},\lambda F_{e_{n2}},\ldots ,\lambda F_{e_{nm}}\right) \\&\quad =\lambda \left\{ FFSWG\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}} ,F_{e_{21}},\right. \right. \\&\qquad \left. \left. F_{e_{22}},\ldots ,F_{e_{2m}},\ldots ,F_{e_{n1}},F_{e_{n2}},\ldots ,F_{e_{nm} }\right) \right\} . \end{aligned}$$

Property 3.6.4

(Boundedness) Let $F_{e_{ij}} ^{-}=\left\langle \underset{j}{\min }\underset{i}{\min }\{ \mu _{ij} \},\underset{j}{~\max }\underset{i}{\max }\{ \nu _{ij}\} \right\rangle$ and $F_{e_{ij}}^{+}=\left\langle \underset{j}{\max }\underset{i}{\max }\text { } \{ \mu _{ij}\},\underset{j}{\min }\underset{i}{\min }\{ \nu _{ij}\} \right\rangle$ then,

$$\begin{aligned}&F_{e_{ij}}^{-}\le FFSWG\left( F_{e_{11}},F_{e_{12}},\ldots ,F_{e_{1m}} ,F_{e_{21}},\right. \\&\quad \left. F_{e_{22}},\ldots ,F_{e_{2m}},\ldots,F_{e_{n1}},F_{e_{n2}},\ldots,F_{e_{nm} }\right) \le \ F_{e_{ij}}^{+} \end{aligned}$$

3.7 Fermatean fuzzy soft ordered weighted geometric (FFSOWG) operator

Definition 14

Let $\Upsilon ^{n\times m}$ be matrix of order $n\times m$ in which entries are from the collection $\left\{ F_{e_{ij}}=\left\langle \mu _{ij},\nu _{ij}\right\rangle ,\left( i=1,2,\ldots,n\ \, \text { and }j=1,2,\ldots,m\right) \right\}$ of FFSNs and $\tau =\left( \tau _{1},\tau _{2},\ldots,\tau _{m}\right) ^{T}$ and $\xi =\left( \xi _{1},\xi _{2},\ldots,\xi _{n}\right) ^{T}$ be the weighted vectors expressing importance of each parameter $e_{j}$ and importance of opinion of experts $x_{i\text { }}$respectively such that $\tau _{j}>0,~\xi _{{\dot{i}}}>0$ and $\underset{j=1}{\overset{m}{\sum }}\tau _{j}=1,$ $\overset{n}{\underset{i=1}{\sum }}\xi _{i}=1$ then FFSOWG operator is a mapping $FFSOWG:\Upsilon ^{n\times m}\longrightarrow \Upsilon$ defined as

$$\begin{aligned}&FFSOWG\left( F_{e_{11}},F_{e_{12}},\ldots,F_{e_{1m}},F_{e_{21}},F_{e_{22} },\ldots,\right. \\&\quad \left. F_{e_{2m}},\ldots,F_{e_{n1}},F_{e_{n2}},\ldots,F_{e_{nm}}\right) = {\displaystyle \bigoplus \limits _{j=1}^{m}} \left( {\displaystyle \bigoplus \limits _{i=1}^{n}} \xi _{i}F_{e_{\sigma \left( _{ij}\right) }}\right) ^{\tau _{j}} \end{aligned}$$

where $\left( \sigma _{12},\sigma _{13},\ldots,\sigma _{nm}\right)$ is a permutation of $\left( 1,2,\ldots,n:~j=1,2,\ldots,m\right)$, such that $F_{e_{\sigma (i-1)(j-1)}}\ge$ $F_{e_{\sigma (ij)}}$ for all $i=2,3,\ldots,n$ and $j=2,3,\ldots,m$.

Theorem 4

Let $F_{e_{ij}}=\left\langle \mu _{ij},\upsilon _{ij}\right\rangle ,$ $\left( i=1,2,\ldots,n:j=1,2,\ldots,m\right)$ be any FFSNs, then the aggregated value by the FFSOWG operator is a FFSN and is given by,

$$\begin{aligned}&FFSOWG\left( F_{e_{11}},F_{e_{12}},\ldots,F_{e_{1m}},F_{e_{21}},F_{e_{22} },\ldots,\right. \nonumber \\&\qquad \left. F_{e_{2m}},\ldots,F_{e_{n1}},F_{e_{n2}},\ldots,F_{e_{nm}}\right) \nonumber \\&\quad =\left\langle \prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{n}\left( \mu _{\sigma _{\left( ij\right) }}\right) ^{\xi _{i}}\right) ^{\tau _{j} },\root 3 \of {1-\prod \limits _{j=1}^{m}\left( \prod \limits _{i=1}^{n}\left( 1-\nu _{\sigma _{\left( ij\right) }}^{3}\right) ^{\xi _{i}}\right) ^{\tau _{j}}}\right\rangle \end{aligned}$$

(9)

Proof

Follow from Theorem 3. $\square$

3.8 Properties of FFSOWG operator

Some properties of FFSOWG operator are stated without proof.

Property 3.8.1

[Idempotency] If $F_{e_{ij}} =F_{e}=(\mu ,\nu )$ $\forall \ i,j$ then

$$\begin{aligned}&FFSOWG\left( F_{e_{11}},F_{e_{12}},\ldots,F_{e_{1m}},F_{e_{21}},F_{e_{22} },\ldots,\right. \\&\qquad \left. F_{e_{2m}},\ldots,F_{e_{n1}},F_{e_{n2}},\ldots,F_{e_{nm}}\right) =F_{e}. \end{aligned}$$

Property 3.8.2

(Shift-Invariance) If $F_{e}=(\mu ,\nu )$, is any other FFSN then

$$\begin{aligned}&FFSWA\left( \begin{array} [c]{c} F_{e_{11}}\oplus F_{e},F_{e_{12}}\oplus F_{e},\ldots,F_{e_{1m}}\oplus F_{e},F_{e_{21}}\oplus F_{e},F_{e_{22}}\oplus F_{e},\\ \ldots,F_{e_{2m}}\oplus F_{e},\ldots,F_{e_{n1}}\oplus F_{e},F_{e_{n2}}\oplus F_{e},\ldots,F_{e_{nm}}\oplus F_{e} \end{array} \right) \\&\quad =FFSWA\left( F_{e_{11}},F_{e_{12}},\ldots,F_{e_{1m}},F_{e_{21}},F_{e_{22} },\ldots,\right. \\ &\left. F_{e_{2m}},\ldots,F_{e_{n1}},F_{e_{n2}},\ldots,F_{e_{nm}}\right) \oplus F_{e}. \end{aligned}$$

Property 3.8.3

(Homogeneity) For any real number$~\lambda$ $>0$ we have

$$\begin{aligned}&FFSOWG\left( \lambda F_{e_{11}},\lambda F_{e_{12}},\ldots,\lambda F_{e_{1m} },\lambda F_{e_{21}},\right. \\&\qquad \left. \lambda F_{e_{22}},\ldots,\lambda F_{e_{2m}},\ldots,\lambda F_{e_{n1}},\lambda F_{e_{n2}},\ldots,\lambda F_{e_{nm}}\right) \\&\quad =\lambda \left\{ FFSOWG\left( F_{e_{11}},F_{e_{12}},\ldots,F_{e_{1m} },F_{e_{21}},\right. \right. \\&\qquad \left. \left. F_{e_{22}},\ldots,F_{e_{2m}},\ldots,F_{e_{n1}},F_{e_{n2}} ,\ldots,F_{e_{nm}}\right) \right\} . \end{aligned}$$

Property 3.8.4

(Boundedness) Let $F_{e_{ij}} ^{-}=\left\langle \underset{j}{\min }\underset{i}{\min }\{ \mu _{ij} \},\underset{j}{~\max }\underset{i}{\max }\{ \nu _{ij}\} \right\rangle$ and $F_{e_{ij}}^{+}=\left\langle \underset{j}{\max }\underset{i}{\max }\text { } \{ \mu _{ij}\},\underset{j}{\min }\underset{i}{\min }\{ \nu _{ij}\} \right\rangle$ then

$$\begin{aligned} F_{e_{ij}}^{-}\le & {} FFSOWG\left( F_{e_{11}},F_{e_{12}},\ldots,F_{e_{1m} },F_{e_{21}},\right. \\&\left. F_{e_{22}},\ldots,F_{e_{2m}},\ldots,F_{e_{n1}},F_{e_{n2}} ,\ldots,F_{e_{nm}}\right) \le \ F_{e_{ij}}^{+}. \end{aligned}$$

4 Decision making approach based upon proposed operators

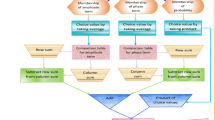
Here we present MCDM method based on the proposed operators. Let $Q=\left\{ x_{1},x_{2},\ldots,x_{r}\right\}$ be the set of r different alternatives, which are going to be evaluated by n experts $y_{1} ,y_{2},\ldots,y_{n}$ under the constraints of m parameters $E=\left\{ e_{1},e_{2},\ldots,e_{m}\right\}$. Suppose $\xi =\left( \xi _{1},\xi _{2} ,\ldots,\xi _{n}\right) ^{T}$ and $\tau =\left( \tau _{1},\tau _{2},\ldots,\tau _{m}\right) ^{T}$ are weighting vectors of experts and parameters respectively for Fermatean fuzzy soft arguments $F_{e_{ij}}$ $\left( i=1,2,\ldots,n:j=1,2,\ldots,m\right)$ with $\xi _{i}\succ 0,$ $\tau _{j}$ $\succ 0$ and $\underset{j=1}{\overset{m}{\sum }}\tau _{j}=1,$ $\underset{i=1}{\overset{n}{\sum }}\xi _{i}=1$. These decision makers will give their opinions about the alternatives in terms of FFSNs,  $F_{e_{ij}}=\left\langle \mu _{ij},\nu _{ij}\right\rangle$ such that $0\le \left( \mu _{ij}\right) ^{3}+\left( \nu _{ij}\right) ^{3}\le 1.$ These information are then collected in a decision matrix $D=\left( F_{e_{ij}}\right) _{n\times m}.$ Using proposed operators, the aggregated matrix $\left( FFSNx_{k}\right)$ for the alternatives $x_{r}$ is obtained. Finally, the score function of the aggregated FFSNs is used to rank the alternatives. Fig. 3 is the pictorial representation of the given approach. The approach is step-wise given as below:

Step 1. Collect the information related to each alternative under different parameters and arrange them in the form of Fermatean fuzzy soft matrix $D_{n\times m}=\langle \ \mu _{ij}\ ,\upsilon _{ij}\rangle ,$

$$\begin{aligned} D_{n\times m}= \begin{pmatrix} \langle \ \mu _{11},\nu _{11}\rangle &{} \langle \ \mu _{12},\nu _{12}\rangle &{} . &{} . &{} . &{} \langle \ \mu _{1m},\nu _{1m}\rangle \\ \langle \ \mu _{21},\upsilon _{21}\rangle &{} \langle \ \mu _{22},\nu _{22}\rangle &{} . &{} . &{} . &{} \langle \ \mu _{2m},\nu _{2m}\rangle \\ . &{} . &{} . &{} &{} &{} .\\ . &{} . &{} &{} . &{} &{} .\\ . &{} . &{} &{} &{} . &{} .\\ \langle \ \mu _{n1}\ ,\nu _{n1}\rangle &{} \langle \ \mu _{n2},\nu _{n2}\rangle &{} . &{} . &{} . &{} \langle \ \mu _{nm}\ ,\nu _{nm}\rangle \end{pmatrix} \end{aligned}$$

Step 2. Normalize the collective information decision matrix by transforming rating values of cost type parameters into benefit type parameters if any by using normalization formula ( Xu and Hu (2010)),

$$\begin{aligned} r_{ij}=\left\{ \begin{array} [c]{c} F_{e_{ij}}^{c}~\ ;~\text {for cost type parameters}\\ ~ \, F_{e_{ij}} \, ;~\text {for benefit type parameters} \end{array} \right. \end{aligned}$$

Step 3. Aggregate the FFSNs, $F_{e_{ij}}$ $(i=1,2,\ldots,n;$ $\ j=1,2,\ldots,m)$ for each alternative $x_{k}$ $(k=1,2,\ldots,r)$ into collective decision matrix by any of the proposed operator. Step 4. Find the score values $S(F_{e_{ij}})$ of $F_{e_{ij}}$ for each alternative $x_{k}(k=1,2,\ldots,r).$ Step 5. Rank the alternatives $x_{k}$, and find out which one is best and which one is the worst, then select the best one.

5 Practical example

Here we present the practical application of our proposed work. We will focus on the investigation of symptomatic treatment of COVID-19 disease by utilizing the presented procedure using Fermatean fuzzy soft operators in the environment of FFS information. But before that, a short background of COVID-19 pandemic is given as under. COVID-19 pandemic: we as a community are fighting against an invisible enemy, the "COVID-19" disease. The disease is caused by sever acute respiratory syndrome coronavirus (SARS-CoV-2) (see e.g. Organization et al. 2020a, b). The first case was reported in Wuhan city of China in December 2019 and spread almost all over the world in a short period of time. So far, more than 80,077,514 cases of COVID-19 and 1,748,352 deaths (up to 27th December 2020) have been reported (Fig. 2).

Fig. 2

COVID-19 cases worldwide

Due to the alarming situations, World Health Organization (WHO) announced public health emergency of international concern on January 30, 2020. The Emergency Committee on COVID-19 reconvened on 1st August 2020, 4th time and agreed that the outbreak of COVID-19 still constitutes a public health emergency of international concern (WHO). The pandemic has changed the way of living, canceling a lots of sports, schools, religious and political activities.

Fig. 3

Clinical representation of a COVID-19 patient

Symptoms: Research have shown that, the symptoms of COVID-19 in a patient appears from 2.5 to 7 days after infection and the maximum period is around 14 days. Moreover, there are several symptoms of the disease like, fever, headache, cough, sore throat, shortness of breath, hemoptysis, and then pneumonia, septic shock, myalgia etc., in late stages as illustrated in Fig. 3.

Since there is no specific treatment so far, and experts are heavily relaying on the symptomatic treatment of the disease. Also, the symptoms are greatly linked to some other infections like Cold, Flu and Seasonal Allergies. Figure 4 shows how the symptoms of these infections are related to each other.

Fig. 4

Comparison of symptoms of COVID-19 with cold, flu and seasonal allergies

That is why, the possibility that an expert may make a wrong decision about a patient can not be ignored. Infect, it has also been observed that, sometimes patients with infections like Cold, Cough and Flu are treated as a case of COVID-19. Therefore, it is very important for experts to investigate any patient with serious care and full attention in order to make their decision more wise and accurate. Pakistan: As all over the world, the novel pandemic has also changed the way of life in Pakistan which is a growing economic state and has less resources to deal with these critical situations (Sarwar et al. 2020). However, local and provincial governments are taking serious action by locking down markets, schools, universities and other public places and raising awareness through social media, T.V channels to reduce the transmission of the pandemic. Up to 27th of December 2020, the total number of confirmed cases in Pakistan are about 473, 309. The government is keen to to control the transmission of the pandemic taking some unusual and hard steps. Due to lockdown (smart lockdown strategy in special) and other precautionary measures, the rate of recovery during the first wave of COVID-19 was incredibly good. Another positive side is that, the death ratio was a lot lower in Pakistan. So far, 423, 892 peoples have recovered while 9929 have lost the run (http://covid-19.gov.pk). The following graph (Fig. 5) shows these details up to 27th of December 2020.

Fig. 5

COVID-19 cases in different areas of Pakistan

Pakistan currently has the 8th-highest number of cases in Asia and the 28th highest number of confirmed cases in the world. To limit and to reduce exposures for other patients and health care personnel, it is imperative to promptly identify and separate active cases by instituting screening system for signs and symptoms of disease along with specific RT-PCR (real time reserve transcription) testing in suspected inpatients and health care personnel (HCP). Application: Keeping social distance is the most important precautionary measure, therefore, to avoid crowds in hospitals/health care centers, it is important to separate patients who have been tested and declared negative for COVID-19 must be sent to the green zone (Area of the hospital reserved for patients declared negative for COVID-19). While those declared positive must be kept in the red zone (Area of the hospital reserved for patients declared positive for COVID-19). In order to provide all necessary health cares, patients in red zone must also be categorized on the basis of severity of the disease as Mild, Moderate, Severe and Critical. In case of,

• Mild: Treatment is symptomatic and can be managed at home and does not require inpatient care.

• Moderate: Can be managed either at home, or as inpatient at red zone.

• Severe: Requires oxygen therapy, has dyspena, hypoxia, or $\succ 50$ percent lung involvement on image within 24–48 h; (In red zone).

• Critical: Requires mechanical ventilation, has respiratory failure, shock, or multiorgan dysfunction (isolation in red zone) (Wang et al. 2020). This plan is also explained in Fig. 6.

Fig. 6

Plan for isolation of COVID-19 patients in red and green zones

We consider the situations of four patients $P_{i}$ $\left( i=1,2,3,4\right)$ from the red zone and will try to find where to keep them on the basis of severity of the disease. A penal of three experts (doctors) is going to treat these patients symptomatically. Considering some parameters, experts will give there opinion about each patient in terms of FFSNs. There are several parameters however, the set of parameters under which these patients are to be treated is arranged by these experts as $E=\left\{ e_{1},e_{2},e_{3} ,e_{4},e_{5}\right\}$ where$~e_{1}\equiv$ Headache, $e_{2}\equiv$ Cough, $e_{3}\equiv$ Shortness of breath, $e_{4}\equiv$ Fever, $e_{5}\equiv$ Sore throat. It is important to note that, if a patient is found to have any of these five symptoms, then it is termed as ’Case’ and if not then termed as ’Control’. We assume that, all the patients $P_{i}$ are infected thus, each of them represents a case. Let $\xi =\left( 0.2,0.3,0.5\right) ^{T}$ and $\tau =\left( 0.2,0.3,0.1,0.25,0.15\right) ^{T}$ be the weighted vectors of experts $d_{i}$ and parameters $e_{j}$ respectively. The rating values by these experts in terms of FFSNs are listed as below,

$$\begin{aligned}&\, \text { Rating values by the experts d}_{1}\text { for the patients}\\&\begin{array} [c]{c} P\left( e_{1}\right) =\left\{ P_{1}/\left( 0.9,0.4\right) ,P_{2}/\left( 0.6,0.3\right) ,P_{3}/\left( 0.9,0.3\right) ,P_{4}/\left( 0.7,0.6\right) \right\} \\ P\left( e_{2}\right) =\left\{ P_{1}/\left( 0.8,0.5\right) ,P_{2}/\left( 0.7,0.5\right) ,P_{3}/\left( 0.6,0.5\right) ,P_{4}/\left( 0.8,0.7\right) \right\} \\ P\left( e_{3}\right) =\left\{ P_{1}/\left( 0.7,0.4\right) ,P_{2}/\left( 0.7,0.3\right) ,P_{3}/\left( 0.5,0.4\right) ,P_{4}/\left( 0.8,0.5\right) \right\} \\ P\left( e_{4}\right) =\left\{ P_{1}/\left( 0.6,0.4\right) ,P_{2}/\left( 0.5,0.3\right) ,P_{3}/\left( 0.9,0.5\right) ,P_{4}/\left( 0.7,0.4\right) \right\} \\ P\left( e_{5}\right) =\left\{ P_{1}/\left( 0.8,0.5\right) ,P_{2}/\left( 0.9,0.3\right) ,P_{3}/\left( 0.7,0.2\right) ,P_{4}/\left( 0.4,0.1\right) \right\} \end{array}\\&\text {Rating values by the experts d}_{2}\text { for the patients}\\&\begin{array} [c]{c} P\left( e_{1}\right) =\left\{ P_{1}/\left( 0.8,0.3\right) ,P_{2}/\left( 0.7,0.5\right) ,P_{3}/\left( 0.6,0.4\right) ,P_{4}/\left( 0.7,0.6\right) \right\} \\ P\left( e_{2}\right) =\left\{ P_{1}/\left( 0.7,0.5\right) ,P_{2}/\left( 0.8,0.5\right) ,P_{3}/\left( 0.9,0.4\right) ,P_{4}/\left( 0.6,0.3\right) \right\} \\ P\left( e_{3}\right) =\left\{ P_{1}/\left( 0.3,0.1\right) ,P_{2}/\left( 0.4,0.2\right) ,P_{3}/\left( 0.5,0.3\right) ,P_{4}/\left( 0.7,0.4\right) \right\} \\ P\left( e_{4}\right) =\left\{ P_{1}/\left( 0.6,0.5\right) ,P_{2}/\left( 0.7,0.3\right) ,P_{3}/\left( 0.8,0.4\right) ,P_{4}/\left( 0.9,0.6\right) \right\} \\ P\left( e_{5}\right) =\left\{ P_{1}/\left( 0.5,0.3\right) ,P_{2}/\left( 0.7,0.5\right) ,P_{3}/\left( 0.9,0.6\right) ,P_{4}/\left( 0.6,0.4\right) \right\} \end{array} \end{aligned}$$

$$\begin{aligned}&\text {Rating values by the experts d}_{3}\text { for the patients}\\&\begin{array} [c]{c} P\left( e_{1}\right) =\left\{ P_{1}/\left( 0.7,0.3\right) ,P_{2}/\left( 0.5,0.2\right) ,P_{3}/\left( 0.6,0.2\right) ,P_{4}/\left( 0.7,0.3\right) \right\} \\ P\left( e_{2}\right) =\left\{ P_{1}/\left( 0.6,0.3\right) ,P_{2}/\left( 0.7,0.5\right) ,P_{3}/\left( 0.9,0.4\right) ,P_{4}/\left( 0.8,0.2\right) \right\} \\ P\left( e_{3}\right) =\left\{ P_{1}/\left( 0.5,0.2\right) ,P_{2}/\left( 0.6,0.5\right) ,P_{3}/\left( 0.7,0.4\right) ,P_{4}/\left( 0.7,0.3\right) \right\} \\ P\left( e_{4}\right) =\left\{ P_{1}/\left( 0.7,0.5\right) ,P_{2}/\left( 0.8,0.3\right) ,P_{3}/\left( 0.3,0.1\right) ,P_{4}/\left( 0.4,0.3\right) \right\} \\ P\left( e_{5}\right) =\left\{ P_{1}/\left( 0.6,0.3\right) ,P_{2}/\left( 0.7,0.4\right) ,P_{3}/\left( 0.9,0.6\right) ,P_{4}/\left( 0.5,0.1\right) \right\} \end{array} \end{aligned}$$

Step 1 In matrix from these information are summarized as (Tables 1, 2, 3, 4).

Table 1 Fermatean fuzzy soft matrix for patient $P_{1}$

Table 2 Fermatean fuzzy soft matrix for patient $P_{2}$

Table 3 Fermatean fuzzy soft matrix for patient $P_{3}$

Table 4 Fermatean fuzzy soft matrix for patient $P_{4}$

Step 2 Since all the parameters are of same type, hence there is no need to normalize the data. Step 3 The aggregated rating values of each patient $P_{i}$ $\left( i=1,2,3,4\right)$ by the proposed operators are given in Table 5.

Table 5 Results by the proposed operators

Step 4 The score values $S\left( F_{e_{ij}}\right)$ are given in Table 6.

Table 6 Score values using score function

Step 5 Final ranking orders are given in the following Table 7.

Table 7 Final ranking orders

From Table 7, it is clear that the ranking orders of the alternatives are same and P$_{3}$ is the patient in the critical stage having respiratory failure, shock, or multiorgan dysfunction and requires mechanical ventilation therefore,

• $P_{3}$ must be isolated in the isolation ward at red zone in the hospital.

• Patient $P_{1}$ is in the severe stage and requires oxygen therapy, having dyspena, hypoxia, or $\succ 50$ percent lung involvement on image within 24–48 h, thus $P_{1}$ (In red zone at hospital).

• $P_{4}$ and $P_{2}$ are respectively in the moderate and mild stages of the disease or vice versa, however treatment is symptomatic and they can be managed at home and does not require inpatient care both of them can be treated as inpatient. For further assistance one can examine Fig. 7.

Fig. 7

Graphical view of score values by the proposed operators

Figure 7 shows the comparison between score values obtained by FFSWA, FFSOWA and FFSWG,  FFSOWG operators. The red line in the figure is representing the ranking order of alternatives $P_{i}$ $\left( i=1,2,3,4\right)$ obtained by FFSWA and FFSWG operator, while the blue line is representing the ranking order of the alternatives obtained by FFSOWA and FFSOWG operator.

6 Comparative analysis

In this final section, we are going to compare our results with results of existing operators. We adopt Fermatean fuzzy soft information from Shahzadi and Akram (2021), where the FFS matrices for four different antivirus masks $x_{i}$ $\left( i=1,2,3,4\right)$ are aggregated using Fermatean fuzzy soft Yager average and geometric operators. The final scores and ranking orders corresponding to FFS Yager average (FFS$_{f}$WA) and FFS Yager geometric (FFS$_{f}$WG) operators are given in Table 8. According to their results, the antivirus mask $x_{1}$ is the most suitable mask (best alternative).

Table 8 Final scores and ranking orders by ${FFS}_{f}\text {WA and FFS}_{f}\text {WG}$

By applying the proposed approach using FFSWA and FFSWG operators, we obtained the aggregated matrix about four antivirus masks $x_{i}$ $\left( i=1,2,3,4\right)$ as given in Table 9.

Table 9 Aggregated matrix about antivirus masks by proposed operators

This matrix is obtained by aggregating the four matrices given in Tables 4 to 7 in Shahzadi and Akram (2021). From this matrix, a comparative study has been established with the existing work developed in Shahzadi and Akram (2021) which is based on Fermatean fuzzy soft Yager aggregation operators on FFS environment. Table 10 shows the final comparison with existing method, which also shows that the best alternative is $x_{1}$.

Table 10 Final scores and ranking orders by proposed operators

Clearly, the ranking orders by the proposed operators are identical with ranking orders of FFS$_{f}$YW operators. This proves the stability of our proposed method. The basic advantage of proposed method is that, it is capable to facilitate the description of real world problems with the help of properties like, parameterization, fuzziness and so, the method can be used in decision making problems instead of other existing methods in the environment of Fermatean fuzzy soft set.

Fig. 8

Comparison of score values by FFSfYWA and FFSWA operators

Figure 8 is the graphical representation of the comparison of score values by FFS$_{f}$YWA and FFSWA operators. The ranking order of the alternatives obtained by FFS$_{f}$YWA operator is represented by the bluish cones in front, while the ranking order of alternatives obtained by FFSWA operator is represented by the red cones behind.

7 Conclusion

We have explored the (MADM) problems with Fermatean fuzzy soft information and introduced FFSWA, FFSOWA, FFSWG, and FFSOWG operators in the environment of Fermatean fuzzy soft sets. The four basic properties of these operators are studied. An approach has been developed to solve the Fermatean fuzzy soft MADM problems. Next, the approach has been tested through a case study of searching out the most serious patient with COVID-19 disease. Lastly, the stability of the proposed method is provided by comparing the work with existing work in the environment of FFSS. In future, we shall extend the idea of Fermatean fuzzy soft information to introduce more operators like, Fermatean fuzzy soft Dombi aggregation operators, Fermatean fuzzy soft Einstein hybrid aggregation operators and Fermatean fuzzy soft Hamacher aggregation operators.