Early infectious diseases identification based on complex probabilistic hesitant fuzzy N-soft information

Abstract

This paper aims to assess and deal with the challenges experienced by medical professionals caring for infectious diseases. In Pakistan, public health is still a serious concern and the main contributor to morbidity and mortality is infectious diseases. The major issue is a resemblance in the clinical symptoms of infectious diseases such as tuberculosis, hepatitis, COVID-19, dengue, and malaria. Early detection of infectious disease is crucial in order to start treatment with counseling and medication. This can only be done if several infections with similar clinical traits can be diagnosed depending on several criteria, including the availability of various kits, the ability to carry out diagnostic procedures, money, and technical staff. But woefully Pakistan’s economy is badly battered due to several circumstances. Therefore, we are unable to provide patients with enough diagnostic testing kits and broadly accessible therapy choices, which makes diagnosis more difficult and create hesitancy with fuzziness and randomness. For this purpose, we introduced the new concept of the complex probabilistic hesitant fuzzy N-soft set. We defined its fundamental operations (like restricted and extended union, restricted and extended intersection, weak, top and bottom weak complements, as well as soft max-AND or soft min-OR) with examples. We also discussed their many properties with their proofs and theorems. Furthermore, we developed the algorithms for decision-making where doctors use the complex probabilistic hesitant fuzzy N-soft information to identify a particular disease. Furthermore, we explained numerical illustration of two case studies. Moreover, a sensitive and comparative analysis is discussed. In the last, we conclude the whole study.

1 Introduction

Decision-making plays a crucial role in our unrealistic world environment. In this enterprising environment, our motive is to figure out the best alternative for any objective or desire from the multifold criteria. Nonetheless, picking out only the prime alternative does not sort out our problem, but the appropriate ranking of all accessible choices is required to be completed to comprehend their classification and nature, so we go ahead with further inspection. The use of decision-making techniques is helpful for those who have to make decisions while keeping both favorable and unfavorable circumstances in mind. But in many real-world circumstances, it might be difficult for decision-makers to evaluate the alternatives due to various types of uncertainties or ambiguity in data. This is a result of incomplete knowledge or errors made by humans when processing data in our daily lives.

In this real world, experts in a variety of sectors, including economic analysis, social sciences, medicine, data sciences, artificial intelligence, physical sciences, natural sciences, environmental sciences, control theory, and engineering, are increasingly understanding the constraints of precise research. Research in these areas is extremely important because we know that the real world is rife with ambiguity, vagueness, and uncertainty. Such issues require the application of mathematical concepts based on uncertainty and imprecision. These days, the procedure of decision-making with multiple criteria is on the rise and usually involves the three steps below.

• Select the appropriate scale to classify the objects you are provided with.

• Assemble the data using the appropriate method to determine each object’s score value.

• To choose the best items, rank the available options.

Due to the significant amount of uncertainty existing in the information, especially when the data exists in crisp form, the decision-making process is becoming more and more complicated. Crisp refers to dichotomous, yes-or-no types instead of more-or-less types. For example, a statement can only be true or false in traditional logic, with nothing in-between. Zadeh (1965) investigated fuzzy theory to overcome these constraints. It is intended to represent the deterministic uncertainty for which he developed the concept of membership function. Making decisions is significantly assisted by fuzzy theory. But sometimes people had a difficult time handling group decision-making issues when they had to choose among many possible membership values for an element in the set. Consider the following scenario: Two experts are debating whether x belongs in category A, and one of them wants to assign a score of 0.6 while the other wants to give a score of 0.7. As a result, the range of possible values has some degree of uncertainty. In order to overcome these restrictions, Torra presented a hesitant fuzzy set to deal with hesitant situations (Torra 2010). In this case, he developed the membership function as a set of possible membership values, namely h(x), where h(x) is a finite subset of [0, 1]. With time, hesitant fuzzy sets have gained popularity and have been applied to a variety of tasks, including medical diagnosis, information retrieval, cluster analysis, and decision-making issues which play a crucial role in decision-making. Researchers in Zhu et al. (2012) presented the model of dual hesitant fuzzy soft set to group forecasting. They used the pharmaceutical company as an example, where the board of directors had to determine the priorities for future investments in the subsidiaries upon net income, a wind power plant site selection algorithms based on hesitancy in Ashraf et al. (2022a, 2022b), etc.

But in many situations in real life during taking decisions, people faced a combination of deterministic and random ones. For instance, weather patterns are both partially random and partially forecastable. To deal with these kinds of circumstances, Meghdadi Meghdadi and Akbarzadeh-T (2001) introduced the concept of probabilistic fuzzy logic. In applications including power systems (Pidre et al. 2003), robotic control systems (Valavanis and Saridis 1991), fog-haze factor Assessment problem (Batool et al. 2020), signal processing (Deshuang et al. 1996), drug selection to treat COVID-19 (Ashraf et al. 2022c), control systems (Liu and Li 2005) and in decision-making (Khan et al. 2020; Ashraf et al. 2022d; Batool et al. 2021), probabilistic modeling is a crucial tool for dealing with random uncertainties. Many scholars work with other hybrid models using probabilistic fuzzy set such as Han et al. (2022); Zhu et al. (2023); Han and Zhan (2023) which plays a very significant role in solving real-life problems. It has been determined from the aforementioned theories that they only have the ability to address vagueness and uncertainty that exist in data while evaluating the decision-making issues under the fuzzy set and its generalizations. These are unable to adequately depict the variations in data at a specific point in time. A complex fuzzy set was introduced by Ramot to solve these constraints (Ramot et al. 2002). Unlike a conventional fuzzy membership function, this range extends to the complex plane’s unit circle rather than being constrained to the range [0, 1]. The Complex Fuzzy Set drew researchers’ attention to itself, and researchers developed many theories related to the complex fuzzy set. For instance, Zhang et al. (2009) on its operation and equalities, Ullah et al. (2020) on some distance measures of complex Pythagorean fuzzy sets and their applications in pattern recognition, Alkouri and Salleh (2012) on complex fuzzy computing to time series prediction and many more.

According to Molodtsov, one major issue with these theories is their inadequate use of parameterizations tools, such as the individual’s ability to determine their level of membership based on the information they receive, making them susceptible to subjective perspectives. Furthermore, it is important to consider all the features of a situation together. In 1999, Molodtsov (1999) created a soft set computing approach to work around these constraints. The soft set theory has the advantage of having problems that take into account several attributes. It has excellent potential to solve issues and is extremely important in many industries (Feng et al. 2016; Feng and Li 2013). Researchers enhanced and developed the soft set theory. Babitha presented the appearance of a fuzzy soft set and described its relations and functions (Babitha and Sunil 2010). Many researchers applied soft set theory to decision-making problems (Roy and Maji 2007; Alcantud 2016; Atagün et al. 2018) rule mining (Herawan and Deris 2011), and business (Xu et al. 2014). The semantics of soft sets are now well studied with the help of the article (Yang and Yao 2020). There are multifold hybrid extensions presented by the investigators. But in reality, non-binary evaluations are common in many contexts in daily life, including (Alcantud and Laruelle 2014) who discuss ternary voting situations in a social choice environment. Rating or ranking systems frequently use non-binary evaluations. Real-world examples demonstrate how ratings may take the form of a star rating, such as “five stars,” “four stars,” “three stars,” “two stars,” or “one star.” Therefore, Fatimah et al. (2018) expanded the soft set model and presented the idea of the N-soft set and discussed the great importance of ordered grades in practical situations. They created decision-making processes for the N-soft set as well. The semantics of N-soft sets are now well studied with the help of the article (Alcantud 2022). The work on N-soft set theory by Akram et al. (2018a) is remarkable. The theory of N-soft set play an interesting and advantageous role therefore many scholars work with this model such as hesitant fuzzy N-soft set (Akram et al. 2019a), complex Fermatean fuzzy N-soft sets (Akram et al. 2022), reduction of N-soft sets (Akram et al. 2021a), complex Pythagorean fuzzy N-soft sets (Akram et al. 2021b) and belief interval valued N-soft sets (Ali et al. 2021) and complex spherical fuzzy N-soft sets (Akram et al. 2021c).

This article aims to broaden the applicability of N-soft set theory where grades yield a parameterized interpretation of alternatives of the universe and most of the time people face difficulty in decision making with the combination of fuzziness, hesitancy, and randomness of uncertain data with a parameterized family of subsets and grades of alternatives of the universe. For example, doctors face many difficulties in dealing with infectious diseases such as lower respiratory infections, heart disease, COVID-19, TB, malaria, and hepatitis, which are included in the top 10 diseases and the leading cause of death globally (Top 10 diseases globally (xxxx)). Because these diseases have common symptoms or clinical characteristics, which create fuzziness, hesitancy, and randomness, it makes early identification difficult, and such complex combinations not only make diagnosis more difficult but also place a double load on the country’s already frail healthcare system. This is only achievable if there are sufficient diagnostic testing kits and widely available treatment options for patients. But unfortunately, Pakistan is an underdeveloped country and in 2020 COVID-19 created a negative impact on its economy. He was trying to stabilize its economy meanwhile floods engulfed Pakistan. The immediate effects of floods include loss of life, property damage, agricultural devastation, animal loss, infrastructure facility failure, and deteriorating health due to waterborne infections which increase the rate of infectious diseases. So, at present we cannot afford sufficient diagnostic testing kits and widely available treatment options for patients. Therefore, we developed the novel model of complex probabilistic hesitant fuzzy N-soft set through which doctors can accurately collect the data from the patient in complex probabilistic hesitant fuzzy information where the amplitude term represents to what extent the symptom belongs to the respective disease, the phase term is typically related to the periodicity or duration of the appearance of the disease or symptoms, the grading indicates the severity, and probability indicates the possibility of the occurrence of the disease. However, hesitant fuzzy approximations increase the flexibility and richness of the decision-maker’s analysis, thereby increasing the dependability of the decisions that rely on them. We also presented the algorithm to run this information by which doctors get the result in a descending order series, which represents the hierarchy of the diseases. This enables the doctors to identify the particular disease and prevent the citizens from contracting infectious diseases, which leads the nation toward development. It is obvious that the modelization by existing theories is insufficient to take these circumstances into account.

The rest of the paper is organized as follows. Preliminaries are covered in Sect. 2, where we carefully review a few fundamental definitions to help us explain more easily the following sections. The notion of a complex probabilistic hesitant fuzzy N-soft set is introduced in Sect. 3. We discussed various fundamental operations, including extended and restricted intersection, extended and restricted union, weak complement, top and bottom weak complement, and soft max-AND and soft min-OR operators. Additionally, we confirm their essential laws. Furthermore, the numerical examples have been resolved to demonstrate the validity and superiority of the research work. In Sect. 5, two distinct decision-making algorithms were established for the use of complex probabilistic hesitant fuzzy information in the presence of multifold attributes. Section 6 presents applications and a case study to help readers make the best choices. In Sect. 7, we discussed the comparative analysis with the existing studies, while we provided the paper’s conclusion in Sect. 8.

2 Preliminaries

The definitions we used to establish the methods in this paper are briefly reviewed in this section.

Definition 2.1

If ${\mathcal {Z}}$ is a universal set, then $\widetilde{{\mathbb {A}}}$ is a fuzzy set defined on ${\mathcal {Z}}$ as:

$$\begin{aligned} \widetilde{{\mathbb {A}}} = \Big \{\langle z_{i},\mu _{\widehat{{\mathbb {A}}}}(z_{i})\rangle \big | z_{i}\in {\mathcal {Z}} \Big \} \end{aligned}$$

where $\mu _{\widehat{{\mathbb {A}}}}(z_{i})$ is a membership degree of $z_{i}$ in $\widehat{{\mathbb {A}}}$ and $\mu _{\widehat{{\mathbb {A}}}}: {\mathcal {Z}} \rightarrow [0, 1]$. If $\mu _{\widehat{{\mathbb {A}}}}(z_{i}) = 0$, is considered to be non- membership of $z_{i}$. If $\mu _{\widehat{{\mathbb {A}}}}(z_{i}) = 1$, is considered to be the entire membership of $z_{i}$. If $\mu _{\widehat{{\mathbb {A}}}}(z_{i})$ value among 0 and 1, is considered to be partial membership of $z_{i}$ (Zadeh 1965).

Definition 2.2

If ${\mathcal {Z}}$ is a universal set, then $\widehat{{\mathbb {B}}}$ is a hesitant fuzzy set in terms of the h function, which returns a subset of [0,1] when it applies to ${\mathcal {Z}}$ which is denoted as:

$$\begin{aligned} \widehat{{\mathbb {B}}} = \Bigg \{\bigg \langle z_{i},h_{\widehat{{\mathbb {B}}}}(z_{i})\bigg \rangle \big | z_{i}\in {\mathcal {Z}} \Bigg \} \end{aligned}$$

where $h_{\widehat{{\mathbb {B}}}}(z_{i})$ is the collection of distinct finite elements in [0,1], represents the possible membership degrees of the element $z_{i}\in {\mathcal {Z}}$ to the set $\widehat{{\mathbb {B}}}$ Torra (2010).

Definition 2.3

If ${\mathcal {Z}}$ is a universal set, then $\widehat{{\mathbb {C}}}$ is a probabilistic hesitant fuzzy set defined as:

$$\begin{aligned} \widehat{{\mathbb {C}}} = \Bigg \{\bigg \langle z_{i},h_{\widehat{{\mathbb {C}}}}\Big (\mu _{m} (z_{i})\big |P_{\widehat{{\mathbb {C}}}_{m}}\Big )\bigg \rangle \big | z_{i}\in {\mathcal {Z}} \Bigg \} \end{aligned}$$

where $h_{ \widehat{{\mathbb {C}}}}\big (\mu _{m} (z_{i})|P_{\widehat{{\mathbb {C}}}_{m}}\big )$ is the collection of distinct finite elements $(\mu _{m} (z_{i})\big |P_{\widehat{{\mathbb {C}}}_{m}})$ representing the hesitant fuzzy information along probabilities to the set $\widehat{{\mathbb {C}}}, m = 1, 2, 3,...,l$ where l is the number of possible elements in $h_{ {\widehat{C}}}\big (\mu _{m} (z_{i})|P_{\widehat{{\mathbb {C}}}_{m}}\big ), P_{\widehat{{\mathbb {C}}}_{m}}\in [0,1]$ is the hesitant probability of $z_{i}$ and $\sum \limits _{m} P_{\widehat{{\mathbb {C}}}_{m}}= 1$Xu and Zhou (2017).

Definition 2.4

If ${\mathcal {Z}}$ is a universal set, then $\widehat{{\mathbb {D}}}$ is a complex fuzzy set defined as:

$$\begin{aligned} \widehat{{\mathbb {D}}} = \Bigg \{\bigg \langle z_{i},r_{\widehat{{\mathbb {D}}}}(z_{i})e^{2\pi i \omega _{\widehat{{\mathbb {D}}}}(z_{i})}\bigg \rangle \big | z_{i}\in {\mathcal {Z}} \Bigg \} \end{aligned}$$

where $r_{\widehat{{\mathbb {D}}}}(z_{i})e^{2\pi i \omega _{\widehat{{\mathbb {D}}}}(z_{i})}$ is a complex valued membership degree of $z_{i}$ in $\widehat{{\mathbb {D}}}$ and it might be given any value that is contained in the complex plane unit circle. and $r_{\widehat{{\mathbb {D}}}}(z_{i})\in [0,1]$, $\omega _{\widehat{{\mathbb {D}}}}(z_{i}) \in (0,1]$ and $i = \sqrt{-1}$ Ramot et al. (2002).

Definition 2.5

If ${\mathcal {Z}}$ is a universal set, then $\widehat{{\mathbb {E}}}$ is a complex probabilistic hesitant fuzzy set (CPHFS) defined as:

$$\begin{aligned} \widehat{{\mathbb {E}}} = \Bigg \{\bigg \langle z_{i},h_{\widehat{{\mathbb {E}}}}\bigg (r_{\widehat{{\mathbb {E}}}_{m}}(z_{i})e^{2\pi i \omega _{\widehat{{\mathbb {E}}}_{m}}(z_{i})}\Big |P_{\widehat{{\mathbb {E}}}_{m}}\bigg )\bigg \rangle \Big | z_{i}\in {\mathcal {Z}} \Bigg \} \end{aligned}$$

where $h_{\widehat{{\mathbb {E}}}}\Big (r_{\widehat{{\mathbb {E}}}_{m}}(z_{i})e^{2\pi i \omega _{\widehat{{\mathbb {E}}}_{m}}(z_{i})}\big |P_{\widehat{{\mathbb {E}}}_{m}}\Big )$ is the collection of finite complex elements denoting the complex hesitant fuzzy information along probabilities to the set $\widehat{{\mathbb {E}}}, r_{\widehat{{\mathbb {E}}}_{m}}(z_{i})\in [0,1]$ and $\omega _{\widehat{{\mathbb {E}}}_{m}}(z_{i}) \in [0, 1], m = 1, 2,...,l$ where l is the number of possible elements in $h_{\widehat{{\mathbb {E}}}}\Big (r_{\widehat{{\mathbb {E}}}_{m}}(z_{i})e^{2\pi i \omega _{\widehat{{\mathbb {E}}}_{m}}(z_{i})}\big |P_{\widehat{{\mathbb {E}}}_{m}}\Big ),$ $P_{\widehat{{\mathbb {E}}}_{m}}\in [0, 1]$ is the complex hesitant probability of $r_{\widehat{{\mathbb {E}}}_{m}}(z_{i})e^{2\pi i \omega _{\widehat{{\mathbb {E}}}_{m}}(z_{i})}$ and $\sum \limits _{m} P_{\widehat{{\mathbb {E}}}_{m}}= 1.$

Definition 2.6

Let ${\mathcal {Z}}$ is a universal set and H be the set of attributes, for any non-empty set ${\mathcal {B}} \subseteq H$. A pair $(\widehat{{\mathbb {F}}},{\mathcal {B}})$ is called soft set over ${\mathcal {Z}}$ if there exists a mapping $\widehat{{\mathbb {F}}}: {\mathcal {B}} \rightarrow {\mathcal {P}}({\mathcal {Z}})$ where ${\mathcal {P}}({\mathcal {Z}})$ indicates the power set of ${\mathcal {Z}}$.

Thus, the soft set is a parametric family of the subsets of universal set. For each $b_{j}\in P$, we can denote $\widehat{{\mathbb {F}}}(b_{j})$ as a subset of universal set ${\mathcal {Z}}$. We can also consider $\widehat{{\mathbb {F}}}(b_{j})$ as a mapping $\widehat{{\mathbb {F}}}(b_{j}): {\mathcal {Z}}\rightarrow \{0,1\}$ and then $\widehat{{\mathbb {F}}}(b_{j})(z_{i}) = 1$ equivalent to $z_{i}\in \widehat{{\mathbb {F}}}(b_{j})$, otherwise $\widehat{{\mathbb {F}}}(b_{j})(z_{i}) = 0$. Molodtsov considered many examples in Molodtsov (1999) to illustrate the soft set.

Definition 2.7

Let ${\mathcal {Z}}$ is a universal set and H be the set of attributes, for any non-empty set ${\mathcal {B}} \subseteq H$. A pair $(\widehat{{\mathbb {G}}},{\mathcal {B}})$ is called fuzzy soft set over ${\mathcal {Z}}$ if there exists a mapping $\widehat{{\mathbb {G}}}: {\mathcal {B}}\rightarrow {\mathcal {I}}({\mathcal {Z}})$ where ${\mathcal {I}}({\mathcal {Z}})$ indicates the fuzzy power set of ${\mathcal {Z}}$(all possible fuzzy subsets of ${\mathcal {Z}}$) Yao et al. (2008).

Definition 2.8

Let ${\mathcal {Z}}$ be the universal set and ${\mathcal {I}}({\mathcal {Z}})$ indicates the set of all fuzzy subsets of ${\mathcal {Z}}$ and let ${\mathcal {R}} = \{0, 1, 2,..., N-1\}$ be a set of ordered grades where $N\in \{2, 3, 4,...\}$ and H be the set of attributes, for any non-empty set ${\mathcal {B}}\subseteq H$. A triple $(\widehat{{\mathbb {H}}}, {\mathcal {B}},N)$ is called fuzzy N-soft set over ${\mathcal {Z}}$ if there exists a mapping $\widehat{{\mathbb {H}}}: {\mathcal {B}}\rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$, with the property that for each $b_{j} \in {\mathcal {B}}$ there exists a unique $(z_{i},\mu ( z_{i}), r_{ij}) \in ({\mathcal {I}}({\mathcal {Z}})\times R)$ such that $(z_{i},\mu ( z_{i}), r_{ij}) \in \widehat{{\mathbb {H}}}(b_{j}),~ b_{j}\in {\mathcal {B}}, ~z_{i} \in {\mathcal {Z}}~ and ~r_{ij} \in {\mathcal {R}}$, where ${\mathcal {I}}({\mathcal {Z}})\times R$ is the collection of all fuzzy soft sets over ${\mathcal {Z}}\times R$Akram et al. (2018b).

Example 2.9

Let ${\mathcal {Z}} = \{ z_{1}, z_{2}, z_{3}\}$ be the set of laptops, $H = \{b_{1}, b_{2}, b_{3},b_{4}, b_{5}\}$ be the set of attributes for the evaluations of laptop by its features, and ${\mathcal {B}}\subseteq H$ such that ${\mathcal {B}} = \{b_{1}=storage, b_{2}=graphics,b_{3}=processor\}$ and let $R = \{0,1,2,3,4\}$ be the set of grade evaluation. Then, $(\widehat{{\mathbb {H}}}, {\mathcal {B}},5)$ is the fuzzy 5-soft set as follows:

$$\begin{aligned}{} & {} \widehat{{\mathbb {H}}}(b_{1}) = \Big \{(z_{1}, 0.3, 3), (z_{2}, 0.5, 1), (z_{3}, 0.2, 2)\Big \}, \\{} & {} \widehat{{\mathbb {H}}}(b_{2}) = \Big \{(z_{1}, 0.7, 2), (z_{2}, 0.2, 3), (z_{3}, 0.4, 4)\Big \}, \\{} & {} \widehat{{\mathbb {H}}}(b_{3}) = \Big \{(z_{1}, 0.2, 0), (z_{2}, 0.6, 4), (z_{3}, 0.8, 1)\Big \}. \end{aligned}$$

It can also be represented in tabular form as follows:

$(\widehat{{\mathbb {H}}},{\mathcal {B}},5)$	$b_{1}$	$b_{3}$	$b_{3}$
$z_{1}$	(0.3, 3)	(0.7, 2)	(0.2, 0)
$z_{2}$	(0.5, 1)	(0.2, 3)	(0.6, 4)
$z_{3}$	(0.2, 2)	(0.4, 4)	(0.8, 1)

For interpretation, the above table is of 5-soft set $(\widehat{{\mathbb {H}}}, {\mathcal {B}},5)$ created on the laptop’s storage, graphics, and processor, where in the bottom middle cell 4 is the ordered grade $(r_{32})$ of the laptop $z_{3}$ with respect to $b_{2}$ = graphics. Similarly, in the top-right cell 0, is the laptop’s ordered grade $(r_{13})$ of the laptop $z_{1}$ with respect to $b_{3}$ = processor. In this case, a grade of 0 does not indicate that the evaluation was insufficient or that the information was inadequate.

3 Complex probabilistic hesitant fuzzy N-soft set

We created a model of a complex probabilistic hesitant fuzzy N-soft set (CPHFNSS) as stated in the Introduction, and we used some numerical examples to show how it works. The soft max-AND and soft min-OR operators are covered along with some fundamental operations. Also, prove their fundamental rules as well. The mathematical examples have also been resolved in order to demonstrate the validity and competency of the research work in this section.

Definition 3.1

Let ${\mathcal {Z}}$ be a universal set and H be the set of attributes, for any non-empty set ${\mathcal {B}} \subseteq H$and let ${\mathcal {R}} = \{0, 1, 2,..., N-1\}$ be a set of ordered grades where $N\in \{2, 3, 4, 5,...\}$. A triple $(\widehat{{\mathbb {I}}},{\mathcal {B}}, N)$ is called complex probabilistic hesitant fuzzy N-soft set over ${\mathcal {Z}}$ if there exists a mapping $\widehat{{\mathbb {I}}}: {\mathcal {B}}\rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$ with the property that for each $b_{j} \in {\mathcal {B}}$ there exists a unique $(z_{i}, r_{ij}) \in ({\mathcal {Z}} \times R)$ such that $((z_{i}, r_{ij}),h_{\widehat{{\mathbb {I}}}} )\in \widehat{{\mathbb {I}}}(b_{j}),~ b_{j}\in {\mathcal {B}}, ~z_{i} \in {\mathcal {Z}}~ and ~r_{ij} \in {\mathcal {R}}$, where ${\mathcal {I}}({\mathcal {Z}})\times R$ indicates the all possible complex probabilistic hesitant fuzzy subset of ${\mathcal {Z}}\times R$. It is expressed as:

$$\begin{aligned}{} & {} \widehat{{\mathbb {I}}}(b_{j}) = \Bigg \{\bigg \langle ( z_{i}, r_{ij}),h_{\widehat{{\mathbb {I}}}}\bigg (r_{\widehat{{\mathbb {I}}}_{m}}( z_{i}, r_{ij})e^{2\pi i\omega _{\widehat{{\mathbb {I}}}_{m}}( z_{i}, r_{ij})}\Big |P_{\widehat{{\mathbb {I}}}_{m}}\bigg )\bigg \rangle \Big | \\{} & {} \quad ( z_{i}, r_{ij})\in {\mathcal {Z}}\times R \Bigg \}, ~\forall b_{j}\in {\mathcal {B}}\subseteq H, \end{aligned}$$

where $h_{\widehat{{\mathbb {I}}}}\Big (r_{\widehat{{\mathbb {I}}}_{m}}(z_{i}, r_{ij})e^{2\pi i \omega _{\widehat{{\mathbb {I}}}_{m}}(z_{i}, r_{ij})}\big |P_{\widehat{{\mathbb {I}}}_{m}}\Big )$ is the collection of complex elements representing the complex hesitant fuzzy information along probabilities to the set $\widehat{{\mathbb {I}}}, r_{\widehat{{\mathbb {I}}}_{m}}(z_{i}, r_{ij})\in [0,1]$ and $\omega _{\widehat{{\mathbb {I}}}_{m}}(z_{i}, r_{ij}) \in [0, 1], m = 1, 2,...,l$ where l is the number of possible elements in $h_{\widehat{{\mathbb {I}}}}\Big (r_{\widehat{{\mathbb {I}}}_{m}}(z_{i}, r_{ij}) e^{2\pi i \omega _{\widehat{{\mathbb {I}}}_{m}}(z_{i}, r_{ij}) }\big |P_{\widehat{{\mathbb {I}}}_{m}}\Big ),$ $P_{\widehat{{\mathbb {I}}}_{m}}\in [0, 1]$ is the complex hesitant probability of $r_{\widehat{{\mathbb {I}}}_{m}}(z_{i}, r_{ij}) e^{2\pi i \omega _{\widehat{{\mathbb {I}}}_{m}}(z_{i}, r_{ij}) }$ and $\sum \limits _{m} P_{\widehat{{\mathbb {I}}}_{m}}= 1.$

Example 3.2

The evaluation of a lecturer at a university is based on the star ratings and grades given by a selection board, which consists of the vice chancellor, subject specialist, chairman, and psychologist. Let ${\mathcal {Z}} = \{ z_{1}, z_{2}, z_{3}\}$ be the set of candidates attending a university interview and ${\mathcal {B}}\subseteq H$ be the set of attributes for the evaluation, by the selection board, such that ${\mathcal {B}}= \big \{b_{1} = Experience, b_{2}= interpersonal~skills, b_{3}= Attitude ~of answering~ the ~questions\big \}$. Table 1 can be used to create a 5-soft set, where four stars indicate excellent, three stars indicate very good, two stars indicate good, one star indicates satisfactory and hole indicates unsatisfactory.

Table 1 Star evaluation by the selection board

Table 2 5-soft set from Table 1

Table 3 Representation of CPHF 5-SS

This star rating is easily identifiable by the numbers for example 0 represents $\circ$, 1 represents $\star$, 2 represents $\star \star$, 3 represents $\star \star \star$, 4 represents $\star \star \star \star$ and we can be used to create 5-soft set, as represented in Table 2.

It is sufficient when this information is accurately and unambiguously extracted from actual data. It has to do with the N-soft set. However, if the assessments are ambiguous, hesitant, and random, we might need to use CPHFNSS, which gives us more flexibility in determining how these grades are assigned to applicants. For this reason, the following CPHFNSS is defined. Then, $(\widehat{{\mathbb {I}}},{\mathcal {B}}, 5)$ is the complex probabilistic hesitant fuzzy 5-soft set, as represented in Table 3.

Definition 3.3

Let ${\mathcal {Z}}$ be a universal set and H be the set of attributes, there exists non-empty set ${\mathcal {B}} \subseteq H$. A triple $(\widehat{{\mathbb {J}}},{\mathcal {B}},N)$ is called empty CPHFNSS over ${\mathcal {Z}}$. If $\widehat{{\mathbb {J}}}(b_{j}) = \phi$ for all $b_{i}\in {\mathcal {B}}.$

Definition 3.4

Let ${\mathcal {M}}$ be a universal set and H be the set of attributes, there exists non-empty set ${\mathcal {B}} \subseteq H$. A triple$(\widehat{{\mathbb {K}}},{\mathcal {B}},N)$ is called full CPHFNSS over ${\mathcal {Z}}$. If $\widehat{{\mathbb {K}}}(b_{j}) = 1$ for all $b_{i}\in {\mathcal {B}}.$

Table 4 Representation of CPHF 6-SS

4 Operations of CPHFNSS

Definition 4.1

Let ${\mathcal {Z}}$ be a universal set. $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$ and $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})$ are two CPHFNSS over ${\mathcal {Z}}$ then the restricted union is described as:

$$\begin{aligned} (\widehat{{\mathbb {L}}},{\mathcal {E}}, {\mathcal {K}}) = (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1}) \Cup (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2}) \end{aligned}$$

where $\widehat{{\mathbb {L}}} = \widehat{{\mathbb {I}}_{1}} \Cup \widehat{{\mathbb {I}}_{2}}$, ${\mathcal {E}} = {\mathcal {B}}_{1} \cap {\mathcal {B}}_{2} \ne \phi$ and ${\mathcal {K}} = max(N_{1},N_{2})$; $\forall e_{j}\in {\mathcal {E}}$ and $z_{i} \in {\mathcal {Z}}$,

$\bigg \langle (z_{i},r_{ij}),h_{\widehat{{\mathbb {L}}}}\bigg (r_{\widehat{{\mathbb {L}}}_{m}}(z_{i}, r_{ij})e^{2\pi i\omega _{\widehat{{\mathbb {L}}}_{m}}(z_{i}, r_{ij})}\Big |P_{\widehat{{\mathbb {L}}}_{m}}\bigg )\bigg \rangle \in \widehat{{\mathbb {L}}}(e_{j}) \Longleftrightarrow$ $r_{ij} = max(r_{ij}^{\shortmid }, r_{ij}^{\parallel })$ and

$r_{\widehat{{\mathbb {L}}}_{m}}(z_{i}, r_{ij})e^{2\pi i\omega _{\widehat{{\mathbb {L}}}_{m}}(z_{i}, r_{ij})}\Big |P_{\widehat{{\mathbb {L}}}_{m}}$

$$\begin{aligned} \ = \left\{ \begin{array}{ll} \ r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid })}\Big |P_{\widehat{{\mathbb {I}}_{1}}_{m}}, {\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}-h_{\widehat{{\mathbb {I}}_{2}}_{m}},\\ ~ r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })}\Big |P_{\widehat{{\mathbb {I}}_{2}}_{m}}, {\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{2}}_{m}}-h_{\widehat{{\mathbb {I}}_{1}}_{m}}, \\ ~ max\Big \{r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid }),r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel }) \Big \}e^{2\pi i max\Big \{\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},} \\ { r_{ij}^{\shortmid }),\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })\Big \}} \Big |P_{\widehat{{\mathbb {I}}_{1}}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{2}}_{m}}, {\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}\cap h_{\widehat{{\mathbb {I}}_{2}}_{m}}. \end{array} \right. \end{aligned}$$

with $r_{ij}^{\shortmid } \in \widehat{{\mathbb {I}}_{1}}(b_{j}^{1})$ and $r_{ij}^{\parallel } \in \widehat{{\mathbb {I}}_{2}}(b_{j}^{2})$, while $b_{j}^{1} \in {\mathcal {B}}_{1}$ and $b_{j}^{2}\in {\mathcal {B}}_{2}$.

Example 4.2

Let two CPHFNSS be represented in Tables 4 and 5, respectively.

Table 5 Representation of CPHF 7-SS

Then, by using Definition 4.1 the restricted union is illustrated in Table 6:

Table 6 Representation of the restricted union

Definition 4.3

Let ${\mathcal {Z}}$ be a universal set. $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$ and $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})$ are two CPHFNSS over ${\mathcal {Z}}$ then the extended union is described as:

$$\begin{aligned} (\widehat{{\mathbb {M}}},{\mathcal {F}}, {\mathcal {K}}) = (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1}) \sqcup (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2}) \end{aligned}$$

where $\widehat{{\mathbb {M}}} = \widehat{{\mathbb {I}}_{1}} \sqcup \widehat{{\mathbb {I}}_{2}}$, ${\mathcal {F}} = {\mathcal {B}}_{1} \cup {\mathcal {B}}_{2}$ and ${\mathcal {K}} = max(N_{1},N_{2})$; $\forall f_{j}\in {\mathcal {F}}$ and $z_{i} \in {\mathcal {Z}}$, with $f_{j}^{1}\in {\mathcal {B}}_{1}$ and $f_{j}^{2}\in {\mathcal {B}}_{2}.$

$$\begin{aligned} \ \widehat{{\mathbb {M}}}(f_{j}) = \left\{ \begin{array}{ll} \ \widehat{{\mathbb {I}}_{1}}(f_{j}^{1}),~ &{}{\text { if}} ~~f_{j} \in {\mathcal {B}}_{1}-{\mathcal {B}}_{2},\\ ~\widehat{{\mathbb {I}}_{2}}(f_{j}^{2}), ~ &{}{\text { if}} ~~f_{j} \in {\mathcal {B}}_{2}-{\mathcal {B}}_{1}, \\ ~\widehat{{\mathbb {I}}_{1}}(f_{j}^{1}) \Cup \widehat{{\mathbb {I}}_{2}}(f_{j}^{2}), ~&{}{\text { if}} ~~f_{j} \in {\mathcal {B}}_{1}\cap {\mathcal {B}}_{2}. \end{array} \right. \end{aligned}$$

Example 4.4

Consider $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, 6)$ and $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, 7)$ two CPHFNSS as described in Example 4.2. Then, by using Definition 4.3 the extended union is illustrated in Table 7:

Table 7 Representation of the extended union

Definition 4.5

Let ${\mathcal {Z}}$ be a universal set. $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$ and $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})$ are two CPHFNSS over ${\mathcal {Z}}$ then the restricted intersection is described as:

$$\begin{aligned} (\widehat{{\mathbb {N}}},{\mathcal {E}}, {\mathcal {J}}) = (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1}) \Cap (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2}) \end{aligned}$$

where $\widehat{{\mathbb {N}}} = \widehat{{\mathbb {I}}_{1}} \Cap \widehat{{\mathbb {I}}_{2}}$, ${\mathcal {E}} = {\mathcal {B}}_{1} \cap {\mathcal {B}}_{2} \ne \phi$ and ${\mathcal {J}} = min(N_{1},N_{2})$; $\forall e_{j}\in {\mathcal {E}}$ and $z_{i} \in {\mathcal {Z}}$,

$\bigg \langle (z_{i},r_{ij}),h_{\widehat{{\mathbb {N}}}}\bigg (r_{\widehat{{\mathbb {N}}}_{m}}(z_{i}, r_{ij})e^{2\pi i\omega _{\widehat{{\mathbb {N}}}_{m}}(z_{i}, r_{ij})}\Big |P_{\widehat{{\mathbb {N}}}_{m}}\bigg )\bigg \rangle \in \widehat{{\mathbb {N}}}(e_{j})$ $\Longleftrightarrow r_{ij} = max(r_{ij}^{\shortmid }, r_{ij}^{\parallel }) and$

$r_{\widehat{{\mathbb {N}}}_{m}}(z_{i}, r_{ij})e^{2\pi i\omega _{\widehat{{\mathbb {N}}}_{m}}(z_{i}, r_{ij})}\Big |P_{\widehat{{\mathbb {N}}}_{m}}$

$$\begin{aligned} \ = \left\{ \begin{array}{ll} \ r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid })}\Big |P_{\widehat{{\mathbb {I}}_{1}}_{m}},~ {\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}-h_{\widehat{{\mathbb {I}}_{2}}_{m}},\\ ~ r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })}\Big |P_{\widehat{{\mathbb {I}}_{2}}_{m}}, ~ {\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{2}}_{m}}-h_{\widehat{{\mathbb {I}}_{1}}_{m}}, \\ ~ min\Big \{r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid }),r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })\Big \}e^{2\pi i min\Big \{\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid }), \omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })\Big \}}\\ \Big |P_{\widehat{{\mathbb {I}}_{1}}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{2}}_{m}}, ~{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}\cap h_{\widehat{{\mathbb {I}}_{2}}_{m}}. \end{array} \right. \end{aligned}$$

with $r_{ij}^{\shortmid } \in \widehat{{\mathbb {I}}_{1}}(b_{j}^{1})$ and $r_{ij}^{\parallel } \in \widehat{{\mathbb {I}}_{2}}(b_{j}^{2})$, while $b_{j}^{1} \in {\mathcal {B}}_{1}$ and $b_{j}^{2}\in {\mathcal {B}}_{2}$.

Example 4.6

Consider $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, 6)$ and $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, 7)$ two CPHFNSS as described in Example 4.2. Then, by using Definition 4.5 the restricted intersection is illustrated in Table 8:

Table 8 Representation of the restricted intersection

Definition 4.7

Let ${\mathcal {Z}}$ be a universal set. $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$ and $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})$ are two CPHFNSS over ${\mathcal {Z}}$ then the extended intersection is described as:

$$\begin{aligned} (\widehat{{\mathbb {O}}},{\mathcal {F}}, {\mathcal {K}}) = (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1}) \sqcap (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2}) \end{aligned}$$

where $\widehat{{\mathbb {O}}} = \widehat{{\mathbb {I}}_{1}} \sqcap \widehat{{\mathbb {I}}_{2}}$, ${\mathcal {F}} = {\mathcal {B}}_{1} \cup {\mathcal {B}}_{2}$ and ${\mathcal {K}} = max(N_{1},N_{2})$; $\forall f_{j}\in {\mathcal {F}}$ and $z_{i} \in {\mathcal {Z}}$, with $f_{j}^{1}\in {\mathcal {B}}_{1}$ and $f_{j}^{2}\in {\mathcal {B}}_{2}.$

$$\begin{aligned} \ \widehat{{\mathbb {O}}}(f_{j}) = \left\{ \begin{array}{ll} \ \widehat{{\mathbb {I}}_{1}}(f_{j}^{1}),~ &{}{\text { if}} ~~f_{j} \in {\mathcal {B}}_{1}-{\mathcal {B}}_{2},\\ ~\widehat{{\mathbb {I}}_{2}}(f_{j}^{2}), ~ &{}{\text { if}} ~~f_{j} \in {\mathcal {B}}_{2}-{\mathcal {B}}_{1}, \\ ~\widehat{{\mathbb {I}}_{1}}(f_{j}^{1}) \Cap \widehat{{\mathbb {I}}_{2}}(f_{j}^{2}), ~&{}{\text { if}} ~~f_{j} \in {\mathcal {B}}_{1}\cap {\mathcal {B}}_{2}. \end{array} \right. \end{aligned}$$

Example 4.8

Consider $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, 6)$ and $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, 7)$ two CPHFNSS as described in Example 4.2. Then, by using Definition 4.7 the extended intersection is illustrated in Table 9:

Table 9 Representation of the extended intersection

Definition 4.9

Let ${\mathcal {Z}}$ be a universal set. $(\widehat{{\mathbb {I}}},{\mathcal {B}}, N)$ is the CPHFNSS over ${\mathcal {Z}}$ then weak CPHFNSS complement is represented by $(\widehat{{\mathbb {I}}}^{c},{\mathcal {B}}, N)$ where $\widehat{{\mathbb {I}}}^{c}(b_{j}) \cap \widehat{{\mathbb {I}}}(b_{j}) = \Phi ;~\forall b_{j}\in {\mathcal {B}}$ and it is defined as:

$$\begin{aligned} \widehat{{\mathbb {I}}}^{c}(b_{j})= & {} \Bigg \{\bigg \langle (z_{i}, r_{ij}), h_{{\widehat{{\mathbb {I}}}}^{c}}\bigg (\big (1 - r_{\widehat{{\mathbb {I}}}_{m}}(z_{i}, r_{ij})\big )e^{2\pi i\big (1 - \omega _{\widehat{{\mathbb {I}}}_{m}}(z_{i}, r_{ij})\big )}\Big |\\{} & {} 1 - P_{\widehat{{\mathbb {I}}}_{m}}\bigg )\bigg \rangle \Big | (z_{i}, r_{ij})\in {\mathcal {Z}} \times R \Bigg \}, ~\forall b_{j}\in {\mathcal {B}}\subseteq H. \end{aligned}$$

Table 10 Representation of weak complement

Table 11 Representation of bottom weak complement

Example 4.10

Consider $(\widehat{{\mathbb {I}}},{\mathcal {B}},5)$ CPHFNSS as described in Example 3.2. Then, by using Definition 4.9 the weak CPHFNSS complement is illustrated in Table 10.

Definition 4.11

Let ${\mathcal {Z}}$ be a universal set. For any CPHFNSS $(\widehat{{\mathbb {I}}},{\mathcal {B}}, N)$ over ${\mathcal {Z}}$ then bottom weak CPHFNSS complement is represented by $(\widehat{{\mathbb {I}}}^{\preccurlyeq },{\mathcal {B}}, N)$; $\forall b_{j}\in {\mathcal {B}}$ and it is defined as:

$$\begin{aligned} \widehat{{\mathbb {I}}}^{\preccurlyeq }(b_{j}) = \left\{ \begin{array}{ll} (z_{i}, 0), h_{{\widehat{{\mathbb {I}}}}^{\preccurlyeq }}\bigg (\big (1 - r_{\widehat{{\mathbb {I}}}_{m}}(z_{i}, r_{ij})\big )e^{2\pi i\big (1 - \omega _{\widehat{{\mathbb {I}}}_{m}}(z_{i}, r_{ij})\big )}\Big |1 - P_{\widehat{{\mathbb {I}}}_{m}}\bigg ), &{} {\text {if}} ~~r_{ij}~>~0,\\ (z_{i}, N - 1), h_{{\widehat{{\mathbb {I}}}}^{\preccurlyeq }}\bigg (\big (1 - r_{\widehat{{\mathbb {I}}}_{m}}(z_{i}, r_{ij})\big )e^{2\pi i\big (1 - \omega _{\widehat{{\mathbb {I}}}_{m}}(z_{i}, r_{ij})\big )}\Big |1 - P_{\widehat{{\mathbb {I}}}_{m}}\bigg ), &{} {\text {if}} ~~ r_{ij}~=~0. \end{array}\right. \end{aligned}$$

Example 4.12

Consider $(\widehat{{\mathbb {I}}},{\mathcal {B}},5)$ CPHFNSS as described in Example 3.2. Then, by using Definition 4.11 the bottom weak CPHFNSS complement is illustrated in Table 11.

Definition 4.13

Let ${\mathcal {Z}}$ be a universal set. For any CPHFNSS $(\widehat{{\mathbb {I}}},{\mathcal {B}}, N)$ over ${\mathcal {Z}}$ then top weak CPHFNSS complement is represented by $(\widehat{{\mathbb {I}}}^{\curlyeqprec },{\mathcal {B}}, N)$; $\forall b_{j}\in {\mathcal {B}}$ and it is defined as:

$$\begin{aligned} \widehat{{\mathbb {I}}}^{\curlyeqprec }(b_{j})= \left\{ \begin{array}{ll} (z_{i}, N - 1), h_{{\widehat{{\mathbb {I}}}}^{\curlyeqprec }}\bigg (\big (1 - r_{\widehat{{\mathbb {I}}}_{m}}(z_{i}, r_{ij})\big )e^{2\pi i\big (1 - \omega _{\widehat{{\mathbb {I}}}_{m}}(z_{i}, r_{ij})\big )}\Big |1 - P_{\widehat{{\mathbb {I}}}_{m}}\bigg ),&{}{\text {if}} ~~r_{ij}<~N - 1,\\ (z_{i}, 0), h_{{\widehat{{\mathbb {I}}}}^{\curlyeqprec }}\bigg (\big (1 - r_{\widehat{{\mathbb {I}}}_{m}}(z_{i}, r_{ij})\big )e^{2\pi i\big (1 - \omega _{\widehat{{\mathbb {I}}}_{m}}(z_{i}, r_{ij})\big )}\Big |1 - P_{\widehat{{\mathbb {I}}}_{m}}\bigg ),&{} {\text {if}} ~~ r_{ij}=~N - 1. \end{array} \right. \end{aligned}$$

Example 4.14

Consider $(\widehat{{\mathbb {I}}},{\mathcal {B}},5)$ CPHFNSS as described in Example 3.2. Then, by using Definition 4.13 the top weak CPHFNSS complement is illustrated in Table 12.

Table 12 Representation of top weak complement

Definition 4.15

Soft max-AND operation of two CPHFSS $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$ and $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})$ $\big ($ where $\widehat{{\mathbb {I}}_{1}}: {\mathcal {B}}_{1} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$ and $\widehat{{\mathbb {I}}_{2}}: {\mathcal {B}}_{2} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R \big )$ defined as:

$$\begin{aligned} (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1}) \wedge (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2}) = (\widehat{{\mathbb {L}}},{\mathcal {G}}, {\mathcal {K}}), \end{aligned}$$

where $\widehat{{\mathbb {L}}}: {\mathcal {G}} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$ such that $\widehat{{\mathbb {L}}} = \widehat{{\mathbb {I}}_{1}} \cup \widehat{{\mathbb {I}}_{2}}$ and ${\mathcal {G}} = {\mathcal {B}}_{1}\times {\mathcal {B}}_{2}$; $\forall (g_{u}, g_{v})\in ({\mathcal {B}}_{1}\times {\mathcal {B}}_{2}),~g_{u},g_{v}\in \Lambda$ and ${\mathcal {K}} = max(N_{1}, N_{2}),$

$\bigg \langle (z_{i}, r_{i(u,v)}),h_{\widehat{{\mathbb {L}}}}\bigg (r_{\widehat{{\mathbb {L}}}_{m}}(z_{i},r_{i(u,v)})e^{2\pi i\omega _{\widehat{{\mathbb {L}}}_{m}}(z_{i},r_{i(u,v)})}\Big |P_{\widehat{{\mathbb {L}}}_{m}}\bigg )\bigg \rangle \in \widehat{{\mathbb {L}}} (g_{u}, g_{v}) \Longleftrightarrow r_{i(u,v)}= max(r_{i(u,v)}^{\shortmid },r_{i(u,v)}^{\parallel })$ and

$$\begin{aligned}{} & {} r_{\widehat{{\mathbb {L}}}_{m}}(z_{i}, r_{i(u,v)})e^{2\pi i\omega _{\widehat{{\mathbb {L}}}_{m}}(z_{i}, r_{i(u,v)})}\Big |P_{\widehat{{\mathbb {L}}}_{m}}\\{} & {} \quad = \left\{ \begin{array}{ll} \ r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{i(u,v)}^{\shortmid })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{i(u,v)}^{\shortmid })}\Big |P_{\widehat{{\mathbb {I}}_{1}}_{m}},~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}-h_{\widehat{{\mathbb {I}}_{2}}_{m}},\\ ~ r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{i(u,v)}^{\parallel })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{i(u,v)}^{\parallel })}\Big |P_{\widehat{{\mathbb {I}}_{2}}_{m}}, ~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{2}}_{m}}-h_{\widehat{{\mathbb {I}}_{1}}_{m}}, \\ ~ max\Big \{r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{i(u,v)}^{\shortmid }),r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{i(u,v)}^{\parallel })\Big \}e^{2\pi i max\Big \{\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{i(u,v)}^{\shortmid }),\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{i(u,v)}^{\parallel })\Big \}} \Big |P_{\widehat{{\mathbb {I}}_{1}}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{2}}_{m}}, ~&{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}\cap h_{\widehat{{\mathbb {I}}_{2}}_{m}}. \end{array}\right. \end{aligned}$$

with $(z_{i},r_{i(u,v)}^{\shortmid }) \in \widehat{{\mathbb {I}}_{1}}({\mathcal {B}}_{1})$ and $(z_{i},r_{i(u,v)}^{\parallel }) \in \widehat{{\mathbb {I}}_{2}}({\mathcal {B}}_{2})$.

Definition 4.16

Soft min-OR operation of two CPHFSS $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$ and $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})$ $\big ($ where $\widehat{{\mathbb {I}}_{1}}: {\mathcal {B}}_{1} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$ and $\widehat{{\mathbb {I}}_{2}}: {\mathcal {B}}_{2} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R \big )$ defined as:

$$\begin{aligned} (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1}) \vee (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2}) = (\widehat{{\mathbb {N}}},{\mathcal {G}}, {\mathcal {J}}), \end{aligned}$$

where $\widehat{{\mathbb {N}}}: {\mathcal {G}} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$ such that $\widehat{{\mathbb {N}}} = \widehat{{\mathbb {I}}_{1}} \cap \widehat{{\mathbb {I}}_{2}}$ and ${\mathcal {G}} = {\mathcal {B}}_{1}\times {\mathcal {B}}_{2}$; $\forall (g_{u}, g_{v})\in ({\mathcal {B}}_{1}\times {\mathcal {B}}_{2}),~g_{u},g_{v}\in \Lambda$ and ${\mathcal {J}} = min(N_{1}, N_{2}),$

$\bigg \langle (z_{i}, r_{i(u,v)}),h_{\widehat{{\mathbb {N}}}}\bigg (r_{\widehat{{\mathbb {N}}}_{m}}(z_{i},r_{i(u,v)})e^{2\pi i\omega _{\widehat{{\mathbb {N}}}_{m}}(z_{i},r_{i(u,v)})}\Big |P_{\widehat{{\mathbb {N}}}_{m}}\bigg )\bigg \rangle \in \widehat{{\mathbb {N}}} (g_{u}, g_{v}) \Longleftrightarrow r_{i(u,v)}= min(r_{i(u,v)}^{\shortmid },r_{i(u,v)}^{\parallel })$ and

$$\begin{aligned}{} & {} r_{\widehat{{\mathbb {N}}}_{m}}(z_{i}, r_{i(u,v)})e^{2\pi i\omega _{\widehat{{\mathbb {N}}}_{m}}(z_{i}, r_{i(u,v)})}\Big |P_{\widehat{{\mathbb {N}}}_{m}}\\{} & {} \quad = \left\{ \begin{array}{ll} \ r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{i(u,v)}^{\shortmid })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{i(u,v)}^{\shortmid })}\Big |P_{\widehat{{\mathbb {I}}_{1}}_{m}},~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}-h_{\widehat{{\mathbb {I}}_{2}}_{m}},\\ ~ r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{i(u,v)}^{\parallel })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{i(u,v)}^{\parallel })}\Big |P_{\widehat{{\mathbb {I}}_{2}}_{m}}, ~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{2}}_{m}}-h_{\widehat{{\mathbb {I}}_{1}}_{m}}, \\ ~ min\Big \{r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{i(u,v)}^{\shortmid }),r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{i(u,v)}^{\parallel })\Big \}e^{2\pi i min\Big \{\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{i(u,v)}^{\shortmid }),\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{i(u,v)}^{\parallel })\Big \}} \Big |P_{\widehat{{\mathbb {I}}_{1}}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{2}}_{m}}, ~&{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}\cap h_{\widehat{{\mathbb {I}}_{2}}_{m}}. \end{array}\right. \end{aligned}$$

with $(z_{i},r_{i(u,v)}^{\shortmid }) \in \widehat{{\mathbb {I}}_{1}}({\mathcal {B}}_{1})$ and $(z_{i},r_{i(u,v)}^{\parallel }) \in \widehat{{\mathbb {I}}_{2}}({\mathcal {B}}_{2})$.

4.1 Fundamental laws

Proposition 4.17

Given that $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$, $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})$ and $(\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3})$ are any three CPHFNSS on ${\mathcal {Z}}$, then following laws holds:

Idempotent Laws:

• i. $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\Cup (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1}) = (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1}),$

• ii. $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\sqcup (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1}) = (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1}),$

• iii. $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\Cap (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1}) = (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1}),$

• iv. $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\sqcap (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1}) = (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1}).$

Commutative Laws:

• v. $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\Cup (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2}) = (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})\Cup (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$,

• vi. $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\sqcup (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2}) = (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})\sqcup (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$,

• vii. $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\Cap (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2}) = (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})\Cap (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$,

• viii. $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\sqcap (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2}) = (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})\sqcap (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$.

Associative Laws:

• ix. $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\Cup \Big ((\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})\Cup (\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3})\Big )= \Big ((\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\Cup (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})\Big )\Cup (\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3})$,

• x. $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\sqcup \Big ((\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})\sqcup (\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3})\Big )= \Big ((\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\sqcup (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})\Big )\sqcup (\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3})$,

• xi. $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\Cap \Big ((\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})\Cap (\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3})\Big )= \Big ((\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\Cap (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})\Big )\Cap (\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3})$,

• xii. $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\sqcap \Big ((\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})\sqcap (\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3})\Big )= \Big ((\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\sqcap (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})\Big )\sqcap (\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3})$.

Proof

Laws from (i) to (viii) are hold by definition.

(ix) L.H.S:

Let $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})$ and $(\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3})$ $\big ($ where $\widehat{{\mathbb {I}}_{2}}: {\mathcal {B}}_{2} \rightarrow {\mathcal {I}}({\mathcal {M}})\times R$ and $\widehat{{\mathbb {I}}_{3}}: {\mathcal {B}}_{3} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R\big )$ be two CPHFNSS on ${\mathcal {Z}}$. By using definition of the restricted union, we have $(\widehat{{\mathbb {P}}}, {\mathcal {M}}, {\mathcal {S}} )$ (where $\widehat{{\mathbb {P}}}: {\mathcal {M}} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R)$ such that,

$$\begin{aligned} (\widehat{{\mathbb {P}}}, {\mathcal {M}},{\mathcal {S}}) = (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})\Cup (\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3}), \end{aligned}$$

where $\widehat{{\mathbb {P}}} = \widehat{{\mathbb {I}}_{2}} \Cup \widehat{{\mathbb {I}}_{3}}$, ${\mathcal {M}} = {\mathcal {B}}_{2} \cap {\mathcal {B}}_{3}$, ${\mathcal {S}} = max( N_{2}, N_{3})$; $\forall m_{j}\in {\mathcal {M}}$ and $z_{i} \in {\mathcal {Z}}$,

$\bigg \langle (z_{i},r_{ij}),h_{\widehat{{\mathbb {P}}}}\bigg (r_{\widehat{{\mathbb {P}}}_{m}}(z_{i},r_{ij})e^{2\pi i\omega _{\widehat{{\mathbb {P}}}_{m}}(z_{i},r_{ij})}\Big |P_{\widehat{{\mathbb {P}}}_{m}}\bigg )\bigg \rangle \in \widehat{{\mathbb {P}}}(m_{j})$ $\Longleftrightarrow r_{ij} = max(r_{ij}^{\parallel }, r_{ij}^{\parallel \shortmid })$ and

$$\begin{aligned}{} & {} r_{\widehat{{\mathbb {P}}}_{m}}(z_{i},r_{ij})e^{2\pi i\omega _{\widehat{{\mathbb {P}}}_{m}}(z_{i},r_{ij})}\Big |P_{\widehat{{\mathbb {P}}}_{m}}\\{} & {} \quad = \left\{ \begin{array}{ll} \ r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })}\Big |P_{\widehat{{\mathbb {I}}_{2}}_{m}},~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{2}}_{m}}-h_{\widehat{{\mathbb {I}}_{3}}_{m}},\\ ~ r_{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid })}\Big |P_{\widehat{{\mathbb {I}}_{3}}_{m}}, ~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{3}}_{m}}-h_{\widehat{{\mathbb {I}}_{2}}_{m}}, \\ ~ max\Big \{r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel }),r_{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid })\Big \}e^{2\pi i max\Big \{\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel }),\omega _{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid })\Big \}} \Big |P_{\widehat{{\mathbb {I}}_{2}}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{3}}_{m}}, ~&{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{2}}_{m}}\cap h_{\widehat{{\mathbb {I}}_{3}}_{m}}. \end{array}\right. \end{aligned}$$

with $r_{ij}^{\parallel } \in \widehat{{\mathbb {I}}_{2}}(b_{j}^{2})$ and $r_{ij}^{\parallel \shortmid } \in \widehat{{\mathbb {I}}_{3}}(b_{j}^{3})$ while $b_{j}^{2} \in {\mathcal {B}}_{2}$ and $b_{j}^{3}\in {\mathcal {B}}_{3}$.

As, $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\Cup \Big ((\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})\Cup (\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3})\Big )= (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\Cup (\widehat{{\mathbb {P}}}, {\mathcal {M}}, {\mathcal {S}}).$ Suppose that $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\Cup (\widehat{{\mathbb {P}}}, {\mathcal {M}}, {\mathcal {S}}) = (\widehat{{\mathbb {Q}}}, {\mathcal {N}}, {\mathcal {T}})$ such that $\widehat{{\mathbb {Q}}}: {\mathcal {N}} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$, where $\widehat{{\mathbb {Q}}} = (\widehat{{\mathbb {I}}_{1}}\Cup \widehat{{\mathbb {P}}})$, ${\mathcal {N}} = {\mathcal {B}}_{1} \cap {\mathcal {M}} = {\mathcal {B}}_{1} \cap {\mathcal {B}}_{2} \cap {\mathcal {B}}_{3}$, ${\mathcal {T}}= max(N_{1}, {\mathcal {S}}) =max(N_{1}, N_{2}, N_{3})$; $\forall n_{j}\in {\mathcal {N}}$,

$\bigg \langle (z_{i},r_{ij}),h_{\widehat{{\mathbb {Q}}}}\bigg (r_{\widehat{{\mathbb {Q}}}_{m}}(z_{i},r_{ij})e^{2\pi i\omega _{\widehat{{\mathbb {Q}}}_{m}}(z_{i}, r_{ij})}\Big |P_{\widehat{{\mathbb {Q}}}_{m}}\bigg )\bigg \rangle \in \widehat{{\mathbb {Q}}}(n_{j})$ $\Longleftrightarrow r_{ij} = max(r_{ij}^{\shortmid }, r_{ij}^{\parallel }, r_{ij}^{\parallel \shortmid })$ and

$$\begin{aligned}{} & {} r_{\widehat{{\mathbb {Q}}}_{m}}(z_{i}, r_{ij})e^{2\pi i\omega _{\widehat{{\mathbb {Q}}}_{m}}(z_{i}, r_{ij})}\Big |P_{\widehat{{\mathbb {Q}}}_{m}} \\{} & {} = \left\{ \begin{array}{ll} \ r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid })}\Big |P_{\widehat{{\mathbb {I}}_{1}}_{m}},~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}-h_{\widehat{{\mathbb {I}}_{2}}_{m}}-h_{\widehat{{\mathbb {I}}_{3}}_{m}},\\ ~ r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })}\Big |P_{\widehat{{\mathbb {I}}_{2}}_{m}},~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{2}}_{m}}-h_{\widehat{{\mathbb {I}}_{3}}_{m}}-h_{\widehat{{\mathbb {I}}_{1}}_{m}},\\ ~ r_{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid })}\Big |P_{\widehat{{\mathbb {I}}_{3}}_{m}}, ~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{3}}_{m}}-h_{\widehat{{\mathbb {I}}_{1}}_{m}}-h_{\widehat{{\mathbb {I}}_{2}}_{m}}, \\ ~ max\Big \{r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid }),r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })\Big \}e^{2\pi i max\Big \{\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid }),\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })\Big \}} \Big |P_{\clubsuit }, ~&{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}\cap h_{\widehat{{\mathbb {I}}_{2}}_{m}}-h_{\widehat{{\mathbb {I}}_{3}}_{m}}, \\ ~ max\Big \{r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel }),r_{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid })\Big \}e^{2\pi i max\Big \{\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel }),\omega _{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid })\Big \}} \Big |P_{\diamondsuit }, ~&{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{2}}_{m}}\cap h_{\widehat{{\mathbb {I}}_{3}}_{m}}-h_{\widehat{{\mathbb {I}}_{1}}_{m}}, \\ ~ max\Big \{r_{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid }),r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid })\Big \}e^{2\pi i max\Big \{\omega _{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid }),\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid })\Big \}} \Big |P_{\spadesuit }, ~&{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{3}}_{m}}\cap h_{\widehat{{\mathbb {I}}_{1}}_{m}} -h_{\widehat{{\mathbb {I}}_{2}}_{m}},\\ ~ max\Big \{r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid }),r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel }), r_{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid })\Big \} \\ ~~~~~~~~~~~~e^{2\pi i max\Big \{\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid }),\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel }), \omega _{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid })\Big \}} \Big |P_{\heartsuit }, ~&{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}\cap h_{\widehat{{\mathbb {I}}_{2}}_{m}} \cap h_{\widehat{{\mathbb {I}}_{3}}_{m}} \end{array} \right. \end{aligned}$$

where $P_{\clubsuit } = P_{\widehat{{\mathbb {I}}_{1}}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{2}}_{m}}, P_{\diamondsuit } = P_{\widehat{{\mathbb {I}}_{2}}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{3}}_{m}}, P_{\spadesuit } = P_{\widehat{{\mathbb {I}}_{3}}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{1}}_{m}}$ and $P_{\heartsuit } =P_{\widehat{{\mathbb {I}}_{1}}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{2}}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{3}}_{m}}$ and $r_{ij}^{\shortmid } \in \widehat{{\mathbb {I}}_{1}}(b_{j}^{1})$, $r_{ij}^{\parallel } \in \widehat{{\mathbb {I}}_{2}}(b_{j}^{2})$ and $r_{ij}^{\parallel \shortmid } \in \widehat{{\mathbb {I}}_{3}}(b_{j}^{3})$ while $b_{j}^{1} \in {\mathcal {B}}_{1}$, $b_{j}^{2}\in {\mathcal {B}}_{2}$ and $b_{j}^{3} \in {\mathcal {B}}_{3}$.

R.H.S:

Let $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$ and $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})$ $\big ($ where $\widehat{{\mathbb {I}}_{1}}: {\mathcal {B}}_{1} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$ and $\widehat{{\mathbb {I}}_{2}}: {\mathcal {B}}_{2} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R\big )$ be two CPHFNSS on ${\mathcal {Z}}$. By using definition of the restricted union, we have $(\widehat{{\mathbb {L}}}, {\mathcal {E}}, {\mathcal {K}} )$ (where $\widehat{{\mathbb {L}}}: {\mathcal {E}} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R)$ such that,

$$\begin{aligned} (\widehat{{\mathbb {L}}}, {\mathcal {E}},{\mathcal {K}}) = (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\Cup (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2}), \end{aligned}$$

where $\widehat{{\mathbb {L}}} = \widehat{{\mathbb {I}}_{1}} \Cup \widehat{{\mathbb {I}}_{2}}$, ${\mathcal {E}} = {\mathcal {B}}_{1} \cap {\mathcal {B}}_{2}$, ${\mathcal {K}} = max( N_{1}, N_{2})$; $\forall e_{j}\in {\mathcal {E}}$ and $z_{i} \in {\mathcal {Z}}$,

$\bigg \langle (z_{i},r_{ij}),h_{\widehat{{\mathbb {L}}}}\bigg (r_{\widehat{{\mathbb {L}}}_{m}}(z_{i},r_{ij})e^{2\pi i\omega _{\widehat{{\mathbb {L}}}_{m}}(z_{i},r_{ij})}\Big |P_{\widehat{{\mathbb {L}}}_{m}}\bigg )\bigg \rangle \in \widehat{{\mathbb {L}}}(e_{j})$ $\Longleftrightarrow r_{ij} = max(r_{ij}^{\shortmid }, r_{ij}^{\parallel })$ and

$$\begin{aligned}{} & {} r_{\widehat{{\mathbb {L}}}_{m}}(z_{i},r_{ij})e^{2\pi i\omega _{\widehat{{\mathbb {L}}}_{m}}(z_{i},r_{ij})}\Big |P_{\widehat{{\mathbb {L}}}_{m}}\\{} & {} \quad = \left\{ \begin{array}{ll} \ r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid })}\Big |P_{\widehat{{\mathbb {I}}_{1}}_{m}},~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}-h_{\widehat{{\mathbb {I}}_{2}}_{m}},\\ ~\ r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })}\Big |P_{\widehat{{\mathbb {I}}_{2}}_{m}},~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{2}}_{m}}-h_{\widehat{{\mathbb {I}}_{1}}_{m}}, \\ ~ max\Big \{r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid }),r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })\Big \}e^{2\pi i max\Big \{\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid }),\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })\Big \}} \Big |P_{\widehat{{\mathbb {I}}_{1}}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{2}}_{m}}, ~&{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}\cap h_{\widehat{{\mathbb {I}}_{2}}_{m}}. \end{array} \right. \end{aligned}$$

with $r_{ij}^{\shortmid } \in \widehat{{\mathbb {I}}_{1}}(b_{j}^{1})$ and $r_{ij}^{\parallel } \in \widehat{{\mathbb {I}}_{2}}(b_{j}^{2})$ while $b_{j}^{1} \in {\mathcal {B}}_{1}$ and $b_{j}^{2}\in {\mathcal {B}}_{2}$.

As,$\Big ($ $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\Cup (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})\Big )\Cup (\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3})= (\widehat{{\mathbb {L}}}, {\mathcal {E}}, {\mathcal {K}})\Cup (\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3}).$ Suppose that $(\widehat{{\mathbb {L}}}, {\mathcal {E}}, {\mathcal {K}})\Cup (\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3}) = (\widehat{{\mathbb {R}}}, {\mathcal {N}}, {\mathcal {T}})$ such that $\widehat{{\mathbb {R}}}: {\mathcal {N}} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$, where $\widehat{{\mathbb {R}}} = (\widehat{{\mathbb {L}}}\Cup \widehat{{\mathbb {I}}_{3}})$, ${\mathcal {N}} = {\mathcal {E}}\cap {\mathcal {B}}_{3} = {\mathcal {B}}_{1} \cap {\mathcal {B}}_{2} \cap {\mathcal {B}}_{3}$, ${\mathcal {T}}= max(N_{1}, N_{2}, N_{3})$; $\forall n_{j}\in {\mathcal {N}}$,

$\bigg \langle (z_{i},r_{ij}),h_{\widehat{{\mathbb {R}}}}\bigg (r_{\widehat{{\mathbb {R}}}_{m}}(z_{i},r_{ij})e^{2\pi i\omega _{\widehat{{\mathbb {R}}}_{m}}(z_{i}, r_{ij})}\Big |P_{\widehat{{\mathbb {R}}}_{m}}\bigg )\bigg \rangle \in \widehat{{\mathbb {R}}}(n_{j})$ $\Longleftrightarrow r_{ij} = max(r_{ij}^{\shortmid }, r_{ij}^{\parallel }, r_{ij}^{\parallel \shortmid })$ and

$$\begin{aligned}{} & {} r_{\widehat{{\mathbb {R}}}_{m}}(z_{i}, r_{ij})e^{2\pi i\omega _{\widehat{{\mathbb {R}}}_{m}}(z_{i}, r_{ij})}\Big |P_{\widehat{{\mathbb {R}}}_{m}} \\{} & {} \quad = \left\{ \begin{array}{ll} \ r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid })}\Big |P_{\widehat{{\mathbb {I}}_{1}}_{m}},~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}-h_{\widehat{{\mathbb {I}}_{2}}_{m}}-h_{\widehat{{\mathbb {I}}_{3}}_{m}},\\ ~ r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })}\Big |P_{\widehat{{\mathbb {I}}_{2}}_{m}},~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{2}}_{m}}-h_{\widehat{{\mathbb {I}}_{3}}_{m}}-h_{\widehat{{\mathbb {I}}_{1}}_{m}},\\ ~ r_{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid })}\Big |P_{\widehat{{\mathbb {I}}_{3}}_{m}}, ~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{3}}_{m}}-h_{\widehat{{\mathbb {I}}_{1}}_{m}}-h_{\widehat{{\mathbb {I}}_{2}}_{m}}, \\ ~ max\Big \{r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid }),r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })\Big \}e^{2\pi i max\Big \{\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid }),\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })\Big \}} \Big |P_{\clubsuit }, ~&{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}\cap h_{\widehat{{\mathbb {I}}_{2}}_{m}}-h_{\widehat{{\mathbb {I}}_{3}}_{m}}, \\ ~ max\Big \{r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel }),r_{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid })\Big \}e^{2\pi i max\Big \{\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel }),\omega _{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid })\Big \}} \Big |P_{\diamondsuit }, ~&{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{2}}_{m}}\cap h_{\widehat{{\mathbb {I}}_{3}}_{m}}-h_{\widehat{{\mathbb {I}}_{1}}_{m}}, \\ ~ max\Big \{r_{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid }),r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid })\Big \}e^{2\pi i max\Big \{\omega _{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid }),\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid })\Big \}} \Big |P_{\spadesuit }, ~&{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{3}}_{m}}\cap h_{\widehat{{\mathbb {I}}_{1}}_{m}} -h_{\widehat{{\mathbb {I}}_{2}}_{m}},\\ ~ max\Big \{r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid }),r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel }), r_{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid })\Big \} \\ ~~~~~~~~~~~~e^{2\pi i max\Big \{\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid }),\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel }), \omega _{\widehat{{\mathbb {I}}_{3}}_{m}}(z_{i},r_{ij}^{\parallel \shortmid })\Big \}} \Big |P_{\heartsuit }, ~&{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}\cap h_{\widehat{{\mathbb {I}}_{2}}_{m}} \cap h_{\widehat{{\mathbb {I}}_{3}}_{m}} \end{array}\right. \end{aligned}$$

where $P_{\clubsuit } = P_{\widehat{{\mathbb {I}}_{1}}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{2}}_{m}}, P_{\diamondsuit } = P_{\widehat{{\mathbb {I}}_{2}}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{3}}_{m}}, P_{\spadesuit } = P_{\widehat{{\mathbb {I}}_{3}}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{1}}_{m}}$ and $P_{\heartsuit } =P_{\widehat{{\mathbb {I}}_{1}}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{2}}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{3}}_{m}}$ and $r_{ij}^{\shortmid } \in \widehat{{\mathbb {I}}_{1}}(b_{j}^{1})$, $r_{ij}^{\parallel } \in \widehat{{\mathbb {I}}_{2}}(b_{j}^{2})$ and $r_{ij}^{\parallel \shortmid } \in \widehat{{\mathbb {I}}_{3}}(b_{j}^{3})$ while $b_{j}^{1} \in {\mathcal {B}}_{1}$, $b_{j}^{2}\in {\mathcal {B}}_{2}$ and $b_{j}^{3} \in {\mathcal {B}}_{3}$.

Then $\widehat{{\mathbb {Q}}}(n_{j}) = \widehat{{\mathbb {R}}}(n_{j})$, $\forall n_{j} \in {\mathcal {N}}$.

Hence L.H.S = R.H.S.

Thus, (ix) is hold. $\square$

Proof

(x) L.H.S:

Let $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})$ and $(\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3})$ $\big ($ where $\widehat{{\mathbb {I}}_{2}}: {\mathcal {B}}_{2} \rightarrow {\mathcal {I}}({\mathcal {M}})\times R$ and $\widehat{{\mathbb {I}}_{3}}: {\mathcal {B}}_{3} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R\big )$ be two CPHFNSS on ${\mathcal {Z}}$. By using definition of the extended union, we have $(\widehat{{\mathbb {S}}}, {\mathcal {O}}, {\mathcal {S}})$ (where $\widehat{{\mathbb {S}}}: {\mathcal {O}} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$ )such that,

$$\begin{aligned} (\widehat{{\mathbb {S}}}, {\mathcal {O}},{\mathcal {S}}) = (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})\sqcup (\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3}), \end{aligned}$$

where $\widehat{{\mathbb {S}}} = \widehat{{\mathbb {I}}_{2}} \sqcup \widehat{{\mathbb {I}}_{3}}$, ${\mathcal {O}} = {\mathcal {B}}_{2} \cup {\mathcal {B}}_{3}$, ${\mathcal {S}} = max( N_{2}, N_{3})$; $\forall o_{j}\in {\mathcal {O}}$ and $z_{i} \in {\mathcal {Z}}$, with $o_{j}^{1}\in {\mathcal {B}}_{2}$ and $o_{j}^{2}\in {\mathcal {B}}_{3}$.

$$\begin{aligned} \ \widehat{{\mathbb {S}}}(o_{j}) = \left\{ \begin{array}{ll} \ \widehat{{\mathbb {I}}_{1}}(o_{j}^{1}),~ &{}{\text { if}} ~~o_{j} \in {\mathcal {B}}_{2}-{\mathcal {B}}_{3},\\ ~\widehat{{\mathbb {I}}_{2}}(o_{j}^{2}), ~ &{}{\text { if}} ~~o_{j} \in {\mathcal {B}}_{3}-{\mathcal {B}}_{2}, \\ ~\widehat{{\mathbb {I}}_{1}}(o_{j}^{1}) \Cup \widehat{{\mathbb {I}}_{2}}(o_{j}^{2}), ~&{}{\text { if}} ~~o_{j} \in {\mathcal {B}}_{2}\cap {\mathcal {B}}_{3}. \end{array} \right. \end{aligned}$$

As, $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\sqcup \Big ((\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})\sqcup (\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3})\Big )= (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\sqcup (\widehat{{\mathbb {S}}}, {\mathcal {O}}, {\mathcal {S}}).$ Suppose that $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\sqcup (\widehat{{\mathbb {S}}}, {\mathcal {O}}, {\mathcal {S}}) = (\widehat{{\mathbb {T}}}, {\mathcal {P}}, {\mathcal {T}})$ such that $\widehat{{\mathbb {T}}}: {\mathcal {P}} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$, where $\widehat{{\mathbb {T}}} = (\widehat{{\mathbb {I}}_{1}}\sqcup \widehat{{\mathbb {S}}})$, ${\mathcal {P}} = {\mathcal {B}}_{1} \cup {\mathcal {O}} = {\mathcal {B}}_{1} \cup {\mathcal {B}}_{2} \cup {\mathcal {B}}_{3}$, ${\mathcal {T}}= max(N_{1}, {\mathcal {S}}) = max(N_{1}, N_{2}, N_{3})$; $\forall p_{j}\in {\mathcal {P}}$, with $p_{j}^{1}\in {\mathcal {B}}_{1}$, $p_{j}^{2}\in {\mathcal {B}}_{2}$ and $p_{j}^{3}\in {\mathcal {B}}_{3}$,

$$\begin{aligned} \ \widehat{{\mathbb {T}}}(p_{j}) = \left\{ \begin{array}{ll} \ \widehat{{\mathbb {I}}_{1}}(p_{j}^{1}),~ &{}{\text { if}} ~~p_{j} \in {\mathcal {B}}_{1} - {\mathcal {B}}_{2} - {\mathcal {B}}_{3},\\ ~\widehat{{\mathbb {I}}_{2}}(p_{j}^{2}), ~ &{}{\text { if}} ~~p_{j} \in {\mathcal {B}}_{2} - {\mathcal {B}}_{3} - {\mathcal {B}}_{1}, \\ ~\widehat{{\mathbb {I}}_{3}}(p_{j}^{3}), ~ &{}{\text { if}} ~~p_{j} \in {\mathcal {B}}_{3} - {\mathcal {B}}_{1} - {\mathcal {B}}_{2},\\ ~\widehat{{\mathbb {I}}_{1}}(p_{j}^{1}) \Cup \widehat{{\mathbb {I}}_{2}}(p_{j}^{2}), ~ &{}{\text { if}} ~~p_{j} \in {\mathcal {B}}_{1}\cap {\mathcal {B}}_{2} - {\mathcal {B}}_{3}, \\ ~\widehat{{\mathbb {I}}_{2}}(p_{j}^{2}) \Cup \widehat{{\mathbb {I}}_{3}}(p_{j}^{3}), ~ &{}{\text { if}} ~~p_{j} \in {\mathcal {B}}_{2}\cap {\mathcal {B}}_{3} - {\mathcal {B}}_{1}, \\ ~\widehat{{\mathbb {I}}_{3}}(p_{j}^{3}) \Cup \widehat{{\mathbb {I}}_{1}}(p_{j}^{1}), ~ &{}{\text { if}} ~~p_{j} \in {\mathcal {B}}_{3}\cap {\mathcal {B}}_{1} - {\mathcal {B}}_{2},\\ ~\widehat{{\mathbb {I}}_{1}}(p_{j}^{1}) \Cup \widehat{{\mathbb {I}}_{2}}(p_{j}^{2})\Cup \widehat{{\mathbb {I}}_{3}}(p_{j}^{3}),~~ &{}{\text {if}} ~~p_{j}\in {\mathcal {B}}_{1}\cap {\mathcal {B}}_{2} \cap {\mathcal {B}}_{3}. \end{array} \right. \end{aligned}$$

R.H.S:

Let $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$ and $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})$ $\big ($ where $\widehat{{\mathbb {I}}_{1}}: {\mathcal {B}}_{1} \rightarrow {\mathcal {I}}({\mathcal {M}})\times R$ and $\widehat{{\mathbb {I}}_{2}}: {\mathcal {B}}_{2} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R\big )$ be two CPHFNSS on ${\mathcal {Z}}$. By using definition of the extended union, we have $(\widehat{{\mathbb {M}}}, {\mathcal {F}}, {\mathcal {K}} )$ (where $\widehat{{\mathbb {M}}}: {\mathcal {F}} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R)$ such that,

$$\begin{aligned} (\widehat{{\mathbb {M}}}, {\mathcal {F}},{\mathcal {K}}) = (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\sqcup (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2}), \end{aligned}$$

where $\widehat{{\mathbb {M}}} = \widehat{{\mathbb {I}}_{1}} \sqcup \widehat{{\mathbb {I}}_{2}}$, ${\mathcal {F}} = {\mathcal {B}}_{1} \cup {\mathcal {B}}_{2}$, ${\mathcal {K}} = max( N_{1}, N_{2})$; $\forall f_{j}\in {\mathcal {F}}$ and $z_{i} \in {\mathcal {Z}}$, with $f_{j}^{1}\in {\mathcal {B}}_{1}$ and $f_{j}^{2}\in {\mathcal {B}}_{2}.$

$$\begin{aligned} \ \widehat{{\mathbb {M}}}(f_{j}) = \left\{ \begin{array}{ll} \ \widehat{{\mathbb {I}}_{1}}(f_{j}^{1}),~ &{}{\text { if}} ~~f_{j} \in {\mathcal {B}}_{1}-{\mathcal {B}}_{2},\\ ~\widehat{{\mathbb {I}}_{2}}(f_{j}^{2}), ~ &{}{\text { if}} ~~f_{j} \in {\mathcal {B}}_{2}-{\mathcal {B}}_{1}, \\ ~\widehat{{\mathbb {I}}_{1}}(f_{j}^{1}) \Cup \widehat{{\mathbb {I}}_{2}}(f_{j}^{2}), ~&{}{\text { if}} ~~f_{j} \in {\mathcal {B}}_{1}\cap {\mathcal {B}}_{2}. \end{array} \right. \end{aligned}$$

As,$\Big ($ $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})\sqcup (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})\Big )\sqcup (\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3})= (\widehat{{\mathbb {M}}}, {\mathcal {F}}, {\mathcal {K}})\sqcup (\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3}).$ Suppose that $(\widehat{{\mathbb {M}}}, {\mathcal {F}}, {\mathcal {K}})\sqcup (\widehat{{\mathbb {I}}_{3}},{\mathcal {B}}_{3}, N_{3}) = (\widehat{{\mathbb {U}}}, {\mathcal {P}}, {\mathcal {T}})$ such that $\widehat{{\mathbb {U}}}: {\mathcal {P}} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$, where $\widehat{{\mathbb {U}}} = (\widehat{{\mathbb {M}}}\Cup \widehat{{\mathbb {I}}_{3}})$, ${\mathcal {P}} = {\mathcal {F}}\cap {\mathcal {B}}_{3} = {\mathcal {B}}_{1} \cup {\mathcal {B}}_{2} \cup {\mathcal {B}}_{3}$, ${\mathcal {T}}= max(N_{1}, {\mathcal {S}}) = max(N_{1}, N_{2}, N_{3})$; $\forall p_{j}\in {\mathcal {P}}$, with $p_{j}^{1}\in {\mathcal {B}}_{1}$, $p_{j}^{2}\in {\mathcal {B}}_{2}$ and $p_{j}^{3}\in {\mathcal {B}}_{3}$,

$$\begin{aligned} \ \widehat{{\mathbb {U}}}(p_{j}) = \left\{ \begin{array}{ll} \ \widehat{{\mathbb {I}}_{1}}(p_{j}^{1}),~ &{}{\text { if}} ~~p_{j} \in {\mathcal {B}}_{1} - {\mathcal {B}}_{2} - {\mathcal {B}}_{3},\\ ~\widehat{{\mathbb {I}}_{2}}(p_{j}^{2}), ~ &{}{\text { if}} ~~p_{j} \in {\mathcal {B}}_{2} - {\mathcal {B}}_{3} - {\mathcal {B}}_{1}, \\ ~\widehat{{\mathbb {I}}_{3}}(p_{j}^{3}), ~ &{}{\text { if}} ~~p_{j} \in {\mathcal {B}}_{3} - {\mathcal {B}}_{1} - {\mathcal {B}}_{2},\\ ~\widehat{{\mathbb {I}}_{1}}(p_{j}^{1}) \Cup \widehat{{\mathbb {I}}_{2}}(p_{j}^{2}), ~ &{}{\text { if}} ~~p_{j} \in {\mathcal {B}}_{1}\cap {\mathcal {B}}_{2} - {\mathcal {B}}_{3}, \\ ~\widehat{{\mathbb {I}}_{2}}(p_{j}^{2}) \Cup \widehat{{\mathbb {I}}_{3}}(p_{j}^{3}), ~ &{}{\text { if}} ~~p_{j} \in {\mathcal {B}}_{2}\cap {\mathcal {B}}_{3} - {\mathcal {B}}_{1}, \\ ~\widehat{{\mathbb {I}}_{3}}(p_{j}^{3}) \Cup \widehat{{\mathbb {I}}_{1}}(p_{j}^{1}), ~ &{}{\text { if}} ~~p_{j} \in {\mathcal {B}}_{3}\cap {\mathcal {B}}_{1} - {\mathcal {B}}_{2},\\ ~\widehat{{\mathbb {I}}_{1}}(p_{j}^{1}) \Cup \widehat{{\mathbb {I}}_{2}}(p_{j}^{2})\Cup \widehat{{\mathbb {I}}_{3}}(p_{j}^{3}),~~&{} {\text {if}} ~~p_{j}\in {\mathcal {B}}_{1}\cap {\mathcal {B}}_{2} \cap {\mathcal {B}}_{3}. \end{array} \right. \end{aligned}$$

Then, $\widehat{{\mathbb {T}}}(p_{j}) = \widehat{{\mathbb {U}}}(p_{j})$, $\forall p_{j} \in {\mathcal {P}}$.

Hence L.H.S = R.H.S.

Thus, (x) is hold. $\square$

The proof of (xi) and (xii) is similar to (ix) and (x).

Proposition 4.18

Given that $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$ and $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})$ are any two CPHFSS on ${\mathcal {Z}}$, then following laws holds:

Involution Law:

• i. $\bigg (\Big (\widehat{{\mathbb {I}}_{1}}^{c}\Big )^{c},{\mathcal {B}}_{1}, N_{1}\bigg )= (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$,

De Morgan’s Laws:

• ii. $\Big (\widehat{{\mathbb {I}}_{1}}^{c},{\mathcal {B}}_{1}, N_{1}\Big )\Cap \Big (\widehat{{\mathbb {I}}_{2}}^{c},{\mathcal {B}}_{2}, N_{2}\Big ) = \Big (\big (\widehat{{\mathbb {I}}_{1}}\Cup \widehat{{\mathbb {I}}_{2}}\big )^{c}, ({\mathcal {B}}_{1}\cap {\mathcal {B}}_{2}), min(N_{1},N_{2}) \Big )$,

• iii. $\Big (\widehat{{\mathbb {I}}_{1}}^{c},{\mathcal {B}}_{1}, N_{1}\Big )\sqcap \Big (\widehat{{\mathbb {I}}_{2}}^{c},{\mathcal {B}}_{2}, N_{2}\Big ) = \Big (\big (\widehat{{\mathbb {I}}_{1}}\sqcup \widehat{{\mathbb {I}}_{2}}\big )^{c}, ({\mathcal {B}}_{1}\cup {\mathcal {B}}_{2}), max(N_{1},N_{2}) \Big )$,

• iv. $\Big (\widehat{{\mathbb {I}}_{1}}^{c},{\mathcal {B}}_{1}, N_{1}\Big )\Cup \Big (\widehat{{\mathbb {I}}_{2}}^{c},{\mathcal {B}}_{2}, N_{2}\Big ) = \Big (\big (\widehat{{\mathbb {I}}_{1}}\Cap \widehat{{\mathbb {I}}_{2}}\big )^{c}, ({\mathcal {B}}_{1}\cap {\mathcal {B}}_{2}), max(N_{1},N_{2}) \Big )$,

• v. $\Big (\widehat{{\mathbb {I}}_{1}}^{c},{\mathcal {B}}_{1}, N_{1}\Big )\sqcup \Big (\widehat{{\mathbb {I}}_{2}}^{c},{\mathcal {B}}_{2}, N_{2}\Big ) = \Big (\big (\widehat{{\mathbb {I}}_{1}}\sqcap \widehat{{\mathbb {I}}_{2}}\big )^{c}, ({\mathcal {B}}_{1}\cup {\mathcal {B}}_{2}), max(N_{1},N_{2}) \Big )$,

• vi $\Big (\widehat{{\mathbb {I}}_{1}}^{c},{\mathcal {B}}_{1}, N_{1}\Big )\wedge \Big (\widehat{{\mathbb {I}}_{2}}^{c},{\mathcal {B}}_{2}, N_{2}\Big ) = \Big (\big (\widehat{{\mathbb {I}}_{1}}\vee \widehat{{\mathbb {I}}_{2}}\big )^{c}, ({\mathcal {B}}_{1}\times {\mathcal {B}}_{2}), max(N_{1},N_{2})\Big )$,

• vii $\Big (\widehat{{\mathbb {I}}_{1}}^{c},{\mathcal {B}}_{1}, N_{1}\Big )\vee \Big (\widehat{{\mathbb {I}}_{2}}^{c},{\mathcal {B}}_{2}, N_{2}\Big ) = \Big (\big (\widehat{{\mathbb {I}}_{1}}\wedge \widehat{{\mathbb {I}}_{2}}\big )^{c}, ({\mathcal {B}}_{1}\times {\mathcal {B}}_{2}), min(N_{1},N_{2})\Big )$.

Proof

Law (i) is hold by definition.

(ii). L.H.S:

Let $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$ and $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})$ $\big ($ where $\widehat{{\mathbb {I}}_{1}}: {\mathcal {B}}_{1} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$ and $\widehat{{\mathbb {I}}_{2}}: {\mathcal {B}}_{2} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R\big )$ be two CPHFNSS on ${\mathcal {Z}}$. By using definition of the weak complement and restricted intersection, we have $(\widehat{{\mathbb {L}}}, {\mathcal {E}}, {\mathcal {K}} )$ (where $\widehat{{\mathbb {L}}}: {\mathcal {E}} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R)$ such that,

$$\begin{aligned} (\widehat{{\mathbb {V}}}, {\mathcal {E}},{\mathcal {J}}) = \Big (\widehat{{\mathbb {I}}_{1}}^{c},{\mathcal {B}}_{1}, N_{1}\Big )\Cap \Big (\widehat{{\mathbb {I}}_{2}}^{c},{\mathcal {B}}_{2}, N_{2}\Big ), \end{aligned}$$

where $\widehat{{\mathbb {V}}} = \widehat{{\mathbb {I}}_{1}}^{c} \Cap \widehat{{\mathbb {I}}_{2}}^{c}$, ${\mathcal {E}} = {\mathcal {B}}_{1} \cap {\mathcal {B}}_{2}$, ${\mathcal {J}} = min( N_{1}, N_{2})$; $\forall e_{j}\in {\mathcal {E}}$ and $z_{i} \in {\mathcal {Z}}$,

$\bigg \langle (z_{i},r_{ij}),h_{\widehat{{\mathbb {V}}}}\bigg (r_{\widehat{{\mathbb {V}}}_{m}}(z_{i},r_{ij})e^{2\pi i\omega _{\widehat{{\mathbb {V}}}_{m}}(z_{i},r_{ij})}\Big |P_{\widehat{{\mathbb {V}}}_{m}}\bigg )\bigg \rangle \in \widehat{{\mathbb {V}}}(e_{j})$ $\Longleftrightarrow r_{ij} = min(r_{ij}^{\shortmid }, r_{ij}^{\parallel })$ and

$$\begin{aligned}{} & {} r_{\widehat{{\mathbb {V}}}_{m}}(z_{i},r_{ij})e^{2\pi i\omega _{\widehat{{\mathbb {V}}}_{m}}(z_{i},r_{ij})}\Big |P_{\widehat{{\mathbb {V}}}_{m}}\\{} & {} \quad = \left\{ \begin{array}{ll} \ r_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}(z_{i},r_{ij}^{\shortmid })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}(z_{i},r_{ij}^{\shortmid })}\Big |P_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}},~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}-h_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}},\\ ~\ r_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}(z_{i},r_{ij}^{\parallel })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}(z_{i},r_{ij}^{\parallel })}\Big |P_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}},~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{2}}_{m}}-h_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}, \\ ~ min\Big \{r_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}(z_{i},r_{ij}^{\shortmid }),r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })\Big \}e^{2\pi i min\Big \{\omega _{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}(z_{i},r_{ij}^{\shortmid }),\omega _{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}(z_{i},r_{ij}^{\parallel })\Big \}} \Big |P_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}, ~&{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}\cap h_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}. \end{array} \right. \end{aligned}$$

with $r_{ij}^{\shortmid } \in \widehat{{\mathbb {I}}_{1}}^{c}(b_{j}^{1})$ and $r_{ij}^{\parallel } \in \widehat{{\mathbb {I}}_{2}}^{c}(b_{j}^{2})$ while $b_{j}^{1} \in {\mathcal {B}}_{1}$ and $b_{j}^{2}\in {\mathcal {B}}_{2}$.

R.H.S:

we have $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$ and $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})$ are two CPHFNSS over ${\mathcal {Z}}$ then taking restricted union with given conditions in R.H.S, is described as:

$$\begin{aligned} (\widehat{{\mathbb {L}}},{\mathcal {E}}, {\mathcal {J}}) = (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1}) \Cup (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2}) \end{aligned}$$

where $\widehat{{\mathbb {L}}} = \widehat{{\mathbb {I}}_{1}} \Cup \widehat{{\mathbb {I}}_{2}}$, ${\mathcal {E}} = {\mathcal {B}}_{1} \cap {\mathcal {B}}_{2} \ne \phi$ and ${\mathcal {J}} = min(N_{1},N_{2})$; $\forall e_{j}\in {\mathcal {E}}$ and $z_{i} \in {\mathcal {Z}}$,

$\bigg \langle (z_{i},r_{ij}),h_{\widehat{{\mathbb {L}}}}\bigg (r_{\widehat{{\mathbb {L}}}_{m}}(z_{i}, r_{ij})e^{2\pi i\omega _{\widehat{{\mathbb {L}}}_{m}}(z_{i}, r_{ij})}\Big |P_{\widehat{{\mathbb {L}}}_{m}}\bigg )\bigg \rangle \in \widehat{{\mathbb {L}}}(e_{j})$ $\Longleftrightarrow r_{ij} = min(r_{ij}^{\shortmid }, r_{ij}^{\parallel })$ and

$$\begin{aligned}{} & {} r_{\widehat{{\mathbb {L}}}_{m}}(z_{i}, r_{ij})e^{2\pi i\omega _{\widehat{{\mathbb {L}}}_{m}}(z_{i}, r_{ij})}\Big |P_{\widehat{{\mathbb {L}}}_{m}} \\{} & {} \quad = \left\{ \begin{array}{ll} \ r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid })}\Big |P_{\widehat{{\mathbb {I}}_{1}}_{m}},~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}-h_{\widehat{{\mathbb {I}}_{2}}_{m}},\\ ~ r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })}\Big |P_{\widehat{{\mathbb {I}}_{2}}_{m}}, ~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{2}}_{m}}-h_{\widehat{{\mathbb {I}}_{1}}_{m}}, \\ ~ max\Big \{r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid }),r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })\Big \}e^{2\pi i max\Big \{\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{ij}^{\shortmid }),\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })\Big \}} \Big |P_{\widehat{{\mathbb {I}}_{1}}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{2}}_{m}}, ~&{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}\cap h_{\widehat{{\mathbb {I}}_{2}}_{m}}. \end{array} \right. \end{aligned}$$

with $r_{ij}^{\shortmid } \in \widehat{{\mathbb {I}}_{1}}(b_{j}^{1})$ and $r_{ij}^{\parallel } \in \widehat{{\mathbb {I}}_{2}}(b_{j}^{2})$ while $b_{j}^{1} \in {\mathcal {B}}_{1}$ and $b_{j}^{2}\in {\mathcal {B}}_{2}$. Now, by the definition of weak complement

$$\begin{aligned}{} & {} \big (\widehat{{\mathbb {I}}_{1}}\Cup \widehat{{\mathbb {I}}_{2}}\big )^{c} \in \widehat{{\mathbb {L}}}^{c}(e_{j}) =\\{} & {} \quad \left\{ \begin{array}{ll} \ r_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}(z_{i},r_{ij}^{\shortmid })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}(z_{i},r_{ij}^{\shortmid })}\Big |P_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}},~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}-h_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}},\\ ~\ r_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}(z_{i},r_{ij}^{\parallel })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}(z_{i},r_{ij}^{\parallel })}\Big |P_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}},~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{2}}_{m}}-h_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}, \\ ~ min\Big \{r_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}(z_{i},r_{ij}^{\shortmid }),r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{ij}^{\parallel })\Big \}e^{2\pi i min\Big \{\omega _{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}(z_{i},r_{ij}^{\shortmid }),\omega _{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}(z_{i},r_{ij}^{\parallel })\Big \}} \Big |P_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}, ~&{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}\cap h_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}. \end{array} \right. \end{aligned}$$

with $r_{ij}^{\shortmid } \in \widehat{{\mathbb {I}}_{1}}^{c}(b_{j}^{1})$ and $r_{ij}^{\parallel } \in \widehat{{\mathbb {I}}_{2}}^{c}(b_{j}^{2})$ while $b_{j}^{1} \in {\mathcal {B}}_{1}$ and $b_{j}^{2}\in {\mathcal {B}}_{2}$.

Then, $\widehat{{\mathbb {V}}}(e_{j}) = \widehat{{\mathbb {L}}}^{c}(e_{j})$; $\forall e_{j}\in {\mathcal {E}}$.

Hence L.H.S = R.H.S.

Thus, (ii) is hold. $\square$

Proof

(iii) L.H.S:

Let $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$ and $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})$ $\big ($ where $\widehat{{\mathbb {I}}_{1}}: {\mathcal {B}}_{1} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$ and $\widehat{{\mathbb {I}}_{2}}: {\mathcal {B}}_{2} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R\big )$ be two CPHFNSS on ${\mathcal {Z}}$. By using definition of the weak complement and extended intersection, we have $(\widehat{{\mathbb {W}}}, {\mathcal {F}}, {\mathcal {K}} )$ (where $\widehat{{\mathbb {W}}}: {\mathcal {F}} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R)$ such that,

$$\begin{aligned} (\widehat{{\mathbb {W}}}, {\mathcal {F}},{\mathcal {K}}) = \Big (\widehat{{\mathbb {I}}_{1}}^{c},{\mathcal {B}}_{1}, N_{1}\Big )\sqcap \Big (\widehat{{\mathbb {I}}_{2}}^{c},{\mathcal {B}}_{2}, N_{2}\Big ), \end{aligned}$$

where $\widehat{{\mathbb {W}}} = \widehat{{\mathbb {I}}_{1}}^{c} \sqcap \widehat{{\mathbb {I}}_{2}}^{c}$, ${\mathcal {F}} = {\mathcal {B}}_{1} \cup {\mathcal {B}}_{2}$, ${\mathcal {K}} = max( N_{1}, N_{2})$; $\forall f_{j}\in {\mathcal {F}}$ and $z_{i} \in {\mathcal {Z}}$, with $f_{j}^{1}\in {\mathcal {B}}_{1}$ and $f_{j}^{2}\in {\mathcal {B}}_{2}.$

$$\begin{aligned} \ \widehat{{\mathbb {W}}}(f_{j}) = \left\{ \begin{array}{ll} \ \widehat{{\mathbb {I}}_{1}}^{c}(f_{j}^{1}),~ &{}{\text { if}} ~~f_{j} \in {\mathcal {B}}_{1}-{\mathcal {B}}_{2},\\ ~\widehat{{\mathbb {I}}_{2}}^{c}(f_{j}^{2}), ~ &{}{\text { if}} ~~f_{j} \in {\mathcal {B}}_{2}-{\mathcal {B}}_{1}, \\ ~\widehat{{\mathbb {I}}_{1}}^{c}(f_{j}^{1}) \Cap \widehat{{\mathbb {I}}_{2}}^{c}(f_{j}^{2}), ~&{}{\text { if}} ~~f_{j} \in {\mathcal {B}}_{1}\cap {\mathcal {B}}_{2}. \end{array} \right. \end{aligned}$$

R.H.S:

we have $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$ and $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})$ are two CPHFNSS over ${\mathcal {Z}}$ then taking extended union with given conditions in R.H.S, is described as:

$$\begin{aligned} (\widehat{{\mathbb {M}}},{\mathcal {F}}, {\mathcal {K}}) = (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1}) \sqcup (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2}) \end{aligned}$$

where $\widehat{{\mathbb {M}}} = \widehat{{\mathbb {I}}_{1}} \sqcup \widehat{{\mathbb {I}}_{2}}$, ${\mathcal {F}} = {\mathcal {B}}_{1} \cup {\mathcal {B}}_{2}$ and ${\mathcal {K}} = max(N_{1},N_{2})$; $\forall f_{j}\in {\mathcal {F}}$ and $z_{i} \in {\mathcal {Z}}$, with $f_{j}^{1}\in {\mathcal {B}}_{1}$ and $f_{j}^{2}\in {\mathcal {B}}_{2}.$

$$\begin{aligned} \ \widehat{{\mathbb {M}}}(f_{j}) = \left\{ \begin{array}{ll} \ \widehat{{\mathbb {I}}_{1}}(f_{j}^{1}),~ &{}{\text { if}} ~~f_{j} \in {\mathcal {B}}_{1}-{\mathcal {B}}_{2},\\ ~\widehat{{\mathbb {I}}_{2}}(f_{j}^{2}), ~ &{}{\text { if}} ~~f_{j} \in {\mathcal {B}}_{2}-{\mathcal {B}}_{1}, \\ ~\widehat{{\mathbb {I}}_{1}}(f_{j}^{1}) \Cup \widehat{{\mathbb {I}}_{2}}(f_{j}^{2}), ~&{}{\text { if}} ~~f_{j} \in {\mathcal {B}}_{1}\cap {\mathcal {B}}_{2}. \end{array} \right. \end{aligned}$$

Now, by using the definition of weak complement we have,

$$\begin{aligned} \ \widehat{{\mathbb {M}}}^{c}(f_{j}) = \left\{ \begin{array}{ll} \ \widehat{{\mathbb {I}}_{1}}^{c}(f_{j}^{1}),~ &{}{\text { if}} ~~f_{j} \in {\mathcal {B}}_{1}-{\mathcal {B}}_{2},\\ ~\widehat{{\mathbb {I}}_{2}}^{c}(f_{j}^{2}), ~ &{}{\text { if}} ~~f_{j} \in {\mathcal {B}}_{2}-{\mathcal {B}}_{1}, \\ ~\widehat{{\mathbb {I}}_{1}}^{c}(f_{j}^{1}) \Cap \widehat{{\mathbb {I}}_{2}}^{c}(f_{j}^{2}), ~&{}{\text { if}} ~~f_{j} \in {\mathcal {B}}_{1}\cap {\mathcal {B}}_{2}. \end{array} \right. \end{aligned}$$

Then, $\widehat{{\mathbb {W}}}(f_{j})) = \widehat{{\mathbb {M}}}^{c}(f_{j})$; $\forall f_{j}\in {\mathcal {F}}$.

Hence L.H.S = R.H.S.

Thus, (iv) is hold. $\square$

Proof

(vi) L.H.S:

Let $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$ and $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})$ $\big ($ where $\widehat{{\mathbb {I}}_{1}}: {\mathcal {B}}_{1} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$ and $\widehat{{\mathbb {I}}_{2}}: {\mathcal {B}}_{2} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R\big )$ be two CPHFNSS on ${\mathcal {Z}}$. Then by using the definition of weak complement and soft max-AND operation, we have,

$$\begin{aligned} (\widehat{{\mathbb {X}}}, {\mathcal {G}},{\mathcal {K}}) = \Big (\widehat{{\mathbb {I}}_{1}}^{c},{\mathcal {B}}_{1}, N_{1}\Big )\wedge \Big (\widehat{{\mathbb {I}}_{2}}^{c},{\mathcal {B}}_{2}, N_{2}\Big ), \end{aligned}$$

where $\widehat{{\mathbb {X}}} = \widehat{{\mathbb {I}}_{1}}^{c} \wedge \widehat{{\mathbb {I}}_{2}}^{c}$, ${\mathcal {G}} = {\mathcal {B}}_{1} \times {\mathcal {B}}_{2}$, ${\mathcal {K}} = max( N_{1}, N_{2})$; $\forall (g_{u}, g_{v})\in ({\mathcal {B}}_{1}\times {\mathcal {B}}_{2}),~g_{u},g_{v}\in \Lambda$and $z_{i} \in {\mathcal {Z}}$,

$\bigg \langle (z_{i},r_{i(u,v)}),h_{\widehat{{\mathbb {X}}}}\bigg (r_{\widehat{{\mathbb {X}}}_{m}}(z_{i},r_{i(u,v)})e^{2\pi i\omega _{\widehat{{\mathbb {X}}}_{m}}(z_{i},r_{i(u,v)})}\Big |P_{\widehat{{\mathbb {X}}}_{m}}\bigg )\bigg \rangle \in \widehat{{\mathbb {X}}}(g_{(u,v)}) \Longleftrightarrow$ $r_{i(u,v)} = max(r_{i(u,v)}^{\shortmid }, r_{i(u,v)}^{\parallel })$ and

$$\begin{aligned}{} & {} r_{\widehat{{\mathbb {X}}}_{m}}(z_{i},r_{i(u,v)})e^{2\pi i\omega _{\widehat{{\mathbb {X}}}_{m}}(z_{i},r_{i(u,v)})}\Big |P_{\widehat{{\mathbb {X}}}_{m}}\\{} & {} = \left\{ \begin{array}{ll} \ r_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}(z_{i},r_{i(u,v)}^{\shortmid })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}(z_{i},r_{i(u,v)}^{\shortmid })}\Big |P_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}},~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}-h_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}},\\ ~\ r_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}(z_{i},r_{i(u,v)}^{\parallel })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}(z_{i},r_{i(u,v)}^{\parallel })}\Big |P_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}},~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{2}}_{m}}-h_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}, \\ ~ max\Big \{r_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}(z_{i},r_{i(u,v)}^{\shortmid }),r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{i(u,v)}^{\parallel })\Big \}e^{2\pi i max\Big \{\omega _{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}(z_{i},r_{i(u,v)}^{\shortmid }),\omega _{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}(z_{i},r_{i(u,v)}^{\parallel })\Big \}} \Big |P_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}, ~&{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}\cap h_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}. \end{array} \right. \end{aligned}$$

with $r_{i(u,v)}^{\shortmid } \in \widehat{{\mathbb {I}}_{1}}^{c}(b_{(u,v)}^{1})$ and $r_{i(u,v)}^{\parallel } \in \widehat{{\mathbb {I}}_{2}}^{c}(b_{(u,v)}^{2})$ while $b_{(u,v)}^{1} \in {\mathcal {B}}_{1}$ and $b_{(u,v)}^{2}\in {\mathcal {B}}_{2}$.

R.H.S:

Let $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$ and $(\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2})$ $\big ($ where $\widehat{{\mathbb {I}}_{1}}: {\mathcal {B}}_{1} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$ and $\widehat{{\mathbb {I}}_{2}}: {\mathcal {B}}_{2} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R \big )$ by using definition of soft min-OR and given conditions in R.H.S, we have

$$\begin{aligned} (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1}) \vee (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2}) = (\widehat{{\mathbb {N}}},{\mathcal {G}}, {\mathcal {K}}), \end{aligned}$$

where $\widehat{{\mathbb {N}}}: {\mathcal {G}} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$ such that $\widehat{{\mathbb {N}}} = \widehat{{\mathbb {I}}_{1}} \cap \widehat{{\mathbb {I}}_{2}}$ and ${\mathcal {G}} = {\mathcal {B}}_{1}\times {\mathcal {B}}_{2}$; $\forall (g_{u}, g_{v})\in ({\mathcal {B}}_{1}\times {\mathcal {B}}_{2}),~g_{u},g_{v}\in \Lambda$ and ${\mathcal {K}} = max(N_{1}, N_{2}),$

$\bigg \langle (z_{i}, r_{i(u,v)}),h_{\widehat{{\mathbb {N}}}}\bigg (r_{\widehat{{\mathbb {N}}}_{m}}(z_{i},r_{i(u,v)})e^{2\pi i\omega _{\widehat{{\mathbb {N}}}_{m}}(z_{i},r_{i(u,v)})}\Big |P_{\widehat{{\mathbb {N}}}_{m}}\bigg )\bigg \rangle \in \widehat{{\mathbb {N}}} (g_{u}, g_{v}) \Longleftrightarrow r_{i(u,v)}= max(r_{i(u,v)}^{\shortmid },r_{i(u,v)}^{\parallel })$ and

Fig. 1

Flowchart of Algorithm 4.1

$$\begin{aligned}{} & {} r_{\widehat{{\mathbb {N}}}_{m}}(z_{i}, r_{i(u,v)})e^{2\pi i\omega _{\widehat{{\mathbb {N}}}_{m}}(z_{i}, r_{i(u,v)})}\Big |P_{\widehat{{\mathbb {N}}}_{m}}\\{} & {} \quad = \left\{ \begin{array}{ll} \ r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{i(u,v)}^{\shortmid })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{i(u,v)}^{\shortmid })}\Big |P_{\widehat{{\mathbb {I}}_{1}}_{m}},~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}-h_{\widehat{{\mathbb {I}}_{2}}_{m}},\\ ~ r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{i(u,v)}^{\parallel })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{i(u,v)}^{\parallel })}\Big |P_{\widehat{{\mathbb {I}}_{2}}_{m}}, ~&{} {\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{2}}_{m}}-h_{\widehat{{\mathbb {I}}_{1}}_{m}}, \\ ~ min\Big \{r_{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{i(u,v)}^{\shortmid }),r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{i(u,v)}^{\parallel })\Big \}e^{2\pi i min\Big \{\omega _{\widehat{{\mathbb {I}}_{1}}_{m}}(z_{i},r_{i(u,v)}^{\shortmid }),\omega _{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{i(u,v)}^{\parallel })\Big \}} \Big |P_{\widehat{{\mathbb {I}}_{1}}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{2}}_{m}}, ~&{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}_{m}}\cap h_{\widehat{{\mathbb {I}}_{2}}_{m}}. \end{array} \right. \end{aligned}$$

with $(z_{i},r_{i(u,v)}^{\shortmid }) \in \widehat{{\mathbb {I}}_{1}}({\mathcal {B}}_{1})$ and $(z_{i},r_{i(u,v)}^{\parallel }) \in \widehat{{\mathbb {I}}_{2}}({\mathcal {B}}_{2})$. Now, by taking the weak complement we get $\widehat{{\mathbb {N}}}^{c} (g_{u}, g_{v})$

$$\begin{aligned} \ = \left\{ \begin{array}{ll} \ r_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}(z_{i},r_{i(u,v)}^{\shortmid })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}(z_{i},r_{i(u,v)}^{\shortmid })}\Big |P_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}},~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}-h_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}},\\ ~\ r_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}(z_{i},r_{i(u,v)}^{\parallel })e^{2\pi i\omega _{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}(z_{i},r_{i(u,v)}^{\parallel })}\Big |P_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}},~ &{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{2}}_{m}}-h_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}, \\ ~ max\Big \{r_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}(z_{i},r_{i(u,v)}^{\shortmid }),r_{\widehat{{\mathbb {I}}_{2}}_{m}}(z_{i},r_{i(u,v)}^{\parallel })\Big \}e^{2\pi i max\Big \{\omega _{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}(z_{i},r_{i(u,v)}^{\shortmid }),\omega _{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}(z_{i},r_{i(u,v)}^{\parallel })\Big \}} \Big |P_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}} \cdot P_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}, ~&{}{\text { if}} ~~m \in h_{\widehat{{\mathbb {I}}_{1}}^{c}_{m}}\cap h_{\widehat{{\mathbb {I}}_{2}}^{c}_{m}}. \end{array} \right. \end{aligned}$$

Fig. 2

Flowchart of Algorithm 4.2

with $r_{i(u,v)}^{\shortmid } \in \widehat{{\mathbb {I}}_{1}}^{c}(b_{(u,v)}^{1})$ and $r_{i(u,v)}^{\parallel } \in \widehat{{\mathbb {I}}_{2}}^{c}(b_{(u,v)}^{2})$ while $b_{(u,v)}^{1} \in {\mathcal {B}}_{1}$ and $b_{(u,v)}^{2}\in {\mathcal {B}}_{2}$.

Then, $\widehat{{\mathbb {X}}}(g_{(u,v)}) = \widehat{{\mathbb {N}}}^{c} (g_{u}, g_{v})$; $\forall (g_{u}, g_{v})\in ({\mathcal {B}}_{1}\times {\mathcal {B}}_{2})$.

Hence L.H.S = R.H.S.

Thus, (vi) is hold. $\square$

The proof of (iv), (v) and (vii) are similar to (ii), (iii) and (vi).

5 Algorithms

Choosing the best approach to solve a problem is frequently essential to get the best result. The method that people use to make decisions is algorithms. An algorithm is a predetermined series of detailed steps that offers the ideal solution to a specific problem. It is preferable to use an algorithm if perfect accuracy is required because accuracy is improved and the likelihood of errors is decreased by the use of an algorithm. Using an algorithm is your quality alternative if you are working in a scenario where you truly need to have the proper or high-quality solution. Here, we introduced two algorithms based on CPHF information with parameterized family and grading for decision-making where the choice of first algorithm is best if there exists a single expert for evaluation or construct a single evaluation by the committee and second algorithm is best if there exist two or more evaluations by the experts.

Algorithm 5.1

Step 1: The input consist of the universal set $\mathcal {Z} = \{z_{1}, z_{2}, z_{3},...,z_{l}\}$ and a set of attributes $\mathcal {B}$ where $\mathcal {B} \subseteq H$.

Step 2: Determine CPHFNSS $(\widehat{\mathbb {I}},\mathcal {B}, N)$ where $\widehat{\mathbb {I}}: \mathcal {B} \rightarrow \mathcal {I}(\mathcal {Z})\times R$ on $\mathcal {Z}$ while using the grading set.

Step 3: Construct tables separately for $r_{\widehat{\mathbb {I}}}$, $\omega _{\widehat{\mathbb {I}}}$, and $P_{\widehat{\mathbb {I}}}$ of complex valued membership of CPHFNSS $(\widehat{\mathbb {I}},\mathcal {B}, N)$.

Step 4: Calculate the choice value $\hat{\mathcal {C}}$ for the amplitude term $\hat{\mathcal {C}}(r_{\widehat{\mathbb {I}}})$ and the phase term $\hat{\mathcal {C}}(\omega _{\widehat{\mathbb {I}}})$ by calculating the average and for the probability $\hat{\mathcal {C}}(P_{\widehat{\mathbb {I}}})$ by calculating their product.

Step 5: Quantify the comparison tables of amplitude term $\bar{\mathbb {C}}(r_{\widehat{\mathbb {I}}})$ and the phase term $\bar{\mathbb {C}}(\omega _{\widehat{\mathbb {I}}})$, where

$\bar{\mathbb {C}}(z_{i}, z_{i'}) = \sum \limits _{b_{j}\in \mathcal {B}}\big ($if $z_{i}$ w.r.t $b_{j}\ge z_{i'}$ w.r.t $b_{j}$ then 1 otherwise 0 $\big )$ where $i,i' = \{1, 2, 3,...$ no. of universal objects$\}$.

Step 6: Design the table for grade sum, row and column sum for amplitude and phase term.

Step 7: Figure out the score of amplitude term $\bar{\mathbb {S}}(r_{\widehat{\mathbb {I}}})$ and phase term $\bar{\mathbb {S}}(\omega _{\widehat{\mathbb {I}}})$ by subtracting the column sum from the row sum and for probability $\bar{\mathbb {S}}(P_{\widehat{\mathbb {I}}})$ by calculating the product of choice values.

Step 8: Compute the final score $\bar{S}$ by multiplying with the probability score value after adding the score of amplitude and phase terms.

Step 9: Any of the alternative is selected as optimal decision with the highest score and highest grade.

The flowchart of Algorithm 4.1 is shown in Fig. 1:

Algorithm 5.2

Step 1: The input consist of the universal set ${\mathcal {Z}} = \{z_{1}, z_{2}, z_{3},...,z_{l}\}$ and a set of attributes ${\mathcal {B}}$ where ${\mathcal {B}} \subseteq H$.

Step 2: Determine CPHFNSSs $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$ and $(\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1})$ where $\widehat{{\mathbb {I}}_{1}}: {\mathcal {B}}_{1} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$ and $\widehat{{\mathbb {I}}_{2}}: {\mathcal {B}}_{2} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$ on ${\mathcal {Z}}$.

Step 3: Evaluate

$$\begin{aligned} (\widehat{{\mathbb {I}}_{1}},{\mathcal {B}}_{1}, N_{1}) \wedge (\widehat{{\mathbb {I}}_{2}},{\mathcal {B}}_{2}, N_{2}) = (\widehat{{\mathbb {L}}},{\mathcal {G}}, {\mathcal {K}}), \end{aligned}$$

where $\widehat{{\mathbb {L}}}: {\mathcal {G}} \rightarrow {\mathcal {I}}({\mathcal {Z}})\times R$ such that $\widehat{{\mathbb {L}}} = \widehat{{\mathbb {I}}_{1}} \cup \widehat{{\mathbb {I}}_{2}}$ and ${\mathcal {G}} = {\mathcal {B}}_{1}\times {\mathcal {B}}_{2}$; $\forall (g_{u}, g_{v})\in ({\mathcal {B}}_{1}\times {\mathcal {B}}_{2}),~g_{u},g_{v}\in \Lambda$ and ${\mathcal {K}} = max(N_{1}, N_{2}),$

Step 4: Calculate choice value $\hat{{\mathcal {C}}}(g_{u}, g_{v})(z_{i});~\forall ~z_{i}\in {\mathcal {Z}},(g_{u}, g_{v})\in ({\mathcal {B}}_{1}\times {\mathcal {B}}_{2})$ defined as:

$$\begin{aligned} \hat{{\mathcal {C}}}(g_{u}, g_{v})(z_{i}) = \frac{\sum \limits _{m}\Big (r_{\widehat{{\mathbb {L}}}_{m}}(z_{i})\times \omega _{\widehat{{\mathbb {L}}}_{m}}(z_{i}) \Big )}{\sum \limits _{m}\Big (r_{\widehat{{\mathbb {L}}}_{m}}(z_{i})\Big )}\Bigg | \prod \limits _{m} P_{\widehat{{\mathbb {L}}}_{m}}, \end{aligned}$$

where $m = 1, 2, 3,...,l$ and l is the possible number of elements in $h_{\widehat{{\mathbb {L}}}}\bigg (r_{\widehat{{\mathbb {L}}}_{m}}(z_{i})e^{2\pi i\omega _{\widehat{{\mathbb {L}}}_{m}}(z_{i})}\Big |P_{\widehat{{\mathbb {L}}}_{m}}\bigg ).$

Step 5: Evaluate score values $\hat{{\mathcal {S}}}(g_{u}, g_{v})(z_{i})$ the product of $\hat{{\mathcal {C}}}(g_{u}, g_{v})$ with corresponding probability and grading against each $z_{i}$.

Step 6: The weighted values for each $\bar{\mathbb {S}}(g_{u}, g_{v})(z_{i})$ is:

$$\begin{aligned} \bar{\mathbb {S}}(z_{i}) = max \bar{\mathbb {S}}(g_{u}, g_{v})(z_{i}). \end{aligned}$$

where ${(g_{u}, g_{v}))\in ({\mathcal {B}}_{1}\times {\mathcal {B}}_{2})}$ and $z_{i}\in {\mathcal {Z}}$.

Step 7: Calculate the sum of each $z_{i}$. Then the optimal decision is in the form of series in the descending order.

The flowchart of Algorithm 4.2 is shown in Fig. 2:

We go on to apply these algorithms to fully developed real-world scenarios in order to demonstrate their value and viability.

Table 13 Star evaluation of anesthesia machine

Table 14 5-soft set by Table 13

Table 15 Representation of CPHF 5-soft set

6 Applications

This section uses applications and case studies of our suggested sets to demonstrate the validity and superiority of the research where we are using parameterized families and grading with fuzziness, hesitancy, and randomness together. Which plays a very significant role in taking decisions in a short interval of time and as accurately as we can.

Case study 6.1

The management of the X hospital wants to purchase an anesthesia machine for its department. Medical professionals use anesthesia machines to deliver a precise and consistent flow of anesthetic gases during anesthesia administration. Oxygen, isoflurane, and nitrous oxide gases are used. The gases should deliver at a secure pressure and in a truly united flow to the patient. Because of this, contemporary anesthesia machines are equipped with a suction unit, a ventilator, and patient monitoring tools. In addition, they comprise touchscreen monitors and displays that remain focused on the patient’s heart rate and oxygen saturation level. Furthermore, an anesthesia machine’s primary function is to regulate a patient’s level of consciousness during a surgical procedure. It’s necessary to buy effective devices because they will ensure the patient’s safety. The management of the hospital accomplishes this by hiring experts and giving them six different machines. Let ${\mathcal {Z}} = \{z_{1}, z_{2}, z_{3}, z_{4}, z_{5}, z_{6}\}$ be the set of anesthesia machines. To choose the best model the concern department wants that following features should be under consideration ${\mathcal {B}}= \{ b_{1} =$ “ventilator system,” $b_{2} =$ “safety features,” $b_{3} =$ “gas delivery system,” $b_{4} =$ “cost and life span,” $b_{5} =$ “vaporizer technology, $b_{6} =$ “dimensions,” $b_{7} =$ “audio-visual alarms for high/low set values of different parameters” $\}$. Table 13 can be used to create a 5-soft set which consists of the evaluation of anesthesia machine by the expert concerning star rating where 4 stars represent excellent working, 3 stars represent good, 2 stars represent normal, 1 star represents satisfactory and the box represents unsatisfactory performance.

For convenience, we will convert Table 13 in 5-soft set, as represented in Table 14.

When this information is precisely and ambiguously extracted from actual data, it is sufficient then it has to do with the N-soft set theory. However, if the rating is ambiguous, hesitant or random then we might need to use CPHFNSS. Then, the CPHF 5-soft set is evaluated in Table 15. By using step 3 of Algorithm 5.1, we construct tables separately for $r_{\widehat{{\mathbb {I}}}}$, $\omega _{\widehat{{\mathbb {I}}}}$, and $P_{\widehat{{\mathbb {I}}}}$ as illustrated in Tables 16, 17 and 18.

By using step 4 of Algorithm 5.1, we will calculate the choice value of $\hat{{\mathcal {C}}}(r_{\widehat{{\mathbb {I}}}})$, $\hat{{\mathcal {C}}}(\omega _{\widehat{{\mathbb {I}}}})$ and $\hat{{\mathcal {C}}}(P_{\widehat{{\mathbb {I}}}})$, as illustrated in Tables 19, 20 and 21.

Table 16 Representation of the amplitude term

Table 17 Representation of the phase term

Table 18 Representation of the probability

After this, we will quantify the comparison tables for amplitude and phase terms by using step 5 of Algorithm 5.1, as represented in Tables 22 and 23.

Then we will construct tables by using step 6 of Algorithm 5.1 for grade sum, row and column sum for amplitude and phase terms, representing in Table 24.

Now, we will design the table for score values by using steps 7 and 8 of Algorithm 5.1, represented in Table 25.

However, $z_{6}$ have highest grading with highest score value. Therefore, the management of the hospital will select the $z_{6}$ anesthesia machine for its department.

The graphical representation of ranking is shown in Fig. 3.

Case study 6.2

Pakistan is the fifth most populous nation in the world with a total population of about 230 million (Population of Pakistan (xxxx)). According to 2020–2022, the poverty rate is around about 39 percent (Poverty rate of Pakistan (xxxx)). Numerous infectious diseases are prevalent in Pakistan as a result of the country’s dense population, poverty, and inadequate healthcare infrastructure. According to World Health Organization (WHO), infectious diseases remained one of the leading causes of death. Infectious diseases are a disorder brought on by microorganisms like bacteria, viruses, fungi, or parasites. Infectious diseases include COVID-19, dengue, TB, malaria, measles, hepatitis, etc., that require proper monitoring or treatment and can result in hospitalizations, long-term impairment, lower quality of life, and even mortality. Infectious diseases have a negative impact on many people’s life quality and health.

According to WHO, the total cases of COVID-19 from January 3, 2020, to August 23, 2022, were 1,566,652 and the death cases were 30,555 (Covid-19 cases of Pakistan (xxxx)). Last year, 52,894 dengue cases together with 224 deaths (Dengue fever cases of Pakistan (2021)). There are more cases of tuberculosis (TB) than ever before, with over 27,000 new cases being reported yearly. The incidence rate of tuberculosis is 5,25,000 per year, according to data from the national TB control program; however, 3,68,589 TB patients are currently receiving treatment, and 56,000 TB-related fatalities occur annually in Pakistan (Tuberculosis cases in Pakistan (2020)). Globally, there were reportedly 229 million cases of malaria in 2019 with an estimated 409,000 deaths. According to Pakistan’s annual report for 2019, 6.5 million malaria suspects were checked at public sector health facilities across the country, resulting in a total of 374,513 verified malaria cases (Butt and Ahmed 2022). One of the top five nations in the world including the highest measles prevalence rates in Pakistan. Although an effective and safe vaccine against measles is available, recent setbacks in the campaign to eradicate the disease are concerning. Measles cases were reported 84 percent fewer times worldwide between 2000 and 2016 thanks to immunization. Unexpectedly, the number of cases of measles surged between 2016 and 2019 (Rana et al. 2022). The laboratory surveillance system recorded more than 34,000 measles cases in 2018 and 8,345 measles cases in 2019. Each year, measles kills about 20,000 children in Pakistan (Mere et al. 2019). Pakistan has the second-highest prevalence of the disease Hepatitis C with 9.8 million persons suffering from chronic Hepatitis C (Hepatitis in Pakistan 2022).

Table 19 Choice value of the amplitude term

Table 20 Choice value of the phase term

Table 21 Choice value of the probability

Table 22 Comparison of the amplitude term

Table 23 Comparison of the phase term

Table 24 Representation of the grade sum

Table 25 Representation of the score values

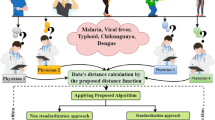
According to WHO these infectious diseases are included in the top 10 diseases which are the globally leading cause of death. But the one major issue with these infectious diseases is that their symptoms or clinical characteristics showed a significant degree of similarity, as indicated in Table 26 Rana et al. (2021). The clinical profile of COVID-19 is frequently mistaken for those of several infectious illnesses, which makes early identification difficult. The co-epidemic of COVID-19 and prevalent infectious disease in Pakistan presents several public health issues, and such complex combinations not only make diagnosis more difficult but also place a double load on the country’s already frail healthcare system. The availability of various kits, the ability to perform diagnostic procedures, available funding, and technical staff are all factors in the diagnostic process of several pathogens with comparable clinical characteristics. While infectious diseases are the main reason for death and disability of the nation. Thus, if society wants to provide citizens with better healthcare and raise their standard of living generally, it is crucial that we understand, manage, and prevent infectious diseases. Doctors can use Algorithm 5.2 scores to determine a patient’s overall prognosis, and researchers can use them to find particular hazards that persons with several infectious conditions face. Here we illustrate the numerical example for better understanding.

Fig. 3

Ranking results

There exist two doctors for the examination of patients. Let ${\mathcal {Z}}= \{z_{1}, z_{2}, z_{3}, z_{4}, z_{5}\}$ be the set of diseases and the set of the attribute consist of common symptoms or clinical characteristics of the set of diseases which is under consideration that is, ${\mathcal {B}}=\{b_{1}, b_{2}, b_{3}\}$ and ${\mathcal {R}}= \{0, 1, 2, 3, 4, 5, 6, 7, 8, 9\}$ be the set of ordered grades concerning the severity of disease, where zero represents that there exists no severity of the disease, while 9 indicates the entire severity of the disease. The doctors will collect the data in CPHFNSS where the amplitude term of membership grade represents the belongingness of the disease and the phase term represents the durability of the symptom concerning the disease while probability indicates how likely is that a particular statement given by the patient is accurate. Tables 27 and 28 represent the data collected by the doctors from the patient.

Table 26 Overlapping of clinical characteristics of infectious diseases

Table 27 Data collected by the doctor 1

Table 28 Data collected by the doctor 2

Table 29 Tabular representation of collected data after applying soft max-AND operation

Now we will run Algorithm 5.2. By using Step 3: we will apply soft max-AND operator, as represented in Table 29.

By using step 4 of Algorithm 5.2, we will calculate the choice value, as represented in Table 30.

Table 30 Tabular representation of choice value

Table 31 Tabular representation of score value

By using step 5 of Algorithm 5.2, we will evaluate the score value, as represented in Table 31.

By using step 6 of Algorithm 5.2, we will evaluate the weighted value, as represented in Table 32.

Table 32 Tabular representation of weighted value

Fig. 4

Ranking results

Table 33 Analytical comparison with existing approaches

Table 34 Characteristic comparison with existing approaches

By using step 7 of Algorithm 5.2.

$$\begin{aligned}{} & {} \bar{\mathbb {S}}(z_{1}) = 8.1, ~~~\bar{\mathbb {S}}(z_{2}) = 5.4, ~~~\bar{\mathbb {S}}(z_{3}) = 21.56, ~~~\\{} & {} \quad \bar{\mathbb {S}}(z_{4}) = 5.6, ~~~\bar{\mathbb {S}}(z_{5}) = 0. \\{} & {} \bar{\mathbb {S}}(z_{3})\ge \bar{\mathbb {S}}(z_{1})\ge \bar{\mathbb {S}}(z_{4})\ge \bar{\mathbb {S}}(z_{2})\ge \bar{\mathbb {S}}(z_{5}) \end{aligned}$$

This indicates that the patient has greater chances to suffer with infectious disease $z_{3}$ as compared to other infectious diseases and the doctor will start laboratory testing for $z_{3}$.

The graphical representation of ranking is shown in Fig. 4.

7 Comparison analysis

In order to solve a real-world difficult issues, we developed a strategy using the theory of constraints in conjunction with multiattribute and multiobjective decision-making techniques. We discussed two algorithms under the CPHFNSS. Without respect to the existence of a unique optimum solution, both methods provide an ordered list of all feasible alternatives. When such information as CPHFNSS is presented to a decision-maker, none of the current works are able to adequately deal with it. While the proposed approach can also deal with the existing approaches (Zadeh 1965; Torra 2010; Akram et al. 2019a, b; Garg et al. 2021; Zhang et al. 2017; Mahmood et al. 2021) information. To illustrate the efficacy of the suggested technique in comparison to the current ones for multi-parameter decision-making, a comparative study employing different structures provided by different researchers was done. The analytical comparison of CPHFNS approach with the existing approaches is given in Table 33 and characteristic comparison is given in Table 34. Thus, our suggested approaches are better and more trustworthy than those now in use.

8 Conclusion

In this research work, we expose and motivate the idea of complex probabilistic hesitant fuzzy N-soft sets (CPHFNSS). It is extremely important for improving the effectiveness of decision-making processes in many theories of uncertainty. In contrast to the soft set theory, the N-soft set theory is emerging as a powerful mathematical tool for handling precision and uncertainty. In this regard, N-soft set theory, complex fuzzy set theory, as well as probabilistic hesitant fuzzy theory, which are modified forms of soft sets and fuzzy sets intended to capture ambiguities and uncertain information in the application settings, are accumulated into CPHFNSS. We split this manuscript into three major sections. Firstly, we broaden the concept of CPHFNSS and presented its restricted and extended union, restricted and extended intersection, weak complement, top and bottom weak complement, soft max-AND, soft min-OR operation and to demonstrate these essential characteristics, we offer numerical examples. Secondly, we established their essential laws, including the De Morgan, idempotent, commutative, associative, involution, and idempotent laws. Finally, we developed a set of algorithms for effective decision-making. Also, we illustrated the examples for the selection of anesthesia machines and make early identification of infectious diseases easier for doctors. Furthermore, improvements in the treatment of infectious diseases, mental health, care quality, and hospitalizations, as well as the potential for enhanced population health. In the future, we may develop innovative decision-making strategies such as TODIM, TAOV or by using possibilities of hybridization with the model “The multi-fuzzy N-soft set and its applications to decision-making” (Fatimah and Alcantud 2021), etc.