GUP modified Wigner function using classical-quantum unified framework

Abstract

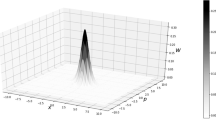
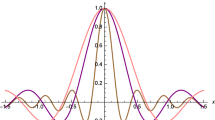
The generalized uncertainty principle (GUP) is a natural consequence of many proposed quantum gravity theories that indicate the modification of quantum mechanics and classical mechanics. A unified classical quantum framework also leads to the interpretation of a Wigner phase-space distribution of a state as a KvN wave function. In this article, we utilize the classical-quantum unified framework to calculate the expression for the GUP-modified Wigner function of a classical harmonic oscillator in the configuration space instead of the conventional approach that uses the momentum space. Further, we plot the modified Wigner functions and show that they are similar to the results obtained in the past literature.

Appendices

Appendix A Wavefunctions expression

The expression for the ground state, first excited state & second excited state of the wave function $\Psi (q_{1},q_{2},t)$ are given as follows:

$$\begin{aligned}&\Psi _{00}(q_{1},q_{2},t) \nonumber \\&\quad = e^{- \xi _{0}^{2}/2} \nonumber \\&\qquad \left[ \phi _{00}(q_{1},q_{2}) +\left( \dfrac{m \omega }{\pi \hbar \kappa } \right) ^{1/2} \right. \nonumber \\&\qquad \quad \left. \dfrac{e^{-(\xi _{1}^{2}+\xi _{2}^{2})/2} \alpha }{32} H_{0}(\xi _{1}) \, H_{0}(\xi _{2}) \times \left( -2 \xi _{0}^{4} + 48 \xi _{0}^{2} \right) \right] , \end{aligned}$$

(44)

$$\begin{aligned}&\Psi _{11}(q_{1},q_{2},t)\nonumber \\&\quad = \dfrac{e^{- \xi _{0}^{2}/2} \xi _{0}^{2}}{2} \nonumber \\&\qquad \left[ \phi _{11}(q_{1},q_{2}) +\left( \dfrac{m \omega }{\pi \hbar \kappa }\right) ^{1/2}\right. \nonumber \\&\qquad \quad \left. \dfrac{e^{-(\xi _{1}^{2}+\xi _{2}^{2})/2} \alpha }{64} H_{1}(\xi _{1}) \, H_{1}(\xi _{2}) \times (-2 \xi _{0}^{4} + 72 \xi _{0}^{2} -96)\right] , \end{aligned}$$

(45)

$$\begin{aligned}&\Psi _{22}(q_{1},q_{2},t)\nonumber \\&\quad = \dfrac{e^{- \xi _{0}^{2}/2} \xi _{0}^{4}}{8} \nonumber \\&\qquad \left[ \phi _{22}(q_{1},q_{2}) +\left( \dfrac{m \omega }{\pi \hbar \kappa }\right) ^{1/2}\right. \nonumber \\&\qquad \quad \left. \dfrac{e^{-(\xi _{1}^{2}+\xi _{2}^{2})/2} \alpha }{256} H_{2}(\xi _{1}) \, H_{2}(\xi _{2}) \times (-2 \xi _{0}^{4} + 96 \xi _{0}^{2} -240)\right] . \end{aligned}$$

(46)

In the derivation of the preceding equations, we have approximated $\beta$ to the first order. Furthermore, we have set $n_{1} = n_{2}$ during the calculation of the ground and excited states to eliminate time dependence, as differing values of $n_{1}$ and $n_{2}$ would introduce such dependence.

Appendix B Expression of modified Wigner function $W(q,\Pi )$

In order to find the modified Wigner function $W(q,\Pi )=\psi (q,\Pi ,t)$, we use the Eq. (34) and we perform transformations of the form $u = q + Q/2$ & $v = q - Q/2$ so that the function $\Psi (q_{1},q_{2},t)$ transforms as $\psi (q, Q, t)$. Now the Fourier transform of the calculated function $\psi (q, Q, t)$ using the Eq. (41) gives the modified Wigner function $W(q,\Pi )$ for the ground state, 1st & 2nd excited states as follows:

$$\begin{aligned}&W_{00}(q,\Pi ) \nonumber \\&\quad = -\frac{1}{2 \sqrt{\pi } x_{0}^{4}}\nonumber \\&\qquad \left[ \sqrt{\frac{2}{\hbar }} \left\{ \left( \Pi ^{4} x_{0}^{8} +6 \Pi ^{2} x_{0}^{6}\right. \right. \right. \nonumber \\&\qquad \quad -6 q^{2} \Pi ^{2} x_{0}^{4} +\left( -6 q^{2}-3 \xi _{0}^{2}\right) x_{0}^{2}\nonumber \\&\qquad \quad \left. \left. +q^{4}+\frac{\xi _{0}^{4}}{8}\right) \alpha -2 x_{0}^{4}\right\} \nonumber \\&\qquad \quad \left. \exp \left[ -\frac{2 \Pi ^{2} x_{0}^{4} +2 q^{2}+\xi _{0}^{2}}{2 x_{0}^{2}}\right] \right] , \end{aligned}$$

(47)

$$\begin{aligned}&W_{11}(q,\Pi ) \nonumber \\&\quad = -\frac{1}{2 \sqrt{\hbar \pi } x_{0}^{8}}\nonumber \\&\quad \left[ \exp \left[ -\frac{2 \Pi ^{2} x_{0}^{4}+2 q^{2} +\xi _{0}^{2}}{2 x_{0}^{2}}\right] \right. \nonumber \\&\qquad \quad \left\{ x_{0}^{12} \alpha \Pi ^{6} +\frac{15 x_{0}^{10} \alpha \Pi ^{4}}{2}\right. \nonumber \\&\qquad +\left( \left( -5 \Pi ^{4} q^{2}-9 \Pi ^{2}\right) \alpha -2 \Pi ^{2}\right) x_{0}^{8}\nonumber \\&\qquad +\left( 1+\left( -3+\left( 15 q^{2} -\frac{9 \xi _{0}^{2}}{2}\right) \Pi ^{2}\right) \alpha \right) x_{0}^{6} \nonumber \\&\qquad +\left( \left( \left( -5 q^{2}+\frac{\xi _{0}^{4}}{8}\right) \Pi ^{2}+21 q^{2}+\frac{9 \xi _{0}^{2}}{4}\right) \alpha -2 q^{2}\right) \nonumber \\&\qquad x_{0}^{4}+q^{2} \alpha \left( q^{4}+\frac{\xi _{0}^{4}}{8}\right) \nonumber \\&\qquad \quad \left. \left. -\frac{25}{2} \alpha \left( q^{4}+\frac{9}{25} q^{2} \xi _{0}^{2} +\frac{1}{200} \xi _{0}^{4}\right) x_{0}^{2}\right\} \sqrt{2} \xi _{0}^{2}\right] , \end{aligned}$$

(48)

$$\begin{aligned}&W_{22}(q,\Pi ) \nonumber \\&\quad =-\frac{1}{8 \sqrt{\pi } x_{0}^{12}}\nonumber \\&\qquad \left[ \textrm{e}^{-\frac{2\Pi ^{2} x_{0}^{4} + 2 q ^ {2} + \xi _ {0} ^ {2}}{2 x _ {0} ^ {2}}} \left( x_{0}^{16} \alpha \Pi ^{8}+8 x_{0}^{14} \alpha \Pi ^{6}\right. \right. \nonumber \\&\qquad +\left( \left( -\frac{67}{2} \Pi ^{4}-4 \Pi ^{6} q^{2}\right) \alpha -2 \Pi ^{4}\right) x_{0}{}^{12}\nonumber \\&\qquad +\left( \left( \left( 44 q^{2}-6 \xi _{0}^{2}\right) \Pi ^{4}+9 \Pi ^{2}\right) \alpha +4 \Pi ^{2}\right) \nonumber \\&\qquad \times x_{0 }^{10}+\left( \left( \frac{15}{2} +\left( -10 q^{4}+\frac{\xi _{0}^{4}}{8}\right) \Pi ^{4}\right. \right. \nonumber \\&\qquad \quad \left. \left. +\left( -15 q^{2}+12 \xi _{0}^{2}\right) \Pi ^{2}\right) \alpha -4 \Pi ^{2}q^{2}-1\right) \nonumber \\&\qquad \times x_{0 }^{8} +\left( \left( \left( -12 q^{2} \xi _{0}^{2}+16 q^{4} -\frac{1}{4} \xi _{0}^{4}\right) \Pi ^{2}\right. \right. \nonumber \\&\qquad \quad \left. \left. -69 q^{2}-3 \xi _{0}^{2}\right) \alpha +4 q^{2}\right) x_{0 }^{6}\nonumber \\&\qquad +\left( \left( \frac{1}{4} q^{2} \xi _{0}^{4}-4 q^{6}\right) \Pi ^{2}\right. \nonumber \\&\qquad \left. \left. +\frac{157 q^{4}}{2}+\frac{\xi _{0}^{4}}{16} +12 q^{2} \xi _{0}^{2}\right) \alpha -2 q^{4}\right) x_{0}^{4}\nonumber \\&\qquad +\left( -20 q^{6}-6 q^{4} \xi _{0}^{2} -\frac{1}{4} q^{2} \xi _{0}^{4}\right) \alpha x_{0}^{2}\nonumber \\&\qquad \quad \left. \left. + q^{4} \alpha \left( q^{4}+\frac{\xi _{0}^{4}}{8}\right) \right) \sqrt{2} \sqrt{\frac{1}{\hbar }} \xi _{0}^{4}\right] . \end{aligned}$$

(49)

Appendix C Expression for probability distributions for harmonic oscillator with GUP

We define the classical probability density for unperturbed ($\beta =0$) HO as

$$\begin{aligned} P_{cl}(q) dq&=\dfrac{2 dt_{cl} }{T_{cl}} = \dfrac{\sqrt{m \omega ^{2}}}{\pi } \dfrac{1}{\sqrt{2 E^{(0)}_{n} - m \omega ^{2} q^{2}}}\nonumber \\&= \text {probability of finding the particle in the interval}\nonumber \\&\quad q\ \text {to}\ q+dq. \end{aligned}$$

(50)

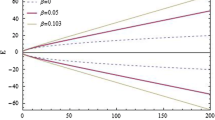
where $E^{(0)}_{n} = (n + 1/2) \hbar \omega \kappa$ & $T_{cl}=\dfrac{2 \pi }{\omega }$ is the time period of the SHO. Similarly, for the modified HO ($\beta \ne 0$), solving the Hamiltonian Eq. (26) we obtain

$$\begin{aligned} dt = \frac{2 \sqrt{2} m^{2} \beta }{\sqrt{m \beta \left( -1+\sqrt{1-16 \beta m^{2}\left( m \omega ^{2} q^{2}-2 E_{n}\right) }\right) }} \, dq. \end{aligned}$$

(51)

Now the modified classical probability density (for $\beta \ne 0$) for the Hamiltonian Eq. (26) is

$$\begin{aligned}&P_{cl-modified}(q) dq \nonumber \\&\quad =\dfrac{2 dt }{T_{cl-modified}}\nonumber \\&\quad = -\frac{4 \sqrt{2} m^{2} \beta \omega }{\sqrt{m \beta \left( -1+\sqrt{1-16 \beta m^{2} \left( m \omega ^{2} q^{2}-2 E_{n}\right) }\right) } \pi \left( 3 \alpha \xi _{0}^{2}-2\right) } \end{aligned}$$

(52)

where the modified time period is given as [26] $T_{cl-modified} = \dfrac{2 \pi }{\omega } \left( 1 - \dfrac{3 \alpha }{2} \xi _{0}^{2} \right)$ and $E_{n} = (n + 1/2) \hbar \omega \kappa + \dfrac{\alpha }{4} (6 n^{2} + 6 n +2) \hbar \kappa \omega$.

The expression for the quantum probability distribution can be calculated by integrating the Wigner functions Eqs. (47), (48), (49) using the Eq. (42) and it can be expressed, for ground state, first excited state, and second excited state respectively as

$$\begin{aligned} |\chi _{0}(q)|^{2}&=\frac{\sqrt{2} \textrm{e}^{-\frac{\left( 2 q^{2} +\xi _{0}^{2}\right) }{2 x_{0}^{2}}} |\left( \frac{15 x_{0}^{4}}{4} +\left( -9 q^{2}-3 \xi _{0}^{2}\right) x_{0}^{2} +q^{4}+\frac{\xi _{0}^{4}}{8}\right) \alpha -2 x_{0}^{4} |\sqrt{\frac{1}{\hbar }}}{2 x_{0}^{5}}, \end{aligned}$$

(53)

$$\begin{aligned} |\chi _{1}(q)|^{2}&= \frac{\sqrt{2} |\left( \frac{99 x_{0}^{4}}{4}+\left( -15 q^{2} -\frac{9 \xi _{0}^{2}}{2}\right) x_{0}^{2}+ q^{4} +\frac{\xi _{0}^{4}}{8}\right) \alpha -2 x_{0}^{4}|e^{-\frac{9\left( 2 q^{2}+\xi _{0}^{2}\right) }{2 x_{0}^{2}}}}{2 \sqrt{\hbar } x_{0}{ }^{9}} q^{2}|\xi _{0}|^{2}, \end{aligned}$$

(54)

$$\begin{aligned} |\chi _{2}(q)|^{2}&= \frac{1}{256 x_{0}^{13}}\nonumber \\&\quad \left[ \sqrt{2} \textrm{e}^{-\frac{\left( 2 q^{2} +\xi _{0}^{2}\right) }{2 x_{0}^{2}}} \xi _{0}^{4}\right. \nonumber \\&\qquad \sqrt{\frac{1}{\hbar }} \mid \left( 16 \alpha q^{6} -344 \alpha q^{4} x_{0}^{2} +1092 \alpha x_{0}^{4} q^{2}\right. \nonumber \\&\qquad -96 \alpha \xi _{0}^{2} q^{2} x_{0}^{2} +2 \alpha \xi _{0}^{4} q^{2}-270 \alpha x_{0}^{6}\nonumber \\&\qquad \left. +48 \alpha \xi _{0}^{2} x_{0}^{4}-\xi _{0}^{4} \alpha x_{0}^{2}-32 q^{2} x_{0}^{4}+16 x_{0}^{6}\right) \nonumber \\&\qquad \quad \left. \left( 2 q^{2} -x_{0}^{2}\right) \mid \right] . \end{aligned}$$

(55)

Appendix D Expression for $\xi _{0}$-free modified Wigner function $W(q,\Pi )$

By employing the methodologies delineated in “Appendix 1” and utilizing Eqs. (34) and (35), it is feasible to compute the $\xi _{0}$ parameter-free Wigner functions $W(q,\Pi )$ for the ground state, first excited state, and second excited state. The Wigner function for the ground state, 1st excited state, and 2nd excited state are given by:

$$\begin{aligned}&W_{00}(q,\Pi ) \nonumber \\&\quad = - \frac{1}{2 \sqrt{\hbar \pi } x_0{ }^4}\nonumber \\&\qquad \left[ \textrm{e}^{\frac{-\Pi ^2 x_0{ }^4-q^2}{x_0{ }^2}} \sqrt{2}\right. \nonumber \\&\quad \quad \left( x_0{ }^8 \alpha \Pi ^4+6 x_0{ }^6 \alpha \Pi ^2 +\left( -6 \alpha \Pi ^2 q^2-2\right) x_0{ }^4 \right. \nonumber \\&\quad \quad \left. \left. -6 \alpha q^2 x_0{ }^2+\alpha q^4\right) \right] , \end{aligned}$$

(56)

$$\begin{aligned}&W_{11}(q,\Pi ) \nonumber \\&\quad = -\frac{1}{2 \sqrt{\pi \hbar } x_0^6}\nonumber \\&\quad \left[ \sqrt{2}\left\{ 2 x_0^{12} \alpha \Pi ^6 -10 x_0^8 \alpha q^2 \Pi ^4\right. \right. \nonumber \\&\quad \quad +15 x_0^{10} \alpha \Pi ^4-10 \alpha q^4 \Pi ^2 x_0^4 +30 \alpha q^2 \Pi ^2 x_0^6-30 x_0^8 \alpha \Pi ^2\nonumber \\&\quad \quad -4 x_0^8 \Pi ^2+2 \alpha q^6-25 \alpha q^4 x_0^2 +30 \alpha q^2 x_0^4 \nonumber \\&\quad \quad \left. \left. -4 q^2 x_0^4+2 x_0^6\right\} \textrm{e}^{- (\Pi ^{2} x_{0}^{4} + q^2)/x_{0}^2} \right] , \end{aligned}$$

(57)

$$\begin{aligned}&W_{22}(q,\Pi ) \nonumber \\&\quad = - \frac{\sqrt{2}}{\sqrt{\hbar \pi } x_{0}^8} \nonumber \\&\qquad \left[ e^{-(\Pi ^{2} x_{0}^4 + q^2)/x_{0}^{2}}\right. \nonumber \\&\qquad \left\{ x_0^{16} \alpha \Pi ^8+8 x_0^{14} \alpha \Pi ^6 +\left( \left( -4 \Pi ^6 q^2-\frac{97}{2} \Pi ^4\right) \alpha -2 \Pi ^4\right) x_0^{12} \right. \nonumber \\&\qquad +\left( \left( 44 \Pi ^4 q^2+39 \Pi ^2\right) \alpha +4 \Pi ^2\right) x_0^{10}\nonumber \\&\quad \quad +\left( \left( -10 \Pi ^4 q^4 -45 \Pi ^2 q^2\right) \alpha -4 \Pi ^2 q^2-1\right) x_0^8\nonumber \\&\quad \quad +\left( \left( 16 \Pi ^2 q^4-39 q^2\right) \alpha +4 q^2\right) x_0^6 \nonumber \\&\quad \quad + ((- 4 \Pi ^2 q^6 + \frac{127}{2} q^4) \alpha - 2 q^4) x_{0}^{4} \nonumber \\&\quad \quad \left. \left. - 20 \alpha q^6 x_{0}^2 + \alpha q^8 \right\} \right] . \end{aligned}$$

(58)

Notice that Wigner functions $W(q,\Pi )$ for $\alpha = 0$ is same as in the Ref. [39].