1 Introduction

Inorganic phosphors are among the most effective materials currently available for use in lighting applications [1, 2]. Additionally, rare-earth (RE)-doped phosphors have been extensively studied and utilized in the realm of thermoluminescence dosimetry (TLD) [3, 4]. This technique entails measuring the amount of light emitted from a material when it is subjected to heat, which can be employed to determine the amount of radiation to which the material has been exposed. The dopants serve to enhance the thermoluminescence properties of the materials by virtue of the unique electronic structure of rare-earth ions, which facilitates efficient energy transfer and luminescence in the phosphors. The dopants create defect energy levels in the host matrix, which function as trap/recombination centers. Thus, TL can be employed as a characteristic of a specific host and dopant combination [5]. The TL glow curve analysis is widely utilized as a research tool for elucidating complex details about defect states and properties. By meticulously examining the shape, height, and peak of the glow curves, valuable information pertaining to trap energy, lifetime, and electron density can be extracted, among other parameters [6]. Consequently, RE-doped phosphors offer several advantages over other materials employed in thermoluminescence dosimetry, including their high sensitivity and stability, and their capacity to detect both ionizing [7] and non-ionizing radiation [8]. They have been employed in a broad spectrum of applications, encompassing medical dosimetry [9], environmental monitoring [10], and radiation protection [11].

The phosphors are categorized based on their chemical composition into nitrides [12], phosphates [13], sulfates [14], silicates [15], oxides [16], and aluminosilicates [17]. The selection of the phosphor matrix and dopants is dependent on the specific requirements. Aluminates are being considered for their potential application in LEDs and dosimeters due to their exceptional thermal and chemical stability, long afterglow, high quantum efficiency, and tunable emission properties [18,19,20]. These materials also have applications in various fields, including lamps [21], TLDs [22, 23], scintillators [24, 25], field emission, and plasma display panels [26].

BaMgAl10O17 (BAM) is a widely studied commercial phosphor due to its exceptional luminescence properties [27]. Several methods have been employed to synthesize BAM, including combustion synthesis [28], microwave-assisted heating [29], radio-frequency sputtering [30], co-precipitation [31], solid-state reaction [32, 33], and spray pyrolysis [27]. Furthermore, studies have been carried out to investigate the TL properties of UV-irradiated BAM: Eu [34,35,36], optical properties of BAM: Cr [37,38,39], and BAM: Ce, Tb [40].

Thus, we have chosen cerium as dopant since it is an excellent candidate for radiation detection applications [41, 42]. Although some studies have reported on the TL features of BAM: Ce [40, 43], there is a lack of theoretical understanding of the TL mechanism and trap origin. Previous published TL parameter studies [36, 44, 45] have provided numerical values and fitted results without exploring the possible origins of the trapping sites responsible for TL.

To address these gaps in the literature, this paper presents a detailed theory and mechanism of TL, interpretation of defect levels, and structural and morphological characteristics. Moreover, we have calculated trap energy values using five different approaches, including computerized glow curve deconvolution (CGCD), Chen’s shape method, Halperin and Braner method with Chen’s correction (HB&C), Lushchik, and Balarin’s method. These approaches will help to obtain more accurate results and provide a more comprehensive understanding of the TL properties of BAM: Ce phosphors.

2 Experimental details

2.1 Synthesis

The BaMgAl10O17:Ce3+ phosphor was prepared using the combustion method. Initial materials are taken in the nitrate form, and fuel is added to enhance the combustion. The metal nitrates taken are Ba(NO3)2, Mg(NO3)2·6H2O, Al(NO3)3·9H2O, Ce(NO3)3·4H2O, and urea (NH2CONH2) is used as a fuel. The compositions are mixed according to the stoichiometric ratio. The stoichiometric compositions are calculated using the basic rules of propellant chemistry. All reagents are combined and crushed in an agate mortar for 30 min. The resulting product was transferred to a crucible and heated in a furnace at 600 °C. This will form a white foamy product that is ground into fine powder. The powder obtained after grinding is used for characterizations. The sample notation is given in Table 1.

Table 1 Sample notation
Full size table

2.2 Characterization

X-ray diffraction (XRD) investigations are conducted to establish the polycrystalline structure and phase composition of the samples. XRD measurement was performed using Rigaku Miniflex 600 (5th gen) with K-α (λ = 1.54 Å) radiation (40 kV, 15 mA). The scanning angle was varied from 10° to 70° at a rate of 2°/min. The morphological properties and elemental composition of the samples were determined using scanning electron microscopy (SEM) and energy-dispersive X-ray spectroscopy (EDS), which were performed using a sigma Zeiss instrument. The luminescence properties were recorded using the JASCO-FP 8500 spectrofluorometer. Phosphor powders were subjected to gamma irradiation using the Gamma Chamber-5000, with 60Co γ radiation doses ranging from 5 Gy to 10 kGy. The TL spectra were acquired for 10 mg of phosphor samples using the TLD reader 1009I Nucleonix India, with heating carried out at a constant rate. The TL glow curves were deconvoluted, and the kinetic parameters were calculated. The trap energy was elucidated using additional graphical methods.

3 Result and discussion

3.1 Phase analysis

XRD analysis is a non-destructive method that employs diffraction phenomena to confirm the crystal structure of a substance. The XRD pattern of BAM-2 Ce phosphor matches JCPDS CARD 26-0163 (Fig. 1), thus confirming the hexagonal arrangement [38]. The phosphor crystallizes into β alumina structure with P63/mmc space group (Fig. 2). The unit cell of the BAM-2 Ce phosphor comprises closely packed oxygen spinel blocks, with BaO mirror planes present in-between. The Al ions coexist in tetrahedral and octahedral sites along the spinel network, with four Al sites present in the unit cell, two of which are tetrahedral and two are octahedral [33]. The Mg may occupy any one of the four sites, but the unit cell is more stable when Mg substitutes in the tetrahedral sites [46]. The dopant occupies one of the Ba sites in the mirror plane due to the similarity of ionic radii [27] (with Ba2+ ionic radius = 0.143 nm and Ce3+ ionic radius = 0.114 nm).

Fig. 1
figure 1

XRD pattern of BAM- 2 Ce phosphors

Full size image
Fig. 2
figure 2

Crystal structure of BAM-Ce hexagonal unit cell

Full size image

3.2 FTIR studies

The investigation of molecular vibrations utilizes FTIR spectroscopy. The presence of functional groups is determined by analyzing the FTIR transmission spectra (Fig. 3) [47]. The O–H stretching peak is observed at 3610 cm−1, while the Mg–O and Ba–O peaks correspond to 1508 and 1366 cm−1 vibrations, respectively [28]. The BAM-Ce phosphor possesses a β-alumina structure comprising AlO6 octahedral and AlO4 tetrahedral structures, resulting in two Al3+ sites. Consequently, distinct bands are observed corresponding to these sites [48]. The AlO6 absorption peak is observed at 1003, 522, and 770 cm−1, while the AlO4 absorption results in a band at 770 cm−1 [49, 50]. These findings are consistent with the X-ray diffraction (XRD) data and the spinel structure of the unit cell. The band assignment is given in Table 2.

Fig. 3
figure 3

FTIR spectrum of BAM-2 Ce phosphor

Full size image
Table 2 FTIR peak assignment
Full size table

3.3 Morphological study and elemental analysis

The morphological characteristics of the BAM-2 Ce phosphor were examined utilizing scanning electron microscopy (SEM). The SEM images depict rod-shaped grains (as illustrated in Fig. 4a). A magnified view of the grains (as shown in Fig. 4b) reveals interconnected crystallites exhibiting high agglomeration. Furthermore, the presence of pores on the surface of the BAM-2 Ce phosphor may be attributed to the escape of gases during the combustion synthesis process [51].

Fig. 4
figure 4

SEM image of a) BAM- 2 Ce, b) enlarged image

Full size image

The analysis of the elements in the prepared BAM-2 Ce phosphors was carried out using EDS, as shown in Fig. 5. The results confirmed the formation of BAM: Ce phosphor, as the presence of Ba, Mg, Al, Si, O, and Ce peaks was observed [52].

Fig. 5
figure 5

EDS spectra of BAM- 2 Ce

Full size image

3.4 Photoluminescence (PL) studies

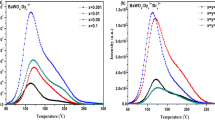
BAM-Ce phosphors exhibit a characteristic blue emission upon exposure to suitable radiation. PL excitation spectrum was recorded by maintaining the emission at 420 nm (see Fig. 6). The PL excitation plot indicates two peaks at 273 and 330 nm. The peak at 330 nm is chosen as the excitation wavelength for the emission spectra (see Fig. 7). The intensity of the emission increases with an increase in Ce3+ concentration up to 2 mol%. However, beyond 2 mol% Ce3+, the intensity drops, indicating concentration quenching. As a result, 2 mol% Ce3+ is determined to be the optimum concentration, and the same samples are used for thermoluminescence studies.

Fig. 6
figure 6

Excitation spectrum of BAM- 2 Ce

Full size image
Fig. 7
figure 7

Emission spectra of BAM- Ce

Full size image

The capability of the dopant ions to transfer energy from one another is truly remarkable, resulting in a phenomenon referred to as quenching. Several distinct interaction mechanisms contribute to the reduction in intensity. The critical radius separating Ce3+ ions within the BAM host matrix serves as a crucial parameter for elucidating the nature of these interactions [53] (Eq. 1).

$${\text{Rc}} = 2\left. {\left( {\frac{3V}{{4\pi X_{{\text{c}}} N}}} \right.} \right)^{1/3}$$
(1)

The unit cell volume V = 620.995 (Å)3, N = 2, and Xc = 0.02 [38], Rc = 30.95 Å (> 5 Å).

If the distance between activator ions is greater than 5 Å, energy transfer occurs due to multipolar exchange. There are various types of multipolar interactions, such as dipole–dipole, dipole–quadrupole, and quadrupole–quadrupole. The corresponding multipolar interaction in BAM-Ce phosphors can be determined using Dexter’s theory [54, 55]. The emission intensity of the phosphor depends solely on the concentration of the dopant ions (Eq. 2). By taking the logarithm and simplifying, a straight-line equation can be obtained, where the y-axis represents \({\text{log}}\frac{I}{x}\), the x-axis represents\({\text{log}}x\), and the slope is \(-\frac{\theta }{3}\) (Eq. 3). The value of θ determines the type of multipolar interaction. For θ = 6, 8, and 10, the reactions are dipole–dipole, dipole–quadrupole, and quadrupole–quadrupole, respectively [56, 57]. The slope of log(I/x) versus log(x) is plotted in Fig. 8, and the slope is − 1.57655. Since θ = 4.73 ~ 6, the dipole–dipole interaction is responsible for energy transfer [38].

$$\frac{I}{x} = k\left[ {1 + \beta x^{{\frac{\theta }{3}}} } \right]^{ - 1}$$
(2)
$$\log \frac{I}{x} = c - \frac{\theta }{3}\log x$$
(3)
Fig. 8
figure 8

log(I/x) versus log(x) of BAM- Ce

Full size image

3.5 Thermoluminescence (TL)

The BAM-2 Ce phosphor samples, with a weight of 10 mg each, were subjected to gamma radiation ranging from 5 to 10 kGy. The irradiated samples were then heated at a rate of 2.85 °K/S, and the number of counts per second was recorded. The plot of emission intensity for each dose value, as a function of temperature, is given in Fig. 9. The TL intensity rises with an increased absorbed dose. The glow curve peaks around 425 K. According to the one trap one recombination (OTOR) model, defect levels in the phosphor act as traps or recombination centers. When gamma rays with high energy levels strike the phosphor sample, electron–hole pairs are produced in the valence band, and the electrons become trapped in these defect states. The trapped electrons acquire sufficient energy upon heating to overcome the traps and combine with the hole at the recombination center. This results in the production of light, the intensity of which is directly proportional to the incident radiation. Consequently, as the incident dose increases, the TL glow peak should become more intense (Fig. 9). The mechanism by which BAM-2 Ce phosphors emit light can be attributed to the presence of defect energy states in the vicinity of the conduction band, which function as electron traps. The spinel network of BAM-2 Ce consists of Al3+ and Mg2+ ions occupying both tetrahedral and octahedral sites (as illustrated in Fig. 2). The formation of antisite defects is possible when divalent or trivalent cations occupy tetrahedral or octahedral sites, leading to the exchange of cation positions. Antisite formation is a point defect and results in the creation of numerous trapping centers within the crystal lattice.

Fig. 9
figure 9

TL glow curves of BAM- 2 Ce irradiated with different γ-doses

Full size image

Irradiation causes changes in the charge states of defect centers and impurities, resulting in the formation of a large number of trap centers, two of which are most likely to exist. The F+ center is formed when an electron becomes trapped in an oxygen vacancy after irradiation. In this case, oxygen acts as the anion, and the electrons are trapped in the oxygen vacancies. O− ions, another predominant trap, are formed when a hole localizes on the O2− ion, leading to an unstable situation that is stabilized via electrostatic interaction with an adjacent cationic vacancy (Ba2+/Mg2+/Al3+) [58, 59]. Upon irradiation, the BAM-2 Ce phosphor may exhibit trapping of electrons in the F+ center, which can only escape the trap level by applying heat. The trapped electrons recombine with holes and emit light upon heat treatment. The existence of F+ centers and O− ions has been experimentally confirmed using electron spin resonance (ESR) studies in SrMgAl10O17: Sm3+ and Eu2+ phosphors by Singh et al. [60, 61].

3.5.1 Optimum range of operation

The dosimeter material has an optimum working region where the integrated TL intensity depends linearly on the incident γ dose. For BAM-2, Ce phosphors, Fig. 9 inset shows a linear trend from 5 to 250 Gy doses. Hence, the prepared phosphor could be used as dosimeters in this range.

3.5.2 Sensitivity and minimum detectable dose (MDD)

The sensitivity of BAM-2 Ce is the slope of TL response versus the dose graph (Fig. 10), and the value is 9.85 × 107 counts/g/kGy. High sensitivity is preferred for dosimetry applications. The threshold value of the dose that can be detected using the prepared phosphor is calculated using Eq. (4),

$${\text{MDD}} = \frac{{3\sigma_{{\text{b}}} }}{{{\text{Sensitivity}}}}$$
(4)

\({\sigma }_{{\text{b}}}\)—the standard deviation of TL reading for 6 unirradiated phosphor samples [3] And MDD = 21.8 μGy.

Fig. 10
figure 10

TL response of BAM- 2 Ce

Full size image

3.5.3 Kinetic parameters

The presence of defects, such as dopant addition or structural defects, in BAM-2 Ce phosphors creates electron traps. Several types of defects may serve as potential traps, including oxygen vacancies in the spinel structure, point defects resulting from charge compensation, and symmetry changes caused by the substitution of Mg for Al ions. And the traps can be characterized by the parameters such as trap energy (E): the energy required to escape from the trap, lifetime (τ): the time duration of trapping, the escape factor (s): determines how often the trapped electron hits the trap wall considering it as potential well, and the order of kinetics followed by each trap (b): the possibility of recombination (b = 1) or re-trapping (b = 2). Various methods can be used to estimate the traps and trap parameters, including computerized glow curve deconvolution (CGCD), Chen’s shape method, Halperin and Braner method with Chen’s correction (HB&C), Lushchik, and Balarin’s method for elucidating trap parameters.

3.5.4 CGCD method

In the CGCD method, the TL glow curves are fitted using Kiti’s general order relation (Eq. 5), and the deconvolution of peaks would give peak parameters [62].

$$I\left( T \right) = I_{{\text{m}}} b^{{\left( {\frac{b}{b - 1}} \right)}} \exp \left( {\frac{E}{{k_{{\text{B}}} T}}\frac{{T - T_{{\text{m}}} }}{{T_{{m{\text{m}}}} }}} \right)\left[ {\left( {b - 1} \right)\left( {1 - \frac{{2k_{{\text{B}}} T}}{E}} \right)\frac{{T^{2} }}{{T_{{\text{m}}}^{2} }}\exp \left( {\frac{E}{{k_{{\text{B}}} T}}\frac{{T - T_{{\text{m}}} }}{{T_{{\text{m}}} }}} \right) + 1\left( {b - 1} \right)\frac{{2k_{{\text{B}}} T}}{E}} \right]^{{ - \left( {\frac{b}{b - 1}} \right)}}$$
(5)

where b is the order of kinetics, Im is the highest TL intensity, and E is the trap activation energy. The accuracy of the fit is given using the figure of merit (FOM). The values are acceptable if FOM is less than 5% [63]. The τ and s are calculated using Eqs. (6) and (7)

$$\tau = \frac{{s^{ - 1} e^{{\frac{E}{{Tk_{{\text{B}}} }}}} }}{2 - b}$$
(6)
$$s = \frac{\beta E}{{k_{{\text{B}}} T_{{\text{m}}}^{{2 \left( {1 + \left( {b - 1} \right)\frac{{2k_{{\text{B}}} T_{{\text{m}}} }}{E}} \right) }} }} \exp \left( {\frac{E}{{k_{{\text{B}}} T_{{\text{m}}} }}} \right)$$
(7)

where β = heating rate, T = storage temperature, and b = order of kinetics.

The deconvolution and trap parameter calculations are given in Fig. 11 and Table 3, respectively.

Fig. 11
figure 11

Deconvoluted TL curves of BAM- 2 Ce

Full size image
Table 3 Trap characteristics of BAM- 2 Ce using CGCD method
Full size table

Each TL glow curve possesses four traps, which correspond to four deconvoluted peaks. These traps exhibit a gradual progression from shallower peaks at the lower temperature end to deeper peaks at the higher temperature side. The trap activation energy follows an increasing trend with an increase in gamma dose. Also, the lifetime of the traps increases with the rise in gamma dose. The temperature corresponding to maximum height is 450–466 K; hence, this phosphor has deeper traps and could be used as a γ dosimeter. The deeper traps have a longer lifetime, showing less fading [64].

3.5.5 Graphical methods

3.5.5.1 Chen’s method

Chen’s peak shape method is one of the famous techniques for trap parameter evaluation [65] (Eqs. 8–10)

$$\omega = T_{2 } - T_{1}$$
(8)
$$\tau = T_{{\text{m }}} - T_{1}$$
(9)
$$\delta = T_{2 } - T_{{\text{m}}}$$
(10)

where Tm is the peak temperature with the highest intensity, and T1 and T2 are the temperatures at a half-width intensity to the lower and higher temperature side of Tm [66, 67]. The order of kinetics is determined using μg [68].

$$\mu_{{\text{g}}} = \frac{\delta }{\omega }$$
(11)

First-order kinetics—μg ~ 0.42, Second-order kinetics—μg ~ 0.52.

The phosphor powders exhibit emission when the trapped electrons are released by supplying external energy (heat). This is called activation energy (Eα) and is calculated using equations below [69,70,71]

$$C_{\tau } = 1.51 + 3 \left( {\mu_{{\text{g }}} - 0.42} \right);\; b_{\tau } = 1.58 + 4.2 \left( {\mu_{{\text{g}}} - 0.42} \right)$$
(12)
$$C_{\delta } = 0.976 + 7.3 \left( {\mu_{{\text{g }}} - 0.42} \right);\; b_{\delta } = 0$$
(13)
$$C_{\omega } = 2.52 + 10.2 \left( {\mu_{{\text{g }}} - 0.42} \right);\; b_{\omega } = 1$$
(14)
$$E_{\alpha } = C_{\alpha } \frac{{k_{{\text{B}}} T_{{\text{m}}}^{2} }}{\alpha } - b_{\alpha } \left( {2k_{{\text{B}}} T_{{\text{m}}} } \right)$$
(15)

where α = τ, δ, ω. Energy E is the average of Eδ, Eω, and Eτ. Kinetic parameters are estimated using Chen’s peak shape method and are tabulated in Table 4.

Table 4 Trap parameters of BAM- 2 Ce by Chen’s method
Full size table
3.5.5.2 HB&C method

Halperin and Branner used a different approach for activation energy calculation. As per their method, there may be two types of recombination leading to light emission. The electron may excite to an energy level below the conduction band and recombines with the hole via tunneling. Also, there is a possibility that the recombination takes place from the CB. In the first approach, the energy value is [72].

$$E = H_{1} \frac{{k T_{{\text{m}}}^{2} }}{\delta }$$
(16)

And for the second one,

$$E = \frac{{H_{2} kT_{{\text{m}}}^{2} }}{\delta } \left( {1 - \Delta_{{\text{M }}} } \right)$$
(17)

where \({\Delta }_{{\text{m}}}= \frac{{2 k T}_{{\text{m}}}}{E}\)

This can only be solved using an iterative method. Hence, Chen introduced a new approximation to solve trap energy without cumbersome iteration. Thus, the following equations with Chen’s correction give the energy for first- and second-order kinetics, respectively [73].

$$E = { }1.52\frac{{kT_{{\text{m}}}^{2} }}{\tau } - 3.16\;kT_{{\text{M}}}$$
(18)
$$E = 1.813\frac{{kT_{{\text{m}}}^{2} }}{\tau } - 4\;kT_{{\text{M}}}$$
(19)
3.5.5.3 Lushchik method

Lushchik approximated the higher-temperature tail of the glow curve as a triangle. Using the δ value, he gave the expressions for first- and second-order kinetics, respectively, as given below [72].

$$E = \frac{{kT_{{\text{m}}}^{2} }}{\delta }$$
(20)
$$E = \frac{{2kT_{{\text{m}}}^{2} }}{\delta }$$
(21)
3.5.5.4 Balarin’s method

Balarin’s approximation uses the half width (ω) of the TL glow peak for the trap energy calculation. Balarin proposed this method by assuming that the trap energy is related to the FWHM of the glow peak [74]. Using Eqs. (22) and (23), the energy value is calculated.

$$E = \frac{{T_{{\text{m}}}^{2} }}{\omega . 4998}$$
(22)
$$E = \frac{{T_{{\text{m}}}^{2} }}{\omega . 3542}$$
(23)

Table 5 compares trap energy values obtained by all the methods for 250 Gy gamma-irradiated BAM-2 Ce phosphors.

Table 5 Trap energies of BAM-2 Ce phosphors using different methods
Full size table

The results obtained from four distinct methods for calculating trap energies indicate a consistent increase in trap energies as peak temperature increases. This finding lends credence to the notion that peak temperature is correlated with trap energy. Therefore, the creation of deeper traps at higher temperatures is supported, while the formation of shallower traps with lesser energy is attributed to lower temperatures. These conclusions are consistent with the results obtained through the CGCD method.

4 Conclusions

Ce3+-doped BaMgAl10O17 phosphors were synthesized using the combustion technique. The prepared samples exhibit a hexagonal crystal structure. FTIR spectra confirmed the presence of AlO4 and AlO6 vibrations which is consistent with the spinel structure of the phosphors. The SEM images demonstrated an interconnected morphology of rod-shaped features with surface pores. Upon excitation at 338 nm, the phosphors exhibited a broad blue emission at 420 nm. Additionally, it was observed that concentration quenching occurred at Ce3+ concentrations greater than 2 mol%. The TL glow curve of BAM-2 Ce phosphors exhibited a rise in luminescence intensity as the gamma dose increased. Moreover, a linear relationship was observed between the dosage and the TL intensity within the range of 5–250 Gy. Consequently, these phosphors can be utilized as dosimeters within this range. The samples exhibited high sensitivity and low MDD value. Four trap centers were confirmed in BAM-2 Ce samples, and the trap energies calculated using five different methods were consistent with one another. The results of the trap analysis demonstrate that as the dose is increased, electrons become trapped in deeper traps with a longer lifetime. Thus, the prepared phosphors are potential candidates as gamma dosimeters.