Influence of Annealing Temperature on the Structural and Luminescence Features and Thermoluminescence Trap Parameters of Ca₂Al₂SiO₇: Ce³⁺ Phosphors

Abstract

Cerium-doped Ca₂Al₂SiO₇ phosphors were synthesized via the combustion technique and annealed at 1073 K, 1173 K, and 1373 K. X-ray diffraction (XRD), Fourier-transform infrared spectroscopy (FTIR), scanning electron microscopy (SEM), photoluminescence (PL), and thermoluminescence (TL) studies were performed to explore the variation of structural, morphological, luminescence, and TL properties with annealing temperature. The XRD plot showed an increase in crystallinity with an increase in annealing temperature. Similarly, the enhancement of PL intensity with an increase in annealing temperature supports the increased crystallinity of the phosphor samples. Detailed analysis of traps and trap parameters was carried out using the principle of TL. Samples were irradiated with different γ-ray doses, and, on heating, luminescence was observed. Thus, TL glow curves were drawn and deconvoluted using computerized glow curve deconvolution (CGCD) and Chen’s peak shape method to study the traps and trap parameters. With increasing annealing temperature, an increase in TL intensity was observed. Regardless of annealing temperature, every sample displayed a linear dose–response for doses ranging from 3 Gy to 500 Gy. TL investigations suggested that the produced phosphors are suitable candidates for gamma dosimetry applications.

Introduction

The luminescent phosphors are inorganic insulators where a dopant is used as an activator. The host matrix can be modified based on the application by adding dopant ions, usually transition metals or rare-earth ions.¹ The dopant shows a characteristic emission peak and luminescence properties when incident with a suitable excitation wavelength. Persistent luminescence (PeLu) is the long-lasting emission even after removing the excitation source.² The PeLu is used in the field of radiation detection³ and sensors to identify structural damage or materials fracture.^4,5 The suitability of inorganic phosphors in the field of dosimetry can be determined by studying the defect energy levels (traps) and trap parameters. Thermoluminescence (TL) studies are of high interest as they help to analyze the defects in the crystal lattice. There are two types of defects in the host crystal: (1) naturally existing defects, such as negative ion vacancy, and (2) defects created by adding dopants, such as the formation of cationic vacancies to maintain charge neutrality when trivalent impurities replace divalent cations.⁶ The thermal treatment-induced light emission from an inorganic insulator due to the recombination of radiation-induced holes or electrons is a highly recommended technique for defect energy state exploration.^7,8 The emitted light intensity is plotted as a function of temperature and is called the TL glow curve. The shape, area, position, and height of the glow curves give information about the traps and trap parameters, such as trap energy, trap lifetime, carrier density, etc. They can also be used to measure the absorbed radiation and the number of traps. In general, TL can be explained using the one trap one recombination (OTOR) model, where the electrons get trapped in trap centers between the forbidden energy gaps upon irradiation. The thermal treatment releases the trapped electrons, and they move through the conduction band. The recombination occurs at recombination centers where the electron and holes recombine, leading to luminescence. The OTOR model assumes that the electrons are only trapped once before reaching the recombination centers. This need not be true in the actual case. Thus, the order of kinetics is another important trap feature indicating the order of trapping of charge carriers.^6,9

Melilite crystals have been extensively studied because of their PeLu characteristics.^{10,11,12,13,14,15} Among them, Ca₂Al₂SiO₇ phosphors are suitable candidates for studying the effect of dopants, defect energy levels, trap lifetimes, etc. Many studies have reported the photoluminescence (PL) and TL properties of a Ca₂Al₂SiO₇ host with different dopants. There are reports on the luminescence properties of Ca₂Al₂SiO₇: Sm³⁺,¹⁶ Ca₂Al₂SiO₇: Eu²⁺,^17,18,19 Ca₂Al₂SiO₇: Eu³⁺,^20,21 Ca₂Al₂SiO₇: Ce³⁺, Sm³⁺, Tb³⁺,²² Ca₂Al₂SiO₇: Tm³⁺ , Dy³⁺,²³ Ca₂Al₂SiO₇: Bi³⁺, Eu³⁺, Tb³⁺,²⁴ Ca₂Al₂SiO₇: Ce³⁺,^11,25 and Ca₂Al₂SiO₇: Ce³⁺, Tb³⁺,²⁶ the TL properties of Ca₂Al₂SiO₇: Ce³⁺,^27,28 Ca₂Al₂SiO₇: Ce³⁺, Tb³⁺,²⁹ Ca₂Al₂SiO₇: Dy³⁺,³⁰ Ca₂Al₂SiO₇: Ce³⁺, Eu²⁺,³¹ and Ca₂Al₂SiO₇: Eu³⁺,³² and the scintillation applications of Ca₂Al₂SiO₇: Pr³⁺,³³ and Ca₂Al₂SiO₇: Ce³⁺.³⁴ However, no studies have been reported examining the impact of annealing temperature (AT) on the structural, morphological, luminescence, and TL features of Ca₂Al₂SiO₇: Ce³⁺ phosphors. Thus, this study investigates the effect of heat treatment on the structural, luminescence, and TL features of Ca₂Al₂SiO₇: Ce³⁺ phosphors prepared using the combustion synthesis technique.

Experimental

The combustion method was used to prepare the Ca₂Al₂SiO₇: Ce³⁺ samples. Analytical research-grade chemicals Al (NO₃)₃.9H₂O, Ce (NO₃)₃.6H₂O, NH₂CONH_2, Ca (NO₃)₂, and SiO₂ were weighed according to stoichiometry and thoroughly mixed. The mixture was transferred to a muffle furnace and heated at 873 K. The fluffy material, after combustion, was milled into a fine powder and annealed at 1073 K, 1173 K, and 1373 K for 4 h. The obtained white powder was further ground and used to perform different characterizations, which were repeated three times to ensure consistency and repeatability.

X-ray diffraction (XRD) analysis was performed with a Rigaku Miniflex 600 (5th gen) using K-α (λ 1.54 Å) radiation (40 kV, 15 mA) with a scanning angle of 10–80° at 2°/min. PL studies were carried out using a Jasco Spectrofluorometer FP-8500, and a Shimadzu FTIR spectrometer (IRSpirit) was used to perform Fourier-transform infrared spectroscopy (FTIR). The morphological features and elemental composition were analyzed using a Sigma Zeiss instrument, and TL studies were carried out using a TLD reader 1009I (Nucleonix, India) for pre-irradiated samples (from 3 Gy to 5 kGy) with a ⁶⁰Co γ dose. The samples, weighing 0.15 g, were irradiated, and the TL properties were analyzed by heating them at 2.85 K/s from 310 K to 620 K at a fixed bias voltage (600 V). Three batches of samples (annealed at 1073 K, 1173 K, and 1373 K) with five samples in each batch (with = 0.5, 0.75, 1, 1.5, and 2 mol.% Ce³⁺ concentration) were prepared. The sample notation is given in Table I.

Table I Sample notation

Results and Discussion

XRD Analysis

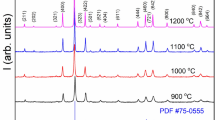
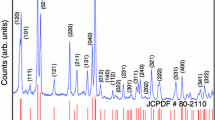
Figure 1 shows the XRD patterns of the C1, C2, and C3 samples, which were crystallized into a tetragonal phase with space group P-421 m. The XRD peaks of all the phosphors showed a similar XRD pattern as per the reference JCPDS file, and there was no change in the crystal structure with a change in AT (see online supplementary material Figure S-1). Also, there were no extra phases with increasing the Ce³⁺ concentration.³⁰ There was a slight shift of XRD peaks towards lower angles as the Ce³⁺ concentration increased (Fig. 1), which can be explained as an effect of replacing smaller Ca²⁺ ions (0.112 nm) with larger Ce³⁺ ions (0.114 nm).³⁵ However, as the trivalent cation (Ce³⁺) replaces the divalent cation (Ca²⁺), a charge imbalance would arise due to the difference in their valence states. Hence, to maintain neutrality, calcium vacancies are formed that act as hole traps.³⁶ The prepared samples have eightfold coordinated Ca²⁺ ions forming the Thomson cube, and Al³⁺ and Si⁴⁺ ions occupy distorted tetrahedral sites.^24,37 The decrease in the full width at half-maximum (FWHM) of the highest intensity peak accounts for the increase in crystallinity with the rise in AT.^38,39 A similar observation has been reported by other researchers.^18,40,41

Figure 1

XRD peaks of (a) C1—Ce, (b) C2—Ce, and (c) C3—Ce samples.

The crystallite size was found by Debye–Scherrer’s equation:

$$ D = \frac{K \lambda }{{\beta \cos \theta }} $$

(1)

where D is the crystallite size, β is the full width at half the maximum height of the diffraction peak, λ is the X-ray wavelength, θ is Bragg’s angle, and k is Scherrer’s constant (0.9).

The variation in crystallite size and FWHM with temperature is shown in Table S-1 (refer to online Supplementary material). It is evident that there is an increase in the crystallite size with increasing temperature.

FTIR Analysis

The identification of functional groups or bonds can be carried out using FTIR spectra. The transmittance of the prepared samples as a function of wavenumber was recorded, and the wavenumbers corresponding to different vibrations were identified and are given in Table II. The FTIR spectra of C1—1.5 Ce, C2—1.5 Ce, and C3—1.5 Ce phosphors are shown in Fig. 2.

Table II Band assignment of phosphor samples

Figure 2

FTIR spectra of (a) C1—1.5 Ce, (b) C2—1.5 Ce, and (c) C3—1.5 Ce samples.

The wavenumbers corresponding to the Ca-O stretch, Si-O asymmetric stretch, Al-O stretch, and SiO₄ bending were obtained from the FTIR spectra.³⁰ The presence of the same functional groups for all the samples and the negligible shift in wavenumber confirmed that no structural changes in the crystal lattice occurred, which correlates with the XRD results.

Scanning Electron Microscopy (SEM) and Energy Dispersive X-ray Spectroscopy (EDS)

The morphology of the prepared samples was highly agglomerated and irregular, and the nonuniformity can be seen in all the series irrespective of the AT (Fig. 3). There is an increase in the grain size with the rise in AT. These results agree with published reports.^42,43 It is difficult to calculate the exact particle size due to inhomogeneous microstructures.

Figure 3

SEM images of (a) C1—1.5 Ce, (b) C2—1.5 Ce, and (c) C3—1.5 Ce; and EDS images of (d) C1—1.5 Ce, (e) C2—1.5 Ce, and (f) C3—1.5 Ce samples.

The EDS studies confirm the presence of Ca, Al, Si, O, and Ce elements in the samples (Fig. 3), confirming the incorporation of Ce³⁺ ions into the host lattice.

Diffuse Reflectance Spectroscopy

Diffuse reflectance is observed when the light illuminates powder samples (rough surface). Changing the angle of incidence does not affect the diffuse reflectance. The band gap calculation of phosphors can be carried out by recording the reflectance spectra.^44,45 The reflectance of phosphors is measured as a function of wavelength, then it is transformed into absorption data with the help of the Kubelka–Munk function:

$$ F\left( R \right) = \frac{{(1 - R)^{2} }}{2R} = \frac{K}{S} $$

(2)

where F(R), R, K, and S are the Kubelka–Munk function, reflectivity, absorption, and scattering coefficients, respectively.

The spectra (Fig. 4, inset) show a sharp decrease of reflectance around 450–350 nm, which is due to the host absorption. The reflection intensity drop of around 350 to 250 nm accounts for the absorption of the Ce³⁺ ions.^46,47 The x-intercept of the graph (F(R) hν)² as a function of energy gives the band gap, E_g.

Figure 4

Absorption spectra of (a) C1—1.5 Ce, (b) C2—1.5 Ce, and (c) C3—1.5 Ce samples; insets diffuse reflectance spectra.

The E_g values of C1—1.5 Ce, C2—1.5 Ce, and C3—1.5 Ce are 5.10 ± 0.04 eV, 5.23 ± 0.03 eV, and 5.42 ± 0.05 eV, respectively (Fig. 4), and E_g increases with an increase in AT. These band gaps are lower than the pure matrix band gap (5.74 eV)⁴⁷ due to the effect of doping,^48,49 which is due to the band gap narrowing effect.⁵⁰ New defect levels were created between the energy gaps when the dopant was added. There is a possibility that these sublevels merge with the conduction band and decrease the E_g. The increase in E_g with increased AT can be attributed to the removal of structural defects. As the structural defects are removed, the energy levels corresponding to them will disappear, which leads to an increase in E_g.^51,52,53

The increase in crystallite size with AT significantly influences the optical properties. As discussed in Sect. “XRD Analysis,” the crystallinity increase indicates crystallite size enhancement. Since the energy band gap is inversely proportional to the interatomic distance,⁴¹ the larger the crystallite size, the smaller the interatomic spacing. Hence, the band gap shows an increasing trend with crystallite size (see supplementary Figure S-2).⁵⁴

PL Spectra

The excitation spectra recorded for a 420-nm emission (for the 1.5 Ce-doped samples) are shown in Fig. 5a. There are two excitation peaks, at 278 nm (weak) and 354 nm (strong), which correspond to the transition from the ground state (4f) of the Ce³⁺ ions to the excited state (5d).^55,56 Hence the excitation was fixed at 354 nm. The excitation spectra show an increase in intensity with annealing temperature. Further, the emission spectra (Fig. 5b–d) for the C1, C2, and C3 samples for different concentrations of dopants (0.5 mol.%, 0.75 mol.%, 1 mol.%, 1.5 mol.%, 2 mol.%, 2.5 mol.%) for different annealing temperatures, were compared and the intensity variation was analyzed.

Figure 5

(a) Excitation spectra of C1—1.5 Ce, C2—1.5 Ce, and C3—1.5 Ce; emission spectra of (b) C1—Ce, (c) C2—Ce, and (d) C3—Ce; and (e) variation of emission intensity with AT of C1—1.5 Ce, C2—1.5 Ce, and C3—1.5 Ce samples.

The emission spectra were observed due to 5d → 4f transitions of the activator, and show a broadband emission. The emission intensity increases with the Ce³⁺ concentration up to 1.5 mol.%, and the luminescence intensity reduces beyond 1.5 mol.% Ce³⁺, leading to concentration quenching.⁵⁷ The drop in intensity occurs due to nonradiative energy transfer. Calculating the critical distance between the dopant ions can identify the mode of energy transfer:^58,59

$$ Rc = 2\left. {\left( {\frac{3V}{{4\pi X_{c} N}}} \right.} \right)^{1/3} $$

(3)

where N is the number of dopant ions in the unit cell, V the volume of the unit cell, and X_c the optimum dopant ion concentration. For the host matrix, dopant ions per unit cell = 8, X_c = 1.5 mol.%, volume = 299.05 (Å)³,²³ and R_c = 3.96 Å. As the R_c < 5 Å, exchange interaction is responsible for the energy exchange.^60,61 The emission intensity is enhanced with an increase in AT (Fig. 5e), which can be due to the increase in crystallinity, the destruction of optical quenching centers at higher temperatures,^62,63 and the reduction of surface defects, which coincides with the XRD results.

Thermoluminescence

The TL glow curves for the C1—1.5 Ce, C2—1.5 Ce, and C3—1.5 Ce samples have been plotted for different gamma doses (Fig. 6). The TL intensity increases with an increase in the γ dose from 3 Gy to 5 kGy. At higher irradiation doses, the TL glow curves appear clipped-off due to the large number of photons emitted from the samples (for a fixed bias voltage at 600 V). When the TL intensities of C1—1.5 Ce, C2—1.5 Ce, and C3—1.5 Ce for 500 Gy irradiation are compared, the enhancement in intensity is seen with increasing annealing temperature (see supplementary Figure S-3), without appreciable changes in the peak shape. This might be due to the increased homogeneity and lowered internal stress of the samples as a result of annealing.⁶² The defects present in the inorganic solids are responsible for the TL phenomenon. Exposure of the samples to heat treatment affects the cationic or anionic vacancies, or the arrangements of dopant ions, thus influencing the TL emissions.⁶³

Figure 6

TL glow curves of (a) C1—1.5 Ce, (b) C2—1.5 Ce, and (c) C3—1.5 Ce irradiated with different γ-doses.

The suitable range of γ doses for the dosimetry applications of prepared samples can be estimated by analyzing the integrated TL intensity versus the irradiated dose graph (see supplementary Figure S-4). TL intensity should be linearly proportional to the γ dose, which is a criterion for dosimeter material.⁶⁴ For all the samples, the linear region has been observed from 3 Gy to 500 Gy, irrespective of the AT. Hence, the optimum dose for the sample series was 500 Gy.

Sensitivity

The slope of integrated TL intensity/unit mass versus γ dose plot gives the sensitivity (Fig. 7). The sensitivity of the C1—1.5 Ce, C2—1.5 Ce, and C3—1.5 Ce samples are 17,178,800, 19,314,900, and 69,075,300 counts/g/kGy, respectively. Sensitivity depends on the radiation type, the measurement system and the TL sample.⁶⁵

Figure 7

TL response (counts/g) of (a) C1—1.5 Ce, (b) C1—1.5 Ce, and (c) C1—1.5 Ce samples as a function of the irradiated dose.

Kinetic Parameters

TL occurs when the trapped carriers are liberated upon heating. The TL mechanism can be different for different host lattices as the origin of traps varies from one to another. In the prepared phosphors, as the Ce³⁺ cation replaces Ca²⁺ in the host matrix, charge-compensating Ca²⁺ vacancies are formed (V_ca), which act as hole traps in the phosphor sample.^31,66 Some studies have discussed the formation of O²⁻ vacancies (V_o) which act as electron traps.^67,68 The electrons and holes are liberated when the sample is exposed to γ radiation. The holes produced travel to Si⁴⁺ sites and get self-trapped in Al⁴⁺ sites via electron–phonon interaction.¹¹ On applying heat, the holes become re-trapped in Ce³⁺ sites, and the recombination leads to light emission.

The trap parameters give information about the defect energy levels, and calculating the escape factor (s), trap energy (E), lifetime (t), and the order of kinetics (b) gives a rough estimation of the suitability of the prepared phosphor in the field of dosimetry. Among various methods, we have used the computerized glow curve deconvolution (CGCD) method to calculate the trap parameters. The experimental glow curve was fitted with the theoretical glow curve plotted using Kitti’s general order equation Eq. 4.⁶⁹ The procedure is to establish approximate positions of the traps (trap temperatures), while the values of trap energy (E) and order of kinetics (b) are found using the iteration method. The iterations were repeated until the theoretical and experimental results converged and the lowest value of the figure of merit (FOM) was obtained:

$$ I\left( T \right) = I_{m} b^{{\left( {\frac{b}{b - 1}} \right)}} \exp \left( {\frac{E}{{k_{B} T}}\frac{{T - T_{m} }}{{T_{m} }}} \right)\left[ {\left( {b - 1} \right)\left( {1 - \frac{{2k_{B} T}}{E}} \right)\frac{{T^{2} }}{{T_{m}^{2} }}\exp \left( {\frac{E}{{k_{B} T}}\frac{{T - T_{m} }}{{T_{m} }}} \right) + 1\left( {b - 1} \right)\frac{{2k_{B}T }}{E}} \right]^{{ - \left( {\frac{b}{b - 1}} \right)}} $$

(4)

where I(T) is the intensity of the glow peak at temperature T, b the order of kinetics, I_m the maximum intensity, k_B the Boltzmann constant, T_m the temperature at maximum intensity, T the absolute temperature, and E the activation energy. The glow curve was deconvoluted, keeping the error or FOM < 5%.⁷⁰ Equations 5 and 6 have been used to determine the trap lifetime and frequency factor (s):

$$ t = \frac{{s^{ - 1} e^{{\frac{E}{{Tk_{B} }}}} }}{2 - b} $$

(5)

$$ s = \frac{\beta E}{{k_{B} T_{m}^{{2 \left( {1 + \left( {b - 1} \right)\frac{{2k_{B} T_{m} }}{E}} \right) }} }} \exp \left( {\frac{E}{{k_{B} T_{m} }}} \right) $$

(6)

where t is the trap lifetime, s a frequency factor, T_m the temperature corresponding to maximum intensity, T the storage temperature (300 K), β the heating rate (2.85 K/s), and b the order of kinetics.

Deconvoluted TL curves of C1—1.5 Ce, C2—1.5 Ce, and C3—1.5 Ce phosphors for the 500-Gy dose are plotted in Fig. 8, and the trap parameters are given in Table III.

Figure 8

Deconvoluted TL glow curves of 500-Gy irradiated (a) C1—1.5 Ce, (b) C2—1.5 Ce, and (c) C3—1.5 Ce samples.

Table III Kinetic parameters of 500-Gy irradiated samples by the CGCD technique

Each TL glow curve for each dose was deconvoluted into four peaks, denoting that there were four traps present in the samples. Lower temperature traps were shallower, and higher temperature traps were deeper. On analyzing the trap parameters obtained, it is clear that the temperature of the traps shifts to a higher temperature with a rise in AT, and that the increase in deeper trap levels is the reason for the shift. Also, the traps around 460–475 K have the highest intensity. This indicates that the samples have the highest number of deep traps.^42,71 Hence, more energy should be supplied for the liberation from these traps. This confirms the suitability of the prepared samples in γ dosimetry applications.⁶² Higher energy traps are more stable than lower energy traps and will show less fading with time.

Kinetic Parameter Calculation by Chen’s Method

The trapping parameters are also calculated using Chen’s peak shape method.⁷² Equations 7–10 have been used to extract the kinetic parameters:

$$ \omega = T_{2 } - T_{1} $$

(7)

$$ \tau = T_{m } - T_{1} $$

(8)

$$ \delta = T_{2 } - T_{m} $$

(9)

$$ {\upmu }_{g = } { }\frac{\delta }{\omega } $$

(10)

where T_m is the peak temperature, and T₁ and T₂ are half-width intensity temperatures below and above T_m, respectively, μ_g is the symmetrical geometrical factor, ω the total half-width, and τ and δ the half-widths at the low temperature side and the high temperature side of the glow peak, respectively. The traps follow first-order kinetics if μ_g $\sim$ 0.42, and second-order kinetics, if μ_g $\sim$ 0.52.⁷³ The activation energy (E_α) can be calculated using:⁷⁴

$$ C_{\tau } = 1.51 + 3 \left( {\mu_{g } - 0.42} \right) ; b_{\tau } = 1.58 + 4.2 \left( {\mu_{g} - 0.42} \right) $$

(11)

$$ C_{\delta } = 0.976 + 7.3 \left( {\mu_{g } - 0.42} \right) ; b_{\delta } = 0 $$

(12)

$$ C_{\omega } = 2.52 + 10.2 \left( {\mu_{g } - 0.42} \right) ; b_{\omega } = 1 $$

(13)

where C_τ, b_τ, C_δ, b_δ, C_ω, and b_ω are correction factors.

$$ E_{\alpha } = C_{\alpha } \frac{{k_{B} T_{m}^{2} }}{\alpha } - b_{\alpha } \left( {2k_{B} T_{m} } \right) $$

(14)

where α = τ, δ, and ω and the average of E_δ, E_ω, and E_τ give the trap activation energy. Kinetic parameters have been estimated using Chen’s peak shape method and are set out in Table IV.

Table IV Kinetic parameters of 500-Gy irradiated phosphors by Chen’s peak shape method

The trapping and recombination follow second-order kinetics, as most trap levels have μ_g close to 0.52.⁷³ The activation energies of C1—1.5 Ce, C2—1.5 Ce, and C3—1.5 Ce for the 500-Gy dose for both methods are identical. The trap lifetime increases with the rise in AT, and the same trend is observed for the calculated trap lifetimes using the CGCD technique, confirming that the electrons trapped in deeper traps stay there longer.

Conclusion

Blue light-emitting Ca₂Al₂SiO₇ doped with Ce³⁺ phosphors was synthesized using the combustion technique at different annealing temperatures. The samples produced had a tetragonal structure, and their crystalline nature improved with higher annealing temperatures, with samples annealed at 1373 K having the highest crystallinity. SEM images showed a highly agglomerated irregular surface, with the grain size increasing with AT. EDX studies confirmed the elements present in the phosphor samples. Upon excitation, the phosphors show a broad blue emission at 420 nm. Concentration quenching was observed beyond 1.5 mol.% of Ce³⁺ concentration. The PL intensity increased at higher AT, peaking in the 1373-K annealed phosphors. The TL glow curves of samples doped with 1.5 mol.% Ce³⁺ showed that, as the annealing temperature increased, so did the TL intensity. All the samples had a linear response from 3 Gy to 500 Gy, making them appropriate for use as dosimeters with high sensitivity in this range. TL glow curve analysis confirmed the occurrence of four trap centers. As the annealing temperature increases, more electrons become trapped in deeper traps with longer lifetimes. Thus, the prepared phosphors are promising candidates for gamma radiation detection.