1 Introduction

The classical thermoelasticity theory has two paradoxes the first one is that the speed of propagation for the thermal field is infinite and the second is that elastic change has no effect on temperature. Lord and Shulman [1] presented, instead of classical Fourier’s law, wave-type heat conduction contains a heat flux vector and its time-derivative as well as new thermal relaxation. Green and Lindsay [2] developed the generalized theory with two thermal relaxations. Green and Naghdi [3] provided that not accommodate the dissipation of thermal energy. Tzou [4, 5] proposed a model known as dual-phase-lag (DPL). It would be convenient to use this model to investigate heat transfer in micro-structures. Chandrasekharaiah [6] proposed a DPL model to modify the classical thermoelasticity. The three-phase-lag model of thermoelasticity was given by Choudhuri [7]. Zenkour [8] discussed a refined two-temperature multi-phase-lags theory in the thermomechanical response of microbeams using the modified couple stress analysis. Dual-phase-lag model for a micro-stretch thermoelastic medium with diffusion under the influence of gravity and Laser Pulse was investigated by Othman et al. [9]. Said et al. [10] used the multi-phase-lags with fractional derivative heat transfer thermoelasticity to study wave propagation on a nonlocal fiber-reinforced thermoelastic medium. The effect of multi-phase-lag and Coriolis acceleration on a fiber-reinforced isotropic thermoelastic medium was discussed by Alharbi et al. [11]. Said and Othman [12] introduced the wave propagation in a two-temperature fiber-reinforced magneto-thermoelastic medium with three-phase-lag model.

Fractional calculus has been used to modify many existing models of physical processes in the field of heat conduction, diffusion, viscoelasticity, solids mechanics, control theory, and electricity [13,14,15,16]. Povstenko [17] proposed a quasistatic uncoupled theory of thermoelasticity which is based on the heat conduction equation with a time-fractional order derivative. Youssef [18] constructed a new consideration of heat conduction with fractional order, and its uniqueness theorem has been approved also. Abouelregal [19] solved a problem of a semi-infinite piezoelectric medium with temperature-dependent properties with the theory of fractional order. Yu et al. [20] formulated the fractional order generalized electro-magneto-thermoelastic theory and presented the effect of the fractional order parameter. Various approaches and definitions of fractional derivatives have become the main object of numerous studies (see [10, 21,22,23,24,25,26,27,28,29,30,31,32,33,34]).

A problem of the hollow cylinder has been noticed by various methods of transform technique and temperature distribution, thermal stresses have been determined by the Hankel transform technique; Laplace transforms technique, Green’s theorem, etc. The Bessel function finds it suitable for agreement between the surface and end boundary conditions. Chen [35] has considered the transversely isotropic hollow cylinder for finding the solution of linear thermoelasticity. Youssef [36] investigated a generalized thermoelastic infinite medium with a cylindrical cavity subjected to a moving heat source. Othman and Abbas [37] studied the thermal shock problem in a homogeneous isotropic hollow cylinder with energy dissipation. Manthena and Kedar [38] investigated the transient thermal stress analysis of a functionally graded thick hollow cylinder with temperature-dependent material properties. Said [39] solved a generalized magneto-thermoelastic problem for a half-space with G-N theory. Problems of the hollow cylinder have been studied by many researchers (see [40,41,42,43]).

The aim of the present contribution is to consider a rotating thick hollow cylinder with two temperatures under the influence of a magnetic field in the context of the multi-phase-lags model. The numerical results for the physical quantities have been obtained and presented graphically to estimate and highlight the effects of the magnetic field, temperature discrepancy, two-temperature parameter, and rotation.

2 The description of the problem

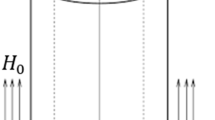
We consider a thermoelastic solid occupying the region of an infinitely long hollow circular cylinder of internal radius ‘\(a\)’ and external radius ‘\(b\)’. We shall use a cylindrical system of coordinates (r, θ, z) with the z axis coincides with the axis of the cylinder. Also, we consider that the cylinder rotates uniformly with angular velocity \({{\varvec{\Omega}}} = \Omega n,\) where n is a unit vector representing the direction of the axis of rotation. Assuming that the initial state of the medium is quiescent and that the outer surface of the cylinder is traction free and subjected to a harmonic varying heat, while the inner surface is thermally insulated and also traction free. Due to the radial symmetry of the problem, all the considered fields are functions of \(r\) and \(t\) only (see Fig. 1). The displacement vector \(u = (u,\,0,0)\).

Fig. 1
figure 1

Schematic diagram for the infinitely hollow cylinder

Full size image

The stress–displacement–temperature relations as Chandrasekharaiah [6]

$$ \sigma_{rr} = \lambda \,e + 2 \mu \,e_{rr} - \gamma \,\hat{T}\,, $$
(1)
$$ \sigma_{\theta \theta } = \lambda \,e + 2 \mu \,e_{\theta \theta } - \gamma \,\hat{T}\,, $$
(2)

where \(\sigma_{ij}\) are the components of stress, \(\lambda ,\;\mu\) are elastic constants, \(\hat{T} = T - T_{0} ,\) where \(T\) is the temperature above the reference temperature \(T_{0} .\)

$$ \begin{aligned} & e_{{rr}} = \frac{{\partial u}}{{\partial r}}, \\ & e_{{\theta \theta }} = \frac{u}{r}, \\ & e = e_{{rr}} + e_{{\theta \theta }} = = \frac{1}{r}\frac{{\partial {\mkern 1mu} (ru)}}{{\partial {\mkern 1mu} r}}, \\ & e_{{zz}} = e_{{rz}} = e_{{r\theta }} = 0. \\ \end{aligned} $$
(3)

The equation of motion as Schoenberg and Censor [44]

$$ \frac{{\partial \,\sigma_{rr} }}{\partial r} + \frac{{\sigma_{rr} - \sigma_{\theta \theta } }}{r}\, + \,\mu_{0} H_{0}^{2} \,\frac{\partial \,e}{{\partial r}} - \,\varepsilon_{0} \mu_{0}^{2} H_{0}^{2} \,\frac{{\partial^{2} \,u}}{{\partial t^{2} }} = \rho \frac{{\partial^{2} \,u}}{{\partial t^{2} }} + R_{r} $$
(4)

where \(R_{r} = - \rho \,\Omega^{2} u\) is the component of body force due to rotation, \(\,F_{r} = \mu_{0} H_{0}^{2} \,\frac{\partial \,e}{{\partial r}} - \,\varepsilon_{0} \mu_{0}^{2} H_{0}^{2} \,\frac{{\partial^{2} \,u}}{{\partial t^{2} }}\) is the component of Lorentz force due to the presence of the magnetic field with constant intensity \({\varvec{H}} = (0,\,0,H_{0} )\) as Abbas [37].

  1. (1)

    The heat conduction equation as Zenkour [8], Youssef [18], Miller and Ross [21], and Podlubny [22]

    $$ I^{s - 1} \,K\,\left( {1 + \sum\limits_{r = 1}^{N} {\,\frac{{\tau_{\theta }^{r} }}{r!}\,\,\frac{{\partial^{r} }}{{\partial t^{r} }}} } \right)\,\nabla^{2} \Phi = \left( {\delta \, + \tau_{0} \frac{\partial }{\partial t} + \sum\limits_{r = 1}^{N} {\,\,\,\frac{{\tau_{q}^{r + 1} }}{r + 1!}\,\,\frac{{\partial^{r} + 1}}{{\partial t^{r + 1} }}} } \right)\,(\,\rho \,C_{E} \dot{T} + \gamma \,T_{0} \,\dot{e}), $$
    (5)
    $$ \Phi - T = \delta_{0} \,\Phi_{,ii} $$
    (6)

    where \(K\) is the coefficient of thermal conductivity, \(\rho \,\) is the mass density, \(C_{E}\) is the specific heat at constant strain, \(\tau_{0}\) is the first relaxation time,\(\tau_{\theta }\) is the phase-lag of the temperature gradient, \(\tau_{q}\) is the phase-lag of heat flux, \(\delta\) is a parameter takes values either 0 or 1 according to the thermoelasticity theory applied, \(\Phi\) is the conductive temperature, \(\delta_{0} > 0\) a constant called two-temperature parameter, and \(\nabla^{2} = \frac{{\partial^{2} }}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial }{\partial r}\). The value of \(N\) may reach 5 or more according to the refined phase-lags (RPL) theory required.

Definite the fractional order derivative as:

$$ \frac{{\partial^{s} f(x,\,t)}}{{\partial t^{s} }} = \left\{ {\begin{array}{*{20}l} {f(x,\,t) - f(x,\,0),} & {s \to 0} \\ {I^{1 - s} \,\,\frac{\partial f(x,\,t)}{{\partial t}},\,} & {0 < s < 1} \\ {\frac{\partial f(x,\,t)}{{\partial t}},} & {s = 1} \\ \end{array} } \right. $$
(7)

and \(I^{s}\) is the Riemann–Liouville integral operator of order \(s\) as:

$$ I^{s} I^{n} f(t) = I^{n} I^{s} f(t) = I^{s + n} f(t),\;\;\;\;I^{s} f(t) = \frac{1}{\Gamma (s)}\,\,\int\limits_{0}^{t} {\frac{1}{{(t - \tau )^{1 - s} }}f(\tau )\,d} \tau ,\;\;\;\;0 < s < 1 $$
(8)

where \(\Gamma (s)\) is the Gamma function and \(f(t)\) is a Lebesgue integrable continuous function satisfies.

$$ \mathop {\lim }\limits_{s \to 1} \,\,\frac{{{\text{d}}^{{\rm{s}}} \,f(t)}}{{{\text{d}}t^{s} }} = f^{\prime}(t) $$
(9)

For convenience, we used the non-dimensional variables as:

$$ \begin{aligned} (r^{\prime},\,u^{\prime})& = c_{0} \eta \,\,(r,\,u),\;\;\;\;(t^{\prime},\,\tau_{q}^{^{\prime}} ,\,\tau_{0}^{^{\prime}} ,\,\tau_{\theta }^{^{\prime}} ) = c_{0}^{2} \eta \,\,(t,\,\tau_{q} ,\,\tau_{0} ,\,\tau_{\theta } ), \hfill \\ \theta^{\prime}& = \frac{\gamma \,\theta }{{\lambda + 2\mu }},\;\;\;\;\Phi^{\prime} = \frac{{\gamma \,(\Phi - T_{0} )}}{\lambda + 2\mu },\;\;\;\;\sigma^{\prime}_{ij} = \frac{{\sigma_{ij} }}{\lambda + 2\mu }, \hfill \\ \Omega^{\prime} &= \frac{\Omega }{{c_{0}^{2} \eta }},\;\;\;\;\eta = \frac{{\rho \,C_{E} }}{K},\;\;\;\;c_{0} = \sqrt {\frac{\lambda + 2\mu }{\rho }} \hfill \\ \end{aligned} $$
(10)

Using Eqs. (1), (2), and (10), then Eqs. (4) and (5) will be as

$$ \,\,(1 + A_{1} )\frac{\partial \,e\,}{{\partial \,r}} - \frac{\partial \,\theta \,}{{\partial \,r}} = A_{2} \frac{{\partial^{{2}} u\,}}{{\partial \,t^{{2}} }} - \Omega^{2} u, $$
(11)
$$ I\,^{s - 1\,} \left( {1 + \sum\limits_{r = 1}^{N} {\,\frac{{\tau_{\theta }^{r} }}{r!}\,\,\frac{{\partial^{r} }}{{\partial t^{r} }}} } \right)\,\,\nabla^{2} \Phi = \left( {\delta \, + \tau_{0} \frac{\partial }{\partial t} + \sum\limits_{r = 1}^{N} {\,\,\,\frac{{\tau_{q}^{r + 1} }}{r + 1!}\,\,\frac{{\partial^{r} + 1}}{{\partial t^{r + 1} }}} } \right)\,(\,\,A_{3} \,\dot{T} + A_{4\,} \dot{e}), $$
(12)

where \(A_{1} = \frac{{\mu \,_{0} \,H_{0}^{2} }}{\lambda + 2\mu }\), \(A_{2} = \frac{{\left( {\rho + \varepsilon \,_{0} \,\mu_{0}^{2} \,H_{0}^{2} } \right)\,c_{0}^{2} }}{\lambda + 2\mu }\), \(A_{3} = \frac{{\rho \,C_{E} }}{\eta \,K}\), \(A_{4} = \frac{{\gamma \,^{2} T\,_{0} \,}}{(\lambda + 2\mu )\,\eta \,K}\).

Multiplying both sides by \(r\) and then using the operator \(\frac{1}{r}\frac{\partial }{\partial \,r}\) to both sides of Eq. (11), we obtain

$$ \,\,(1 + A_{1} )\nabla^{2} e - \nabla^{2} \theta = A_{2} \frac{{\partial^{{2}} e\,}}{{\partial \,t^{{2}} }} - \Omega^{2} e. $$
(13)

3 The harmonic wave analysis method

We solve the problem of generalized thermoelasticity by using the harmonic wave analysis:

$$ (e,\Phi ,\,\theta )\,(r,t) = (\overline{e},\overline{\Phi },\,\overline{\theta })\,(r)\exp \,(mt) $$
(14)

where \(\overline{\theta } (r)\), etc. is the amplitude of the function \(\theta \,(r,\,t)\) etc., and \(m\) (complex) is the time constant.

The harmonic wave analysis, in fact, comprises seeking the solution in the Fourier-transformed domain.

Assuming that all the field quantities are sufficiently smooth on the real line such that harmonic wave analysis of these functions exists.

Using Eqs. (14) in Eqs. (12) and (13), we get

$$ (A_{5} \,\nabla^{2} - A_{6} )\,\overline{e} - \nabla^{2} {(}1 - \,\delta_{0} \,\nabla^{2} {)}\,\overline{\Phi } = 0, $$
(15)
$$ A_{8} \,\overline{e} + \, [A_{9} - \,(A_{9} \delta_{0} + A_{10} )\,\nabla^{2} ]\,\,\overline{\Phi } = 0, $$
(16)

where \(A_{5} = 1 + A_{1} ,\) \(A_{6} = m^{2} A_{2} - \Omega^{2} ,\) \(A_{7} = m\,[\delta + \tau_{0} m + \sum\nolimits_{r = 1}^{N} {\,\,\,\frac{{\tau_{q}^{r + 1} }}{r + 1!}\,\,m^{r + 1} } ],\) \(A_{8} = A_{4} A_{7} ,\) \(A_{9} = A_{3} A_{7} ,\) \(A_{10} = 1 + G_{1} ,\) \(G_{1} = m^{*} \sum\nolimits_{r = 1}^{N} {\,\frac{{\tau_{\theta }^{r} }}{r!}\,\,m^{r} } ,\) \(\,m^{*} = e^{ - mt} \,t^{ - s} \,\sum\nolimits_{n = 1}^{\infty } {\,\,\frac{{(mt)^{n} }}{\Gamma (n + 1 - s)}} \,.\)

The solution of Eqs. (15) and (16) is:

$$ (\nabla^{{4}} - B_{1} \nabla^{{2}} + B_{2} ){\kern 1pt} {\kern 1pt} \overline{e}{(}r{)} = 0, $$
(17)

where \(B_{1} = \frac{{A_{12} }}{{A_{11} }},\) \(B_{2} = \frac{{A_{6} A_{9} }}{{A_{11} }},\) \(A_{11} = A_{5} (A_{9} \delta_{0} + A_{10} ) + \delta_{0} A_{8} ,\) \(A_{12} = A_{5} A_{9} + A_{6} (A_{9} \delta_{0} + A_{10} ) + A_{8} ,\)

The solution of Eq. (17) can be expressed as:

$$ \overline{e}(r) = \sum\limits_{{i = {1}}}^{{2}} {\,\left\{ {A_{i} I_{0} {(}m_{i} r{)} + \,B_{i} K_{0} {(}m_{i} r{)}\,} \right\}} \,{,} $$
(18)
$$ \overline{\Phi }(r) = \sum\limits_{{i = {1}}}^{{2}} {\,\left\{ {A_{i} J_{1i} I_{0} {(}m_{i} r{)} + \,B_{i} J_{1i} K_{0} {(}m_{i} r{)}\,} \right\}} \,{,} $$
(19)

where \(A_{i} ,\,B_{i}\) are parameters, \(I_{n} (m_{i} r)\) is the modified Bessel functions of order \(n\) of the first kind and \(\,K_{n} (m_{i} r)\) second kind. \(m_{i} (i = 1,\,2)\) is the square root of the positive real part of the roots \(m_{{_{i} }}^{2}\) of the following characteristic equation:

$$ m^{{4}} - B_{1} m^{{2}} + B_{2} = 0. $$
(20)
$$ I_{n} (m) \approx \frac{{e^{m} }}{{\sqrt {2\pi m} }}\left( {1 - \frac{{(4n^{2} - 1)}}{8m} + \frac{{(4n^{2} - 1)(4n^{2} - 9)}}{{2!\,\,\left( {8m} \right)^{2} }} - \frac{{(4n^{2} - 1)(4n^{2} - 9)(4n^{2} - 25)}}{{3!\,\,\left( {8m} \right)^{3} }} + \ldots } \right) $$
(21)
$$ K_{n} (m) \approx \frac{{e^{m} }}{{\sqrt {2\pi m} }}\left( {1 + \frac{{(4n^{2} - 1)}}{8m} + \frac{{(4n^{2} - 1)(4n^{2} - 9)}}{{2!\,\,\left( {8m} \right)^{2} }} + \frac{{(4n^{2} - 1)(4n^{2} - 9)(4n^{2} - 25)}}{{3!\,\,\left( {8m} \right)^{3} }} + \ldots } \right) $$
(22)

Using the above equations, we get

$$ \overline{\theta }(r) = \sum\limits_{{i = {1}}}^{{2}} {\,\,\left\{ {A_{i} J_{2i} I_{0} {(}m_{i} r{)} + \,B_{i} J_{2i} K_{0} {(}m_{i} r{)}\,} \right\}} \,{,} $$
(23)
$$ \overline{u}(r) = \sum\limits_{{i = {1}}}^{{2}} {\,\left\{ {\frac{{A_{i} }}{{m_{i} }}I_{1} {(}m_{i} r{)} - \,\frac{{B_{i} }}{{m_{i} }}K_{1} {(}m_{i} r{)}} \right\}} \,{,} $$
(24)
$$ \overline{{\sigma_{rr} }} (r) = \sum\limits_{{i = {1}}}^{{2}} {\,\left\{ {A_{i} J_{3i} I_{0} {(}m_{i} r{)} + \,B_{i} J_{3i} K_{0} {(}m_{i} r{)} - A_{i} J_{4i} I_{1} \,{(}m_{i} r{)} + \,B_{i} J_{4i} K_{1} {(}m_{i} r{)}} \right\}} \,{,} $$
(25)
$$ \overline{{\sigma_{\theta \theta } }} (r) = \sum\limits_{{i = {1}}}^{{2}} {\,\left\{ {A_{i} J_{5i} I_{0} {(}m_{i} r{)} + \,B_{i} J_{5i} K_{0} {(}m_{i} r{)} + A_{i} J_{4i} I_{1} \,{(}m_{i} r{)} - \,B_{i} J_{4i} K_{1} {(}m_{i} r{)}} \right\}} \,{,} $$
(26)

where \(J_{1i} = \frac{{A_{8} }}{{m_{i}^{2} (A_{9} \delta_{0} + A_{10} ) - A_{9} }},\) \(J_{2i} = (1 - \delta_{0} m_{i}^{2} )J_{1i} ,\) \(J_{3i} = \lambda + 2\mu - \gamma J_{2i} ,\) \(J_{4i} = \frac{2\mu }{{m_{i} r}},\) \(J_{5i} = \lambda - \gamma J_{2i} .\)

4 Boundary conditions

The boundary conditions may be expressed as:

$$ \theta (a,t) = \theta_{0} f(t),\;\;\;\;\sigma_{rr} (a,t) = \sigma_{\theta \theta } (a,t) = u\,\,(a,t) = 0, $$
(27)

where \(\theta_{0}\) is a constant and \(f(t)\) is an arbitrary function.

Introducing Eqs. (27) to Eqs. (23, 24, 25, 26) we get

$$ \sum\limits_{{i = {1}}}^{{2}} {\,A_{i} } J_{{{2}i}} \,I_{0} (m_{i} a) + B_{i} J_{{{2}i}} \,K_{0} (m_{i} a) = \theta_{0} , $$
(28)
$$ \sum\limits_{{i = {1}}}^{{2}} {\,A_{i} } J_{{{3}i}} \,I_{0} (m_{i} a) + B_{i} J_{{{3}i}} \,K_{0} (m_{i} a) - A_{i} J_{{{4}i}} \,I_{1} (m_{i} a) + B_{i} J_{{{4}i}} \,K_{1} (m_{i} a) = 0, $$
(29)
$$ \sum\limits_{{i = {1}}}^{{2}} {\,A_{i} } J_{{{5}i}} \,I_{0} (m_{i} a) + B_{i} J_{{{5}i}} \,K_{0} (m_{i} a) + A_{i} J_{{{4}i}} \,I_{1} (m_{i} a) - B_{i} J_{{{4}i}} \,K_{1} (m_{i} a) = 0, $$
(30)
$$ \sum\limits_{{i = {1}}}^{{2}} {\,\frac{{A_{i} }}{{m_{i} }}} \,I_{1} (m_{i} a) - \frac{{B_{i} }}{{m_{i} }}\,K_{1} (m_{i} a) = 0, $$
(31)

Solving the above system of Eqs. (28, 29, 30, 31), we obtain \(A_{i} ,\,B_{i} \,\,{(}i = {1,}\,\,{2)}.\)

$$ \left( {\begin{array}{*{20}c} {A_{1} } \\ {A_{2} } \\ {B_{1} } \\ {B_{2} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {W_{1} } & {W_{2} } & {W_{3} } & {W_{4} } \\ {W_{5} } & {W_{6} } & {W_{7} } & {W_{8} } \\ {W_{9} } & {W_{10} } & {W_{11} } & {W_{12} } \\ {W_{13} } & {W_{14} } & {W_{15} } & {W_{16} } \\ \end{array} } \right)^{ - 1} \left( {\begin{array}{*{20}c} {\theta_{0} } \\ 0 \\ 0 \\ 0 \\ \end{array} } \right) $$
(32)

where \(W_{1} \,\, = J_{21} I_{0} {(}m_{1} a{),}\) \(W_{2} \,\, = J_{22} I_{0} {(}m_{2} a{),}\) \(W_{3} \,\, = J_{21} K_{0} {(}m_{1} a{),}\) \(W_{4} \,\, = J_{22} K_{0} {(}m_{2} a{),}\) \(W_{5} \,\, = J_{31} I_{0} {(}m_{1} a{)} - J_{41} I_{1} {(}m_{1} a{),}\) \(W_{6} \,\, = J_{32} I_{0} {(}m_{2} a{)} - J_{42} I_{1} {(}m_{2} a{),}\) \(W_{7} \,\, = J_{31} K_{0} {(}m_{1} a{)} + J_{41} K_{1} {(}m_{1} a{),}\) \(W_{8} \,\, = J_{32} K_{0} {(}m_{2} a{)} + J_{42} K_{1} {(}m_{2} a{),}\) \(W_{9} \,\, = J_{51} I_{0} {(}m_{1} a{)} + J_{41} I_{1} {(}m_{1} a{),}\) \(W_{10} \,\, = J_{52} I_{0} {(}m_{2} a{)} + J_{42} I_{1} {(}m_{2} a{),}\) \(W_{11} \,\, = J_{51} K_{0} {(}m_{1} a{)} - J_{41} K_{1} {(}m_{1} a{),}\) \(W_{12} \,\, = J_{52} K_{0} {(}m_{2} a{)} - J_{42} K_{1} {(}m_{2} a{),}\) \(W_{13} \,\, = \frac{{I_{1} {(}m_{1} a{)}}}{{m_{1} }}{,}\) \(W_{14} \,\, = \frac{{I_{1} {(}m_{2} a{)}}}{{m_{2} }}{,}\) \(W_{15} \,\, = - \frac{{K_{1} {(}m_{1} a{)}}}{{m_{1} }}{,}\) \(W_{16} \,\, = - \frac{{K_{1} {(}m_{2} a{)}}}{{m_{2} }}{.}\)

5 Special case

  1. (1)

    The corresponding equations for a thermoelastic solid occupying the region of an infinitely long hollow circular cylinder without the magnetic field from the above-mentioned cases by taking \(H_{0} \,\, = 0.\)

  2. (2)

    The corresponding equations for a thermoelastic solid occupying the region of an infinitely long hollow circular cylinder without temperature-dependent properties from the above-mentioned cases by taking \(\alpha^{*} = 0.\)

  3. (3)

    The corresponding equations for a thermoelastic solid occupying the region of an infinitely long hollow circular cylinder without rotation from the above-mentioned cases by taking \(\Omega = 0.\)

  4. (4)

    The coupled thermoelasticity (CT) theory, if we take \(\tau_{q} = \tau_{\theta } = \tau_{0} = 0\), \(\delta = 1\), then the above analysis reduces for theory.

  5. (5)

    The Lord-Shulman (L-S) theory, If we take \(\tau_{q} = \tau_{\theta } = 0\), \(\delta = 1,\) \(\tau_{0} > \,\,0\).

  6. (6)

    The G-N: II theory without energy dissipation, if we take \(\tau_{q} = \tau_{\theta } = 0\), \(\delta = 0\), \(\tau_{0} = 1\).

  7. (7)

    The simple phase-lags (DuaL) model of Tzou [4] is obtained, if \(\tau_{q} = \tau_{0} > \tau_{\theta } \ge 0\) , \(\delta = 1\),\(N = 1,\)\(\tau_{q}^{2} = 0\).

  8. (8)

    The refined phase-lags (RPL) model is given when \(\tau_{q} = \tau_{0} > \tau_{\theta } \ge 0\), \(\delta = 1,\) and \(N \ge 1\).

6 Numerical results and discussion

We now consider a numerical example for which computational results are given. The copper material is taken as the thermoelastic material for which we take the following values of the different physical constants as Abbas [38]. All the units of the used parameters are given in SI units.

$$ \begin{aligned} \lambda = & 7.76 \times 10^{10} {\text{N}}/{\rm{m}}^{2} ,\;\mu = 3.86 \times 10^{10} {\text{N}}/{\rm{m}}^{2} ,\;\rho = {8954}\;{\text{kg}}/{\rm{m}}^{3} ,\;T_{0} = 293\;{\text{K}},\;K = 386\;{\text{N}}/{\rm{s}} \cdot {\text{K}}, \\ & \theta_{0} = 0.2,\;\alpha_{t} = {1}{{.78}} \times 10^{ - 5} \;{\text{K}}^{ - 1} ,\;C_{E} = {383}{{.1}}\;{\text{J}}/{\rm{kg}} \cdot {\text{K}},\;\mu_{0} = 4 \times \pi \times 10^{ - 2} {\text{N}}/{\rm{m}}^{2} , \\ & a = 1\;{\text{m}},\;H_{0} = 10^{5} {\text{Col}}^{2} /{\text{Cal}}.{\rm{cm}}.\sec ,\;\sigma_{0} = 9.36 \times 10^{5} \;{\text{Col}}^{2} /{\text{Cal}}.{\rm{cm}}.{\text{sec,}} \\ & f_{0} = 0.1\,\,{\text{N}},\;\tau_{0} = 0.6\;{\text{rad}}/{\text{s}},\;\tau_{q} = 0.6\;{\text{rad}}/{\text{s}},\,\tau_{\theta } = 0.3\;{\text{rad}}/{\text{s}},\;0 \le r \le 1. \\ \end{aligned} $$

The numerical code has been prepared using (MATLAB R2007b) programming language. The comparison of the displacement component \(u,\) the strain \(e,\) the thermodynamic temperature \(\theta ,\) and the radial and hoop stress \(\sigma_{rr} ,\) with the radius \(r,\) has been made in these cases for \(t = 0.02\;s:\)

Case I: Effect of the magnetic field, rotation, and two-temperature parameter introduced as.

  1. (1)

    Refined-phase-lags in a rotating thick hollow cylinder with a magnetic field and two-temperature [RPL(HRT)] by the solid line.

  2. (2)

    Refined-phase-lags in a rotating thick hollow cylinder with a two-temperature (without magnetic field) [RPL(RT)] by a dashed line with dots.

  3. (3)

    Refined-phase-lags in a thick hollow cylinder with a two-temperature and magnetic field (without rotation) [RPL(HT)] by a dashed line with stars.

  4. (4)

    Refined-phase-lags in a rotating thick hollow cylinder with a magnetic field (without two-temperature parameter) [RPL(HR)] by a dotted line.

Case II: Different theories of thermoelasticity, namely; the refined-phase-lag theory (RPL), Green and Naghdi theory of type II (G-N: II), Lord and Shulman theory (L-S), and coupled theory (CT).

Case III: Different values of the fractional order parameter \(s\)(\(s = 0.1,\;0.3,\;0.5\;{\text{and}}\;0.9\)), in the presence of the magnetic field, rotation, and two-temperature parameter.

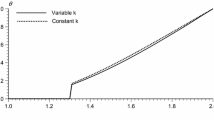
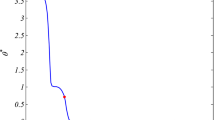
Figures 2, 3, 4 and 5 (Case I) show the effect of a magnetic field, rotation, and two-temperature parameter on the physical quantities against the radial distance \(r\) in the range \(0 \le r \le 1.\) Figure 2 depicts the space variation of the horizontal displacement \(u\) versus \(r.\) It can be seen that, the presence of a magnetic field, rotation, and two temperature parameter show decreasing effect on the magnitude of horizontal displacement. Figures 3, 4, and 5 clarify that the values of the strain \(e,\) the thermodynamic temperature \(\theta ,\) and the radial and hoop stress \(\sigma_{rr} ,\) for RPL(HRT) are large compared to those for RPL(RT), RPL(HT), and RPL(HR), this means that the presence of a magnetic field, rotation and two temperature parameter show increasing effect on the magnitude of these variables.

Fig. 2
figure 2

Variation of the displacement \(u\) versus the radius \(r\) for different values of rotation and magnetic field

Full size image
Fig. 3
figure 3

Variation of the strain \(e\) versus the radius \(r\) for different values of rotation and magnetic field

Full size image
Fig. 4
figure 4

Variation of the thermodynamic temperature \(\theta\) versus the radius \(r\) for different values of rotation and magnetic field

Full size image
Fig. 5
figure 5

Variation of the radial stress \(\sigma_{rr}\) versus the radius \(r\) for different values of rotation and magnetic field

Full size image

Figures 6, 7, 8 and 9 (Case II) show the variations of some physical variables at \(H_{0} = 100\,{\text{col}}^{{2}} {\text{/cal}}.{\text{cm}}.{\text{sec}}\) \(\Omega = 0.39\) and \(\delta_{0} = 0.03,\) for different theories of thermoelasticity, namely; the refined-phase-lag theory (RPL), Green and Naghdi theory of type II (G-N: II), Lord and Shulman theory (L-S) and coupled theory (CT). Figure 6 depicts that the relative difference between theorems for \(u.\) It can be seen that; along \(r{ - }\) direction, the G-N: II theory gives the smallest value of \(u,\) while the CT theory yields the highest value of \(u,\) Figs. 7, 8, and 9 illustrate the variations of the strain \(e,\) thermodynamic temperature \(\theta ,\) and the radial and hoop stress \(\sigma_{rr} ,\) respectively. It is observed that, along \(r{ - }\) direction, the CT theory gives the smallest value for these variables while the G-N: II theory yields the highest value.

Fig. 6
figure 6

Variation of the displacement \(u\) versus the radius \(r\) for different theories

Full size image
Fig. 7
figure 7

Variation of the strain \(e\) versus the radius \(r\) for different theories

Full size image
Fig. 8
figure 8

Variation of the thermodynamic temperature \(\theta\) versus the radius \(r\) for different theories

Full size image
Fig. 9
figure 9

Variation of the radial stress \(\sigma_{rr}\) versus the radius \(r\) for different theories

Full size image

Figures 10, 11, 12 and 13 (case III) show the variations of the non-dimensional displacement \(u,\) strain, thermodynamic temperature \(\theta\) and radial and hoop stress \(\sigma_{rr} ,\) respectively, which demonstrate the effects of the fractional order parameter on the variations of the considered variables. Two different values of fractional order parameter \(s\) were considered (\(s = 0.1,\;0.3,\)\(0.5,\)\(0.9\)). In this case: it is noticed that the fractional order parameter \(s\) is more pronounced and has significant effects on all considered functions. From this figure, all considered variables increase with the increasing the fractional order parameter except the value of displacement \(u\) decrease.

Fig. 10
figure 10

Variation of the displacement \(u\) versus the radius \(r\) for different values of the fractional order parameter

Full size image
Fig. 11
figure 11

Variation of the strain \(e\) versus the radius \(r\) for different values of the fractional order parameter

Full size image
Fig. 12
figure 12

Variation of the thermodynamic temperature \(\theta\) versus the radius \(r\) for different values of the fractional order parameter

Full size image
Fig. 13
figure 13

Variation of the radial stress \(\sigma_{rr}\) versus the radius \(r\) for different values of the fractional order parameter

Full size image

7 Conclusions

A two-temperature and fractional order derivative in a rotating thick hollow cylinder with a magnetic field. All coupled equations have been resolved exactly. The method used in the present article, the harmonic wave technique, is applicable to a wide range of problems in thermodynamics. The results provided the following most notable conclusions:

  1. (1)

    Theoretical, as well as numerical results, reveal that all the field variables are sensitive to rotation, magnetic field, and two-temperature parameter.

  2. (2)

    The deformation of a body depends on the nature of the force applied as well as the type of boundary conditions.

  3. (3)

    All figures display the variations of all field quantities in the context of the RPL, G-N II, L-S, and CT theories of thermoelasticity following similar trends.

  4. (4)

    The effects of the fractional parameter on all the considered variables are very significant, as clearly evidenced by the peak values of the curves.

  5. (5)

    The results presented in this paper should prove useful for researchers in material sciences, designers of new materials, low-temperature physics researchers, and those working to further develop the theory of thermoelasticity with fractional calculus.