Skip to main content
SpringerLink
Log in

Generalized magneto-thermoelasticity in a nonhomogeneous isotropic hollow cylinder using the finite element method

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

An Erratum to this article was published on 03 February 2009

Abstract

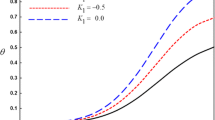
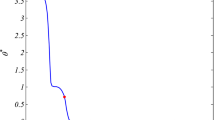
In this paper, we constructed the equations of generalized magneto-thermoelasticity in a perfectly conducting medium. The formulation is applied to generalizations, the Lord–Shulman theory with one relaxation time, and the Green–Lindsay theory with two relaxation times, as well as to the coupled theory. The material of the cylinder is supposed to be nonhomogeneous isotropic both mechanically and thermally. The problem has been solved numerically using a finite element method. Numerical results for the temperature distribution, displacement, radial stress, and hoop stress are represented graphically. The results indicate that the effects of nonhomogeneity, magnetic field, and thermal relaxation times are very pronounced. In the absence of the magnetic field or relaxation times, our results reduce to those of generalized thermoelasticity and/or classical dynamical thermoelasticity, respectively. Results carried out in this paper can be used to design various nonhomogeneous magneto-thermoelastic elements under magnetothermal load to meet special engineering requirements.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bargmann H. (1974). Recent developments in the field of thermally induced waves and vibrations. Nrecl. Eng. Des. 27: 372

    Article  Google Scholar 

  2. Anisimov S.I., Kapeliovich B.L. and Perelman T.L. (1974). Electron emission from metal surfaces exposed to ultra-short llaser pulses. Sov. Phys. JETP 39: 375–377

    Google Scholar 

  3. Boley, B.A.: In: Thermal Stresses: Hasselman, D.P.H., Heller, R.A. (eds.), pp. 1-ll. Plenum, New York (1980)

  4. Qiu T.Q. and Tien C.L. (1993). Heat transfer mechanism during short-pulse laser heating of metals. ASME J. Heat Transf. 115: 835–841

    Article  Google Scholar 

  5. Chen J.K., Beraun J.E. and Tham C.L. (2004). Ultrafast thermoelasticity for short-pulse laser heating. Int. J. Eng. Sci. 42: 793–807

    Article  Google Scholar 

  6. Chandrasekhariah D.S. (1986). Thermoelasticity with second sound a-review. Appl. Mech. Rev. 39: 355

    Article  Google Scholar 

  7. Lord H. and Shulman Y. (1967). A generalized dynamical theory of thermoelasticity. J. Mech. Phys. Solids 15: 299–309

    Article  MATH  Google Scholar 

  8. Green A.E. and Lindsay K.A. (1972). Thermoelasticity. J. Elast. 2: 1–7

    Article  MATH  Google Scholar 

  9. Erbay S. and Suhubi E.S. (1986). Longitudinal wave propagation in a generalized thermo-elastic cylinder. J. Therm. Stresses 9: 279

    Article  Google Scholar 

  10. Furukawa T., Noda N. and Ashida F. (1990). Generalized thermoelasticity for an infinite bode with cylindrical hole. JSME Int. J. 31: 26

    Google Scholar 

  11. Nowinski, J.L.: Theory of Thermoelasticity with Applications. Sijthoff & Noordhoff International, Alphen Aan Den Rijn (1978)

  12. Bahar, L., Hetnarski, R.: State space approach to thermoelasticity. In: Proceedings of 6th Canadian Congress on Applied Mechanics, pp. 17–18. University of British Columbia, Vancouver (1977)

  13. Bahar, L., Hetnarski, R.: Transfer matrix approach to thermoelasticity. In: Proceedings of the 15th Midwest Mechanic Conference, pp. 161–163. University of Illinois, Chicago (1977)

  14. Furukawa T., Noda N. and Ashida F. (1990). Generalized thermoelasticity for an infinite bode with cylindrical hole. JSME Int. J. 31: 26

    Google Scholar 

  15. Sharma J.N. and Chand D. (1992). On the axisymmetrical and plane strain problems of generalized thermoelasticity. Int J. Eng. Sci. 30: 223–230

    Article  MATH  Google Scholar 

  16. Chandrasekharaiah D.S. and Murthy H.N. (1993). Thermoelastic interactions in an unbounded body with a spherical cavity. J. Therm. Stresses 16: 55–71

    Article  Google Scholar 

  17. Misra J.C., Chattopadhyay N.C. and Samanta S.C. (1994). Thermoviscoelastic waves in an infinite aeolotropic body with a cylindrical cavity-a study under the review of generalized theory of thermoelasticity. Comp. Struc. 52(4): 705–717

    Article  MATH  Google Scholar 

  18. Chandrasekharaiah D.S. (1996). One-dimensional wave propagation in the linear theory of thermoelasticity with energy dissipation. J. Therm. Stresses 19: 695–710

    Article  MathSciNet  Google Scholar 

  19. Abd-alla A.N. and Abbas I.A. (2002). A problem of generalized magnetothermoelasticity for an infinitely long, perfectly conducting cylinder. J. Therm. Stresses 25: 1009–1025

    Article  Google Scholar 

  20. Misra J.C., Samanta S.C., Chakraborty A.K. and Misra S.C. (1991). Magnetothermoelastic interaction in an infinite elastic continuum with a cylindrical hole subjected to ramp-type heating. Int. J. Eng. Sci. 29(12): 1505–1514

    Article  MATH  Google Scholar 

  21. Misra J.C., Samanta S.C. and Chakraborty A.K. (1991). Magnetothermoelastic interaction in an aeolotropic solid cylinder subjected to a ramp-type heating. Int. J. Eng. Sci. 29(9): 1065–1075

    Article  MATH  Google Scholar 

  22. Zienkiewicz O.C. and Taylor R.L. (2000). The Finite Element Method Fluid Dynamics, 5th edn. Butterworth-Heinemann, London

    Google Scholar 

  23. Reddy J.N. (1993). An Introduction to the Finite Element Method, 2nd edn. McGraw-Hill, New York

    Google Scholar 

  24. Cook R.D., Malkus D.S. and Plesha M.E. (1989). Concepts and Applications of Finite Element Analysis, 3rd edn. Wiley, New York

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Faculty of Science, Sohag University, Sohag, Egypt

    Ibrahim A. Abbas

Authors
  1. Ibrahim A. Abbas
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ibrahim A. Abbas.

Additional information

An erratum to this article can be found at http://dx.doi.org/10.1007/s00419-009-0301-6

Rights and permissions

Reprints and permissions

About this article

Cite this article

Abbas, I.A. Generalized magneto-thermoelasticity in a nonhomogeneous isotropic hollow cylinder using the finite element method. Arch Appl Mech 79, 41–50 (2009). https://doi.org/10.1007/s00419-008-0206-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-008-0206-9

Keywords

Search

Navigation