1 Introduction

In classical theory, such as general relativity (GR), the black holes absorb every thing approaching the event horizon including light and also emit nothing. Our perspectives of GR are radically revised by the discovery that the black holes can be directly connected with some aspects of quantum mechanics, such as particle creation and annihilation [1,2,3,4,5,6,7]. Apparently, the black hole radiation could be characterized by thermodynamic quantities such as temperature and entropy, which are found in direct relations with the Plank constant and the gravitational constant.

Literature is full of publications assuming that the black holes follow the laws of thermodynamics, for example [8,9,10,11,12], it was also pointed out that the black hole radiation seems to violate the second law of thermodynamics [13]. This might be avoided when recent developments on QM are taken into account, such as the gravitational impacts on the Heisenberg uncertainty principle [14,15,16,17,18].

The black hole temperature known as Hawking temperature is also an intensive quantity. It has a much lower value than that of the cosmic microwave background [19]. The Bekenstein entropy was verified with various assumptions. On the other hand, there is an essential difference between the extensive entropy of an ordinary system and that of a black hole. In earlier, the entropy is scaling as volume, while in latter the entropy is scaling as area [20]. The holographic nature of the black hole entropy assumes that the micro-states or degrees of freedom in space or volume likely collapse to form black hole, where entropy is scaling as area.

If main thermodynamic properties of any system are well known, as the case of black holes, various equation-of-state (EoS) could straightforwardly be deduced [21,22,23,24,25]. In literature, there are different sets of EoS deduced from the black holes. A set depending on volume and pressure has been suggested for Bañados, Teitelboim, and Zanelli (BTZ) [26] and Reissner–Nordström (RN) anti-de Sitter (AdS) black holes [9, 27, 28]. Another set of EoS depending on energy density and pressure has been proposed for black hole neutron star (BHNS) [29, 30] and for white dwarf black hole (WDBH) [31]. Also, this set of EoS can be deduced in dependence of the concept that the entropy satisfying shock wave solutions [32,33,34] of the Einstein equations for a perfect fluid inside the black hole [35]. This present paper deals with the second set of EoS of different types of (a) Schwarzschild, (b) Reissner–Nordström, (c) Kerr, and (d) Kerr–Newman black holes. The paper aims to propose EoS for different kinds of black holes and calculate the corresponding squared speed of sound for each kind of BH. Also, from the squared speed of sound, the ratio of bulk viscosity to shear viscosity for each type of black holes would be determined.

The present paper is organized as follows. Various types of black holes are discussed in Sect. 2. In Sect. 3, black holes thermodynamics is reviewed. The results are given in Sect. 4. Section 5 is devoted to the final conclusions.

2 Various types of black holes

The black hole is a maximally warped region of spacetime where gravity is huge so that no particles or even radiations can escape from it [36]. On the other hand, the quantum field theory allows event horizons, the boundaries of the warped region, to emit radiations with temperatures inversely proportional to the mass of the black hole [2].

Based on their various properties, such as mass (m), electric charge (Q), and angular momentum (J) there are different types of black holes. Any black hole has also a characteristic event horizon created as a result of the string gravitational attraction [4].

Neutral and spinless black holes, \(Q=J=0\), are classified as Schwarzschild black holes [4],

$$\begin{aligned} ds^2 = (1-2GM/R_{\rm{Sch}})~\!dt^2 - \frac{1}{1-2GM/R_{\rm{Sch}}}~\!dR^2, \end{aligned}$$
(1)

where R refers to the space, t indicates the time, and \(R_{\rm{Sch}}\) is the Schwarzschild radius, \(G=1/2 \sigma \) is known as the gravitational constant with \(\sigma \) is defined as the string tension, and here \(\sigma =0.19\) GeV\(^2\). The Schwarzschild metric \(ds^2\) diverges, at \(R_{\rm{Sch}} = 2GM\).

The second type is the electrically charged black holes which are known as Reissner–Nordström black hole. This type of black hole is spinless, \(J=0\) [37]. The space–time line element is given as

$$\begin{aligned} ds^2 = \left( 1 - \frac{2GM}{R_{\rm{RN}}} + \frac{GQ^2}{R_{\rm{RN}}^2}\right) dt^2 - \left( 1- \frac{2GM}{R_{\rm{RN}}} + \frac{GQ^2}{R_{\rm{RN}}^2}\right) ^{-1}dR^2. \end{aligned}$$
(2)

The radius of a Reissner–Nordström black hole reads

$$\begin{aligned} R_{\rm{RN}} = GM\left( 1 + \sqrt{1 - \frac{Q^2}{GM^2}}\right) , \end{aligned}$$
(3)

which reduces to \(R_{\rm{Sch}}=2GM\), at \(Q=0\).

The third type considered in the present study is Kerr black holes [4]. It is neutral charged (\(Q=0\)) but has spin (\(J\ne 0\)). Their rotation takes place around an axis. The finite spin angular momentum J strengthens the gravitational attraction due to the centripetal force [38]. The Kerr metric is given as [4]

$$\begin{aligned} ds^2= & {} \left( 1 - {\frac{2 G M R_{\rm{K}}}{R_{\rm{K}}^2 + j^2 \cos ^2 \theta }}\right) dt^2 - (R_{\rm{K}}^2 + j^2 \cos ^2 \theta )~\!d\theta ^2 \nonumber \\ {}- & {} \left( \frac{ R_{\rm{K}}^2 + j^2 \cos ^2 \theta }{R_{\rm{K}}^2 - 2 G M R_{\rm{K}} + j^2}\right) ~\!dR^2, \end{aligned}$$
(4)

where the polar axis vanishes [4]. The spin angular momentum reads \(J=j M\) with j is the angular momentum parameter. The Kerr radius is given as

$$\begin{aligned} R_{\rm{K}} = \frac{R_{\rm{Sch}}}{2}\left( 1 + \sqrt{1 - \frac{j^2}{G^2M^2}}~\!\right) . \end{aligned}$$
(5)

The Fourth type of black hole is called Kerr–Newman; charged and rotating black hole, i.e., \(Q\ne 0\) and \(J\ne 0\). The Kerr–Newman metric reads [39]

$$\begin{aligned} ds^2= & {} \left( 1 + {\frac{Q^2 G - 2GMR_{\rm{KN}}}{R_{\rm{KN}}^2 + j^2 \cos ^2 \theta }}\right) dt^2 - (R_{\rm{KN}}^2 + j^2 \cos ^2 \theta )~\!d\theta ^2 \nonumber \\- & {} \left( \frac{R_{\rm{KN}}^2 + j^2 \cos ^2 \theta }{R_{\rm{KN}}^2 - 2GMR_{\rm{KN}} + j^2 + Q^2 G}\right) ~\!dR^2. \end{aligned}$$
(6)

The event horizon radius is given as

$$\begin{aligned} R_{\rm{KN}} =\frac{R_{\rm{Sch}}}{2}\left( 1 + \sqrt{1 - \frac{Q^2}{GM^2} - \frac{j^2}{G^2M^2}}\right) , \end{aligned}$$
(7)

3 Thermodynamics and equations of state of black holes

The Bekenstein entropy with its geometric nature is the quantum condition needed to be fulfilled in order to allow black holes fulfil the laws of thermodynamics which are apparently interpreted by observers whose spacetime coordinates are external to the black holes [40]. The Bekenstein entropy estimates information about the absorption of emission, at event horizon. Based on laws of thermodynamics, the black hole energy is conjectured to increase as it should be in closed systems, so does the event horizon area. Thus, it was assumed that the black hole entropy is directly proportional to the horizon area [12]

$$\begin{aligned} S = \frac{\pi (R^2+j^2)}{G}. \end{aligned}$$
(8)

At \(j=0\), the entropy reduces to the Schwarzschild one. The first Law of thermodynamics for electrically charged and rotating Kerr–Newman black hole is given by

$$\begin{aligned} dM = T_{\rm{BH}}(M,J)\;dS_{\rm{K}} + \mu _{\rm{Q}} dQ + \mu _{\rm{J}} dJ, \end{aligned}$$
(9)

where TdS is the heat exchanged between the black hole and its surrounding. \(\mu _{\rm{Q}} = 1.4 Q/R_{\rm{RN}}\) gives the chemical potential related to the variation of the electrical charge of the black holes [10, 11] and \(\mu _{\rm{J}}\) is associated with the variation of the black hole’s angular momentum. The chemical potential \(\mu \) describing the change in the electrical charge and the angular momentum of the black holes can be combined as [12]

$$\begin{aligned} \mu = \mu _{\rm{Q}} + \mu _{\rm{J}} = \sqrt{\frac{w J}{0.1 R}}+ \frac{1.4 Q}{R}, \end{aligned}$$
(10)

where \(w=\frac{4 \pi a}{S}\) is the angular velocity [4].

Based on the analogy between the black hole thermodynamics with the thermodynamics of heavy-ion collisions [4, 10,11,12], various thermodynamic properties could be comparatively evaluated. First, the pressure p of the grand-canonical ensemble (black hole) can be given as [41, 42]

$$\begin{aligned} p=\frac{g T^2}{2 \pi ^2} M^2 K_2\left( \frac{M}{T}\right) \exp {\frac{\mu }{T}}, \end{aligned}$$
(11)

where \(g=2j+1\) is the degeneracy factor and \(M=1.629~\)GeV is the black hole’s mass. Figure 1 shows the dependence of the normalized pressure on the temperature for various types of black holes, Sect. 4. The same behaviour was obtained for grand-canonical ensemble in the hadron resonance gas (HRG) model and from lattice quantum chromodynamics (LQCD) simulations [41,42,43].

Second, the black hole’s energy density \(\varepsilon \) can be expressed as

$$\begin{aligned} \varepsilon =\frac{\langle E \rangle }{V} \; = \frac{\langle E \rangle }{N} \frac{N}{V}, \end{aligned}$$
(12)

where \(V=\frac{4 \pi (R^3 +j^3)}{3}\) is the volume of the black hole. Since, the average energy density per particle \(\frac{\langle E \rangle }{N}\) [12] reads

$$\begin{aligned} \frac{\langle E \rangle }{N} = \sigma (R+j) \left[ 1.0-\frac{\mu }{\mu _0}\right] , \end{aligned}$$
(13)

where \(\mu _0=1.2\) is a free parameter [44] and N is the total number of particles [41, 42]

$$\begin{aligned} N =\frac{g V}{2\pi ^2} M^2 \;T K_2\left( \frac{M}{T}\right) \exp {\frac{\mu }{T}} \end{aligned}$$
(14)

In the following section, we introduce results on the thermodynamic properties of different types of black holes. Also, we elaborate the corresponding EoS and their dependence on the pressure and energy density for each type of black hole.

4 Results and discussion

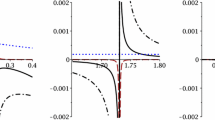
Figure 1 presents the normalized pressure \(p/T^4\) as a function of the temperature T. The double-dotted, dashed, solid, and dotted curves refer to the different types of black holes (non-charged non-rotating, rotating, charged, and charged-rotating, respectively), Eq. (11). We find that the normalized pressure increases rapidly with the increase in temperature for all types of studied black holes, especially at low T. Then, \(p/T^4\) increases slowly till reach to plateau behaviour with the increase in T especially for charge-rotating black hole. This transition with the increase in temperature refers to the phase transition from the confined hadrons to the de-confined phase (Quark gluon plasma).

Figure 2 shows the normalized energy density \(\varepsilon /T^4\) in dependence of the temperature T. The double-dotted, dashed, solid, and dotted curves refer to the different types of black holes (non-charged non-rotating, rotating, charged, and charged-rotating, respectively), Eq. (12). At low temperature (\(T<0.2\) GeV), the normalized energy density for all types of BHs increase rapidly. Then, with the increase in T, \(\varepsilon /T^4\) will increases slowly till reach to plateau behaviour for all types of BHs. But values of \(\varepsilon /T^4\) for charged BHs are less than values for rotating BHs at high T and all of them are less than values for charged-rotating BH. So, we conclude that the transition of \(\varepsilon /T^4\) refers also to the transition form the hadronization to the de-confined state.

Fig. 1
figure 1

Normalized pressure \(p/T^4\) as a function of temperature T for the various types of black holes

Full size image
Fig. 2
figure 2

Normalized energy density \(\varepsilon /T^4\) is given in dependence on the temperatures T for the different types of black holes

Full size image

We propose EoS for each type of studied black holes as

  • for Sch BH

    $$\begin{aligned} p(\varepsilon ) = a_1 \varepsilon ^{b_1}, \end{aligned}$$
    (15)

    where \(a_1=0.3319\pm 0.0003\) and \(b_1=1.1767\pm 0.001\), as represented in Fig. 3.

  • for RN BH

    $$\begin{aligned} p(\varepsilon ) = a_2 \varepsilon ^{b_2}, \end{aligned}$$
    (16)

    where \(a_2=0.5823\pm 0.0005\) and \(b_2=1.2086\pm 0.0012\), as depicted in Fig. 3.

  • for K BH

    $$\begin{aligned} p(\varepsilon ) = a_3 \varepsilon ^{b_3}, \end{aligned}$$
    (17)

    where \(a_3=0.2648\pm 0.0002\) and \(b_3=1.186\pm 0.0011\), as presented in Fig. 3.

  • for KN BH

    $$\begin{aligned} p(\varepsilon ) = a_4 \varepsilon ^{b_4}, \end{aligned}$$
    (18)

    where \(a_4=0.535\pm 0.0005\) and \(b_4=1.2326\pm 0.0014\), as represented in Fig. 3.

Figure 3 depicts the dependence of the pressure p on the energy density \(\varepsilon \) for the fourth types of black holes. The symbols show the values of pressure as a function of energy density for the fourth types of black holes which calculated from Eqs. (11, 12). Cross, square, circle, and triangle symbols refer to non-charged non-rotating BH (Sch BH), charged BH (RN BH), rotating BH (K BH), and charged-rotating BH (KN BH), respectively. The double-dotted, dashed, solid, and dotted curves refer to the proposed EoS for each type of black hole, Eqs. (15–18). We find that \(\varepsilon \) increases with the increase in p. We note that values of constants \(a, \;b\) differ with the type of BH and b ranges from \(1.177-1.233\) depending on the type of BH.

Fig. 3
figure 3

Pressure p is shown in dependence on \(\varepsilon \) for the all types of black holes. Our calculations for pressure and energy density using Eqs. (11, 12) are depicted by symbols. The statistical fits are given by curves, Eqs. (15–18)

Full size image

We calculate the squared speed of sound \(C_s^2\) which can be derived as \(C_s^2=\partial p/\partial \varepsilon \). Differentiate Eqs. (15–18) with respect to \(\varepsilon \) for each type of black holes, then plot the relation between the squared speed of sound and the temperature as depicted in Fig. 4. Results for \(C_s^2\) also describe the equation of state for all types of black holes [45, 46]. We find that \(C_s^2\) increases with the increase in T for all types of BHs. But \(C_s^2\) for rotating BH is lower than \(C_s^2\) for non-charged non-rotating BH which is lower than charged BH and all of them are lower than the ones of charged-rotating BH.

The ratio of bulk viscosity to shear viscosity for each type of black hole can be calculated using the squared speed of sound. Substitute about the squared speed of sound for each type of black hole in the following expression [47]

$$\begin{aligned} \frac{\zeta }{\eta } = 15 \sigma _0 \left( \frac{1}{3}-C_s^2\right) ^2, \end{aligned}$$
(19)

where \(\sigma _0=0.01\) [47]. Figure 5 shows the ratio of the bulk viscosity to shear viscosity \(\zeta /\eta \) as a function of the temperature T for different types of black holes. The double-dotted, dashed, solid, and dotted curves refer to the different types of black holes (non-charged non-rotating, rotating, charged, and charged-rotating, respectively), Eq. (19). We find that \(\zeta /\eta \) decrease with the increasing in T for all types of black holes. Also, we notice that \(\zeta /\eta \) for rotating BH and non-charged non-rotating BH greater than for other types of black holes and also decreases rapidly with the increasing in T. While, \(\zeta /\eta \) decreases slowly for the other types of BHs which indicate that the charge of the black hole effect on the viscosity. This means that the bulk viscosity for the charged black holes decreases rapidly with the increase in the temperature.

Fig. 4
figure 4

The speed of sound squared \(C_s^2\) is depicted in dependence of the temperature T for different types of black holes

Full size image
Fig. 5
figure 5

The ratio of the bulk viscosity to shear viscosity \(\zeta /\eta \) is depicted in dependence of the temperature T for different types of black holes

Full size image

5 Conclusions

In the present paper, we study the thermodynamic properties of various kinds of black holes to propose EoS for each type of black holes using the thermodynamics laws of black holes. We estimate the pressure and energy density for Schwarzschild, Reissner–Nordström, Kerr, and Kerr-Newman black holes and compare results with each other. We noticed that the normalized pressure and the normalized energy density increases rapidly with the increase in temperature for all types of studied black holes, especially at low T. Then, both of them (\(p/T^4\), \(\varepsilon /T^4\)) increases slowly till reach to plateau behaviour with the increase in T especially for charge-rotating black hole. This transition with the increase in temperature refers to the phase transition from hadronization to QGP.

We also have proposed EoS for each type of studied black holes. We have found that \(\varepsilon \) increases with the increase in p. We have showed that values of constants \(a, \;b\) differ with the type of BH and b ranges from 1.177–1.233 depending on the type of BH. Then, we estimate the squared speed of sound \(C_s^2\) and plot the \(C_s^2\)-T curves for these black holes. We find that \(C_s^2\) increases with the increase in T for all types of BHs. But \(C_s^2\) for rotating BH is lower than \(C_s^2\) for non-charged non-rotating BH which is lower than charged BH and all of them are lower than the ones of charged-rotating BH.

Finally, the ratio of the bulk viscosity to shear viscosity \(\zeta /\eta \) has estimated for each type of black holes. We calculated \(\zeta /\eta \) as a function of the temperature T for different types of black holes using the squared speed of sound values. We found that \(\zeta /\eta \) decrease with the increasing in T for all types of black holes. Also, we notice that \(\zeta /\eta \) for rotating BH and non-charged non-rotating BH greater than for other types of black holes and also decreases rapidly with the increasing in T. While, \(\zeta /\eta \) decreases slowly for the other types of BHs which indicate that the charge of the black hole effect on the viscosity which means that the bulk viscosity for the charged black holes decreases rapidly with the increase in the temperature.