Tidal properties of D-dimensional Tangherlini black holes

Abstract

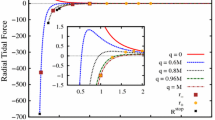
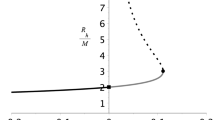
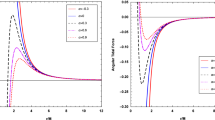
The aim of this paper is to investigate tidal forces in multidimensional spherically simmetric spacetimes. We consider geodesic deviation equation in Schwarzschild–Tangherlini metric and its electrically charged version. We show that these equations can be solved explicity for radial geodesics as quadratures in spaces of any dimension. In the cases of five, six and seven dimensional spaces, these solutions can be represented in terms of elliptic integrals. For spacetimes of higher dimension asymptotics of the solution are found instead. We established that the greater the dimension of space is, the stronger the tidal stretch along the radial direction in the vicinity of physical singularity is, whereas the tidal compression in direction transverse to the radial one, does not change in the leading order starting from a certain dimension. Also, in the case of non-radial geodesics, the presence of black hole electric charge does not affect the force of transverse compression in the leading order. Finally, for non-radial geodesics with nonzero angular momentum, the local properties of solutions of geodesic deviation equations in the vicinity of a singularity are studied.

Appendices

Fuchs’ equations and Frobenius method

Second-order differential equation for a complex variable function y(z)

$$\begin{aligned} y''(z)+p(z)y'(z)+q(z)y(z)=0 \end{aligned}$$

(80)

has a regular singular point at $z=z_0$, if the coefficients p(z), q(z) have pole at $z=z_0$ not higher than the first and second order, respectively. In other words, the coefficients are decomposed into Laurent series as follows:

$$\begin{aligned} p(z)= & \sum _{k=-1}^{\infty }a_k(z-z_0)^{k}, \end{aligned}$$

(81a)

$$\begin{aligned} q(z)= & \sum _{k=-2}^{\infty }b_k(z-z_0)^{k}. \end{aligned}$$

(81b)

In the vicinity of a regular singular point $z=z_0$ two linearly independent solutions of Eq. (80) can be found using the generalized series

$$\begin{aligned} y_1(z)= & (z-z_0)^{\zeta _1}\sum _{k=0}^{\infty }c_k(z-z_0)^k, \end{aligned}$$

(82a)

$$\begin{aligned} y_2(z)= & (z-z_0)^{\zeta _2}\sum _{k=0}^{\infty }d_k(z-z_0)^k, \end{aligned}$$

(82b)

where $\zeta _1$ and $\zeta _2$ are roots of quadratic equation

$$\begin{aligned} \zeta (\zeta -1)+a_{-1}\zeta +b_{-2}=0. \end{aligned}$$

(83)

If difference $\zeta _1-\zeta _2$ is not integer, then both solutions of Eq. (80) coincide with the power series (82), but if difference $\zeta _1~-~\zeta _2$ is positive integer, then the first solution for higher $\zeta _1$ remains the same (82a) while the second linearly independent solution has another form

$$\begin{aligned} y_2=(z-z_0)^{\zeta _2}\sum _{k=0}^{\infty }d_k(z-z_0)^k+Ay_1(z)\ln (z-z_0). \end{aligned}$$

(84)

Elliptic integrals

The simplest indefinite elliptic integral is the expression

$$\begin{aligned} \int R\left( z,y(z)\right) \textrm{d}z, \end{aligned}$$

(85)

where $y(z)=\sqrt{a_0+a_1z+a_2z^2+a_3z^3+a_4z^4}$ and R(z, y) is rational function of two variables. Any elliptic integral can be brought to the form

$$\begin{aligned} \int R_1(z)\textrm{d}z+\int \frac{R_2(z)}{y(z)}\textrm{d}z, \end{aligned}$$

(86)

where $R_1(z)$ and $R_2(z)$ are rational functions of one variable. Linear fractional transformation

$$\begin{aligned} z=\frac{ax+b}{cx+d} \end{aligned}$$

(87)

can turn the second term of (86) into

$$\begin{aligned} \int \frac{\tilde{R}_2(x)}{\tilde{y}(x)}\textrm{d}x, \end{aligned}$$

(88)

where $\tilde{R}_2(x)$ is another rational function, and $\tilde{y}(x)$ is reduced to Weierstrass form

$$\begin{aligned} \tilde{y}(x)=\sqrt{4x^3-g_2x-g_3}, \end{aligned}$$

(89)

or Legendre form

$$\begin{aligned} \tilde{y}(x)=\sqrt{\left( 1-x^2\right) \left( 1-k^2x^2\right) }. \end{aligned}$$

(90)

As a result, expression (88) can be represented as a sum of integrals of three kinds.

• In Weierstrass form integrals of three kinds are

  $$\begin{aligned} J_0(x|g_2,g_3)= & \int \frac{\textrm{d}x}{\sqrt{4x^3-g_2x-g_3}}, \end{aligned}$$

  (91a)
  $$\begin{aligned} J_1(x|g_2,g_3)= & \int \frac{x\textrm{d}x}{\sqrt{4x^3-g_2x-g_3}}, \end{aligned}$$

  (91b)
  $$\begin{aligned} H(x|g_2,g_3)= & \int \frac{\textrm{d}x}{(x-c)\sqrt{4x^3-g_2x-g_3}}. \end{aligned}$$

  (91c)

• In Legendre form integrals of three kinds are

  $$\begin{aligned} F(x,k)= & \int \frac{\textrm{d}x}{\sqrt{\left( 1-x^2\right) \left( 1-k^2x^2\right) }}, \end{aligned}$$

  (92a)
  $$\begin{aligned} E(x,k)= & \int \sqrt{\frac{1-k^2x^2}{1-x^2}}\textrm{d}x, \end{aligned}$$

  (92b)
  $$\begin{aligned} \Pi (x,k,c)= & \int \frac{\textrm{d}x}{\left( 1-\frac{x^2}{c^2}\right) \sqrt{\left( 1-x^2\right) \left( 1-k^2x^2\right) }}. \end{aligned}$$

  (92c)

Where c is some pole of the function $\tilde{R}_2(x)$, which can be complex.