1 Introduction

Black holes are objects of great fascination for the scientific community as well as for the general public, especially because of their remarkable physical properties. Schwarzschild (uncharged) black holes – the simplest case – have been extensively investigated over the years. However, less attention has been given to Reissner–Nordström (electrically charged) and Kerr (rotating) black holes. The importance of studying these more complex black holes lies in the fact that they present a new set of phenomena that are not present in Schwarzschild spacetimes. Examples are the Penrose process [1], superradiance [2], and interconversion between spin 1 and 2 fields [3, 4], as well as electromagnetic helicity-reversing processes [5]. Reissner–Nordström black holes are of special interest because they allow one to analyze extreme spacetime configurations with spherical symmetry. For example, it has recently been found that extreme Reissner–Nordström black holes absorb and scatter gravitational and electromagnetic waves equally [6, 7]. This equality is a consequence of the supersymmetry that relates photons and gravitons in the extreme Reissner–Nordström spacetime [8].

In this paper we focus on Reissner–Nordström black holes, which are spherically symmetric, and which have a non-zero electric charge but no angular momentum. They are exact solutions of the Einstein–Maxwell equations [9], and in the case of vanishing electric charge, they reduce to the Schwarzschild black holes.

It is well known that a body falling toward the event horizon of a static uncharged black hole experiences stretching in the radial direction and compression in the angular directions [10–14]. However, whether a body may experience stretching or compression in either direction (radial or angular) in Reissner–Nordström spacetime depends on the charge-to-mass ratio of the black hole and where the body is located (see, e.g., Ref. [15]). At certain points of Reissner–Nordström spacetimes, the tidal forces in the radial or angular direction change their sign unlike in Schwarzschild spacetime. In this paper we describe the tidal forces in Reissner–Nordström spacetime in detail. We then solve the geodesic deviation equations to analyze the changes in size of a test body consisting of neutral dust particles in-falling radially toward the Reissner–Nordström black hole. We also point out that the tidal forces can be understood within Newtonian Mechanics if an extra force coming from General Relativity is added, while the geodesic deviation needs to be analyzed using full General Relativity. The remainder of this paper is organized as follows. In Sect. 2 we briefly review relevant facts about Reissner–Nordström black holes. We analyze geodesics in Reissner–Nordström spacetime in Sect. 3 and study tidal forces for charged static black holes in Sect. 4. In Sect. 5 we obtain the solutions of the geodesic deviation equations. Then we present our conclusion in Sect. 6. We use the metric signature \((+,-,-,-)\) and set the speed of light c and Newtonian gravitational constant G to 1 throughout this paper.

2 Reissner–Nordström black holes

The line element of a static charged black hole is given by [9]

$$\begin{aligned} \mathrm{d}{s}^2= & {} g_{\mu \nu }\mathrm{d}x^{\mu }\mathrm{d}x^{\nu }\nonumber \\= & {} f(r)\mathrm{d}t^2 - f(r)^{-1}\mathrm{d}r^2 - r^2(\mathrm{d}\theta ^2 + \sin ^2\theta \mathrm{d}\phi ^2), \end{aligned}$$
(1)

with

$$\begin{aligned} f(r) = 1-\frac{2M}{r} + \frac{q^2}{r^2}, \end{aligned}$$
(2)

where M and q are the mass and charge (in gaussian units) of the black hole, respectively.

There are three possible configurations (with \(q\ne 0\)) for the Reissner–Nordström spacetime:

  1. (i)

    For \(q^2/M^2< 1\), we have a Reissner–Nordström black hole with two horizons.

  2. (ii)

    For \(q^2/M^2 = 1\), we have an extremely charged Reissner–Nordström black hole, with the event horizon located at \(r_{+}=r_{-}=M\).

  3. (iii)

    For \(q^2/M^2 > 1\), we have a naked singularity.

Here we will only consider the cases in which \(q^2/M^2 \le 1\) (black hole spacetimes). (Naked singularities do not occur in nature if the cosmic censor conjecture [16] is true.) The radial coordinates of the horizons, i.e. the zero(s) of the function f(r), are

$$\begin{aligned} r_{+}= & {} M+ \sqrt{M^2- q^2}, \end{aligned}$$
(3)
$$\begin{aligned} r_{-}= & {} M - \sqrt{M^2- q^2}. \end{aligned}$$
(4)

Equation (3) gives the location of the external horizon, or the event horizon, of the black hole and Eq. (4) gives the location of the internal horizon, or the Cauchy horizon, of the black hole [17].

3 Radial geodesics in Reissner–Nordström spacetimes

We consider a radial geodesic motion in spherically symmetric spacetimes with line element (1). By letting \(\mathrm{d}s=\mathrm{d}\tau \) in Eq. (1) we obtain [18]

$$\begin{aligned} f(r)\dot{t}^2 - f(r)^{-1}\dot{r}^2 = 1, \end{aligned}$$
(5)

where the dot represents the differentiation with respect to the proper time \(\tau \). We have let \(\dot{\theta } = \dot{\phi } = 0\) because the motion is radial by assumption. As is well known, \(E=f(r)\dot{t}\) is conserved and is interpreted as the mechanical energy per unit mass of the particle. Substituting this equation into Eq. (5), we obtain

$$\begin{aligned} \frac{\dot{r}^2}{2} = \frac{E^2-f(r)}{2}. \end{aligned}$$
(6)

For the radial infall of a test particle from rest at position b, we obtain \(E=\sqrt{f(r=b)}\) from Eq. (6) [19].

By defining the “Newtonian radial acceleration” [20] as

$$\begin{aligned} A^{(R)} \equiv \ddot{r}, \end{aligned}$$
(7)

we find from Eq. (6) that

$$\begin{aligned} A^{(R)} = -\frac{f'(r)}{2}, \end{aligned}$$
(8)

where the prime denotes the differentiation with respect to the radial coordinate r. For Reissner–Nordström spacetime this becomes

$$\begin{aligned} A^{(R)} = -\frac{M}{r^2} + \frac{q^2}{r^3}. \end{aligned}$$
(9)

This gives us the “Newtonian radial acceleration” that the Reissner–Nordström black hole “exerts” on a neutral free-falling massive test body.

The term \(q^2/r^3\) in Eq. (9) represents a purely relativistic effect. It has been analyzed in the literature (see Ref. [21]) and has been a theme of discussion (see Refs. [22, 23]). It is interesting to note that the test particle falling freely from rest at \(r=b> r_{+}\) (for \(q\ne 0\)) would bounce back at \(R^{\text {stop}}\). The radius \(R^{\text {stop}}\) can readily be found as a root of \(E^2 - f(r)\) as

$$\begin{aligned} R^{\text {stop}} = \frac{bq^2}{2Mb-q^2}, \end{aligned}$$
(10)

where we recall that b is the initial position of test particle (starting from rest). The radius \(R^{\text {stop}}\) is always located inside the internal (Cauchy) horizon. In the limit \(b\rightarrow \infty \), one finds \(R^{\text {stop}} \rightarrow q^2/2M\). In the maximal analytic extension of Reissner–Nordström spacetime the particle, after bouncing back at \(R^{\text {stop}}\), would emerge in a different asymptotically flat region of the spacetime [11]. For more details as regards the physics of free-falling neutral particles in Reissner–Nordström black holes, we refer the reader to Refs. [10, 11]. We note in passing that the Cauchy horizon is known to be unstable [24]. Thus, the part of the spacetime beyond the Cauchy horizon in the maximal analytic extension of Reissner–Nordström spacetime is unphysical.

4 Tidal forces in Reissner–Nordström spacetime on a neutral body in radial free fall

Now let us turn our attention to the tidal forces acting in Reissner–Nordström spacetime. As is well known [10, 11], the equation for the spacelike components of the geodesic deviation vector \(\eta ^{\mu }\) that describes the distance between two infinitesimally close particles in free fall is given by

$$\begin{aligned} \frac{\mathrm{D}^2\eta ^\mu }{\mathrm{D}\tau ^2} - R^{\mu }_{\ \sigma \nu \rho }v^{\sigma }v^{\nu }\eta ^\rho =0, \end{aligned}$$
(11)

where \(v^\nu \) is the unit vector tangent to the geodesic. We introduce the tetrad basis for radial free-fall reference frames:

$$\begin{aligned}&\hat{e}^{\ \mu }_{\widehat{0}} = \left( \frac{E}{f},\,-\sqrt{E^2-f},\,0,\,0\right) ,\\&\hat{e}^{\ \mu }_{\widehat{1}} = \left( \frac{-\sqrt{E^2-f}}{f},\,E,\,0,\,0\right) ,\\&\hat{e}^{\ \mu }_{\widehat{2}} = r^{-1} \left( 0,\,0,\,1,\,0\right) , \\&\hat{e}^{\ \mu }_{\widehat{3}} = \left( r\sin {\theta }\right) ^{-1} \left( 0,\,0,\,0,\,1\right) , \end{aligned}$$

where \((x^0,x^1,x^2,x^3) = (t,r,\theta ,\phi )\). These unit vectors satisfy the following orthonormality condition:

$$\begin{aligned} \hat{e}^{\ \alpha }_{\widehat{\mu }}\hat{e}_{\widehat{\nu } \alpha } = \eta _{\widehat{\mu }\widehat{\nu }}, \end{aligned}$$
(12)

where \(\eta _{\widehat{\mu }\widehat{\nu }}\) is the Minkowski metric (for more details, see Ref. [10]). We have \(\hat{e}^{\ \mu }_{\widehat{0}} = v^\mu \). The geodesic deviation vector, also called the Jacobi vector, can be expanded as

$$\begin{aligned} \eta ^{\mu } = \hat{e}_{\widehat{\nu }}^{\ \mu }\eta ^{\widehat{\nu }}. \end{aligned}$$
(13)

Here we note that \(\eta ^{\widehat{0}} =0\) [10].

The non-vanishing independent components of the Riemann tensor in spherically symmetric spacetimes, including the Reissner–Nordström spacetime, are (see, e.g., Ref. [18])

$$\begin{aligned}&R^1_{\ 212}= -\frac{rf^{\prime }}{2},\quad R^1_{\ 313}= -\frac{rf^{\prime }}{2}\sin ^2\theta ,\\&R^1_{\ 010}= \frac{ff^{\prime \prime }}{2},\quad R^2_{\ 323}= \left( 1-f\right) \sin ^2\theta ,\\&R^2_{\ 020}= \frac{ff^{\prime }}{2r},\quad R^3_{\ 030}= \frac{ff^{\prime }}{2r}. \end{aligned}$$

Using these expressions in Eq. (11) and noting that the vectors \({\hat{e}_{\widehat{\nu }}}^{\ \mu }\) are all parallelly transported along the geodesic, we find the following equations for tidal forces in radial free-fall reference frames (see, e.g., Ref. [15]):

$$\begin{aligned} \ddot{\eta }^{\widehat{1}}= & {} -\frac{f^{\prime \prime }}{2}\eta ^{\widehat{1}}, \end{aligned}$$
(14)
$$\begin{aligned} \ddot{\eta }^{\widehat{i}}= & {} -\frac{f^{\prime }}{2r}\eta ^{\widehat{i}}, \end{aligned}$$
(15)

where \(i=2,3\).

Substituting the explicit form (2) of f(r) in Reissner–Nordström spacetime into Eqs. (14) and (15) we see that the tidal forces in this spacetime depend on the mass and charge of a black hole. We also see that the radial and angular tidal forces may vanish, in contrast to what happens in the Schwarzschild spacetime (\(q=0\)) [10–13]. We note that the expressions of the tidal forces, given by Eqs. (14) and (15), are identical to the Newtonian tidal forces with the force \(-f'/2\) in the radial direction. In the remainder of this paper we study Eqs. (14) and (15) for Reissner–Nordström spacetime in detail.

4.1 Radial tidal force

From Eqs. (2) and (14) it can readily be shown that the radial tidal force vanishes at \(r=R^{\text {rtf}}_0\), where

$$\begin{aligned} R^{\text {rtf}}_0 = \frac{3q^2}{2M}. \end{aligned}$$
(16)

By comparing this and the expression (3) for the event horizon we find that, if \(2\sqrt{2}/3 \le q/M \le 1\),Footnote 1 the radial tidal force inverts its direction and becomes compressing just outside the event horizon. The radial tidal force takes a maximum value at \(R^{\text {rtf}}_{\text {max}}\) where

$$\begin{aligned} R^{\text {rtf}}_{\text {max}} = \frac{2q^2}{M}. \end{aligned}$$
(17)

The maximum radial stretching at \(r = R^{\text {rft}}_{\text {max}}\) is [21]

$$\begin{aligned} \ddot{\eta }^{\widehat{1}}|_{\text {max}}= \frac{M^4}{16q^6} \eta ^{\widehat{1}}. \end{aligned}$$
(18)

In Fig. 1 we plot the radial tidal force given by Eq. (14) for Reissner–Nordström black holes for different values of the black hole charge. For \(q\ne 0\) there is always a local maximum of the radial tidal force. In the Schwarzschild case (\(q=0\)) the radial tidal force is always positive and diverges (infinite radial stretching) as the body approaches the singularity.

Fig. 1
figure 1

Radial tidal force for Reissner–Nordström black holes with different choices of q / M (\(q=0.6M\), \(q=0.8M\), \(q=0.96M\), and \(q=M\)), as well as for the Schwarzschild black hole (\(q=0\)). The positions of \(R^{\text {stop}}\), \(r_{-}\), and \(r_{+}\), are exhibited in each plot. We have chosen \(b=100M\)

Full size image

4.2 Angular tidal forces

We find from Eqs. (2) and (15) that the angular tidal forces vanish at

$$\begin{aligned} \frac{R^{\text {atf}}_{0}}{M} = \frac{q^2}{M^2}. \end{aligned}$$
(19)

From Eqs. (3), (4) and (19), we obtain

$$\begin{aligned} r_{-} \le {R^{\text {atf}}_{0}} \le r_{+}, \end{aligned}$$
(20)

i.e., the angular tidal forces are zero at some point between the external and internal horizons, with the equality in Eq. (20) holding for the extremely charged black hole. In Fig. 2 we plot the angular tidal forces given by Eq. (15). We note that for \(q=0\) (Schwarzschild black hole) angular tidal forces are never zero and tend to minus infinity (infinite angular compressing) as the body approaches the singularity.

Fig. 2
figure 2

Angular tidal forces for different choices of the charge-to-mass ratio (\(q/M=0, \ 0.6, \ 0.8, \ 0.96, \ 1.0\)). The positions of \(R^{\text {stop}}\), \(r_{-}\), and \(r_{+}\), are exhibited in each plot. We have chosen \(b=100M\)

Full size image

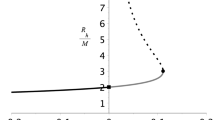
In Fig. 3 we plot \(r_{+}\), \(r_{-}\), \(R^{\text {stop}}\), \(R_0^{\text {rtf}}\), and \(R_0^{\text {atf}}\), given by Eqs. (3), (4), (10), (16), and (19), respectively, as functions of q / M. We used \(b=100M\) to compute \(R^{\text {stop}}\).

Fig. 3
figure 3

\(R^{\text {stop}}\), \(R_0^{\text {rtf}}\), \(R_0^{\text {atf}}\), \(r_{-}\), and \(r_{+}\), plotted as functions of q / M. The intersection point of \(R_0^{\text {rtf}}\) and \(r_{+}\) (black dot) happens at \(q/M=2\sqrt{2}/3\), where the radial tidal force inverts its direction on the event horizon. \(R^{\text {stop}}\) is always located inside the internal (Cauchy) horizon. We have chosen \(b=100M\)

Full size image
Fig. 4
figure 4

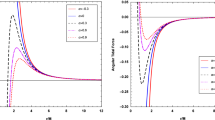
Radial components of the geodesic deviation vector for several values of charge-to-mass ratio with \(b=100M\) and for \(q/M=0.6\) with several values of b. The figures on the left correspond to IC I, whereas the figures on the right correspond to IC II. The positions of \(R^{\text {stop}}\), \(r_{-}\), and \(r_{+}\) are exhibited in each plot

Full size image
Fig. 5
figure 5

Angular components of the geodesic deviation vector for several values of charge-to-mass ratio with \(b=100M\) and for \(q/M=0.6\) with several values of b. The positions of \(R^{\text {stop}}\), \(r_{-}\), and \(r_{+}\), are exhibited in each plot

Full size image

5 Solutions of the geodesic deviation equations in Reissner–Nordström spacetimes

In this section we solve the geodesic deviation equations (14) and (15) and find the geodesic deviation vectors for radially free-falling geodesics as functions of r. As stated in the Introduction, we are considering a test body consisting of neutral dust particles in-falling radially toward the Reissner–Nordström black hole. It is straightforward to convert Eqs. (14) and (15) to differential equations in r by using \(\mathrm{d}r/\mathrm{d}\tau = - \sqrt{E^2 - f(r)}\), which results immediately from Eq. (6). Thus, we find

$$\begin{aligned} (E^2-f)\eta ^{\widehat{1} \prime \prime } -\frac{f^{\prime }}{2}\eta ^{\widehat{1} \prime }+\frac{f^{\prime \prime }}{2}\eta ^{\widehat{1}}= & {} 0, \end{aligned}$$
(21)
$$\begin{aligned} (E^2-f)\eta ^{\widehat{i} \prime \prime } -\frac{f^{\prime }}{2}\eta ^{\widehat{i} \prime }+\frac{f^{\prime }}{2r}\eta ^{\widehat{i}}= & {} 0. \end{aligned}$$
(22)

The analytical solutions of Eqs. (21) and (22) may be expressed in the following general form: for the radial component

$$\begin{aligned} \eta ^{\widehat{1}}(r) = \sqrt{E^2-f}\left[ C_1+C_2\int \frac{\mathrm{d}r}{(E^2 - f)^{3/2}}\right] , \end{aligned}$$
(23)

and for the angular components

$$\begin{aligned} \eta ^{\widehat{i}}(r) = \left[ C_3 +C_4\int \frac{\mathrm{d}r}{r^2(E^2-f)^{1/2}}\right] r, \end{aligned}$$
(24)

where \(C_1\), \(C_2\), \(C_3\), and \(C_4\) are constants of integration. Now we specialize to Reissner–Nordström spacetime. We consider the geodesic corresponding to a body released from rest at \(r=b > r_{+}\). Then the solutions to the geodesic deviation equations about this geodesic can be written as follows:

$$\begin{aligned} \eta ^{\widehat{1}}(r)= & {} \frac{b^3}{Mb-q^2}\dot{\eta }^{\widehat{1}}(b)(E^2-f)^{1/2}\nonumber \\&+\, \frac{Mb-q^2}{b(2Mb-q^2)}\eta ^{\widehat{1}}(b)g(r), \end{aligned}$$
(25)

where

$$\begin{aligned} g(r)= & {} \frac{q^2}{M^2 - (1-E^2)q^2}\left( M - \frac{q^2}{r}\right) + 2r \nonumber \\&+\, \frac{3}{1-E^2}\left[ r(E^2 -f) + \frac{M(E^2-f)^{1/2}}{(1-E^2)^{1/2}}\right. \nonumber \\&\times \left. \cos ^{-1}\frac{(1-E^2)r - M}{M-q^2/b}\right] , \end{aligned}$$
(26)

for \( 0 \le q \le 1\).

For \(q> 0\), the angular components read

$$\begin{aligned} \eta ^{\widehat{i}}(r) = \left[ \frac{1}{b}\eta ^{\widehat{i}}(b) + \frac{b}{q}\dot{\eta }^{\widehat{i}}(b) \cos ^{-1}\frac{M-q^2/r}{M-q^2/b}\right] r, \end{aligned}$$
(27)

and, for \(q=0\), they read

$$\begin{aligned} \eta ^{\widehat{i}}(r) = \left[ \frac{1}{b}\eta ^{\widehat{i}}(b) + \dot{\eta }^{\widehat{i}}(b) \left[ \frac{2b}{M}\left( \frac{b}{r} - 1\right) \right] ^{1/2}\right] r. \end{aligned}$$
(28)

Here, \(\eta ^{\widehat{1}}(b)\) and \(\eta ^{\widehat{i}}(b)\) are the radial and angular components of the initial geodesic deviation vector at \(r=b\) and \(\dot{\eta }^{\widehat{1}}(b)\) and \(\dot{\eta }^{\widehat{i}}(b)\) are the corresponding derivatives with respect to the proper time \(\tau \). We plot in Figs. 4 and 5 the radial and angular components, respectively, of the geodesic deviation vector of a body in-falling from rest at \(r = b\) toward the black hole for different choices of the black hole charge. Here we consider two different initial conditions, IC I and IC II, for the radial and angular components of the geodesic deviation vector at \(r=b\). For the first type, IC I, we choose \(\eta ^{\widehat{1}}>0\), \(\eta ^{\widehat{i}}>0\), \(\dot{\eta }^{\widehat{1}}=0\), and \(\dot{\eta }^{\widehat{i}}=0\), at \(r = b\). For the second type, IC II, we choose \(\eta ^{\widehat{1}}=0\), \(\eta ^{\widehat{i}}=0\), \(\dot{\eta }^{\widehat{1}}>0\), and \(\dot{\eta }^{\widehat{i}}>0\), at \(r = b\). The condition IC I corresponds to releasing a body consisting of dust at rest with no internal motion. The condition IC II, on the other hand, corresponds to letting such a body ‘explode’ from a point at \(r=b\). The behavior of the geodesic deviation vector is almost identical for different values of q until r becomes of the same order as the horizon radius. This is as expected because for large r the spacetime looks similar for all values of q. It can be seen from Fig. 4 that, for IC II (figures on the right), during the infall from \(r=b\) to \(r_{+}\), the radial component always increases. If \(q \ne 0\), while the body falls from the outer horizon (\(r=r_{+}\)) to the inner horizon (\(r_{-}\)), the radial component of the geodesic deviation vector keeps increasing, reaches a maximum, and then starts decreasing until it reaches \(r_{-}\). While the body falls in the region between \(r_{-}\) and \(R^{\text {stop}}\), the radial component of the geodesic deviation vector keeps decreasing, finally shrinking to zero at \(R^{\text {stop}}\). (Recall, however, that, since the inner (Cauchy) horizon is unstable, the region between \(r=r_{-}\) and \(R^{\text {stop}}\) is unphysical.) The radial component of the geodesic deviation vector with the initial condition IC I (shown on the left of Fig. 4) behaves similarly to IC II, except that in the former case it becomes zero at some r satisfying \(R^{\text {stop}} < r < r_{-}\).Footnote 2

With the initial conditions IC II, it can be seen from Fig. 5 (figures on the right) that the angular components increase in the beginning but start decreasing around \(r=b/2\), reflecting the compressing nature of the angular tidal force. They then start increasing at some point before the body reaches \(r=R^{\text {stop}}\) if \(q \ne 0\) because of the change in the sign of the angular components of the tidal force. If the initial conditions are IC I, the angular components of the geodesic deviation vector decrease linearly in r, as shown in the figures on the left of Fig. 5. This is expected because all geodesics with no angular velocity trace out straight radial lines.

We also can see from these figures that for Schwarzschild spacetime (\(q=0\)) the radial component of the geodesic deviation vector becomes infinite at the singularity \(r=0\) whereas the angular components vanish there, as expected [13, 25].

6 Conclusion

In this paper we investigated tidal forces in Reissner–Nordström spacetimes, which depend on the charge-to-mass ratio of the black hole. For certain values of these parameters, the radial tidal force can change from stretching to compressing outside the event horizon. We also noted that the angular tidal forces can only be zero between the two horizons of the charged black hole.

We pointed out that the tidal forces in Schwarzschild and Reissner–Nordström spacetimes can be quite different close to the black hole. In Schwarzschild spacetime the tidal forces always cause stretching in the radial direction and compression in the angular directions whereas in Reissner–Nordström spacetime they may cause either stretching or compression in any direction, depending on the charge-to-mass ratio of the Reissner–Nordström black hole and the radial coordinate.

We also noted that the geodesic deviation equations about a radially free-falling geodesic can be solved analytically. In particular, we examined the behavior of the geodesic deviation vector for such a geodesic under the influence of tidal forces created by static charged black holes. We noted that the behavior of the geodesic deviation vector is qualitatively the same for both Schwarzschild and Reissner–Nordström black holes away from the horizon. However, its behavior is considerably different for Schwarzschild and Reissner–Nordström black holes inside the event horizon, as we showed in Sect. 5. For instance, for a charged black hole, at its closest approach to the singularity, the radial component of the geodesic deviation vector becomes zero for a certain initial condition though its angular components remain finite there (though this point is beyond the Cauchy horizon and, hence, in an unphysical region). In contrast, for the uncharged black hole the radial component of the geodesic deviation vector increases all the way to the singularity whereas the angular components shrink to zero at the singularity.