Based on insurance processes, the article analyzes automation decisions in business processes. A method to economically decide between the comparative advantages of manual and automated execution is developed. Applying criteria of value-based management to each claim, the execution that generates the optimal net present value of cash-flow is selected. Contrary to heuristic business rules this approach allows a specific control of the method of execution ex ante and during execution. Capacity restrictions are considered and thus considerations regarding resource planning and resources utility can be included.

1 Introduction

In all industrial nations the service sector is the largest and fastest growing sector of the economy (Maglio et al. 2006, p. 82). Increasing competitive pressure in combination with technological and regulatory changes drive the transformation of business processes of service providers like insurance companies (Drew 1996, p. 23). To improve the efficiency of business processes and therefore their value proposition, process orientation is not sufficient. In fact, insurance providers need to realize a higher level of standardization, automation, and flexibility in their operations and structures (Walter et al. 2007, p. 7). At the same time a flexible reaction to customer needs is essential for competition.

Banks have recognized this trend that leads not only to standardization, automation, and flexibility of information technology (IT) itself (Walter et al. 2007, p. 7) but also of workflows with IT (Grob et al. 2008, p. 268): German Postbank established the “Betriebscenter für Banken” to handle a high quantity of transactions with standardized processes efficiently (Achenbach 2006, p. 210). Insurance providers are following this example and refer to these activities as industrialization of their processes (Uzquiano 2008, p. 14): 39% of those interviewed in Capgemini 2006 (p. 8) are pursuing actions of process optimization, standardization, and automation in insurance business. Even after accomplishing business process reengineering the automated and standardized processes can potentially be optimized. This potential is rarely used as is done in the project “Dark Process Optimization” of Postbank (Berensmann 2005, p. 277). It is the goal of this article to analyze the evaluation of the benefits of fast and cheap automated processing on the one hand and those of manual handling on the other hand (creativity and the ability to solve complex problems) from a financial perspective.

The article is structured as follows: In Sect. 2 the requirements for an evaluation and optimization of service processes are identified and they are compared to approaches applied in science and industry in order to show the present gap in research. Applying a formal-deductive method (Wilde and Hess 2007, p. 282) and taking a value-based management into consideration, a model to support automation decisions in processing is developed in Sect. 3. The application is illustrated using a case study for the regulation of glass claims in Sect. 4. Section 5 summarizes the implications of the model, evaluates them critically and presents further research needs.

2 Decisions on Process Automation in Service Processes – Particularly in Insurance Processes

Insurance companies deal not only with the completion of policies and the reinsurance of parts of the taken risks, but amongst others they are also occupied with processing various insurance claims e.g. property or car insurance claims. Depending on the class of insurance and the policy the claim can be designed differently and will thus be processed differently, e.g. an auto insurance claim will be processed in a different way according to if the customer has a fully comprehensive or part insurance cover. While the claims are being processed, various actions will be performed either by the actor “human” or “machine” (Ferstl et al. 1996, p. 8). According to Ferstl and Sinz (1995, pp. 209 ff) there is a differentiation between “automated systems with operations performed by machines, non-automated systems with manual operations and partially automated systems”. We distinguish between actions processed entirely manually and in an exclusively automated way. Consequently there are also various degrees of automation (DA), i.e. different combinations of manually and automated processed actions.

2.1 Requirements for a Financial Evaluation of the Degree of Automation

We are looking at insurance processes which have already been subject to Business Process Reengineering to achieve standardized and automated paths through the process. The question is now, how to determine the optimal configuration.

The optimal path through the process is usually identified by business rules that indicate which processes and resources are used to produce an artifact (Grob et al. 2008, p. 269). These rules are hardly ever uniformly specified (Schacher and Grässler 2006, p. 1), they are often not well-grounded in economical theory, they are complicated to use in dynamic environments and they make multifaceted demands on personnel and machines (Grob et al. 2008, p. 269). The performance of processes and subsequently their optimization has to be determined using monetary and comparable measurements. An evaluation that grounds in a criterion of value-based management additionally makes it possible to calculate the value proposition of a single process to the enterprise value, which contains not only returns but also risks. We postulate:

  1. (R1)

    Processes are examined future-oriented and monetarily on the basis of discounted cash flows (CF), i.e. applying the present value of future incoming and outgoing payment allows to include long-term effects like changes in customer relationships. Risk is also taken into account.

After acquisition there are only few ongoing payments for automated systems. Due to the high capacity and productivity of these systems it can be assumed that a maximum DA is targeted. However, to solve highly dynamic and complex problems the flexibility and creativity of humans is required. Exempli gratia, the absence of contact with customers that comes along with full automation of whole processes can lead to customer dissatisfaction. There are also various disadvantages of manual processing: Employees have only a limited work schedule and repetitive activities exhaust them, both of which can lead to an increasing error rate (Malitz 2007, p. 2). Since the process environment changes dynamically, it must be possible to consider the choice of manual or automated processing during the realization of the process.

  1. (R2)

    The method to evaluate the appropriate DA is applicable ex ante and during realization.

To select an optimal path through the process, it is essential to possess the required creativity and ability to solve problems. Lewis and Jones (1990, p. 39) suggest the following categorization: frequently occurring routine tasks, tasks with a medium degree of complexity, unplanned and unknown tasks (i.e. project activities) which do not have any references. We focus on tasks with a medium degree of complexity which depend on the specification of the process input e.g. the insurance claim.

  1. (R3)

    The selection of the appropriate DA depends on the complexity of the specific process input.

Different methods of processing and a changing number of arriving process instances (e.g. peaks because of thunderstorms vs. summer depression) result in different capacity loads. In contrast to long-term capacity planning, we analyze the effects that occur when additional resources are required in manual processing or when different quantities arrive at the process.

  1. (R4)

    The evaluation and optimization includes a capacity consideration, i.e. responses to changes in the number of arriving process inputs and available resources are regarded.

The selected capacity level influences the process quality and thus the quality of the service which is perceived by the customer (Adenso-Diaz et al. 2002, p. 300). Customer-orientation is of high importance in service delivery (Lamberti 2004, p. 3) as customers show their satisfaction with the service through modifications in their future payment patterns. This has an effect on the customer and thus on the enterprise value and has to be integrated – like all payments that incur before, during, and after the process realization – into the valuation.

  1. (R5)

    An extensive evaluation of the process realization is carried out, i.e. all direct and indirect process-outcomes which occur currently and in future must be factored in the valuation of business processes.

All above mentioned requirements should be satisfied by an approach dealing with the financial evaluation of the DA of insurance processes.

2.2 Related Work

Based on the presented requirements the approaches of Delpachitra (2008), Adenso-Diaz et al. (2002), Balasubramanian and Gupta (2005) and Grob et al. (2008) are compared in Table  1 . Even though the discussed approaches can be applied for automated processes, only Balasubramanian and Gupta (2005) enable an ex-ante determination of the DA using metrics (e.g. activity automation factor). In literature, there is an intense discussion about the evaluation and optimization of processes using target achievement of structural metrics as process costs, cycle time, and reliability (Nissen 1994; Tjaden et al. 1996; Kueng and Kawalek 1997). Nissen (2002) points out that these metrics can only be calculated ex post and are therefore not suitable for an ex ante control. Grob et al. (2008) determine the DA by integrating business rules. Including capacity restrictions using business rules results in the shortcoming that the quantity of applied business rules escalates over time (Beck 2006, pp. 282 and 293). Grob et al. (2008) consider capacity restrictions and different utilization ratios (cf. Table  1 ).

Table 1 Comparison of previous work with respect to requirements
Full size table

Only the approach of Adenso-Diaz et al. (2002) enables an evaluation that incorporates all assignable results of a process instance. Costs which are independent from evaluation are regarded by Köster (2004) and Gerboth (2000) in activity-based costing as a facet of process management. Delpachitra (2008) uses activity-based costing with eight different cost categories which do not include indirectly allocable process results in combination with a process benchmarking approach. Table  1 shows that none of the approaches is concerned with a method based on future oriented cash flows that are independent from evaluation – as required in (R1).

Based on this assessment we develop a model for the determination of the optimal path for the process instance that supports a flexible decision even in different capacity situations.

3 Formulating the Decision Model

Below a model that meets the requirements quoted in Sect. 2.1 is developed.

3.1 Definitions and Basic Assumptions

First we will define the fundamental terms:

  • A process model is a precise abstract illustration of a business process in a specific notation. A process consists of actions in a control flow which defines a sequence relationship. In the control flow there are decision nodes and mergers.

Below, following Ferstl et al. (1996, p. 26), we assume a given semiformal process model, an activity diagram of UML 2.0 (OMG 2007, pp. 295 ff). A formal model consisting of variables, constants, and operators can be deduced from this model.

  • A specific path through the process from beginning to end is called path. A path j (j=1,2,…,J) is thus an explicit sequence of actions for which exactly one outgoing branch is chosen at each decision node (schema level).

  • A claim F (F=1,2,…) is a single execution of a path. Hence it is a concrete instance which is consecutively processed in the actions of a path. For a process input the optimal path through the process and thus the appropriate DA are to be identified (instance level). A claim in a path is a process instance (instance level).

  • Each claim has nominal and cardinal attributes which allow drawing conclusions concerning the claim’s properties before processing. Nominal attributes (e.g. the type of a claim or the customer group) are regarded as discrete variables and have a limited number of characteristics. The cardinal attributes (e.g. amount of loss or age of customer) are regarded as continuous and normally distributed variables. There is a database consisting of a set Ω of past claims which contains the nominal and cardinal attributes and the results of process execution (e.g. execution time (ET) and resulting CFs) for each of those claims.

  • We distinguish between different types of decision nodes: The decision at so called functional decision nodes is already provided by the properties of the claim (e.g. it depends on the age of the car). At so called procedural decision nodes a decision is made for different methods of execution representing different levels of automation. We focus on procedural nodes.

After defining the fundamental terms for the model, we assume:

Assumption 1

(Process) There is a semi-formal model of a loop-free process. At procedural nodes, we can decide on different methods of execution resulting in different DA.

To consider capacity restrictions in the model (cf. (R3)) the actions are regarded independently.

Assumption 2

(Actions) The process consists of actions  a (a=1,2,…,A) which are executed by resources (humans or systems). Single resources are attributed to specific actions and cannot be prorated for different actions. Each action is modeled as an M/M/1-system (Kendall notation), i.e. we assume that arrival and execution time are exponentially distributed and there is one operating unit (i.e. the action) with arrival rate λ a for a time interval and execution rate η a . The set of actions on path j is  A j .

In terms of queuing system theory we regard actions as operating units which execute process instances. For this purpose available mathematical models for measuring the effects of random arrival and execution times can be consulted. We can determine the resulting stabilization in number of instances and waiting time in the system (Neumann and Morlock 2004, pp. 665 ff). Each action is modeled as a separate M/M/1-system. This represents infrequent events with great risk (e.g. thunderstorms), which are typical for the insurance industry, as a Poisson-process (Bamberg and Baur 2002, p. 103) and will be of relevance in Sect. 3.2.

According to (R1) the approach is aimed at integrating all results of process execution. Hence, we assume the following taking into consideration (R4) and (R5):

Assumption 3

(Cash-flow-effectiveness of in- and outgoing payments) There are variable cash-flows for executing the process instance \(B\in \mathopen{]}-\infty;0]\) , for direct process-outcomes \(D\in\mathopen{]}-\infty;\infty \mathclose{[}\) and for indirect process-outcomes \(I\in\mathopen{]}-\infty;\infty \mathclose{[}\) . Fix CF are considered separately or proportionally. To take those effects which are cash-flow-effective in the long-term into consideration the cash-flows are discounted applying a common interest rate. Cash-flows are measured for a claim F which is processed in path  j.

The present value of the overall cash-flow \(\mathit{CF}_{F,j}\in \mathopen{]}-\infty ;\infty\mathclose{[}\) of a claim F in path j can be summarized as follows:

$$\mathit{CF}_{F,j}=B_{F,j}+D_{F,j}+I_{F,j}.$$
(1)

Assumption 3a

(Cash-flow for execution of process instance in an action B F,j) Cash outflows B F,j occur during the execution of claim F for each action a on path  j. We distinguish between manually (ma) and automatically (au) executed actions:

For each manually executed action (binary variables\(b^{ma}_{a}=1\)and\(b^{au}_{a}=0\) ) there are cash-outflows for resources. They are calculated using the execution time\(t_{F,a}\in\mathopen{[}0;\infty \mathclose{[}\)and the wage rate\(z^{ma}_{a}\in[0;\infty\mathclose{[}\)of actiona, which can escalate because of short-term adjustments or the need of additional resources (cf. Sect. 3.2). Waiting times, break times and down times, which are flexibly compensated by colleagues, are already included.

For each automatically executed action (binary variables\(b^{ma}_{a}=0\)and\(b^{au}_{a}=1\) ) there are cash outflows for the system. These are composed of cash outflows for processing\(z^{au}_{a}\in[-\infty ;0\mathclose{[}\) , of a failure probabilityp a ∈[0;1] and the resulting costs of a failure\(y_{a}\in[-\infty;0\mathclose{[}\)in action a. Automatically executed actions can also be performed by external service providers (e.g. as web services).

Considering the cash-flow for execution in automated actions, the restriction on the license model pay-per-use is justifiable (Boles and Schmees 2003, pp. 385 ff), as also for other license models (e.g. time licenses, resource licenses) planning values for employment costs can be calculated applying a pre-calculation (Braunwarth and Heinrich 2008, p. 102). These can be used as input data for the model.

In conclusion the sum of cash-flows for the executions of claim F in path j can be obtained as follows:

(2)

Alongside there are cash flows as a consequence of the execution, e.g. the customer pays for the service or the company delivers the service. They are also assignable to a specific path.

Assumption 3b

(Direct process-outcomes D F,j) Direct process-outcomes D F,j are cash-flows which are linked to the execution of claim F in path  j. Independent from the number of available resources and the quantity of arriving process instances the direct process-outcomes are one and the same if process instances are executed identically.

Furthermore we consider indirect effects of the execution of a process instance. The customer perceives a certain quality and this influences her satisfaction (Matzler 2000, p. 291). In combination with other factors e.g. competitor actions and customer behavior this in turn effects customer loyalty. Only loyal customers generate returns for the company e.g. through repetitive buying (Homburg and Giering 2000, p. 61). A higher degree of customer satisfaction thus reduces the migration of customers (Oliver 1997) and increases the probability of customer recovery (Homburg et al. 2004; Maxham and Netemeyer 2003). Together with higher revenue and more frequent recommendations this leads to higher expected customer cash-flows (Krafft 1999, p. 523). Finally, it results in an alteration of the customer lifetime value. According to (R5) these expected changes are integrated in an exhaustive valuation of the process as the customer lifetime value can influence the enterprise value. Customer satisfaction can moreover change the reference potential, i.e. the number of potential customers that a customer can reach during her lifetime (Rudolf-Sipötz 2001, p. 108). The result of the process execution, e.g. the fact whether and how a claim is settled, influences the customer satisfaction significantly. For claim settlement in insurance companies we distinguish between rejection and payment of a claim. In the first case, the effect on customer satisfaction depends, above all, on the claim, e.g. the rejection of a low loss amount might not be clear to the customer. The resulting decision between the potential savings because of intensive checking, which also causes costs, and the possible reduction of customer lifetime value are not focused in this approach. We consider claims that lead to the result that is expected by the customer, e.g. settlement of the claim. The functional choice of the most appropriate process result would be an advanced decision problem but is not integrated into the present approach to avoid any bias in the optimization.

Assumption 3c

(Indirect process-outcomes I F,j) Depending on the satisfaction with the result of the process execution customers will extend or reduce their relationship with the company. This leads to positive or negative changes of the customer lifetime value which are referred to as indirect process-outcomes I F,j. I F,j summarizes the present value of all cash in- and outflows that can in the long-term be attributed to the customer relationship. We estimate the indirect process outcomes in dependency of the most important influencing factors: I F,j=I(DLZ F,j,g,q). These are not only the cycle time in the process \(\mathit{DLZ}_{F,j}\in [0;\infty\mathclose{[}\) but also the customer group g (one of the nominal attributes) and the complexity \(q\in\mathopen{]}-\infty;\infty\mathclose{[}\) . It is not essential to know the absolute customer lifetime value but its alteration.

In Sect. 4, we specify one of these relations and the calculation in detail.

3.2 Optimization

Regarding a new process instance that has not been processed yet, we want to define the most appropriate DA, i.e. the path that fits best. The decision for a specific path depends on the number of available resources and the quantity of process instances that arrive at the process or are processed temporarily in the specific process.

To chose the appropriate path j for claim F functional restrictions which prohibit the execution of a claim in specific paths have to be considered. Subsequently, there is a decision for one of the remaining paths j by calculating the present value of CF F,j which is the result of processing claim F in this path. For each claim F path \(\tilde{j}_{F}\) , which generates the maximum present value of CF F,j in the specific capacity load, should be chosen:

$$\tilde{j}_{F}=\mathop{\mathrm{arg\,max}}_{j}\mathit{CF}_{F,j}.$$
(3)

To determine this optimal path, the single components of CF F,j for each path j have to be calculated or at least estimated. Ex ante, the direct process-outcomes D F,j for a newly arriving claim F and the BZ in the action t F,a, are neither known nor calculable, but we know the characteristics of the attributes. Based on former reference claims whose nominal and cardinal attributes, direct process-outcomes D F,j and ET t F,a are known we can draw conclusions for the present claim. However, it has to be taken into consideration that past data is only partly suitable for conclusions on future claims and thus the results are estimations. As there are various reference claims which are similar to the regarded claim we can assume, according to the central limit theorem, that the sums of D F,j and t F,a of the reference claims are normally distributed for a specific claim or specific action.

Assumption 4

(Properties of direct process-outcomes and processing times) Direct process-outcomes D F,j and processing time ET t F,a of the actions are independent and normally distributed.

Following, we present a method for a risk-adjusted estimation of direct process-outcomes \(\tilde{D}_{F,j}\) and processing times \(\tilde{t}_{F,a}\) in action a for claim F. A detailed description of the method can be found in the Appendix.

First, some representative example claims are selected based on characteristics of known attributes. Within this set, the arithmetical average of direct process-outcomes and processing times are calculated as estimation for the new claim. Using the standard deviation as a measurement of risk we adjust for risk using a function that takes the decision maker’s attitude towards risk into account.

To determine the path that delivers the maximum present value of CF, the components of CF are calculated respectively estimated.

3.2.1 Process Execution B F,j

The calculation of B F,j is based on (2) and will be enlarged for optimization to consider different capacity loads. For each action a we examine how many resources R a are available respectively necessary to process the claims there. A change in the quantity of available resources or arriving process instances results in changes in manual processing. E.g. if all routine claims are checked by a specialist there will be a bottleneck. Similar effects on automated processing can be neglected since there are no relevant capacity restrictions because of the high performance of automated systems. Following, we present a method to obtain the resulting CF for manual processing.

  1. (1)

    Determine the current workload applying a M/M/1-queuing system for each action (cf. Assumption 2):

    To determine the optimal path the current workload has to be considered. A workflow management system can provide the necessary data. For the simulation of a process the amount of process instances in the system \(\varLambda _{a}\in[0;\infty\mathclose{[}\) must be estimated using an M/M/1-queuing system:

    The arrival rate of the previous period is used as the parameter of the Poisson-distribution of the arrival rate \(\lambda_{a}\in[0;\infty \mathclose{[}\) . The execution time \(\eta_{a}\in[0;\infty \mathclose{[}\) is determined according to the execution rate of the resources \(R_{a}^{Plan}\) which are allocated for action a. There is a temporal restriction \(k_{a}\in[0;\infty \mathclose{[}\) which represents the available time of each resource for the execution of process instances in a given time period (e.g. a day). To calculate the processing time, we revert to the average ET \(\bar{t}_{a}\) of the action for all known process instances of path j:

    $$\eta_{a}=\frac{R_{a}^{Plan}\cdot k_{a}}{\bar{t}_{a}}.$$
    (4)

    According to Neumann and Morlock (2004, p. 671) there are

    $$\varLambda _{a}=\frac{\lambda_{a}}{\eta_{a}-\lambda_{a}}$$
    (5)

    process instances that are to be processed in the system of action a.

  2. (2)

    Period-based determination of the appropriate number of resources for action a:

    As introduced in Assumption 2, resources are assigned to single actions and a proportional allocation is not possible. We need an integral number of resources R a ∈{1,2,…} in action a to execute Λ a process instances. The processing time of these process instances is the sum of ET for which we assume the average ET \(\bar{t}_{a}\) . As an additional resource has to be brought in when the capacity restriction is reached, there is a step cost structure:

    $$R_{a}=\biggl\lceil\frac{ \varLambda _{a}\cdot\bar{t}_{a}}{k_{a}}\biggr\rceil.$$
    (6)
  3. (3)

    Determinate of the wage rate\(z_{a}^{akt}\)that goes along with the current workload:

    There are additional costs if we need supplementary short-term resources on top of the long-term planned resources \(R_{a}^{Plan}\) for action a in order to process the current workload. Besides the step cost structure there are costs that depend on the number of required resources R a in each period: \(S_{a}(R_{a}-R_{a}^{Plan})\) . The more resources are needed, the higher the “penalty” is for short-term adjustments and thus the current wage rate \(z_{a}^{akt}\) :

    (7)

    For each period we are therefore able to respond to capacity variations in action a by changing the execution rate η a by bringing in additional resources and accepting a penalty payment S a . Additional resources are only applied for one period and after that the demand is recalculated.

  4. (4)

    Determination of CF for the execution of a specific claimFin action a in a period:

    Based on the current wage rate \(z_{a}^{akt}\) and the above mentioned risk-adjusted estimation of ET \(\tilde{t}_{F,a}\) there is a redefinition of formula (2):

    (8)

3.2.2 Direct Process-Outcomes D F,j

In path j the risk-adjusted expected CF of the direct process-outcomes of the reference claims in a specific path \(\tilde{D}_{F,j}\) can be used as an estimation of the CF of the direct process-outcomes D F,j.

$$D_{F,j}=\tilde{D}_{F,j}.$$
(9)

A detailed description of the method can be found in the Appendix.

3.2.3 Indirect Process-Outcomes I F,j

The indirect process-outcomes of the various possible paths are not known before the process is executed and thus they have to be estimated. According to Assumption 3c, there is a relation that depends on the most important influencing factors cycle time DLZ F,j in path j, customer group g and the subjectively perceived complexity q. DLZ contains not only the ET but also the waiting time and can be calculated using the sum of the DLZ of all actions on path j. As above, we consider a manually executed action as a M/M/1-system with arrival rate λ a and execution rate η a and the know ET (beginning with the request and ending with receiving the executed process instances) t F,a for automatically executed actions is taken into consideration:

(10)

The customer group g is one of the nominal attributes of each claim. To determine the complexity q (as expected DLZ in days) the claim is classified by reference to its attributes (e.g. type of claim or amount of loss). Based on this analysis we can identify how complex the customers perceive the execution of process instances in these classes: each customer group is interviewed to find out how many days are expected for the execution of each type of process instances. Therefore, applying the relation of Assumption 3c, there is a monetary estimation of indirect process-outcomes.

As a result of the optimization for a specific newly arriving claim F we obtain a decision for the optimal path \(\tilde{j}_{F}\) in the moment of execution in due consideration of current capacity load on the basis of the maximum (estimated) CF of a claim.

3.3 Process Valuation

In the following we present a cross-claim view of a process to evaluate the process configuration. Thus the quality of the conduct of a claim in respect of the DA can be measured and the improvements by applying the presented optimization can be assessed. Additionally, the aggregated key figures are a basis for control and planning of resources.

3.3.1 Resulting Cash-Flow of an Average Process Execution \(\overline{CF}\)

Regarding averages as an aggregated view on a sample of process executions allows drawing uniformly valid conclusions on the performance of the process and the method to determine the DA for single process instances. Apart from problems that come along with calculating averages, the cash-flow of an average process execution is calculated as a key figure of a sample of regarded process instances.

3.3.2 Rates of Utilization of Paths

For each claim F the appropriate DA i.e. a path j is chosen according to the approach presented in Sect. 3.2. Aggregately regarding a process, the partition in manual and automated processing is remarkable. The utilization of paths allows having resources available in the long term where the majority of process instances are processed. Hence, an uneconomic short term reallocation can be avoided. To calculate the utilization of paths, the number of process instances that are assigned to a path is divided through the total number of observed process instances. Thus benchmarks for the workload of actions which are part of paths are determined and resources can be planned based on historical data. Purpose and application of these key figures are made clear in the following case study.

4 Case Study

Hereinafter, the model presented in Sect. 3 is applied using the example of an insurance company. The examined process of handling own damage glass claims is executed in the back-office of insurance providers without direct customer contact. But there remains the possibility that the perceived service quality influences customer satisfaction.

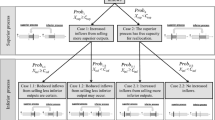
In Fig.  1 the considered section of the process is simplified. After recording the data of the claim in the action “classification and extraction” there is an either manual or automated acquisition of the claim. The calculation of the customer payment goes along with these process steps. After that an expert can determine whether a reduction of the claim amount is applicable by means of a manual check. As an alternative, an automated report can be generated followed by an automated check and will then automatically be processed further. Finally, there is a manual or automated payment and closure of the claim. Thus, there are twelve different paths.

Fig. 1
figure 1

Observed process with different DA

Full size image

The data for the application of the model is derived from an industry project and is modified for the purpose of anonymization. In total approx. 4000 claims are processed in the regarded workflow – three of them are shown in Table  3 . From the record we know the discrete attributes like type of claim and customer group and the cardinal attributes like amount of loss and the age of the vehicle.

The claims are executed in a specific path of the process and thus in specific manually or automatically executed actions for which specific data must be known. A certain number of resources is assigned for each action (e.g. for action “manual checking” there are two resources with eight hours per day each; per resource and day costs amount to 466.66 €). If additional resources are required the associated costs S a are calculated as follows with R a being the total number of required resources: \(S_{a}(R_{a})=66,67\cdot e^{(R_{a}-2)}\) .

To determine the direct process-outcomes and ET of a claim, we draw on 10,000 reference claims. The data of the reference claims is stored in a company-wide repository which contains not only transaction data but also historical data. This is relevant to the determination of indirect process-outcomes: By analyzing the reference claims in the repository with respect to the effects of one claim on the customer value and portfolio of policies and by interviewing customers, a coherence between the realized DLZ, the expected execution time q (each measured in days) and the indirect process-outcomes I can be deduced, e.g. I(DLZ,Standard customer,q)=5.2778⋅(DLZ−q)3−4.8701(DLZ−q)2+8.0556(DLZ−q). Table  2 shows an overview of the necessary data for the model and some exemplary sources of information.

Table 2 Data-oriented requirements for the application of the model and each source of information in the case study
Full size table

The execution of the process is analyzed from two different perspectives. An average day is compared to purely automated respectively manual execution and to the outcomes that result from either an application of business rules or from the application of the optimization approach presented in Sect. 3.

Table  3 illustrates the chosen paths for three selected claims and the resulting CFs. Claim C is a standard claim which should be executed automatically (the path schemas in Table  3 relate to Fig. 1 – used actions are marked in black). Nevertheless there is a variety of claims for which neither of the extremes is appropriate (cf. claim A and B). This can be seen in the comparison of average CFs of all claims of a day in Table  4 . It is remarkable, that manual processing leads to increased costs but reduces customer satisfaction (payments of indirect process-outcomes show this effect). In contrast, automated execution leads to an improved customer satisfaction because of fast processing. Footnote 1

Table 3 Comparison of different methods for choosing the appropriate DA for example claims (selected execution is marked)
Full size table
Table 4 Comparison of different methods for choosing the DA for an average day
Full size table

The presented approach for process control suggests e.g. substituting the automated checking by manually checking for claim A which results in a significant improvement of the CF (Table  3 ). On average, the increased flexibility of the optimization model is reflected in savings. Compared to business rules, the payments for process execution and the insurance benefits can be reduced and the customer satisfaction can be improved (Table  4 ). This improvement is a result of the selection of the appropriate DA for each claim.

Now we will analyze the ability of the model to be responsive to changes in the quantity of arriving claims and the resulting consequences. Due to the fact that each day a different volume of claims arrives, there are various load situations. Extraordinary high load occurs e.g. after thunderstorms when a lot of customers report their claims. Fig.  2 shows the number of daily arriving claims, the average CF of a claim per day and the partition on different paths (cf. Sect. 3.3) for 20 workdays of a month. However there is a simplification: We only regard the automation decision for checking because this decision influences the result most significantly.

Fig. 2
figure 2

Analysis of a month with 20 workdays

Full size image

There are two different effects regarding the selection of an appropriate method of execution: First, different quantities of claims arrive and due to capacity restrictions different methods of processing are preferred. Second, because of different properties of the claims different DA are appropriate. This explains the changes in partitions of paths on days with similar load (e.g. 4 and 5). On quiet days (e.g. 9 to 11) the share of manual checking is increased to use the free capacity of the agents. Simultaneously, the standard deviation of the CFs increases (e.g. compare day 10 to day 16) because the manual processing implies greater variations. The daily results are mostly based on the load of the previous day which is the estimation of the expected demand. Thus, changes in demand only become effective in the subsequent period, e.g. decreased demand on day 8 will become effective on day 9. In high load situations (day 14 to 18) systems absorb the increased effort but the payments per claim only increase moderately.

For this case study only the number of arriving claims is variable and the resources are regarded as constant. But this is equivalent to a vice-versa approach and a day with increased appearance is comparable to vacation time when only a few agents are available.

Hence, for back office processes of insurance companies the DA that generates the optimal present value of CF can be selected. Thus, the presented approach fulfills (R1) to (R5) and enables a financial evaluation and optimization.

5 Summary and Conclusion

In this article we presented a model that supports automation decisions in insurance processes on the basis of maximum present values of CF. For this, amongst others, reference claims are identified from historical data and cash-flows are extrapolated from this data for the current claim. Constitutively, a method for evaluation and optimization of the degree of automation of these processes is suggested and the application is illustrated using a case study. We also present how risks and capacity restrictions influence the decision for manual or automated execution.

The presented approach has some advantages:

  1. (1)

    Comparative advantages of manual and automated execution can be compared. As in the case study neither manual processing (average CF: −452.17 €) nor automated execution (average CF: −509.69 €) is optimal but a financially oriented selection of the DA as the model proposes (average CF: −369.82 €). The model thus supports the statements that purely automated processing of whole processes and the corresponding reduction of jobs and the dependency on automated execution are of financial disadvantage.

  2. (2)

    Furthermore, the approach allows an application ex ante and during the execution as no inflexible heuristic rules are used. The optimal manner of processing rather depends on the current work load: In the case study the model suggests manual checking in 80% of all claims if there is capacity underload, but if there is extraordinary high load only 5% are checked manually. Despite the high degree of flexibility a standardized and automated execution is possible. Moreover, the presented approach allows drawing conclusions on how many resources should be provided to enable frictionless execution in extreme situations.

The presented approach currently focuses on service processes without direct customer contact in which the performance of existing contractual duties is central. To apply the approach, a process that accepts these limitations and the assumptions of the model is required. Furthermore, the required data (cf. Table  2 ) needs to be available or foreseeable. Our approach aims to render specific services for a minimum of payment required. It is of particular interest to analyze the behavior of the model in value-generating processes e.g. in sales where direct and indirect process-outcomes lead to revenues and thus prerequisites are changed. Now we focus on insurances – a further starting point is the adaption to specific requirements of service processes of other industries.