1 Introduction

A fundamental problem of decision theory is how to derive the weights for a set of criteria (activities, alternatives, objects, etc.), according to their importance, prominence, quality, etc., which is usually judged according to several criteria, aspects, viewpoints, etc. Each criterion may be shared by some or all of the activities. The criteria may, for example, also be taken as objectives, which the activities have been devised fulfill to. This is called a process of multiple criteria decision making which is a theory of measurement in a hierarchical structure consisting of the goal, the criteria and sub-criteria, and the alternatives, see [29].

The main subproblem of AHP is to calculate the priority vectors – weights assigned to the elements of the hierarchy: criteria (or sub-criteria) and alternatives (or variants). The decision maker (DM) is to rank the elements from the set \({\mathcal {C}} = \{c_{1},c_{2},\ldots ,c_{n}\}\), where \(n>1\), from the best to the worst (or vice versa, which is equivalent), using the information given in the form of an \(n\times n\) pairwise comparisons matrix (PCM). The ranking of the alternatives is determined by the priority vector of positive numbers \(w = (w_1,w_2,\ldots ,w_n)\), which is calculated from the corresponding PCM. There exist various methods for calculating the vector of weights based on the DM problem, particularly, on the pairwise comparisons matrix, e.g., Saaty’s Eigenvector Method, the Geometric Mean Method and others, see [26, 27].

Fuzzy sets as the elements of the pairwise comparisons matrix can be used in the decision making problem, whenever the DM is not sure about the preference degree of his/her evaluations of the pairs in question. We can primarily find them in Fuzzy Analytic Hierarchy Process (FAHP), PROMETHEE and TOPSIS oriented methods, and various exact and heuristic algorithms, [16, 22, 32]. They are also useful in aggregating pairwise comparisons, particularly in consensus group decision making problems, see e.g. [8, 19], and they form the basis for many decision-making models as intuitionistic fuzzy relations, pythagorean, q-rung orthopair fuzzy preference relations, hesitant or interval fuzzy sets, [14, 15, 17, 31], and also found in stochastic judgment models, see e.g. [7]. Effectiveness of FAHP together with applications to models in environmental risk assessment and other big projects can be found in [9, 16, 18, 20, 21, 30]. Such an approach, usually structured to Goal – Criteria – Alternatives, is also well known in the Fuzzy Analytic Hierarchy Process (FAHP) originated by T. Saaty in [29], and also in [10, 33]. Fuzzy elements are useful in order to capture the uncertainty stemming from the subjectivity of the human thinking and from the incompleteness of information, which is an integral part of multi-criteria decision-making problems. Fuzzy elements may also be useful as aggregations of crisp pairwise comparisons of a group DM in the group decision making problem. Recent development of the problem can be found in [18, 33].

Recently, [12, 18] deal with fuzzy eigenvector methods for obtaining fuzzy weights from pairwise comparisons matrices with fuzzy elements. They improve the approach published earlier in [3, 4] and [10]. The output is, however, a normalized fuzzy vector of weights, which is not, from the perspective of the DM, directly applicable to the final decision, and/or ranking of alternatives, see e.g. [18]. Another suitable defuzzification or ranking procedure is necessary prior to making a final decision. The eigenvector method itself is criticized by some authors for unsuitable properties, see, e.g. [18, 40]. Moreover, the concept of the fuzzy eigenvalue of the matrix with fuzzy elements does not seem to be properly justified. For these reasons we do not follow this way of the fuzzy eigenvector method for deriving the priority vector of the pairwise comparisons matrix with fuzzy elements and propose our own approach based on investigation of crisp priority vector.

In [26,27,28], the authors presented a general approach for PCM with fuzzy number elements based on alo-groups unifying the previous approaches which enable unifying of multiplicative, additive and fuzzy PCMs. Then we define a novel concept of consistency, coherence and intensity of FPCMs, and propose a number of optimization methods for finding a consistent vector (CSV), coherent vector (CV) and intensity vector (IV) of a FPCM satisfying the desirable properties. Fuzzy intervals are elements of the PCM called Fuzzy Pairwise Comparisons matrix (FPCM). In this paper we apply the observation and analysis from [1, 13] to FPC matrices defining the coherent vector, and intensity vector of a FPCM based on \(\alpha\)-cuts, called desirable properties. In general, the most popular methods for deriving the priority vector, i.e., the Eigenvector Method, [29], and the Geometric Mean Method, see e.g. [11, 13], do not always satisfy the desirable properties, see, e.g., [6, 40].

Later on, many authors proposed various approaches and methods of generating priority vectors with different properties. A method of obtaining the priority weights from an interval fuzzy preference relation was presented in [17]. Nedashovskaya, in [23,24,25] proposed a method for weights calculation based on interval multiplicative PCM. In [28], when comparing to this paper, the author proposes another type of optimization method for calculating the crisp weights of FPCMs. In a series of papers, Wang et al., see [34,35,36,37,38,39] published the goal programming approaches to deriving interval weights in analytic form from interval FPCMs.

Here, we derive new sufficient conditions for the existence of consistent vector (CSV), coherent vector (CV), intensity vector (IV) of a FPCM. Then, we formulate special optimization problems and algorithms for deriving the priority vector satisfying the desirable properties under appropriate assumptions. Furthermore, the proposed methods solve the problem of finding a priority vector satisfying the desirable properties by minimizing the corresponding global error index, already proposed in [13]. Finally, we give some numerical examples in order to illustrate the new concepts, their properties and the algorithms for solving the problem.

2 Preliminaries

The reader can find the corresponding basic definitions, concepts and results e.g. in [26]. Here, we summarize some necessary concepts, however, for a more detailed information we refer to [27].

A fuzzy subset S of a nonempty set X (or a fuzzy set on X) is a family \(\{S_{\alpha }\}_{\alpha \in [0;1]}\) of subsets of X such that \(S_{0}=X, S_{\beta }\subset S_{\alpha }\) whenever \(0\le \alpha \le \beta \le 1\), and \(S_{\beta }=\cap _{0\le \alpha <\beta }S_{\alpha }\) whenever \(0 < \beta \le 1.\) The membership function of S is the function \(\mu _S\) from X into the unit interval [0; 1] defined by \(\mu _{S}(x)=\sup \{\alpha \mid x\in S_{\alpha }\}\). Given \(\alpha \in ]0;1]\), the set \([S]_{\alpha }=\{x\in X\mid \mu _{S}(x)\ge \alpha \}\) is called the \(\alpha\)-cut of fuzzy set S. We say that a fuzzy subset S of \({\textbf{R}}^{*}={\textbf{R}} \cup \{-\infty \} \cup \{+\infty \}\) is a fuzzy interval whenever S is normal and its membership function \(\mu _{S}\) satisfies the following condition: S is closed, compact and convex, i.e. the \(\alpha\)-cut \([S]_{\alpha }\) are closed, compact and convex subset of X for every \(\alpha \in ]0;1]\), respectively.

A bounded fuzzy interval S called the triangular fuzzy number is denoted by \(S=(a,b,c)\). Notice that each crisp number is also a bounded fuzzy interval \(S=(a,b,c)\) with \(a=b=c\).

In order to unify various approaches and prepare a more flexible presentation, we apply abelian linearly ordered groups, shortly, alo-groups, see [5]. Recall that an abelian group is a set, G, together with an operation \(\odot\) and corresponding "group axioms" that combine any two elements \(a,b\in G\) to form another element in G denoted by \(a \odot b\). The well known examples of alo-groups can be found in [5] or [26].

Example 2.1

Additive alo-group \({\mathcal {R}}=({\textbf{R}},+,\le )\) with the usual addition operation and natural ordering is a continuous alo-group with:

\(e=0,\ a^{(-1)}=-a.\)

Example 2.2

Multiplicative alo-group \({\mathcal {R}}_{+}=({\textbf{R}}_{+}, \bullet ,\le )\) with the usual multiplication operation and natural ordering is a continuous alo-group with:

\(e=1,\ a^{(-1)}=a^{-1}=1/a.\) Here, by \(\bullet\) we denote the usual operation of multiplication.

Example 2.3

Fuzzy additive alo-group \({\mathcal {R}}_a\)=\(({\textbf{R}}, +_{f}, \le )\) with a special addition operation and natural ordering, see [5], is a continuous alo-group with: \(a +_f b=a+b-0.5,\ e=0.5,\ a^{(-1)}=1-a.\)

Example 2.4

Fuzzy multiplicative alo-group \({\mathcal {R}}_m\)=\((]0;1[,\bullet _f,\le )\), see [5], with a special multiplication operation and natural ordering is a continuous alo-group with: \(a \bullet _f b=\frac{ab}{ab+(1-a)(1-b)}, e=0.5, a^{(-1)}=1-a.\)

3 FPC matrices, reciprocity and consistency

Our general approach based on alo-groups is useful, as it unifies various important approaches known from the literature, see [5, 27]. This fact has been already demonstrated on 4 examples presented above, where the well known alo-groups are shown. Particularly, all concepts and properties which will be presented bellow can be easily applied to any alo-group. Before we shall investigate PC matrices with fuzzy elements we remember some concepts and properties of PC matrices on alo-group with crisp elements.

A crisp PC matrix \(A=\{a_{ij} \}\) is said to be \(\odot\) -reciprocal, if the following condition holds:

For every \(i,j \in N=\{1,...,n\}\)

$$\begin{aligned} a_{ij}\odot ~a_{ji}=e, \text { or, equivalently, } a_{ji}=a_{ij}^{(-1)}. \end{aligned}$$
(1)

A crisp FPC matrix \(A=\{a_{ij}\}\) is \(\odot\)-consistent if for all \(i,j,k \in N\)

$$\begin{aligned} a_{ik}=a_{ij} \odot a_{jk}, \text { or, equivalently, } a_{ij}\odot a_{jk}\odot a_{ki}=e. \end{aligned}$$
(2)

Remember that an \(\odot\)-consistent PC matrix \(A=\{a_{ij}\}\) is \(\odot\)-reciprocal, but not vice-versa. The following equivalent condition for consistency of PC matrices is well known, see e.g. [5, 29].

A crisp PC matrix \(A=\{a_{ij}\}\) is \(\odot\)-consistent if and only if there exists a vector \(w=(w_{1},...,w_{n})\), \(w_{i}\in G,\) such that

$$\begin{aligned} a_{ij}=w_{i}\div w_{j}\text { for all }i,j\in N \text {.} \end{aligned}$$
(3)

Here, \(w_{i}\div w_{j}=w_{i}\odot w_{j}^{(-1)}.\)

In [26], we extended the above stated definition of \(\odot\)-reciprocity and \(\odot\)-consistency to non-crisp matrices with fuzzy elements. In particular, we introduced a new concept of reciprocity and consistency based on \(\alpha\)-cuts: \(\alpha\)-\(\odot\)-reciprocity and \(\alpha\)-\(\odot\)-consistency. Let us start with the \(\alpha\)-\(\odot\)-reciprocity in the fuzzy case.

Let \({\mathcal {G}}=(G,\odot ,\le )\) be a divisible and continuous alo-group over an open interval G of \({\textbf{R}}\), see [5]. Let \(\alpha \in [0;1],\) \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) be an \(n \times n\) matrix, where each element is a bounded fuzzy interval of the alo-group \({\mathcal {G}},\) let \([{\tilde{a}}_{ij}]_{\alpha } =[a_{ij}^L(\alpha ), a_{ij}^R(\alpha )]\) be an \(\alpha\)-cut of \({\tilde{a}}_{ij}\).

Matrix \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) is said to be \(\alpha\)-\(\odot\)-reciprocal, if the following two conditions hold for each \(i,j \in N\):

$$\begin{aligned} a_{ii}^L(\alpha ) = a_{ii}^R(\alpha )=e, \end{aligned}$$
(4)
$$\begin{aligned} a_{ij}^L(\alpha ) \odot a_{ji}^R(\alpha )=e. \end{aligned}$$
(5)

If \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) is \(\alpha\)-\(\odot\)-reciprocal for all \(\alpha \in [0;1],\) then it is called \(\odot\)-reciprocal.

If \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) is \(\odot\)-reciprocal, then \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) is called the fuzzy pairwise comparisons matrix, fuzzy PC matrix, FPC matrix, or, shortly, FPCM.

Now, we turn to the concept of consistency of FPC matrices. We start with the definition of \(\alpha\)-\(\odot\)-consistent FPC matrix, see [26].

Definition 3.1

Let \(\alpha \in [0;1].\) A FPC matrix \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) is said to be \(\alpha\)-\(\odot\)-consistent, if the following condition holds:

There exists a crisp matrix \(A'=\{a_{ij}' \}\) with \(a_{ik}' \in [{\tilde{a}}_{ik}]_{\alpha }\), \(a_{ij}' \in [{\tilde{a}}_{ij}]_{\alpha }\), \(a_{jk}' \in [{\tilde{a}}_{jk}]_{\alpha }\), such that \(A'=\{a_{ij}' \}\) is consistent, i.e. for each \(i,j,k \in N\) it holds

$$\begin{aligned} a_{ik}'=a_{ij}' \odot a_{jk}'. \end{aligned}$$
(6)

The FPC matrix \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) is said to be \(\odot\)-consistent, if \({\tilde{A}}\) is \(\alpha\)-\(\odot\)-consistent for all \(\alpha \in [0;1]\).

If for some \(\alpha \in [0;1]\) the FPC matrix \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) is not \(\alpha\)-\(\odot\)-consistent, then \({\tilde{A}}\) is called \(\alpha\)-\(\odot\)-inconsistent.

If for all \(\alpha \in [0;1]\) the FPC matrix \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) is \(\alpha\)-\(\odot\)-inconsistent, then \({\tilde{A}}\) is called \(\odot\)-inconsistent.

Ramarks. Let \(\alpha ,\beta \in [0;1], \alpha \ge \beta\).

  • For a crisp PCM, definitions of \(\odot\)-reciprocity and \(\odot\)-consistency coincide with the classical definitions.

  • If \({\tilde{A}}=\{{\tilde{a}}_{ij}\}\) is \(\alpha\)-\(\odot\)-consistent, then it is \(\beta\)-\(\odot\)-consistent.

  • If \({\tilde{A}}=\{{\tilde{a}}_{ij}\}\) is \(\beta\)-\(\odot\)-inconsistent, then it is \(\alpha\)-\(\odot\)-inconsistent.

  • (5) holds for all \(i,j \in \{1,...,n\}\) if and only if (5) holds for all \(i,j \in N,1 \le i < j \le n.\)

  • (6) holds for all \(i,j,k \in N\) if and only if (shortly: iff) (6) holds for all \(i,j,k \in N, 1 \le i< j < k \le n.\)

The next proposition gives an equivalent condition for a FPC matrix to be \(\alpha\)-\(\odot\)-consistent, see e.g. [26].

Proposition 3.2

Let \(\alpha \in [0;1]\), \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) be a FPC matrix, \([{\tilde{a}}_{ij}]_{\alpha } =[a_{ij}^L(\alpha ), a_{ij}^R(\alpha )]\) be an \(\alpha\)-cut of \({\tilde{a}}_{ij}, i,j \in N\).

Then \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) is \(\alpha\)-\(\odot\)-consistent iff there exists a vector \(w=(w_1,...,w_n)\) with \(w_i~\in ~G, i \in N,\) such that for each \(i,k \in N,\) it holds:

$$\begin{aligned} a_{ik}^L(\alpha ) \le w_i \div w_k. \end{aligned}$$
(7)

Remark 3.3

Notice that an \(\alpha\)-\(\odot\)-consistent FPC matrix is not necessarily \(\alpha\)-\(\odot\)-reciprocal, as it is true in the crisp case. In real DM problems, \(\alpha\)-\(\odot\)-reciprocity condition is, however, a natural assumption, as the DM usually evaluates only one of the reciprocal elements \({\tilde{a}}_{ij},{\tilde{a}}_{ji},\) the other element is automatically set up as the reciprocal one. Therefore, in the sequel we assume that FPC matrices are always \(\alpha\)-\(\odot\)-reciprocal. The following proposition gives a characterization of \(\alpha\)-\(\odot\)-reciprocal matrix to become a mean \(\alpha\)-\(\odot\)-consistent FPC matrix, see [27].

Remark 3.4

Let \(\alpha \in [0;1]\), let \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) be a FPC matrix. Notice that \(\alpha\)-\(\odot\)-consistency of FPC matrix \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) is equivalent to the feasibility of the system of inequalities

$$\begin{aligned} a_{ij}^L(\alpha ) \le w_i \div w_j, w_j \in G \text { for all } i,j \in N, \bigodot _{k=1}^{n} w_k=e. \end{aligned}$$
(8)

Here, we denote the matrix

$$\begin{aligned} A^L(\alpha )=\{a_{ij}^L(\alpha )\}. \end{aligned}$$
(9)

The feasible solution of system (8) will be important in deriving a corresponding priority vector of the FPC matrix as we shall see in Sect. 5.

Example 3.5

Consider the additive alo-group \({\mathcal {R}}=({\textbf{R}},\odot ,\le )\) with \(\odot =+\), see Example 2.1. Let \({\tilde{A}}=\{{\tilde{a}}_{ij}\}\) be given by triangular fuzzy number elements as follows

$$\begin{aligned} {\tilde{A}}=\left[ \begin{array}{ccc} (0,0,0) &{} (1,3,4) &{} (4,6,8) \\ (-4,-3,-1) &{} (0,0,0) &{} (2,4,5) \\ (-8,-6,-4) &{} (-5,-4,-2) &{} (0,0,0) \end{array} \right] , \end{aligned}$$

or, equivalently, by \(\alpha\)-cut representation, we obtain

$$\begin{aligned} {\tilde{A}} = \left[ \begin{matrix} [0;0] &{} [1+2\alpha ;4-\alpha ] &{} [4+2\alpha ;8-2\alpha ] \\ [-4+\alpha ;-1-2\alpha ] &{} [0;0] &{} [2+2\alpha ;5-\alpha ] \\ [-8+2\alpha ;-4-2\alpha ] &{} [-5+\alpha ;-2-2\alpha ] &{} [0;0] \end{matrix} \right] . \end{aligned}$$

Moreover, the \(\alpha\)-\(+\) PC matrix of \({\tilde{A}},\) \(A^L(\alpha ),\) \(\alpha \in [0,1],\) is calculated as

$$\begin{aligned} A^L(\alpha )=\left[ \begin{array}{ccc} \ 0 &{} 1+2\alpha &{} 4+2\alpha \\ \ -4+\alpha &{} 0 &{} 2+2\alpha \\ \ -8+2\alpha &{} -5+\alpha &{} 0 \end{array} \right] . \end{aligned}$$

By solving system (8), we obtain that \({\tilde{A}}\) is \(\alpha\)-\(+\)-consistent PCM for \(0 \le \alpha \le 0.833.\)

4 More desirable properties of the priority vector, error indexes

Pairwise comparisons matrices may violate some desirable properties of multiple criteria decision making: e.g. the best alternative with respect to DM’s preferences is selected from the set of non-dominated alternatives, on condition this set is non-empty. The other PCMs may violate the preservation order preference conditions (the so called POP/POIP conditions, see [1]), or, the reliable preference conditions (RP conditions, see [6]). Here, we introduce the coherent vector (CV) of PC matrix and intensity vector (IV) of PC matrix as follows, see also [6] or [27].

Definition 4.1

Let \(A=\{a_{ij}\}\) be a PC matrix with crisp elements. A priority vector \(w = (w_1,\cdots ,w_n)\) is said to be the coherent vector (CV) of PC matrix\(A=\{a_{ij}\}\) if for all \(i,j \in N\)

$$\begin{aligned} a_{ij}>e \text { iff } w_i > w_j. \end{aligned}$$
(10)

On the other hand, a PC matrix \(A=\{a_{ij}\}\) is said to be the coherent PC matrix if there exists a priority vector \(w = (w_1,\cdots ,w_n)\) satisfying (10).

A priority vector \(w = (w_1,\cdots ,w_n)\) is said to be the intensity vector (IV) of PC matrix\(A=\{a_{ij}\}\) if for all \(i,j,k \in N\)

$$\begin{aligned} a_{ij}> e, a_{kl}>e, a_{ij}>a_{kl} \text { iff } w_i \div w_j > w_k \div w_l. \end{aligned}$$
(11)

On the other hand, a PC matrix \(A=\{a_{ij}\}\) is said to be the intensity PC matrix if there exists a priority vector \(w = (w_1,\cdots ,w_n)\) satisfying (11).

From (10) in the above definition it is evident that any CV w of a crisp PC matrix A satisfies the POP condition with respect to priority vector w,  see [26], defined in [1]. Also, the alternative with the highest weight of CV w corresponding to DM’s preferences is always non-dominated. The similar property holds for any IV w, resp. POIP condition of a crisp PC matrix A. The opposite is evidently not true. Clearly, each \(\alpha\)-mean IV is also a CV for a given FPC matrix \({\tilde{A}}\) and given priority vector w, see also [27].

Let \(A=\{a_{ij}\}\) be a crisp consistent PC matrix, and let \(w = (w_1,\cdots ,w_n)\) be a priority vector associated with A satisfying (3). Then it is obvious that conditions (10) and (11) are satisfied. Moreover, it is well known (see e.g. [29]), that for each crisp consistent PC matrix, the priority vector satisfying (3) can be generated either by the eigenvalue method (EVM), or, by the geometric mean method (GMM).

Now, we are ready to define the concepts of CV and IV for a FPC matrix \({\tilde{A}}=\{{\tilde{a}}_{ij} \}.\) Further, if there is no danger of misunderstanding, the symbol \(\odot\) will be usually omitted in what follows.

Definition 4.2

Let \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) be a FPC matrix on the alo-group \({\mathcal {G}}=(G,\odot ,\le ),\) \(w=(w_{1},w_{2},\cdots ,w_{n})\), \(w_{i}\in G,\) be a priority vector, \(\alpha \in [0;1].\)

We say that the vector w is \(\alpha\) -coherent vector of FPC matrix\({\tilde{A}}\) (\(\alpha\)-CV) if for all \(i,j \in N\)

$$\begin{aligned} a^{R}_{ij}(\alpha )>e \text { iff } w_{i} > w_{j}. \end{aligned}$$
(12)

Moreover, the vector w is coherent vector of FPC matrix \({\tilde{A}}\) (or, CV) if for all \(i,j,k \in N\)

$$\begin{aligned} a^{R}_{ij}(\beta )>e \text { iff } w_{i} > w_{j} \text { for all } \beta \in [0;1]. \end{aligned}$$
(13)

Definition 4.3

Let \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) be a FPC matrix on the alo-group \({\mathcal {G}}=(G,\odot ,\le ),\) \(w=(w_{1},w_{2},\cdots ,w_{n})\), \(w_{i}\in G,\) be a priority vector, \(\alpha \in [0;1].\)

We say that the vector w is \(\alpha\) -intensity vector of FPC matrix \({\tilde{A}}\) (\(\alpha\)-IV) if for all \(i,j,k \in N\)

$$\begin{aligned} a_{ij}^{L}(\alpha )> a_{kl}^{R}(\alpha ) \text { iff } w_{i} \div w_{j} > w_{k} \div w_{l}. \end{aligned}$$
(14)

Moreover, the vector w is intensity vector of FPC matrix \({\tilde{A}}\) (or, IV) if for all \(i,j,k \in N\)

$$\begin{aligned} a_{ij}^{L}(\beta )> a_{kl}^{R}(\beta ) \text { iff } w_{i} \div w_{j} > w_{k} \div w_{l} \text { for all } \beta \in [0;1]. \end{aligned}$$
(15)

Remark 4.4

Notice, that the concepts of the \(\alpha\)- IV/CV is introduced for a given FPC matrix \({\tilde{A}}\) and given priority vector w. If \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) is a crisp FPC matrix, then the priority vectors IV/CV introduced in Definitions 4.2 and 4.3 coincide with the usual IV/CV vectors defined by Definition 4.1. Clearly, by setting \(k=l\) in Definition 4.3, each \(\alpha\)-intensity vector of FPC matrix \({\tilde{A}}\) is also an \(\alpha\)-coherent vector of FPC matrix \({\tilde{A}},\) see also [27]. The same is true for each intensity vector of \({\tilde{A}}\) versus a coherent vector of FPC matrix \({\tilde{A}}.\) Moreover, by Proposition 3.2 and Definition 4.1, each \(\alpha\)-consistent vector of FPC matrix \({\tilde{A}}\) is also an \(\alpha\)-intensity vector of FPC matrix \({\tilde{A}},\) and, consequently, an \(\alpha\)-coherent vector of FPC matrix \({\tilde{A}}\).

Notice that the property of \(\alpha\)-consistency depends on the left end \(a_{ij}^{L}(\alpha )\) of the \(\alpha\)-cut of \({\tilde{A}},\) whereas \(\alpha\)-coherence property depends on the right end \(a_{ij}^{R}(\alpha ).\) This property will be essential in deriving the priority vectors with the given properties, see Sect. 5.

In what follows we introduce the local error indexes and global error index based on the end points of \(\alpha\)-cuts of the fuzzy elements of the FPCM.

Definition 4.5

Let \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) be an FPC matrix on alo-group \({\mathcal {G}}=(G,\odot ,\le ).\) For each pair \(i,j\in N\), and a priority vector \(w=(w_{1},w_{2},\cdots ,w_{n})\), \(w_{i}\in G,\) \(\alpha \in [0;1],\) let us denote

$$\begin{aligned} \varepsilon (i,j,w,\alpha )=\max \left\{a_{ij}^{L}(\alpha ) \odot w_{j}\div w_{i},(a_{ij}^{L}(\alpha ) \odot w_{j}\div w_{i})^{(-1)} \right\}, \end{aligned}$$
(16)

Moreover, define the \(n \times n\) matrix \(\varepsilon (w,\alpha )\) of local error indexes as

$$\begin{aligned} \varepsilon (w,\alpha ) =\{ \varepsilon (i,j,w,\alpha ) \}. \end{aligned}$$
(17)

Definition 4.6

Let \(\alpha \in [0;1]\). The global error index \({\mathcal {E}}({\tilde{A}},w,\alpha ),\) for a FPC matrix \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) and a priority vector \(w=(w_{1},\ldots ,w_{n})\) is defined as the maximal element of matrix of local errors \(\varepsilon (w,\alpha ),\) i.e.

$$\begin{aligned} {\mathcal {E}}({\tilde{A}},w,\alpha )=\max _{i,j\in N}\varepsilon (i,j,w,\alpha ). \end{aligned}$$
(18)

Proposition 4.7

Let \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) be an FPC matrix and \(w=(w_{1},\ldots ,w_{n})\) be a priority vector, \(\alpha \in [0;1].\) Then the global error index satisfies

$$\begin{aligned} {\mathcal {E}}({\tilde{A}},w,\alpha )\ge e. \end{aligned}$$
(19)

Moreover,

$$\begin{aligned} {\mathcal {E}}({\tilde{A}},w,\alpha )= e \end{aligned}$$
(20)

iff \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) is \(\alpha\)-\(\odot\)-consistent.

Proof

Inequality (19) follows directly from definitions (16), (17) and (18).

Now, let \({\mathcal {E}}({\tilde{A}},w,\alpha )= e\). Then for all \(i,j\in \{1,\ldots ,n\}\) it holds

$$\begin{aligned} a_{ij}^{L}(\alpha ) \odot w_{j}\div w_{i}= e, \end{aligned}$$
(21)

or, in other words

$$\begin{aligned} a_{ij}^{L}(\alpha )= w_{i}\div w_{j}, \end{aligned}$$
(22)

hence, by Proposition 3.2, \({\tilde{A}}\) is \(\alpha\)-\(\odot\)-consistent.

On the other hand, let \({\tilde{A}}\) be mean \(\alpha\)-\(\odot\)-consistent. Then, by Proposition 3.2, (22) holds for all \(i,j\in \{1,\ldots ,n\},\) therefore, (21) is true for all \(i,j\in \{1,\ldots ,n\}.\)

Consequently, by Definition 4.6, we obtain \({\mathcal {E}}({\tilde{A}},w,\alpha )= e.\) \(\square\)

5 Deriving priority vectors and measuring inconsistency of FPC matrices

In this section we consider a given FPC matrix \({\tilde{A}}=\{{\tilde{a}}_{ij} \}.\) Here, we propose a couple of methods for calculating the priority vector of \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) for the purpose of rating the alternatives \(c_1,...,c_n \in {\mathcal {C}}\). We do not follow the way of calculating the fuzzy priority vector as it is proposed e.g. in [4], and others. Here, we shall generate a crisp priority vector, therefore, no defuzzification is necessary for final ranking of the alternatives. The proposed methods for calculating the priority vector satisfying the formerly defined desirable properties can be divided into several corresponding categories. Moreover, we look for priority vector for various given possibility degrees \(\alpha \in [0;1],\) eventually we shall look for the maximal such \(\alpha .\) Let us start with a suitable notation.

Definition 5.1

Given a FPC matrix \({\tilde{A}}=\{{\tilde{a}}_{ij} \},\) let \(\alpha \in [0;1].\) Denote the sets of \(\alpha\)-priority vectors of corresponding desirable properties of FPC \({\tilde{A}}.\) Firstly, we denote the basic set of normalized n-vectors, possible priority vectors with no other requirements.

$$\begin{aligned} W({\tilde{A}}) =\{w|w=(w_{1},w_{2},\cdots ,w_{n}), \bigodot _{k=1}^{n} w_k, w_k \in G, \text { for all }k \in N\}. \end{aligned}$$
(23)

Now, for given \(\alpha \in [0;1],\) we denote the sets of priority vectors satisfying specific desirable properties.

$$\begin{aligned} W_{CSV}({\tilde{A}},\alpha ) =\{w|w \in W({\tilde{A}}), w \text { is } \alpha -CSV \text {priority vector of} {\tilde{A}}\}, \end{aligned}$$
(24)
$$\begin{aligned} W_{IV}({\tilde{A}},\alpha ) =\{w|w \in W({\tilde{A}}), w \text { is } \alpha -IV \text {priority vector of} {\tilde{A}}\}, \end{aligned}$$
(25)
$$\begin{aligned} W_{CV}({\tilde{A}},\alpha ) =\{w|w \in W({\tilde{A}}), w \text { is } \alpha -CV \text {priority vector of} {\tilde{A}}\}. \end{aligned}$$
(26)

Proposition 5.2

Let \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) be a FPC matrix, let \(\alpha \in [0;1].\) Then

$$\begin{aligned} W_{CSV}({\tilde{A}},\alpha ) \subset W_{IV}(\alpha ,{\tilde{A}}) \subset W_{CV}({\tilde{A}},\alpha ). \end{aligned}$$
(27)

Proof

Suppose that \(w=(w_{1},w_{2},\cdots ,w_{n}) \in W_{CSV}({\tilde{A}},\alpha ).\) Then by Proposition 3.2 it holds \(a_{ik}^L(\alpha ) \le w_i \div w_k\) for all \(i,j\in \{1,\ldots ,n\}.\) By Definition 4.3, formula (14), then for some i, j, k, l it holds \(w_i \div w_j > w_k \div w_l,\) therefore, w is an \(\alpha\)-IV priority vector of \({\tilde{A}}\).

By setting \(k=l,\) we obtain that w is an \(\alpha\)-CV priority vector of \({\tilde{A}}.\) See also Remark 4.4. \(\square\)

Let \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\), \(\alpha \in [0;1].\) We denote

$$\begin{aligned} I^{(2)}({\tilde{A}},\alpha )=\{ (i,j)|i,j \in N, a_{ij}^R(\alpha )>e \}, \end{aligned}$$
(28)
$$\begin{aligned} I^{(4)}({\tilde{A}},\alpha )=\{ (i,j,k,l)|i,j,k,l \in N, a_{ij}^L(\alpha )>a_{kl}^R(\alpha )\}. \end{aligned}$$
(29)

Proposition 5.3

Let \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) be a FPC matrix, let \(\alpha \in [0;1],\) let \(\eta , \eta >e\) be a “sufficiently small” number converting the strict inequality > to the non-strict one, i.e. \(\ge .\)

Then

$$\begin{aligned} W_{CSV}({\tilde{A}},\alpha ) =\{w|w \in W({\tilde{A}}), a_{ij}^L(\alpha ) \le w_i \div w_j, w_k \in G, \text { for all } i,j \in N \}, \end{aligned}$$
(30)
$$\begin{aligned} W_{IV}({\tilde{A}},\alpha ) =\{w|w \in W({\tilde{A}}), w_{i} \div w_{j} \ge w_{k} \div w_{l} \odot \eta \text { , } (i,j,k,l) \in I^{(4)}({\tilde{A}},\alpha ) \}, \end{aligned}$$
(31)
$$\begin{aligned} W_{CV}({\tilde{A}},\alpha ) =\{w|\in W({\tilde{A}}), w_{i} \ge w_{j} \odot \eta \text { for all } (i,j) \in I^{(2)}(\alpha ,{\tilde{A}})\}. \end{aligned}$$
(32)

Proof

Formula (30) is evident by Proposition 3.2.

Formula (31) follows from the fact that \(w_{i} \div w_{j} \ge w_{k} \div w_{l} \odot \eta\) iff \(w_{i} \div w_{j} > w_{k} \div w_{l}\) for some \(\eta >e,\) for all \((i,j,k,l) \in I^{(4)}({\tilde{A}},\alpha ).\)

The similar argument can be used for proving (32). \(\square\)

The following proposition says that a "monotonicity" property of the individual sets of priority vectors is true. Later on, this property enables us to find out the \(\alpha\)-PV with the maximal \(\alpha \in [0;1].\)

Proposition 5.4

Let \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) be a FPC matrix, let \(\alpha , \beta \in [0;1], \beta \le \alpha .\) Then

$$\begin{aligned} W_{CSV}({\tilde{A}},\beta ) \subset W_{CSV}({\tilde{A}},\alpha ), \end{aligned}$$
(33)
$$\begin{aligned} W_{IV}({\tilde{A}},\beta ) \subset W_{IV}({\tilde{A}},\alpha ), \end{aligned}$$
(34)
$$\begin{aligned} W_{CV}({\tilde{A}},\beta ) \subset W_{CV}({\tilde{A}},\alpha ). \end{aligned}$$
(35)

Proof

  1. (i)

    Suppose that \(w \in W_{CSV}({\tilde{A}},\beta ), \alpha , \beta \in [0;1], \beta \le \alpha .\) Then \(a_{ij}^L(\beta ) \le w_i \div w_j \text { for all } i,j \in N.\) Moreover, by monotonicity of \(a_{ij}^L,\) we obtain \(a_{ij}^L(\beta ) \le a_{ij}^L(\alpha )\) for \(\beta \le \alpha .\) Hence, \(a_{ij}^L(\beta ) \le a_{ij}^L(\alpha ) \text { for all } i,j \in N.\) Consequently, \(w \in W_{CSV}({\tilde{A}},\alpha )\) and (33) holds.

  2. (ii)

    Suppose that \(w \in W_{CV}({\tilde{A}},\beta ), \alpha , \beta \in [0;1], \beta \le \alpha ,\) and let \(a_{ij}^R(\alpha )>e.\) By monotonicity of \(a_{ij}^R,\) we obtain \(a_{ij}^R(\beta ) \ge a_{ij}^R(\alpha )\) for \(\beta \le \alpha .\) Hence, \(a_{ij}^R(\beta ) > e,\) consequently, \(w_i \div w_j >e,\) therefore, \(w \in W_{CV}({\tilde{A}},\alpha )\) and (35) holds.

  3. (iii)

    By arguments similar to (ii) we obtain (34).

\(\square\)

Let \({\tilde{A}}=\{{\tilde{a}}_{ij} \}\) be a FPC matrix, let \(\alpha \in [0;1].\) Now, we propose three methods for finding priority vectors with a specific desirable properties for a given \(\alpha \in [0;1]:\) consistency, intensity and coherence.

5.1 Finding \(\alpha\)-CSV priority vector of \({\tilde{A}}\)

(P-CSV):

$$\begin{aligned} {\mathcal {E}}({\tilde{A}},w,\alpha ) \longrightarrow \text {min;} \end{aligned}$$
(36)

subject to

$$\begin{aligned} w \in W_{CSV}({\tilde{A}},\alpha ) \cap {\mathcal {E}}({\tilde{A}},w,\alpha ). \end{aligned}$$
(37)

5.2 Finding \(\alpha\)-IV priority vector of \({\tilde{A}}\)

(P-IV):

$$\begin{aligned} {\mathcal {E}}({\tilde{A}},w,\alpha ) \longrightarrow \text {min;} \end{aligned}$$
(38)

subject to

$$\begin{aligned} w \in W_{IV}({\tilde{A}},\alpha ) \cap {\mathcal {E}}({\tilde{A}},w,\alpha ). \end{aligned}$$
(39)

5.3 Finding \(\alpha\)-CV priority vector of \({\tilde{A}}\)

(P-CV):

$$\begin{aligned} {\mathcal {E}}({\tilde{A}},w,\alpha ) \longrightarrow \text {min;} \end{aligned}$$
(40)

subject to

$$\begin{aligned} w \in W_{CV}({\tilde{A}},\alpha ) \cap {\mathcal {E}}({\tilde{A}},w,\alpha ). \end{aligned}$$
(41)

Remark 5.5

It is evident that any \(\alpha -CV\) priority vector w of \({\tilde{A}}\) has the property, that the alternative with the highest weight of CV w corresponding to DM’s alternative \(c_{i_0}\) is always non-dominated, see [26]. The similar property holds for any IV w, resp. of a crisp PC matrix A. Another problem is to find a priority vector with specific desirable properties (consistency, intensity and coherence) with the maximal \(\alpha \in [0;1].\)

5.4 Finding \(\alpha ^{CSV}\)-CSV priority vector of \({\tilde{A}}\)

$$\begin{aligned} \alpha \longrightarrow \text {max;} \end{aligned}$$
(42)

subject to

$$\begin{aligned} w \in W_{CSV}({\tilde{A}},\alpha ) \cap {\mathcal {E}}({\tilde{A}},w,\alpha ). \end{aligned}$$
(43)

The optimal solution \(w^{(CSV)} \in G\) of problem (42), (43) is an \(\alpha ^{(CSV)}\)-CSV priority vector of \({\tilde{A}}.\)

5.5 Finding \(\alpha ^{(IV)}\)-IV priority vector of \({\tilde{A}}\)

$$\begin{aligned} \alpha \longrightarrow \text {max;} \end{aligned}$$
(44)

subject to

$$\begin{aligned} w \in W_{IV}({\tilde{A}},\alpha ) \cap {\mathcal {E}}({\tilde{A}},w,\alpha ). \end{aligned}$$
(45)

The optimal solution \(w^{(IV)} \in G\) of problem (42), (45) is an \(\alpha ^{(IV)}\)-IV priority vector of \({\tilde{A}}.\)

5.6 Finding \(\alpha ^{(CV)}\)-CV priority vector of \({\tilde{A}}\)

$$\begin{aligned} \alpha \longrightarrow \text {max;} \end{aligned}$$
(46)

subject to

$$\begin{aligned} w \in W_{CV}({\tilde{A}},\alpha ) \cap {\mathcal {E}}({\tilde{A}},w,\alpha ). \end{aligned}$$
(47)

The optimal solution \(w^{(CV)} \in G\) of problem (42), (47) is an \(\alpha ^{(CV)}\)-CV priority vector of \({\tilde{A}}.\)

Remark 5.6

In general, problem (P-T) where \(T \in \{CSV, IV, CV \},\) are nonlinear optimization problems that may be solved by a numerical method, e.g. by the well known dichotomy method, which is a sequence of relatively simple optimization problems, or by one of other available optimization methods, see e.g. [2].

Remark 5.7

Notice that here, strict inequalities have been changed to non-strict ones by including a sufficient constant \(\varepsilon >e.\) The objective function of (36) is the global error index, which is minimized with respect to w,  subject to the given constraints.

Remark 5.8

Evidently, for a given FPC matrix \({\tilde{A}},\) eventually, \(\alpha \in [0;1],\) some, and/or all sets of priority vectors \(W_{T}({\tilde{A}},\alpha ),\) \(T \in \{CSV, IV, CV \},\) in Subsects. 5.1–5.6, could be empty, i.e. the corresponding optimization problems are infeasible. If this situation happens for all \(T \in \{CSV, IV, CV \},\) then the DM should reconsider the elements of original FPC matrix \({\tilde{A}},\) eventually, should redesign it in some sense.

Remark 5.9

In general, the uniqueness of optimal solution of (36) and/or (42) subject to the given constraint is not saved. Depending on the particular operation \(\odot\), these problems may have multiple optimal solutions which is an unfavorable fact from the point of view of the DM. In this case, the DM should reconsider particular (fuzzy) evaluations in the original fuzzy pairwise comparison matrix.

Finally, we illustrate the above mentioned methods of calculating priority vectors with desirable properties by two examples.

Example 5.10

Consider the usual multiplicative alo-group \({\mathcal {R}}_{+}=({\textbf{R}}_{+}, \bullet ,\le )\) with \(\odot = \bullet\), see Example 2.2. Let \(\tilde{A_1}=\{{\tilde{a}}_{1ij}\}\) be given by triangular fuzzy number elements as follows:

$$\begin{aligned} \tilde{A_1}=\left[ \begin{array}{ccc} {[}1,1,1] &{} [1,2,3] &{} [7,8,9] \\ {[}\frac{1}{3},\frac{1}{2},1] &{} [1,1,1] &{} [2,3,4] \\ {[}\frac{1}{9},\frac{1}{8},\frac{1}{7}] &{} {[}\frac{1}{4},\frac{1}{3},\frac{1}{2}] &{} [1,1,1] \end{array} \right] , \end{aligned}$$

or, equivalently, by \(\alpha\)-cut notation, for \(\alpha \in [0;1]\), we obtain

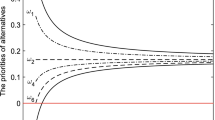
$$\begin{aligned} \tilde{A_1}=\left[ \begin{array}{ccc} {[}1;1] &{} [1+\alpha ;3-\alpha ] &{} [7+\alpha ;9-\alpha ] \\ {[}\frac{1}{3-\alpha };\frac{1}{1+\alpha }] &{} [1;1] &{} [2+\alpha ;4-\alpha ] \\ \frac{1}{9-\alpha };\frac{1}{7+\alpha }] &{} [\frac{1}{4-\alpha };\frac{1}{2+\alpha }] &{} [1;1] \end{array} \right] . \end{aligned}$$

Here, \(\tilde{A_1}\) is a \(3\times 3\) matrix with triangular fuzzy number elements and the corresponding piece-wise linear membership functions.

By solving problem (P-CSV), see Subsect. 5.1, we obtain the maximal \(\alpha ^{(CSV)}= 0.683\) and minimal global error index \({\mathcal {E}}(\tilde{A_1},w^{(CSV)},0.683)= 1.378.\) Hence, \(\tilde{A_1}\) is \(\alpha\)-\(\bullet\)-consistent for all \(0 \le \alpha \le 0.683\).

The priority vector of \(\tilde{A_1}\) is obtained as the optimal solution of problem (P-CSV), particularly, \(w^{(CSV)}=(w_1^{*},w_2^{*},w_3^{*}) = (2.611, 1.127, 0.340).\)

Moreover, by solving problem (P-CV), see Subsect. 5.3, we obtain the maximal \(\alpha ^{(CV)}= 1.000\) and minimal global error index \({\mathcal {E}}(\tilde{A_1},w^{(CV)},1.000)= 1.101.\) Hence, \(\tilde{A_1}\) is \(\alpha\)-\(\bullet\)-coherent for all \(0 \le \alpha \le 1.000\), i.e. it is \(\bullet\)-coherent.

The coherent priority vector of \(\tilde{A_1}\) is obtained as the optimal solution of problem (P-CV), particularly, \(w^{(CV)}=(w_1^{**},w_2^{**},w_3^{**}) = (2.520, 1.145, 0.347).\)

The corresponding ranking of alternatives is in both cases \(c_{1}> c_{2} > c_{3}.\)

Example 5.11

Consider the multiplicative alo-group \({\mathcal {R}}_{+}=({\textbf{R}}_{+}, \bullet ,\le )\) with \(\odot = \bullet\) (see Example 2.2). Let \(\tilde{A_2}=\{{\tilde{a}}_{2ij}\}\) be given by triangular fuzzy number elements as

$$\begin{aligned} \tilde{A_2}=\left[ \begin{array}{ccc} {[}1,1,1] &{} [1,\frac{3}{2},2] &{} [7,8,9] \\ {[}\frac{1}{3},\frac{2}{3},1] &{} [1,1,1] &{} [2,\frac{5}{2},3] \\ {[}\frac{1}{9},\frac{1}{8},\frac{1}{7}] &{} {[}\frac{1}{3},\frac{2}{5},\frac{1}{2}] &{} [1,1,1] \end{array} \right] , \end{aligned}$$

or, equivalently, by \(\alpha\)-cut notation, for \(\alpha \in [0;1]\), we obtain

$$\begin{aligned} \tilde{A_2}=\left[ \begin{array}{ccc} {[}1;1] &{} [1+\frac{\alpha }{2};2-\frac{\alpha }{2}] &{} [7+\alpha ;9-\alpha ] \\ {[}\frac{2}{4-\alpha };\frac{2}{2+\alpha }] &{} [1;1] &{} [2+0.5\alpha ;3-0.5\alpha ] \\ \frac{1}{9-\alpha };\frac{1}{7+\alpha }] &{} [\frac{2}{6-\alpha };\frac{2}{4+\alpha }] &{} [1;1] \end{array} \right] . \end{aligned}$$

Here, problem (P-CSV) has no feasible solution, hence, \(\tilde{A_2}\) is \(\bullet\)-inconsistent.

Moreover, by solving problem (P-CV), see Subsect. 5.3, we obtain the maximal \(\alpha ^{(CV)}= 1.000\) and minimal global error index \({\mathcal {E}}(\tilde{A_2},w^{(CV)},1.000)= 1.287.\) Hence, \(\tilde{A_2}\) is \(\alpha\)-\(\bullet\)-coherent for all \(0 \le \alpha \le 1.000\), i.e., it is \(\bullet\)-coherent.

The coherent priority vector of \(\tilde{A_2}\) is obtained as the optimal solution of problem (P-CV), particularly, \(w^{(CV)}=(w_1^{***},w_2^{***},w_3^{***}) = (2.289, 1.186, 0.368).\)

The corresponding ranking of alternatives is in both cases \(c_{1}> c_{2} > c_{3}.\)

6 Conclusion

This paper deals with PC matrices with fuzzy elements and it solves an important problem of finding their priority vectors having the desirable properties of consistency, intensity and coherence. In comparison with PC matrices investigated in the literature, here we investigate PCMs with elements from abelian linearly ordered group (alo-group) over a real interval. We also define the concept of crisp priority vector which is an extension of the well known concept in crisp case and is used for ranking of the given alternatives. Such an approach allows for extending various approaches known from the literature and enables practical computations of the priority vectors. Here, we derive new sufficient conditions for the existence of consistent vector, coherent vector, intensity vector of a FPCM. Then, we formulate special optimization problems and algorithms for deriving the priority vector satisfying the desirable properties under appropriate assumptions. Furthermore, the proposed methods solve the problem of finding a priority vector satisfying the desirable properties by minimizing the corresponding global error index, formerly proposed in [13]. Finally, we give some numerical examples in order to illustrate the new concepts, their properties and the algorithms for solving the problem.

In the future, we shall focus our research to the problems of non-reciprocal pairwise comparisons matrices being also frequent in the practice of MCDM. Without the assumption of reciprocity some interesting results can be achieved and corresponding algorithms for finding priority vectors can be verified. There is also an interesting problem of under what conditions the classical priority vectors generated by the Eigenvector method and/or Geometric average method could become intensity and/or coherent PVs. Up till now, sufficient theoretical results are not known, hence simulation experiments should be performed and analyzed.