Introduction

A considerable amount of advances have been made with the concatenation model ever since its inception during 2014 [1, 2]. This model is a combination of the three well known equations that are individually considered and frequently talked about in fiber optics [3, 4]. They are the nonlinear Schrödinger’s equation (NLSE), Lakshmanan–Porsezian–Daniel (LPD) equation and the Sasa–Satsuma equation (SSE) [5, 6]. The model was first proposed about a decade ago [7, 8]. Thereafter, a wide range of results have followed through for this model [9, 10]. These include the identification of the conservation laws, addressing the model using several forms of integration algorithms including undetermined coefficients and Kudryashov’s approaches [11]. The current paper moves over to the next phase of the project. This work is to address gap solitons that emerge from the Bragg gratings structure which is introduced to compensate for the low count of CD. These gap solitons are thus retrieved from the model equation by the application of the new mapping method. A full spectrum of gap solitons are revealed for the model in Bragg gratings. The soliton solutions are thus enumerated and the parameter restrictions that appear as constraints are also enumerated. The details of the integration scheme as well as the mathematical derivation procedure are presented in details and are exhibited in the rest of the paper.

Mathematical model

The expression of the concatenation model for polarization-preserving fibers can be summarized as follows:

$$\begin{aligned}{} & {} i\psi _{t}+a\psi _{xx}+b\left| \psi \right| ^{2}\psi +c_{1}\left[ \sigma _{1}\psi _{xxxx}+\sigma _{2}\left( \psi _{x}\right) ^{2}\psi ^{*}\right. +\sigma _{3}\left| \psi _{x}\right| ^{2}\psi \nonumber \\{} & {} \quad \left. +\sigma _{4}\left| \psi \right| ^{2}\psi _{xx}+\sigma _{5}\psi ^{2}\psi _{xx}^{*}+\sigma _{6}\left| \psi \right| ^{4}\psi \right] \nonumber \\{} & {} \quad +ic_{2}\left[ \sigma _{7}\psi _{xxx}+\sigma _{8}\left| \psi \right| ^{2}\psi _{x}+\sigma _{9}\psi ^{2}\psi _{x}^{*}\right] =0,\quad i= \sqrt{-1}, \end{aligned}$$
(1)

In Equation (1), the variable \(\psi (x,t)\) represents the complex wave profile, where x corresponds to the spatial component and t represents the temporal component. a represents the CD term, b and \(\sigma _{6}\) represent the self-phase modulation (SPM) coefficients. Next, \(\sigma _{1}\) and \(\sigma _{7}\) are the coefficients of third–order dispersion (3OD) and the fourth–order dispersion (4OD), respectively. Finally, the coefficients \(\sigma _{2},\sigma _{3},\sigma _{8}\) and \(\sigma _{9}\) imply the additional nonlinear effects, while the coefficients \(\sigma _{4}\) and \(\sigma _{5}\) give the nonlinear dispersive effects.

For fiber Bragg gratings, Eq. (1) is split into two separate components as:

$$\begin{aligned}{} & {} iq_{t}+a_{1}r_{xx}+\left( b_{11}\left| q\right| ^{2}+b_{12}\left| r\right| ^{2}\right) q \nonumber \\{} & {} \quad +c_{11}\left\{ \dfrac{{}}{{}}b_{1}r_{xxxx}+\left[ d_{11}\left( q_{x}\right) ^{2}+d_{12}\left( r_{x}\right) ^{2}\right] q^{*}+\left[ e_{11}\left| q_{x}\right| ^{2}+e_{12}\left| r_{x}\right| ^{2}\right] q+\left[ f_{11}\left| q\right| ^{2}+f_{12}\left| r\right| ^{2}\right] q_{xx}\right. \nonumber \\{} & {} \quad \left. +\left[ g_{11}q^{2}+g_{12}r^{2}\right] q_{xx}^{*}+\left[ h_{11}\left| q\right| ^{4}+h_{12}\left| q\right| ^{2}\left| r\right| ^{2}+h_{13}\left| r\right| ^{4}\right] q \dfrac{{}}{{}}\right\} \nonumber \\{} & {} \quad +ic_{12}\left[ c_{1}r_{xxx}+\left( k_{11}\left| q\right| ^{2}+k_{12}\left| r\right| ^{2}\right) q_{x}+\left( l_{11}q^{2}+l_{12}r^{2}\right) q_{x}^{*}\right] +i\alpha _{1}q_{x}+\beta _{1}r+\gamma _{1}q^{*}r^{2}=0, \end{aligned}$$
(2)

and

$$\begin{aligned}{} & {} ir_{t}+a_{2}q_{xx}+\left( b_{21}\left| r\right| ^{2}+b_{22}\left| q\right| ^{2}\right) r \nonumber \\{} & {} \quad +c_{21}\left\{ \dfrac{{}}{{}}b_{2}q_{xxxx}+\left[ d_{21}\left( r_{x}\right) ^{2}+d_{22}\left( q_{x}\right) ^{2}\right] r^{*}+\left[ e_{21}\left| r_{x}\right| ^{2}+e_{22}\left| q_{x}\right| ^{2}\right] r+\left[ f_{21}\left| r\right| ^{2}+f_{22}\left| q\right| ^{2}\right] r_{xx}\right. \nonumber \\{} & {} \quad \left. +\left[ g_{21}r^{2}+g_{22}q^{2}\right] r_{xx}^{*}+\left[ h_{21}\left| r\right| ^{4}+h_{22}\left| r\right| ^{2}\left| q\right| ^{2}+h_{23}\left| q\right| ^{4}\right] r \dfrac{{}}{{}}\right\} \nonumber \\{} & {} \quad +ic_{22}\left[ c_{2}q_{xxx}+\left( k_{21}\left| r\right| ^{2}+k_{22}\left| q\right| ^{2}\right) r_{x}+\left( l_{21}r^{2}+l_{22}q^{2}\right) r_{x}^{*}\right] +i\alpha _{2}r_{x}+\beta _{2}q+\gamma _{2}r^{*}q^{2}=0. \end{aligned}$$
(3)

The constrants \(a_{j}\), \(b_{j}\), \(c_{j}\), \(b_{j1}\), \(b_{j2}\), \(d_{j1}\), \(d_{j2}\), \(e_{j1}\), \(e_{j2}\), \(f_{j1}\), \(f_{j2}\), \(g_{j1}\), \(g_{j2}\), \(h_{j1}\), \(h_{j2}\), \(h_{j3}\), \(k_{j1}\), \(k_{j2}\), \(l_{j1}\), \(l_{j2}\), \(\alpha _{j}\), \(\beta _{j}\) and \(\gamma _{j},\) \((j=1,2)\) are parameters, while, \(q\left( x,t\right)\), r(x, t) are the complex wave profiles. Respectively, the coefficients \(a_{j}\), \(b_{j}\) and \(c_{j}\) are CD, 3OD and 4OD terms along the two components. Next, \(b_{j1}\) and \(h_{j1}\) are the SPM terms, while \(b_{j2},h_{j2}\) and \(h_{j3}\) are the cross-phase modulation (XPM) effect. The coefficients \(\alpha _{j},\beta _{j}\) and \(\gamma _{j}\) give inter-modal dispersion (IMD), detuning parameter and four–wave mixing effect (4WM) for Kerr part of the nonlinearity, respectively. Finally, the coefficients \(d_{j1}\), \(d_{j2}\), \(e_{j1}\) and \(e_{j2}\), give the nonlinear dispersive effects and the remaining coefficients give the effect of additional dispersions. The concatenation model integrates these three equations into a unified framework, offering a comprehensive and precise depiction of soliton behavior in Bragg grating fibers. This model proves valuable in various applications within fiber optic communication systems, where solitons play a crucial role in transmitting information over long distances while experiencing minimal distortion.

The primary objective of this article is to utilize a new mapping method in order to identify the dark, bright, and singular soliton solutions, as well as the combined bright-singular soliton solutions, for Eqs. (2) and (3).

The structure of this article can be outlined as follows: Section Preliminary analysis provides a mathema4tical analysis. Section New mapping method presents the solutions of Eqs. (2) and (3) utilizing the new mapping method. Finally, in Section Results and discussion, the conclusions are presented and discussed.

Preliminary analysis

In this section, we assume that the solutions for Eqs. (2) and (3) are given by:

$$\begin{aligned} \left. \begin{array}{c} q(x,t)=\varphi _{1}\left( \zeta \right) \exp \left[ iZ\left( x,t\right) \right] , \\ \\ r(x,t)=\varphi _{2}\left( \zeta \right) \exp \left[ iZ\left( x,t\right) \right] , \end{array} \right. \end{aligned}$$
(4)

and

$$\begin{aligned} \left. \begin{array}{c} \zeta =x-vt,\quad Z\left( x,t\right) =-\kappa x+\omega t+\theta _{0}, \\ \end{array} \right. \end{aligned}$$
(5)

Assuming that \(v,\kappa ,\omega\) and \(\theta _{0}\) are all non-zero parameters, where v represents the soliton’s velocity, \(\kappa\) denotes its wave number, \(\omega\) represents its frequency, and \(\theta _{0}\) is the phase constant, we have real functions \(\varphi _{1}\left( \zeta \right) ,\varphi _{2}\left( \zeta \right)\) and \(Z\left( x,t\right)\) that represent the amplitude and phase components of the soliton, respectively. By substituting Eqs. (4) and (5) into Eqs. (2) and (3) and separating their real and imaginary parts, we can infer that:

$$\begin{aligned}{} & {} \Re _{1}:c_{11}b_{1}\varphi _{2}^{(4)}+\left( a_{1}+3c_{12}c_{1}\kappa -6c_{11}b_{1}\kappa ^{2}\right) \varphi _{2}^{\prime \prime }\nonumber \\{} & {} \quad +c_{11}\left[ \left( d_{11}+e_{11}\right) \varphi _{1}\varphi _{1}^{\prime 2}+\left( d_{12}+e_{12}\right) \varphi _{1}\varphi _{2}^{\prime 2}\right] \nonumber \\{} & {} \quad +c_{11}\left[ \left( f_{11}+g_{11}\right) \varphi _{1}^{2}\varphi _{1}^{\prime \prime }+\left( f_{12}+g_{12}\right) \varphi _{1}^{\prime \prime }\varphi _{2}^{2}\right] +\left( \alpha _{1}\kappa -\omega \right) \varphi _{1}\nonumber \\{} & {} \quad + \left( \beta _{1}-a_{1}\kappa ^{2}-c_{12}c_{1}\kappa ^{3}+c_{11}b_{1}\kappa ^{4}\right) \varphi _{2} \nonumber \\{} & {} \quad +\left[ b_{11}-c_{11}\left( d_{11}-e_{11}+f_{11}+g_{11}\right) \kappa ^{2}+c_{12}\left( k_{11}-l_{11}\right) \kappa \right] \varphi _{1}^{3} \nonumber \\{} & {} \quad +\left[ \gamma _{1}+b_{12}-c_{11}\left( d_{12}-e_{12}+f_{12}+g_{12}\right) \kappa ^{2}+c_{12}\left( k_{12}-l_{12}\right) \kappa \right] \varphi _{1}\varphi _{2}^{2} \nonumber \\{} & {} \quad +c_{11}\left[ h_{11}\varphi _{1}^{5}+h_{12}\varphi _{1}^{3}\varphi _{2}^{2}+h_{13}\varphi _{1}\varphi _{2}^{4}\right] =0, \end{aligned}$$
(6)
$$\begin{aligned}{} & {} \Re _{2}:c_{21}b_{2}\varphi _{1}^{(4)}+\left( a_{2}+3c_{22}c_{2}\kappa -6c_{21}b_{2}\kappa ^{2}\right) \varphi _{1}^{\prime \prime }\nonumber \\{} & {} \quad +c_{21}\left[ \left( d_{21}+e_{21}\right) \varphi _{2}\varphi _{2}^{\prime 2}+\left( d_{22}+e_{22}\right) \varphi _{2}\varphi _{1}^{\prime 2}\right] \nonumber \\{} & {} \quad +c_{21}\left[ \left( f_{21}+g_{21}\right) \varphi _{2}^{2}\varphi _{2}^{\prime \prime }+\left( f_{22}+g_{22}\right) \varphi _{2}^{\prime \prime }\varphi _{1}^{2}\right] +\left( \alpha _{2}\kappa -\omega \right) \varphi _{2}\nonumber \\{} & {} \quad +\left( \beta _{2}-a_{2}\kappa ^{2}-c_{22}c_{2}\kappa ^{3}+c_{21}b_{2}\kappa ^{4}\right) \varphi _{1} \nonumber \\{} & {} \quad +\left[ b_{21}-c_{21}\left( d_{21}-e_{21}+f_{21}+g_{21}\right) \kappa ^{2}+c_{22}\left( k_{21}-l_{21}\right) \kappa \right] \varphi _{2}^{3} \nonumber \\{} & {} \quad +\left[ \gamma _{2}+b_{22}-c_{21}\left( d_{22}-e_{22}+f_{22}+g_{22}\right) \kappa ^{2}+c_{22}\left( k_{22}-l_{22}\right) \kappa \right] \varphi _{2}\varphi _{1}^{2} \nonumber \\{} & {} \quad +c_{21}\left[ h_{21}\varphi _{2}^{5}+h_{22}\varphi _{2}^{3}\varphi _{1}^{2}+h_{23}\varphi _{2}\varphi _{1}^{4}\right] =0, \end{aligned}$$
(7)

and

$$\begin{aligned}{} & {} \Im _{1}:\left( c_{12}c_{1}-4c_{11}b_{1}\kappa \right) \varphi _{2}^{\prime \prime \prime }+\left[ 2c_{11}\left( g_{11}-d_{11}-f_{11}\right) \kappa \right. \nonumber \\{} & {} \quad \left. +c_{12}\left( k_{11}+l_{11}\right) \right] \varphi _{1}^{2}\varphi _{1}^{\prime }-2c_{11}d_{12}\kappa \varphi _{1}\varphi _{2}\varphi _{2}^{\prime }\nonumber \\{} & {} \quad +\left[ 2c_{11}\left( g_{11}-f_{11}\right) \kappa +c_{12}\left( k_{12}+l_{12}\right) \right] \varphi _{1}^{\prime }\varphi _{2}^{2}+\left( \alpha _{1}-v\right) \varphi _{1}^{\prime }\nonumber \\{} & {} \quad +\left( 4c_{11}b_{1}\kappa ^{3}-3c_{12}c_{1}\kappa ^{2}-2a_{1}\kappa \right) \varphi _{2}^{\prime }=0, \end{aligned}$$
(8)
$$\begin{aligned}{} & {} \Im _{2}:\left( c_{22}c_{2}-4c_{21}b_{2}\kappa \right) \varphi _{1}^{\prime \prime \prime }+\left[ 2c_{21}\left( g_{21}-d_{21}-f_{21}\right) \kappa \right. \nonumber \\{} & {} \quad \left. +c_{22}\left( k_{21}+l_{21}\right) \right] \varphi _{2}^{2}\varphi _{2}^{\prime }-2c_{21}d_{22}\kappa \varphi _{2}\varphi _{1}\varphi _{1}^{\prime } \nonumber \\{} & {} \quad +\left[ 2c_{21}\left( g_{21}-f_{21}\right) \kappa +c_{22}\left( k_{22}+l_{22}\right) \right] \varphi _{2}^{\prime }\varphi _{1}^{2}+\left( \alpha _{2}-v\right) \varphi _{2}^{\prime }\nonumber \\{} & {} \quad +\left( 4c_{21}b_{2}\kappa ^{3}-3c_{22}c_{2}\kappa ^{2}-2a_{2}\kappa \right) \varphi _{1}^{\prime }=0. \end{aligned}$$
(9)

Set

$$\begin{aligned} \varphi _{2}\left( \zeta \right) =\chi \varphi _{1}\left( \zeta \right) , \end{aligned}$$
(10)

provided \(\chi \ne 0,1.\) Now, Eqs. (6)–(9) become

$$\begin{aligned}{} & {} \Re _{1}:c_{11}b_{1}\chi \varphi _{1}^{(4)}+\left( a_{1}+3c_{12}c_{1}\kappa -6c_{11}b_{1}\kappa ^{2}\right) \chi \varphi _{1}^{\prime \prime }\nonumber \\{} & {} \quad +c_{11} \left[ d_{11}+e_{11}+\left( d_{12}+e_{12}\right) \chi ^{2}\right] \varphi _{1}\varphi _{1}^{\prime 2} \nonumber \\{} & {} \quad +c_{11}\left[ f_{11}+g_{11}+\left( f_{12}+g_{12}\right) \chi ^{2}\right] \varphi _{1}^{2}\varphi _{1}^{\prime \prime }\nonumber \\{} & {} \quad +\left[ \alpha _{1}\kappa -\omega +\left( \beta _{1}-a_{1}\kappa ^{2}-c_{12}c_{1}\kappa ^{3}+c_{11}b_{1}\kappa ^{4}\right) \chi \right] \varphi _{1} \nonumber \\{} & {} \quad +\left\{ \dfrac{{}}{{}}b_{11}-c_{11}\left( d_{11}-e_{11}+f_{11}+g_{11}\right) \kappa ^{2}+c_{12}\left( k_{11}-l_{11}\right) \kappa \right. \nonumber \\{} & {} \quad +\left[ \gamma _{1}+b_{12}+c_{12}\left( k_{12}-l_{12}\right) \kappa \right] \chi ^{2} \nonumber \\{} & {} \quad \left. -c_{11}\kappa ^{2}\left( d_{12}-e_{12}+f_{12}+g_{12}\right) \chi ^{2} \dfrac{{}}{{}}\right\} \varphi _{1}^{3}\nonumber \\{} & {} \quad +c_{11}\left[ h_{11}+h_{12}\chi ^{2}+h_{13}\chi ^{4}\right] \varphi _{1}^{5}=0, \end{aligned}$$
(11)
$$\begin{aligned}{} & {} \Re _{2}:c_{21}b_{2}\varphi _{1}^{(4)}+\left( a_{2}+3c_{22}c_{2}\kappa -6c_{21}b_{2}\kappa ^{2}\right) \varphi _{1}^{\prime \prime }\nonumber \\{} & {} \quad +c_{21}\left[ \left( d_{21}+e_{21}\right) \chi ^{3}+\left( d_{22}+e_{22}\right) \chi \right] \varphi _{1}\varphi _{1}^{\prime 2} \nonumber \\{} & {} \quad +c_{21}\left[ \left( f_{21}+g_{21}\right) \chi ^{3}+\left( f_{22}+g_{22}\right) \chi \right] \varphi _{1}^{2}\varphi _{1}^{\prime \prime }\nonumber \\{} & {} \quad +\left[ \left( \alpha _{2}\kappa -\omega \right) \chi +\beta _{2}-a_{2}\kappa ^{2}-c_{22}c_{2}\kappa ^{3}+c_{21}b_{2}\kappa ^{4}\right] \varphi _{1} \nonumber \\{} & {} \quad +\left\{ \dfrac{{}}{{}}\left[ b_{21}-c_{21}\left( d_{21}-e_{21}+f_{21}+g_{21}\right) \kappa ^{2}+c_{22}\left( k_{21}-l_{21}\right) \kappa \right] \chi ^{3}\right. \nonumber \\{} & {} \quad +\left[ \gamma _{2}+b_{22}+c_{22}\left( k_{22}-l_{22}\right) \kappa \right] \chi \nonumber \\{} & {} \quad \left. -c_{21}\chi \kappa ^{2}\left( d_{22}-e_{22}+f_{22}+g_{22}\right) \dfrac{{}}{{}}\right\} \varphi _{1}^{3}\nonumber \\{} & {} \quad +c_{21}\left[ h_{21}\chi ^{5}+h_{22}\chi ^{3}+h_{23}\chi \right] \varphi _{1}^{5}=0, \end{aligned}$$
(12)

and

$$\begin{aligned}{} & {} \Im _{1}:\left( c_{12}c_{1}-4c_{11}b_{1}\kappa \right) \chi \varphi _{1}^{\prime \prime \prime }\nonumber \\{} & {} \quad +\left[ \alpha _{1}-v+\left( 4c_{11}b_{1}\kappa ^{3}-3c_{12}c_{1}\kappa ^{2}-2a_{1}\kappa \right) \chi \right] \varphi _{1}^{\prime } \nonumber \\{} & {} \quad +\left\{ 2c_{11}\left( g_{11}-d_{11}-f_{11}\right) \kappa +c_{12}\left( k_{11}+l_{11}\right) \right. \nonumber \\{} & {} \quad \left. +\left[ 2c_{11}\left( g_{11}-f_{11}\right) \kappa +c_{12}\left( k_{12}+l_{12}\right) -2c_{11}d_{12}\kappa \right] \chi ^{2}\right\} \varphi _{1}^{\prime }\varphi _{1}^{2}=0, \end{aligned}$$
(13)
$$\begin{aligned}{} & {} \quad \Im _{2}:\left( c_{22}c_{2}-4c_{21}b_{2}\kappa \right) \varphi _{1}^{\prime \prime \prime }+\left[ \left( \alpha _{2}-v\right) \chi +4c_{21}b_{2}\kappa ^{3}\right. \nonumber \\{} & {} \quad \left. -3c_{22}c_{2}\kappa ^{2}-2a_{2}\kappa \right] \varphi _{1}^{\prime } \nonumber \\{} & {} \quad +\left\{ \left[ 2c_{21}\left( g_{21}-d_{21}-f_{21}\right) \kappa +c_{22}\left( k_{21}+l_{21}\right) \right] \chi ^{2} \right. \nonumber \\{} & {} \quad \left. +2c_{21}\left( g_{21}-f_{21}\right) \kappa +c_{22}\left( k_{22}+l_{22}\right) -2c_{21}d_{22}\kappa \right\} \chi \varphi _{1}^{\prime }\varphi _{1}^{2}=0, \end{aligned}$$
(14)

By equating the coefficients of the linearly independent functions in Eqs. (13) and (14) to zero, we obtain:

$$\begin{aligned}{} & {} \left. \kappa =\frac{c_{j2}c_{j}}{4c_{j1}b_{j}},\quad j=1,2,\right. \end{aligned}$$
(15)
$$\begin{aligned}{} & {} v=\alpha _{1}+\left( 4c_{11}b_{1}\kappa ^{3}-3c_{12}c_{1}\kappa ^{2}-2a_{1}\kappa \right) \chi , \nonumber \\{} & {} v=\dfrac{\alpha _{2}\chi +4c_{21}b_{2}\kappa ^{3}-3c_{22}c_{2}\kappa ^{2}-2a_{2}\kappa }{\chi }, \end{aligned}$$
(16)
$$\begin{aligned}{} & {} 2c_{11}\left( g_{11}-d_{11}-f_{11}\right) \kappa +c_{12}\left( k_{11}+l_{11}\right) \nonumber \\ & \quad +\left[ 2c_{11}\left( g_{11}-f_{11}\right) \kappa +c_{12}\left( k_{12}+l_{12}\right) -2c_{11}d_{12}\kappa \right] \chi ^{2}=0,\nonumber \\ & \quad \left[ 2c_{21}\left( g_{21}-d_{21}-f_{21}\right) \kappa +c_{22}\left( k_{21}+l_{21}\right) \right] \chi ^{2}\nonumber \\ & \quad +2c_{21}\left( g_{21}-f_{21}\right) \kappa +c_{22}\left( k_{22}+l_{22}\right) -2c_{21}d_{22}\kappa =0. \end{aligned}$$
(17)

Equations (11) and (12) exhibit identical forms, under the following constraint conditions:

$$\begin{aligned} \left. \begin{array}{l} c_{11}b_{1}\chi =c_{21}b_{2}, \\ \left( a_{1}+3c_{12}c_{1}\kappa -6c_{11}b_{1}\kappa ^{2}\right) \chi =a_{2}+3c_{22}c_{2}\kappa -6c_{21}b_{2}\kappa ^{2}, \\ c_{11}\left[ d_{11}+e_{11}+\left( d_{12}+e_{12}\right) \chi ^{2}\right] =c_{21}\left[ \left( d_{21}+e_{21}\right) \chi ^{3}+\left( d_{22}+e_{22}\right) \chi \right] , \\ c_{11}\left[ f_{11}+g_{11}+\left( f_{12}+g_{12}\right) \chi ^{2}\right] \\ \quad =c_{21}\left[ \left( f_{21}+g_{21}\right) \chi ^{3}+\left( f_{22}+g_{22}\right) \chi \right] , \\ \alpha _{1}\kappa -\omega +\left( \beta _{1}-a_{1}\kappa ^{2}-c_{12}c_{1}\kappa ^{3}+c_{11}b_{1}\kappa ^{4}\right) \chi =\left( \alpha _{2}\kappa -\omega \right) \chi \\ \quad +\beta _{2}-a_{2}\kappa ^{2}-c_{22}c_{2}\kappa ^{3}+c_{21}b_{2}\kappa ^{4}, \\ b_{11}-c_{11}\left( d_{11}-e_{11}+f_{11}+g_{11}\right) \kappa ^{2}+c_{12}\left( k_{11}-l_{11}\right) \kappa \\ \quad +\left[ \gamma _{1}+b_{12}+c_{12}\left( k_{12}-l_{12}\right) \kappa \right] \chi ^{2} \\ \quad -c_{11}\kappa ^{2}\left( d_{12}-e_{12}+f_{12}+g_{12}\right) \chi ^{2}=\left[ b_{21}\right. \\ \quad \left. -c_{21}\left( d_{21} -e_{21}+f_{21}+g_{21}\right) \kappa ^{2}+c_{22}\left( k_{21}-l_{21}\right) \kappa \right] \chi ^{3} \\ \quad +\left[ \gamma _{2}+b_{22}+c_{22}\left( k_{22}-l_{22}\right) \kappa \right] \chi -c_{21}\chi \kappa ^{2}\left( d_{22}-e_{22}+f_{22}+g_{22}\right) , \\ c_{11}\left[ h_{11}+h_{12}\chi ^{2}+h_{13}\chi ^{4}\right] =c_{21}\left[ h_{21}\chi ^{5}+h_{22}\chi ^{3}+h_{23}\chi \right] . \\ \end{array} \right\} \end{aligned}$$
(18)

From (15)–(18), one derives the following:

$$\begin{aligned} \left. \begin{array}{l} \omega =\frac{\left( 3\,c_{{12}}c_{{1}}{\kappa }^{3}-4\,c_{{11}}b_{{1}}{ \kappa }^{4}+2\,a_{{1}}{\kappa }^{2}\right) {\chi }^{2}+\left( \beta _{{1} }-3\,c_{{12}}c_{{1}}{\kappa }^{3}+4\,c_{{11}}b_{{1}}{\kappa }^{4}-\alpha _{{1 }}\kappa -2\,a_{{1}}{\kappa }^{2}\right) \chi -\beta _{{2}}+\alpha _{{1} }\kappa }{\chi -1},\text { }c_{{22}}={\frac{c_{{1}}c_{{12}}\chi }{c_{{2}}}}, \\ \\ \alpha _{{2}}=4\,c_{{11}}b_{{1}}\left( \chi -1\right) {\kappa }^{3}-3\,c_{{12 }}c_{{1}}\left( \chi -1\right) {\kappa }^{2}-2\,a_{{1}}\left( \chi -1\right) \kappa +\alpha _{{1}},\text { }a_{{2}}=\chi \,a_{{1}},\text { }b_{{2}}={\frac{ c_{{11}}b_{{1}}\chi }{c_{{21}}},} \\ \\ b_{{22}}={\tfrac{\left\{ \left[ 2\,c_{{11}}\left( f_{{11}}-g_{{11}}\right) { \kappa }^{2}-2\,c_{{12}}\kappa \,l_{{12}}+b_{{12}}+\gamma _{{1}}\right] { \chi }^{2}-\left[ 2\,c_{{21}}\left( f_{{21}}-g_{{21}}\right) {\kappa } ^{2}+b_{{21}}\right] {\chi }^{3}-\left[ 2\,c_{{21}}\left( f_{{21}}-g_{{21} }\right) {\kappa }^{2}+\gamma _{{2}}\right] \chi \right\} c_{{2}}}{\chi \,c_{ {2}}}} \\ \qquad +\frac{\left[ 2\,c_{{11}}\left( f_{{11}}-g_{{11} }\right) {\kappa }^{2}-2\,c_{{12}}\kappa \,l_{{11}}+b_{{11}}\right] c_{{2} }+2\,{\chi }^{2}\kappa \,c_{{1}}c_{{12}}\left( l_{{21}}{\chi }^{2}+l_{{22} }\right) }{\chi \,c_{{2}}}{,} \\ \\ d_{{22}}={\frac{-c_{{21}}\left( d_{{21}}+e_{{21}}\right) {\chi }^{3}+c_{{11} }\left( d_{{12}}+e_{{12}}\right) {\chi }^{2}-c_{{21}}\chi \,e_{{22}}+c_{{11} }\left( d_{{11}}+e_{{11}}\right) }{c_{{21}}\chi },}\\ f_{{22}}={\frac{ -c_{{21}}\left( f_{{21}}+g_{{21}}\right) {\chi }^{3}+c_{{11}}\left( f_{{12} }+g_{{12}}\right) {\chi }^{2}-c_{{21}}\chi \,g_{{22}}+c_{{11}}\left( f_{{11} }+g_{{11}}\right) }{c_{{21}}\chi },} \\ \\ h_{{22}}={\frac{c_{{11}}h_{{11}}+c_{{11}}h_{{12}}{\chi }^{2}+c_{{11}}h_{{13}} {\chi }^{4}-c_{{21}}h_{{21}}{\chi }^{5}-c_{{21}}h_{{23}}\chi }{c_{{21}}{\chi }^{3}},}\\ k_{{12}}={\frac{2\,\left( \left( -g_{{11}}+f_{{11}}+d_{{12} }\right) {\chi }^{2}-g_{{11}}+d_{{11}}+f_{{11}}\right) \kappa \,c_{{11}}-c_{{ 12}}\left( k_{{11}}+{\chi }^{2}l_{{12}}+l_{{11}}\right) }{{\chi }^{2}c_{{12}} },} \\ \\ k_{{22}}={\tfrac{2\,\kappa \,c_{{11}}c_{{2}}\left( d_{{11}}+e_{{11}}\right) -c_{{1}}c_{{12}}\left( k_{{21}}+l_{{21}}\right) {\chi }^{4}-2\,\kappa \,c_{{ 21}}c_{{2}}\left( -f_{{21}}+g_{{21}}+e_{{21}}\right) {\chi }^{3}+\left( 2\,c_{{11}}\kappa \,\left( d_{{12}}+e_{{12}}\right) c_{{2}}-c_{{1}}c_{{12} }l_{{22}}\right) {\chi }^{2}-2\,\kappa \,c_{{21}}c_{{2}}\left( g_{{21}}-f_{{ 21}}+e_{{22}}\right) \chi }{{\chi }^{2}c_{{1}}c_{{12}}}.} \end{array} \right\} \end{aligned}$$
(19)

We can express Eq. (11) in an alternative form as follows:

$$\begin{aligned}{} & {} \varphi _{1}^{(4)}+\Delta _{1}\varphi _{1}^{\prime \prime }+\Delta _{2}\varphi _{1}\varphi _{1}^{\prime 2}+\Delta _{3}\varphi _{1}^{2}\varphi _{1}^{\prime \prime }\nonumber \\{} & {} \quad +\Delta _{4}\varphi _{1}+\Delta _{5}\varphi _{1}^{3}+\Delta _{6}\varphi _{1}^{5}=0, \end{aligned}$$
(20)

where

$$\begin{aligned} \left. \begin{array}{l} \Delta _{1}=\frac{a_{1}+3c_{12}c_{1}\kappa -6c_{11}b_{1}\kappa ^{2}}{ c_{11}b_{1}},\;\;\Delta _{2}=\frac{d_{11}+e_{11}+\left( d_{12}+e_{12}\right) \chi ^{2}}{b_{1}\chi }, \\ \\ \Delta _{3}=\frac{f_{11}+g_{11}+\left( f_{12}+g_{12}\right) \chi ^{2}}{ b_{1}\chi },\;\;\Delta _{4}=\frac{\alpha _{1}\kappa -\omega +\left( \beta _{1}-a_{1}\kappa ^{2}-c_{12}c_{1}\kappa ^{3}+c_{11}b_{1}\kappa ^{4}\right) \chi }{c_{11}b_{1}\chi }, \\ \\ \Delta _{5}=\frac{b_{11}-c_{11}\left( d_{11}-e_{11}+f_{11}+g_{11}\right) \kappa ^{2}+c_{12}\left( k_{11}-l_{11}\right) \kappa +\left[ \gamma _{1}+b_{12}+c_{12}\left( k_{12}-l_{12}\right) \kappa \right] \chi ^{2}-c_{11}\kappa ^{2}\left( d_{12}-e_{12}+f_{12}+g_{12}\right) \chi ^{2}}{ c_{11}b_{1}\chi }, \\ \\ \Delta _{6}=\frac{h_{11}+h_{12}\chi ^{2}+h_{13}\chi ^{4}}{b_{1}\chi }. \end{array} \right\} \end{aligned}$$
(21)

In the upcoming section, we will employ the following approach to solve equation (20).

New mapping method

We make the assumption that Eq. (20) possesses the following formal solution:

$$\begin{aligned} \varphi _{1}\left( \zeta \right) =\sum _{m=0}^{2N}\delta _{m}\Psi ^{m}(\zeta ). \end{aligned}$$
(22)

In this context, \(\Psi (\zeta )\) is subject to the following first-order ordinary differential equation (ODE):

$$\begin{aligned} \Psi ^{\prime 2}(\zeta )=r+p\Psi ^{2}(\zeta )+\frac{1}{2}h\Psi ^{4}(\zeta )+ \frac{1}{3}s\Psi ^{6}(\zeta ). \end{aligned}$$
(23)

The arbitrary constants \(\delta _{m}\) (where m ranges from 0 to 2N), r, p, h,  and s need to be determined, with the condition that \(\delta _{2N}\ne 0\) and \(s\ne 0\). It is widely recognized that the solutions of Eq. (23) take on the following forms:

Form-1: Assuming that \(s=\frac{3h^{2}}{16p},r=\frac{16p^{2}}{27h}\), Eq. (23) exhibits the following soliton solutions:

$$\begin{aligned} \Psi (\zeta )=4\sqrt{\frac{-p\tanh ^{2}\left( \epsilon \sqrt{-\frac{p}{3}} \zeta \right) }{3h\left[ 3+\tanh ^{2}\left( \epsilon \sqrt{-\frac{p}{3}} \zeta \right) \right] }},p<0,h>0, \end{aligned}$$
(24)

and

$$\begin{aligned} \Psi (\zeta )=4\sqrt{\frac{-p\coth ^{2}\left( \epsilon \sqrt{-\frac{p}{3}} \zeta \right) }{3h\left[ 3+\coth ^{2}\left( \epsilon \sqrt{-\frac{p}{3}} \zeta \right) \right] }},p<0,h>0, \end{aligned}$$
(25)

Form-2: Assuming that \(s=\frac{3h^{2}}{16p},r=0\), Eq. (23) exhibits, respectively the dark and singular soliton solutions:

$$\begin{aligned} \Psi (\zeta )=\sqrt{\frac{-2p}{h}\left[ 1+\tanh \left( \epsilon \sqrt{p} \zeta \right) \right] },p>0, h<0. \end{aligned}$$
(26)

and

$$\begin{aligned} \Psi (\zeta )=\sqrt{\frac{-2p}{h}\left[ 1+\coth \left( \epsilon \sqrt{p} \zeta \right) \right] },p>0, h<0. \end{aligned}$$
(27)

Form-3: Assuming that \(r=0\), Eq. (23) exhibits the following solutions:

(I): Soliton solutions:

$$\begin{aligned} \Psi (\zeta )= & {} \sqrt{\frac{-6ph\text{ sech}^{2}\left( \sqrt{p}\zeta \right) }{ 3h^{2}-4ps\left[ 1+\epsilon \tanh \left( \sqrt{p}\zeta \right) \right] ^{2}}},p>0, \end{aligned}$$
(28)
$$\begin{aligned} \Psi (\zeta )= & {} \sqrt{\frac{6pq_{2}\text{ csch}^{2}\left( \sqrt{p}\zeta \right) }{3h^{2}-4ps\left[ 1+\epsilon \coth \left( \sqrt{p}\zeta \right) \right] ^{2} }},p>0, \end{aligned}$$
(29)
$$\begin{aligned} \Psi (\zeta )= & {} \sqrt{\frac{-6p\text{ sech}^{2}\left( \sqrt{p}\zeta \right) }{ 3h+4\epsilon \sqrt{3ps}\tanh \left( \sqrt{p}\zeta \right) }},p>0,s>0, \end{aligned}$$
(30)

and

$$\begin{aligned} \Psi (\zeta )=\sqrt{\frac{6p\text{ csch}^{2}\left( \sqrt{p}\zeta \right) }{ 3h+4\epsilon \sqrt{3ps}\coth \left( \sqrt{p}\zeta \right) }},p>0,s>0. \end{aligned}$$
(31)

(II): Bright solitons:

$$\begin{aligned} \Psi (\zeta )=2\sqrt{\frac{3p}{\epsilon \sqrt{9h^{2}-48ps}\cosh \left( 2 \sqrt{p}\zeta \right) -3h}},p>0,9h^{2}-48ps>0. \end{aligned}$$
(32)

(III): Singular solitons:

$$\begin{aligned} \Psi (\zeta )=2\sqrt{\frac{3p}{\epsilon \sqrt{-\left( 9h^{2}-48ps\right) } \sinh \left( 2\sqrt{p}\zeta \right) -3h}},p>0,9h^{2}-48ps<0. \end{aligned}$$
(33)

where \(\epsilon =\pm 1.\)

With this aim, we first balance \(\varphi _{1}^{(4)}\) and \(\varphi _{1}^{5}\) in Eq. (20), one deduces the balance number \(N=1\). Consequently, Eq. (20) reveals the formal solution:

$$\begin{aligned} \varphi _{1}(\zeta )=\delta _{0}+\delta _{1}\Psi (\zeta )+\delta _{2}\Psi ^{2}(\zeta ), \end{aligned}$$
(34)

where the constants \(\delta _{0},\delta _{1}\) and \(\delta _{2}\) need to be determined, assuming that \(\delta _{2}\ne 0\). By substituting (34) and (23) into Eq. (20), the result is a set of algebraic equations as follows:

$$\begin{aligned} \left. \begin{array}{l} {4\Delta _{{2}}{\delta _{{2}}^{3}}s+\,8\Delta _{{3}}{\delta _{{2}}^{3}}s+{128 }\,\delta _{{2}}{s}^{2}+3\Delta _{{6}}{\delta _{{2}}^{5}}=0,} \\ \\ 16\Delta _{{3}}{\delta _{{2}}^{2}}\delta _{{0}}s+6\,\Delta _{{2}}{\delta _{{ 2}}^{3}}h+15\,\Delta _{{6}}\delta _{{0}}{\delta _{{2}}^{4}}+9\,\Delta _{{3}}{ \delta _{{2}}^{3}}h\\ \quad +240\delta _{{2}}hs+4\,\Delta _{{2}}{\delta _{{2}}^{2}} \delta _{{0}}s=0, \\ \\ 3\Delta _{{5}}{\delta _{{2}}^{3}}+12\Delta _{{2}}{\delta _{{2}}^{3}}p+{320} \,\delta _{{2}}ps+6\,\Delta _{{2}}{\delta _{{2}}^{2}}\delta _{{0}}h\\ \quad +12\Delta _{{3}}{\delta _{{2}}^{3}}p+8\,\Delta _{{1}}\delta _{{2}}s+90\,\delta _{{2}}{h }^{2} \\ \quad +18\,\Delta _{{3}}{\delta _{{2}}^{2}}\delta _{{0}}h+30\,\Delta _{{6}}{ \delta _{{0}}^{2}\delta _{{2}}^{3}}\\ \quad +8\,\Delta _{{3}}\delta _{{2}}{\delta _{{0 }}^{2}}s=0, \\ \\ 8\,\Delta _{{3}}{\delta _{{2}}^{2}}\delta _{{0}}p+4\,\Delta _{{2}}{\delta _{ {2}}^{2}}\delta _{{0}}p+2\,\Delta _{{3}}{\delta _{{2}}^{3}}r+60\,\delta _{{2} }ph\\ \quad +4\,\Delta _{{2}}{\delta _{{2}}^{3}}r+10\,\Delta _{{6}}{\delta _{{0} }^{3}\delta _{{2}}^{2}} \\ \quad +3\,\Delta _{{1}}\delta _{{2}}h+80\,\delta _{{2}}rs+3\,\Delta _{{3}}\delta _{{2}}{\delta _{{0}}^{2}}h+3\,\Delta _{{5}}\delta _{{0}}{\delta _{{2}}^{2}} =0, \\ \\ 4\,\Delta _{{3}}\delta _{{2}}{\delta _{{0}}^{2}}p+\Delta _{{4}}\delta _{{2} }+36\,\delta _{{2}}rh+4\,\Delta _{{3}}{\delta _{{2}}^{2}}\delta _{{0} }r\\ \quad +16\,\delta _{{2}}{p}^{2}+4\,\Delta _{{1}}\delta _{{2}}p \\ \quad +4\,\Delta _{{2}}{\delta _{{2}}^{2}}\delta _{{0}}r+5\,\Delta _{{6}}{\delta _{{0}}^{4}}\delta _{{2}}+3\,\Delta _{{5}}{\delta _{{0}}^{2}}\delta _{{2}}=0, \\ \\ +2\,\Delta _{{3}}\delta _{{2}}{\delta _{{0}}^{2}}r+\Delta _{{4}}\delta _{{0} }+\Delta _{{5}}{\delta _{{0}}^{3}}+\Delta _{{6}}{\delta _{{0}}^{5}} \\ \quad +8\,\delta _{{2}}rp+2\,\Delta _{{1}}\delta _{{2}}r=0. \end{array} \right\} \end{aligned}$$
(35)

According to the used method, one arrives at the following solutions for Eqs. (2) and (3):

Set-1: By assigning the values \(s=\frac{3\,h^{2}}{16p}\) and \(r=\frac{16p^{2}}{27\,h}\) to the algebraic equations obtained in (35), and utilizing the Maple software to solve them, the following outcomes are obtained:

$$\begin{aligned}{} & {} \delta _{{0}}=\epsilon \Delta _{{1}}\sqrt{\frac{3}{2\Delta _{{5} }-\Delta _{{1}}\Delta _{{3}}}},\text { }\delta _{{1}}=0,\nonumber \\{} & {} \quad \delta _{{2} }=\epsilon h\sqrt{\frac{3}{2\Delta _{{5}}-\Delta _{{1}}\Delta _{{3}}}},\text { }p=\,{\tfrac{1}{2}}\Delta _{{1}},\text { }h=h, \end{aligned}$$
(36)

and

$$\begin{aligned}{} & {} \Delta _{{2}}=\frac{2\Delta _{{1}}\Delta _{{3}}-5\Delta _{{5}}}{\Delta _{{1}} },\text { }\Delta _{{4}}=\frac{5\Delta _{{1}}^{2}\Delta _{{5}}}{18\left( \Delta _{{1}}\Delta _{{3}}-2\Delta _{{5}}\right) },\nonumber \\{} & {} \quad \Delta _{{6}}= \frac{\Delta _{{5}}\left( \Delta _{{1}}\Delta _{{3}}-2\Delta _{{5}}\right) }{ 2\Delta _{{1}}^{2}}{,}\nonumber \\{} & {} \quad \text{ provided } ~~ \epsilon =\pm 1, ~~ 2\Delta _{{5}}-\Delta _{{1}}\Delta _{{3}}>0, ~~ \text{ and } ~~ \Delta _{{1}}\ne 0. \end{aligned}$$
(37)

By substituting (36) into (34) and employing (24) and (25), the bright soliton solutions of Eqs. (2) and (3) can be derived as follows:

$$\begin{aligned} q(x,t){} & {} =\pm \Delta _{{1}}\sqrt{\frac{1}{3\left( 2\Delta _{{5}}-\Delta _{{1} }\Delta _{{3}}\right) }}\nonumber \\{} & {} \quad \left[ 1+\frac{6}{1+2\epsilon \cosh \left( \sqrt{ \frac{2\Delta _{{1}}}{3}}\left( x-vt\right) \right) }\right] \text{ e } ^{i\left( -\kappa x+\omega t+\theta _{0}\right) }, \end{aligned}$$
(38)
$$\begin{aligned} r(x,t){} & {} =\pm \chi \Delta _{{1}}\sqrt{\frac{1}{3\left( 2\Delta _{{5}}-\Delta _{{ 1}}\Delta _{{3}}\right) }}\nonumber \\{} & {} \quad \left[ 1+\frac{6}{1+2\epsilon \cosh \left( \sqrt{ \frac{2\Delta _{{1}}}{3}}\left( x-vt\right) \right) }\right] \text{ e } ^{i\left( -\kappa x+\omega t+\theta _{0}\right) },\nonumber \\{} & {} \quad \text{ provided } ~~ \Delta _{{1}}>0, ~~ \text{ and } ~~ 2\Delta _{{5}}-\Delta _{{1}}\Delta _{{3}}>0. \end{aligned}$$
(39)

The solutions (38) and (39) meet the requirements specified by the constraint conditions (37).

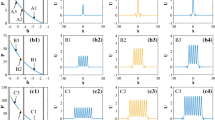
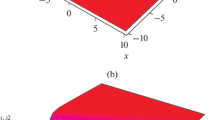
Figure 1 and 2 represent the surface plot, contour plot and 2D plot of bright soliton (38). The parameter values that have been chosen are:

Fig. 1
figure 1

Profile of a bright soliton solution

Full size image

Set–2: By assigning the values \(s=\frac{3\,h^{2}}{16p}\) and \(r=0\) to the algebraic equations obtained in (35), and utilizing the Maple software to solve them, the following outcomes are obtained:

$$\begin{aligned}{} & {} \delta _{{0}}=-2\epsilon \Delta _{{1}}\sqrt{-\frac{1}{10\Delta _{{5} }+\Delta _{{1}}\Delta _{{3}}}},\text { }\delta _{{1}}=0,\nonumber \\{} & {} \delta _{{2} }=10\epsilon h\sqrt{-\frac{1}{10\Delta _{{5}}+\Delta _{{1}}\Delta _{{3}}}}, \text { }p=\,-{\tfrac{1}{20}}\Delta _{{1}},\text { }h=h, \end{aligned}$$
(40)

and

$$\begin{aligned}{} & {} \Delta _{{2}}=-\frac{3\left( \Delta _{{1}}\Delta _{{3}}+5\Delta _{{5} }\right) }{\Delta _{{1}}},\text { }\Delta _{{4}}=\frac{4}{25}\Delta _{{1} }^{2},\nonumber \\{} & {} \Delta _{{6}}=\frac{150\Delta _{{5}}^{2}+\left( 5\Delta _{{5} }-\Delta _{{1}}\Delta _{{3}}\right) \Delta _{{1}}\Delta _{{3}}}{100\Delta _{{ 1}}^{2}}{,}\nonumber \\{} & {} \text{ provided } ~~ \epsilon =\pm 1, ~~ 10\Delta _{{5}}+\Delta _{{1}}\Delta _{{3}}<0, ~~ \text{ and } ~~ \Delta _{{1}}\ne 0. \end{aligned}$$
(41)

By substituting (40) into (34) and employing (26) and (27), the dark and singular soliton solutions of Eqs. (2) and (3) can be derived as:

$$\begin{aligned} q(x,t){} & {} =\epsilon \Delta _{{1}}\sqrt{-\frac{1}{10\Delta _{{5}}+\Delta _{{1} }\Delta _{{3}}}}\nonumber \\{} & {} \quad \left[ 1-\tanh \left( \sqrt{-\frac{\Delta _{{1}}}{20}}\left( x-vt\right) \right) \right] \text{ e}^{i\left( -\kappa x+\omega t+\theta _{0}\right) }, \end{aligned}$$
(42)
$$\begin{aligned} r(x,t){} & {} =\epsilon \chi \Delta _{{1}}\sqrt{-\frac{1}{10\Delta _{{5}}+\Delta _{{1 }}\Delta _{{3}}}}\nonumber \\{} & {} \quad \left[ 1-\tanh \left( \sqrt{-\frac{\Delta _{{1}}}{20}} \left( x-vt\right) \right) \right] \text{ e}^{i\left( -\kappa x+\omega t+\theta _{0}\right) }, \end{aligned}$$
(43)

and

$$\begin{aligned} q(x,t)= & {} \epsilon \Delta _{{1}}\sqrt{-\frac{1}{10\Delta _{{5}}+\Delta _{{1} }\Delta _{{3}}}}\nonumber \\{} & {} \left[ 1-\coth \left( \sqrt{-\frac{\Delta _{{1}}}{20}}\left( x-vt\right) \right) \right] \text{ e}^{i\left( -\kappa x+\omega t+\theta _{0}\right) }, \end{aligned}$$
(44)
$$\begin{aligned} r(x,t)= & {} \epsilon \chi \Delta _{{1}}\sqrt{-\frac{1}{10\Delta _{{5}}+\Delta _{{1 }}\Delta _{{3}}}}\nonumber \\{} & {} \left[ 1-\coth \left( \sqrt{-\frac{\Delta _{{1}}}{20}} \left( x-vt\right) \right) \right] \text{ e}^{i\left( -\kappa x+\omega t+\theta _{0}\right) },\nonumber \\{} & {} \text{ respectively, } \text{ provided } ~~ 10\Delta _{{5}}+\Delta _{{1}}\Delta _{{3}}<0, ~~ \text{ and } ~~ \Delta _{{1}}<0. \end{aligned}$$
(45)

The solutions (42)–(45) meet the requirements specified by the constraint conditions (41).

Fig. 2
figure 2

Profile of a dark soliton solution

Full size image

Set-3: By assigning the value \(r=0\) to the algebraic equations obtained in (35), and utilizing the Maple software to solve them, the following results are revealed:

$$\begin{aligned} \left. \begin{array}{l} \delta _{{0}}=0,\text { }\delta _{{1}}=0,\text { }\delta _{{2}}=\dfrac{ 30\epsilon h}{\sqrt{(4\Delta _{{2}}+3\Delta _{{3}})\Delta _{{1}}-30\Delta _{{ 5}}}}, \\ \\ p=\,-{\tfrac{1}{20}}\Delta _{{1}},\text { }s=-{\dfrac{45{h}^{2}\left( 2\,\Delta _{{2}}+3\,\Delta _{{3}}\right) }{\left( 4\Delta _{{2}}+3\,\Delta _{ {3}}\right) \Delta _{{1}}-30\,\Delta _{{5}}},}\text { }h=h, \end{array} \right. \end{aligned}$$
(46)

and

$$\begin{aligned}{} & {} \Delta _{{4}}={\frac{4}{25}}\,{\Delta _{{1}}}^{2},\text { }\Delta _{{6}}={ \frac{1}{300}}\,\left( 2\Delta _{{2}}+3\Delta _{{3}}\right) \left( \Delta _{{ 2}}+4\,\Delta _{{3}}\right) ,\nonumber \\{} & {} \text{ provided } ~~ \epsilon =\pm 1, ~~ \text{ and } ~~ (4\Delta _{{2}}+3\Delta _{{3}})\Delta _{{1}}-30\Delta _{{5}}>0. \end{aligned}$$
(47)

By substituting (46) into (34) and employing (28)–(33), the following solutions of Eqs. (2) and (3) can be derived as follows:

(I) Bright–Singular straddled solitons:

$$\begin{aligned} q(x,t)= & {} {\tfrac{\pm 12\Delta _{{1}}\sqrt{\left( 4\,\Delta _{{2}}+3\,\Delta _{{ 3}}\right) \Delta _{{1}}-30\,\Delta _{{5}}}}{\left[ \left( 2\,\Delta _{{2} }-3\,\Delta _{{3}}\right) \Delta _{{1}}-60\,\Delta _{{5}}\right] \left[ \cosh \left( \sqrt{-\frac{\,\Delta _{{1}}}{5}}(x-vt)\right) +\epsilon \right] -3\,\Delta _{{1}}\left( 2\,\Delta _{{2}}+3\,\Delta _{{3}}\right) \left[ \sinh \left( \sqrt{-\frac{\,\Delta _{{1}}}{5}}(x-vt)\right) -\epsilon \right] }}\text{ e}^{i\left( -\kappa x+\omega t+\theta _{0}\right) }, \end{aligned}$$
(48)
$$\begin{aligned} r(x,t)= & {} {\tfrac{\pm 12\chi \Delta _{{1}}\sqrt{3\,\Delta _{{3}}\Delta _{{1} }+4\,\Delta _{{1}}\Delta _{{2}}-30\,\Delta _{{5}}}}{\left[ \left( -3\,\Delta _{{3}}+2\,\Delta _{{2}}\right) \Delta _{{1}}-60\,\Delta _{{5}}\right] \left[ \cosh \left( \sqrt{-\frac{\,\Delta _{{1}}}{5}}(x-vt)\right) +\epsilon \right] -3\,\Delta _{{1}}\left( 2\,\Delta _{{2}}+3\,\Delta _{{3}}\right) \left[ \sinh \left( \sqrt{-\frac{\,\Delta _{{1}}}{5}}(x-vt)\right) -\epsilon \right] }}\text{ e}^{i\left( -\kappa x+\omega t+\theta _{0}\right) }, \end{aligned}$$
(49)
$$\begin{aligned}{} & {} \text{ for } ~~ \left( 4\,\Delta _{{2}}+3\,\Delta _{{3}}\right) \Delta _{{1}}-30\,\Delta _{{5}}>0, ~~ \Delta _1 (2\Delta _2 + 3\Delta _3) > 0; ~~ \text{ and } ~~ \Delta _{{1}}<0,\nonumber \\{} & {} q(x,t)=\,{\tfrac{\pm 6\Delta _{{1}}}{\sqrt{\left( 3\,\Delta _{{3}}+4\,\Delta _{{2}}\right) \Delta _{{1}}-30\,\Delta _{{5}}}\left[ \cosh \left( \sqrt{- \frac{\Delta _{{1}}}{5}}(x-vt)\right) +\epsilon \right] +\sqrt{3\Delta _{{1} }\left( 2\,\Delta _{{2}}+3\,\Delta _{{3}}\right) }\sinh \left( \sqrt{-\frac{ \Delta _{{1}}}{5}}(x-vt)\right) }}\text{ e}^{i\left( -\kappa x+\omega t+\theta _{0}\right) }, \end{aligned}$$
(50)
$$\begin{aligned}{} & {} r(x,t)=\tfrac{\pm 6\chi \Delta _{{1}}}{\sqrt{\left( 3\,\Delta _{{3} }+4\,\Delta _{{2}}\right) \Delta _{{1}}-30\,\Delta _{{5}}}\left[ \cosh \left( \sqrt{-\frac{\Delta _{{1}}}{5}}(x-vt)\right) +\epsilon \right] +\sqrt{ 3\Delta _{{1}}\left( 2\,\Delta _{{2}}+3\,\Delta _{{3}}\right) }\sinh \left( \sqrt{-\frac{\Delta _{{1}}}{5}}(x-vt)\right) }\text{ e}^{i\left( -\kappa x+\omega t+\theta _{0}\right) }, \nonumber \\{} & {} \text{ whenever } ~~ \left( 4\,\Delta _{{2}}+3\,\Delta _{{3}}\right) \Delta _{{1}}-30\,\Delta _{{5}}>0, ~~ \Delta _{{1}}\left( 2\,\Delta _{{2}}+3\,\Delta _{{3}}\right) >0, ~~ \text{ and } ~~ \Delta _{{1}}<0. \end{aligned}$$
(51)

(II) Bright solitons:

$$\begin{aligned}{} & {} q(x,t)={\tfrac{\pm 6\Delta _{{1}}}{\sqrt{-2\left[ \left( 3\Delta _{{3} }+\Delta _{{2}}\right) \,\Delta _{{1}}+15\,\Delta _{{5}}\right] }\cosh \left( \sqrt{-\frac{\Delta _{{1}}}{5}}(x-vt)\right) -\sqrt{\left( 3\,\Delta _{{3}}+4\,\Delta _{{2}}\right) \Delta _{{1}}-30\,\Delta _{{5}}}}}\text{ e } ^{i\left( -\kappa x+\omega t+\theta _{0}\right) }, \end{aligned}$$
(52)
$$\begin{aligned}{} & {} r(x,t)={\tfrac{\pm 6\chi \Delta _{{1}}}{\sqrt{-2\left[ \left( 3\Delta _{{3} }+\Delta _{{2}}\right) \,\Delta _{{1}}+15\,\Delta _{{5}}\right] }\cosh \left( \sqrt{-\frac{\Delta _{{1}}}{5}}(x-vt)\right) -\sqrt{\left( 3\,\Delta _{{3}}+4\,\Delta _{{2}}\right) \Delta _{{1}}-30\,\Delta _{{5}}}}}\text{ e } ^{i\left( -\kappa x+\omega t+\theta _{0}\right) },\nonumber \\{} & {} \text{ provided } ~~ \left( 3\Delta _{{3}}+\Delta _{{2}}\right) \,\Delta _{{1}}+15\,\Delta _{{5}}<0, ~~ \text{ and } ~~ \Delta _{{1}}<0. \end{aligned}$$
(53)

(III) Singular solitons:

$$\begin{aligned} q(x,t)= & {} {\tfrac{\pm 6\Delta _{{1}}}{\sqrt{2\left[ \left( 3\Delta _{{3} }+\Delta _{{2}}\right) \,\Delta _{{1}}+15\,\Delta _{{5}}\right] }\sinh \left( \sqrt{-\frac{\Delta _{{1}}}{5}}(x-vt)\right) -\sqrt{\left( 3\,\Delta _{{3}}+4\,\Delta _{{2}}\right) \Delta _{{1}}-30\,\Delta _{{5}}}}}\text{ e } ^{i\left( -\kappa x+\omega t+\theta _{0}\right) }, \end{aligned}$$
(54)
$$\begin{aligned} r(x,t)= & {} {\tfrac{\pm 6\chi \Delta _{{1}}}{\sqrt{2\left[ \left( 3\Delta _{{3} }+\Delta _{{2}}\right) \,\Delta _{{1}}+15\,\Delta _{{5}}\right] }\sinh \left( \sqrt{-\frac{\Delta _{{1}}}{5}}(x-vt)\right) -\sqrt{\left( 3\,\Delta _{{3}}+4\,\Delta _{{2}}\right) \Delta _{{1}}-30\,\Delta _{{5}}}}}\text{ e } ^{i\left( -\kappa x+\omega t+\theta _{0}\right) }, \nonumber \\{} & {} \text{ as } \text{ long } \text{ as } ~~ \left( 3\Delta _{{3}}+\Delta _{{2}}\right) \,\Delta _{{1}}+15\,\Delta _{{5}}>0 ~~ \text{ and } ~~ \Delta _{{1}}<0. \end{aligned}$$
(55)

The solutions (48)–(55) meet the requirements specified by the constraint conditions (47).

Results and discussion

Figure 1 depicts the evolution of a bright soliton solution q(x, t), characterized by the complex-valued solution (38), through surface plots, contour plots, and 2D plots. The soliton dynamics are analyzed over a temporal range from \(t=2\) to \(t=3\), with intervals of 0.2. The parameters governing the system are set to specific values: \(\chi =2\), \(\epsilon =1.1\), \(\gamma _{1}=3.2\), \(\alpha _{1}=1.3\), \(\alpha _{2}=2.4\), \(a_{1}=0.5\), \(a_{2}=1.6\), \(b_{1}=0.7\), \(b_{2}=1.8\), \(c_{1}=1.9\), \(c_{2}=2\), \(b_{11}=2.1\), \(b_{12}=2.2\), \(c_{11}=0.3\), \(c_{12}=2.4\), \(d_{11}=0.5\), \(d_{12}=2.6\), \(e_{11}=2.7\), \(e_{12}=2.8\), \(f_{11}=0.9\), \(f_{12}=-1.1\), \(g_{11}=-1.2\), \(g_{12}=-1.3\), \(k_{11}=-2.4\), \(k_{12}=-0.5\), \(l_{11}=-2.6\), \(l_{12}=-0.7\), \(c_{21}=-3.8\), and \(c_{22}=-0.9\).. The surface plot illustrates the spatial distribution of the soliton solution q(x, t) over the domain x and t, revealing the propagation and behavior of the soliton. The contour plot provides further insight into the soliton’s profile, highlighting regions of different intensity. Additionally, the 2D plot offers a concise representation of the soliton’s evolution at specific time points. The observed evolution of the bright soliton solution demonstrates characteristic features such as wavepacket localization and preservation of shape over time. As time progresses, the soliton maintains its structure while propagating through the medium. The interplay of the system parameters influences the soliton’s behavior, including its speed and stability. The prescribed parameter values contribute to the observed dynamics, with each parameter exerting specific effects on the soliton’s evolution. Figure 2 presents the evolution of a dark soliton solution q(x, t), described by the complex-valued solution (42), through surface plots, contour plots, and 2D plots. Similar to Fig. 1, the temporal evolution is analyzed over the interval from \(t=2\) to \(t=3\), with increments of 0.2. The same set of parameters as in Fig. 1 is employed to govern the system dynamics. The surface plot, contour plot, and 2D plot in Fig. 2 provide visual representations of the dark soliton’s behavior and evolution. The surface plot captures the spatiotemporal dynamics of the soliton, highlighting its characteristic depression within the medium. The contour plot offers detailed information on the soliton’s intensity profile, while the 2D plot succinctly illustrates its evolution at discrete time points. The dark soliton solution exhibits distinct features compared to its bright counterpart, characterized by a localized intensity minimum within the medium. As time progresses, the dark soliton maintains its shape and travels through the medium, albeit with different dynamics influenced by the system parameters. The specific parameter values chosen for this analysis play a crucial role in shaping the dark soliton’s evolution, influencing its speed, depth, and stability. As a result, Figs. 1 and 2 provide valuable insights into the evolution of bright and dark soliton solutions, respectively, under the specified parameter regime. The visualizations offer a comprehensive understanding of the soliton dynamics and highlight the influence of system parameters on their behavior. These findings contribute to the broader understanding of soliton phenomena and their potential applications in various physical systems.

Conclusions

The current paper has moved the literature of the concatenation model one step forward. The model has been applied to Bragg gratings that led to the emergence of the gap solitons. A full spectrum has been recovered. The new mapping method has made the revelation possible and a reality. Thus, the crisis of low CD has been overcome for the concatenation model with the introduction of Bragg gratings. Hence, another chapter from this concatenation model is now complete. It is now time to venture into additional aspects of the model. Several issues are yet to be explored. These range from the control of Internet bottleneck effects, a study of the model in dispersion flattened fibers, moving over to dispersive concatenation model and their corresponding follow–up concepts. Therefore, a plethora of grounds are yet to be covered. The results of such promising projects are sequentially going to be disseminated across a wide range of outlets after getting these results aligned with the pre–existing works [5].